Suppression of the High-Frequency Errors in Surface Topography Measurements Based on Comparison of Various Spline Filtering Methods
Abstract
1. Introduction
1.1. Introduction to the High-Frequency Errors in Surface Topography Analysis
1.2. State-of-the-Art in the High-Frequency Errors Characterisation
1.3. Selection of Various Types of Surface Topographies for Noise Analysis Improvement
1.4. Motivation
2. Materials, Measurement Process, and Applied Methods
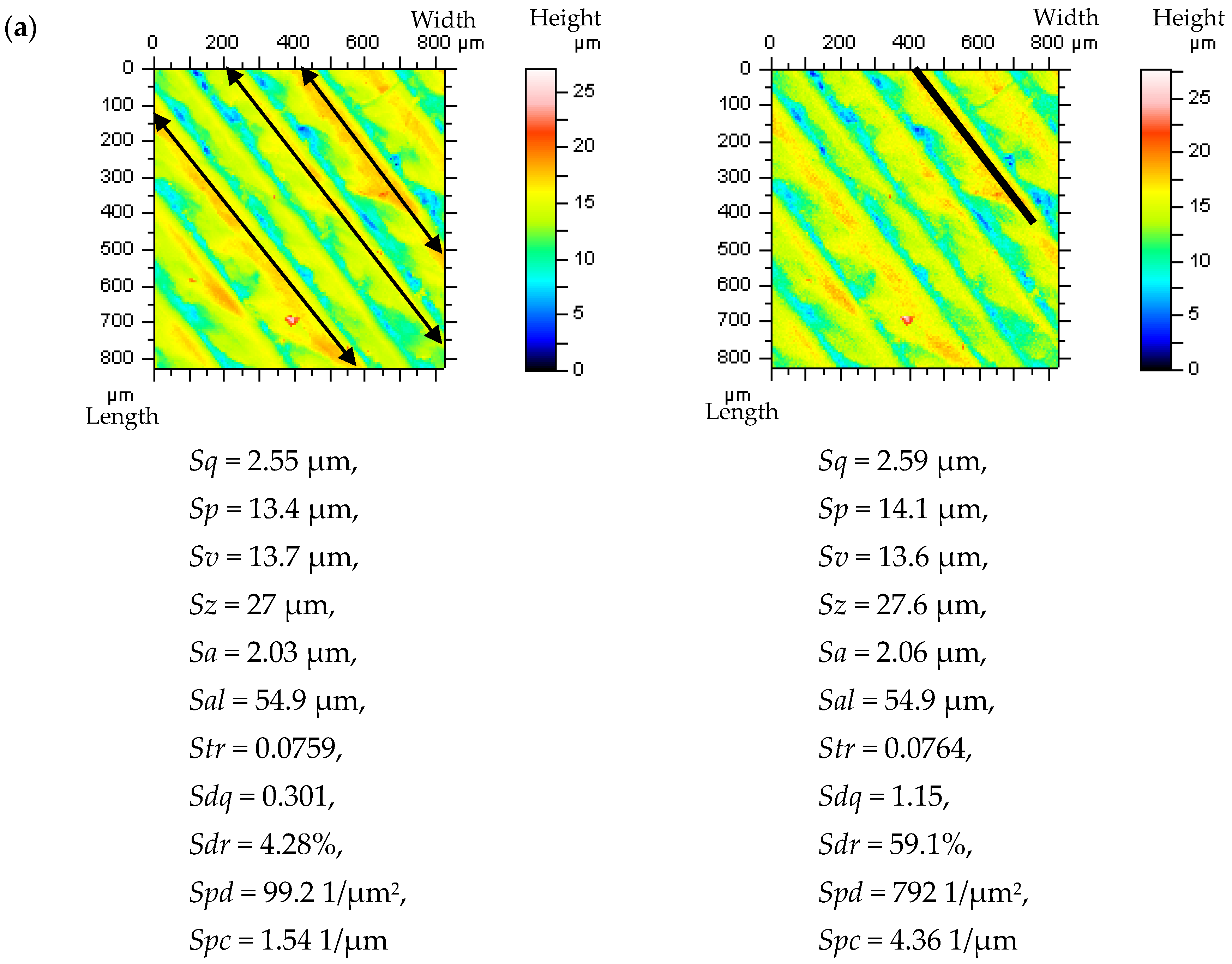
2.1. Analyzed Surfaces
2.2. Measurement Process
2.3. Compared Spline Filters for Noise Suppressions
2.4. Proposals of Procedures for the Detection of High-Frequency Errors from the Raw Measured Data
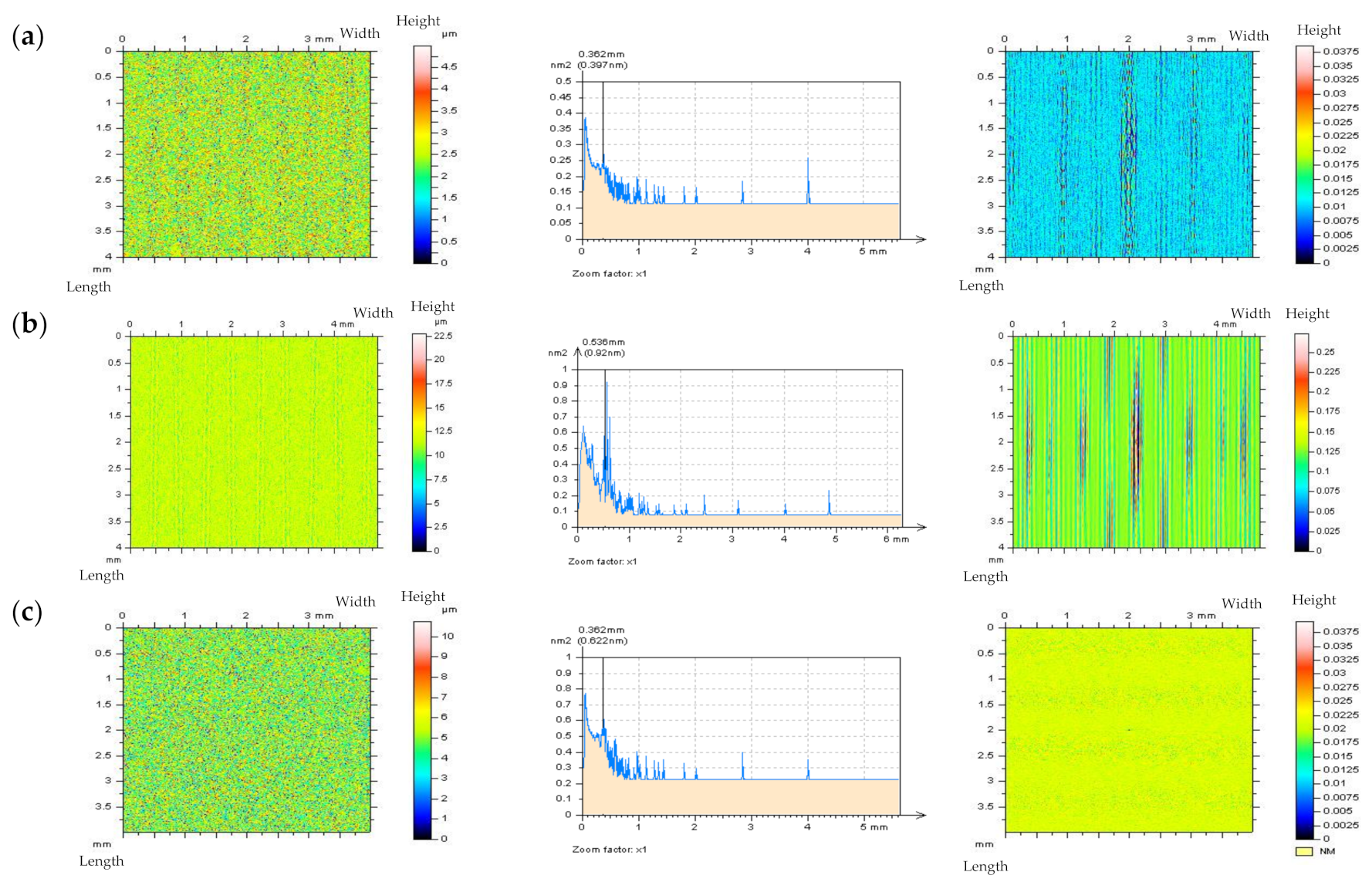
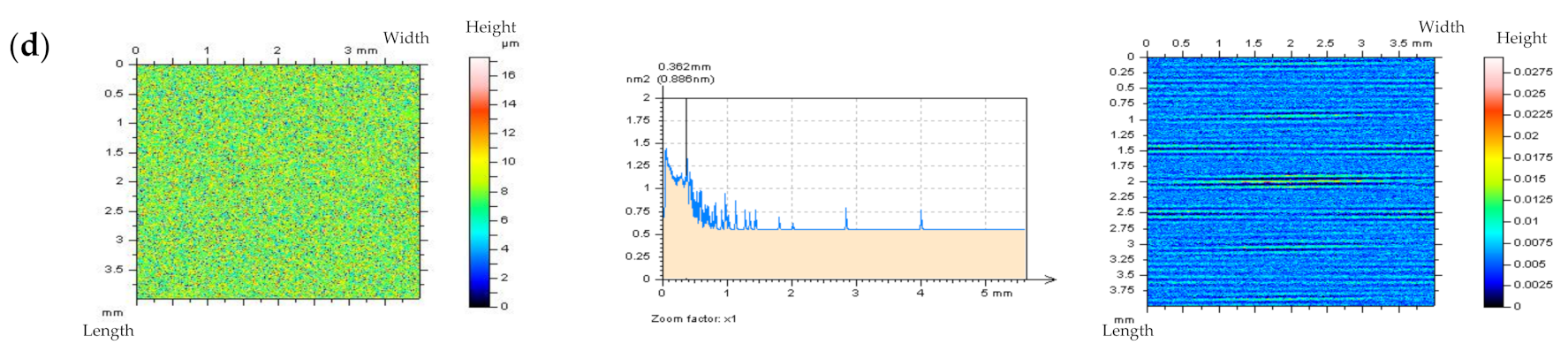
2.4.1. Detection of Noise with Power Spectral Density Applications
2.4.2. Noise Suppressions with Spline Modifications of Surface Texture Profiles
2.4.3. Definition of Noise by the Analysis of the Shape of Autocorrelation Function
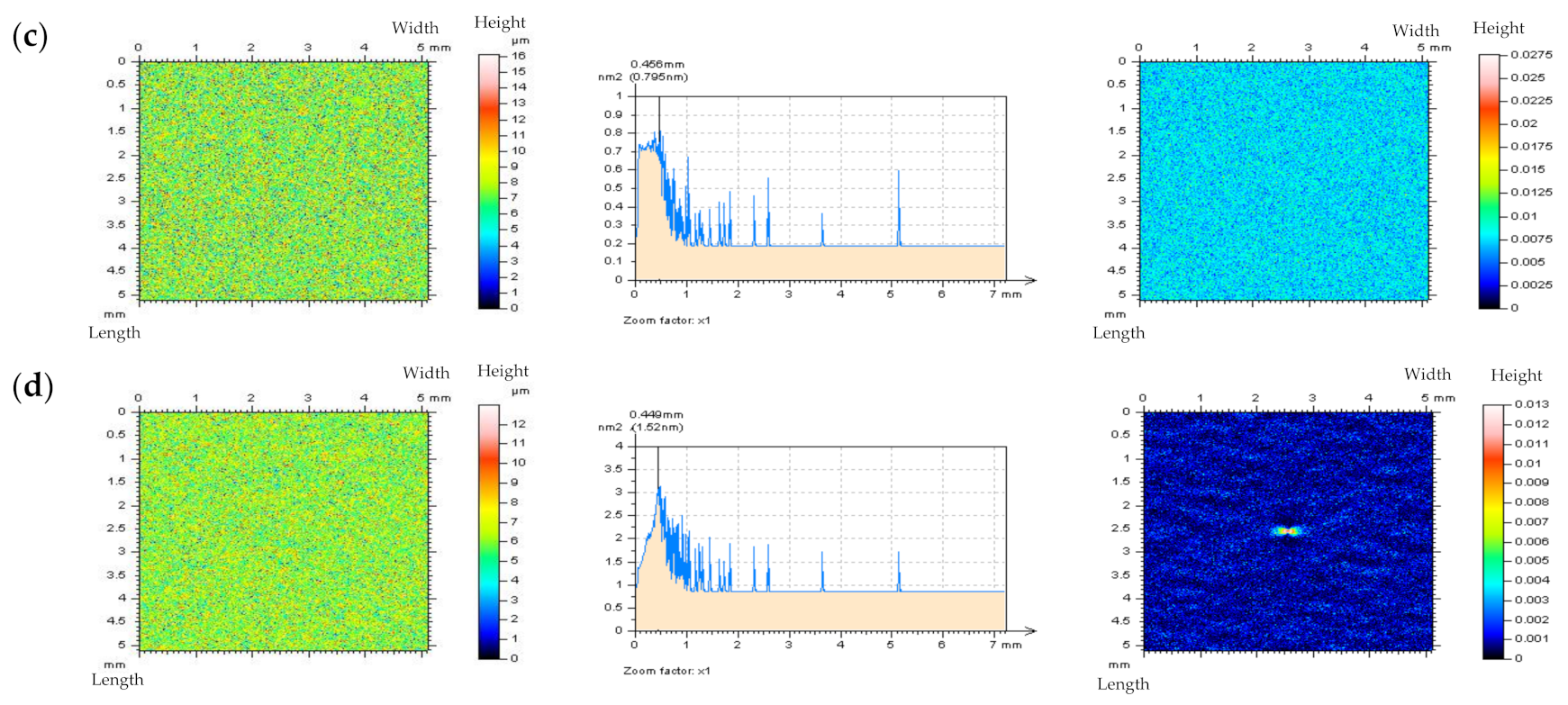
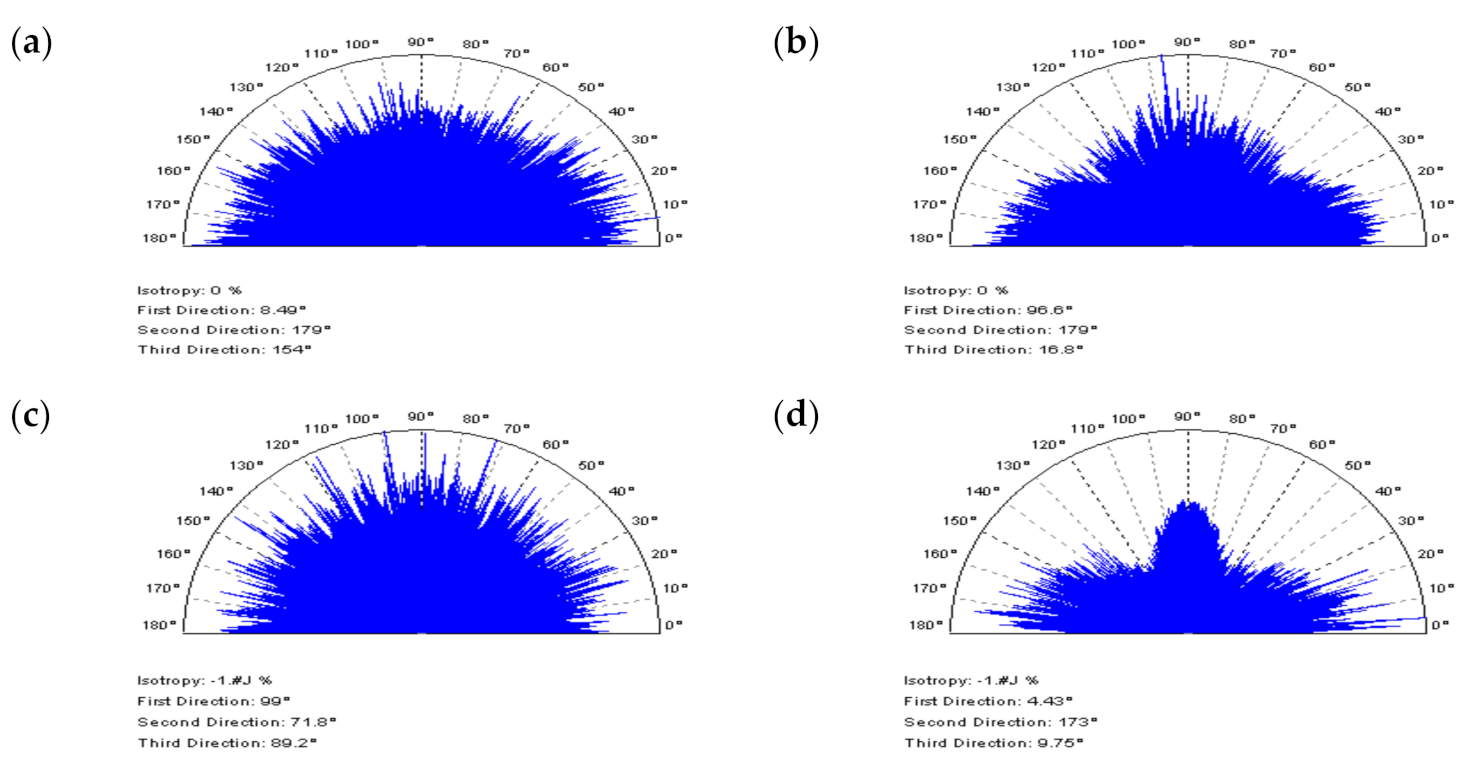
3. Results and Discussion
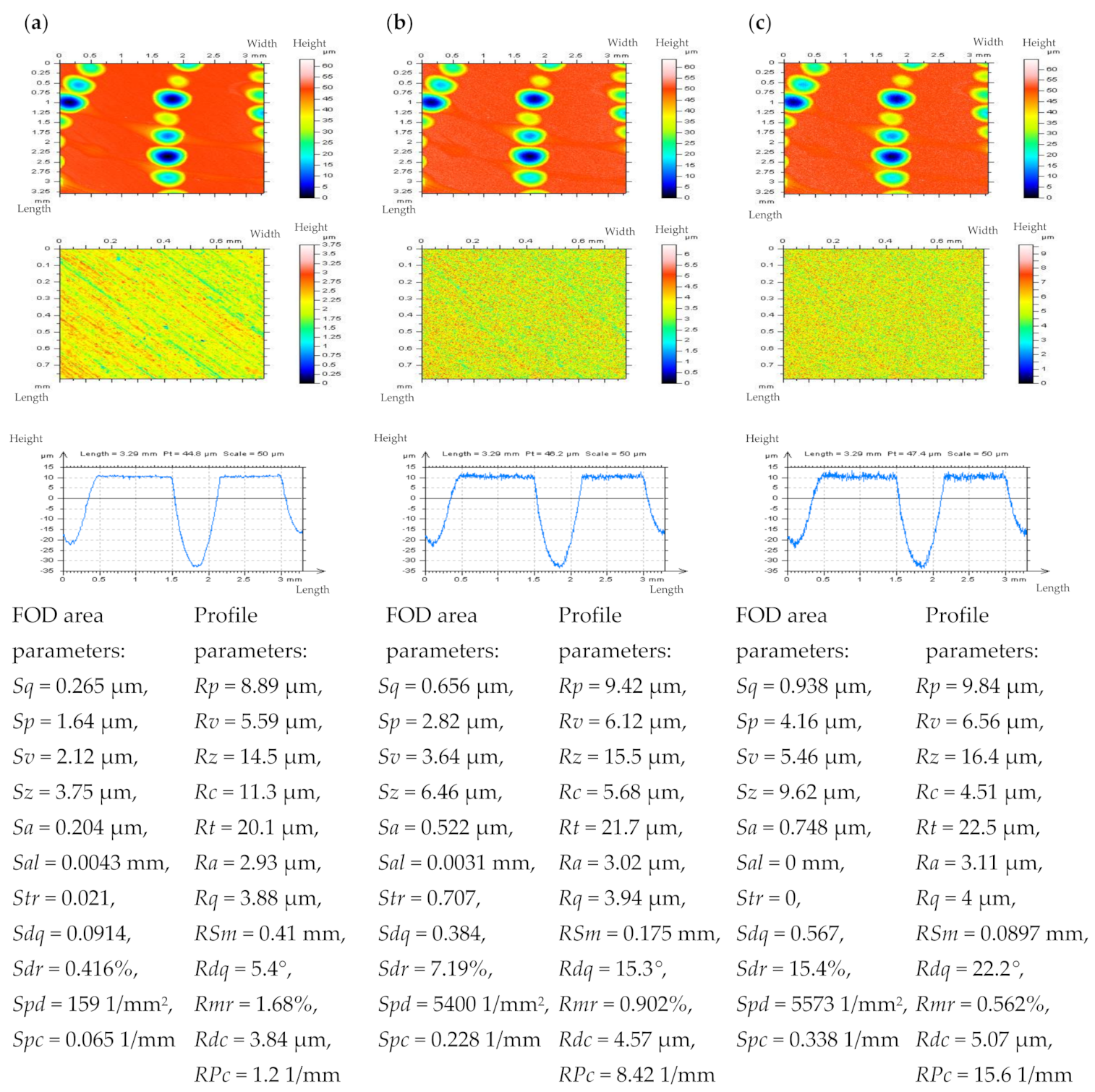
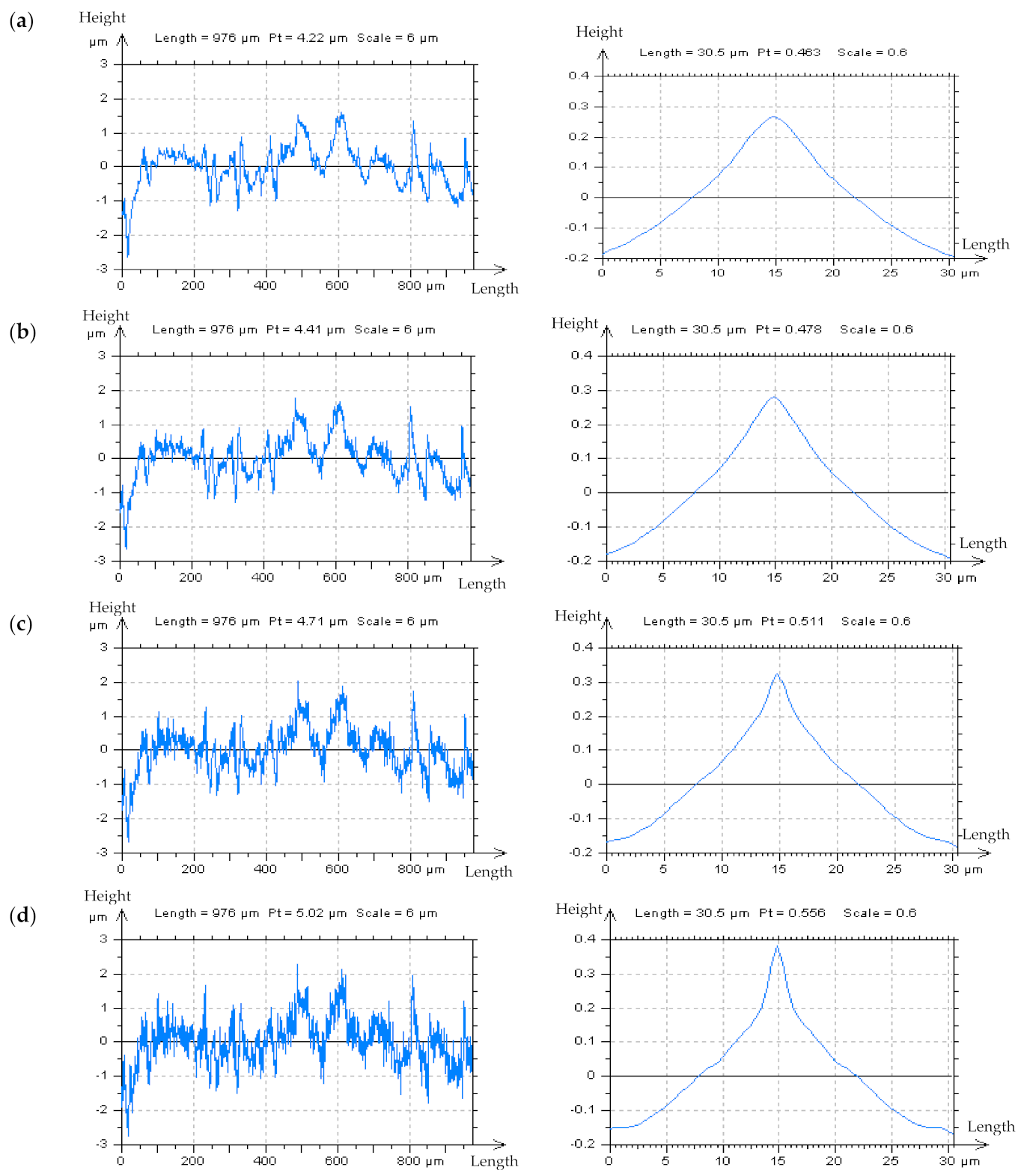
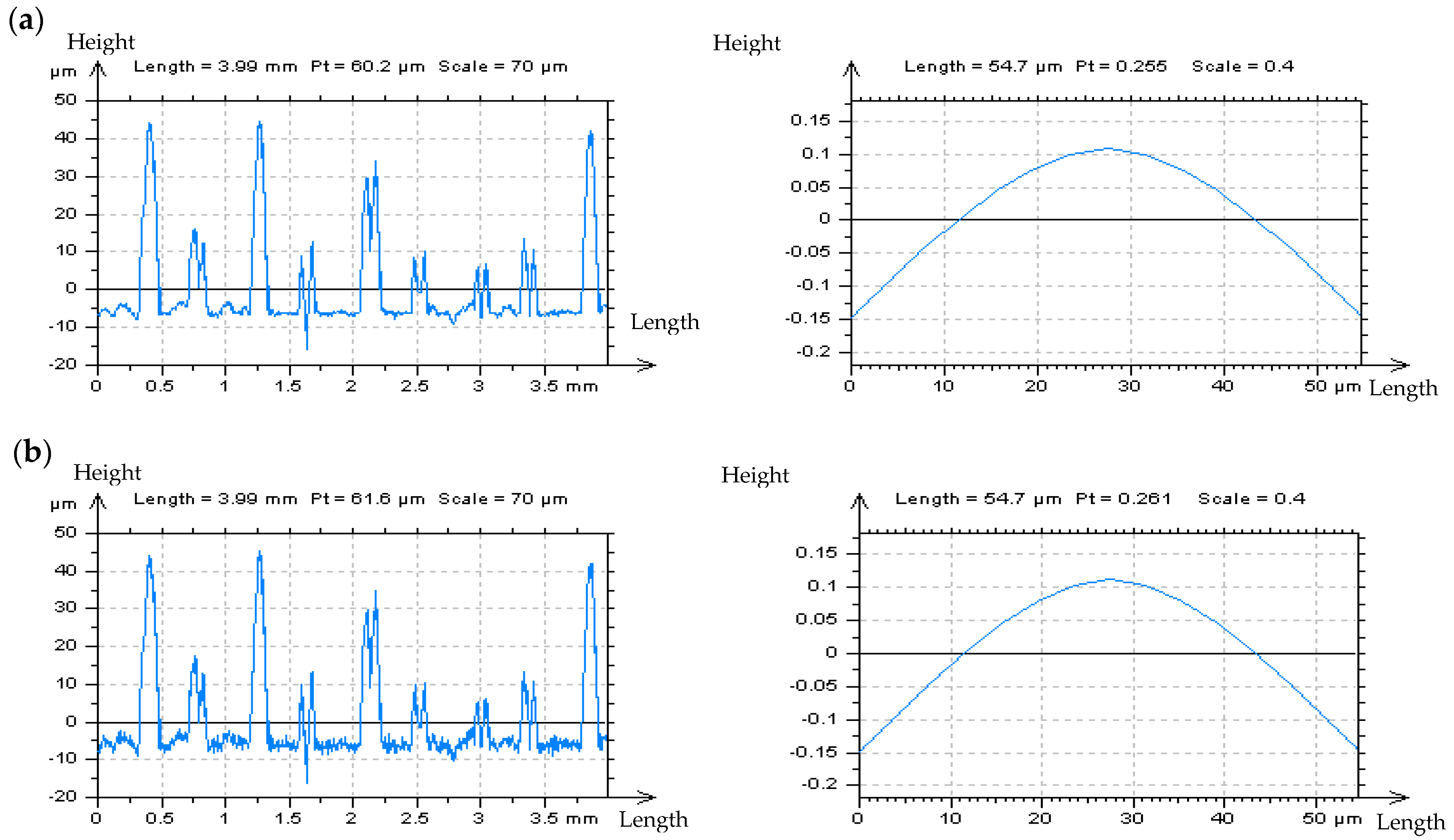
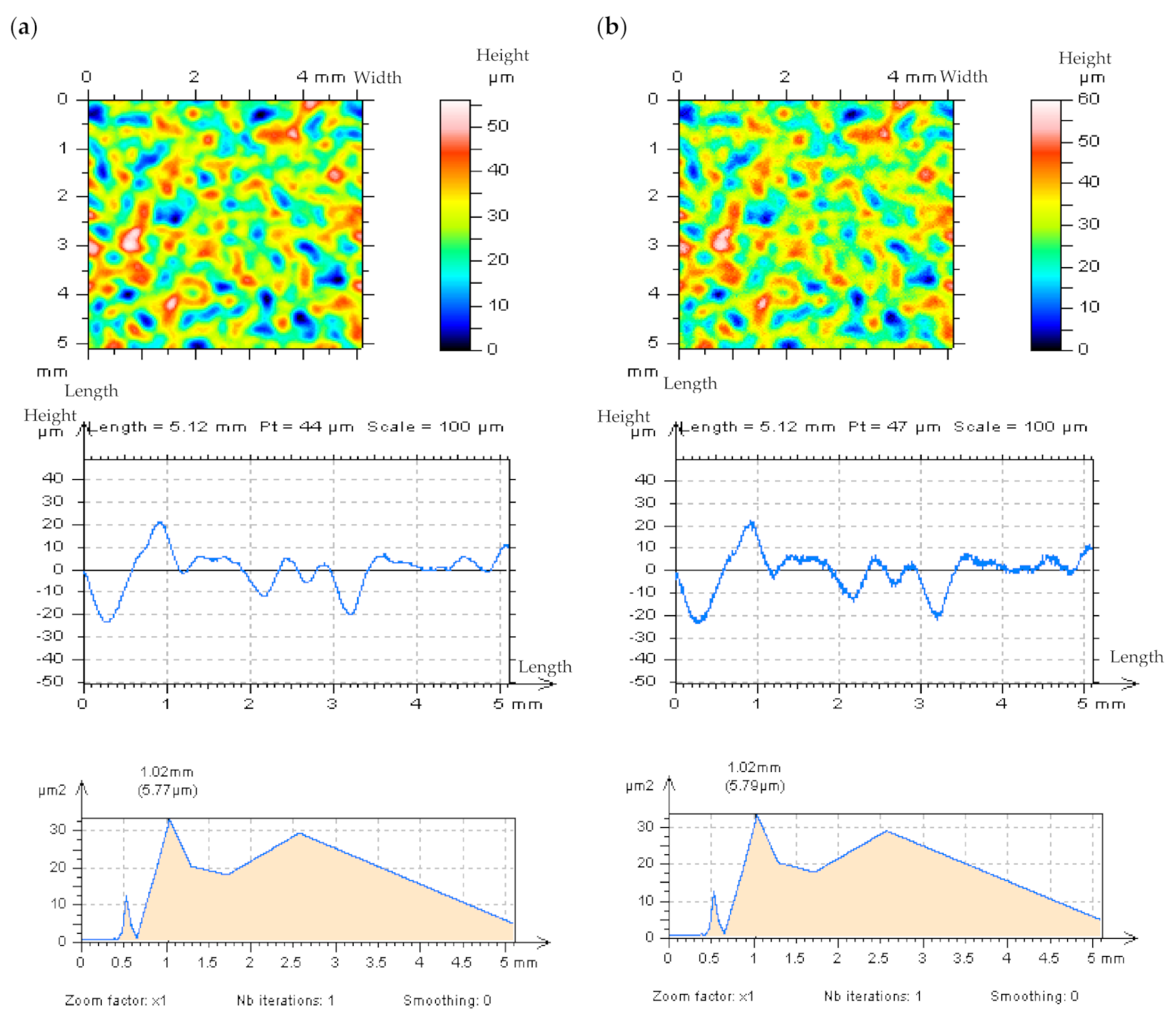
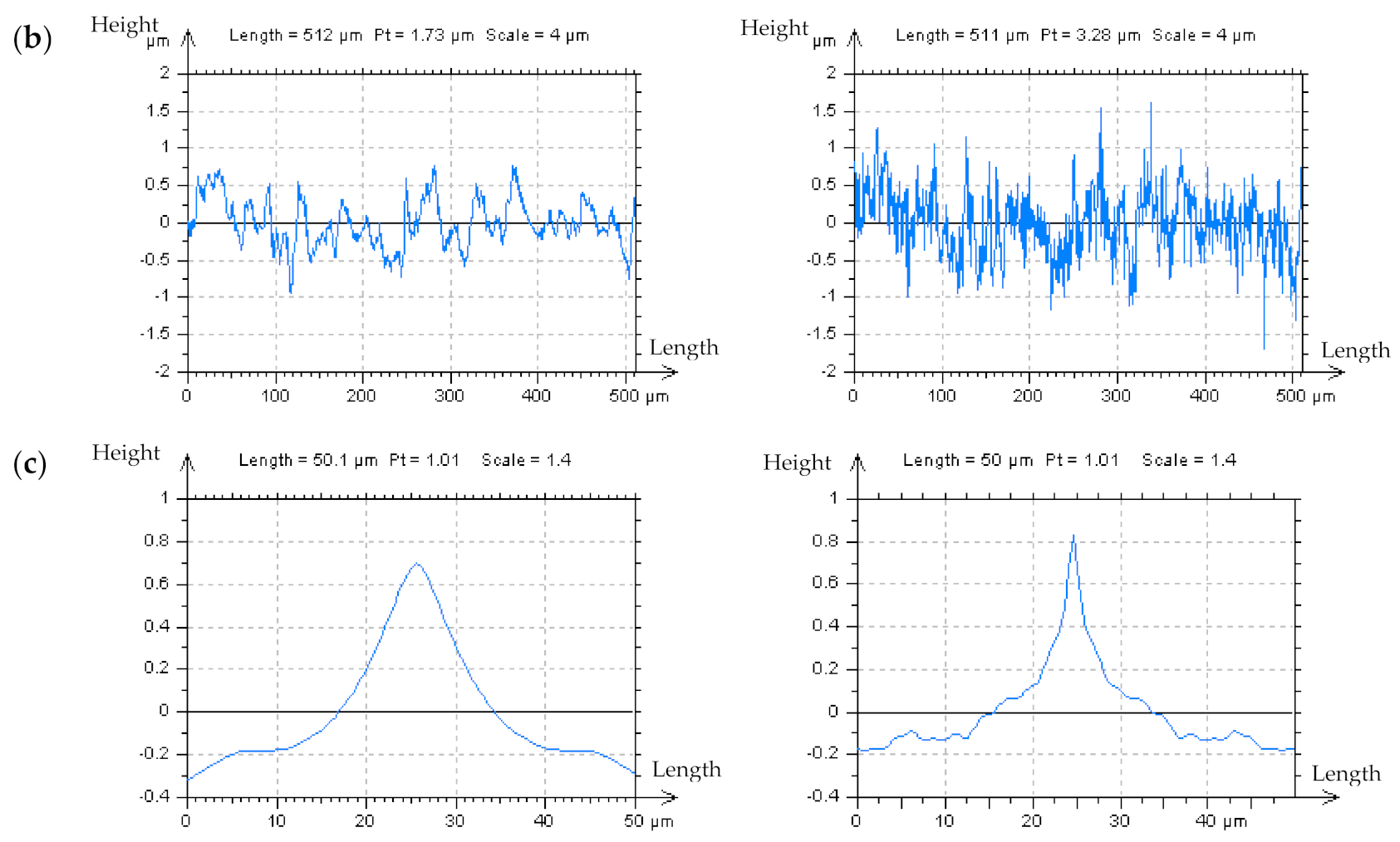
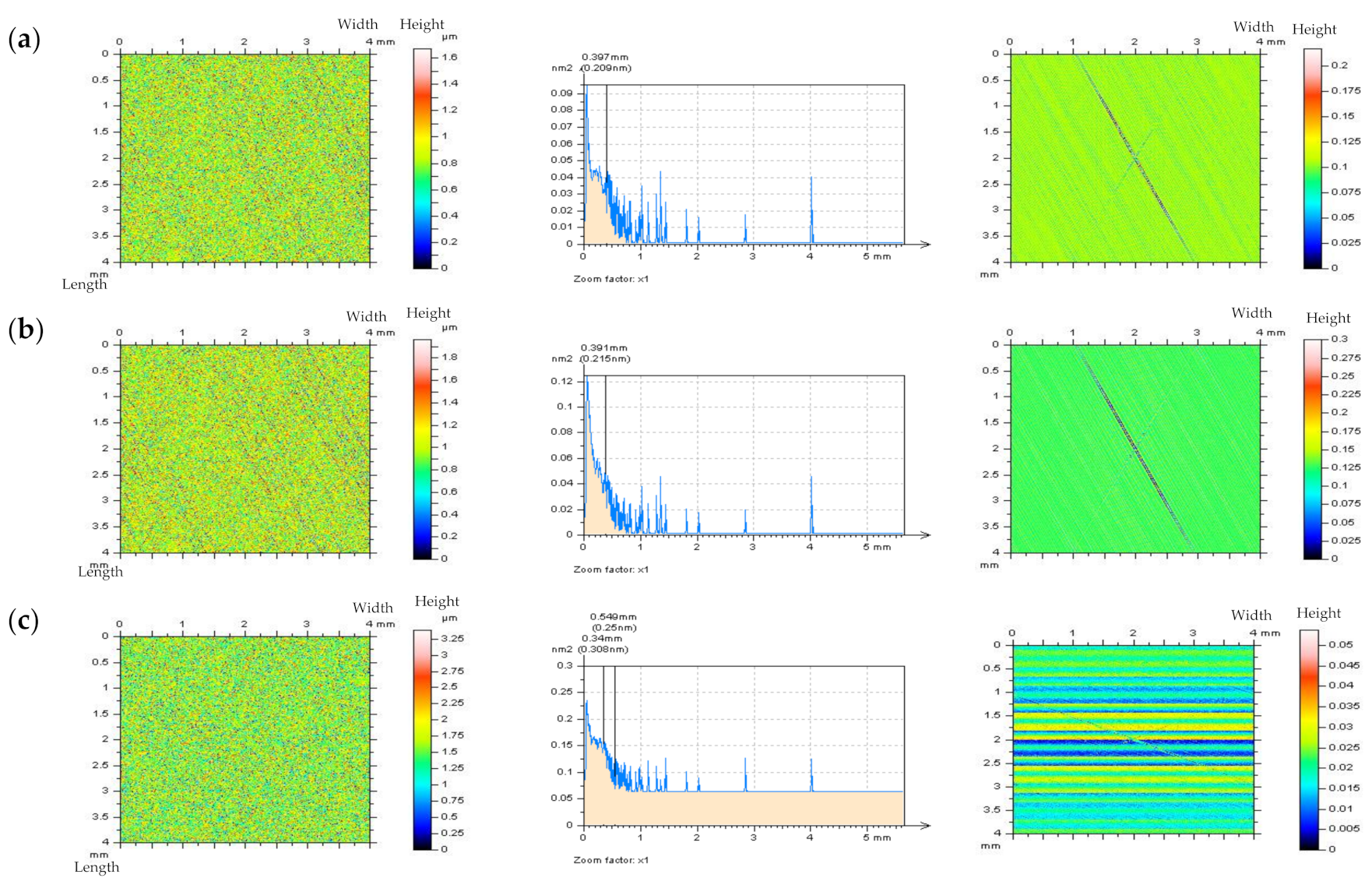
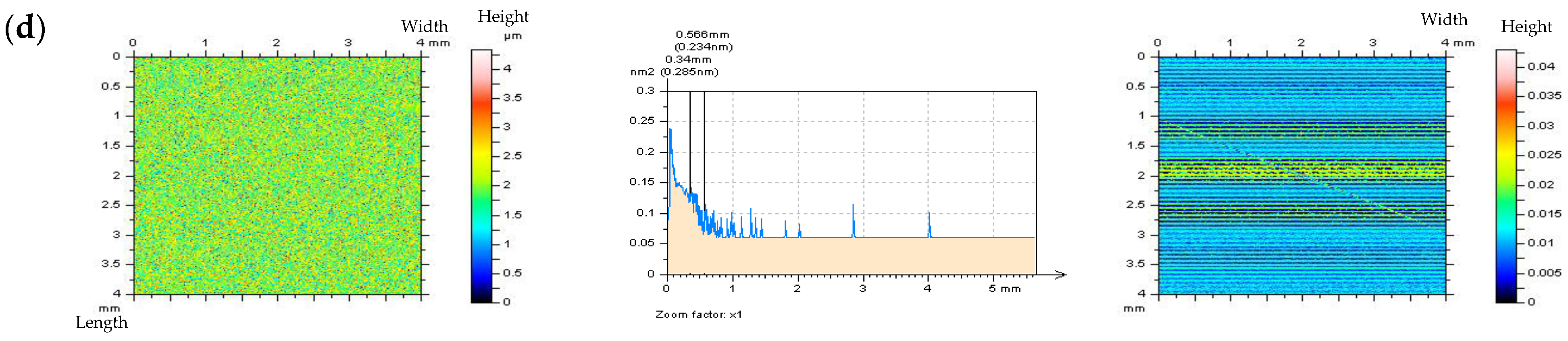
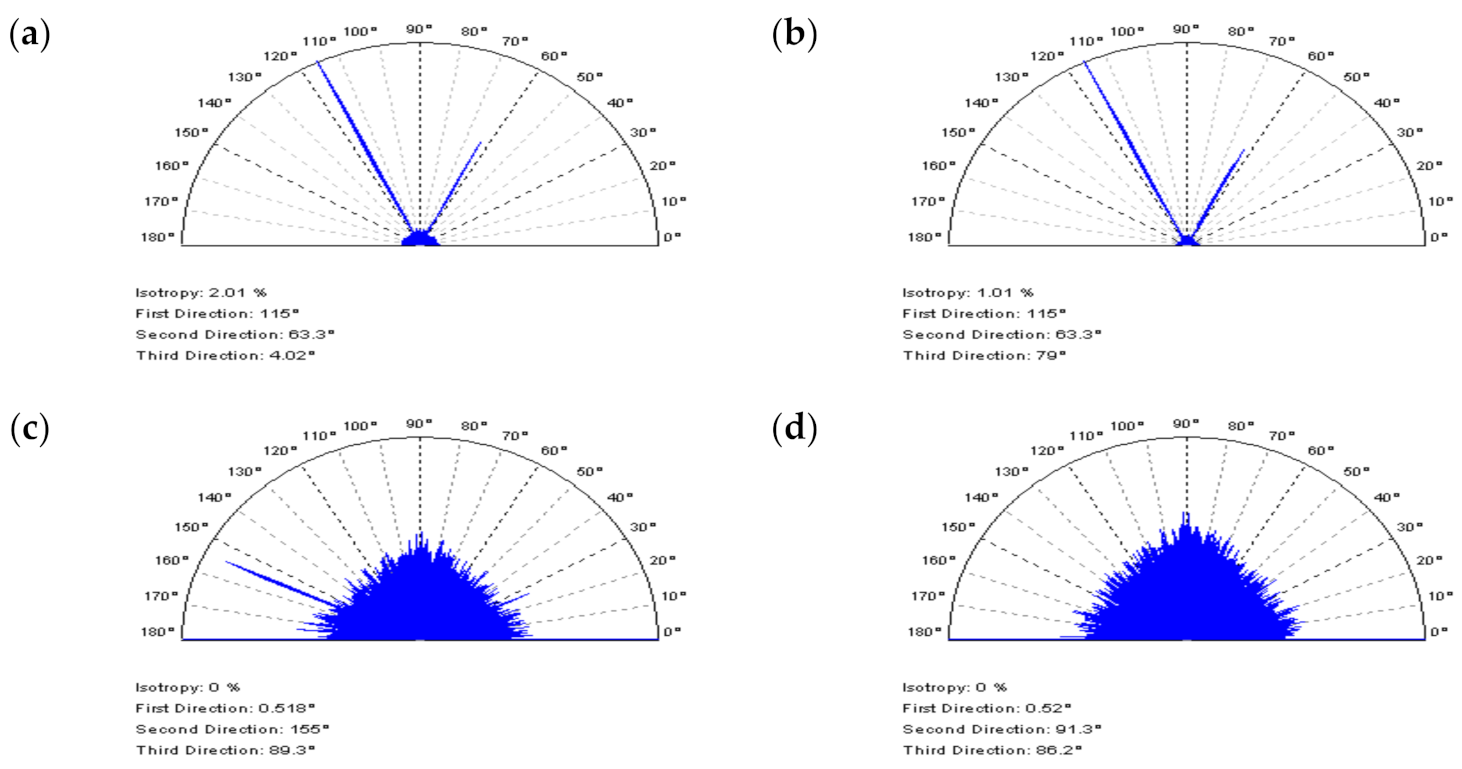
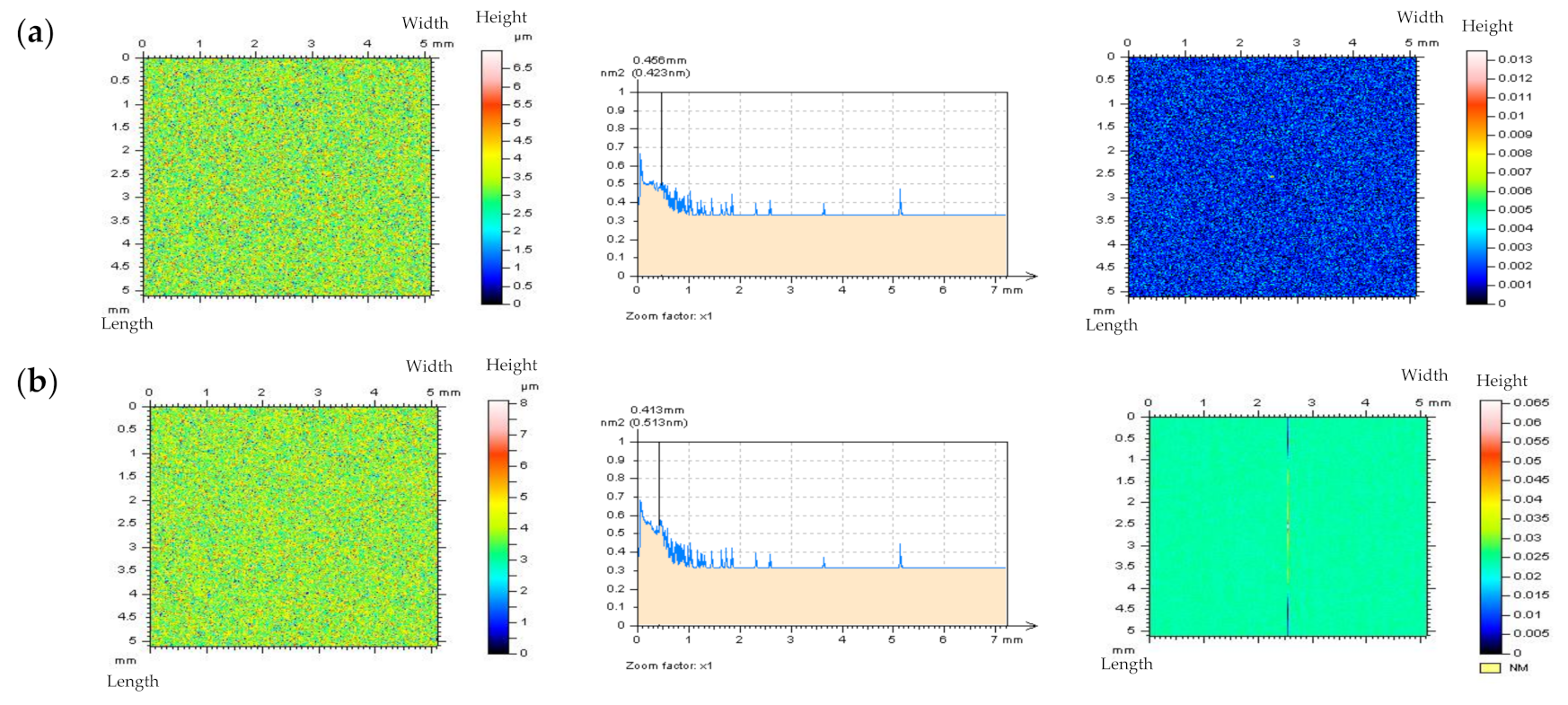
3.1. Resolving Problems in the Extraction of Irrelevant Features from Surface Textures
- (i)
- Observe the difference in the isometric view of the measured data.
- (ii)
- When the difference in point (i) is not visible, examine the non-plateau and non-valley details.
- (iii)
- When the difference in point (ii) is not visible, extract some non-peak and non-dimple profiles.
- (iv)
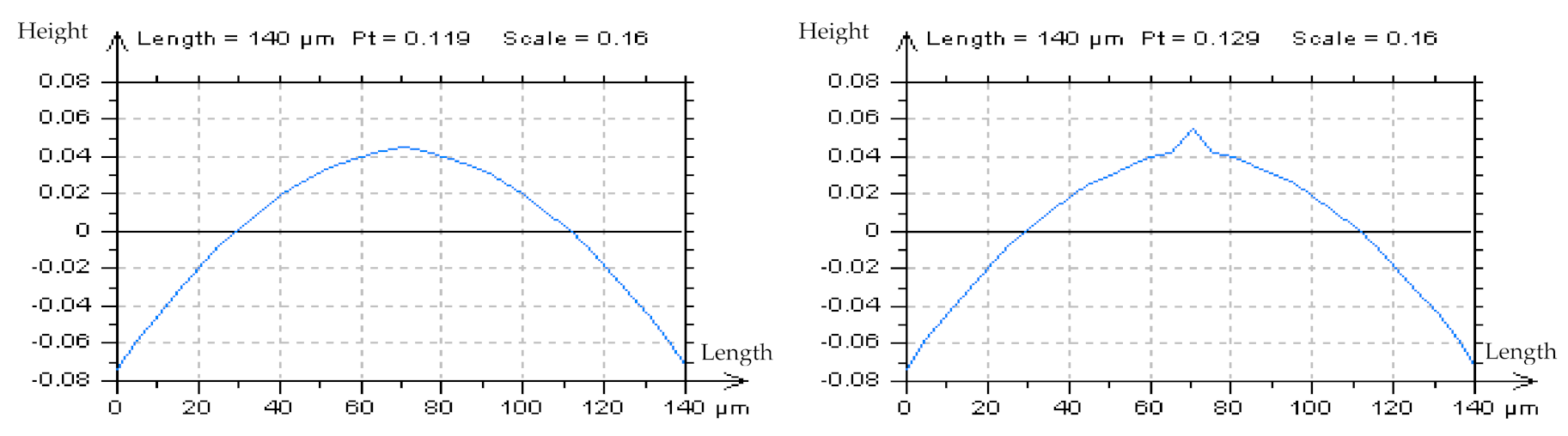
- An analysis of the PSD or ACF of the profiles from point (iii) proves to be valuable for HFN detection.
- (v)
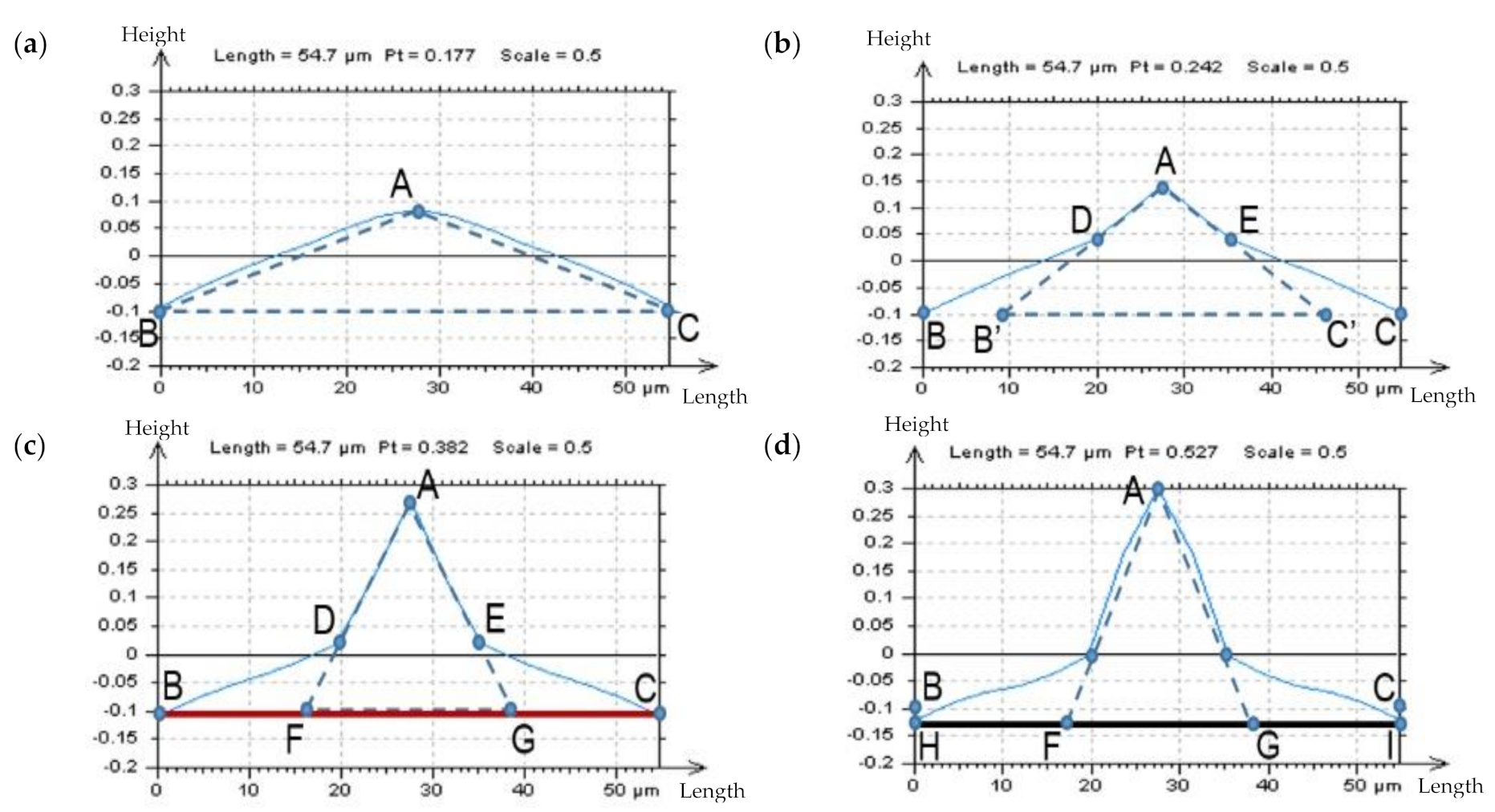
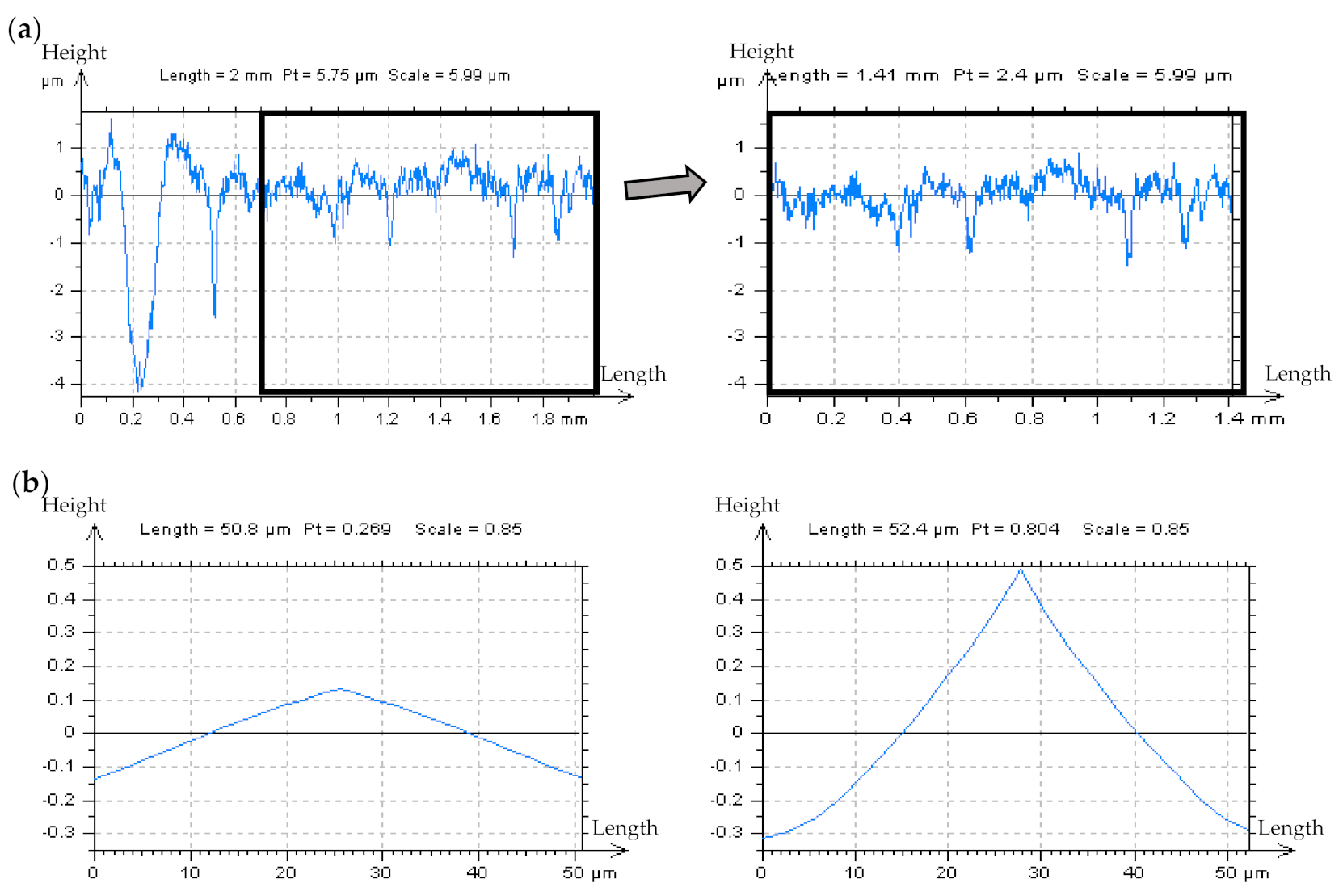
- If the above points, (i) to (iv), are ineffective and give no appropriate response, an analysis of an enlarged and extracted centre-part of the ACF of the non-valley/non-peak profile is necessary. When the frame of the received function is accelerating near the maximum value (“1”) of the ACF, the HFN occurrence can be observed.
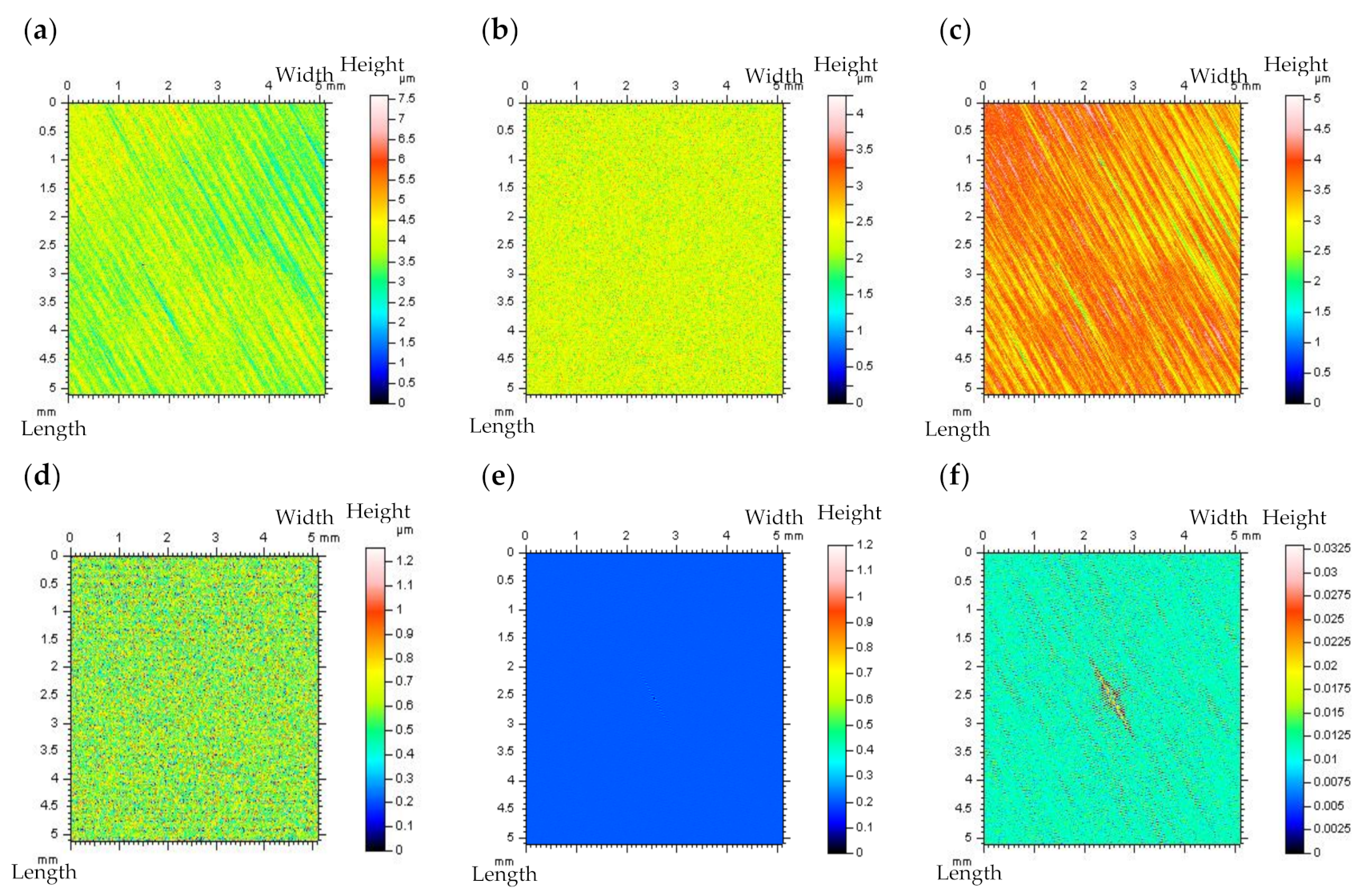
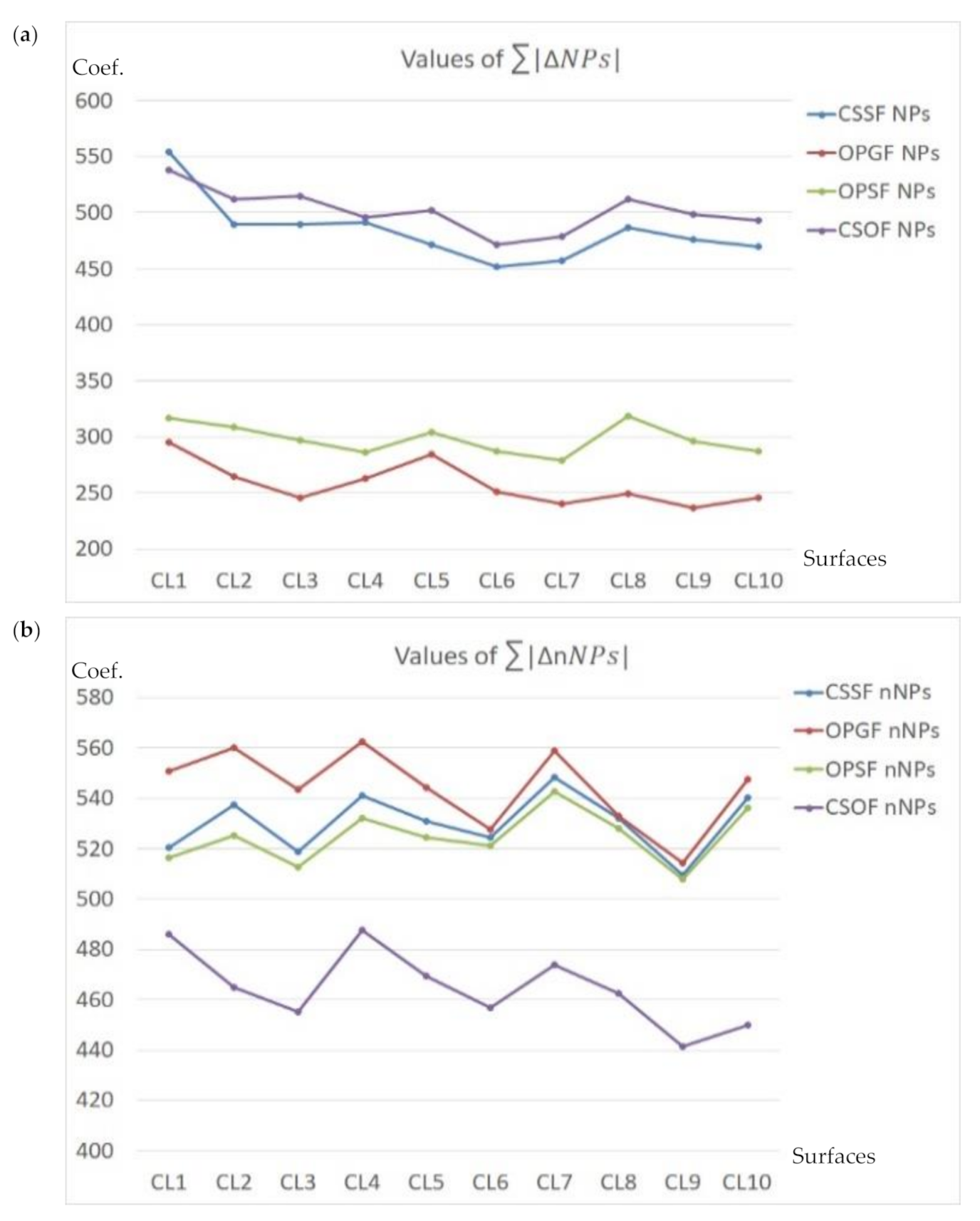
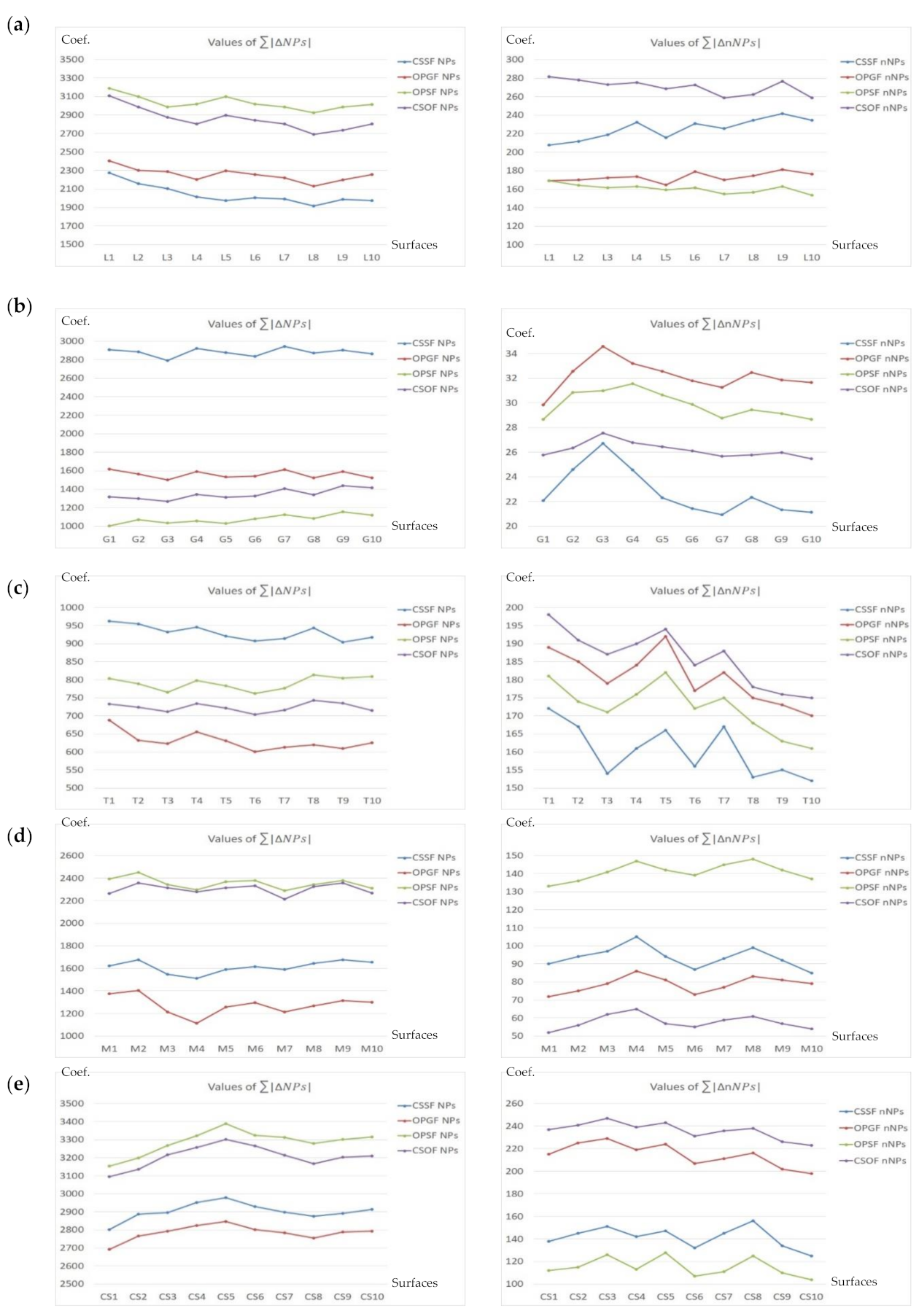
3.2. Reduction of the High-Frequency Errors with Comparisons of Various Spline Filters
3.3. Improving Procedures with a Modelled Data
4. The Outlook
- Primarily, the influence of wear on the occurrence of high-frequency measurement noise (and vice versa), which was not considered in this paper and deserves close attention in further research, as does the HFN for worn surface (details).
- The presented procedures for noise estimation might not be sufficient, outside of simulation tests. Furthermore, the recommended approaches might prove to be futile in cases when the amplitude errors are too small to eradicate. Moreover, some non-noise (in particular, non-HFN) components are also directly exposed to raw measured data when S-filtration is accomplished.
- There should also be a proposed research method for cases in which the raw data received is compared with the results which were obtained while the measurement is relatively small, e.g., 0.5 mm/s. Subsequently, the difference between fast measurement (e.g., 1.5 mm/s) after filtration (i.e., using spline schemes) and raw measured data with a low velocity (e.g., 0.5 mm/s), should be minimized. The smaller the difference separating the results of the processed fast measurement (for HFN reduction) and the unprocessed results measured at a slower pace, the better. There is a considerable advantage of the procedure.
- The NPs were defined as common “noise parameters” for all of the studied details. Nonetheless, the number of NPs can be slightly or, in some cases, considerably enlarged for each type of the analyzed textures. Thus, the non-general designated NPs and factors might be more commonly useful, considering their relative difference changes.
- A serious problem remains with edge-effect minimization in surface topography measurements. This type of data processing errors method is especially concerned with the extraction of waviness from the raw data. The edge limitations increase when deep or wide features (e.g., dimples, scratches, oil pockets, or valleys in general) are situated near the edge of a studied surface topography detail. The influence of density and amplitude of errors on the sides (edges) of the measured component on the HFN occurrence and their effect on the surface texture parameter calculation were not fully analyzed. Sharp-edge noise can also be considered for sharp-edged features, such as deep holes. However, the results of the received (extracted) noise (HFN in general) might be of different amplitudes in each NS area. The noise gathering process was also omitted.
- Establishing the locations in which the noise is easy to detect constitutes another challenge. Free-of-dimple or profile spline methods are typical examples of this form of HFN detection. Moreover, the noise amplitude might be falsely estimated when non-feature details are considered, as opposed to the in-depth valley analysis. Distinguishing the studies involving valley-part or plateau-part might prove useful for noise detection but not for the minimization of the considered frequency errors. Therefore, much attention should be directed to the analysis of the entirety of the measured detail.
5. Conclusions
- It was found that when the number of features (e.g., dimples, valleys, scratches) increased in the plateau-honed cylinder liner surfaces, the accuracy of the high-frequency noise detection by optical analysis of Power Spectral Density graphs decreased. Consequently, the chosen solution was an out-of-feature analysis of the specific details. The optical detection of noise was more effective during the 2D (profile) analysis than in the 3D (areal) surface topography assessment. The paper proves that in the plateau-honed cylinder liner surface containing additionally burnished dimples, the detection of high-frequency noise is entirely dependent on the valley occurrence. When a certain profile contains only scratches (of a width < 50 um) and their number (density) is relatively small (profile < 3 mm, length equal to 4 or 5 mm), the detection of noise using the Power Spectral Density plot analysis becomes possible.
- When considering the valley profiles (profiles with dimples), the problems with noise detection using the PSD graph analysis increased. Severe problems with noise detection appeared in cases with the largest number (density) of dimples. Therefore, the out-of-dimple (valley or scratch) detail (and, usually, profile) analysis is required for the detection of high-frequency noise within the raw measured data, rather than the entire measured detail assessment.
- An alternative is the profile spline method. It is proposed rather than the out-of-feature (e.g., dimple) noise detection. This approach extracts the out-of-valley parts of the profile from the raw measurement profile data and connects them. The free-of-dimple profile is not required for this type of examination. The plateau-and-valley extraction accuracy was not studied in detail in this paper. However, some papers already cover the efficiency of various distinguishing methods.
- Similar to the out-of-dimple method is a “treatment trace-profile” analysis, where the studied profiles are extracted along the trace of treatment received directly from the manufacturing process. This type of analysis can be applied to other kinds of surface textures than the plateau-honed topographies. The “treatment trace profile” analysis is particularly valuable, in some cases, for turned or ground details assessments.
- According to the applied approach, each spline filtering method is adequate for the noise extraction of various types of surface textures, e.g., Open Profile Spline Filter seems to be the most useful in the analysis of laser-textured or composite surfaces, Cubic Spline Outlier Filter is valuable in studying the honed, ceramic, or milled topographies, Cubic Smoothing Spline Filter gave encouraging results for the turned or ground details. The suggested minimization approach can also be applied for other types of surface topographies. Additionally, alternative types of filtering methods may be used for the characterization of engineering surfaces. The achieved results can also be compared with those presented in recent studies.
- Finally, high-frequency noise analysis with multithreaded intention is suggested. The analysis of the Power Spectral Density and the Autocorrelation Function graphs can provide much valuable information about noise identification, especially with regard to the analysis of “noise surface” (defined as a result of the noise-removal S-filtering process). The proposal was that “noise surface” should only contain the frequencies needing to be removed, i.e., after the high-frequency noise reduction process, the received noise data (NS) should only consist of high-frequency components, non-noise features should not be present. When other unrequired surface features are present, the less popular approach (filter) is suitable for the reduction of high-frequency measurement errors.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ACF | autocorrelation function | Sa | arithmetic mean height Sa, µm |
| ACF-CSM | Autocorrelation Function Centre-Shape Method | Sal | auto-correlation length, mm |
| CPSF | Close Profile Spline Filter | Sbi | surface bearing index |
| CSSF | Cubic Smoothing Spline Filter | Sci | core fluid retention index |
| EDM | Empirical Mode Decomposition | Sdq | Root-mean-square gradient |
| FOD | free of dimple (valley) surface or profile Gauss | Sdr | developed interfacial areal ratio, % |
| FFTF | Fast Fourier Transform Filter | Sk | core roughness depth, µm |
| HFN | high-frequency noise | Sku | kurtosis |
| MA | multithreaded approach | Sp | maximum peak height, µm |
| MQCL | Minimum Quantity Cooling Lubrication | Spc | arithmetic mean peak curvature, 1/mm |
| NURBS | non-uniform rational B-spline surfaces | Spd | peak density, 1/mm2 |
| OPGF | Open Profile Gaussian Filter | Spk | reduced summit height, µm |
| OPSF | Open Profile Spline Filter | Sq | Root-mean-square height, µm |
| PSD | power spectral density | Ssk | skewness |
| PSM | Profile Spline Method | Std | texture direction, ° |
| PSWF | Polynomial Spline Wavelet Filter | Str | texture parameter |
| RSM | root-mean-square | Sv | maximum valley depth, µm |
| TTP | treatment-trace-profiles approach | Svi | valley fluid retention index |
| WLIAFM | white light interference-based atomic force microscopy | Svk | reduced valley depth, µm |
| ω | vector of output data values | Sz | the maximum height of surface, µm |
| cut-off value | Ra | arithmetic mean deviation of rough. profile, µm | |
| s(x) | the weighting function | Rc | mean height of roughness profile element, µm |
| a “noisy-data” vector | Rdc | roughness profile Section height difference, µm | |
| the example of “noisy data” | Rdq | root-mean-square slope of roughness profile, ° | |
| cubic spline smoothing curve | Rmr | relative material ratio of roughness profile, % | |
| a smoothed vector | Rp | maximum peak height of roughness profile, µm | |
| a symmetric three-diagonal matrix with the non-null elements of the th row or column | RPc | peak count of the raw profile, 1/mm | |
| the B-spline coefficients | Rq | root-mean-square (RSM) dev. of r. profile, µm | |
| the indicator function | RSm | mean width of roughness profile element, mm | |
| the B-spline function constructed by a repeated convolution of a B-spline of order 0 | Rt | total height of roughness profile, µm | |
| the central B-spline | Rv | maximum valley depth of roughness profile, µm | |
| the B-spline waelet | Rz | maximum height of roughness profile, µm | |
| th order B-spline | |||
| the bi-cubic spline element | |||
| the coefficients | |||
| the values of | |||
| the Kronecker product of two-band matrices of small size |
References
- Thomas, T.R. Roughness and functions. Surf. Topogr. Metrol. Prop. 2014, 2, 014001. [Google Scholar] [CrossRef]
- Dagnall, H. Exploring Surface Texture; Rank Taylor Hobson Limited: Leicester, UK, 1986. [Google Scholar]
- Muhamedsalih, H.; Jiang, X.; Gao, F. Accelerated surface measurement using wavelength scanning interferometer with compensation of environmental noise. Procedia CIRP 2013, 10, 70–76. [Google Scholar] [CrossRef][Green Version]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterisation of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- De Groot, P. Principles of interference microscopy for the measurement of surface topography. Adv. Opt. Photonics 2015, 7, 65. [Google Scholar] [CrossRef]
- Servin, M.; Estrada, J.C.; Quiroga, J.A.; Mosiño, J.F.; Cywiak, M. Noise in phase shifting interferometry. Opt. Express 2009, 17, 8789–8794. [Google Scholar] [CrossRef]
- Šarbort, M.; Holá, M.; Pavelka, J.; Schovánek, P.; Rerucha, Š.; Oulehla, J.; Fo, T.; Lazar, J. Comparison of three focus sensors for optical topography measurement of rough surfaces. Opt. Express 2019, 27, 33459. [Google Scholar] [CrossRef] [PubMed]
- Blateyron, F. The areal field parameters. In Characterisation of Areal Surface Texture; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 2; pp. 15–43. [Google Scholar]
- Geometrical Product Specifications (GPS). Surface Texture: Areal—Part 600: Metrological Characteristics for Areal-Topography Measuring Methods (DRAFT); ISO WD 25178-600:2014(E); International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Schimmack, M.; Mercorelli, P. A wavelet packet tree denoising algorithm for images of atomic-force microscopy. Asian J. Control 2018, 24, 1367–1378. [Google Scholar] [CrossRef]
- Zhong, C.; Gao, Z.; Wang, X.; Gao, C.; Yang, S.; Sun, X.; Wen, X.; Feng, Z.; Wang, S. The machine learning method of phase extraction in interferometry. Opt. Lasers Eng. 2018, 110, 384–391. [Google Scholar] [CrossRef]
- Zuo, X.; Peng, M.; Zhou, Y. Influence of noise on the fractal dimension of measured surface topography. Measurement 2020, 152, 107311. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann.-Manuf. Technol. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Hu, C.; Liu, X.; Yang, W.; Lu, W.; Yu, N.; Chang, S. Improved zero-order fringe positioning algorithms in white light interference based atomic force microscopy. Opt. Lasers Eng. 2018, 100, 71–76. [Google Scholar] [CrossRef]
- Pavliček, P.; Michálek, V. White-light interferometry—Envelope detection by Hilbert transform and influence of noise. Opt. Lasers Eng. 2012, 50, 1063–1068. [Google Scholar] [CrossRef]
- De Groot, P.; De Lega, X.C.; Kramer, J.; Turzhitsky, M. Determination of fringe order in white-light interference microscopy. Appl. Opt. 2002, 41, 4571–4578. [Google Scholar] [CrossRef]
- Sharma, A.; Sheoran, G.; Jaffery, Z.A.; Moinuddin. Improvement of signal-to-noise ratio in digital holography using wavelet transform. Opt. Lasers Eng. 2008, 46, 42–47. [Google Scholar] [CrossRef]
- Schimmack, M.; Mercorelli, P. An on-line orthogonal wavelet denoising algorithm for high-resolution surface scans. J. Frankl. Inst. 2018, 355, 9245–9270. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Suo, T.; Liang, J. De-noising of digital image correlation based on stationary wavelet transform. Opt. Lasers Eng. 2017, 90, 161–172. [Google Scholar] [CrossRef]
- Jiang, X.; Scott, P.; Whitehouse, D.J. Wavelets and their applications for surface metrology. CIRP Ann. Manuf. Technol. 2008, 57, 555–558. [Google Scholar] [CrossRef]
- Huang, L.; Kemao, Q.; Pan, B.; Krishna, A.; Asundi, A.K. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase extraction from a single fringe pattern in fringe projection profilometry. Opt. Lasers Eng. 2010, 48, 141–148. [Google Scholar] [CrossRef]
- Kiela, K.; Navickas, R. A method for continuous tuning of MOSFET–RC filters with extended control range. J. Electr. Eng. 2016, 67, 449–453. [Google Scholar] [CrossRef][Green Version]
- Podulka, P. Comparisons of envelope morphological filtering methods and various regular algorithms for surface texture analysis. Metrol. Meas. Syst. 2020, 27, 243–263. [Google Scholar]
- Boashash, B. Signal denoising by time-frequency peak filtering (TFPF). In Time-Frequency Signal Analysis and Processing; Boashash, B., Ed.; Elsevier: New York, NY, USA, 2016; pp. 663–670. [Google Scholar]
- Sun, J.; Song, Z.; Heb, G.; Sang, Y. An improved signal determination method on machined surface topography. Precis. Eng. 2018, 51, 338–347. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Proc. Let. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Tanaka, T.; Mandic, D.P. Complex Empirical Mode Decomposition. IEEE Signal Proc. Let. 2007, 14, 101–104. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Janecki, D. Edge effect elimination in the recursive implementation of Gaussian filters. Precis. Eng. 2012, 36, 128–136. [Google Scholar] [CrossRef]
- Seewig, J. Linear and robust Gaussian regression filters. J. Phys. Conf. Ser. 2005, 13, 254–257. [Google Scholar] [CrossRef]
- ISO 16610-28:2016. Geometrical Product Specifications (GPS). Filtration—Part 28: Profile Filters: End Effects; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Goto, T.; Yanagi, K. An optimal discrete operator for the two-dimensional spline filter. Meas. Sci. Tech. 2009, 20, 125105. [Google Scholar] [CrossRef]
- Huang, S.; Tong, M.; Huang, W.; Zhao, X. An isotropic areal filter based on high-order thin-plate spline for surface metrology. IEEE Access 2019, 7, 116809–116822. [Google Scholar] [CrossRef]
- Zhang, H.; Tong, M.; Chu, W. An areal isotropic spline filter for surface metrology. J. Res. Natl. Inst. Stan. 2015, 120, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Tong, M.; Zhang, H.; Ott, D.; Zhao, X.; Song, J. Analysis of the boundary conditions of the spline filter. Meas. Sci. Technol. 2015, 26, 095001. [Google Scholar] [CrossRef]
- Gogolewski, D. Fractional spline wavelets within the surface texture analysis. Measurement 2021, 179, 109435. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, K.; Du, S.; Xi, L. High definition metrology enabled three dimensional discontinuous surface filtering by extended tetrolet transform. J. Manuf. Syst. 2018, 49, 75–92. [Google Scholar] [CrossRef]
- Krommweh, J. Tetrolet transform: A new adaptive Haar wavelet algorithm for sparse image representation. J Vis. Commun. Image R. 2010, 21, 364–374. [Google Scholar] [CrossRef]
- Hanada, H.; Saito, T.; Hasegawa, M.; Yanagi, K. Sophisticated filtration technique for 3D surface topography data of rectangular area. Wear 2008, 264, 422–427. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Problem of non-measured points in surface texture measurements. Metrol. Meas. Syst. 2017, 24, 525–536. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, H.-Y. A rotating scan scheme for automatic outlier removal in laser scanning of reflective surfaces. Int. J. Adv. Manuf. Syst. 2015, 81, 705. [Google Scholar] [CrossRef]
- Harasaki, A.; Wyant, J.C. Fringe modulation effect in white-light vertical scanning interferometry. Appl. Opt. 2000, 39, 2107–2115. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T.; Zhou, Y.; Butler, D. A non-contact measuring system for in-situ surface characterisation based on laser confocal microscopy. Sensors 2018, 18, 2657. [Google Scholar] [CrossRef]
- Raja, J.; Muralikrishnan, B.; Fu, S. Recent advances in separation of roughness, waviness and form. Precis. Eng. 2002, 26, 222–235. [Google Scholar] [CrossRef]
- Ismail, F.M.; Yanagi, K.; Fujii, A. An outlier correction procedure and its application to areal surface data measured by optical instruments. Meas. Sci. Technol. 2010, 21, 105105. [Google Scholar] [CrossRef]
- Le Goic, G.; Brown, C.A.; Favreliere, H.; Samper, S.; Formosa, F. Outlier filtering: A new method for improving the quality of surface measurements. Meas. Sci. Techol. 2012, 24, 015001. [Google Scholar] [CrossRef]
- Podulka, P.; Pawlus, P.; Dobrzański, P.; Lenart, A. Spikes removal in surface measurement. J. Phys. Conf. Ser. 2014, 483, 012025. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Piao, W. The spline filter: A regularisation approach for the Gaussian filter. Precis. Eng. 2012, 36, 586–592. [Google Scholar] [CrossRef]
- Tong, M.; Zhang, H.; Ott, D.; Chu, W.; Song, J. Applications of the spline filter for areal filtration. Meas. Sci. Technol. 2015, 26, 127002. [Google Scholar] [CrossRef]
- Janecki, D. A two-dimensional isotropic spline filter. Precis. Eng. 2013, 37, 948–965. [Google Scholar] [CrossRef]
- Janecki, D. A generalised L2-Spline Filter. Measurement 2009, 42, 937–943. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. B-spline signal processing. II. Efficiency design and applications. IEEE Trans. Signal Proces. 1993, 41/2, 834–848. [Google Scholar] [CrossRef]
- Krystek, M. Form filtering by Splines. Measurement 1996, 18, 9–15. [Google Scholar] [CrossRef]
- Auger, D.; Wang, Q.; Trevelyan, J.; Huang, S.; Zhao, W. Investigating the quality inspection process of offshore wind turbine blades using B-spline surfaces. Measurement 2018, 115, 162–172. [Google Scholar] [CrossRef]
- Savio, E.; De Chiffre, L.; Schmitt, R. Metrology of freeform shaped parts. CIRP Ann. Manuf. Technol. 2007, 56, 810–835. [Google Scholar] [CrossRef]
- Zeng, W.; Jiang, X.; Scott, P.J. A generalised linear and nonlinear spline filter. Wear 2011, 271, 544–547. [Google Scholar] [CrossRef][Green Version]
- Abdul-Rahman, H.S.; Jiang, X.J.; Scott, P.J. Freeform surface filtering using the lifting wavelet transform. Precis. Eng. 2013, 37/1, 187–202. [Google Scholar] [CrossRef][Green Version]
- Bonneau, G.P. Multiresolution analysis on irregular surface meshes. IEEE Trams. Vis. Comput. 1998, 4, 365–378. [Google Scholar] [CrossRef]
- Ortiz-Gracia, L.; Masdemont, J.J. Peaks and jumps reconstruction with -splines scaling functions. J. Comput. Appl. Math. 2014, 272, 258–272. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Piao, W. A universal spline filter for surface metrology. Measurement 2010, 43, 1575–1582. [Google Scholar] [CrossRef]
- Bai, F.; Han, F.; Xu, Y.; Bao, X.; Gan, S. Modified Fourier-transform method for phase-shift calibration. Opt. Lasers Eng. 2011, 49, 932–936. [Google Scholar] [CrossRef]
- ISO 25178 Part 600 Geometrical Product Specifications (GPS). Surface Texture: Areal—Part 600: Metrological Characteristics for Areal-Topography Measuring Methods; International Organization for Standardization: Geneva, Switzerland, 2019. [Google Scholar]
- Leach, R.K.; Haitjema, H.; Su, R.; Thompson, A. Metrological characteristics for the calibration of surface topography measuring instruments: A review. Meas. Sci. Technol. 2021, 32, 032001. [Google Scholar] [CrossRef]
- Koszela, W.; Pawlus, P.; Rejwer, E.; Ochwat, S. Possibilities of oil pockets creation by the burnishing technique. Arch. Civ. Mech. Eng. 2013, 13, 465–471. [Google Scholar] [CrossRef]
- Kacalak, W.; Lipiński, D.; Różański, R.; Królczyk, G.M. Assessment of the classification ability of parameters characterizing surface topography formed in manufacturing and operation processes. Measurement 2021, 170, 108715. [Google Scholar] [CrossRef]
- Jiang, X. Robust solution for the evaluation of stratified functional surfaces. CIRP Ann.-Manuf Technol. 2010, 59, 573–576. [Google Scholar] [CrossRef]
- Zębala, W.; Struzikiewicz, G.; Rumian, K. Cutting Forces and Tool Wear Investigation during Turning of Sintered Nickel-Cobalt Alloy with CBN Tools. Materials 2021, 14, 1623. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Lin, B.; Han, X.; Chen, S. Fractal analysis of engineering ceramics ground surface. Appl. Surf. Sci. 2012, 258/17, 6406–6415. [Google Scholar] [CrossRef]
- Niemczewska-Wójcik, M.; Gawlik, J.; Sładek, J. The measurement and analysis of surface geometric structure of ceramic femoral heads. Scanning 2014, 36, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Szpunar, M.; Trzepieciński, T.; Żaba, K.; Ostrowski, R.; Zwolak, M. Effect of Lubricant Type on the Friction Behaviours and Surface Topography in Metal Forming of Ti-6Al-4V Titanium Alloy Sheets. Materials 2021, 14, 3721. [Google Scholar] [CrossRef]
- Podulka, P. Improved procedures for feature-based suppression of surface texture high-frequency measurement errors in the wear analysis of cylinder liner topographies. Metals 2021, 11, 143. [Google Scholar] [CrossRef]
- Szala, M.; Łatka, L.; Walczak, M.; Winnicki, M. Comparative study on the cavitation erosion and sliding wear of cold-sprayed Al/Al2O3 and Cu/Al2O3 coatings, and stainless steel, aluminium alloy, copper and brass. Metals 2020, 10, 856. [Google Scholar] [CrossRef]
- Szala, M.; Walczak, M.; Pasierbiewicz, K.; Kamiński, M. Cavitation Erosion and Sliding Wear Mechanisms of AlTiN and TiAlN Films Deposited on Stainless Steel Substrate. Coatings 2019, 9, 340. [Google Scholar] [CrossRef]
- Mandal, S. Applicability of Tool Condition Monitoring Methods Used for Conventional Milling in Micromilling: A Comparative Review. J. Ind. Eng. 2014, 2014, 837390. [Google Scholar] [CrossRef]
- De Groot, P.; DiSciacca, J. Definition and evaluation of topography measurement noise in optical instruments. Opt. Eng. 2020, 59, 064110. [Google Scholar] [CrossRef]
- Giusca, C.L.; Leach, R.K.; Helary, F.; Gutauskas, T.; Nimishakavi, L. Calibration of the scales of areal surface topography-measuring instruments: Part 1. Measurement noise and residual flatness. Meas. Sci. Technol. 2012, 23, 03500. [Google Scholar] [CrossRef]
- Gomez, C.; Su, R.; de Groot, P.; Leach, R.K. Noise Reduction in Coherence Scanning Interferometry for Surface Topography Measurement. Nanomanuf. Metrol. 2020, 3, 68–76. [Google Scholar] [CrossRef]
- Podulka, P. Fast Fourier Transform detection and reduction of high-frequency errors from the results of surface topography profile measurements of honed textures. Eksploat. Niezawodn. 2021, 23, 84–89. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Szala, M.; Marciniak, Z.; Ulewicz, R.; Sczygiol, N.; Kardasz, P. Profile and areal surface parameters for fatigue fracture characterisation. Materials 2020, 13, 3691. [Google Scholar] [CrossRef]
- ISO 4287:1997 Geometrical Product Specifications (GPS). Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Janecki, D.; Cedro, L.; Zwierzchowski, J. Separation of non-periodic and periodic 2D profile features using B-Spline functions. Metrol. Meas. Syst. 2015, 22, 289–302. [Google Scholar] [CrossRef]
- Mathia, T.G.; Pawlus, P.; Wieczorowski, M. Recent trends in surface metrology. Wear 2011, 273, 494–508. [Google Scholar] [CrossRef]
- Krystek, M.; Scott, P.J.; Srinivasan, V. Discrete linear filters for metrology. In Proceedings of the 16th IMEKO World Congress 2000, Vienna, Austria, 25–28 September 2000. [Google Scholar]
- ISO 16610-22:2015. Geometrical Product Specifications (GPS). Filtration—Part 22: Linear Profile Filters: Spline Filters; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Jiang, X.J.; Whitehouse, D.J. Technological shifts in surface metrology. CIRP Ann.-Manuf. Technol. 2012, 61, 815–836. [Google Scholar] [CrossRef]
- Krystek, M. Discrete L-spline filtering in roundness measurements. Measurement 1996, 18, 129–138. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; De Hoog, F.R. Smoothing Noisy Data with Spline Functions. Numer. Math. 1985, 47, 99–106. [Google Scholar] [CrossRef]
- Feng, G. Data smoothing by cubic spline filters. IEEE Trams. Signal Proces. 1998, 46, 2790–2796. [Google Scholar] [CrossRef]
- Marchouk, G. Methodes de Calcul Numerique; Moscow, Russia, 1980; Chapter 3; pp. 127–149. [Google Scholar]
- Isomichi, Y. Inverse-quantization method for digital signals and images point-approximation type. Trans. Inst. Electron. Commun. Eng. 1980, 63, 815–821. (In Japanese) [Google Scholar]
- Hummel, R. Sampling for Spline Reconstruction. SIAM J. Appl. Math. 1983, 43, 278–288. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. Polynomial spline signal approximations: Filter design and asymptotic equivalence with Shannon’s sampling theorem. IEEE Trans. Inform. Theory 1992, 38, 95–103. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. A family of polynomial spline wavelet transforms. Signal Process. 1993, 30, 41–162. [Google Scholar] [CrossRef]
- Patrick, J. The B-spline Wavelet Recurrence Relation and B-spline Wavelet Interpolation; Honors Project; Illinois Wesleyan University: Bloomington, IL, USA, 1996. [Google Scholar]
- Renner, G.; Weiß, V. Exact and approximate computation of B-spline curves on surfaces. Comput. Aided Des. 2004, 36, 351–362. [Google Scholar] [CrossRef]
- Dierckx, P. An algorithm for least-squares fitting of cubic spline surfaces to functions on a rectilinear mesh over a rectangle. J Comput. Appl. Math. 1977, 3, 113–129. [Google Scholar] [CrossRef]
- Dierckx, P. Computation of least-squares spline approximations to data over incomplete grids. Comput. Math. Appl. 1984, 10, 283–289. [Google Scholar] [CrossRef][Green Version]
- Elson, J.M.; Bennett, J.M. Calculation of the power spectral density from surface profile data. Appl. Opt. 1995, 34, 201–208. [Google Scholar] [CrossRef]
- ISO 25178: Geometric Product Specifications (GPS). Surface Texture: Areal; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- Krolczyk, G.M.; Maruda, R.W.; Nieslony, P.; Wieczorowski, M. Surface morphology analysis of Duplex Stainless Steel (DSS) in Clean Production using the Power Spectral Density. Measurement 2016, 94, 464–470. [Google Scholar] [CrossRef]
- Martínez, J.F.G.; Nieto-Carvajal, I.; Abad, J.; Colchero, J. Nanoscale measurement of the power spectral density of surface roughness: How to solve a difficult experimental challenge. Nanoscale Res. Lett. 2012, 7, 174. [Google Scholar]
- Alcock, S.G.; Ludbrook, G.D.; Owen, T.; Dockree, R. Using the power spectral density method to characterise the surface topography of optical surfaces. Proc. SPIE 2010, 7801, 780108. [Google Scholar]
- Gavrila, R.; Dinescu, A.; Mardare, D. A Power Spectral Density study of thin films morphology based on AFM profiling. Raman J. Inf. Sci. Technol. 2007, 3, 291–300. [Google Scholar]
- Raoufi, D. Fractal analyses of ITO thin films: A study based on power spectral density. Phys. B Condens. Matter 2010, 405, 451–455. [Google Scholar] [CrossRef]
- Pawlus, P. Change of cylinder surface topography in the initial stage of engine life. Wear 1997, 209, 69–83. [Google Scholar] [CrossRef]
- Pawlus, P.; Chetwynd, D.G. Efficient characterization of surface topography in cylinder bores. Precis. Eng. 1996, 19, 164–174. [Google Scholar] [CrossRef]
- Podulka, P. The effect of surface topography feature size density and distribution on the results of a data processing and parameters calculation with a comparison of regular methods. Materials 2021, 14, 4077. [Google Scholar] [CrossRef]
- Podulka, P. Reduction of influence of the high-frequency noise on the results of surface topography measurements. Materials 2021, 14, 333. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Surface metrology. Meas. Sci. Tech. 1997, 8, 955. [Google Scholar] [CrossRef]
- ISO 25178-3:2012 Geometrical Product Specifications (GPS). Surface Texture: Areal—Part 3: Specification Operators; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- Li, L.; Tang, J.; Wen, Y.; Zhu, C. Numerical simulation of ultrasonic-assisted grinding surfaces with Fast Fourier Transform. J. Tribol. 2020, 142, 092301. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M.; Krolczyk, G. Material ratio curve as information on the state of surface topography—A review. Precis. Eng. 2020, 65, 240–258. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podulka, P. Suppression of the High-Frequency Errors in Surface Topography Measurements Based on Comparison of Various Spline Filtering Methods. Materials 2021, 14, 5096. https://doi.org/10.3390/ma14175096
Podulka P. Suppression of the High-Frequency Errors in Surface Topography Measurements Based on Comparison of Various Spline Filtering Methods. Materials. 2021; 14(17):5096. https://doi.org/10.3390/ma14175096
Chicago/Turabian StylePodulka, Przemysław. 2021. "Suppression of the High-Frequency Errors in Surface Topography Measurements Based on Comparison of Various Spline Filtering Methods" Materials 14, no. 17: 5096. https://doi.org/10.3390/ma14175096
APA StylePodulka, P. (2021). Suppression of the High-Frequency Errors in Surface Topography Measurements Based on Comparison of Various Spline Filtering Methods. Materials, 14(17), 5096. https://doi.org/10.3390/ma14175096





