A Mandible with the Temporomandibular Joint—A New FEM Model Dedicated to Strength and Fatigue Calculations of Bonding Elements Used in Fracture and Defect Surgery
Abstract
1. Introduction
- Creation of an accurate model of the mandible together with the temporomandibular joint. The main assumption was to create a model that could be used for numerical analyses of various clinical cases, allowing the simulation of the work of fixing elements, assessment of the strength and durability of the fixation, and at the same time, without unnecessary simplifications, reflect real human anatomy. The input data were DICOM images obtained from medical imaging using computed tomography. Obtaining three-dimensional models of individual anatomical structures required the segmentation of tomographic images and then edition of the generated surface objects. Reverse engineering software for free modeling and a CAD program for parametric modeling were used.
- Taking into account the current achievements and shortcomings of the existing models of the mandible, it was necessary to investigate the effect of simplifications of the temporomandibular joint. Various degrees of simplification of the mandible model were designed, which made it possible to check various configurations of the FEM analysis assumptions and to select the variant that best reflects real conditions. The most important criterion for simplifications was a sufficient reflection of the system biomechanics. This required the creation of a force action scheme based on the actual impact of muscles on the mandible and the introduction of boundary conditions to simulate the appropriate load state. As a result of the performed calculations, maps of stresses in the mandible were obtained, and their analysis allowed to assess the influence of the studied simplifications.
- Verification of the possibility of modifying the model and applying it in various cases.
2. Materials and Methods
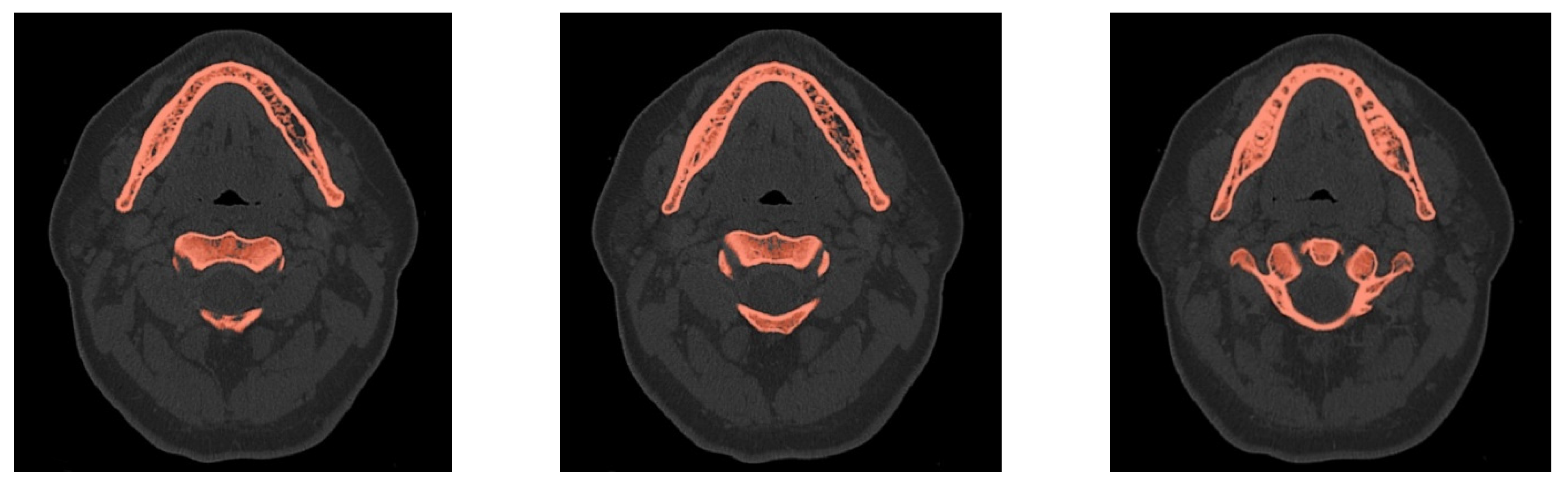
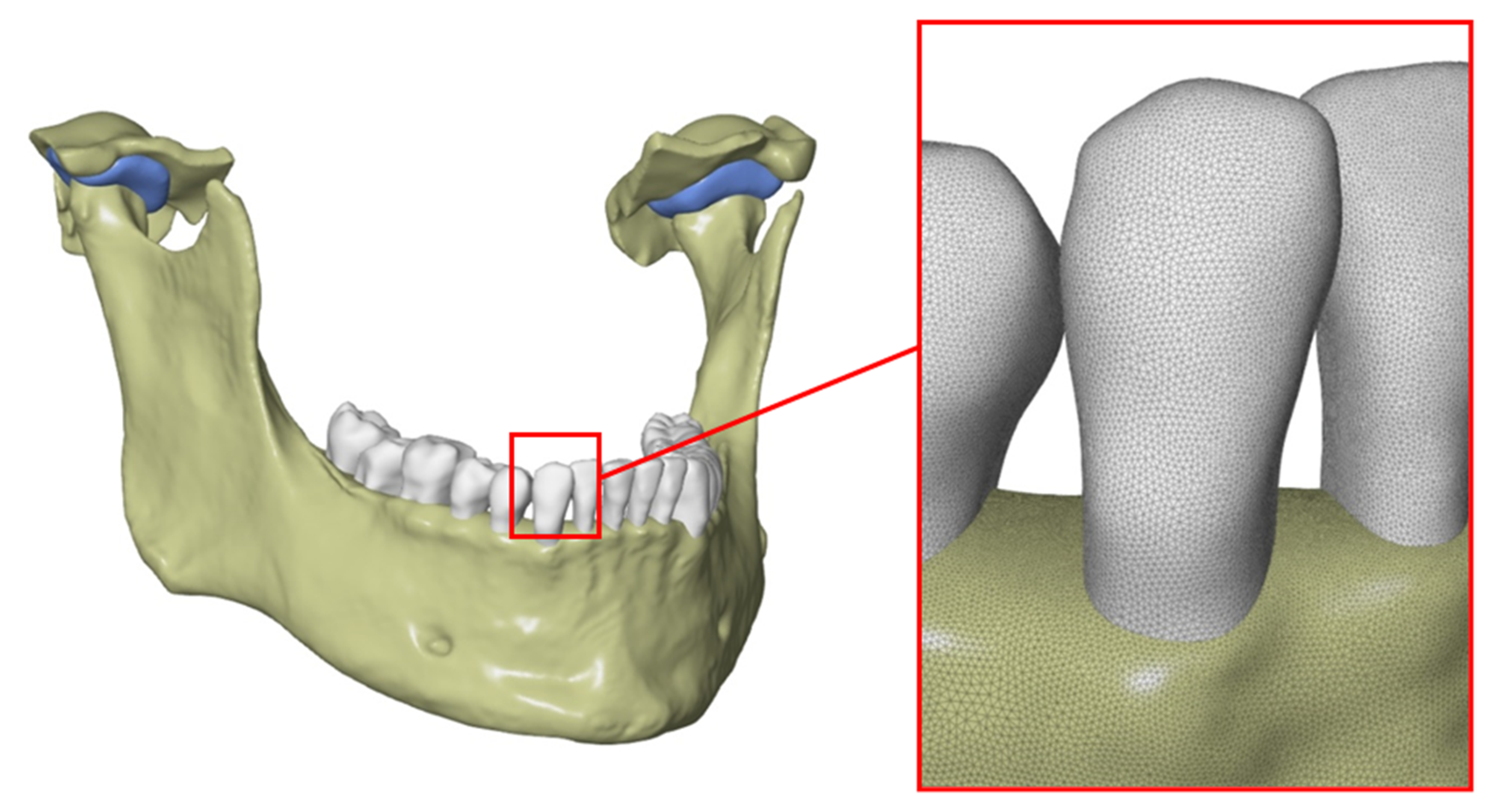
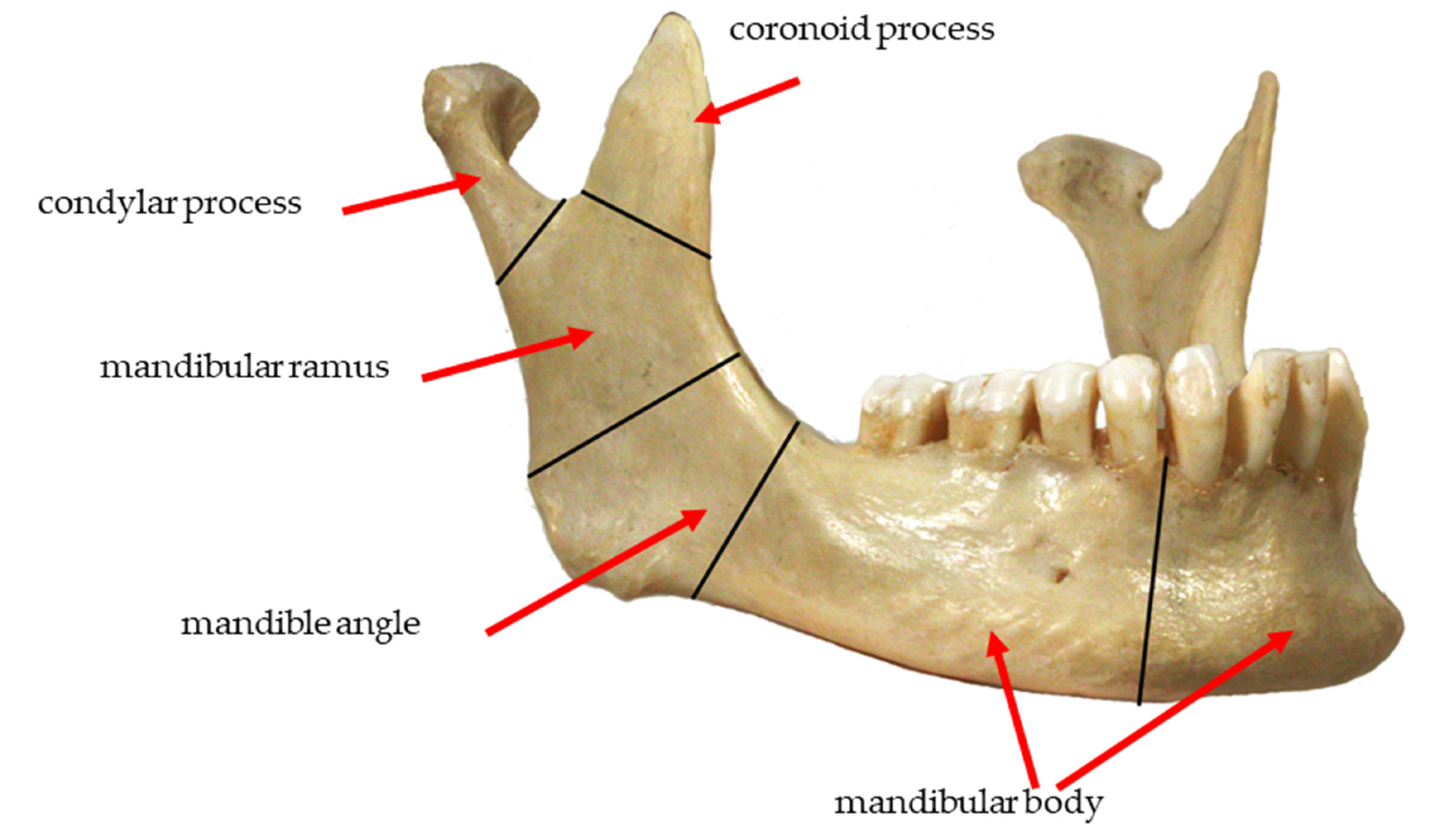
2.1. Obtaining Anatomical Data
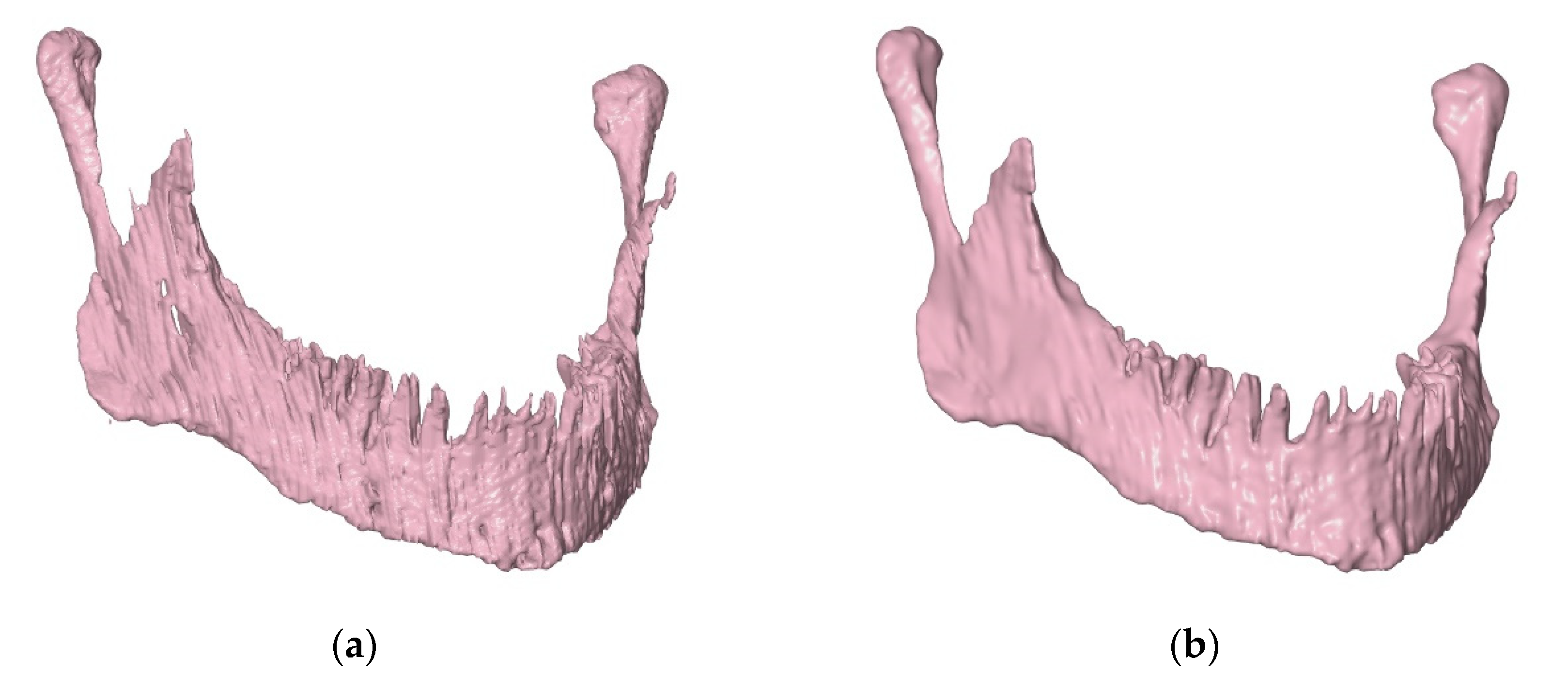
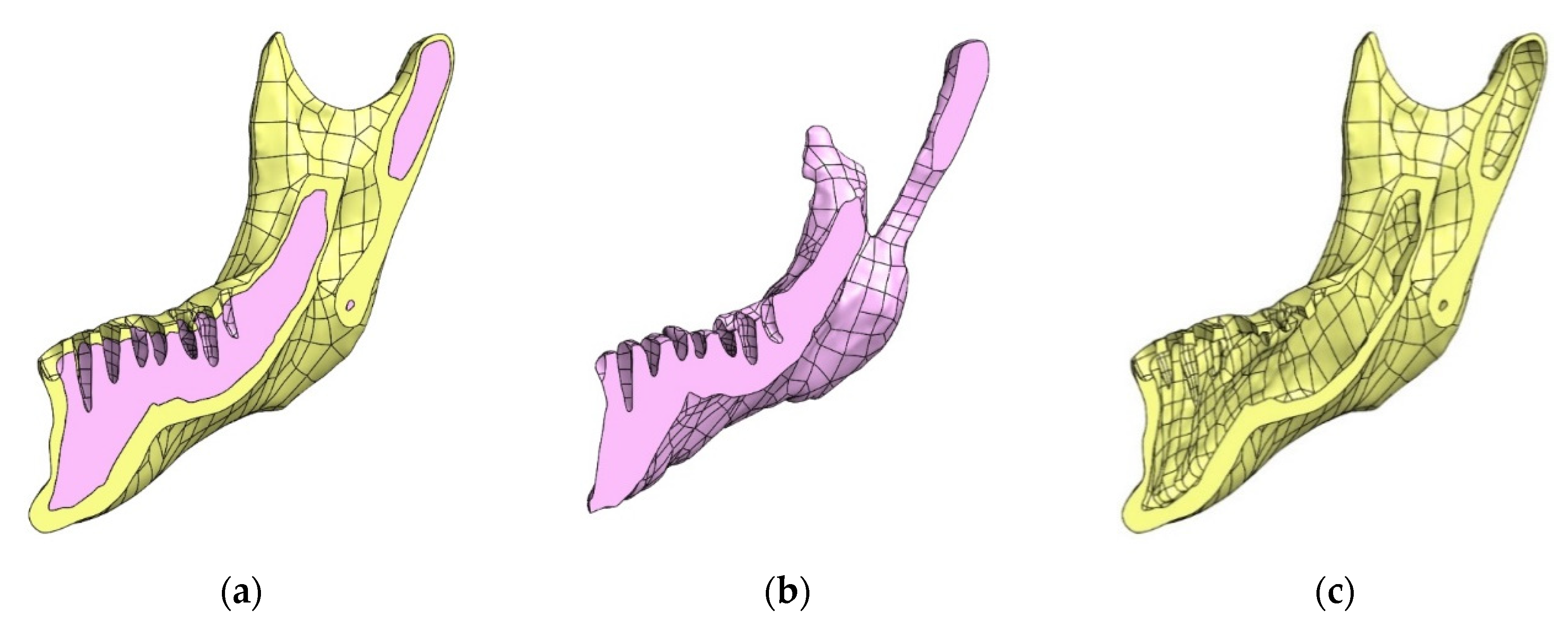
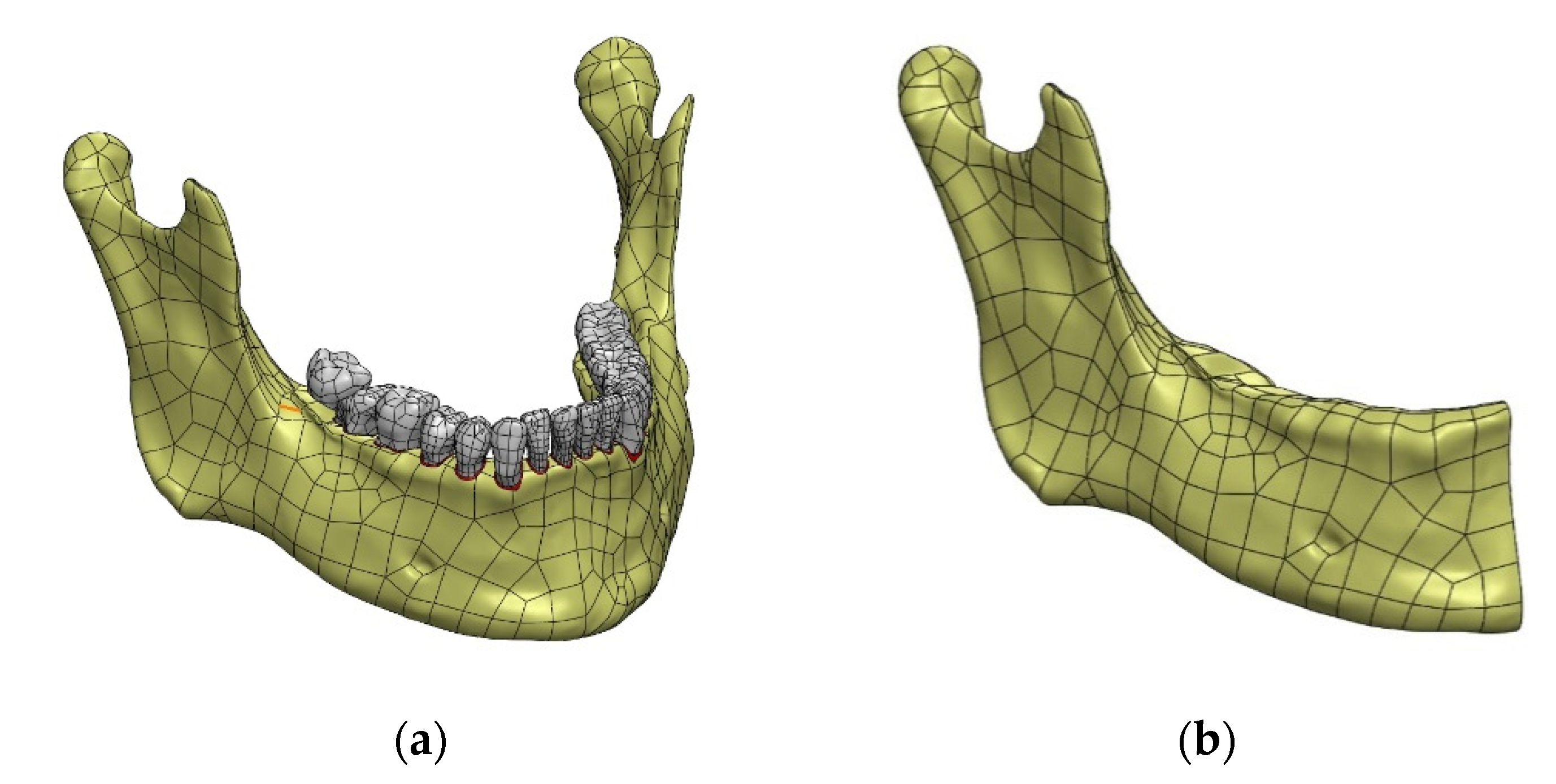
2.2. Generation of a Three-Dimensional Model of Selected Anatomical Structures
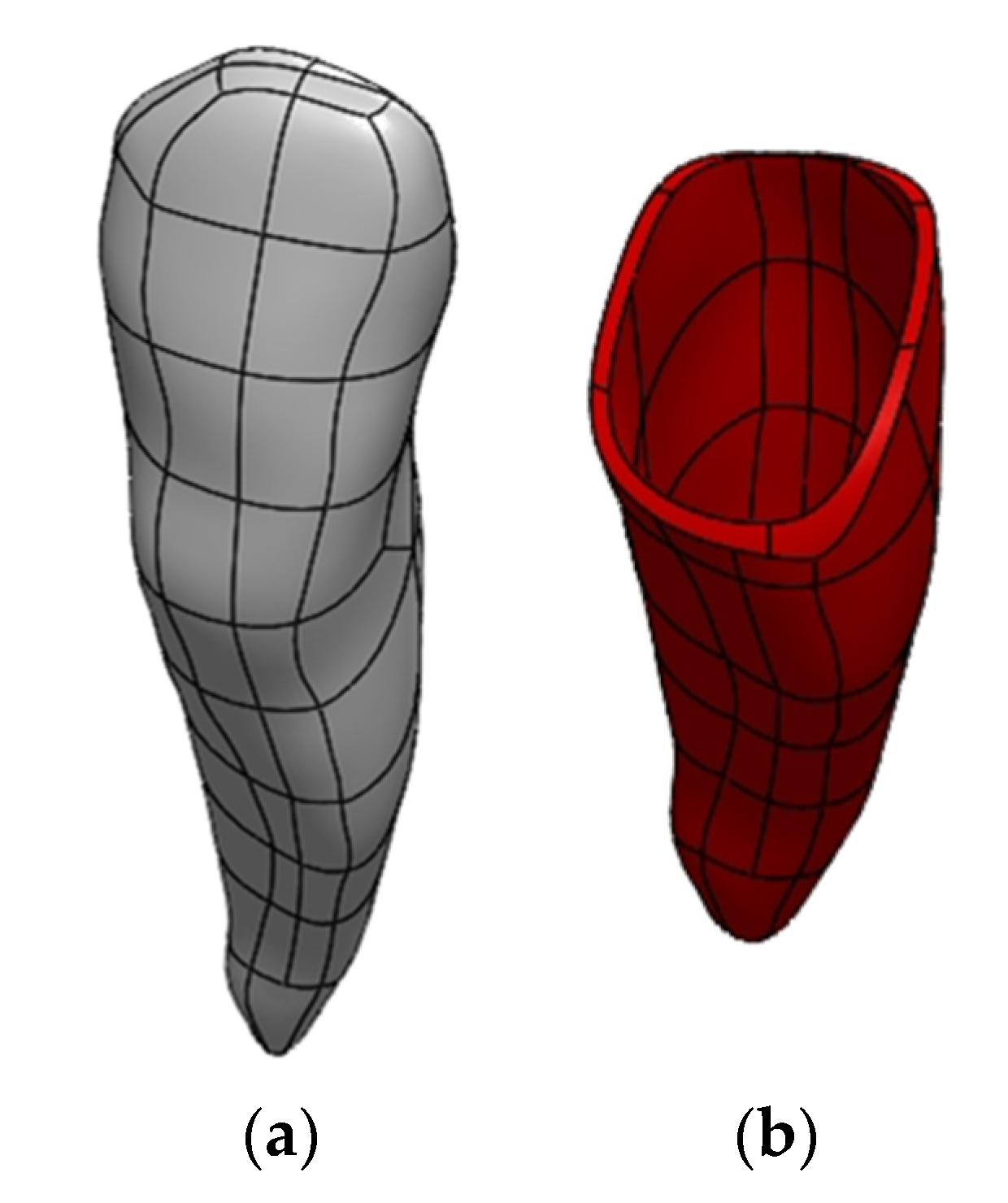
2.3. Edition of STL Models
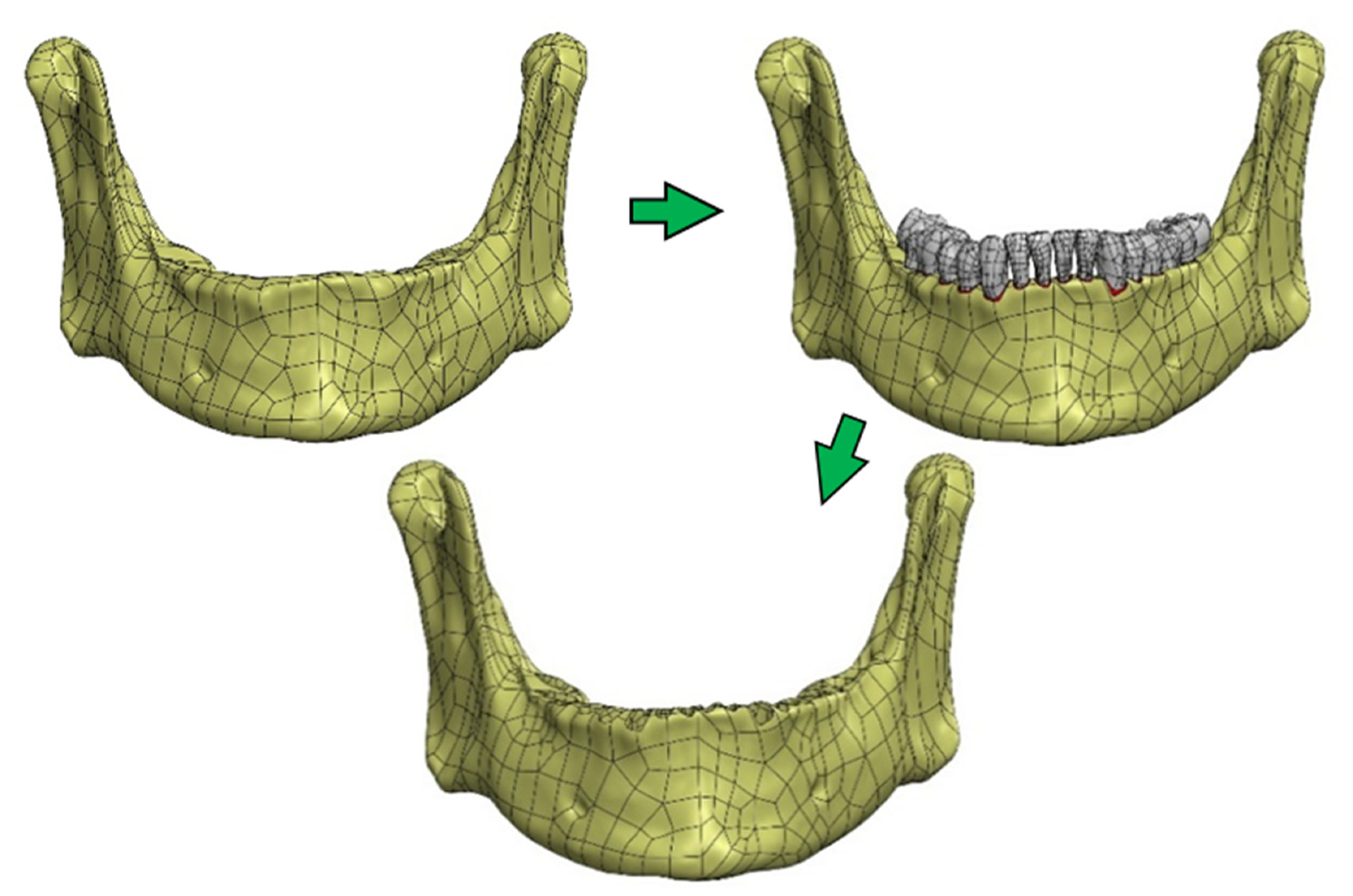
2.4. Preparation of a Solid CAD Model
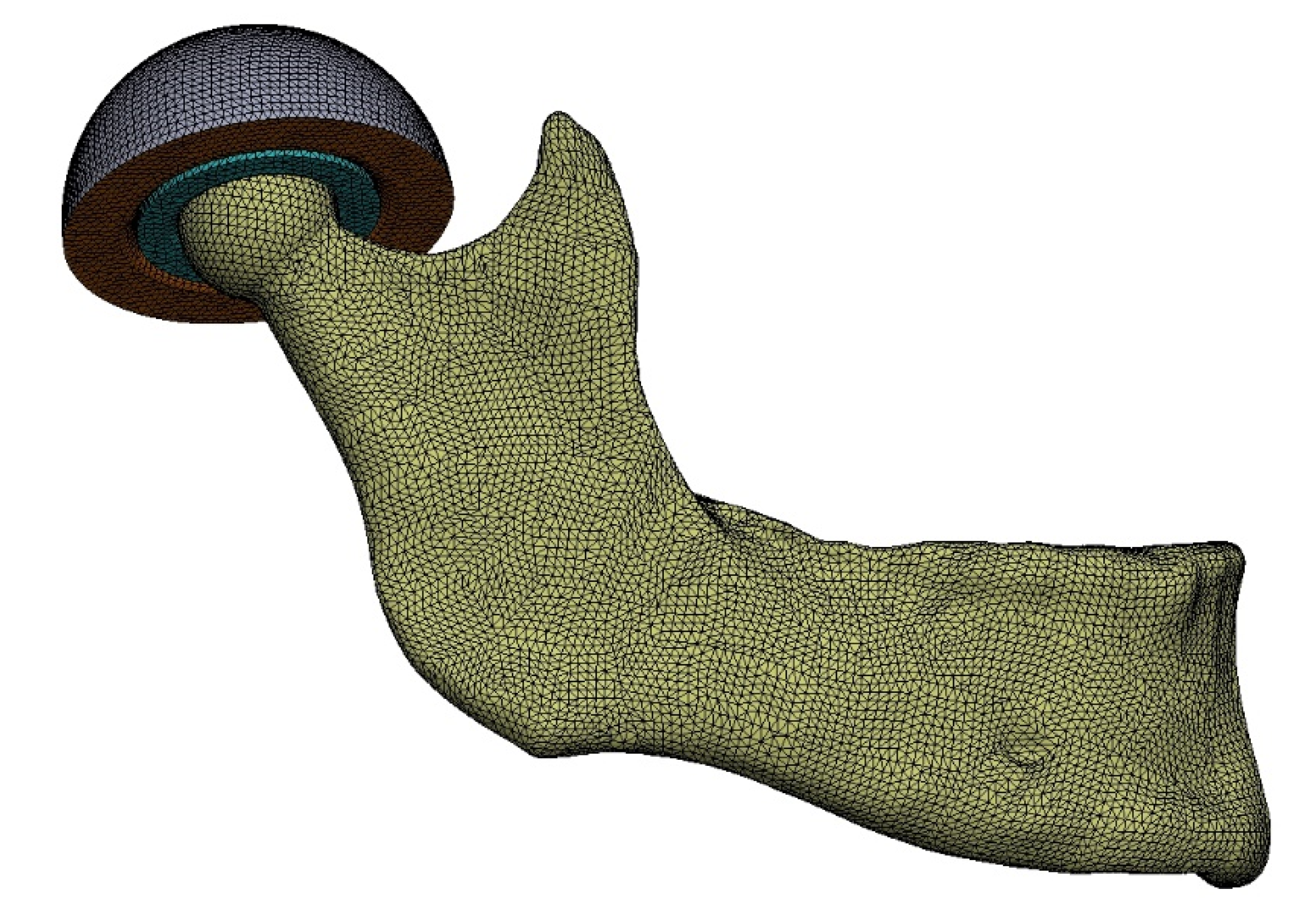
2.5. Preparation of an FEM Model
2.6. Material Data
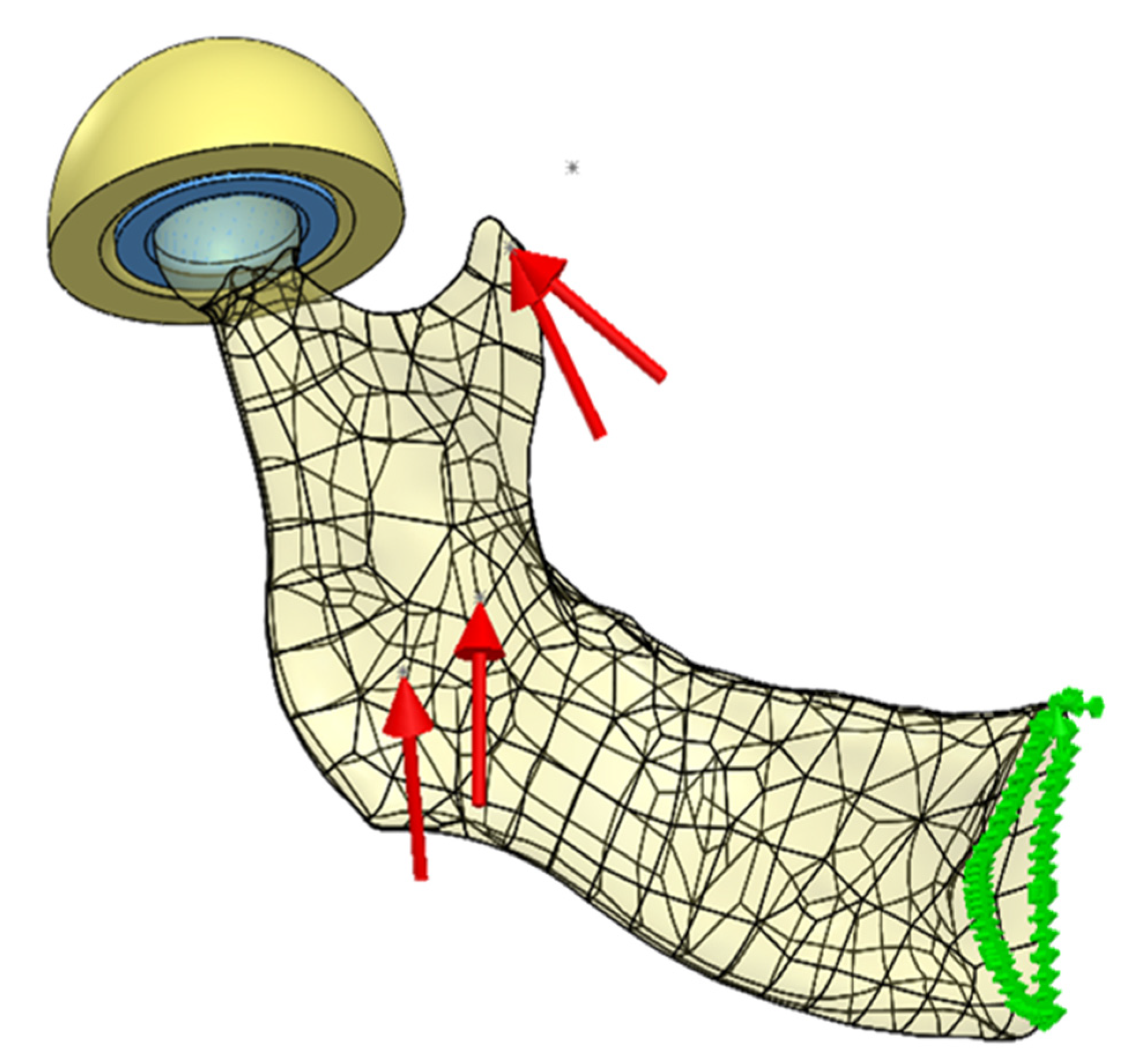
2.7. Loading Scheme
2.8. Boundary Conditions
2.9. FEM Model
3. Results
3.1. CAD Model
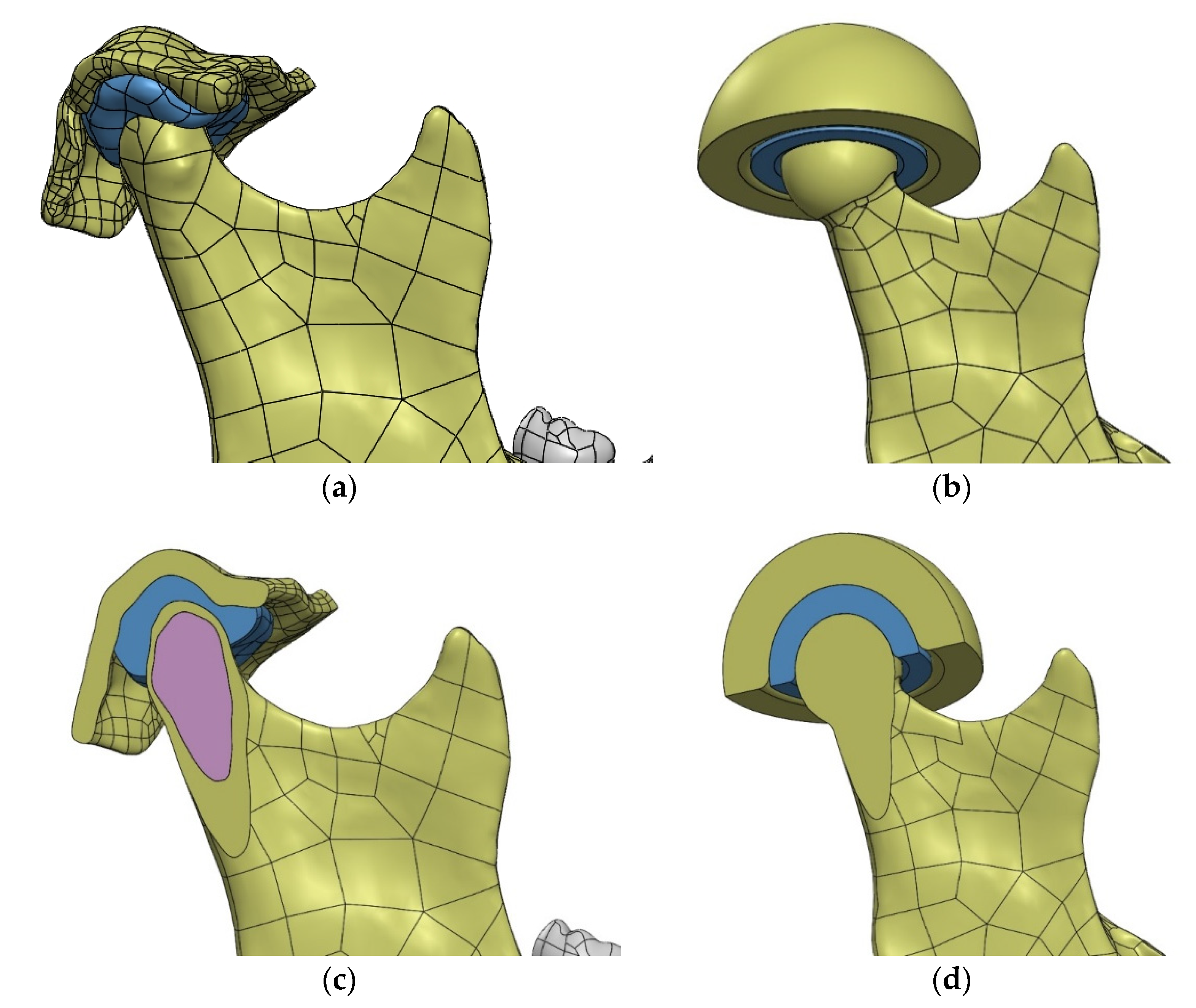
3.2. Possibilities of Simplifying the Model
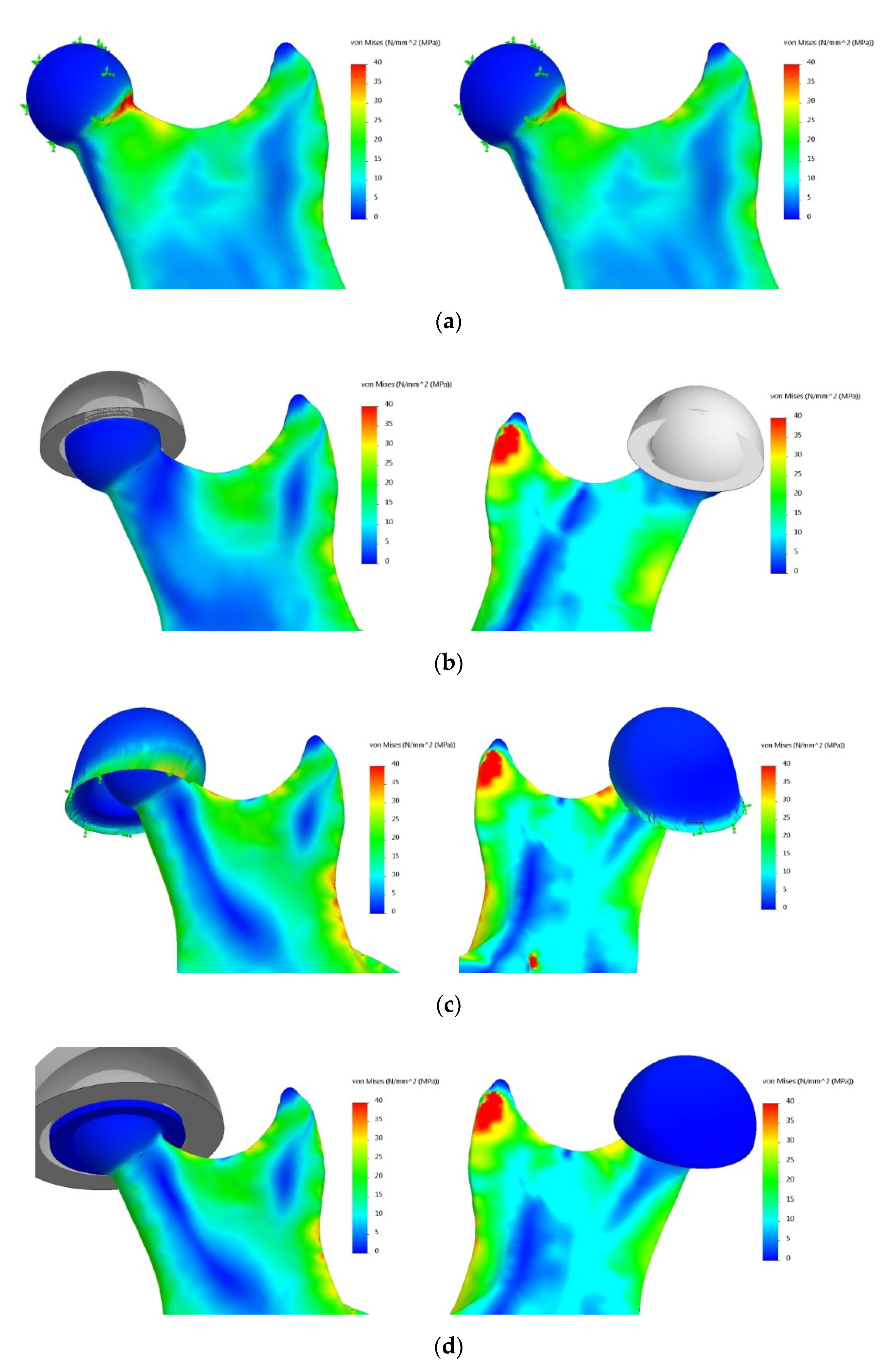
3.3. Examination of the Influence of the Simplification of the Temporomandibular Joint on the Correctness of the Assessment of Mandibular Strain
3.3.1. Model
3.3.2. Examined Cases of Simplifications
3.3.3. Results of the Experiment
4. Discussion
- The most simplified model of the mandible with the blocked displacement of nodes on the articular surface of the head of the mandible (Variant 1) should not be used in strength calculations due to large discrepancies between the obtained results and the reference model (Variant 4). The differences can be as high as 216%, as in the case of stresses in the area of the condylar process.
- Simplification of the temporomandibular joint to the model of a non-deformable disc (Variant 2) does not provide a sufficiently accurate representation of the state of mandibular strain, despite recreating the kinematics of the examined bone (hinge movement with possible lateral adductions).
- Modelling the temporomandibular joint as a joint (contact task) has a significant impact on the obtained stress distribution on the mandible (Variants 3 and 4).
- For the analysis of mandibular strain, it is not necessary to build an exact (Variant 4) model of the temporomandibular joint. The reduction of the system to a deformable articular disc provides a sufficiently good representation of stress distribution.
- Simplification of the temporomandibular joint to a deformable articular disc (Variant 3) does not ensure an appropriate state of displacement, which may affect the results of the analysis of fixation stability based on the study of displacement of broken bone fragments.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erdmann, B.; Kober, C.; Lang, J.; Deuflhard, P.; Zeilhofer, H.F.; Sader, R. Efficient and Reliable Finite Element Methods for Simulation of the Human Mandible, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Report ZIB 01-14. 2001. Available online: http://webdoc.sub.gwdg.de/ebook/e/2003/zib_2/reports/ZR-01-14.pdf (accessed on 13 July 2021).
- Misch, C.E. Progressive Bone Loading: Increasing the Density of Bone with a Prosthetic Protocol, Pocket Dentistry. Available online: https://pocketdentistry.com/32-progressive-bone-loading/ (accessed on 13 July 2021).
- Netter, F.H. Atlas of Human Anatomy E-Book, 7th ed.; Elsevier: Philadelphia, PA, USA, 2017. [Google Scholar]
- Hansen, J.T. Netter’s Anatomy Coloring Book, 2nd ed.; Elsevier: Philadelphia, PA, USA, 2019. [Google Scholar]
- Thibodeau, G.A.; Patton, K.T. Brief Atlas of the Human Body; Elsevier: St Louis, MO, USA, 2007. [Google Scholar]
- Gorzałek, J. Biomechanics of the temporomandibular joint (TMJ) in terms of the manual therapy. Man. Med. 2009, 2009, 44–48. [Google Scholar]
- Perry, M.; Brown, A.; Banks, P. Fractures of the Facial Skeleton, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2015. [Google Scholar]
- Staszak, K.; Kurlej, W.; Pawlak, W.; Domagała, Z.; Gworys, B.; Nelke, K. Anatomical Possibilities of Repositioning the Mandible, XXXIV International Congress of the Polish Anatomical Society. Available online: https://zjazdanatomiczny.gumed.edu.pl/attachment/attachment/20967/P1_03_Staszak.pdf (accessed on 12 January 2018).
- Vranis, N.M.; Mundinger, G.S.; Bellamy, J.L.; Schultz, B.D.; Banda, A.; Yang, R.; Dorafshar, A.H.; Christy, M.R.; Rozdiguez, E.D. Extracapsular Mandibular Condyle Fractures Are Associated with Severe Blunt Internal Carotid Artery Injury: Analysis of 605 Patients. Plast. Reconstr. Surg. 2015, 136, 811–821. [Google Scholar] [CrossRef]
- Edward, E., III; Warren, S. Mandible. Available online: https://surgeryreference.aofoundation.org/cmf/trauma/mandible (accessed on 12 July 2018).
- Vollmer, D.; Meyer, U.; Joos, U.; Vègh, A.; Piffko, J. Experimental and finite element study of a human mandible. J. Cranio-Maxillofac. Surg. 2000, 28, 91–96. [Google Scholar] [CrossRef]
- Ichim, I.; Kieser, J.A.; Swain, M.V. Functional significance of strain distribution in the human mandible under masticatory load: Numerical predictions. Arch. Oral Biol. 2007, 52, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Torreira, M.G.; Fernandez, J.R. A three-dimensional computer model of the human mandible in two simulated standard trauma situations. J. Cranio-Maxillofac. Surg. 2004, 32, 303–307. [Google Scholar] [CrossRef]
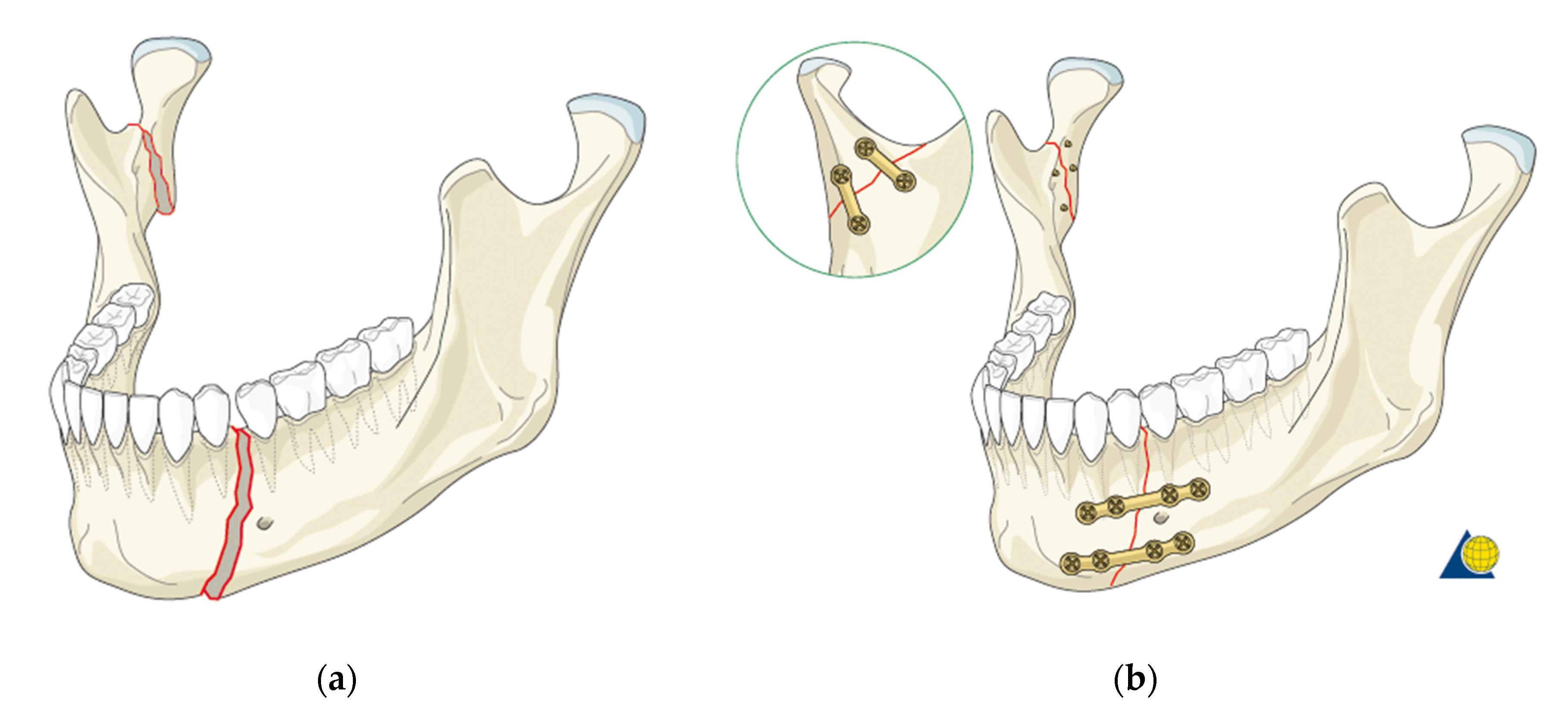
- Arbag, H.; Korkmaz, H.H.; Ozturk, K.; Uyar, Y. Comparative Evaluation of Different Miniplates for Internal Fixation of Mandible Fractures Using Finite Element Analysis. J. Oral Maxillofac. Surg. 2008, 66, 1225–1232. [Google Scholar] [CrossRef]
- Lovald, S.T.; Wagner, J.D.; Baack, B. Biomechanical optimization of bone plates used in rigid fixation of mandibular fractures. J. Oral Maxillofac. Surg. 2009, 67, 973–985. [Google Scholar] [CrossRef]
- Kozakiewicz, M.; Swiniarski, J. “A” shape plate for open rigid internal fixation of mandible condyle neck fracture. J. Cranio-Maxillofac. Surg. 2014, 42, 730–737. [Google Scholar] [CrossRef]
- Aquilina, P.; Chamoli, U.; Parr, W.C.; Clausen, P.D.; Wroe, S. Finite element analysis of three patterns of internal fixation of fractures of the mandibular condyle. Br. J. Oral Maxillofac. Surg. 2013, 51, 326–331. [Google Scholar] [CrossRef]
- De Jesus, G.P.; Vaz, L.G.; Gabrielli, M.F.; Passeri, L.A.; Oliveira, T.V.; Noritomi, J.P. Finite element evaluation of three methods of stable fixation of condyle base fractures. Int. J. Oral Maxillofac. Surg. 2014, 43, 1251–1256. [Google Scholar] [CrossRef]
- Różyło-Kalinowska, I. Contemporary Dental Radiology; Publishing House Czelej: Lublin, Poland, 2012. [Google Scholar]
- Wang, M. Industrial Tomography: Systems and Applications; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Foley, J.D.; van Dam, A.; Feiner, S.K.; Hughes, J. Computer Graphics: Principles and Practice, 2nd ed.; Addison Wesley: Wokingham, UK, 1990. [Google Scholar]
- Holbert, J.M.; Costello, P.I.; Federle, M.P. Role of Spiral Computed Tomography in the Diagnosis of Pulmonary Embolism in the Emergency Department. Ann. Emerg. Med. 1999, 33, 520–528. [Google Scholar] [CrossRef]
- Heiken, J.P.; Brink, J.A.; Vannier, M.W. Spiral (helical) CT. Radiology 1993, 189, 647–656. [Google Scholar] [CrossRef]
- Schnoll, R.A.; Wileyto, E.P.; Hornik, R.; Schiller, J.; Lerman, C. Spiral computed tomography and lung cancer: Science, the media, and public opinion. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2007, 25, 5695–5697. [Google Scholar] [CrossRef] [PubMed]
- Świderska, A. To See the Invisible—Industrial Computed Tomography. Raven Media Sp. z o.o, 01 February 2016. Available online: https://www.magazynprzemyslowy.pl/artykuly/zobaczyc-niewidzialne-przemyslowa-tomografia-komputerowa (accessed on 21 July 2021).
- DICOM. Digital Imaging and Communications in Medicine. Available online: https://www.dicomstandard.org/ (accessed on 15 January 2020).
- DICOM. 3D Slicer Documentation. Available online: https://slicer.readthedocs.io/en/latest/user_guide/modules/dicom.html (accessed on 21 July 2021).
- Zhang, Y.; Wu, L. Optimal Multi-Level Thresholding Based on Maximum Tsallis Entropy via an Artificial Bee Colony Approach. Entropy 2011, 13, 841–859. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146. [Google Scholar] [CrossRef]
- Broder, J. Diagnostic Imaging for the Emergency Physician; Elsevier: Philadelphia, PA, USA; Saunders: Philadelphia, PA, USA, 2011. [Google Scholar]
- De Vos, W.; Casselman, J.; Swennen, G.R.J. Cone-beam computerized tomography (CBCT) imaging of the oral and maxillofacial region: A systematic review of the literature. Int. J. Oral Maxillofac. Surg. 2009, 38, 609–625. [Google Scholar] [CrossRef]
- Hughes, J.F.; van Dam, A.; Morgan, M.; Sklar, D.F.; Foley, J.D.; Feiner, S.K.; Akeley, K. Computer Graphics: Principles and Practice, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2014. [Google Scholar]
- Roth, S.D. Ray casting for modeling solids. Comput. Graph. Image Process. 1982, 18, 109–144. [Google Scholar] [CrossRef]
- AZoM.com. Properties: Titanium Alloys—Ti6Al7Nb Properties and Applications. Available online: https://www.azom.com/properties.aspx?ArticleID=2064 (accessed on 21 July 2021).
- AUREMO. The Use of Titanium in Medicine. Available online: https://auremo.pl/reference/titan-v-mediczine.html (accessed on 21 July 2021).
- Supra Alloys. Titanium Metal: Titanium Medical Metal of Choice—Supra Alloys. Available online: http://www.supraalloys.com/medical-titanium.php (accessed on 21 July 2021).
- Froes, F.; Qian, M. Titanium in Medical and Dental Applications; Woodhead Publishing: Sawston, UK, 2018. [Google Scholar]
- Brunette, D.M.; Tengvall, P.; Textor, M.; Thomsen, P. Titanium in Medicine; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Wang, K. The use of titanium for medical applications in the USA. Mater. Sci. Eng. A 1996, 213, 134–137. [Google Scholar] [CrossRef]
- Ackland, D.C.; Moskaljuk, A.; Hart, C.; Vee Sin Lee, P.; Dimitroulis, G. Prosthesis loading after temporomandibular joint replacement surgery: A musculoskeletal modeling study. J. Biomech. Eng. 2015, 137, 41001. [Google Scholar] [CrossRef] [PubMed]
- May, B.; Saha, S.; Saltzman, M. A three-dimensional mathematical model of temporomandibular joint loading. Clin. Biomech. 2001, 16, 489–495. [Google Scholar] [CrossRef]
- Wagner, A.; Krach, W.; Schicho, K.; Undt, G.; Ploder, O.; Ewers, R. A 3-dimensional finite-element analysis investigating the biomechanical behavior of the mandible and plate osteosynthesis in cases of fractures of the condylar process. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endod. 2002, 94, 678–686. [Google Scholar] [CrossRef]
- Iwasaki, L.R.; Baird, B.W.; McCall, W.D.; Nickel, C.C. Muscle and temporomandibular joint forces associated with chincup loading predicted by numerical modeling. Am. J. Orthod. Dentofac. Orthop. 2003, 124, 530–540. [Google Scholar] [CrossRef]
- Mesnard, M.; Ramos, A.; Ballu, A.; Morlier, J.; Cid, M.; Simoes, J.A. Biomechanical analysis comparing natural and alloplastic temporomandibular joint replacement using a finite element model. J. Oral Maxillofac. Surg. Off. J. Am. Assoc. Oral Maxillofac. Surg. 2011, 69, 1008–1017. [Google Scholar] [CrossRef]
- Kobylarz, J.; Bird, J.J.; Faria, D.R.; Ribeiro, E.P.; Ekárt, A. Thumbs up, thumbs down: Non-verbal human-robot interaction through real-time EMG classification via inductive and supervised transductive transfer learning. J. Ambient Intell. Hum. Comput. 2020, 11, 6021–6031. [Google Scholar] [CrossRef]
- Kamen, G.; Gabriel, D.A. Essentials of Electromyography; Human Kinetics: Champaign, IL, USA, 2010. [Google Scholar]
- Chang, H.W.; Lin, H.H.; Chortrakarnkij, P.; Kim Sun, G.; Lo, L.J. Intraoperative navigation for single-splint two-jaw orthognathic surgery: From model to actual surgery. J. Cranio-Maxillo-Facial Surg. Off. Publ. Eur. Assoc. Cranio-Maxillo-Facial Surg. 2015, 43, 1119–1126. [Google Scholar] [CrossRef] [PubMed]
- BioPortal. Foundational Model of Anatomy. Available online: https://bioportal.bioontology.org/ontologies/FMA/?p=classes&conceptid=http%3A%2F%2Fpurl.org%2Fsig%2Font%2Ffma%2Ffma49450#mappings (accessed on 22 July 2021).
- Cheng, Y.; Leow, W.K.; Lim, T.C. Automatic identification of Frankfurt plane and mid-sagittal plane of skull. In Proceedings of the 2012 IEEE Workshop on the Applications of Computer Vision (WACV), Breckenridge, CO, USA, 9–11 January 2012. [Google Scholar]
- Abaqus Analysis User’s Guide. 2016. Available online: http://130.149.89.49/v2016/books/usb/default.htm (accessed on 21 July 2021).
- Motoyoshi, M.; Ueno, S.; Okazaki, K.; Shimizu, N. Bone stress for a mini-implant close to the roots of adjacent teeth—3D finite element analysis. Int. J. Oral Maxillofac. Surg. 2009, 2009, 363–368. [Google Scholar] [CrossRef]
- Gröning, F.; Fagan, M.; O’Higgins, P. Modeling the human mandible under masticatory loads: Which input variables are important? Anat. Rec. Adv. Integr. Anat. Evol. Biol. 2012, 2012, 853–863. [Google Scholar] [CrossRef]
- McCormack, S.W.; Witzel, U.; Watson, P.J.; Fagan, M.J.; Gröning, F. Inclusion of periodontal ligament fibres in mandibular finite element models leads to an increase in alveolar bone strains. PLoS ONE 2017, 12, e0188707. [Google Scholar] [CrossRef]
- Armentani, E.; Caputo, F.; Citarella, R. Fem sensitivity analyses on the stress levels in a human mandible with a varying atm modelling complexity. Open Mech. Eng. J. 2010, 4, 8–15. [Google Scholar] [CrossRef][Green Version]
- Citarella, R.; Armentani, E.; Caputo, F.; Naddeo, A. FEM and BEM analysis of a human mandible with added temporomandibular joints. Open Mech. Eng. J. 2012, 6, 100–114. [Google Scholar] [CrossRef]


| Structure | Young’s Modulus (MPa) | Poisson’s Ratio | Re (Compressive Strength) (MPa) |
|---|---|---|---|
| Compact bone | 14,700 | 0.3 | 159 |
| Dentin (tooth) | 14,700 | 0.3 | - |
| Spongy bone | 490 | 0.3 | 1.86 |
| Articular disc | 6.1 | 0.49 (0.46 in the analyses due to convergence) | - |
| Parameter | Ti-6Al-7Nb | Ti-Grade-4 |
|---|---|---|
| Tensile Strength MPa (ksi) sheet | 1000 (145) | 552 |
| 0.2% Proof Stress MPa (ksi) | 900 (130) | 483 |
| Elongation over 5D% | 12 | 15 |
| Reduction in Area % | 35 | 30 |
| Elastic Modulus GPa (Msi) | 105 (15) | 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mańkowski, J.; Piękoś, J.; Dominiak, K.; Klukowski, P.; Fotek, M.; Zawisza, M.; Żach, P. A Mandible with the Temporomandibular Joint—A New FEM Model Dedicated to Strength and Fatigue Calculations of Bonding Elements Used in Fracture and Defect Surgery. Materials 2021, 14, 5031. https://doi.org/10.3390/ma14175031
Mańkowski J, Piękoś J, Dominiak K, Klukowski P, Fotek M, Zawisza M, Żach P. A Mandible with the Temporomandibular Joint—A New FEM Model Dedicated to Strength and Fatigue Calculations of Bonding Elements Used in Fracture and Defect Surgery. Materials. 2021; 14(17):5031. https://doi.org/10.3390/ma14175031
Chicago/Turabian StyleMańkowski, Jarosław, Jakub Piękoś, Karol Dominiak, Piotr Klukowski, Michał Fotek, Maciej Zawisza, and Piotr Żach. 2021. "A Mandible with the Temporomandibular Joint—A New FEM Model Dedicated to Strength and Fatigue Calculations of Bonding Elements Used in Fracture and Defect Surgery" Materials 14, no. 17: 5031. https://doi.org/10.3390/ma14175031
APA StyleMańkowski, J., Piękoś, J., Dominiak, K., Klukowski, P., Fotek, M., Zawisza, M., & Żach, P. (2021). A Mandible with the Temporomandibular Joint—A New FEM Model Dedicated to Strength and Fatigue Calculations of Bonding Elements Used in Fracture and Defect Surgery. Materials, 14(17), 5031. https://doi.org/10.3390/ma14175031






