Numerical Simulation on Seismic Behavior of Steel Fiber Reinforced Concrete Beam—Column Joints
Abstract
1. Introduction
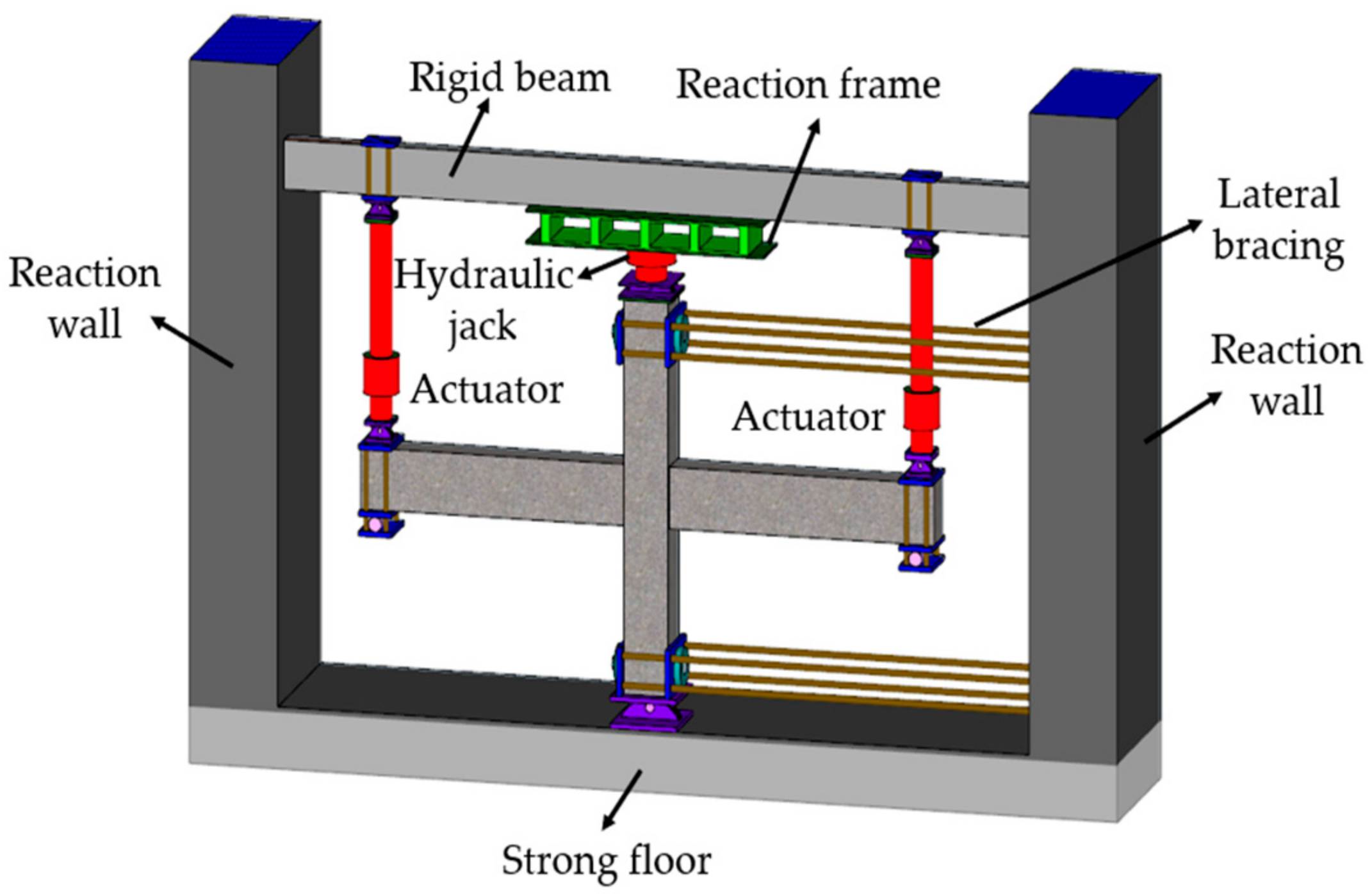
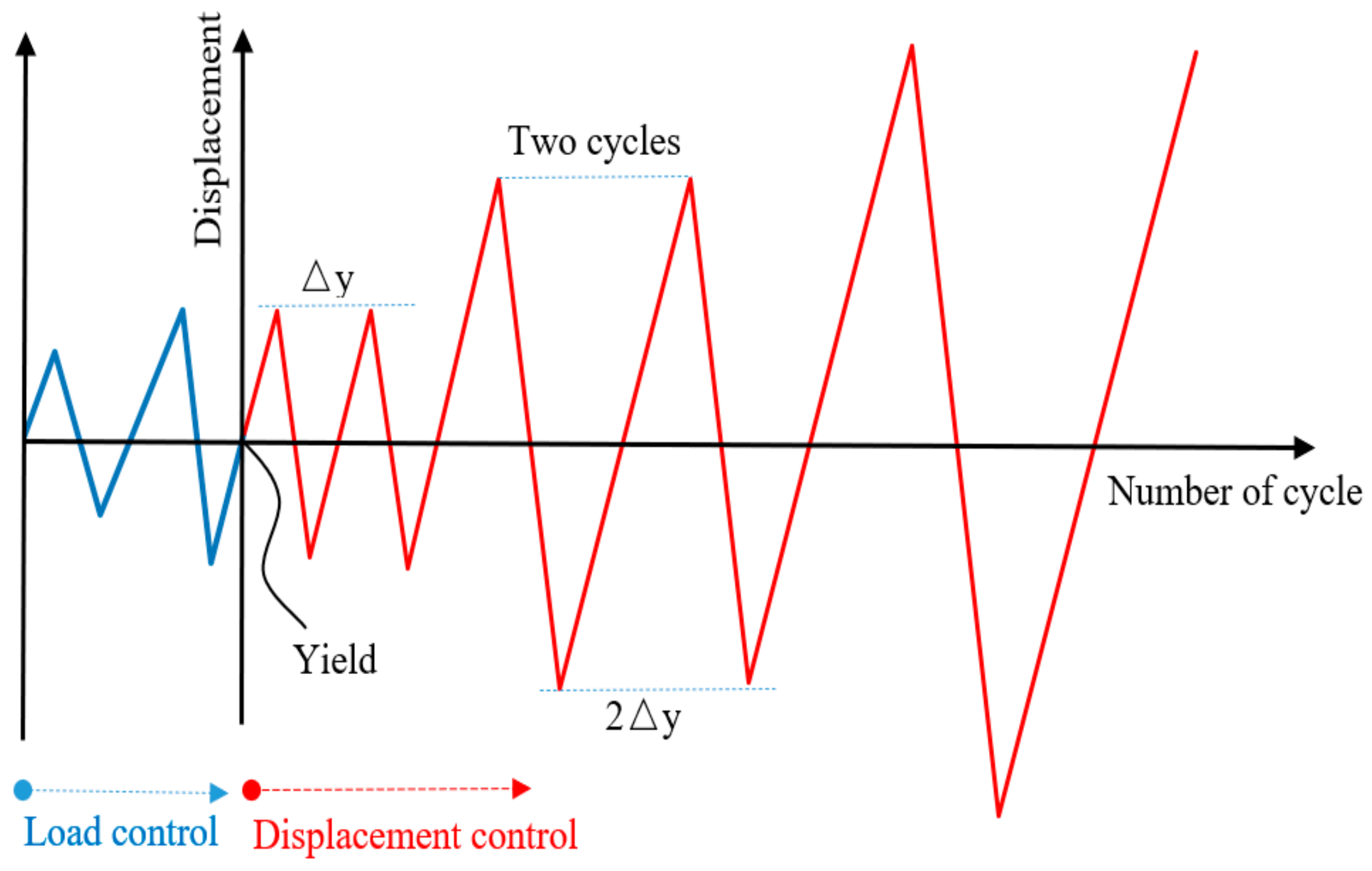
2. Experimental Introduction
3. Finite Element Model
3.1. Element Model
3.1.1. Nonlinear Fiber Beam–Column Element
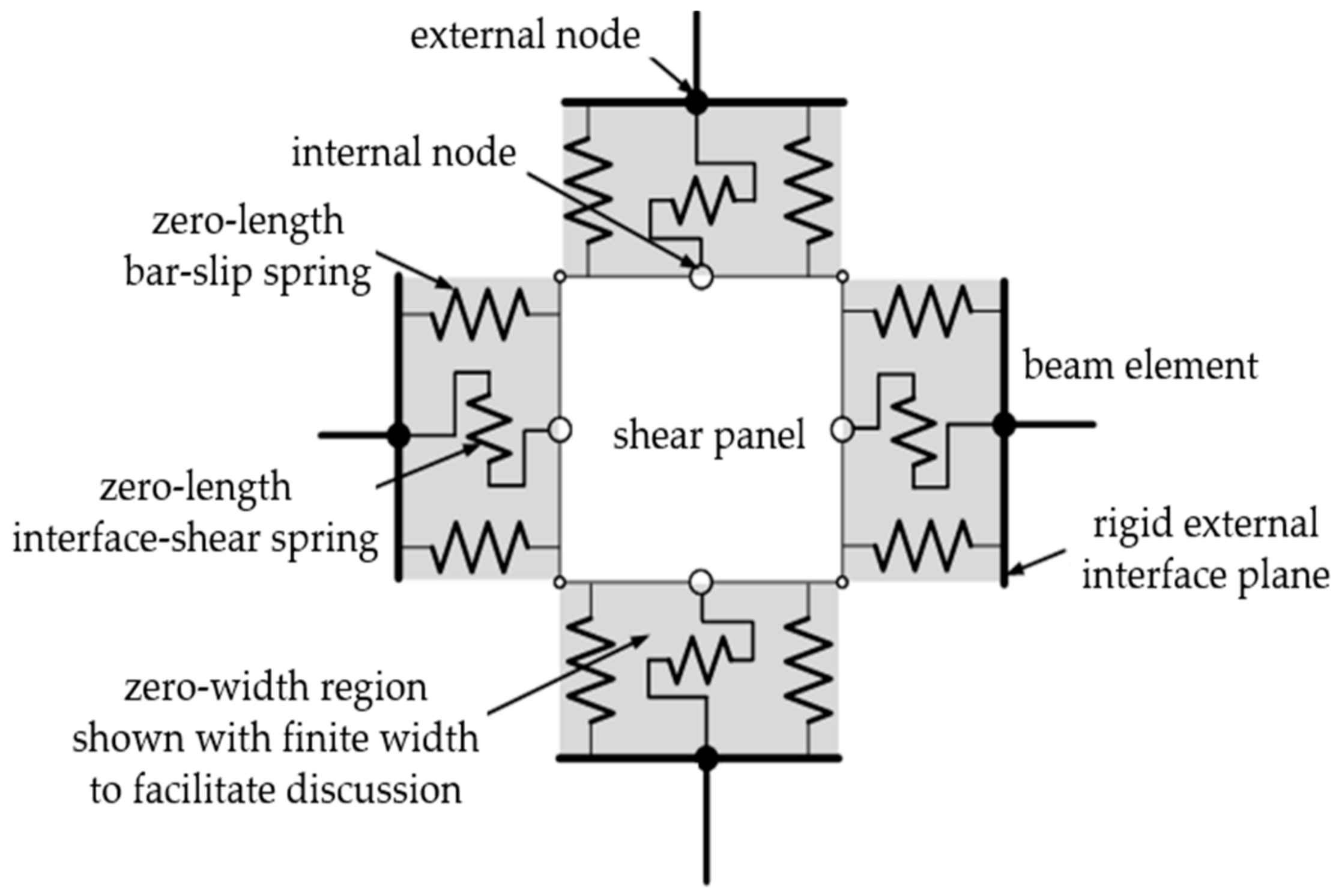
3.1.2. Beam–Column Joint Element
3.1.3. Constitutive Model of Concrete
3.1.4. Constitutive Model of Reinforcement
3.1.5. Analysis Module
3.2. Applicability Analysis of Beam–Column Joint Element Model
3.3. Improvement of Beam–Column Joint Element Mode
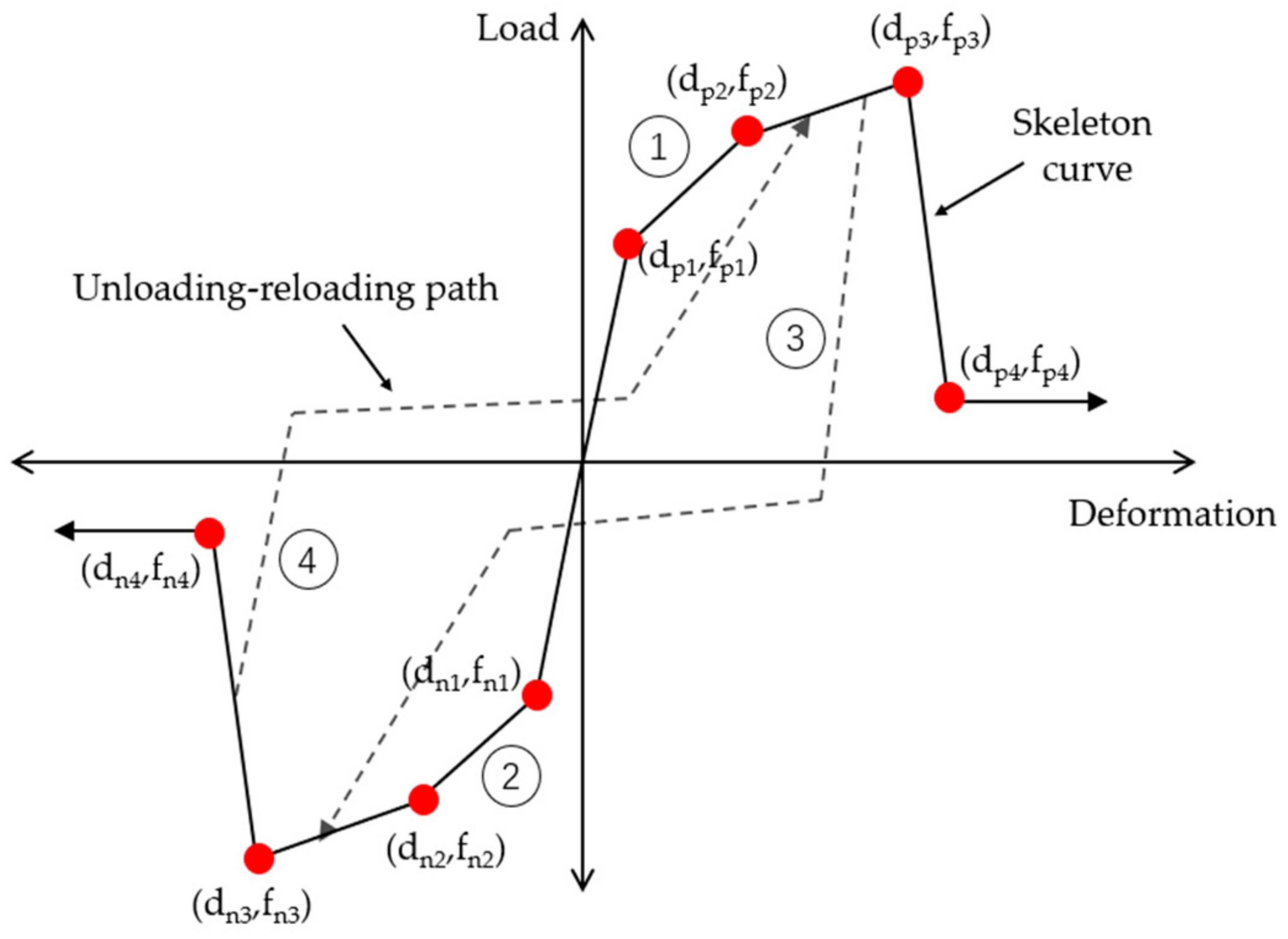
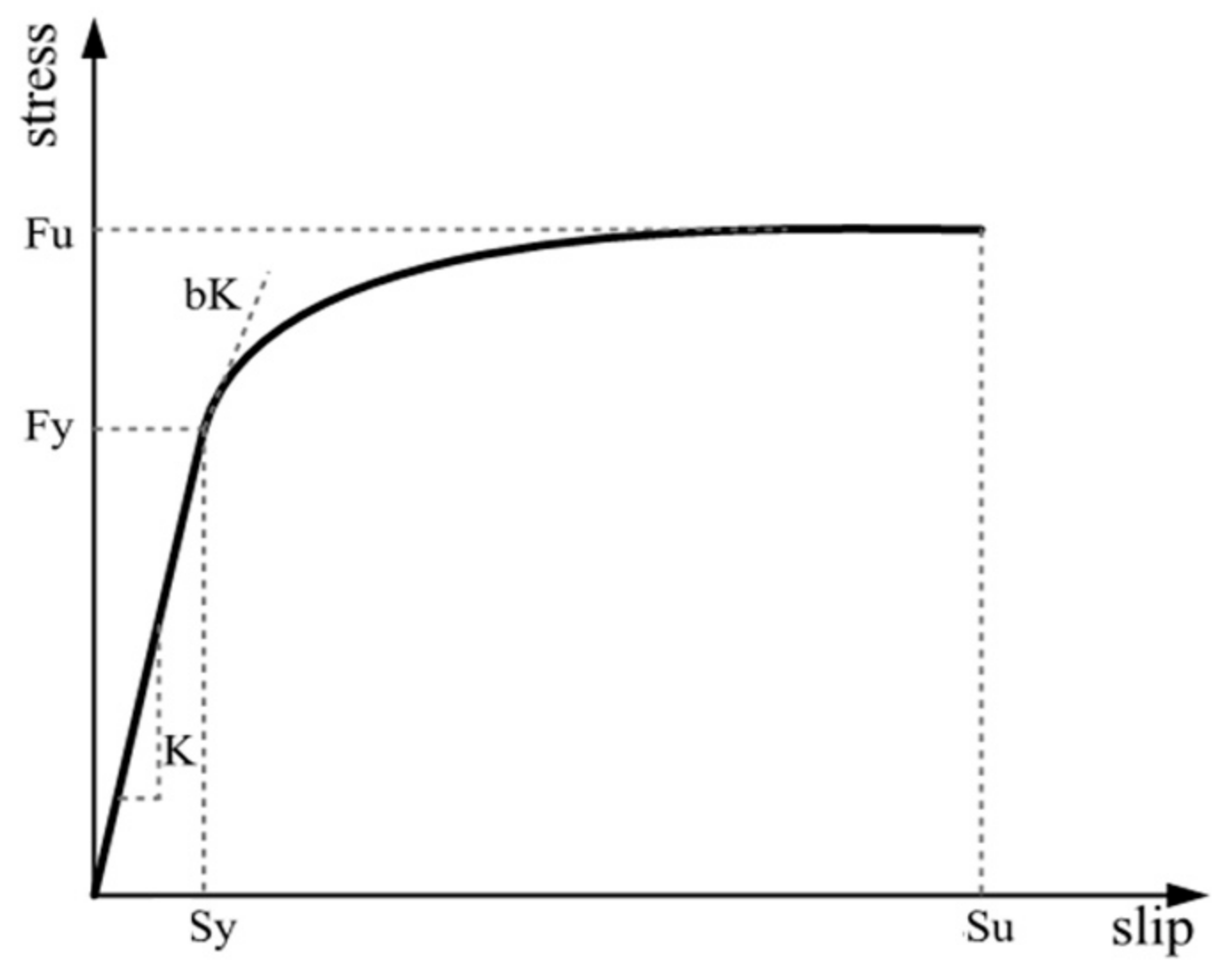
3.3.1. Constitutive Model of Reinforced Bond–Slip Spring
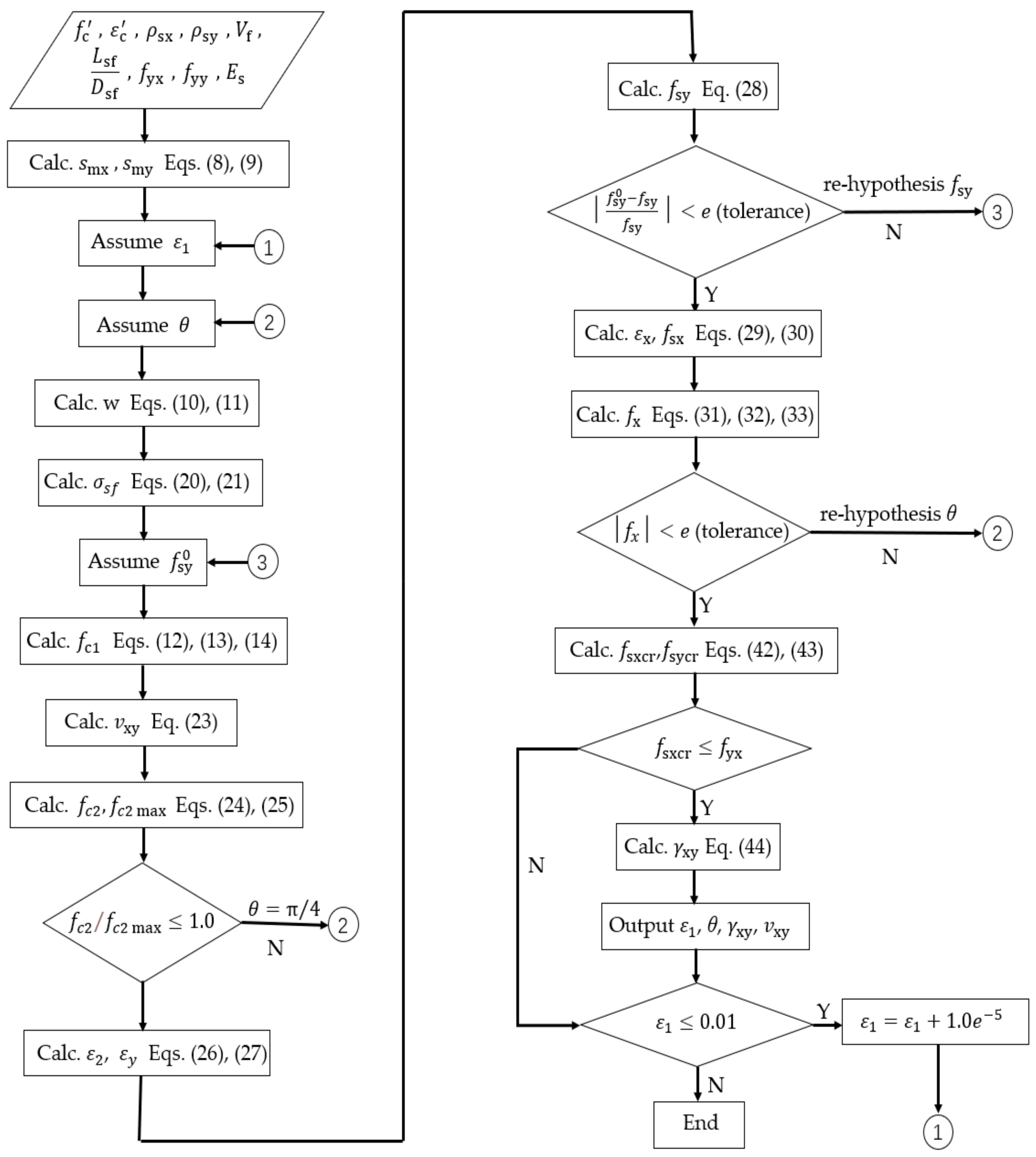
3.3.2. Constitutive Model of Joint Shear Block
4. Numerical Result Analysis
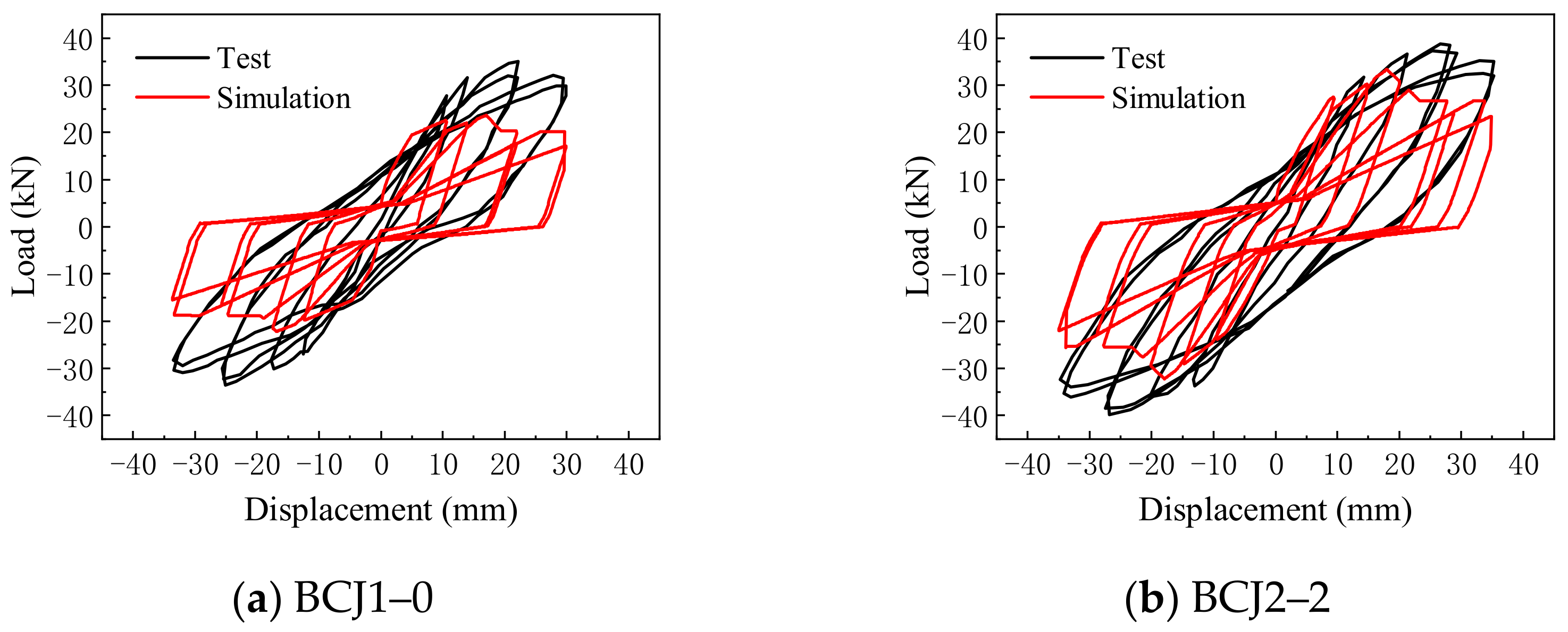
4.1. Hysteretic Curve
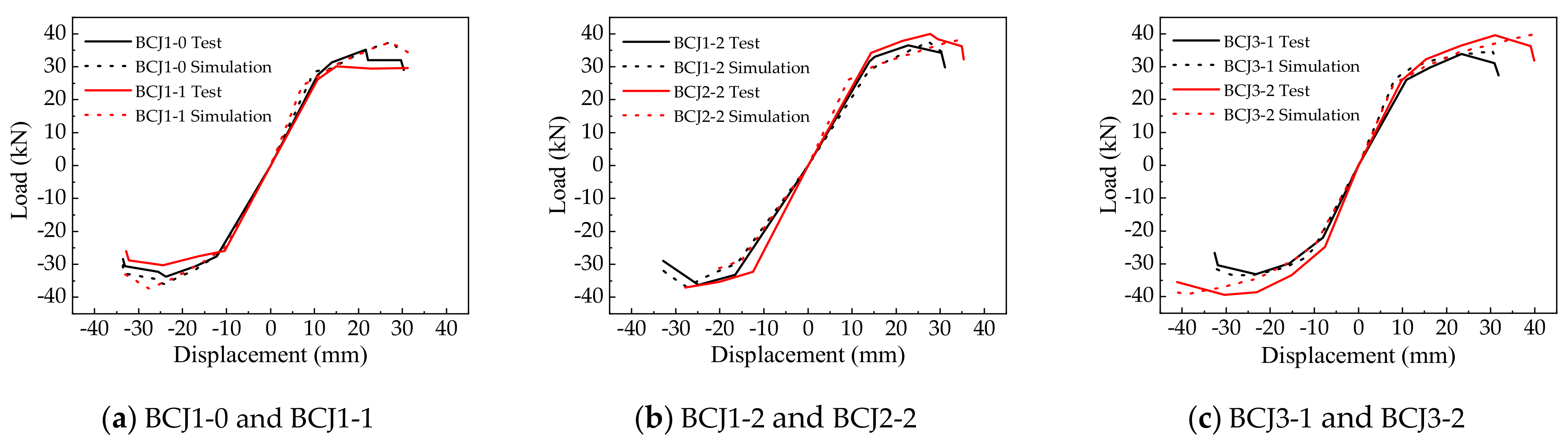
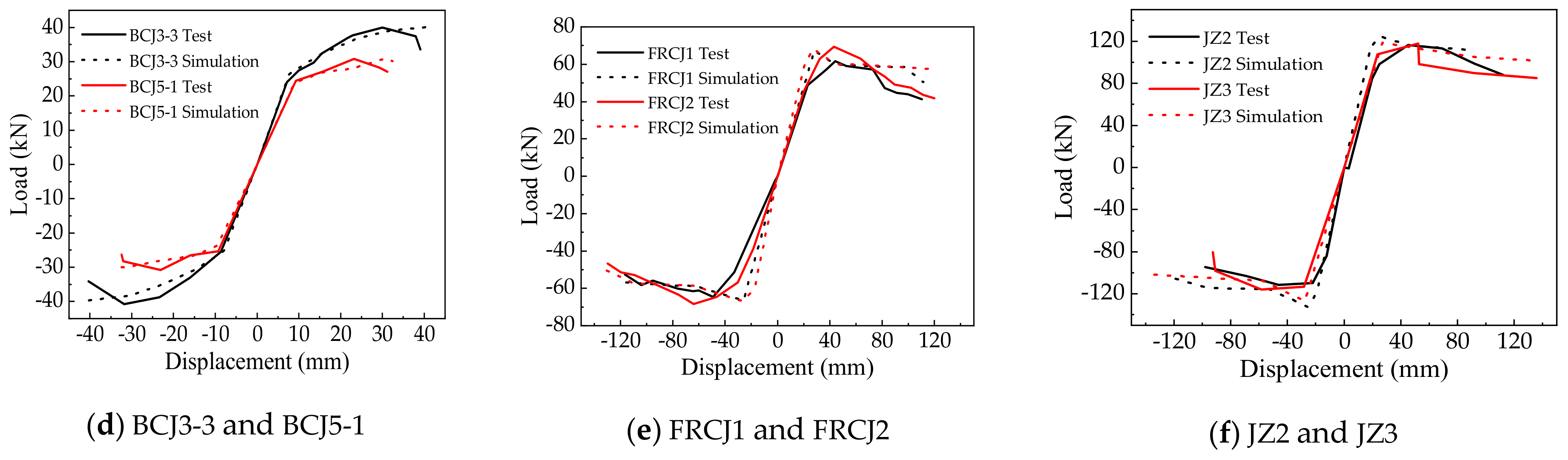
4.2. Skeleton Curve
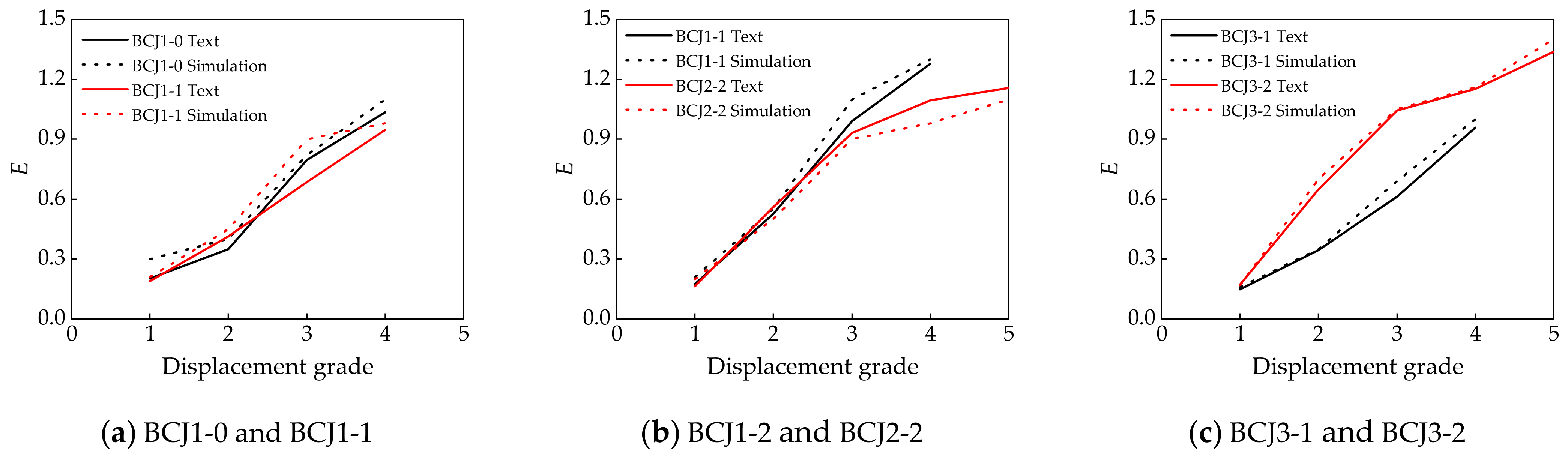
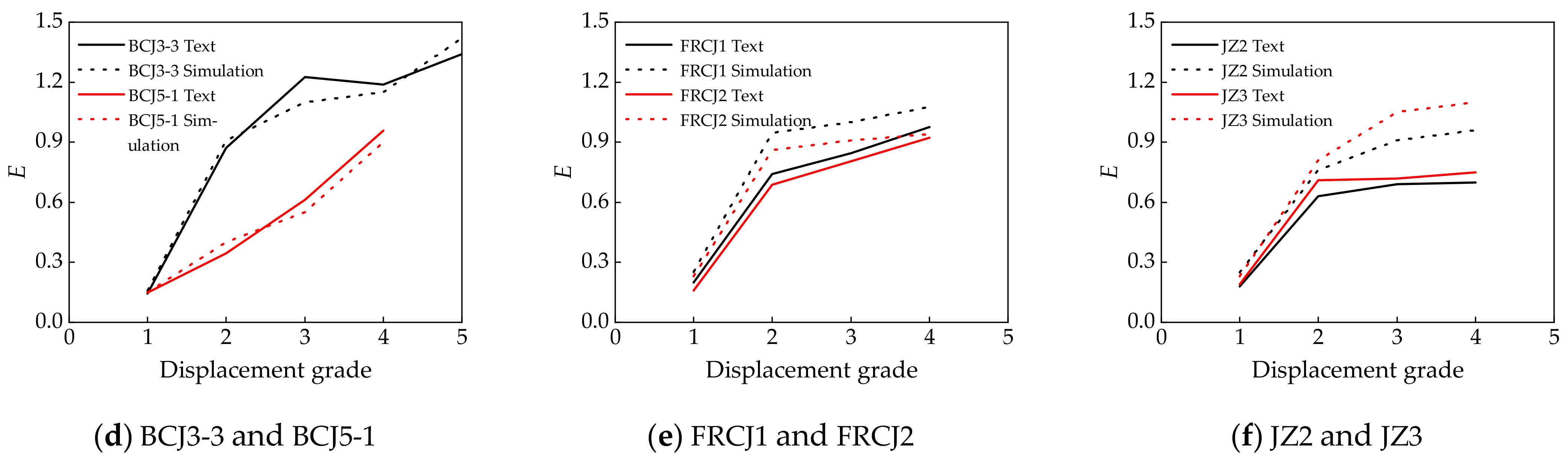
4.3. Energy Dissipation and Stiffness Degradation
5. Parameter Expansion Analysis
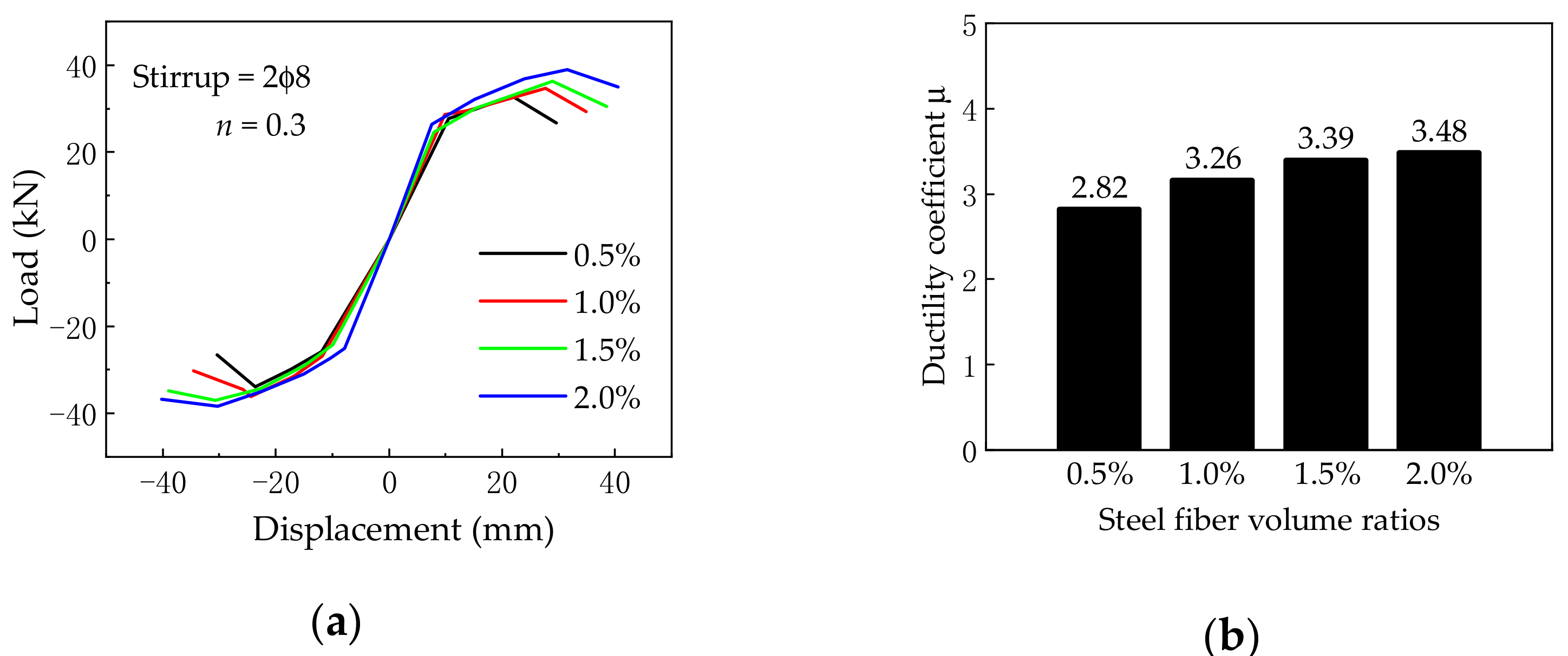
5.1. Steel Fiber Volume Ratio
5.2. Stirrup Amount of Joint Core Area
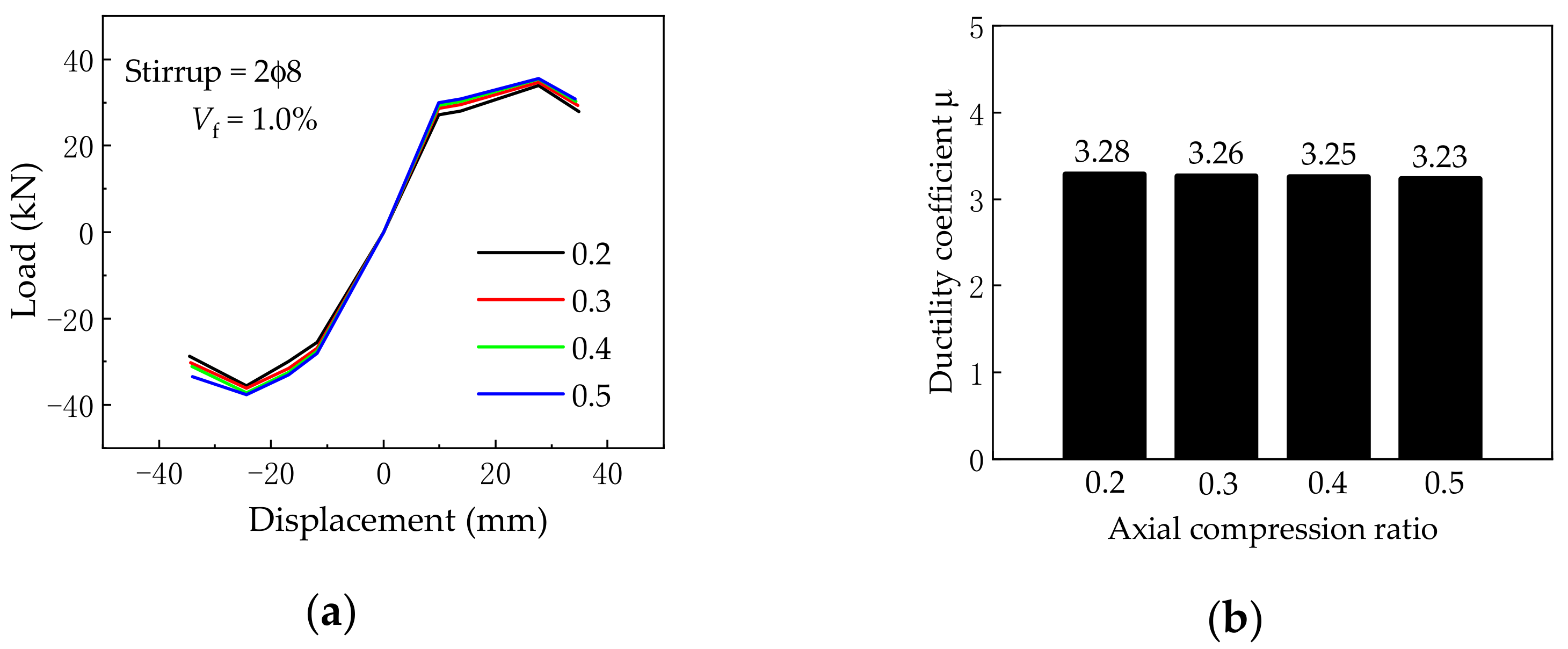
5.3. Axial Compression Ratio
6. Ultimate Shear Capacity of SFRC–BCJs
7. Conclusions
- A numerical simulation method on investigating the seismic behavior of SFRC–BCJs was proposed by modifying the calculation method of shear deformation in the core area of joint and bond–slip deformation of longitudinal reinforcement of beam. The numerical modeling approach can accurately reflect the development of SFRC–BCJs, and the numerical results agreed well with the experimental results.
- Adding the steel fiber volume ratio can effectively improve the seismic behavior of SFRC–BCJs, in terms of the initial stiffness, yield load, ultimate load, and ductility. Besides, increasing the stirrup amount contribute to enhance the yield load, ultimate load, and ductility. However, the axial compression ratio has no obvious influence on the seismic behavior of SFRC–BCJs.
- Based on the numerical simulation results, the formula for calculating the shear capacity of joints is established. Furthermore, the results show that the proposed formula can reflect the influence of steel fibers and stirrups, which is in good agreement with the numerical simulation results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsonos, A.G. Cyclic load behaviour of reinforced concrete beam–column subassemblages designed according to modern codes. WIT Trans. Built Environ. 2006, 3, 3–21. [Google Scholar]
- Tsonos, A.G. Cyclic Load Behavior of Reinforced Concrete Beam–Column Subassemblages of Modern Structures. ACI Struct. J. 2007, 104, 468–478. [Google Scholar]
- Kotsovou, G.; Mouzakis, H. Seismic behaviour of RC external joints. Mag. Concr. Res. 2011, 63, 247–264. [Google Scholar] [CrossRef]
- Kotsovou, G.; Mouzakis, H. Seismic design of RC external beam-column joints. Bull. Earthq. Eng. 2011, 10, 645–677. [Google Scholar] [CrossRef]
- Hong, Y. Elastoplastic earthquake response of structure considering slippage between longitudinal steel bar and concrete of beam in nodes. China Civ. Eng. J. 2004, 37, 16–22. [Google Scholar]
- Alath, S. Modeling Inelastic Shear Deformation in RC Beam-Column Joints. Master’s Thesis, University of Central Florida, Orlando, FL, USA, 1995. [Google Scholar]
- Biddah, A.; Ghobarah, A. Modelling of shear deformation and bond slip in reinforced concrete joints. Struct. Eng. Mech. 1999, 7, 413–432. [Google Scholar] [CrossRef]
- Fleury, F.; Reynouard, J.-M.; Merabet, O. Multicomponent Model of Reinforced Concrete Joints for Cyclic Loading. J. Eng. Mech. 2000, 126, 804–811. [Google Scholar] [CrossRef]
- Youssef, M.; Ghobarah, A. Modelling of Rc Beam-Column Joints and Structural Walls. J. Earthq. Eng. 2001, 5, 93–111. [Google Scholar] [CrossRef]
- Lowes, L.N.; Altoontash, A. Modeling Reinforced-Concrete Beam-Column Joints Subjected to Cyclic Loading. J. Struct. Eng. 2003, 12, 1686–1697. [Google Scholar] [CrossRef]
- Mitra, N.; Lowes, L.N. Evaluation, Calibration, and Verification of a Reinforced Concrete Beam–Column Joint Model. J. Struct. Eng. 2007, 133, 105–120. [Google Scholar] [CrossRef]
- Dizaj, E.A.; Madandoust, R.; Kashani, M.M. Exploring the impact of chloride-induced corrosion on seismic damage limit states and residual capacity of reinforced concrete structures. Struct. Infrastruct. Eng. 2017, 14, 714–729. [Google Scholar] [CrossRef]
- Santos, J.B.; Da Silva, T.J.; Alva, G. Influence of the stiffness of beam-column connections on the structural analysis of reinforced concrete buildings. Rev. Ibracon Estruturas Mater. 2018, 11, 834–855. [Google Scholar] [CrossRef]
- Adom-Asamoah, M.; Osei, J.B. A comparative seismic fragility analysis of a multi and single component beam-column joint models. Cogent Eng. 2018, 5, 1426204. [Google Scholar] [CrossRef]
- Bayhan, B.; Özdemir, G.; Gülkan, P. Impact of Joint Modeling Approach on Performance Estimates of Older-Type RC Buildings. Earthq. Spectra 2017, 33, 1101–1123. [Google Scholar] [CrossRef]
- Pan, Z.; Guner, S.; Vecchio, F.J. Modeling of interior beam-column joints for nonlinear analysis of reinforced concrete frames. Eng. Struct. 2017, 142, 182–191. [Google Scholar] [CrossRef][Green Version]
- Del Vecchio, C.; Di Ludovico, M.; Prota, A.; Manfredi, G. Modelling beam-column joints and FRP strengthening in the seismic performance assessment of RC existing frames. Compos. Struct. 2016, 142, 107–116. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Zhang, J.; Liu, Y. Bond Degradation–Induced Incompatible Strain between Steel Bars and Concrete in Corroded RC Beams. J. Perform. Constr. Facil. 2016, 30, 04016058. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation User Command-Language Manual; Pacific Earthquake Engineering Research Center: Berkley, CA, USA, 2009; pp. 33–236. [Google Scholar]
- Zhao, W.; Yang, H.; Fu, J.; Li, B. Calibration of beam-column joint element model and comparison of loading methods of beam-column subassemblages. J. Build. Struct. 2017, 38, 133–142. [Google Scholar]
- Shafaei, J.; Zareian, M.S.; Hosseini, A.; Marefat, M.S. Effects of joint flexibility on lateral response of reinforced concrete frames. Eng. Struct. 2014, 81, 412–431. [Google Scholar] [CrossRef]
- Tang, C.; Huang, C. Research on hysteretic performance of concrete frame with beam-column joint bonding–slip model. J. Railw. Sci. Eng. 2019, 16, 729–736. [Google Scholar]
- Xie, L.L.; Ye, X.G.; Chong, X.; Jiang, Q. Research and verification on joint model of RC frame structure in OpenSEES. Eng. Mech. 2014, 31, 116–121. [Google Scholar] [CrossRef]
- Shin, M.; Lafave, J.M. Testing and modeling for cyclic joint shear deformations in RC beam–column connections. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; pp. 1–15. [Google Scholar]
- Sumathi, A.; Mohan, K.S.R. Effect of Steel Fiber on Structural Characteristics of High-Strength Concrete. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 43, 117–130. [Google Scholar] [CrossRef]
- Choi, W.-C.; Jung, K.-Y.; Jang, S.-J.; Yun, H.-D. The Influence of Steel Fiber Tensile Strengths and Aspect Ratios on the Fracture Properties of High-Strength Concrete. Materials 2019, 12, 2105. [Google Scholar] [CrossRef] [PubMed]
- Conforti, A.; Zerbino, R.; Plizzari, G.A. Influence of steel, glass and polymer fibers on the cracking behavior of reinforced concrete beams under flexure. Struct. Concr. 2018, 20, 133–143. [Google Scholar] [CrossRef]
- Smarzewski, P. Effect of Curing Period on Properties of Steel and Polypropylene Fibre Reinforced Ultra-High Performance Concrete. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 032059. [Google Scholar] [CrossRef]
- Cuenca, E.; Ferrara, L. Self–healing capacity of fiber reinforced cementitious composites. State of the art and perspectives. KSCE J. Civ. Eng. 2017, 21, 2777–2789. [Google Scholar] [CrossRef]
- Gribniak, V.; Arnautov, A.K.; Norkus, A.; Kliukas, R.; Tamulenas, V.; Gudonis, E.; Sokolov, A.V. Steel fibers: Effective way to prevent failure of the concrete bonded with FRP sheets. Adv. Mater. Sci. Eng. 2016, 10, 4913536. [Google Scholar] [CrossRef]
- Gribniak, V.; Tamulenas, V.; Ng, P.-L.; Arnautov, A.K.; Gudonis, E.; Misiunaite, I. Mechanical Behavior of Steel Fiber-Reinforced Concrete Beams Bonded with External Carbon Fiber Sheets. Materials 2017, 10, 666. [Google Scholar] [CrossRef]
- Gribniak, V.; Ng, P.-L.; Tamulenas, V.; Misiūnaitė, I.; Norkus, A.; Šapalas, A. Strengthening of Fibre Reinforced Concrete Elements: Synergy of the Fibres and External Sheet. Sustainability 2019, 11, 4456. [Google Scholar] [CrossRef]
- Perceka, W.; Liao, W.-C.; Wang, Y.-D. High Strength Concrete Columns under Axial Compression Load: Hybrid Confinement Efficiency of High Strength Transverse Reinforcement and Steel Fibers. Materials 2016, 9, 264. [Google Scholar] [CrossRef]
- Song, W.; Yin, J. Hybrid Effect Evaluation of Steel Fiber and Carbon Fiber on the Performance of the Fiber Reinforced Concrete. Materials 2016, 9, 704. [Google Scholar] [CrossRef]
- Pazdera, L.; Cajka, R.; Topolář, L.; Mateckova, P.; Bilek, V.; Sucharda, O. Measurement and Utilization of Acoustic Emission for the Analysis and Monitoring of Concrete Slabs on the Subsoil. Period. Polytech. Civ. Eng. 2019, 63, 608–620. [Google Scholar] [CrossRef]
- Mures, J.K.; Chkheiwer, A.H.; Ahmed, M.A. Experimental Study on Torsional Behavior of steel Fiber Reinforced Concrete Members under Pure Torsion. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1090, 12065–12069. [Google Scholar] [CrossRef]
- Bencardino, F.; Nisticò, M.; Verre, S. Experimental Investigation and Numerical Analysis of Bond Behavior in SRG-Strengthened Masonry Prisms Using UHTSS and Stainless-Steel Fibers. Fibers 2020, 8, 8. [Google Scholar] [CrossRef]
- Martinelli, E.; Lima, C.; Pepe, M.; Caggiano, A.; Faella, C. Post-cracking response of hybrid recycled/industrial steel fiber-reinforced concrete. ACI Spec. Publ. 2018, 326, 1–10. [Google Scholar]
- Tsonos, A.G. Ultra-high-performance fiber reinforced concrete: An innovative solution for strengthening old R/C structures and for improving the FRP strengthening method. WIT Trans. Eng. Sci. 2009, 64, 273–284. [Google Scholar] [CrossRef]
- Leone, M.; Centonze, G.; Colonna, D.; Micelli, F.; Aiello, M.A. Fiber-reinforced concrete with low content of recycled steel fiber: Shear behavior. Constr. Build. Mater. 2018, 161, 141–155. [Google Scholar] [CrossRef]
- Li, C.; Zhao, M.; Zhang, X.; Li, J.; Li, X.; Zhao, M. Effect of Steel Fiber Content on Shear Behavior of Reinforced Expanded-Shale Lightweight Concrete Beams with Stirrups. Materials 2021, 14, 1107. [Google Scholar] [CrossRef]
- Tadepalli, P.R.; Mo, Y.L.; Hsu, T.T.C. Mechanical properties of steel fibre concrete. Mag. Concr. Res. 2013, 65, 462–474. [Google Scholar] [CrossRef]
- Yang, K.; He, Z.; Li, D.; Xu, H.; Kong, L. Experimental Study on Basalt Fiber Crack Resistance of Asphalt Concrete Based on Acoustic Emission. Materials 2021, 14, 4096. [Google Scholar] [CrossRef]
- Ganesan, N.; Indira, P.V.; Abraham, R. Steel fibre reinforced high performance concrete beam–column joints subjected to cyclic loading. ISET J. Earthq. Technol. 2007, 44, 445–456. [Google Scholar]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G.G.; Elenas, A. Effect of Steel Fibers on the Hysteretic Performance of Concrete Beams with Steel Reinforcement—Tests and Analysis. Materials 2020, 13, 2923. [Google Scholar] [CrossRef] [PubMed]
- Shannag, M.J.; Abu-Dyya, N.; Abu-Farsakh, G. Lateral load response of high performance fiber reinforced concrete beam–column joints. Constr. Build. Mater. 2005, 19, 500–508. [Google Scholar] [CrossRef]
- Shi, K. Seismic Behavior and Calculation Method of Steel Fiber Reinforced High–Strength Concrete Beam–Column Joints; Zhengzhou University: Zhengzhou, China, 2016. [Google Scholar]
- Scott, M.H.; Fenves, G.L. Plastic Hinge Integration Methods for Force-Based Beam–Column Elements. J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Feng, D.; Wang, Z.; Wu, G. Progressive collapse performance analysis of precast reinforced concrete structures. Struct. Des. Tall Spéc. Build. 2019, 28, e1588. [Google Scholar] [CrossRef]
- Feng, D.-C.; Wu, G.; Sun, Z.-Y.; Xu, J.-G. A flexure-shear Timoshenko fiber beam element based on softened damage-plasticity model. Eng. Struct. 2017, 140, 483–497. [Google Scholar] [CrossRef]
- Mazzoni, S.; Mckenna, F.; Fenves, G.L. OpenSees command language manual. Pac. Earthq. Eng. Res. (PEER) Center 2006, 264, 137–158. [Google Scholar]
- Song, M. Study on Modeling Method of Reinforced Concrete Beam–Column Joint; Chongqing University: Chongqing, China, 2009. [Google Scholar]
- Lin, Y.; Zhang, X. The slab effect of composite frames: From modified fiber modeling to seismic fragility assessment. J. Constr. Steel Res. 2021, 186, 106877. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.D.; Hong, W.-K.; Kim, J. Nonlinear finite element model for the novel mechanical beam-column joints of precast concrete-based frames. Comput. Struct. 2017, 189, 31–48. [Google Scholar] [CrossRef]
- B. D. Scott, Park, R.; Priestley, M.J.N. Stress-Strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. ACI J. Proc. 1982, 79. [Google Scholar] [CrossRef]
- Xin, Z.; Ai, Q.; Melina, B. Slotted Beam-Column Energy Dissipating Connections: Applicability and Seismic Behavior. Adv. Civ. Eng. 2021, 2021, 5530083. [Google Scholar] [CrossRef]
- Ma, H.; Xue, J.; Liu, Y.; Dong, J. Numerical analysis and horizontal bearing capacity of steel reinforced recycled concrete columns. Steel Compos. Struct. 2016, 22, 797–820. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded RC Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending; IABSE Symposium: Lisbon, Portugal, 1973. [Google Scholar]
- Mitra, N. An Analytical Study of Reinforced Concrete Beam-Column Joint Behavior under Seismic Loading; Citeseer: Pennsylvania, PA, USA, 2007; Volume 68. [Google Scholar]
- Harajli, M.H. Bond Behavior in Steel Fiber-Reinforced Concrete Zones under Static and Cyclic Loading: Experimental Evaluations and Analytical Modeling. J. Mater. Civ. Eng. 2010, 22, 674–686. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression–field theory for reinforced concrete elements subjected to shear. Aci. J. 1986, 83, 219–231. [Google Scholar]
- Feng, W.; Feng, H.; Zhou, Z.; Shi, X. Analysis of the Shear Capacity of Ultrahigh Performance Concrete Beams Based on the Modified Compression Field Theory. Adv. Mater. Sci. Eng. 2021, 2021, 5569733. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Zhang, R.J.; Huang, C.K. Sectional analysis of steel fiber reinforced concrete beams using modified compression field theory. Eng. Mech. 2008, 25, 144–150. [Google Scholar]
- Gao, D.; Shi, K. Calculation method for shear behavior of steel fiber reinforced concrete beam–column joints based on modified compression field theory. China Civ. Eng. J. 2016, 36, 82–89. [Google Scholar] [CrossRef]
- Stevens, N.J.; Uzumeri, S.M.; Collins, P.M.; Will, G.T. Constitutive Model for Reinforced Concrete Finite Element Analysis. Struct. J. 1991, 88, 49–59. [Google Scholar]
- Liang, X.-W.; Wang, Y.-J.; Tao, Y.; Deng, M.-K. Seismic performance of fiber-reinforced concrete interior beam-column joints. Eng. Struct. 2016, 126, 432–445. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Rong, X.; Ding, C. Experimental Research on Seismic Behavior of High Strength Bar Concrete Beam-Column Joints Reinforced by Steel Fiber. J. Northeast. Univ. Nat. Sci. 2020, 41, 1465. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, X. Principle and Analysis of Reinforced Concrete; Tsinghua University: Beijing, China, 2003. [Google Scholar]
- Zhao, G. Advanced Theory for Reinforced Concrete Structures; Machine Industry Press: Beijing, China, 2005. [Google Scholar]
- Jiang, Y.; Wei, L.; Xu, J.; Lu, Z. Experimental study on the performance of steel fiber high-strength concrete frame joints. J. Southeast Univ. 1991, 2, 72–79. [Google Scholar]
- Jra, B.; Ksa, B.; Nik, C.; Kib, D.; Sm, E. Data–driven shear strength prediction of steel fiber reinforced concrete beams using machine learning approach. Eng. Struct. 2021, 233, 111743. [Google Scholar] [CrossRef]
- Shi, M. The Performance and Calculation Method on the Compression and Splitting Tension of Concrete Reinforced by the Steel Fibers with Hooked–End; Zhengzhou University: Zhengzhou, China, 2020. [Google Scholar]
- Zhou, L.; Liu, H.T. Calculation Method of Flexural Bearing Capacity of Carbon Fiber Reinforced Concrete Beam. Appl. Mech. Mater. 2011, 71–78, 5080–5083. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M. Seismic design of reinforced concrete and masonry buildings. In Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Ghomi, S.; El–Salakawy, E.F. Effect of geometrical configuration on seismic behavior of GFRP-RC beam-column joints. Adv. Concr. Constr. 2020, 9, 313–326. [Google Scholar] [CrossRef]
- Jiuru, T.; Chaobin, H.; Kaijian, Y.; Yongcheng, Y. Seismic Behavior and Shear Strength of Framed Joint Using Steel-Fiber Reinforced Concrete. J. Struct. Eng. 1992, 118, 341–358. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, T. Study on seismic behavior of steel fiber reinforced concrete frame joints. J. Archit. Struct. 1989, 10, 35–45. [Google Scholar]
- Filiatrault, A.; Ladicani, K.; Massicotte, B. Seismic performance of code–designed fiber reinforced concrete joints. Aci Mater. J. 1994, 91, 564–571. [Google Scholar]









| Category | d (mm) | fy (MPa) | fu (MPa) | δ (%) | Es (MPa) |
|---|---|---|---|---|---|
| HRB335 | 22 | 418.2 | 652.1 | 27 | 1.95 × 105 |
| HRB335 | 16 | 360.5 | 594.9 | 23 | 2.01 × 105 |
| HPB235 | 8 | 306.9 | 472.7 | 30 | 2.09 × 105 |
| Joint Number | Concrete Strength (Mpa) | Volume Ratio of Steel Fiber Vf (%) | Axial Compression Ratio n | Core Area Hoop Reinforcement | Cubic Compressive Strength (MPa) | Split Tensile Strength (MPa) | Elasticity Modulus (MPa) |
|---|---|---|---|---|---|---|---|
| BCJ1–0 | CF60 | 1.0 | 0.3 | 0 | 81.7 | 7.3 | 45,300 |
| BCJ1–1 | CF60 | 1.0 | 0.2 | 0 | 79.1 | 7.4 | 43,700 |
| BCJ1–2 | CF60 | 1.0 | 0.4 | 0 | 78.1 | 7.3 | 44,400 |
| BCJ2–2 | CF80 | 1.0 | 0.3 | 2ϕ8 | 89.5 | 7.1 | 44,500 |
| BCJ3–1 | CF60 | 0.5 | 0.3 | 2ϕ8 | 82.1 | 7.5 | 46,600 |
| BCJ3–2 | CF60 | 1.5 | 0.3 | 0 | 86.6 | 8.9 | 40,900 |
| BCJ3–3 | CF60 | 2.0 | 0.3 | 0 | 87.4 | 9.1 | 44,100 |
| BCJ5–1 | C60 | 0 | 0.3 | 5ϕ8 | 68.6 | 4.9 | 42,500 |
| Number | Water (L) | Cement (kg) | Sand (kg) | Stone (kg) | Steel Fiber (kg) | Superplasticizer (kg) |
|---|---|---|---|---|---|---|
| BCJ1–0 | 164 | 547 | 696 | 1044 | 78 | 8.2 |
| BCJ1–1 | 164 | 547 | 696 | 1044 | 78 | 8.2 |
| BCJ1–2 | 164 | 547 | 696 | 1044 | 78 | 8.2 |
| BCJ2–2 | 164 | 547 | 696 | 1044 | 78 | 8.2 |
| BCJ3–1 | 156 | 520 | 710 | 1065 | 39 | 7.8 |
| BCJ3–2 | 172 | 573 | 682 | 1023 | 117 | 8.6 |
| BCJ3–3 | 181 | 599 | 668 | 1001 | 156 | 8.9 |
| BCJ5–1 | 146 | 487 | 623 | 1210 | 0 | 7.3 |
| Component | Py (kN) | Pm (kN) | Pu (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T | S | T/S | T | S | T/S | T | S | T/S | |
| BCJ1–0 | 27.49 | 28.55 | 0.96 | 35.20 | 37.65 | 0.93 | 32.08 | 33.41 | 0.96 |
| BCJ1–1 | 26.18 | 24.32 | 1.08 | 34.12 | 37.37 | 0.91 | 30.63 | 33.42 | 0.92 |
| BCJ1–2 | 31.64 | 29.01 | 1.09 | 36.45 | 37.51 | 0.97 | 29.88 | 32.08 | 0.93 |
| BCJ2–2 | 32.29 | 29.99 | 1.08 | 39.95 | 37.66 | 1.06 | 33.22 | 35.10 | 0.95 |
| BCJ3–1 | 26.01 | 26.29 | 0.99 | 33.86 | 34.58 | 0.98 | 29.41 | 30.75 | 0.96 |
| BCJ3–2 | 25.74 | 24.65 | 1.04 | 39.27 | 39.60 | 0.99 | 33.87 | 36.90 | 0.92 |
| BCJ3–3 | 27.50 | 26.38 | 1.04 | 40.00 | 39.00 | 1.03 | 33.57 | 36.02 | 0.93 |
| BCJ5–1 | 24.41 | 23.83 | 1.02 | 30.76 | 30.75 | 1.00 | 28.12 | 30.16 | 0.93 |
| Average | 1.04 | 0.98 | 0.94 | ||||||
| COV | 0.0020 | 0.0022 | 0.0002 | ||||||
| Joint Number | Vjt (kN) | Vjc (kN) | Vjt/Vjc |
|---|---|---|---|
| SF–7 [76] | 398.6 | 393.561 | 1.013 |
| SF–8 [76] | 456.6 | 486.258 | 0.939 |
| J3–3 [77] | 467.7 | 454.363 | 1.029 |
| J3–4 [77] | 456.0 | 503.451 | 0.906 |
| S3 [78] | 1375.5 | 1238.093 | 1.111 |
| SF–2 [70] | 1087.5 | 980.296 | 1.109 |
| S6 [46] | 34.1 | 38.647 | 0.882 |
| BCJ1–0 | 348.4 | 359.264 | 0.970 |
| BCJ1–1 | 330.9 | 344.214 | 0.961 |
| BCJ1–2 | 360.5 | 347.004 | 1.039 |
| BCJ2–2 | 384.3 | 385.718 | 0.996 |
| BCJ3–1 | 328.1 | 404.009 | 0.812 |
| BCJ3–2 | 375.9 | 323.254 | 1.163 |
| BCJ3–3 | 390.0 | 370.185 | 1.054 |
| BCJ5–1 | 347.6 | 360.635 | 0.964 |
| Average | 0.997 | ||
| COV | 0.094 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Zhu, J.; Li, P.; Zhang, M.; Xue, R.; Zhang, T. Numerical Simulation on Seismic Behavior of Steel Fiber Reinforced Concrete Beam—Column Joints. Materials 2021, 14, 4883. https://doi.org/10.3390/ma14174883
Shi K, Zhu J, Li P, Zhang M, Xue R, Zhang T. Numerical Simulation on Seismic Behavior of Steel Fiber Reinforced Concrete Beam—Column Joints. Materials. 2021; 14(17):4883. https://doi.org/10.3390/ma14174883
Chicago/Turabian StyleShi, Ke, Junpeng Zhu, Pengfei Li, Mengyue Zhang, Ru Xue, and Tao Zhang. 2021. "Numerical Simulation on Seismic Behavior of Steel Fiber Reinforced Concrete Beam—Column Joints" Materials 14, no. 17: 4883. https://doi.org/10.3390/ma14174883
APA StyleShi, K., Zhu, J., Li, P., Zhang, M., Xue, R., & Zhang, T. (2021). Numerical Simulation on Seismic Behavior of Steel Fiber Reinforced Concrete Beam—Column Joints. Materials, 14(17), 4883. https://doi.org/10.3390/ma14174883






