Investigation of Damage Evolution in Heterogeneous Rock Based on the Grain-Based Finite-Discrete Element Model
Abstract
:1. Introduction
2. Basic Principles of FDEM
3. FDEM Simulation of Acoustic Emission
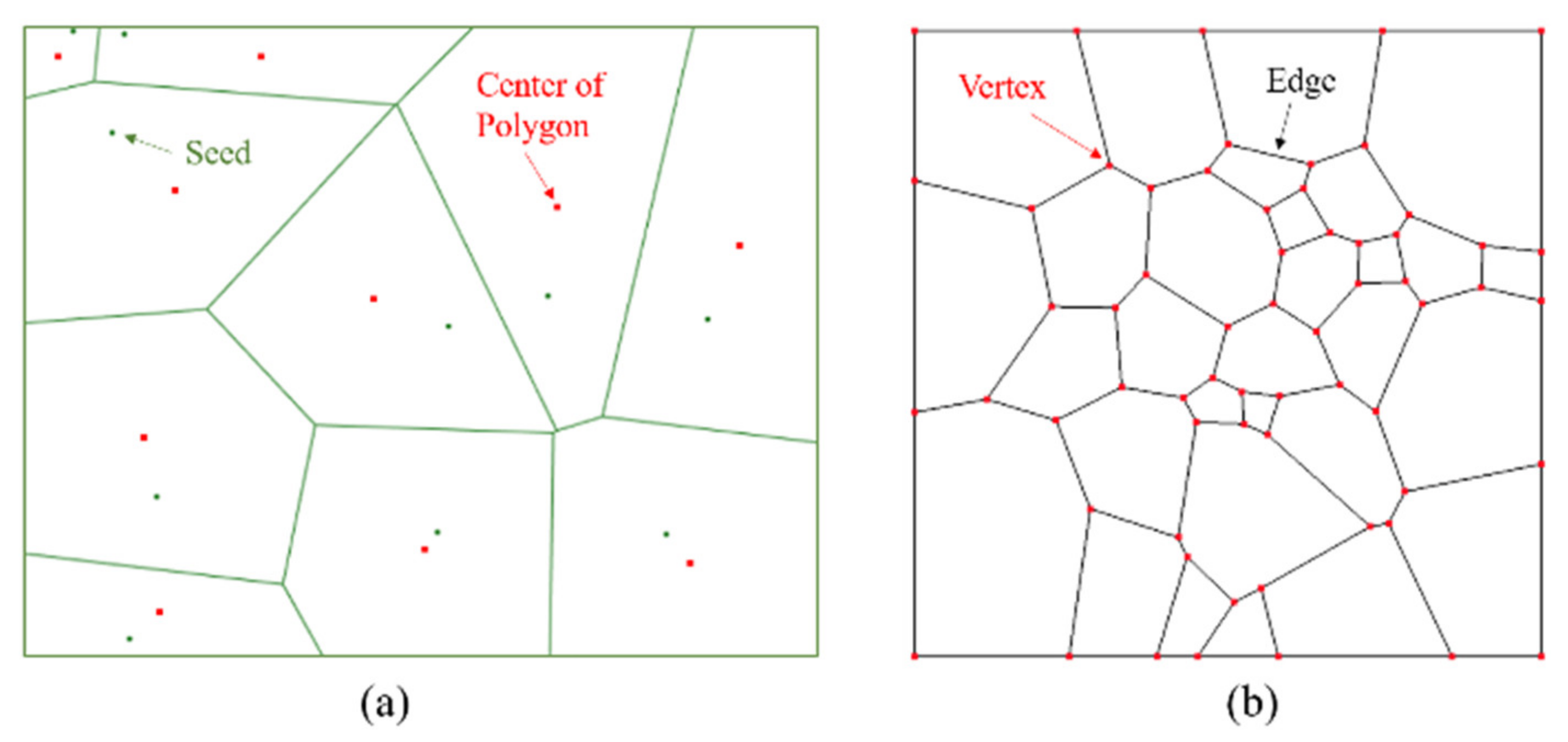
4. Numerical Grain-Based Model
5. Mesoscopic Parameter Verification of Grain-based Model
6. Analysis of the Effect of Meso-Heterogeneity on the Mechanical Properties
6.1. Effect of the Grain Size
6.2. Effect of the Preferred Grain Orientation
7. Conclusions
- The FDEM-GBM considers the complexity of the contacts between different mineral grains in the rock and the physical and mechanical properties of different mineral phases; therefore, the FDEM-GBM has the ability to simulate the effect of the grain size in heterogeneous rocks.
- Because the mineral grain has significant influence on the crack propagation paths, the FDEM-GBM can capture the location of fractures more accurately than the conventional models. Shear cracks occur near the loading area, while tensile and tensile-shear mixed cracks occur far from the loading area. The applied stress must overcome the tensile strength of the intergrain contact.
- The UTS and the ratio of the number of intergrain tensile cracks to the number of intragrain tensile cracks are negatively correlated with the grain size. During the whole process of splitting simulation, shear microcracks play the dominant role in energy release; particularly, they occur in later stage. Under different grain sizes conditions, the crack growth paths are significantly different. The larger the grain size is, the more complicated the crack propagation path. When the grain sizes are 1.5 and 2 mm, the fracture sections are smoother and straighter.
- With the increase of preferred grain orientation, the UTS presents a “V-shaped” characteristic distribution. During the whole process of splitting simulation, shear microcracks play the dominant role in energy release; particularly, they occur in later stage. Under different preferred grain orientation conditions, the crack growth paths are significantly different, especially 30°, 45° and 60°. When the preferred orientations are 30°, 45° and 60°, the fracture sections are more complicated.
- The preferred grain orientation considerably influences the energy storage capacity of Beishan granite. With the increase of grain orientation, the energy storage capacity decreases significantly. The greater the UTS is, the higher the energy storage capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuang, Z.H.; Qiu, S.L.; Li, S.J.; Du, S.H.; Huang, Y.; Chen, X.Q. A new rock brittleness index based on the characteristics of complete stress–strain behaviors. Rock Mech. Rock Eng. 2021, 54, 1109–1128. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Xue, R.X.; Xu, N.W.; Linlu Dong, L.L.; Zhang, Y.H. Analysis on microseismic characteristics and stability of the access tunnel in the main powerhouse, Shuangjiangkou hydropower station, under high in situ stress. B. Eng. Geol. Environ. 2020, 79, 3231–3244. [Google Scholar] [CrossRef]
- Wang, Z.H.; Su, T.; Konietzky, H.; Tan, Y.L.; Zhou, G.L. Hydraulic properties of Beishan granite after different high temperature treatments. B. Eng. Geol. Environ. 2021, 80, 2911–2923. [Google Scholar] [CrossRef]
- Read, R. 20 Years of Excavation Response Studies at Aecl’s Underground Research Laboratory. Int. J. Rock Mech. Min. Sci. 2004, 41, 1251–1275. [Google Scholar] [CrossRef]
- Yilmaz, N.G.; Goktan, R.M.; Kibici, Y. Relations between some quantitative petrographic characteristics and mechanical strength properties of granitic building stones. Int. J. Rock Mech. Min. Sci. 2011, 48, 506–513. [Google Scholar] [CrossRef]
- Tapponnier, P.; Brace, W.F. Development of stress-induced microcracks in Westerly Granite. Int. J. Rock Mech. Min. Sci. 1976, 13, 103–112. [Google Scholar] [CrossRef]
- Onodera, T.F.; Kamura, A.H.M. Relation between texture and mechanical properties of crystalline rocks. Bull. Int. Assoc. Eng. Geol. 1980, 22, 173–177. [Google Scholar]
- Ghazvinian, E.; Diederichs, M.S.; Labrie, D.; Martin, C.D. An investigation on the fabric type dependency of the crack damage thresholds in brittle rocks. Geotech. Geol. Eng. 2015, 33, 1409–1429. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive large-scale movements in blocky rock systems. Proc. Int. Symp. Rock Fract. 1971, 1, 11–18. [Google Scholar]
- Munjiza, A.; Owen, D.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Tech, C.I. Influence of grain size on strength of polymineralic crystalline rock: New insights from DEM grain-based modeling. J. Rock Mech. Geotech. Eng. 2021. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Zhao, J. Transgranular fracturing of crystalline rocks and its influence on rock strengths: Insights from a grain-scale continuum-discontinuum approach. Comput. Method. Appl. M. 2021, 373, 113462. [Google Scholar] [CrossRef]
- Pan, C.; Li, X.; He, L.; Li, J.C. Study on the effect of micro-geometric heterogeneity on mechanical properties of brittle rock using a grain-based discrete element method coupling with the cohesive zone model. Int. J. Rock Mech. Min. Sci. 2021, 140, 104680. [Google Scholar] [CrossRef]
- Lisjak, A.; Mahabadi, O.; He, L. Acceleration of a 2d/3d finite-discrete element code for geomechanical simulations using general purpose GPU computing. Comput. Geotech. 2018, 100, 84–96. [Google Scholar] [CrossRef]
- Zhao, X.G.; Ma, L.; Su, R. Fracture evolution and strength characteristics of Beishan deep granite under compression conditions. Chin. J. Rock Mech. Eng. 2014, 33, 3665–3675. [Google Scholar]
- Liu, Q.; Deng, P.H. Numerical study of rock fragmentation process and acoustic emission by FDEM based on heterogeneous model. Math. Probl. Eng. 2020. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P. Simulating acoustic emissions in bonded-particle models of rock. Int. J. Rock Mech. Min. Sci. 2000, 37, 867–872. [Google Scholar] [CrossRef]
- Lisjak, A.; Liu, Q.; Zhao, Q.; Mahabadi, O.K.; Grasselli, G. Numerical simulation of acoustic emission in brittle rocks by two-dimensional finite-discrete element analysis. Geophys. J. Int. 2013, 195, 423–443. [Google Scholar] [CrossRef] [Green Version]
- Gutenberg, B. The energy of earthquakes. J. Geol. Soc. 1956, 112, 1–14. [Google Scholar] [CrossRef]
- Miao, S.T.; Pan, P.Z.; Zhao, X. Experimental study on damage and fracture characteristics of Beishan granite subjected to high-temperature treatment with DIC and AE techniques. Rock Mech. Rock Eng. 2021, 54, 721–743. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.; Barbe, F. Large-scale 3d random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl Mech Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef] [Green Version]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Zhao, Q.; Grasselli, G. Grain based modelling of rocks using the combined finite-discrete element method. Comput. Geotech. 2018, 103, 75–81. [Google Scholar] [CrossRef]
- Mahabadi, O. Investigating the Influence of Micro-Scale Heterogeneity and Micro-Structure on the Failure and Mechanical Behaviour of Geomaterials. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Zhao, Q.; Tisato, N.; Grasselli, G. Influence of in situ stress variations on acoustic emissions: A numerical study. Geophys. J. Int. 2015, 203, 1246–1252. [Google Scholar] [CrossRef] [Green Version]
- Tatone, B.S.A.; Grasselli, G. A calibration procedure for two-dimensional laboratory-scale hybrid finite-discrete element simulations. Int. J. Rock Mech. Min. Sci. 2015, 75, 56–72. [Google Scholar] [CrossRef]
- Liu, J.F.; Chen, L.; Wang, C.P.; Man, K.; Wang, L.; Wang, J.; Su, R. Characterizing the mechanical tensile behavior of Beishan granite with different experimental methods. Int. J. Rock Mech. Min. Sci. 2014, 69, 50–58. [Google Scholar] [CrossRef]
- Howarth, D.F.; Rowlands, J.C. Quantitative assessment of rock texture and correlation with drillability and strength properties. Rock Mech. Rock Eng. 1987, 20, 57–85. [Google Scholar] [CrossRef]
- Prikryl, R. Some microstructural aspects of strength variation in rocks. Int. J. Rock Mech. Min. Sci. 2001, 38, 671–682. [Google Scholar] [CrossRef]
- Olsson, W.A. Grain size dependence of yield stress in marble. J. Geophys. Res. 1974, 79, 4859–4862. [Google Scholar] [CrossRef]
- Deng, C.F.; Liu, J.F.; Chen, L. Fracture mechanical behaviors and acoustic emission characteristics of Beishan granites with different particle sizes. Rock Soil Mech. 2016, 37, 2507–2514. (In Chinese) [Google Scholar]
- Cowie, S.; Walton, G. The effect of mineralogical parameters on the mechanical properties of granitic rocks. Eng. Geol. 2018, 240, 204–225. [Google Scholar] [CrossRef]
- Nicksiar, M.; Martin, C.D. Factors affecting crack initiation in low porosity crystalline rocks. Rock Mech. Rock Eng. 2014, 47, 1165–1181. [Google Scholar] [CrossRef]
- Hofmann, H.; Babadagli, T.; Yoon, J.S.; Zang, A.; Zimmermann, G. A grain based modeling study of mineralogical factors affecting strength, elastic behavior and micro fracture development during compression tests in granites. Eng. Fract. Mech. 2015, 147, 261–275. [Google Scholar] [CrossRef]
- Mollon, G.; Zhao, J. Fourier-Voronoi-based generation of realistic samples for discrete modelling of granular materials. Granul. Matter. 2012, 14, 621–638. [Google Scholar] [CrossRef]
- Tavallali, A.; Vervoort, A. Effect of layer orientation on the failure of layered sandstone under Brazilian test conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 313–322. [Google Scholar] [CrossRef]



















| Mineral | Density (kg·m−3) | Tensile Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio (-) |
|---|---|---|---|---|
| K-feldspar | 2560 | 5–10 | 69.8 | 0.28 |
| Plagioclase | 2630 | 5–10 | 88.1 | 0.26 |
| Quartz | 2650 | 10–11 | 94.5 | 0.08 |
| Biotite | 3050 | 4–7 | 33.8 | 0.36 |
| Property | Qz | Fsp | Ma | |
|---|---|---|---|---|
| Intragrain | Density (kg·m−3) | 2600 | 2600 | 3050 |
| Young’s modulus (GPa) | 80 | 70 | 40 | |
| Poisson’s ratio (-) | 0.07 | 0.26 | 0.27 | |
| Friction coefficient (-) | 1.2 | 1.2 | 1.2 | |
| Cohesion (MPa) | 25 | 25 | 25 | |
| Tensile strength (MPa) | 20 | 15 | 10 | |
| Mode I fracture energy (J·m−2) | 900 | 300 | 600 | |
| Mode II fracture energy (J·m−2) | 1800 | 600 | 1200 | |
| Fracture penalty (GPa) | 400 | 350 | 200 | |
| Normal penalty (GPa·m) | 80 | 70 | 40 | |
| Tangential penalty (GPa·m−1) | 800 | 700 | 400 | |
| Qz-Qz | Fsp-Fsp | Ma-Ma | ||
| Homophase boundary | Friction coefficient (-) | 1.1 | 1.1 | 1.1 |
| Cohesion (MPa) | 20 | 20 | 20 | |
| Tensile strength (MPa) | 15 | 10 | 10 | |
| Mode I fracture energy (J·m−2) | 700 | 250 | 450 | |
| Mode II fracture energy (J·m−2) | 1400 | 500 | 900 | |
| Fracture penalty (GPa) | 200 | 175 | 100 | |
| Normal penalty (GPa·m) | 40 | 35 | 20 | |
| Tangential penalty (GPa·m−1) | 400 | 350 | 200 | |
| Qz-Fsp | Qz-Ma | Fsp-Ma | ||
| Heterophase boundaries | Friction coefficient (-) | 0.9 | 0.9 | 0.9 |
| Cohesion (MPa) | 20 | 20 | 20 | |
| Tensile strength (MPa) | 10 | 6 | 6 | |
| Mode I fracture energy (J·m−2) | 50 | 20 | 20 | |
| Mode II fracture energy (J·m−2) | 500 | 200 | 200 | |
| Fracture penalty (GPa) | 350 | 200 | 275 | |
| Normal penalty (GPa·m) | 70 | 40 | 55 | |
| Tangential penalty (GPa·m−1) | 700 | 400 | 550 |
| Scheme | Grain Size (mm) | Grain Orientation (º) |
|---|---|---|
| 1 | 1.5, 2.0, 2.5, 3.0 | - |
| 2 | - | 0, 30, 45, 60, 90 |
| Sample | Number of Different Types of Microcracks | |||||
|---|---|---|---|---|---|---|
| Intergranular Cracks | Transgranular Cracks | |||||
| Mode I | Mode III | Mode II | Mode I | Mode III | Mode II | |
| A-1 | 119 | 23 | 2 | 4 | 68 | 1 |
| A-2 | 121 | 43 | 2 | 7 | 48 | 3 |
| A-3 | 150 | 56 | 3 | 10 | 50 | 6 |
| A-4 | 130 | 70 | 3 | 19 | 52 | 10 |
| Sample | Grain Number, NP | Grain Size Coefficient, So | Preferred Orientation, φ (°) |
|---|---|---|---|
| B-1 | 303 | 1.06 | 0 |
| B-2 | 319 | 1.07 | 30 |
| B-3 | 329 | 1.06 | 45 |
| B-4 | 328 | 1.07 | 60 |
| B-5 | 321 | 1.06 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Qiu, S.; Kou, P.; Li, S.; Li, P.; Yan, S. Investigation of Damage Evolution in Heterogeneous Rock Based on the Grain-Based Finite-Discrete Element Model. Materials 2021, 14, 3969. https://doi.org/10.3390/ma14143969
Zhang S, Qiu S, Kou P, Li S, Li P, Yan S. Investigation of Damage Evolution in Heterogeneous Rock Based on the Grain-Based Finite-Discrete Element Model. Materials. 2021; 14(14):3969. https://doi.org/10.3390/ma14143969
Chicago/Turabian StyleZhang, Shirui, Shili Qiu, Pengfei Kou, Shaojun Li, Ping Li, and Siquan Yan. 2021. "Investigation of Damage Evolution in Heterogeneous Rock Based on the Grain-Based Finite-Discrete Element Model" Materials 14, no. 14: 3969. https://doi.org/10.3390/ma14143969
APA StyleZhang, S., Qiu, S., Kou, P., Li, S., Li, P., & Yan, S. (2021). Investigation of Damage Evolution in Heterogeneous Rock Based on the Grain-Based Finite-Discrete Element Model. Materials, 14(14), 3969. https://doi.org/10.3390/ma14143969





