Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method
Abstract
:1. Introduction
2. P-Version Finite Element Method and Contour Integral Method in Three Dimensions
2.1. P-Version Finite Element Method in Three Dimensions
2.2. 3-D Hierarchical Shape Functions for Standard Tetrahedral Elements
2.3. Contour Integral Method in Three Dimensions
3. Numerical Examples and Discussion
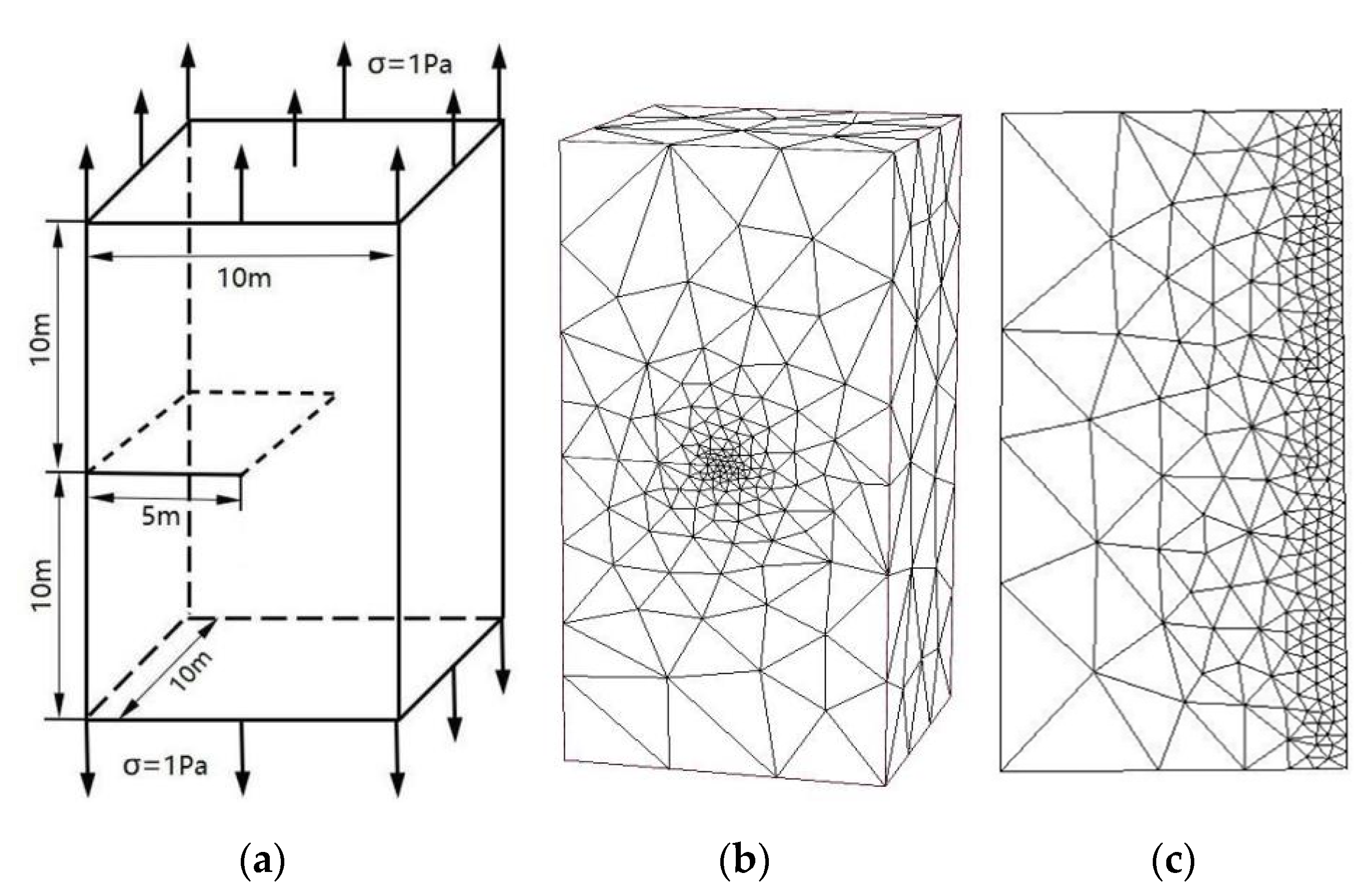
3.1. An Edge Straight Crack
SIFs of an Edge Straight Crack in a Rectangular Block
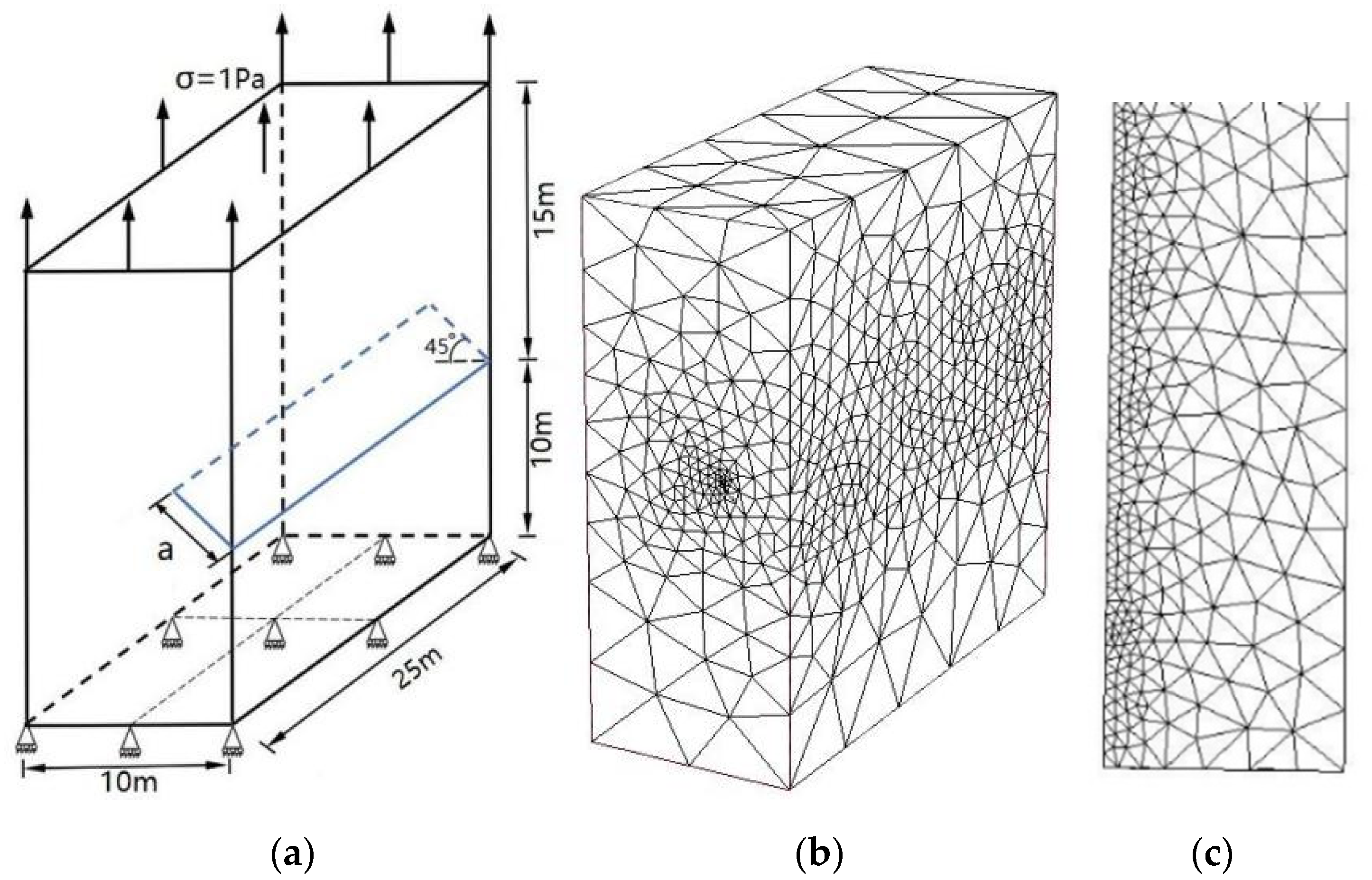
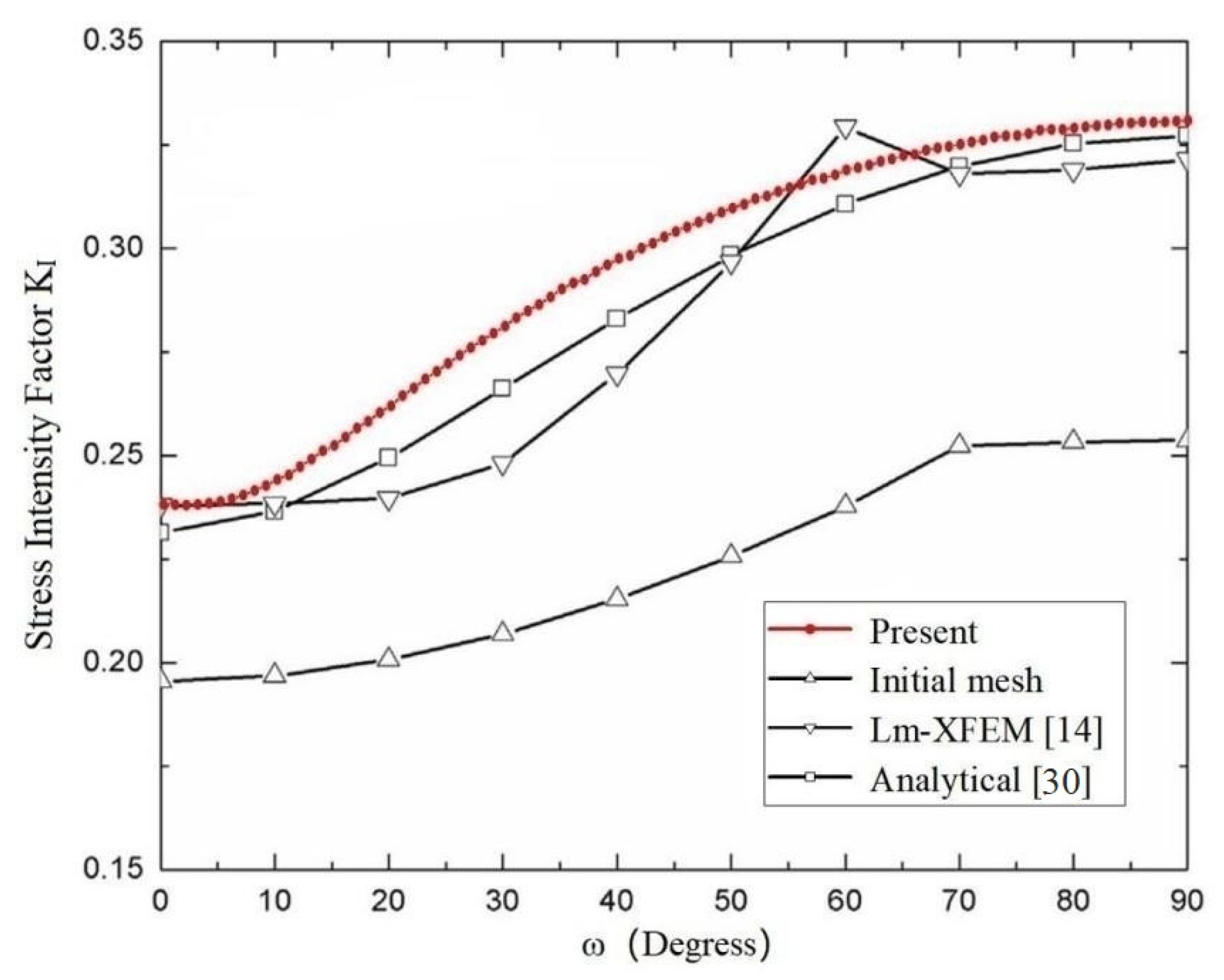
3.2. An Edge Inclined Straight Crack
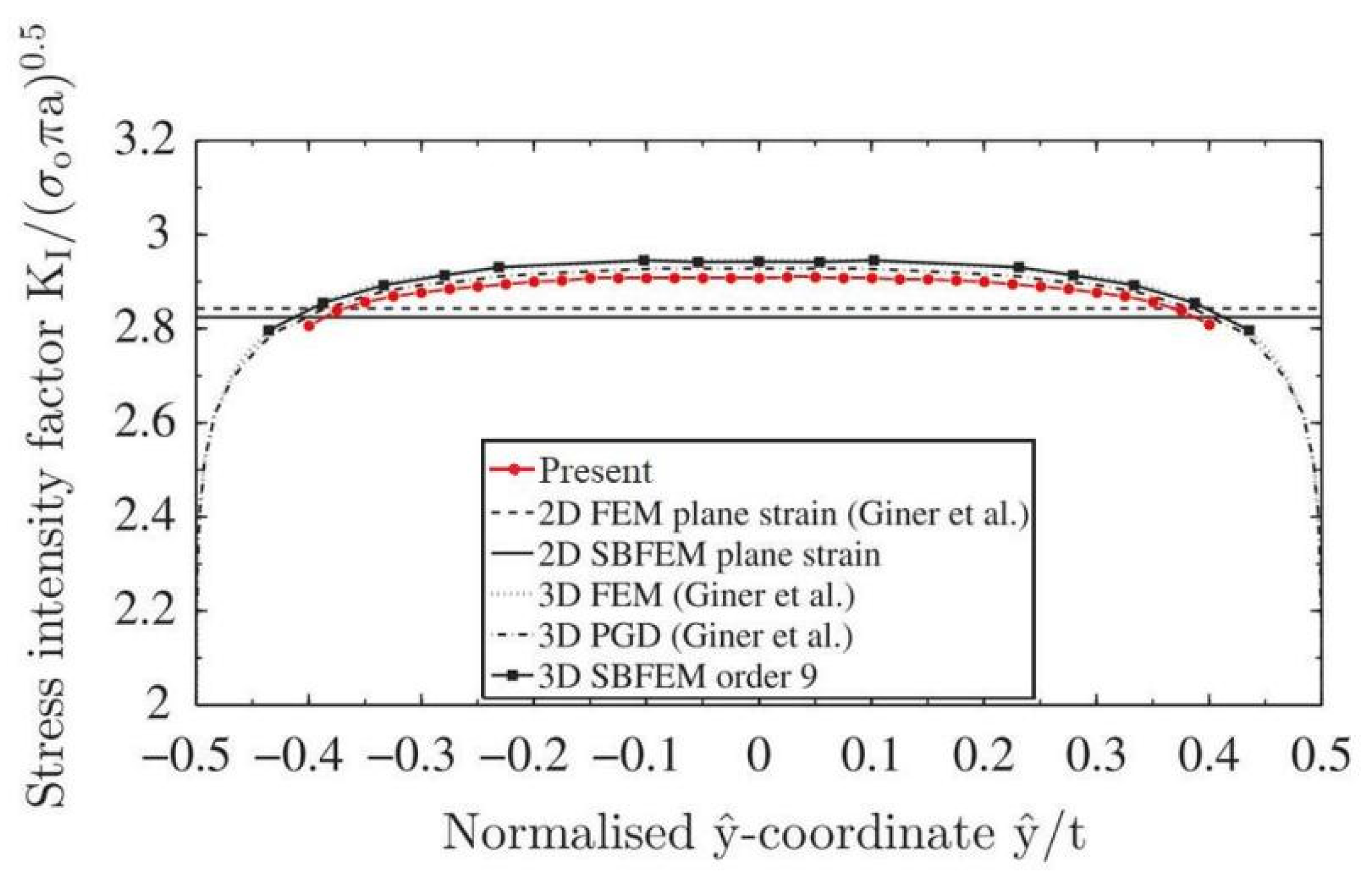
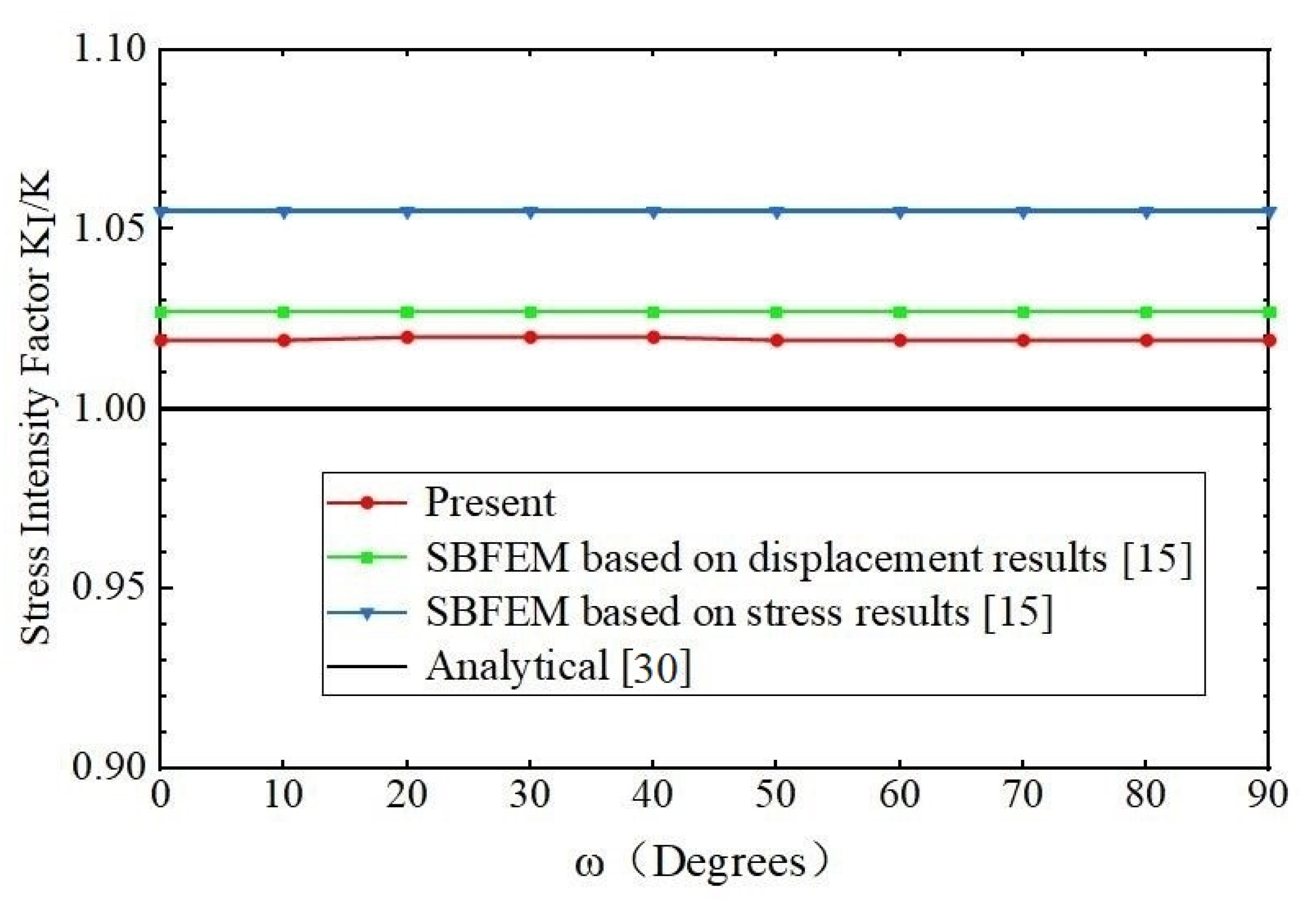
3.3. A Penny-Shaped Crack
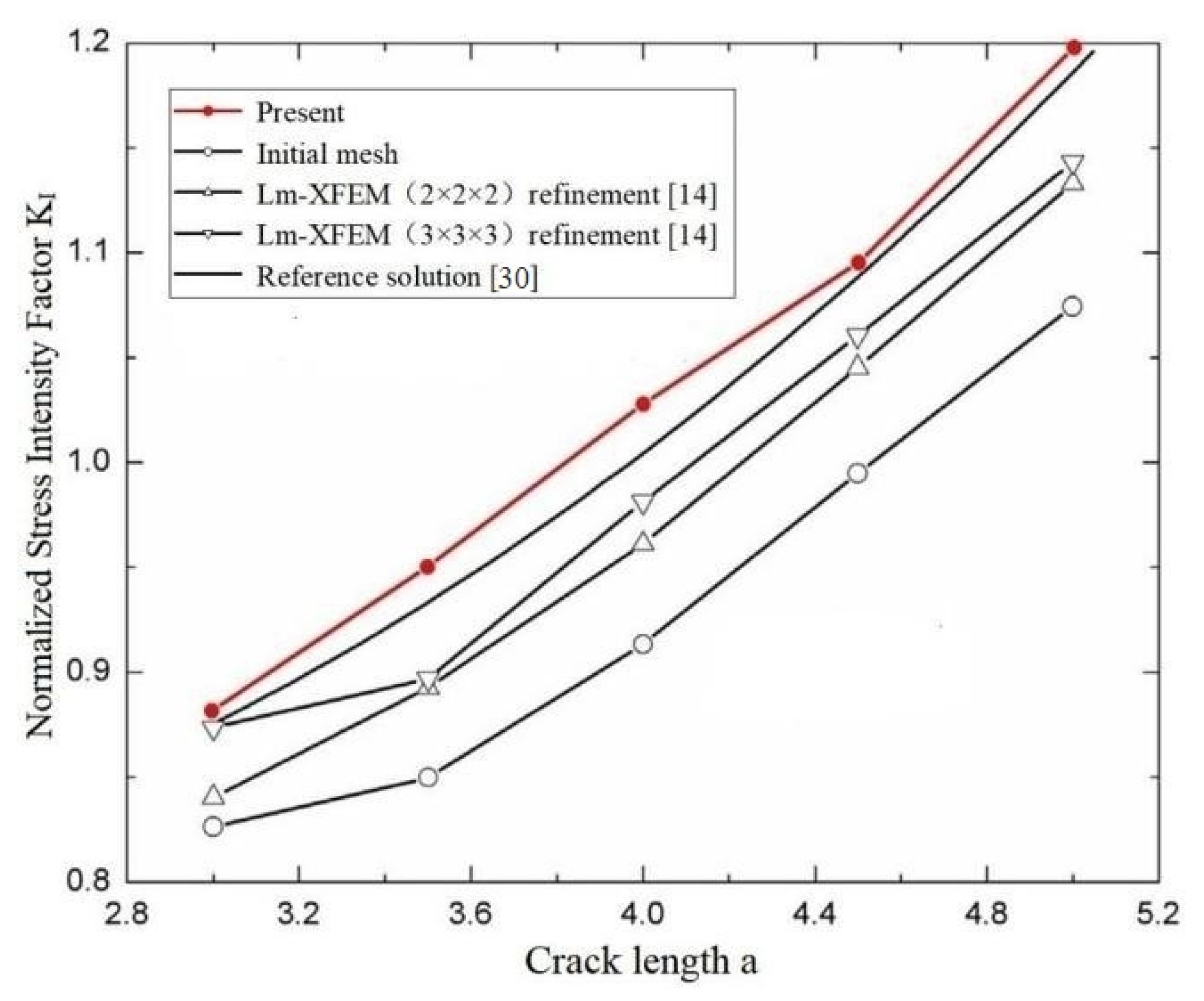
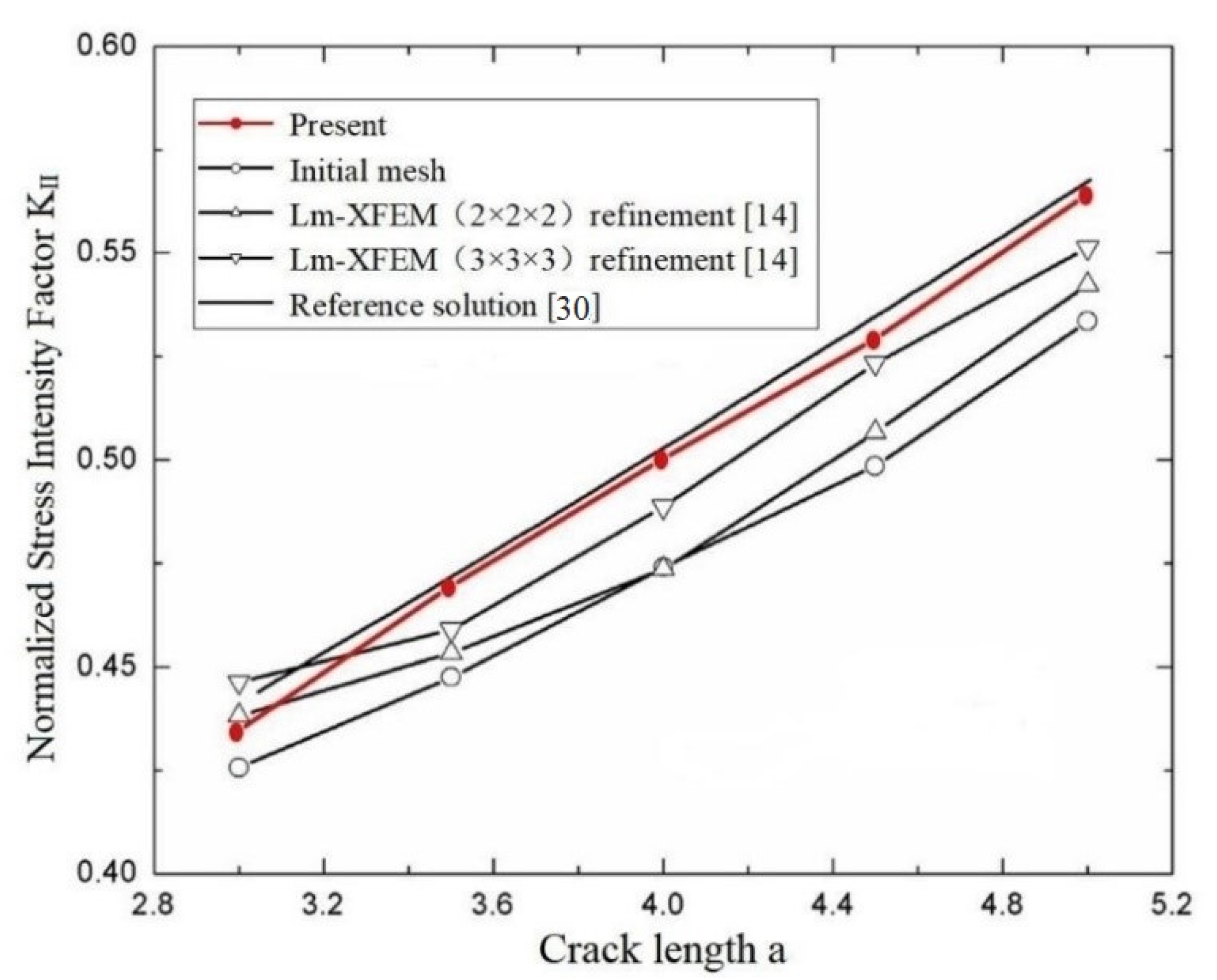
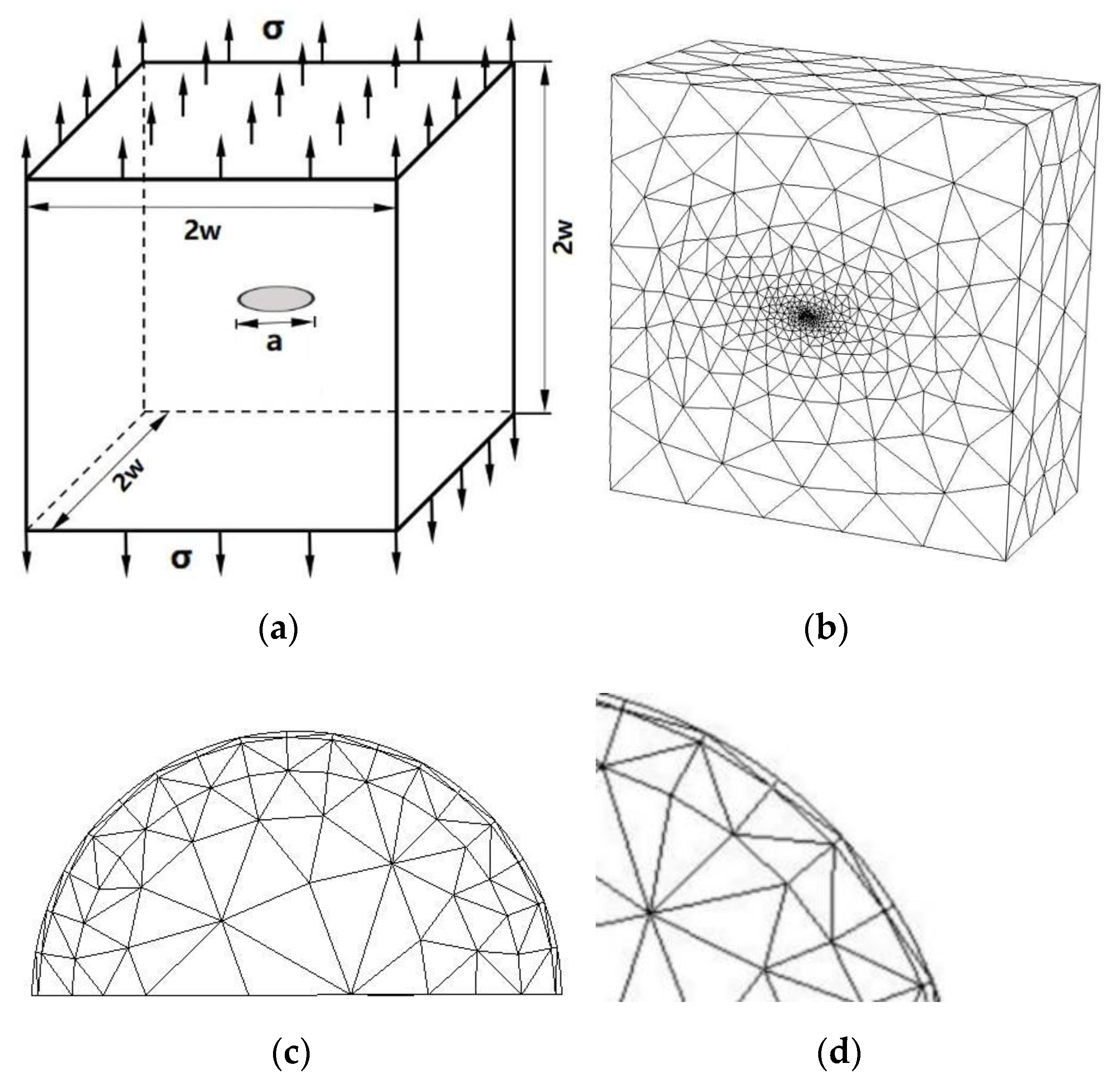
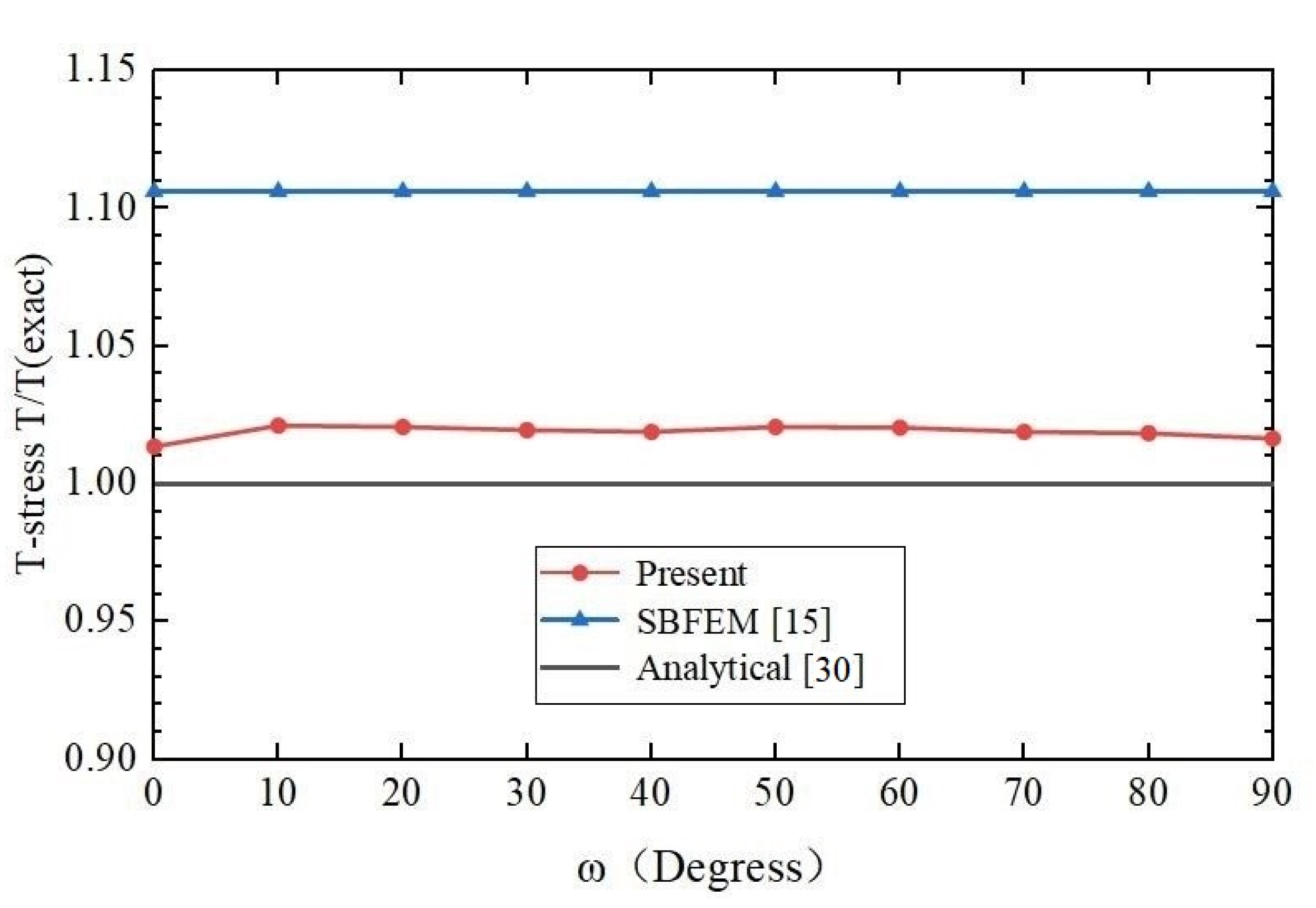
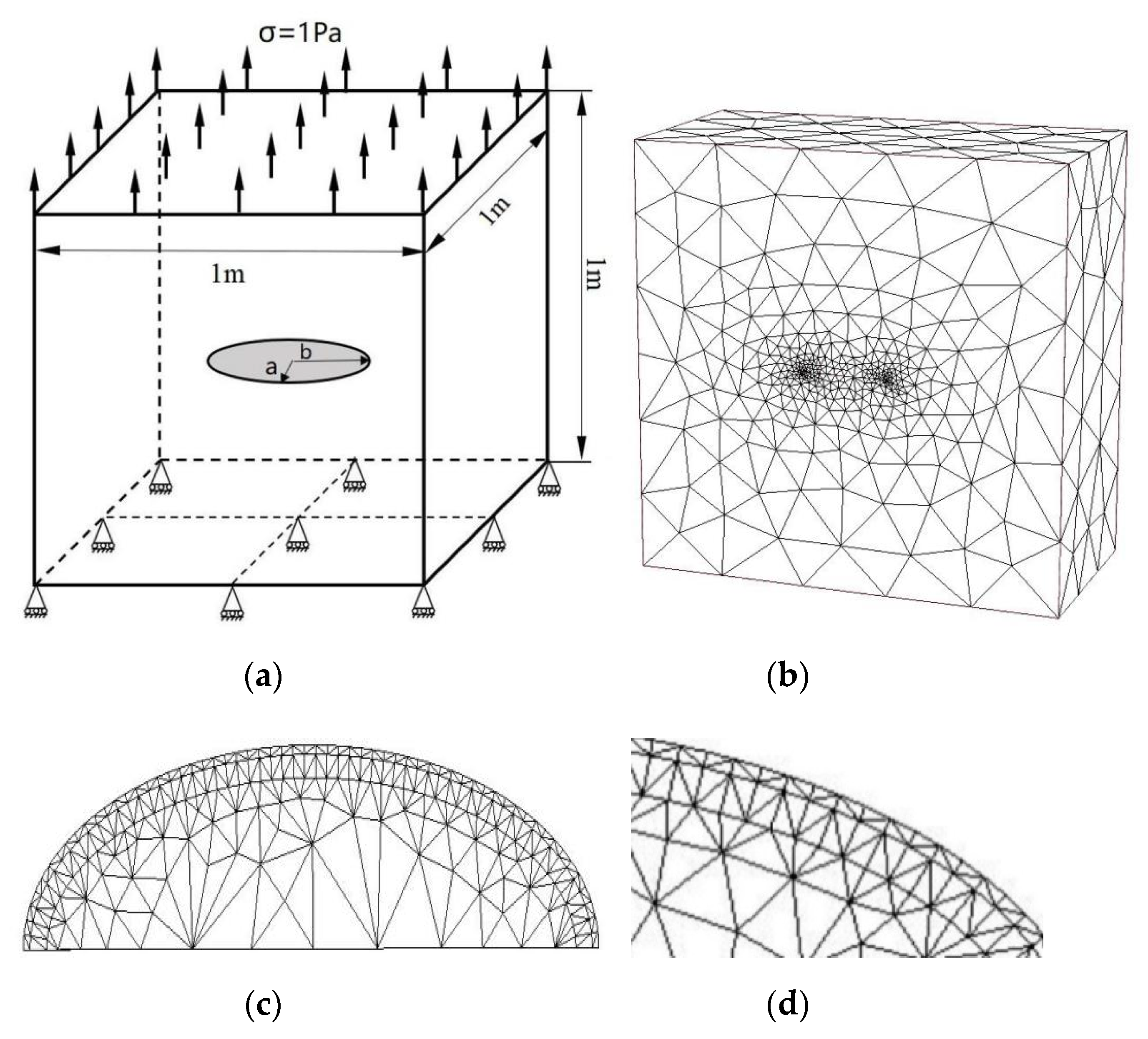
3.4. A Central Ellipse Shaped Crack
SIFs of a Central Ellipse Shaped Crack in a Large Cube
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Y.J.; Zhou, W.Y.; Lin, P. Application of EFG method to three-dimensional fracture mechanics. Rock Soil Mech. 2003, 24, 21–24. [Google Scholar]
- Chen, W.H.; Chen, C.H. On three-dimensional fracture mechanics analysis by an enriched meshless method. Comput. Modeling Eng. Sci. 2005, 8, 177–190. [Google Scholar]
- Duflot, M. A meshless method with enriched weight functions for three-dimensional crack propagation. Int. J. Numer. Methods Eng. 2006, 65, 1970–2006. [Google Scholar] [CrossRef]
- Ayhan, A.O. Stress intensity factors for three-dimensional cracks in functionally graded materials using enriched finite elements. Int. J. Solids Struct. 2007, 44, 8579–8599. [Google Scholar] [CrossRef] [Green Version]
- Ayhan, A.O. Three-dimensional mixed-mode stress intensity factors for cracks in functionally graded materials using enriched finite elements. Int. J. Solids Struct. 2009, 46, 796–810. [Google Scholar] [CrossRef] [Green Version]
- Ayhan, A.O. Three-dimensional fracture analysis using tetrahedral enriched elements and fully unstructured mesh. Int. J. Solids Struct. 2011, 48, 492–505. [Google Scholar] [CrossRef]
- Nejati, M.; Paluszny, A.; Zimmerman, R.W. On the use of quarter-point tetrahedral finite elements in linear elastic fracture mechanics. Eng. Fract. Mech. 2015, 144, 194–221. [Google Scholar] [CrossRef] [Green Version]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Garzon, J.; Duarte, C.A.; Pereira, J.P. Extraction of stress intensity factors for the simulation of 3-D crack growth with the generalized finite element method. Key Eng. Mater. 2013, 560, 1–36. [Google Scholar] [CrossRef]
- Sukumar, N.; Moës, N.; Moran, B.; Belytschko, T. Extended finite element method for three-dimensional crack modeling. Int. J. Numer. Methods Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]
- Areias, P.M.A.; Belytschko, T. Analysis of three-dimensional crack initiation and propagation using the extended finite element method. Int. J. Numer. Methods Eng. 2005, 63, 760–788. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, T. A multiscale extended finite element method for modeling three-dimensional crack problems. Rock Soil Mech. 2014, 35, 2702–2708. [Google Scholar]
- Wang, Z.; Yu, T. Adaptive multiscale extended finite element method for modeling three-dimensional crack problems. Eng. Mech. 2016, 33, 32–38. [Google Scholar]
- Wang, Z.; Yu, T.T.; Bui, T.Q.; Tanaka, S.; Zhang, C.Z.; Hirose, S.; Curiel-Sosa, J.L. 3-D local mesh refinement XFEM with variable-node hexahedron elements for extraction of stress intensity factors of straight and curved planar cracks. Comput. Methods Appl. Mech. Eng. 2017, 313, 375–405. [Google Scholar] [CrossRef] [Green Version]
- Saputra, A.A.; Birk, C.; Song, C.M. Computation of three-dimensional fracture parameters at interface cracks and notches by the scaled boundary finite element method. Eng. Fract. Mech. 2015, 148, 213–242. [Google Scholar] [CrossRef]
- Bhat, M.A.; Shaikh, A.A. Effect of specimen parameters on mixed-mode I/II stress intensity factors for additive manufactured slant edge crack plate. Mater. Today Proc. 2021, 44, 4305–4308. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Zolfagharian, A. Fracture and load-carrying capacity of 3D-printed cracked components. Extrem. Mech. Lett. 2020, 37, 100692. [Google Scholar] [CrossRef]
- Guo, B.Q. Approximation theory for the p-version of the finite element method in three dimensions, Part 1: Approximabilities of singular functions in the framework of the Jacobi-Weighted Besov and Sobolev spaces. SIAM J. Numer. Anal. 2006, 44, 246–269. [Google Scholar] [CrossRef]
- Guo, B.Q.; Zhang, J.M. Stable and compatible polynomial extensions in three dimensions and applications to the p and h-p finite element method. SIAM J. Numer. Anal. 2009, 47, 1195–1225. [Google Scholar] [CrossRef]
- Guo, B.Q. Approximation theory of the p-version of the finite element method in three dimensions, Part 2: Convergence of the p-version of FEM. SIAM J. Numer. Anal. 2009, 47, 2578–2611. [Google Scholar] [CrossRef]
- Ribeiro, P.; Cochelin, B.; Bellizzi, S. Non-linear vibrations of deep cylindrical shells by the p-version finite element method. Shock. Vib. 2010, 17, 21–37. [Google Scholar] [CrossRef]
- Wowk, D.; Gamble, K.; Underhill, R. Influence of p-method finite element parameters on predictions of crack front Geometry. Finite Elem. Anal. Des. 2013, 73, 1–10. [Google Scholar] [CrossRef]
- Düster, A.; Bröker, H.; Rank, E. The p-version of the finite element method for three-dimensional curved thin walled structures. Int. J. Numer. Methods Eng. 2001, 52, 673–703. [Google Scholar] [CrossRef] [Green Version]
- Paolini, A.; Kollmannsberger, S.; Winter, C.; Buchschmid, M. A high-order finite element model for vibration analysis of cross- laminated timber assemblies. Build. Acoust. 2017, 24, 135–158. [Google Scholar] [CrossRef]
- Wu, Y.; Xing, Y.F.; Liu, B. Analysis of isotropic and composite laminated plates and shells using a differential quadrature hierarchical finite element method. Compos. Struct. 2018, 205, 11–25. [Google Scholar] [CrossRef]
- Rachid, Z.; Kaddour, R.; Achache, H. Dynamic calculation of a tapered shaft rotor made of composite material. Adv. Aircr. Spacecr. Sci. 2018, 5, 51–71. [Google Scholar]
- Houmat, A. Three-dimensional free vibration analysis of variable stiffness laminated composite rectangular plates. Compos. Struct. 2018, 194, 398–412. [Google Scholar] [CrossRef]
- Szabó, B.A.; Babuška, I. Finite Element Analysis; John Wiley and Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Szabó, B.A.; Babuška, I. Computation of the amplitude of stress singular terms for cracks and reentrant corners. In Fracture Mechanics: Nineteenth Symposium; ASTM STP 969; Southwest Research Institute: San Antonio, TX, USA, 1988; pp. 101–124. [Google Scholar] [CrossRef]
- Chinese Aeronautical Establishment. Stress Intensity Factors Handbook, revised ed.; Science Press: Beijing, China, 1993. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, R. The Stress Analysis of Cracks Handbook, 3rd ed.; Del Research Corporation: Hellertown, PA, USA, 2000. [Google Scholar]
- Wang, X. Elastic T-stress solutions for penny-shaped cracks under tension and bending. Eng. Fract. Mech. 2004, 71, 2283–2298. [Google Scholar] [CrossRef]

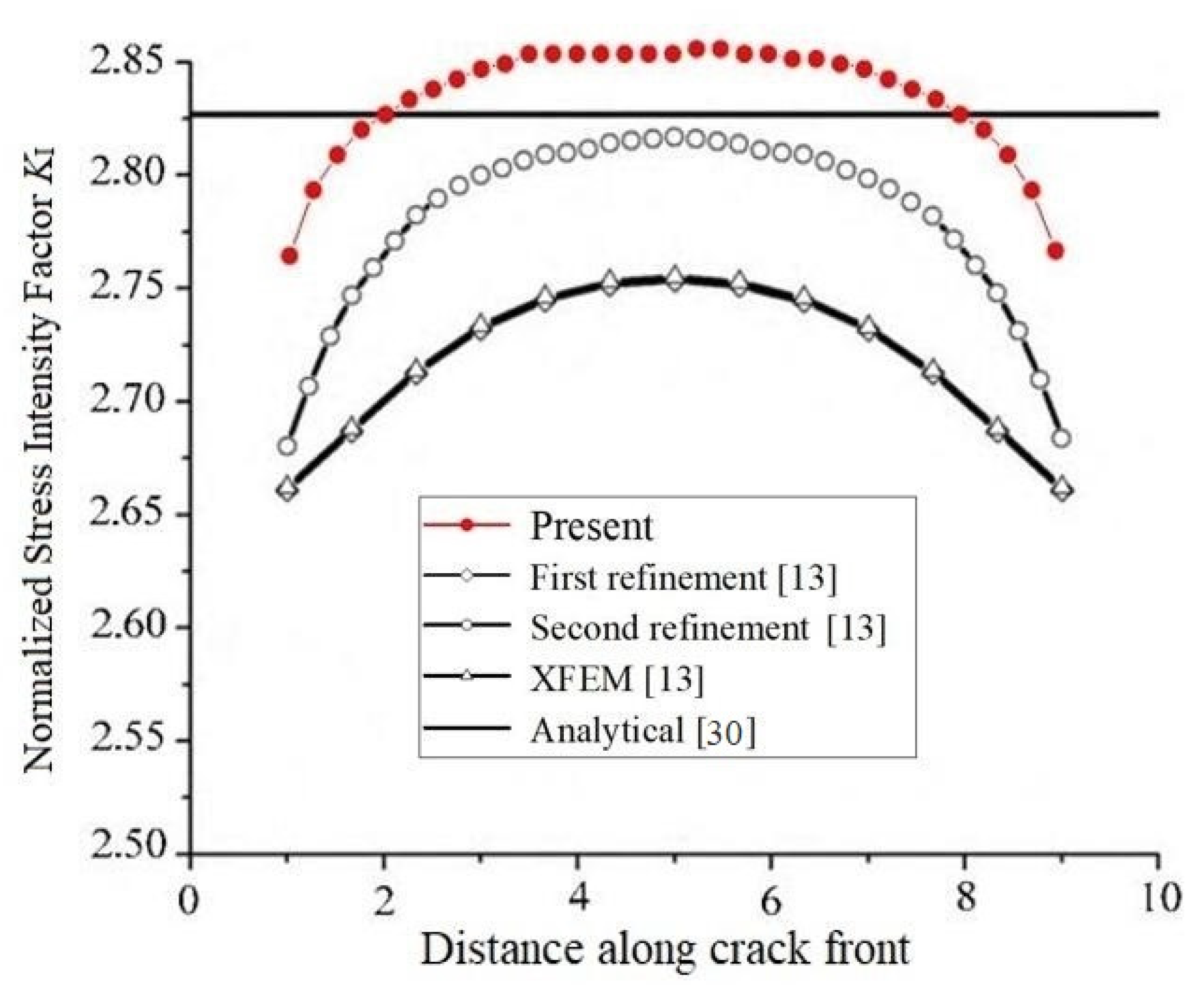
| Distance Along Crack Front (m) | Analytical KI (Pa·m1/2) | Present KI (Pa·m1/2) | Normalized KI (Pa·m1/2) | Relative Error (%) [Present] |
|---|---|---|---|---|
| 1 | 11.202 | 10.92 | 2.755 | −2.50 |
| 2 | 11.202 | 11.18 | 2.821 | −0.18 |
| 3 | 11.202 | 11.29 | 2.849 | 0.80 |
| 4 | 11.202 | 11.32 | 2.856 | 1.07 |
| 5 | 11.202 | 11.34 | 2.861 | 1.25 |
| 6 | 11.202 | 11.32 | 2.856 | 1.07 |
| 7 | 11.202 | 11.29 | 2.849 | 0.80 |
| 8 | 11.202 | 11.18 | 2.821 | −0.18 |
| 9 | 11.202 | 10.93 | 2.758 | −2.41 |
| Distance Along Crack Front (m) | KI (Pa·m1/2) | ||||
|---|---|---|---|---|---|
| a = 3 m | a = 3.5 m | a = 4 m | a = 4.5 m | a = 5 m | |
| 0.9 | 2.703 | 3.153 | 3.603 | 4.168 | 4.730 |
| 1.8 | 2.707 | 3.148 | 3.648 | 4.124 | 4.730 |
| 2.7 | 2.704 | 3.167 | 3.675 | 4.162 | 4.757 |
| 3.6 | - | - | 3.606 | 4.036 | 4.753 |
| 4.5 | - | - | - | - | 4.769 |
| Distance along Crack Front (m) | KII (Pa·m1/2) | ||||
|---|---|---|---|---|---|
| a = 3 m | a = 3.5 m | a = 4 m | a = 4.5 m | a = 5 m | |
| 0.9 | 1.320 | 1.557 | 1.794 | 1.959 | 2.188 |
| 1.8 | 1.334 | 1.612 | 1.746 | 1.945 | 2.237 |
| 2.7 | 1.321 | 1.548 | 1.826 | 1.990 | 2.262 |
| 3.6 | - | - | 1.768 | 1.941 | 2.179 |
| 4.5 | - | - | - | - | 2.198 |
| Degrees | Analytical KI (Pa·m1/2) | Present KI (Pa·m1/2) | SBFEM [15] Stress Results Error (%) | SBFEM [15] Displacement Results Error (%) | Present Error (%) |
|---|---|---|---|---|---|
| 0 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 10 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 20 | 1.1284 | 1.151 | 5.5 | 2.7 | 2.00 |
| 30 | 1.1284 | 1.151 | 5.5 | 2.7 | 2.00 |
| 40 | 1.1284 | 1.151 | 5.5 | 2.7 | 2.00 |
| 50 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 60 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 70 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 80 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| 90 | 1.1284 | 1.150 | 5.5 | 2.7 | 1.91 |
| Degrees | Analytical | Present | SBFEM [15] Results Error (%) | Present Error (%) |
|---|---|---|---|---|
| 0 | −0.8 | −0.811 | 10.6 | 1.35 |
| 10 | −0.8 | −0.817 | 10.6 | 2.12 |
| 20 | −0.8 | −0.817 | 10.6 | 2.07 |
| 30 | −0.8 | −0.816 | 10.6 | 1.95 |
| 40 | −0.8 | −0.816 | 10.6 | 1.89 |
| 50 | −0.8 | −0.817 | 10.6 | 2.07 |
| 60 | −0.8 | −0.816 | 10.6 | 2.04 |
| 70 | −0.8 | −0.815 | 10.6 | 1.89 |
| 80 | −0.8 | −0.815 | 10.6 | 1.84 |
| 90 | −0.8 | −0.813 | 10.6 | 1.65 |
| P | DOF | Error of Energy Norm (%) | Analytical KI (Pa·m1/2) | KI (Pa·m1/2) | Relative Error (%) [Present] |
|---|---|---|---|---|---|
| 1 | 18723 | 30.25 | 1.1284 | 0.810 | −28.2 |
| 2 | 148194 | 17.28 | 1.1284 | 1.088 | −3.58 |
| 3 | 497136 | 12.70 | 1.1284 | 1.141 | 1.12 |
| 4 | 1174290 | 10.16 | 1.1284 | 1.157 | 2.53 |
| 5 | 2288397 | 8.53 | 1.1284 | 1.154 | 2.27 |
| 6 | 3948198 | 7.39 | 1.1284 | 1.153 | 2.18 |
| 7 | 6262434 | 6.55 | 1.1284 | 1.153 | 2.18 |
| 8 | 9339846 | 5.90 | 1.1284 | 1.151 | 2.00 |
| Degrees | Analytical KI (Pa·m1/2) | Present KI (Pa·m1/2) | Present Error (%) |
|---|---|---|---|
| 0 | 0.2314 | 0.2393 | 3.41 |
| 10 | 0.2365 | 0.2439 | 3.13 |
| 20 | 0.2495 | 0.2616 | 4.85 |
| 30 | 0.2661 | 0.2807 | 5.49 |
| 40 | 0.2831 | 0.2973 | 5.02 |
| 50 | 0.2983 | 0.3100 | 3.92 |
| 60 | 0.3107 | 0.3190 | 2.67 |
| 70 | 0.3198 | 0.3259 | 1.91 |
| 80 | 0.3254 | 0.3300 | 1.41 |
| 90 | 0.3273 | 0.3320 | 1.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Xu, R.; He, Y.; Yang, W. Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method. Materials 2021, 14, 3949. https://doi.org/10.3390/ma14143949
Zhang J, Xu R, He Y, Yang W. Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method. Materials. 2021; 14(14):3949. https://doi.org/10.3390/ma14143949
Chicago/Turabian StyleZhang, Jianming, Rui Xu, Yong He, and Wensheng Yang. 2021. "Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method" Materials 14, no. 14: 3949. https://doi.org/10.3390/ma14143949
APA StyleZhang, J., Xu, R., He, Y., & Yang, W. (2021). Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method. Materials, 14(14), 3949. https://doi.org/10.3390/ma14143949





