Using Artificial Neural Networks to Predict Influences of Heterogeneity on Rock Strength at Different Strain Rates
Abstract
1. Introduction
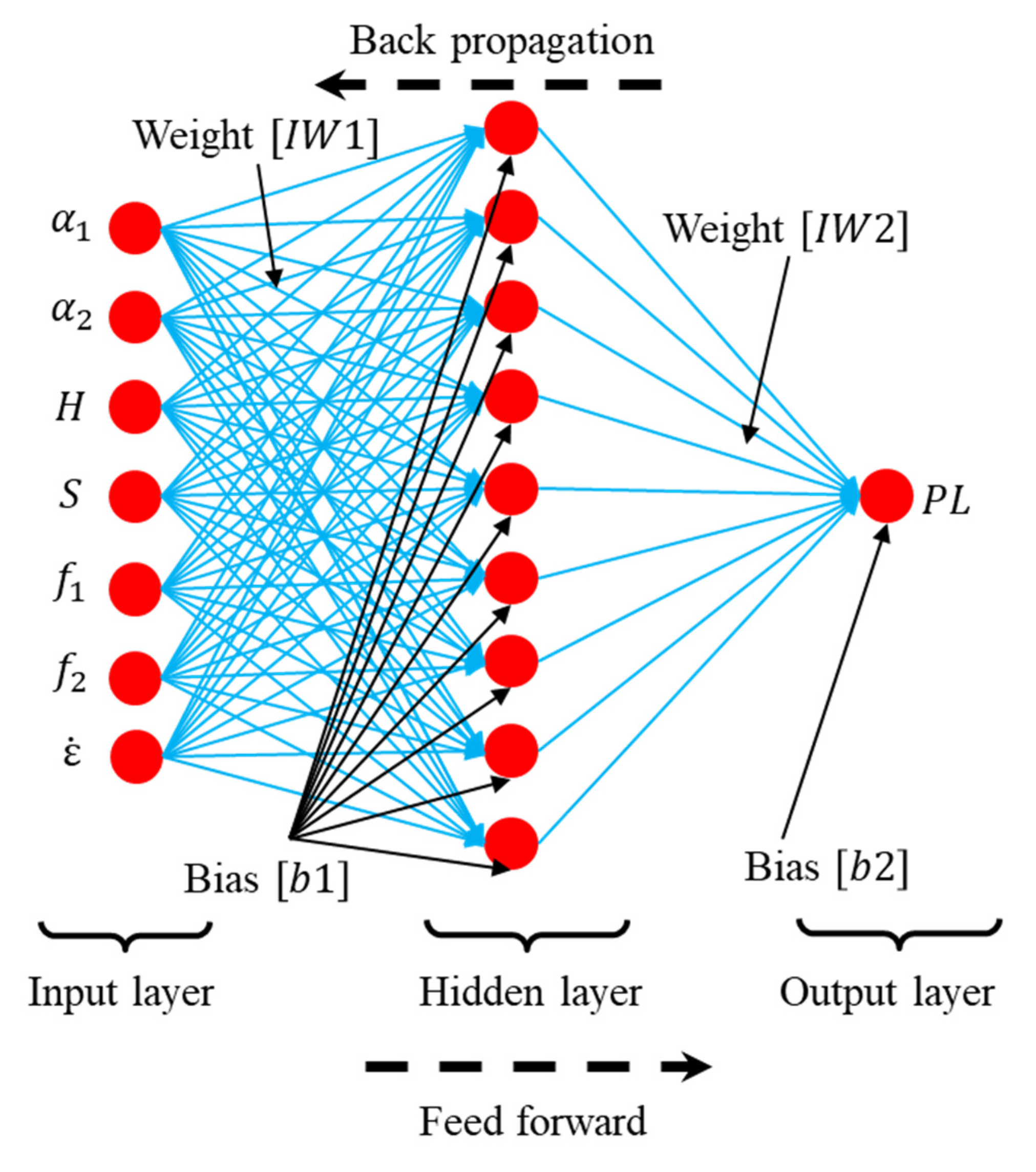
2. Methodology
2.1. Input and Output Variables
2.2. Optimization of ANN
2.2.1. Transfer Functions
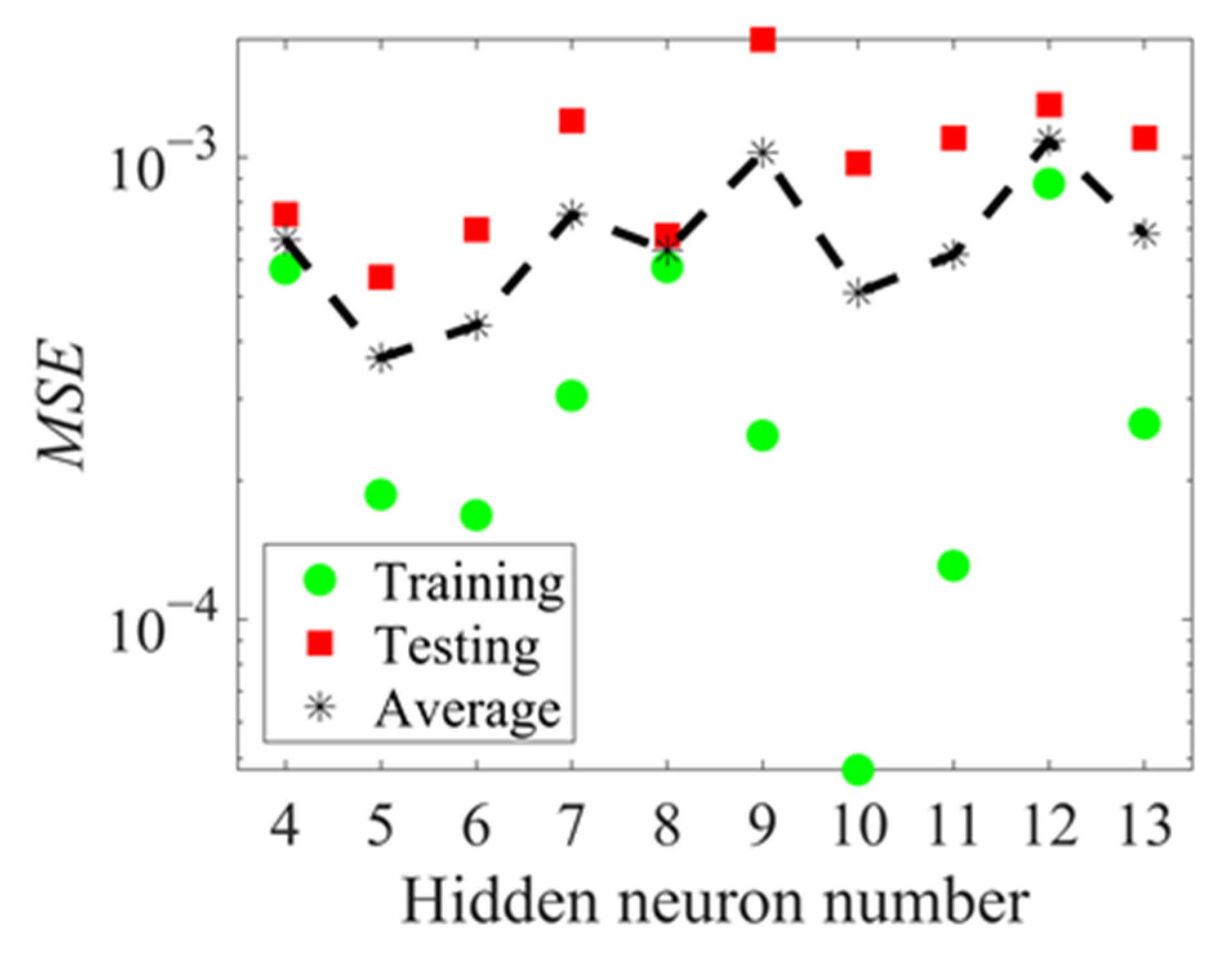
2.2.2. Hidden Layer Neuron Number
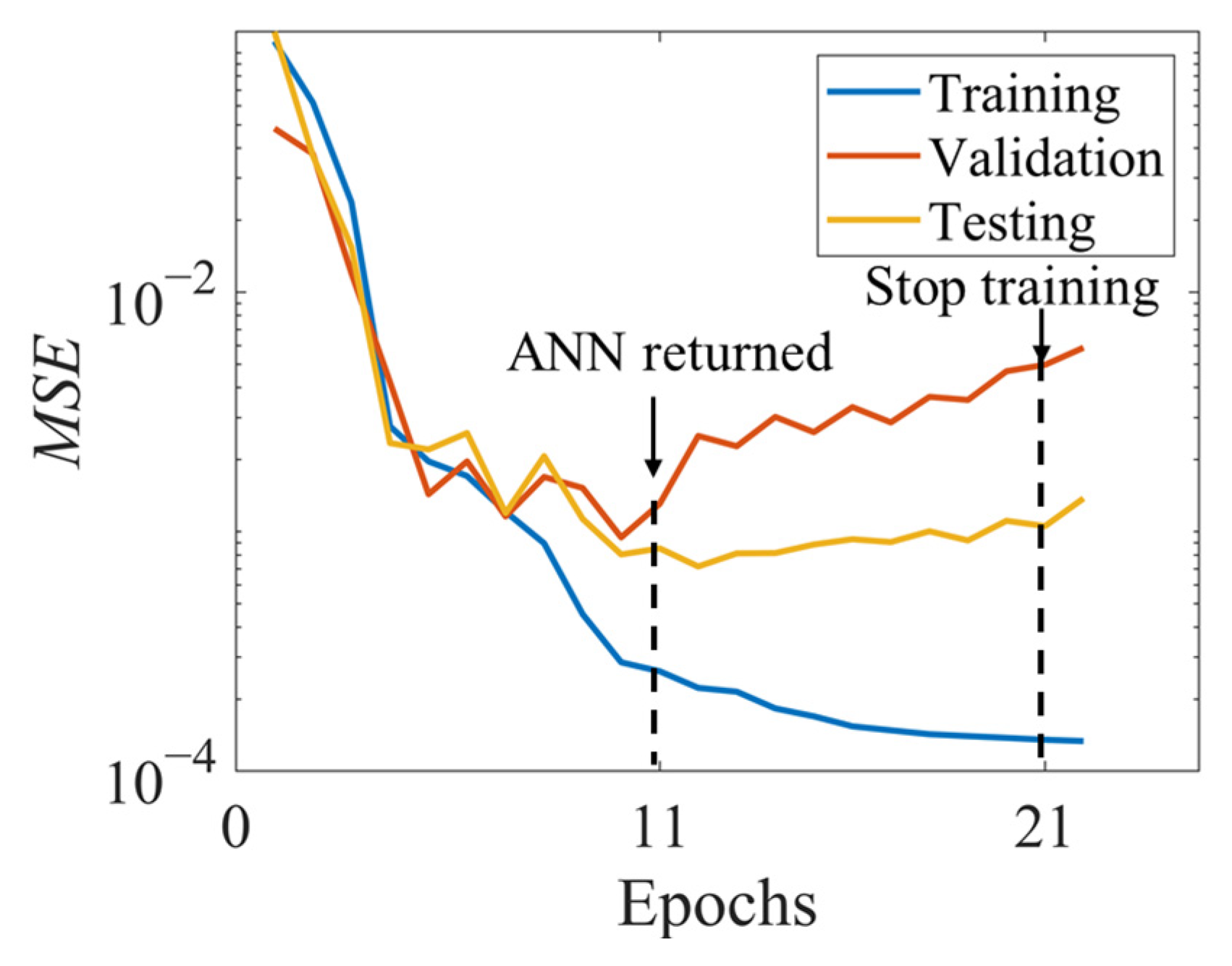
2.3. ANN Training
3. Results and Discussion
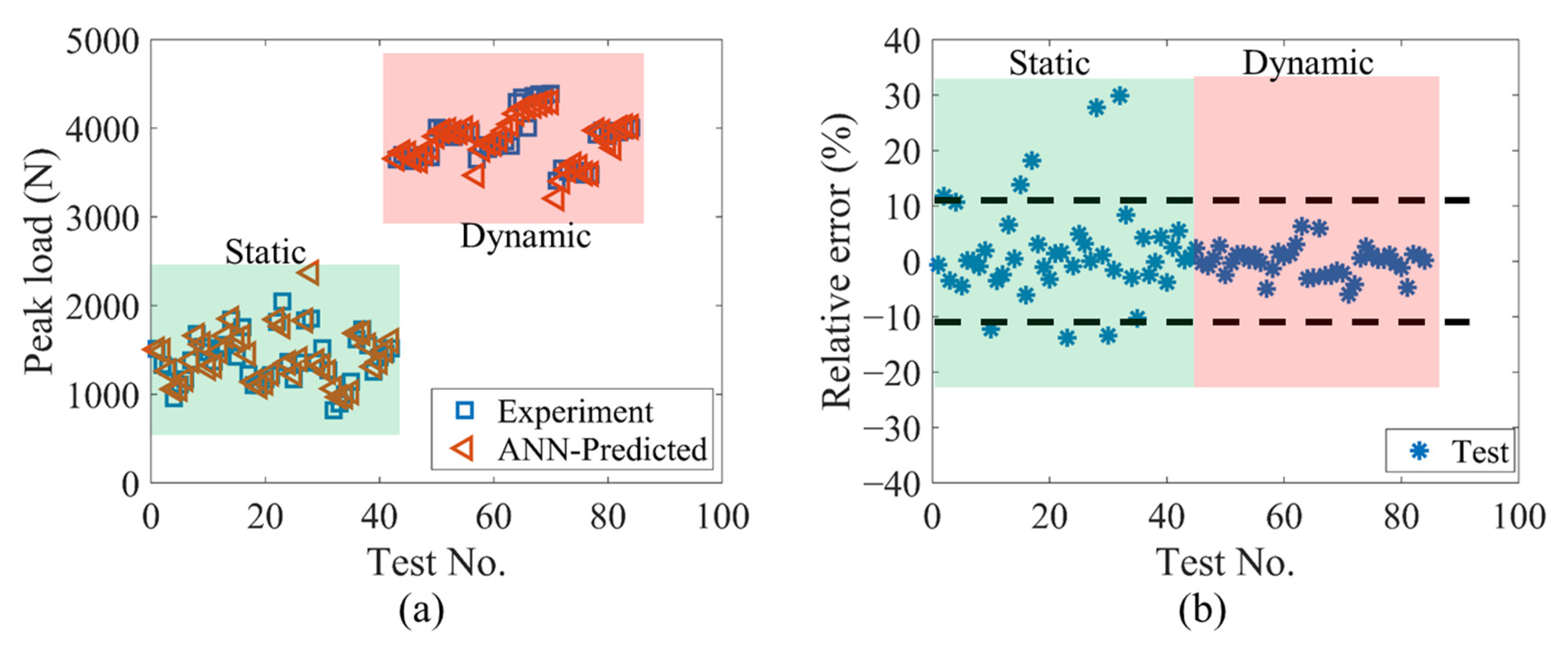
3.1. Predicting Results
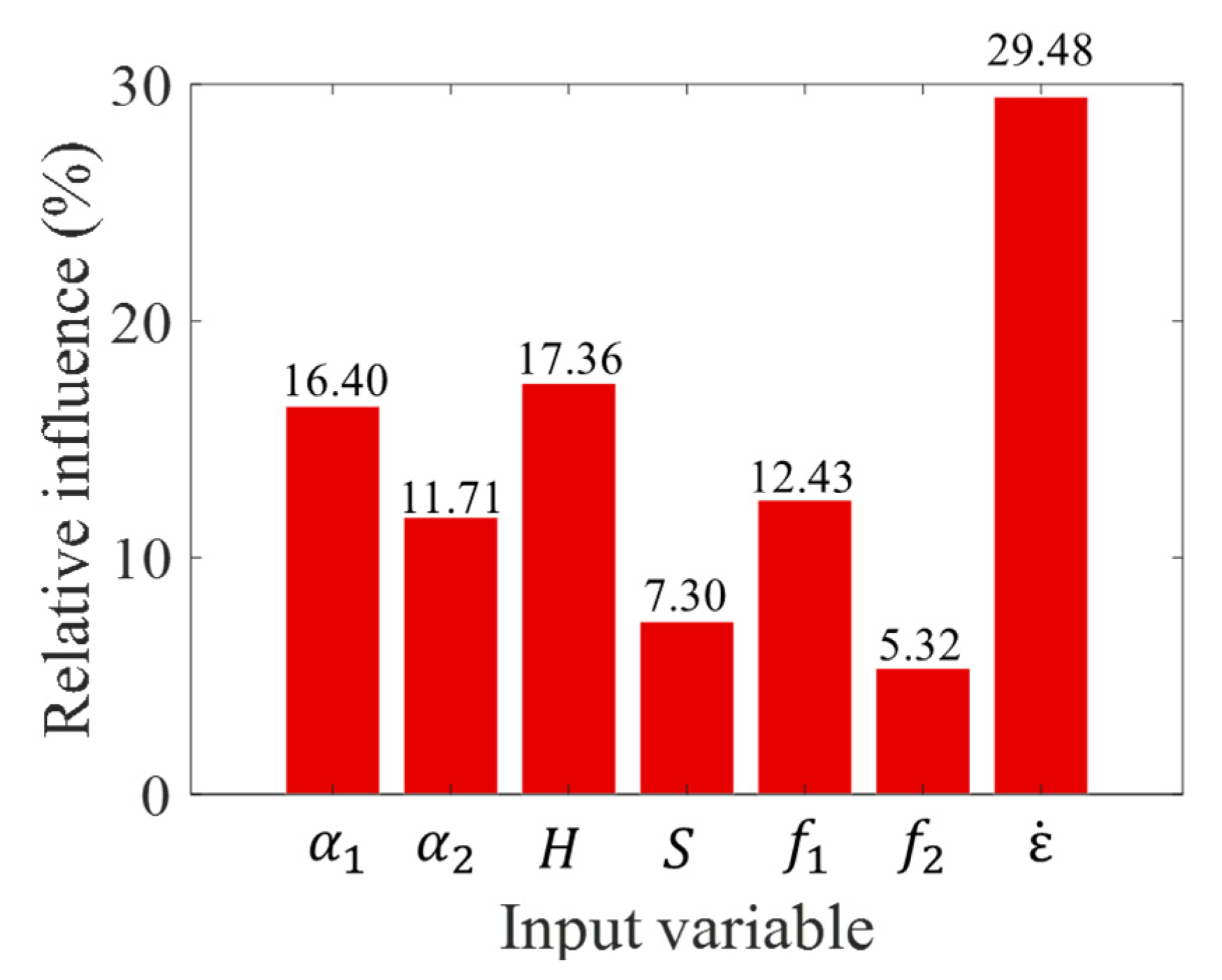
3.2. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Test No. | Input | Output | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Initial Crack Inclination Angle from Loading Axis (o) | Relative Position (mm) | Filling | Strain Rate (s−1) | Peak Load (N) | |||||
| Experiment | ANN | ||||||||
| PL | |||||||||
| 1 | 90 | 90 | 0 | 0 | 0 | 0 | 0.0001 | 1515 | 1486.098 |
| 2 | 75 | 75 | 0 | 0 | 0 | 0 | 0.0001 | 1333 | 1326.732 |
| 3 | 60 | 60 | 0 | 0 | 0 | 0 | 0.0001 | 1306 | 1225.101 |
| 4 | 45 | 45 | 0 | 0 | 0 | 0 | 0.0001 | 956 | 1196.695 |
| 5 | 30 | 30 | 0 | 0 | 0 | 0 | 0.0001 | 1109 | 1204.291 |
| 6 | 15 | 15 | 0 | 0 | 0 | 0 | 0.0001 | 1169 | 1238.981 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0001 | 1380 | 1319.490 |
| 8 | 90 | 90 | 0 | 0 | 1 | 1 | 0.0001 | 1678 | 1725.743 |
| 9 | 75 | 75 | 0 | 0 | 1 | 1 | 0.0001 | 1533 | 1523.316 |
| 10 | 60 | 60 | 0 | 0 | 1 | 1 | 0.0001 | 1476 | 1444.671 |
| 11 | 45 | 45 | 0 | 0 | 1 | 1 | 0.0001 | 1369 | 1445.347 |
| 12 | 30 | 30 | 0 | 0 | 1 | 1 | 0.0001 | 1520 | 1494.781 |
| 13 | 15 | 15 | 0 | 0 | 1 | 1 | 0.0001 | 1557 | 1610.455 |
| 14 | 0 | 0 | 0 | 0 | 1 | 1 | 0.0001 | 1843 | 1849.571 |
| 15 | 90 | 90 | 0 | 7.334 | 0 | 0 | 0.0001 | 1423 | 1443.698 |
| 16 | 75 | 75 | 0 | 7.334 | 0 | 0 | 0.0001 | 1756 | 1305.584 |
| 17 | 60 | 60 | 0 | 7.334 | 0 | 0 | 0.0001 | 1230 | 1195.725 |
| 18 | 45 | 45 | 0 | 7.334 | 0 | 0 | 0.0001 | 1105 | 1159.104 |
| 19 | 30 | 30 | 0 | 7.334 | 0 | 0 | 0.0001 | 1101 | 1164.367 |
| 20 | 15 | 15 | 0 | 7.334 | 0 | 0 | 0.0001 | 1169 | 1200.831 |
| 21 | 0 | 0 | 0 | 7.334 | 0 | 0 | 0.0001 | 1217 | 1288.699 |
| 22 | 90 | 90 | 0 | 7.334 | 1 | 1 | 0.0001 | 1816 | 1643.400 |
| 23 | 75 | 75 | 0 | 7.334 | 1 | 1 | 0.0001 | 2049 | 1453.946 |
| 24 | 60 | 60 | 0 | 7.334 | 1 | 1 | 0.0001 | 1365 | 1367.216 |
| 25 | 45 | 45 | 0 | 7.334 | 1 | 1 | 0.0001 | 1171 | 1368.303 |
| 26 | 30 | 30 | 0 | 7.334 | 1 | 1 | 0.0001 | 1354 | 1428.184 |
| 27 | 15 | 15 | 0 | 7.334 | 1 | 1 | 0.0001 | 1832 | 1568.657 |
| 28 | 0 | 0 | 0 | 7.334 | 1 | 1 | 0.0001 | 1856 | 1855.662 |
| 29 | 90 | 90 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 1359 | 1377.247 |
| 30 | 75 | 75 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 1522 | 1346.187 |
| 31 | 60 | 60 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 1270 | 1262.478 |
| 32 | 45 | 45 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 819 | 1154.207 |
| 33 | 30 | 30 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 894 | 1096.502 |
| 34 | 15 | 15 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 1002 | 1083.879 |
| 35 | 0 | 0 | 5.555 | 5.686 | 0 | 0 | 0.0001 | 1140 | 1093.918 |
| 36 | 90 | 90 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1620 | 1665.344 |
| 37 | 75 | 75 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1732 | 1623.381 |
| 38 | 60 | 60 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1554 | 1489.184 |
| 39 | 45 | 45 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1256 | 1379.604 |
| 40 | 30 | 30 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1419 | 1366.166 |
| 41 | 15 | 15 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1456 | 1417.751 |
| 42 | 0 | 0 | 5.555 | 5.686 | 1 | 1 | 0.0001 | 1518 | 1526.933 |
| 43 | 90 | 90 | 0 | 0 | 0 | 0 | 350 | 3650 | 3663.233 |
| 44 | 75 | 75 | 0 | 0 | 0 | 0 | 350 | 3700 | 3617.357 |
| 45 | 60 | 60 | 0 | 0 | 0 | 0 | 350 | 3630 | 3620.612 |
| 46 | 45 | 45 | 0 | 0 | 0 | 0 | 350 | 3655 | 3639.233 |
| 47 | 30 | 30 | 0 | 0 | 0 | 0 | 350 | 3670 | 3658.648 |
| 48 | 15 | 15 | 0 | 0 | 0 | 0 | 350 | 3697 | 3677.001 |
| 49 | 0 | 0 | 0 | 0 | 0 | 0 | 350 | 3675 | 3695.113 |
| 50 | 90 | 90 | 0 | 0 | 1 | 1 | 350 | 4010 | 3925.057 |
| 51 | 75 | 75 | 0 | 0 | 1 | 1 | 350 | 3980 | 3916.149 |
| 52 | 60 | 60 | 0 | 0 | 1 | 1 | 350 | 3930 | 3929.861 |
| 53 | 45 | 45 | 0 | 0 | 1 | 1 | 350 | 3900 | 3949.114 |
| 54 | 30 | 30 | 0 | 0 | 1 | 1 | 350 | 3945 | 3969.769 |
| 55 | 15 | 15 | 0 | 0 | 1 | 1 | 350 | 3955 | 3991.496 |
| 56 | 0 | 0 | 0 | 0 | 1 | 1 | 350 | 3950 | 4014.363 |
| 57 | 90 | 90 | 0 | 7.334 | 0 | 0 | 350 | 3650 | 3724.057 |
| 58 | 75 | 75 | 0 | 7.334 | 0 | 0 | 350 | 3810 | 3665.866 |
| 59 | 60 | 60 | 0 | 7.334 | 0 | 0 | 350 | 3768 | 3679.004 |
| 60 | 45 | 45 | 0 | 7.334 | 0 | 0 | 350 | 3795 | 3726.472 |
| 61 | 30 | 30 | 0 | 7.334 | 0 | 0 | 350 | 3825 | 3781.462 |
| 62 | 15 | 15 | 0 | 7.334 | 0 | 0 | 350 | 3850 | 3836.380 |
| 63 | 0 | 0 | 0 | 7.334 | 0 | 0 | 350 | 3805 | 3889.384 |
| 64 | 90 | 90 | 0 | 7.334 | 1 | 1 | 350 | 4300 | 4268.950 |
| 65 | 75 | 75 | 0 | 7.334 | 1 | 1 | 350 | 4350 | 4270.513 |
| 66 | 60 | 60 | 0 | 7.334 | 1 | 1 | 350 | 4005 | 4279.144 |
| 67 | 45 | 45 | 0 | 7.334 | 1 | 1 | 350 | 4365 | 4288.077 |
| 68 | 30 | 30 | 0 | 7.334 | 1 | 1 | 350 | 4386 | 4295.510 |
| 69 | 15 | 15 | 0 | 7.334 | 1 | 1 | 350 | 4370 | 4301.435 |
| 70 | 0 | 0 | 0 | 7.334 | 1 | 1 | 350 | 4390 | 4306.144 |
| 71 | 90 | 90 | 5.555 | 5.686 | 0 | 0 | 350 | 3410 | 3400.248 |
| 72 | 75 | 75 | 5.555 | 5.686 | 0 | 0 | 350 | 3550 | 3521.862 |
| 73 | 60 | 60 | 5.555 | 5.686 | 0 | 0 | 350 | 3510 | 3487.539 |
| 74 | 45 | 45 | 5.555 | 5.686 | 0 | 0 | 350 | 3500 | 3492.108 |
| 75 | 30 | 30 | 5.555 | 5.686 | 0 | 0 | 350 | 3520 | 3547.000 |
| 76 | 15 | 15 | 5.555 | 5.686 | 0 | 0 | 350 | 3480 | 3610.143 |
| 77 | 0 | 0 | 5.555 | 5.686 | 0 | 0 | 350 | 3475 | 3667.492 |
| 78 | 90 | 90 | 5.555 | 5.686 | 1 | 1 | 350 | 3930 | 4020.174 |
| 79 | 75 | 75 | 5.555 | 5.686 | 1 | 1 | 350 | 3975 | 3946.840 |
| 80 | 60 | 60 | 5.555 | 5.686 | 1 | 1 | 350 | 3910 | 3964.291 |
| 81 | 45 | 45 | 5.555 | 5.686 | 1 | 1 | 350 | 3970 | 3980.738 |
| 82 | 30 | 30 | 5.555 | 5.686 | 1 | 1 | 350 | 3955 | 3982.104 |
| 83 | 15 | 15 | 5.555 | 5.686 | 1 | 1 | 350 | 3980 | 3936.657 |
| 84 | 0 | 0 | 5.555 | 5.686 | 1 | 1 | 350 | 4010 | 3932.417 |
References
- Jiang, S.; Shen, L.; Guillard, F.; Einav, I. Energy dissipation from two-glass-bead chains under impact. Int. J. Impact Eng. 2018, 114, 160–168. [Google Scholar] [CrossRef]
- Jiang, S.; Shen, L.; Guillard, F.; Einav, I. The effect of inter-grain contact material on the dynamic fracture of short glass bead chains under impact. Powder Technol. 2018, 339, 911–921. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Wang, W.; Pu, C.; Wan, W.; Tang, J. Cracking and stress–strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 2016, 49, 2665–2687. [Google Scholar] [CrossRef]
- Fan, X.; Li, K.; Lai, H.; Xie, Y.; Cao, R.; Zheng, J. Internal stress distribution and cracking around flaws and openings of rock block under uniaxial compression: A particle mechanics approach. Comput. Geotech. 2018, 102, 28–38. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T.; Tang, C.A.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flaws—part I: Experimental approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 909–924. [Google Scholar] [CrossRef]
- Tang, C.A.; Lin, P.; Wong, R.H.C.; Chau, K.T. Analysis of crack coalescence in rock-like materials containing three flaws—part II: Numerical approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 925–939. [Google Scholar] [CrossRef]
- Nicholson, D.T.; Nicholson, F.H. Physical deterioration of sedimentary rocks subjected to experimental freeze–thaw weathering. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2000, 25, 1295–1307. [Google Scholar] [CrossRef]
- Le, H.; Sun, S.; Kulatilake, P.H.; Wei, J. Effect of grout on mechanical properties and cracking behavior of rock-like specimens containing a single flaw under uniaxial compression. Int. J. Geomech. 2018, 18, 04018129. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, Y.; Lai, J. Influence of ground temperature on shotcrete-to-rock adhesion in tunnels. Adv. Mater. Sci. Eng. 2019, 2019, 8709087. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Aliabadian, Z.; Shen, L. Crack initiation and failure development in bimrocks using digital image correlation under dynamic load. Theor. Appl. Fract. Mech. 2020, 109, 102688. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lin, H.; Zhao, Y.; Li, X.; Liu, Y. Mechanical behavior and failure analysis of fracture-filled gneissic granite. Theor. Appl. Fract. Mech. 2020, 108, 102674. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Li, X.; Wu, D.; Zhang, G. Underlying mechanisms of crack initiation for granitic rocks containing a single pre-existing flaw: Insights from digital image correlation (DIC) analysis. Rock Mech. Rock Eng. 2020, 54, 1–17. [Google Scholar]
- Yan, Z.; Dai, F.; Liu, Y.; Du, H.; Luo, J. Dynamic Strength and Cracking Behaviors of Single-Flawed Rock Subjected to Coupled Static–Dynamic Compression. Rock Mech. Rock Eng. 2020, 53, 4289–4298. [Google Scholar] [CrossRef]
- Zhao, C.; Meng Zhou, Y.; Feng Zhao, C.; Bao, C. Cracking processes and coalescence modes in rock-like specimens with two parallel pre-existing cracks. Rock Mech. Rock Eng. 2018, 51, 3377–3393. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Yang, S.-Q.; Tian, W.-L. Crack coalescence behavior of sandstone specimen containing two pre-existing flaws under different confining pressures. Theor. Appl. Fract. Mech. 2019, 99, 118–130. [Google Scholar] [CrossRef]
- Zhou, X.-P.; Li, G.-Q.; Ma, H.-C. Real-time experiment investigations on the coupled thermomechanical and cracking behaviors in granite containing three pre-existing fissures. Eng. Fract. Mech. 2020, 224, 106797. [Google Scholar] [CrossRef]
- Chen, S.; Xia, Z.; Feng, F.; Yin, D. Numerical study on strength and failure characteristics of rock samples with different hole defects. Bull. Eng. Geol. Environ. 2020, 80, 1–18. [Google Scholar] [CrossRef]
- Xi, X.; Wu, X.; Guo, Q.; Cai, M. Experimental investigation and numerical simulation on the crack initiation and propagation of rock with pre-existing cracks. IEEE Access 2020, 8, 129636–129644. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lin, H.; Zhao, Y.; Liu, Y. Fracture behaviour of central-flawed rock plate under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 106, 102503. [Google Scholar] [CrossRef]
- Liu, G.; Peng, J.; Zhang, Z.; Wang, Z.; Yang, Y. Numerical investigation of fluid-driven crack propagation and coalescence in granite specimen with two pre-existing flaws. J. Nat. Gas Sci. Eng. 2020, 75, 103132. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Li, Q.; Wang, H. A method to model the effect of pre-existing cracks on P-wave velocity in rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 493–506. [Google Scholar] [CrossRef]
- Altindag, R. Correlation between P-wave velocity and some mechanical properties for sedimentary rocks. J. South. Afr. Inst. Min. Metall. 2012, 112, 229–237. [Google Scholar]
- Liu, X.; Athanasiou, C.E.; Padture, N.P.; Sheldon, B.W.; Gao, H. A machine learning approach to fracture mechanics problems. Acta Mater. 2020, 190, 105–112. [Google Scholar] [CrossRef]
- Nasiri, S.; Khosravani, M.R.; Weinberg, K. Fracture mechanics and mechanical fault detection by artificial intelligence methods: A review. Eng. Fail. Anal. 2017, 81, 270–293. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Niedostatkiewicz, M.; Kang, S.-B. Model-Based Adaptive Machine Learning Approach in Concrete Mix Design. Materials 2021, 14, 1661. [Google Scholar] [CrossRef] [PubMed]
- Atici, U. Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst. Appl. 2011, 38, 9609–9618. [Google Scholar] [CrossRef]
- Gope, D.; Gope, P.C.; Thakur, A.; Yadav, A. Application of artificial neural network for predicting crack growth direction in multiple cracks geometry. Appl. Soft Comput. 2015, 30, 514–528. [Google Scholar] [CrossRef]
- Yan, Y.; Ren, Q.; Xia, N.; Shen, L.; Gu, J. Artificial neural network approach to predict the fracture parameters of the size effect model for concrete. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1347–1358. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Abdulhamid, S.N.; Salim, S.G.; Ali, H.F.H.; Majeed, M.K. Artificial intelligence forecasting models of uniaxial compressive strength. Transp. Geotech. 2021, 27, 100499. [Google Scholar] [CrossRef]
- Ferentinou, M.; Fakir, M. An ANN approach for the prediction of uniaxial compressive strength, of some sedimentary and igneous rocks in eastern KwaZulu-Natal. Procedia Eng. 2017, 191, 1117–1125. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Shen, L. Experimental Investigation of Dynamic Fracture Patterns of 3D Printed Rock-like Material Under Impact with Digital Image Correlation. Rock Mech. Rock Eng. 2020, 53, 1–19. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Shen, L.; Zheng, Y.; Xiao, J. The effect of flaw filling material on the compressive behaviour of 3D printed rock-like discs. Int. J. Rock Mech. Min. Sci. 2019, 117, 105–117. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Shen, L.; Xu, Q. Characterisation of mechanical behaviour of 3D printed rock-like material with digital image correlation. Int. J. Rock Mech. Min. Sci. 2018, 112, 122–138. [Google Scholar] [CrossRef]
- Mazahery, A.; Shabani, M.O. Process conditions optimization in Al–Cu alloy matrix composites. Powder Technol. 2012, 225, 101–106. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Naderpour, H.; Poursaeidi, O.; Ahmadi, M. Shear resistance prediction of concrete beams reinforced by FRP bars using artificial neural networks. Measurement 2018, 126, 299–308. [Google Scholar] [CrossRef]
- Faisal, A.A.; Naji, L.A. Simulation of ammonia nitrogen removal from simulated wastewater by sorption onto waste foundry sand using artificial neural network. Assoc. Arab Univ. J. Eng. Sci. 2019, 26, 28–34. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection weights. AI EXPERT 1991, 6, 47–51. [Google Scholar]

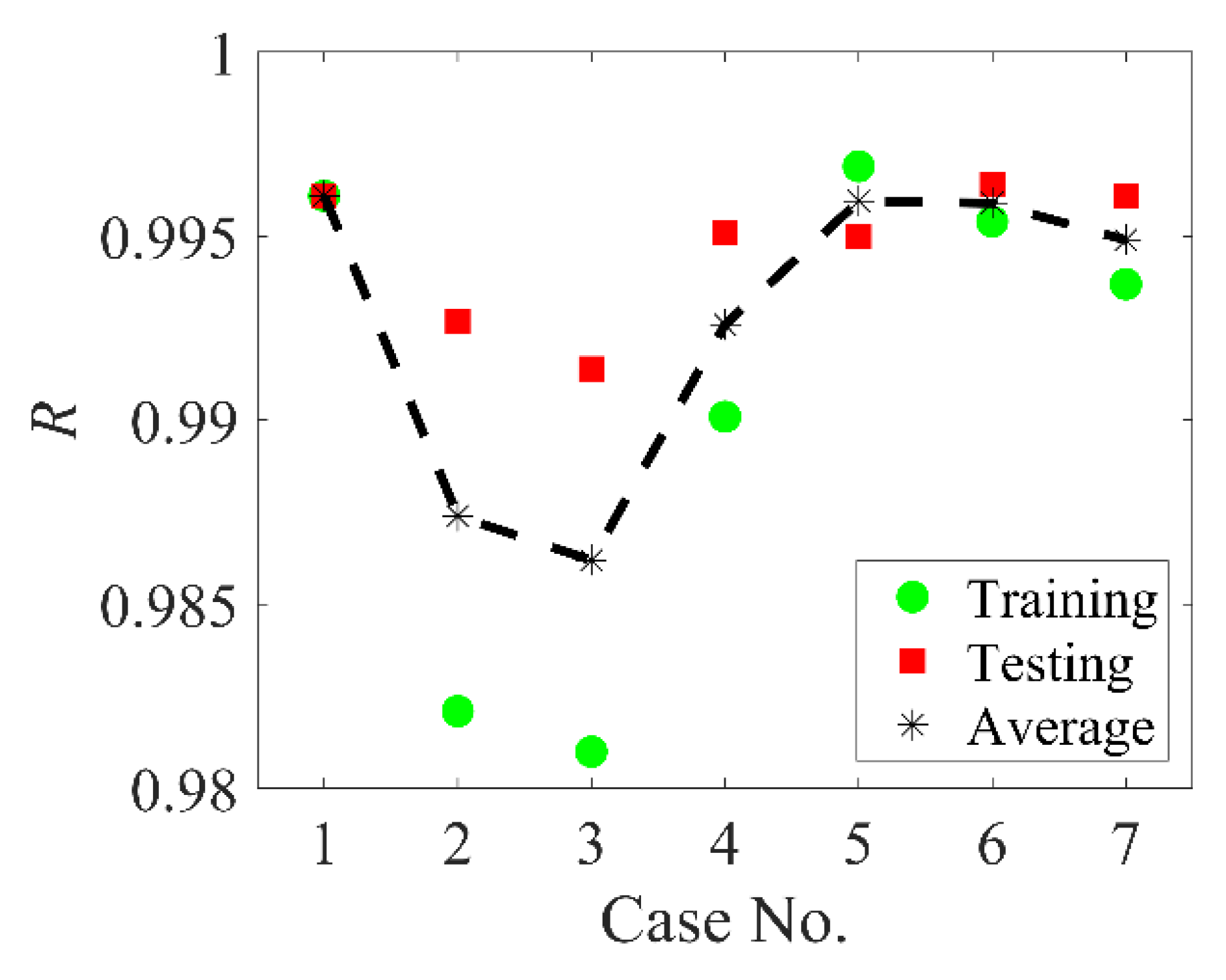

| Case No. | Input Variables | Hidden Layer | Output Layer | Output Variable |
|---|---|---|---|---|
| 1 | Normalized | Tan-sigmoid | Tan-sigmoid | Normalized |
| 2 | Normalized | Tan-sigmoid | Sigmoid | Normalized |
| 3 | Normalized | Sigmoid | Sigmoid | Normalized |
| 4 | Normalized | Tan-sigmoid | Linear | Raw |
| 5 | Normalized | Sigmoid | Linear | Raw |
| 6 | Raw | Tan-sigmoid | Linear | Raw |
| 7 | Raw | Sigmoid | Linear | Raw |
| Input layer neuron number | 7 |
| Hidden layer neuron number | 5 |
| Output layer neuron number | 1 |
| Data division | Randomly (70% training, 15% validation, 15% testing) |
| Hidden layer transfer function | Tan-sigmoid |
| Output layer transfer function | Tan-sigmoid |
| Early stopping criterion | 10 epochs for validation check |
| Target error | 10−6 |
| Training algorithm | Levenberg–Marquardt |
| Test No. | Mean Absolute Relative Error (%) | |||
|---|---|---|---|---|
| Mean | SD | COV (%) | ||
| Static (No.1–No.42) | 1.01 | 0.12 | 1.37 | 7.46 |
| Dynamic (No.43–No.84) | 1.00 | 0.02 | 0.04 | 1.51 |
| Overall (No.1–No.84) | 1.00 | 0.08 | 0.70 | 4.49 |
| Case No. | Number of Inputs | Inputs | Mean Absolute Relative Error (%) |
|---|---|---|---|
| 1 | 7 | , ,, ,, , | 4.49 (Reference) |
| 2 | 6 | ,, ,, , | 6.26 |
| 3 | ,, ,, , | 5.75 | |
| 4 | ,,,, , | 7.39 | |
| 5 | ,,,, , | 6.02 | |
| 6 | ,,, ,, | 5.96 | |
| 7 | ,,, ,, | 6.36 | |
| 8 | ,,,,, | 68.40 | |
| 9 | 5 | ,,,, | 6.38 |
| 10 | ,,,, | 6.43 | |
| 11 | ,,,, | 6.50 | |
| 12 | 4 | ,,, | 6.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Sharafisafa, M.; Shen, L. Using Artificial Neural Networks to Predict Influences of Heterogeneity on Rock Strength at Different Strain Rates. Materials 2021, 14, 3042. https://doi.org/10.3390/ma14113042
Jiang S, Sharafisafa M, Shen L. Using Artificial Neural Networks to Predict Influences of Heterogeneity on Rock Strength at Different Strain Rates. Materials. 2021; 14(11):3042. https://doi.org/10.3390/ma14113042
Chicago/Turabian StyleJiang, Sheng, Mansour Sharafisafa, and Luming Shen. 2021. "Using Artificial Neural Networks to Predict Influences of Heterogeneity on Rock Strength at Different Strain Rates" Materials 14, no. 11: 3042. https://doi.org/10.3390/ma14113042
APA StyleJiang, S., Sharafisafa, M., & Shen, L. (2021). Using Artificial Neural Networks to Predict Influences of Heterogeneity on Rock Strength at Different Strain Rates. Materials, 14(11), 3042. https://doi.org/10.3390/ma14113042







