Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach
Abstract
1. Introduction
2. Experimental Details
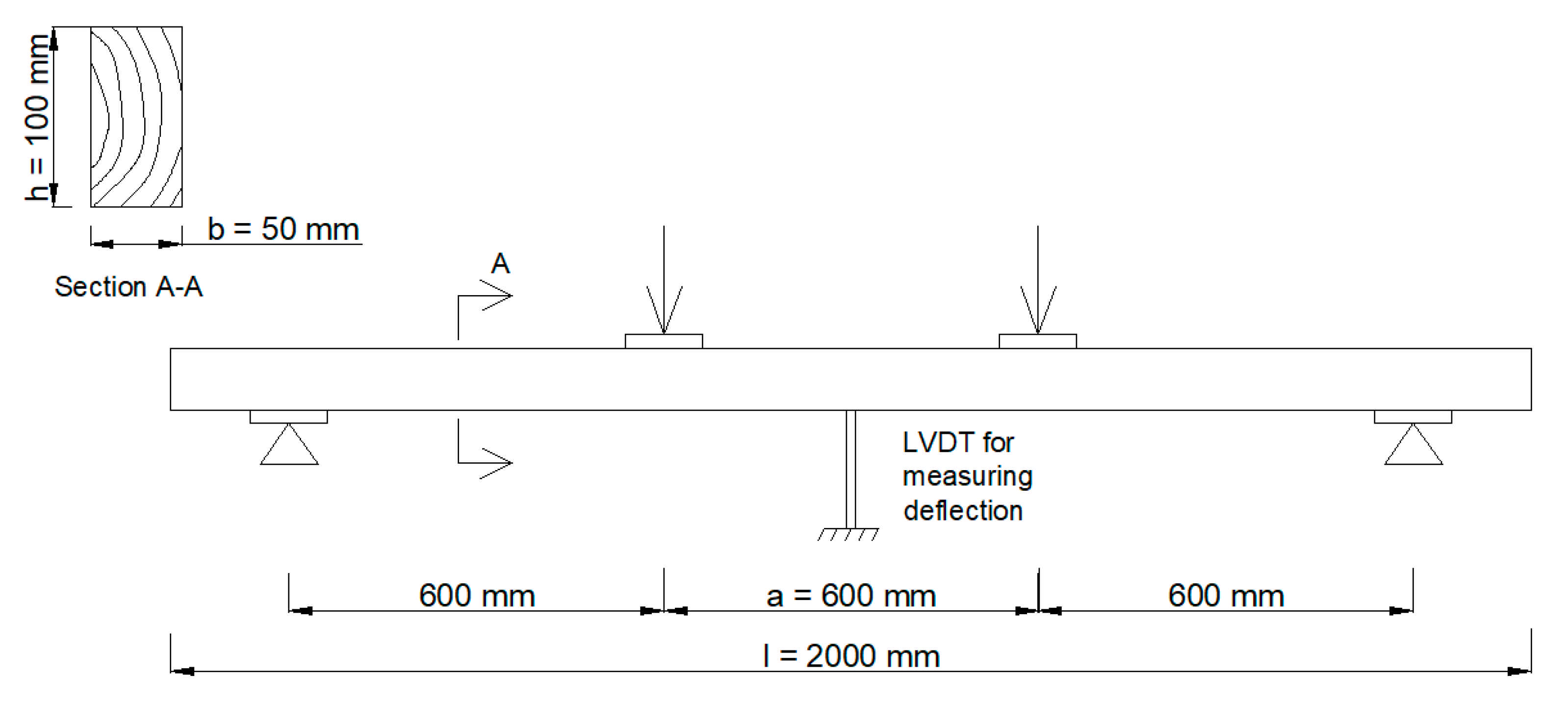
2.1. Material
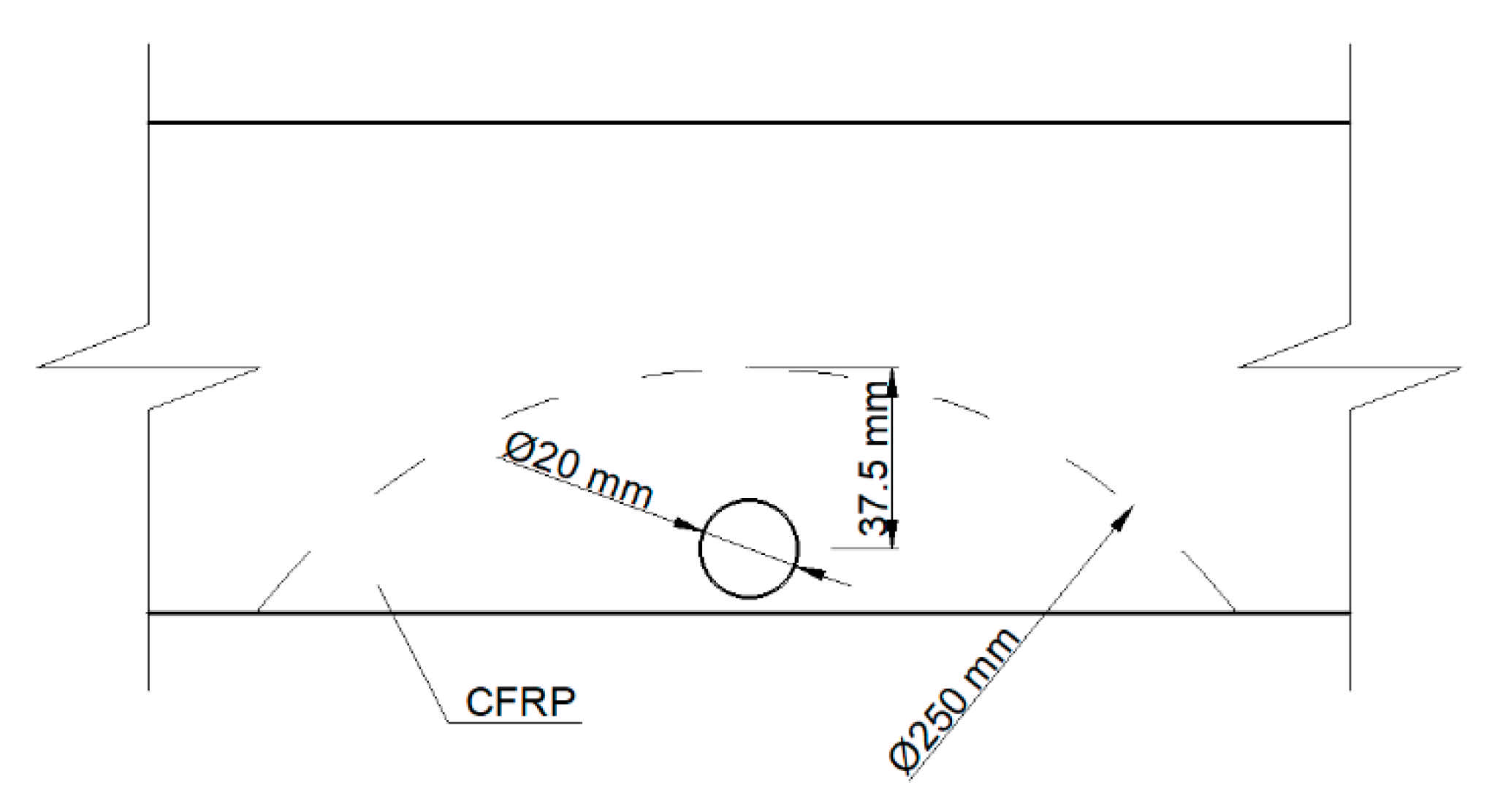
2.2. Methods
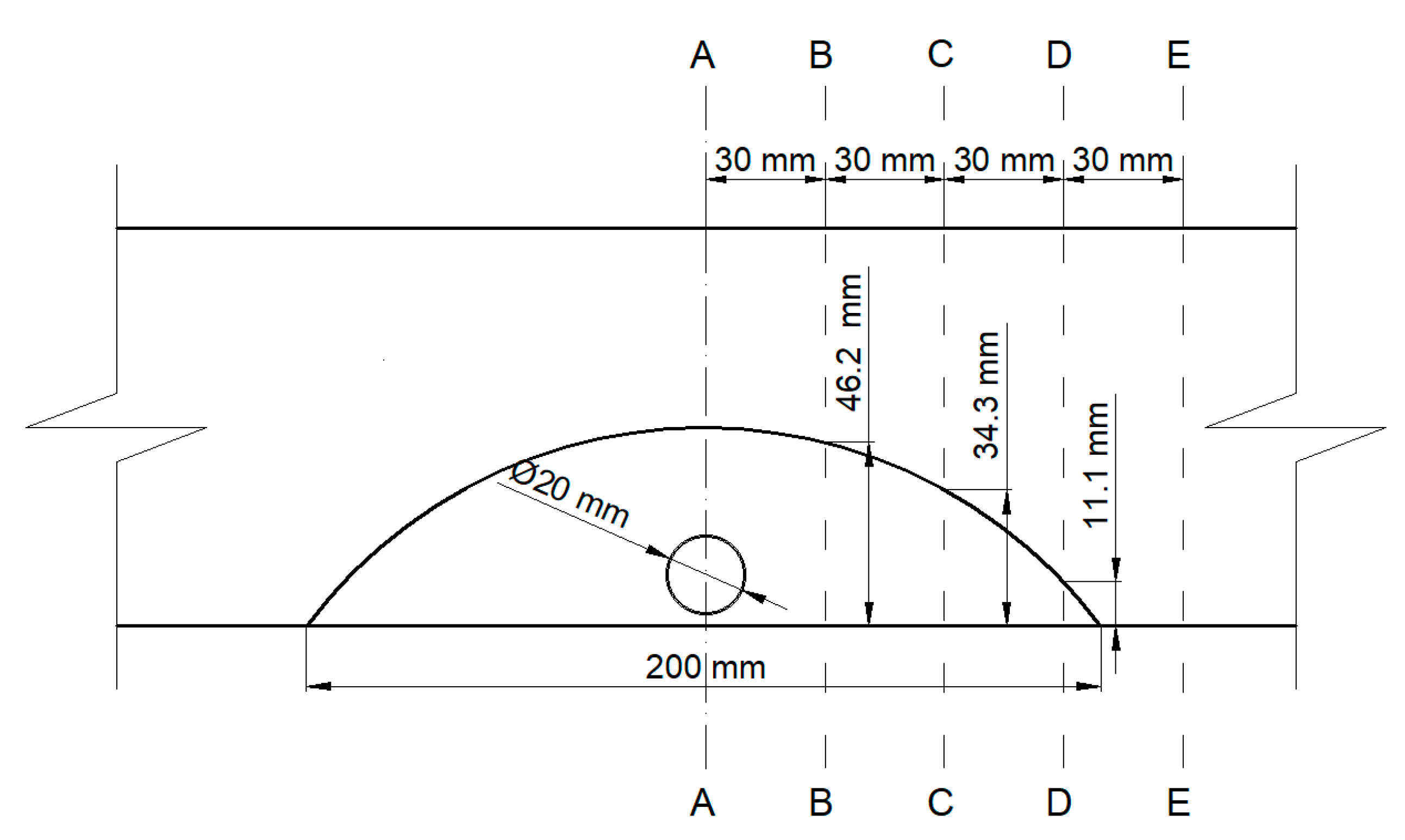
2.3. Results
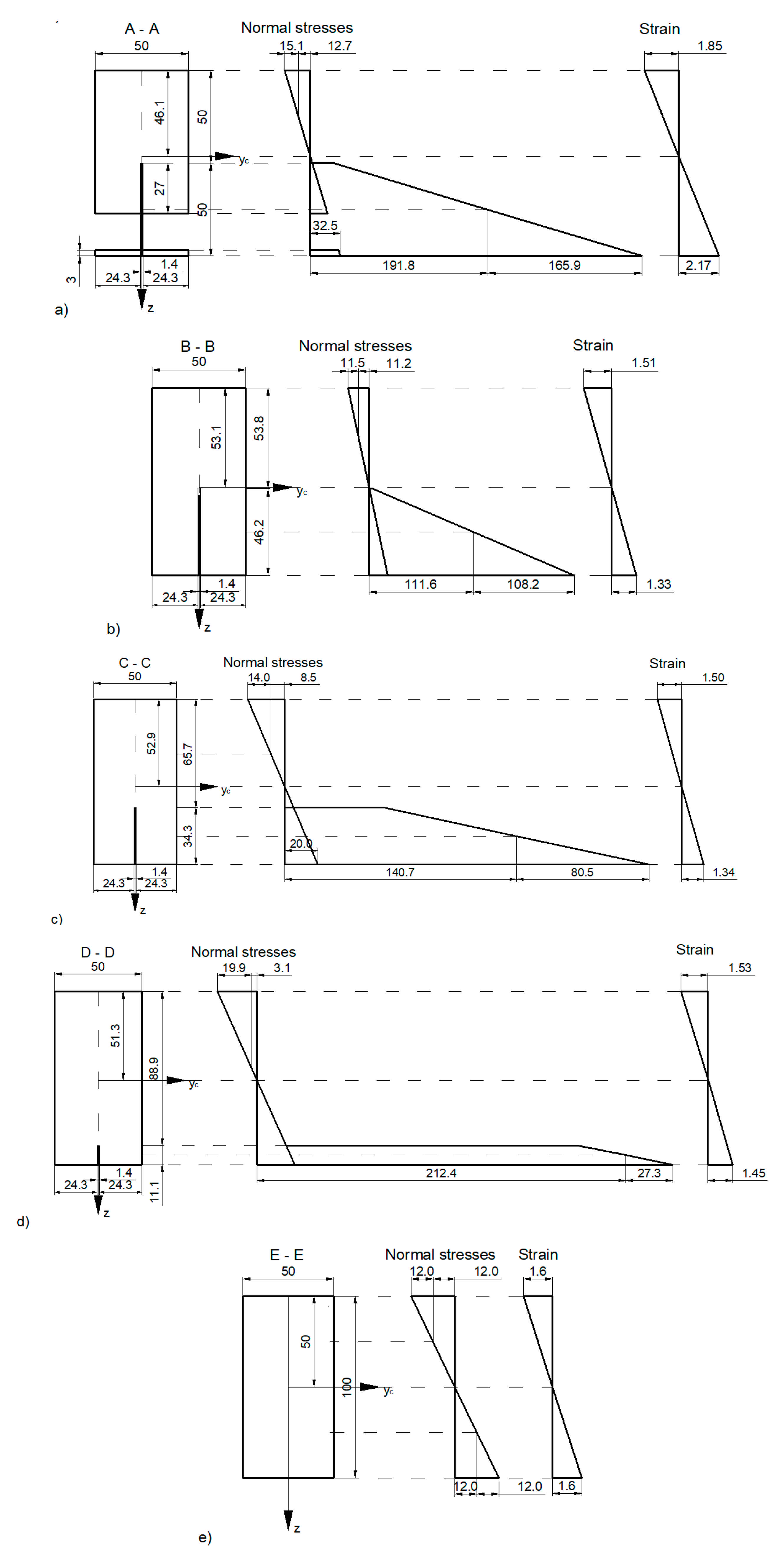
3. Analytical Analysis
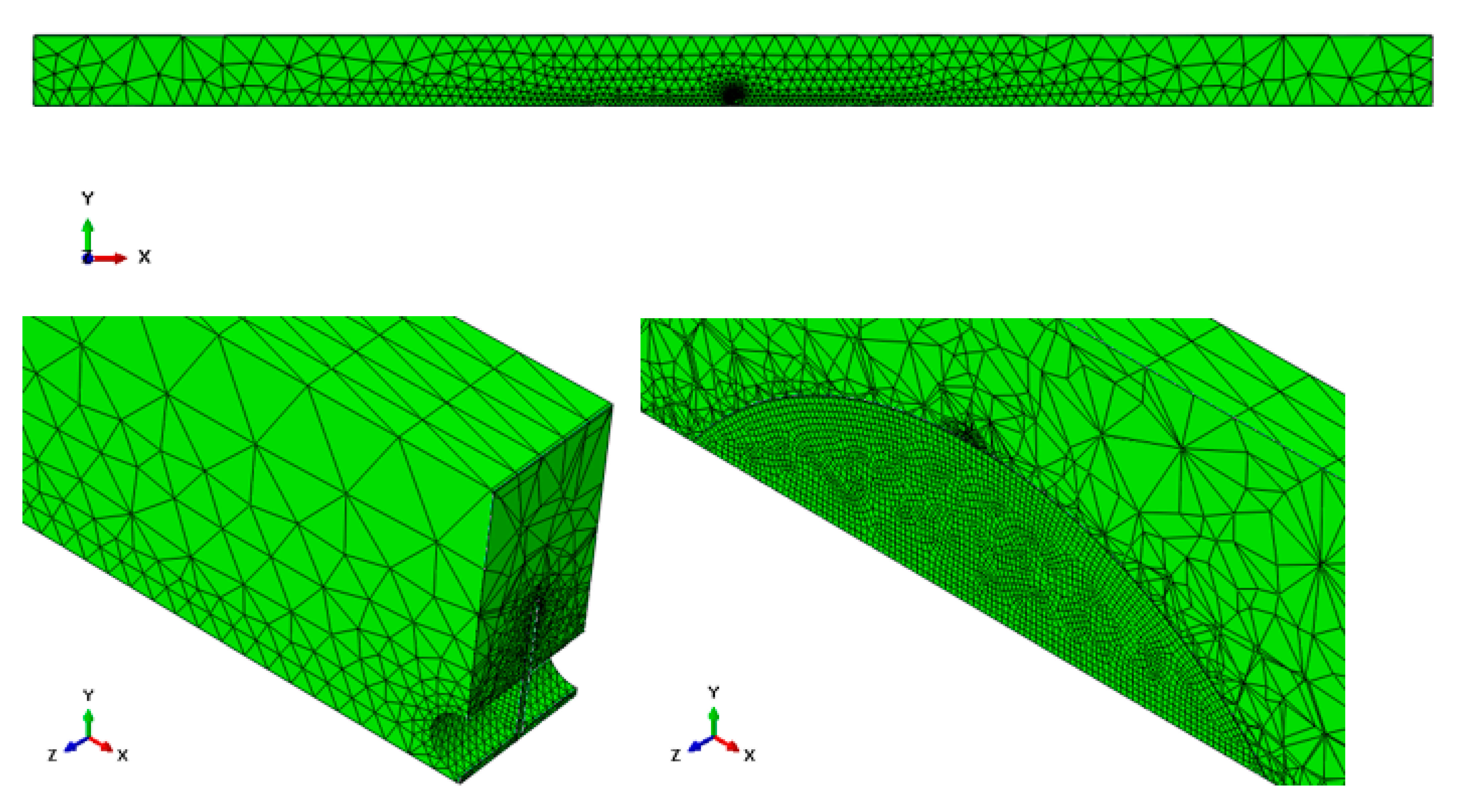
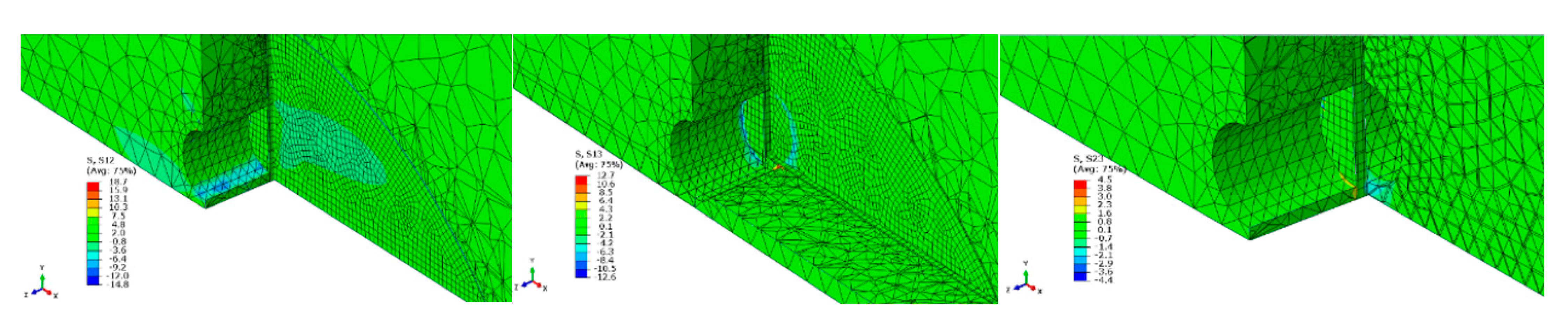
4. FEM Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kretschmann, D.E. Mechanical Properties of Wood—Wood Handbook; Forest Products Laboratory, United States Department of Agricultural Forest Service: Madison, WI, USA, 2010. [Google Scholar]
- Johansson, C.J.; Boström, L.; Bräuner, L.; Hoffmeyer, P.; Holmquist, C.; Solli, K.H. Laminations for Glued Laminated Timber—Establishment of Strength Classes for Visual Strength Grades and Machine Settings for Glulam Laminations of Nordic Origin; A Nordic Wood Project, Sp. Report 38; SP Swedish National Testing and Research Institute: Borås, Sweden, 1998. [Google Scholar]
- Teischinger, A.; Patzelt, M. XXL-Wood. Materialkenngrößen als Grundlage für Innovative Verarbeitungstechnologien und Produkte zur Wirtschaftlichen Nachhaltigen Nutzung der Österreichischen Nadelstarkholzreserven. In Berichte aus Energie und Umweltforschung; 27/2006; Universität für Bodenkultur Wien: Wien, Austria, 2006. [Google Scholar]
- Mettem, C.J. The Principles Involved in Stress Grading with Special Reference to Its Application in Developing Countries; UNIDO—United Nations Industrial Development Organization: Vienna, Austria, 1981. [Google Scholar]
- Ridley-Ellis, D.; Stapel, P.; Baño, V. Strength grading of sawn timber in Europe: An explanation for engineers and researchers. Eur. J. Wood Wood Prod. 2016, 74, 291–306. [Google Scholar] [CrossRef]
- Johansson, C.J. Grading of Timber with Respect to Mechanical Properties. In Timber Engineering; Thelandersson, S., Larsen, H.J., Eds.; Wiley & Sons: London, UK, 2003; pp. 23–43. [Google Scholar]
- PN-D-94021. Tarcica Konstrukcyjna Iglasta Sortowana Metodami Wytrzymałościowymi; Polski Komitet Normalizacyjny: Warsaw, Poland, 2013. [Google Scholar]
- Martínez-Martínez, J.E.; Alonso-Martínez, M.; Rabanal, F.P.Á.; Díaz, J.J.d.C. Finite Element Analysis of Composite Laminated Timber (CLT). Proceedings 2018, 2, 1454. [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M. Three-Dimensional Modelling of Notched Connections for Timber—Concrete Composite Beams. Struct. Eng. Int. 2017, 27, 184–196. [Google Scholar] [CrossRef]
- Phillips, G.E.; Bodig, J.; Goodman, J.R. Flow grain analogy. Wood Sci. 1981, 14, 55–64. [Google Scholar]
- Baňo, V. Numerical Analysis of Wood Strength Loss Due to Presence of Knots. Ph.D. Thesis, Polytechnic University of Madrid, Madrid, Spain, 2009. [Google Scholar]
- Guindos, P.; Guaita, M. The analytical influence of all types of knots on bending. Wood Sci. Technol. 2014, 48, 533–552. [Google Scholar] [CrossRef]
- Foley, C. A three-dimensional paradigm of fiber orientation in timber. Wood Sci. Technol. 2001, 35, 453–465. [Google Scholar] [CrossRef]
- Guindos, P.; Guaita, M. A three-dimensional wood material model to simulate the behavior of wood with any type of knot at the macro-scale. Wood Sci. Technol. 2013, 47, 585–599. [Google Scholar] [CrossRef]
- Lukacevic, M.; Füssl, J.; Lampert, R. Failure mechanisms of clear wood identified at wood cell level by an approach based on the extended finite element method. Eng. Fract. Mech. 2015, 144, 158–175. [Google Scholar] [CrossRef]
- Lukacevic, M.; Lederer, W.; Füssl, J. A microstructure-based multisurface failure criterion for the description of brittle and ductile failure mechanisms of clearwood. Eng. Fract. Mech. 2017, 176, 83–99. [Google Scholar] [CrossRef]
- Oscarsson, J.; Olsson, A.; Enquist, B. Strain fields around knots in Norway spruce specimens exposed to tensile forces. Wood Sci. Technol. 2012, 46, 593–610. [Google Scholar] [CrossRef]
- Baňo, V.; Arriaga, F.; Guaita, M. Determination of the influence of size and position of knots on load capacity and stress distribution in timber beams of Pinus sylvestris using finite element model. Biosyst. Eng. 2013, 114, 214–222. [Google Scholar] [CrossRef]
- Baňo, V.; Arriaga, F.; Soilan, A.; Guaita, M. Prediction of bending load capacity of timber beams using a finite element method simulation of knots and grain deviation. Biosyst. Eng. 2011, 109, 241–249. [Google Scholar] [CrossRef]
- Goodman, J.R.; Bodig, J. Mathematical Model of the Tension Behaviour of Wood with Knots and Cross Grain. In Proceedings of the First International Conference on Wood Fracture, Banff, AB, Canada, 14–16 August 1978. [Google Scholar]
- Foley, C. Modelling the Effects of Knots in Structural Timber. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Konopka, D.; Gebhardt, C.; Kaliske, M. Numerical modelling of wooden structures. J. Cult. Herit. 2016, 27, 93–102. [Google Scholar] [CrossRef]
- Jockwer, R.; Serrano, E.; Gustafsson, P.-J.; Steiger, R. Impact of knots on the fracture propagating along grain in timber beams. Int. Wood Prod. J. 2017, 8, 1–6. [Google Scholar] [CrossRef]
- Lang, R.; Kaliske, M. Description of inhomogeneities in wooden structures: Modelling of branches. Wood Sci. Technol. 2013, 47, 1051–1070. [Google Scholar] [CrossRef]
- Guindos, P. Method for the integral calculation of the fiber orientation and the fundamental material properties of softwood logs and lumber. Holzforschung 2016, 70, 981–991. [Google Scholar] [CrossRef]
- Hu, M.; Olsson, A.; Johansson, M.; Oscarsson, J. Modelling local bending stiffness based on fibre orientation in sawn timber. Eur. J. Wood Wood Prod. 2018, 76, 1605–1621. [Google Scholar] [CrossRef]
- EN 408 +A1. Timber Structures. Structural Timber and Glued Laminated Timber. Determination of Some Physical and Mechanical Properties; European Committee for Standardization (CEN): Brussels, Belgium, 2012. [Google Scholar]
- EN 1995-1-1. Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2010. [Google Scholar]
- Kollmann, F.F.P.; Côté, A.C.J. Principles of Wood Science and Technology: Solid Wood; Springer: Berlin, Germany, 1968. [Google Scholar]
- Nowak, T. Analiza Pracy Statycznej Zginanych Belek Drewnianych Wzmacnianych Przy Użyciu CFRP. Ph.D. Thesis, Wroclaw University of Science and Technology, Wrocław, Poland, 2007. [Google Scholar]



| Property | CFRP Strip |
|---|---|
| density (kg/m3) | 1500 |
| Young’s modulus (N/mm2) | >165 |
| tensile strength (N/mm2) | >2800 |
| Property | All Samples | Weakened Samples | Reinforced Samples |
|---|---|---|---|
| density (kg/m3) | 563 (62.5) | 556 (69.7) | 561 (55.3) |
| bending stiffness (Nm2) | 51,993 (9557) | 48,140 (9688) | 46,446 (8641) |
| bending strength (N/mm2) | - | 24.4 (7.5) | 41.9 (7.7) |
| Parameter | σ11 | σ22 | σ33 | σ12 | σ13 | σ23 | σ0 |
|---|---|---|---|---|---|---|---|
| N/mm2 | 15.5 | 3.6 | 3.6 | 6.0 | 6.0 | 3.0 | 15.5 |
| Beam/Parameter | E1 N/mm2 | E2 N/mm2 | E3 N/mm2 | μ12 - | μ13 - | μ23 - | G12 N/mm2 | G13 N/mm2 | G23 N/mm2 |
|---|---|---|---|---|---|---|---|---|---|
| Beam 1 46 × 100 × 1995 mm3 | 13,500 | 1080 | 675 | 0.42 | 0.37 | 0.47 | 964 | 906 | 96 |
| Beam 2 47 × 100 × 2002 mm3 | 13,050 | 1044 | 653 | 0.42 | 0.37 | 0.47 | 932 | 876 | 93 |
| Beam 3 47 × 100 × 2002 mm3 | 10,663 | 853 | 533 | 0.42 | 0.37 | 0.47 | 762 | 716 | 76 |
| Parameter | E N/mm2 | μ - |
|---|---|---|
| 3000 | 0.3 |
| Parameter | E1 N/mm2 | E2 N/mm2 | E3 N/mm2 | μ12 - | μ13 - | μ23 - | G12 N/mm2 | G13 N/mm2 | G23 N/mm2 |
|---|---|---|---|---|---|---|---|---|---|
| 165,000 | 10,000 | 10,000 | 0.3 | 0.3 | 0.03 | 5000 | 5000 | 500 |
| Beam/Parameter | Destructive Force (N) | Deflection (mm) | |
|---|---|---|---|
| Experimental | FEM | ||
| Beam 1 | 11,030 | 19.1 | 17.2 |
| Beam 2 | 11,369 | 23.6 | 20.3 |
| Beam 3 | 10,214 | 27.2 | 24.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burawska-Kupniewska, I.; Beer, P. Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach. Materials 2021, 14, 2780. https://doi.org/10.3390/ma14112780
Burawska-Kupniewska I, Beer P. Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach. Materials. 2021; 14(11):2780. https://doi.org/10.3390/ma14112780
Chicago/Turabian StyleBurawska-Kupniewska, Izabela, and Piotr Beer. 2021. "Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach" Materials 14, no. 11: 2780. https://doi.org/10.3390/ma14112780
APA StyleBurawska-Kupniewska, I., & Beer, P. (2021). Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach. Materials, 14(11), 2780. https://doi.org/10.3390/ma14112780






