Relationships among the Characteristic Tensile Strain, Curing Age, and Strength of Reactive Powder Concrete
Abstract
1. Introduction
2. Experimental Program
2.1. Production of Test Materials and Test Samples
2.2. Test Method
3. Analysis of Experimental Results
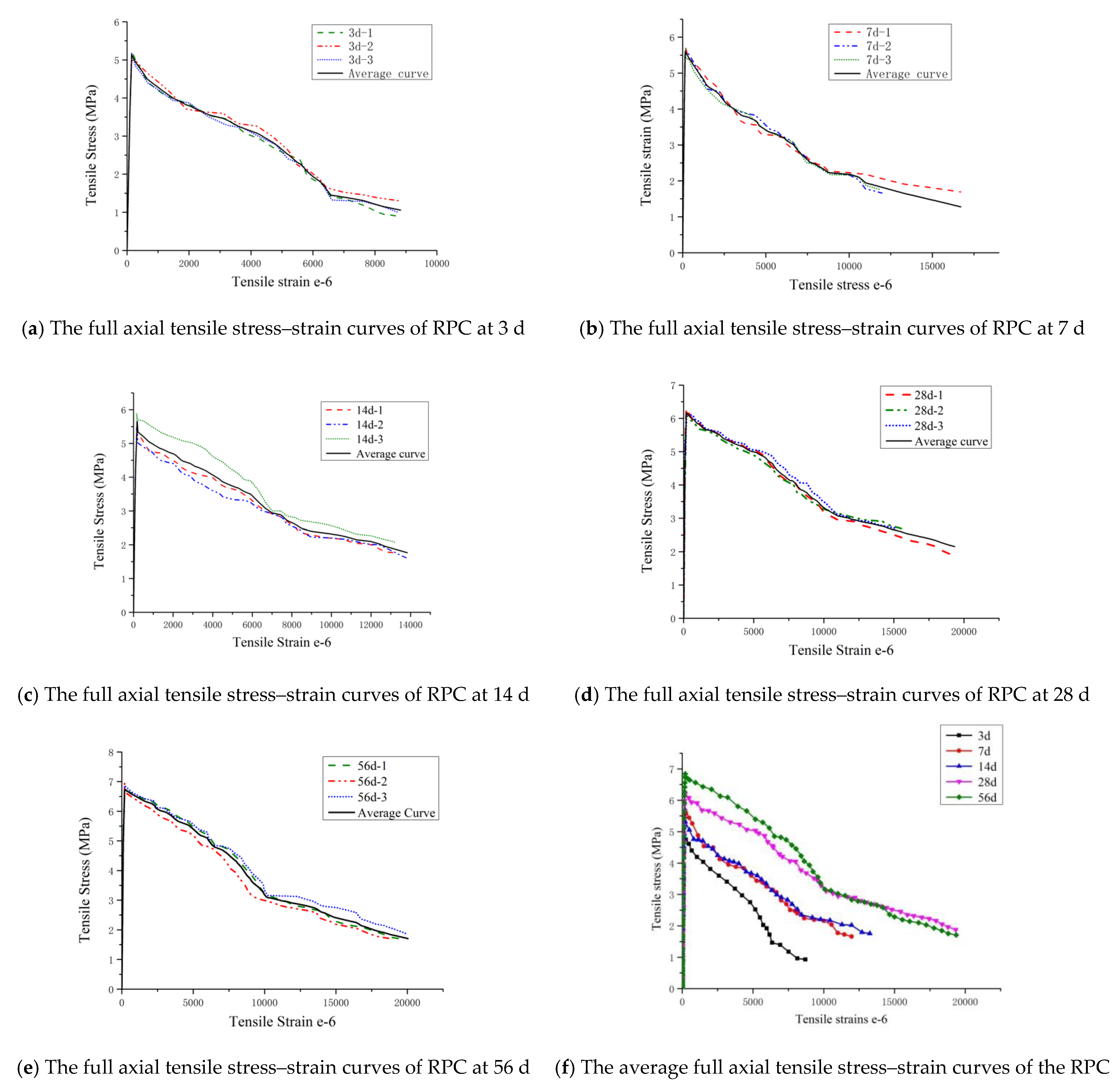
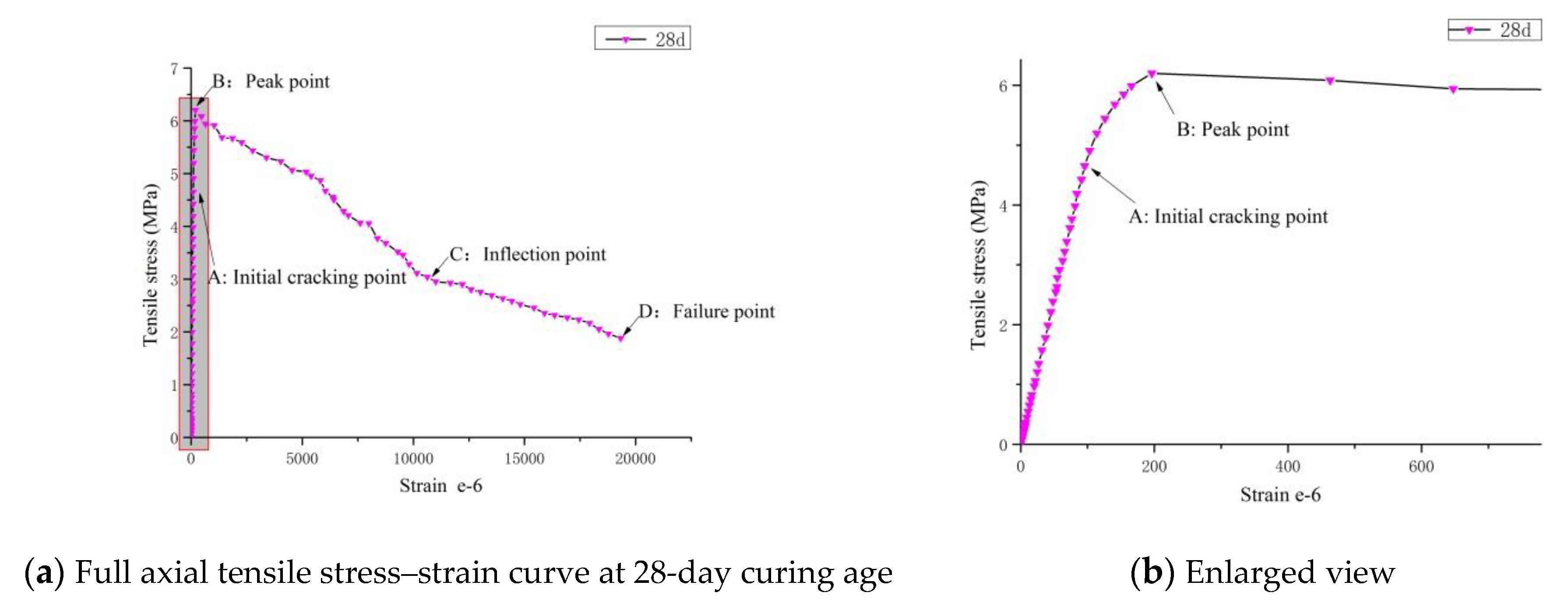
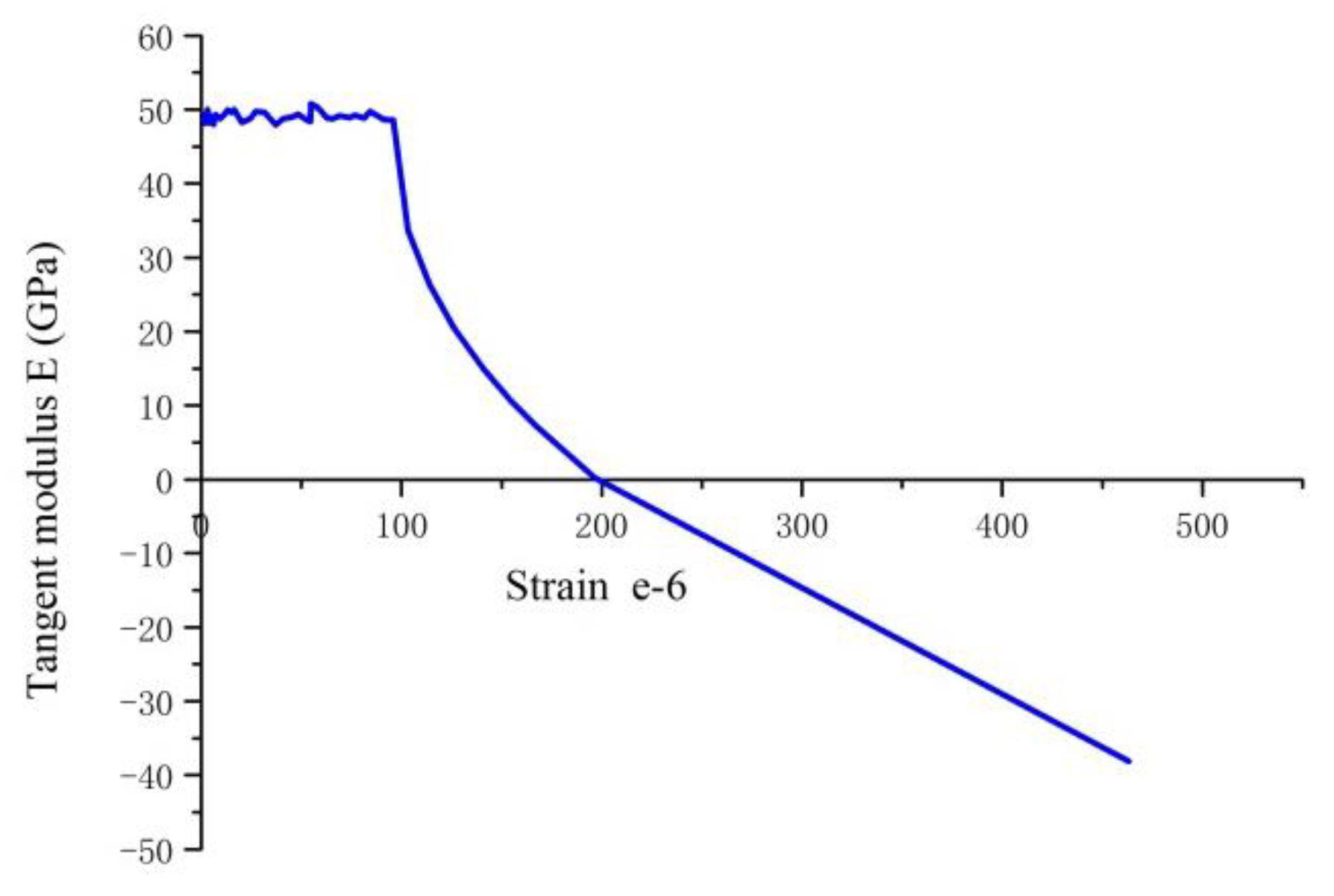
3.1. Full Axial Tensile Stress–Strain Curves
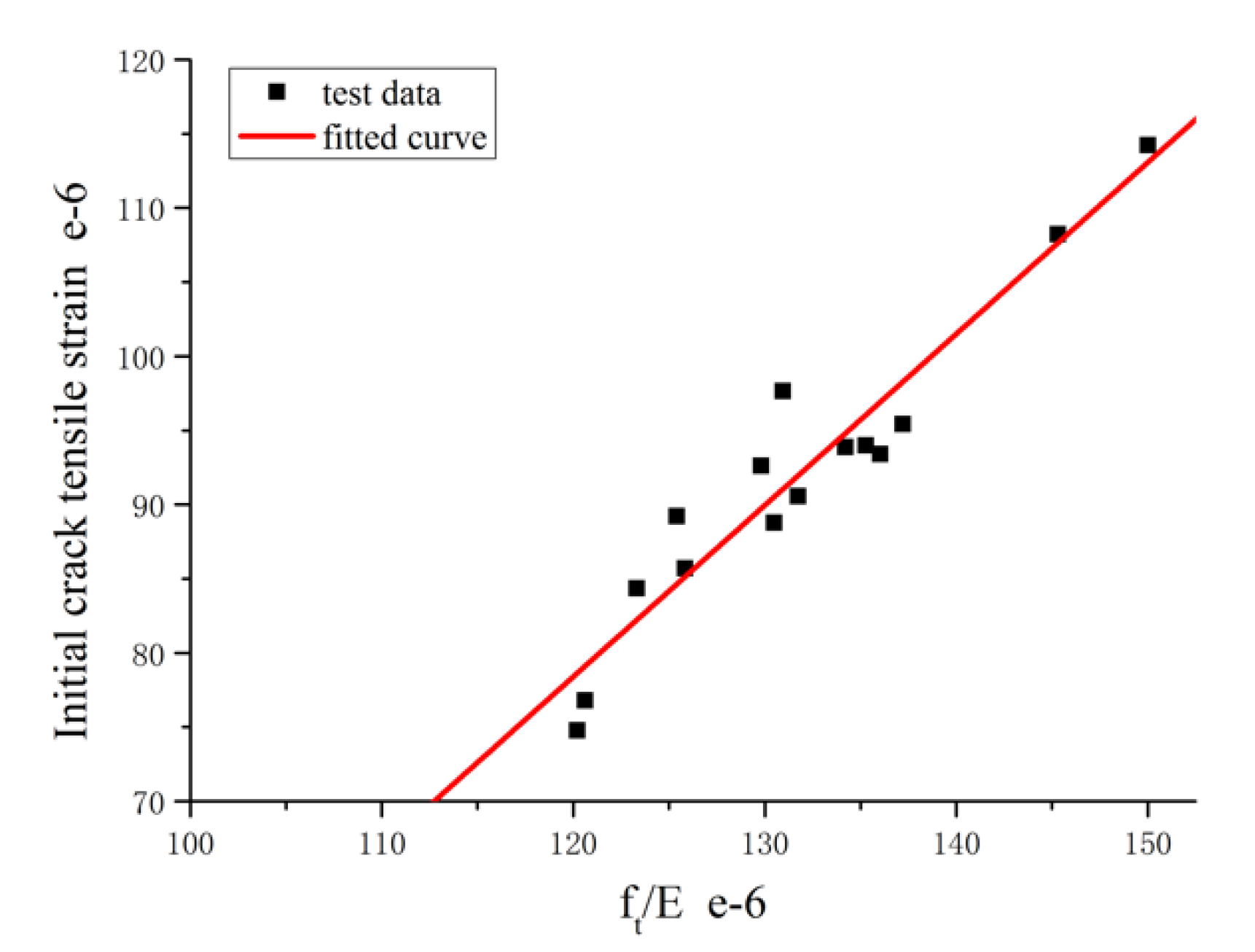
3.2. Relationship between Initial Tensile Strain and Age
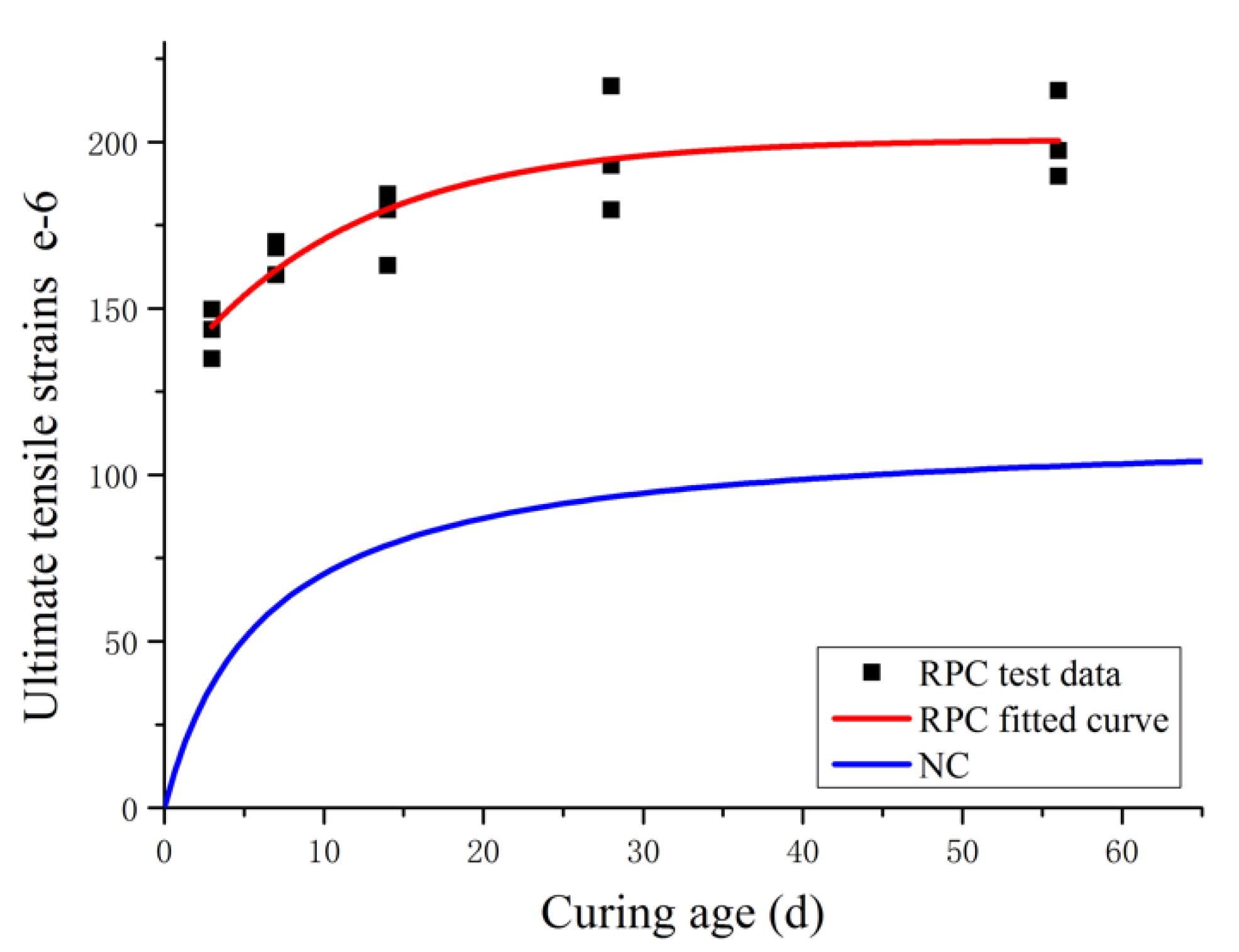
3.3. Relationship between Ultimate Tensile Strain and Age
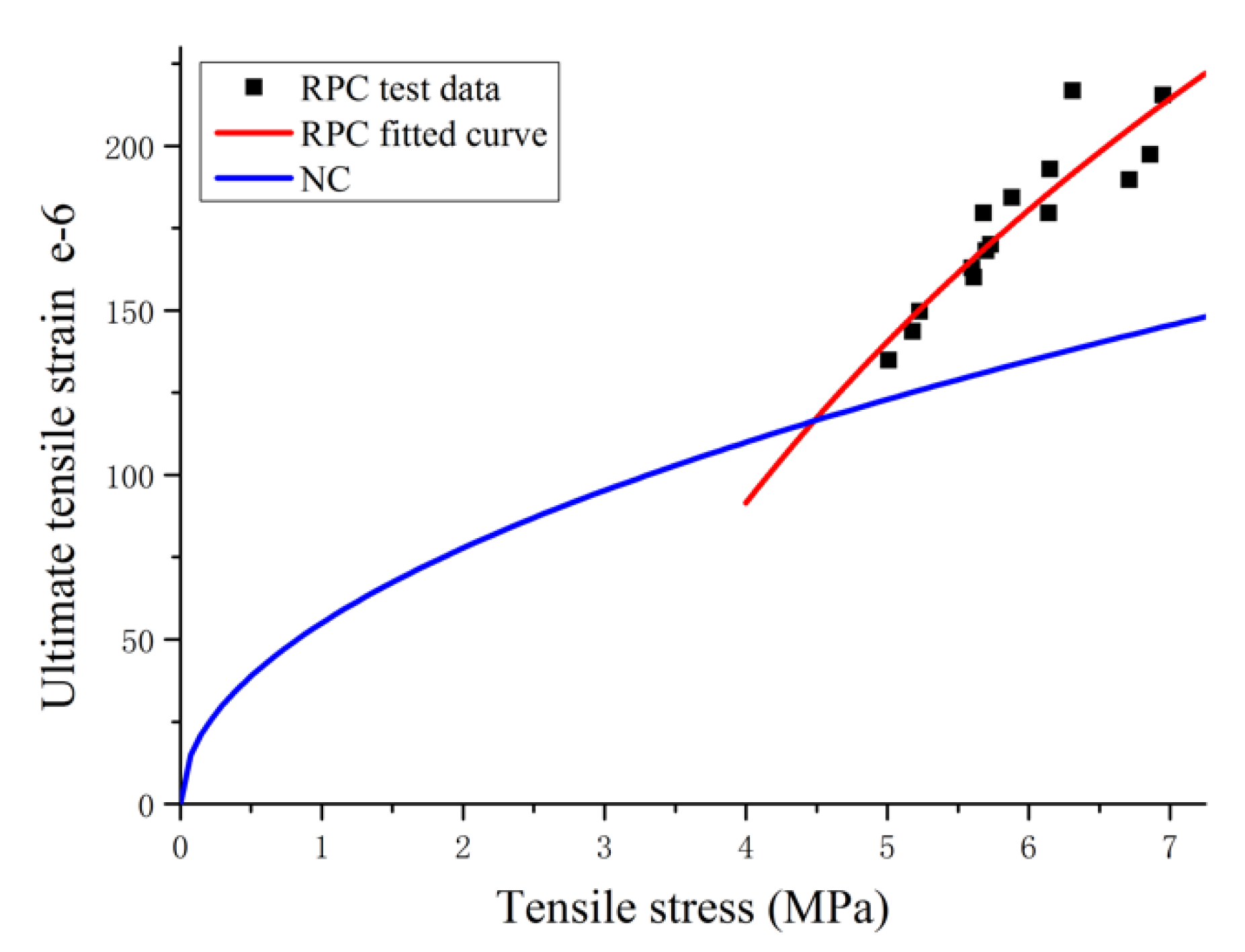
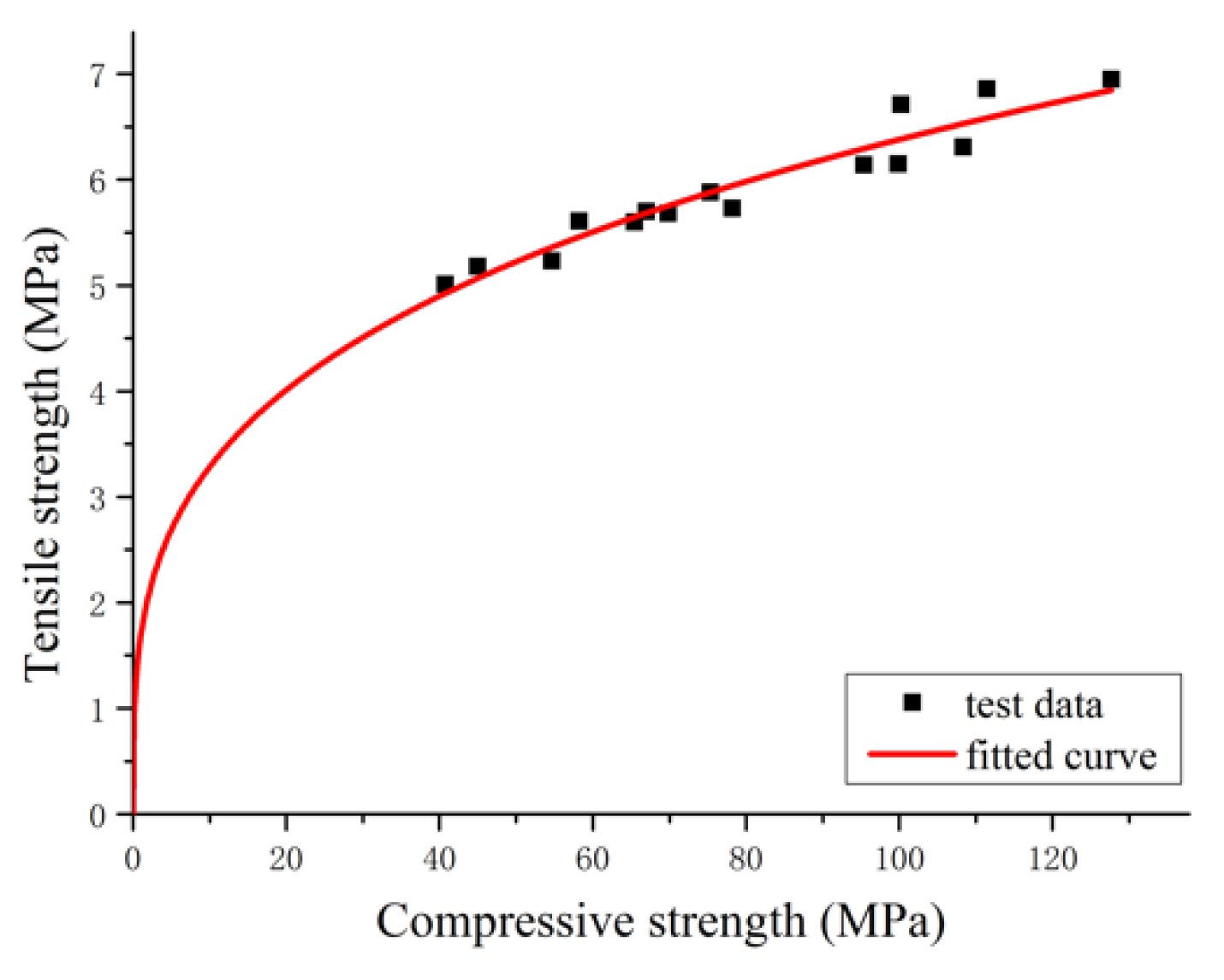
3.4. Relationship between Ultimate Tensile Strain and Strength
3.4.1. Relationship between Ultimate Tensile Strain and Tensile Strength
3.4.2. Relationship between Ultimate Tensile Strain and Compressive Strength
4. Conclusions
- The trend of changes in the axial tension stress–strain curves of RPC at all curing ages is similar, all the curves involve three stages, i.e., the elastic, strain hardening, and stress softening stages. There is an obvious difference in the tensile strength of RPC with curing age.
- There is a typical linear relationship between the axial tensile crack strain at different curing ages and the ratio of tensile strength to elastic modulus at the corresponding curing ages. According to the test data, the relationships between tensile strength and curing age and between elastic modulus and curing age are obtained, therefore, the relationship between tensile strain and curing age of initial crack could be established. The initial crack tensile strain of RPC is an important sign of material cracking; it directly reflects the crack resistance of the material. Therefore, in this study, we have shown the influence of curing age on the crack resistance of RPC.
- The ultimate tensile strain of RPC increases with an increase in the curing age and, at a late stage, becomes flattened. The ultimate tensile strain can reflect the crack width control ability of RPC. Compared with ordinary concrete, the crack width control ability of RPC has obvious advantages, and the earlier the curing age, the more obvious the advantage.
- A method for calculating the characteristic age of RPC is presented in this study. In addition, the relationships between RPC ultimate tensile strain and compressive strength and between ultimate tensile strain and tensile strength are proposed for estimating ultimate tensile strain exhibited by known RPC strength for applications in the field of engineering.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmidt, M.; Fehling, E. Ultra-high-performance concrete: Research, development, and application in Europe. ACI Spec. Publ. 2005, 228, 51–78. [Google Scholar]
- Chen, X.; Wan, D.W.; Jin, L.Z.; Qian, K.; Fu, F. Experimental studies and microstructure analysis for ultra-high-performance reactive powder concrete. Constr. Build. Mater. 2019, 229, 116924–116938. [Google Scholar] [CrossRef]
- Wang, Y.; An, M.Z.; Yu, Z.R.; Su, J.J.; Li, Z.G. Research on the mechanical properties of reactive powder concrete: A review. Concrete 2013, 12, 21–26. (In Chinese) [Google Scholar] [CrossRef]
- Wille, K.; Naaman, A.E.; Parra-Montesinos, G.J. Ultra-high performance concrete with compressive strength exceeding 150MPa (22ksi): Asimpler way. ACI Mater. J. 2011, 108, 46–54. [Google Scholar] [CrossRef]
- Shi, C.J.; Wu, Z.M.; Xiao, J.F.; Wang, D.H.; Huang, Z.Y.; Fang, Z. A review on ultra-high performance concrete: Part 1. Raw materials and mixture design. Constr. Build. Mater. 2015, 101, 741–751. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wu, B.; Wang, J.; Liu, M.; Zhang, X. Reactive Powder Concrete Mix Ratio and Steel Fiber Content Optimization under Dierent Curing Conditions. Materails 2019, 12, 3615. [Google Scholar] [CrossRef]
- Marcalikova, Z.; Cajka, R.; Bilek, V.; Bujdos, D.; Sucharda, O. Determination of Mechanical Characteristics for Fiber-Reinforced Concrete with Straight; Hooked Fibers. Crystals 2020, 10, 545. [Google Scholar] [CrossRef]
- Wang, J.Y.; Geng, L.P.; Guo, J.Y.; Liu, C.; Liu, G.P. Experimental study on crack width control ability of ultra-high performance concrete. J. Harbin Inst. Technol. 2017, 49, 165–169. (In Chinese) [Google Scholar] [CrossRef]
- Graybeal, B.A.; Baby, F. Tension Testing of Ultra-High Performance Concrete, Report No. FHWA-HRT-17-053; US Department of Transportation Federal Highway Administration: McLean, VA, USA, 2019.
- Yu, K.Q.; Lu, Z.D.; Yu, J.T. Residual compressive properties of strain-hardening cementitious composite with different curing ages exposed to high temperature. Constr. Build. Mater. 2015, 98, 146–155. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Qiao, P.Z. Direct Tension Test for Characterization of Tensile Behavior o Uitra-High Performance Concrete. J. Test. Eval. 2020, 7. [Google Scholar] [CrossRef]
- An, M.Z.; Yang, Z.H.; Yu, Z.R.; Zhai, Y.F.; Gao, K. Experimental study on the tensile performance of reactive powder concrete. J. China Railw. Soc. 2010, 32, 54–58. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, X.D.; Li, W.G.; Zhu, P.; Chen, H. Axial tensile behavior test of ultra high performance concrete. China J. Highw. Transp. 2015, 28, 50–58. [Google Scholar] [CrossRef]
- Yuan, H.Y. Experimental Study and Theoretical Analysis on Tensile Properties of Reinforced Reactive Powder Concrete. Ph.D. Thesis, School of Civil Engineering, Beijing Jiaotong University, Beijing, China, 2009. [Google Scholar]
- Kaplan, M.F. Strains and stresses of concrete at initiation of cracking and near failure. J. Am. Concr. Inst. Proc. 1963, 60, 853–880. [Google Scholar]
- Tasdemir, M.A.; Lydon, F.D.; Bart, B.G. The tensile strain capacity of concrete. Mag. Concr. Res. 1996, 48, 211–218. [Google Scholar] [CrossRef]
- Park, G.K.; Park, G.J.; Park, J.J.; Lee, N.; Kim, S.W. Residual Tensile Properties and Explosive Spalling of High-Performance Fiber-Reinforced Cementitious Composites Exposed to Thermal Damage. Materials 2021, 14, 1608. [Google Scholar] [CrossRef]
- Smarzewski, P. Effect of curing period on properties of steel and polypropylene fibre reinforced ultra-high performance concrete. Mater. Sci. Eng. 2017, 245, 1–7. [Google Scholar] [CrossRef]
- Rong, Q.; Hou, X.M.; Ge, C. Quantifying curing and composition effects on compressive and tensile strength of 160-250 MPa RPC. Constr. Build. Mater. 2020, 241, 117987–117996. [Google Scholar] [CrossRef]
- Lu, D.; Zhong, J.; Yan, B.B.; Gong, J.; He, Z.Y.; Zhang, G.H.; Song, C.Z. Effects of curing conditions on the mechanical and microstructural properties of ultra-high-performance concrete (UHPC) incorporating iron tailing powder. Materials 2021, 14, 215. [Google Scholar] [CrossRef] [PubMed]
- GB/T50081-2019. Standard for Test Methods of Concrete Physical and Mechanical Properties; China Architecture & Building Press: Beijing, China, 2019. [Google Scholar]
- Klink, T.; Stegmann, F.; Slowik, V. Age dependence of cracking and deformability of a strain-hardening cement-based composite. Constr. Build. Mater. 2019, 214, 641–647. [Google Scholar] [CrossRef]
- Yu, J.; Yao, J.; Lin, X.Y. Tensile performance of sustainable strain-hardening cementitious composites with hybrid PVA and recycled PET fibers. Cem. Concr. Res. 2018, 5, 110–123. [Google Scholar] [CrossRef]
- Hu, J.H.; Sun, M.Q.; Li, J.; Wei, Y.P.; Chen, J.Z. Tensile characteristics of strain-hardening cement-based composites with different curing ages. Constr. Build. Mater. 2019, 221, 709–719. [Google Scholar] [CrossRef]
- Boshoff, W.P.; Adedorff, C.J. Effect of sustained tensile loading on SHCC crack widths. Cem. Concr. Compos. 2013, 37, 119–125. [Google Scholar] [CrossRef]
- Yan, G.J.; Yan, G.P.; An, M.Z.; Chen, Y.Z. Experimental Study on 200 Mpa Reactive Powder Concrete. J. China Railw. Soc. 2004, 26, 116–119. [Google Scholar] [CrossRef]
- Ju, Y.Z.; Zhou, G.N.; Zheng, W.Q. The Compounding and test study of 200MPa reactive powder concrete. J. N. Dianli Univ. Nat. Sci. Ed. 2007, 27, 18–21. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, H.Z.; Shi, Q.X.; Chen, J.F. State of art of mix design theory of reactive powder concrete. J. Xi’an Univ. Arch. Tech. 2016, 48, 840–845. [Google Scholar]
- Li, J.Y. The Mix Proportion Design and Application Research of RPC130. Master's Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2013. [Google Scholar]
- GB/T31387-2015. Reactive Powder Concrete; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; Standardization Administration of China: Beijing, China, 2015. [Google Scholar]
- Blakey, F.A.; Beresford, F.D. Tensile Strains in Concrete; Australian Division of Building Research: Melbourne, Australia, 1955. [Google Scholar]
- Blakey, F.A.; Beresford, F.D. A note on strain distribution in concrete beam. Civ. Eng. Public Work. Rev. 1955, 50, 415–416. [Google Scholar]
- Nicholas, J.C.; Floyd, O.S. Limiting tensile strain criterion for failure of concrete. J. Am. Concr. Inst. Proc. 1976, 73, 160–165. [Google Scholar] [CrossRef]
- Tian, Y.; Jin, N.G.; Jin, X.Y. Relationship between characteristic tensile strain and curing age of concrete. J. Zhejiang Univ. 2008, 42, 1076–1079. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, B.F. Relation Between Extensibility, Age, Tensile and Compressive Strength of Concrete. China Civ. Eng. J. 1996, 29, 72–76. (In Chinese) [Google Scholar] [CrossRef]


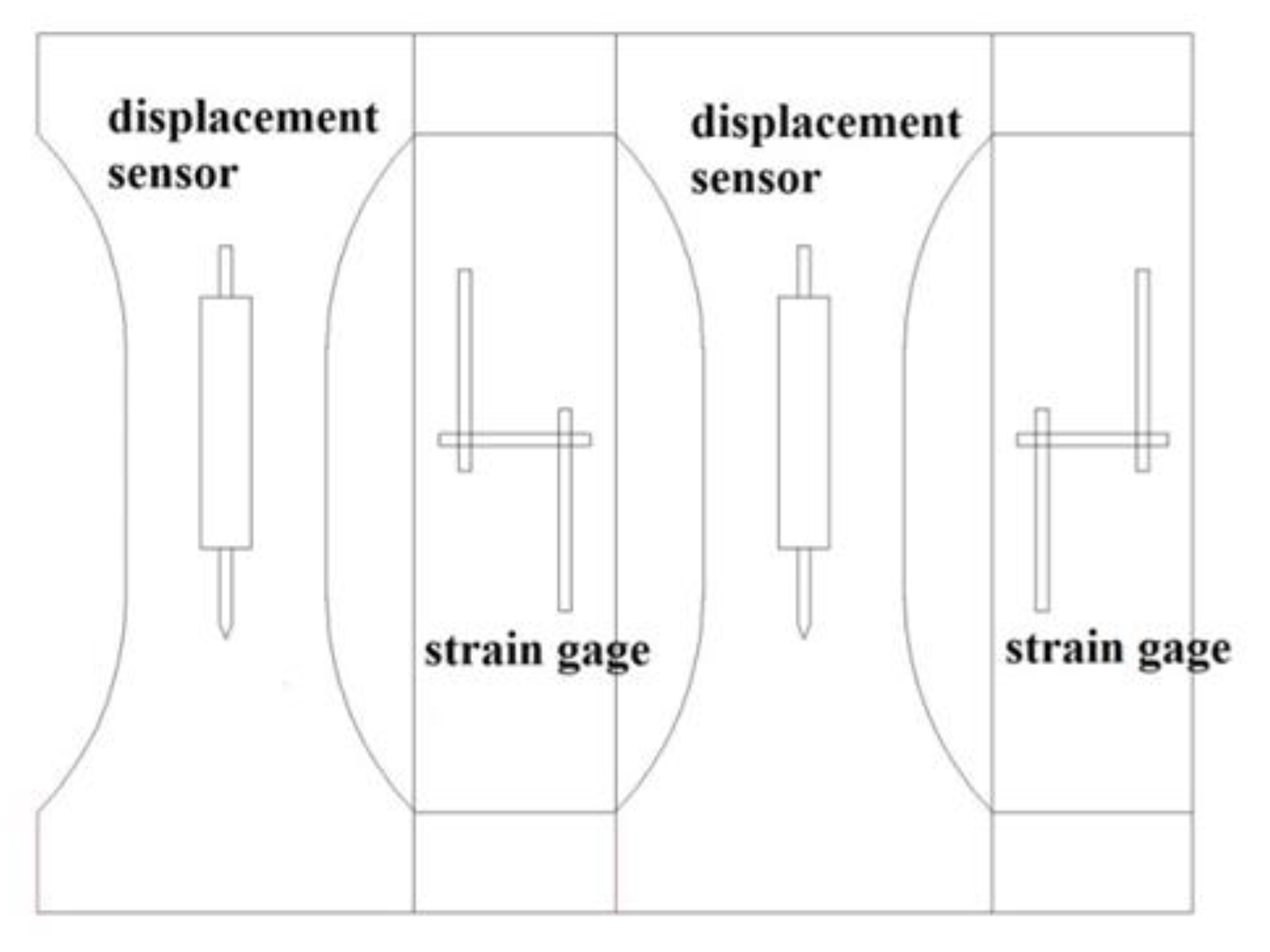

| Cement | Silica Fume | Quartz Sand | Steel Fiber | Water Reducing Agent | Water | |||
|---|---|---|---|---|---|---|---|---|
| Coarse | Medium | Fine | ||||||
| Dosage kg/m3 | 920 | 170 | 460 | 340 | 280 | 120 () 1 | 22 | 174 |
| Mix ratio | 1 | 0.18 | 0.5 | 0.37 | 0.3 | 0.024 | 0.19 | |
| Test Batch | Slump (mm) | Expand Slump (mm) | Conclusion |
|---|---|---|---|
| 1 | 270 | 450 | The workability is good, the mixer is slightly wet |
| 2 | 260 | 408 | The workability is good |
| 3 | 270 | 410 | The workability is good |
| 4 | 280 | 490 | The workability is good |
| Age | Average Compressive Strength | Average Tensile Strength | Average Initial Tensile Strain | Average Ultimate Tensile Strain | Elastic Modulus |
|---|---|---|---|---|---|
| 3 d | 46.8/2.45 | 5.14/0.139 | 84.67/4.31 | 142.76/6.492 | 3.97 × 104 |
| 7 d | 67.8/2.44 | 5.68/0.143 | 92.00/5.65 | 166.10/8.672 | 4.55 × 104 |
| 14 d | 70.2/3.22 | 5.72/0.277 | 86.21/3.35 | 175.62/7.171 | 4.53 × 104 |
| 28 d | 101.2/5.08 | 6.2/0.076 | 95.77/2.92 | 196.44/6.648 | 4.88 × 104 |
| 56 d | 113.1/5.96 | 6.84/0.124 | 101.18/6.82 | 200.85/4.065 | 5.0 × 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Gao, R. Relationships among the Characteristic Tensile Strain, Curing Age, and Strength of Reactive Powder Concrete. Materials 2021, 14, 2660. https://doi.org/10.3390/ma14102660
Guo M, Gao R. Relationships among the Characteristic Tensile Strain, Curing Age, and Strength of Reactive Powder Concrete. Materials. 2021; 14(10):2660. https://doi.org/10.3390/ma14102660
Chicago/Turabian StyleGuo, Min, and Ri Gao. 2021. "Relationships among the Characteristic Tensile Strain, Curing Age, and Strength of Reactive Powder Concrete" Materials 14, no. 10: 2660. https://doi.org/10.3390/ma14102660
APA StyleGuo, M., & Gao, R. (2021). Relationships among the Characteristic Tensile Strain, Curing Age, and Strength of Reactive Powder Concrete. Materials, 14(10), 2660. https://doi.org/10.3390/ma14102660





