Improving the Blast Resistance of Large Steel Gates—Numerical Study
Abstract
1. Introduction
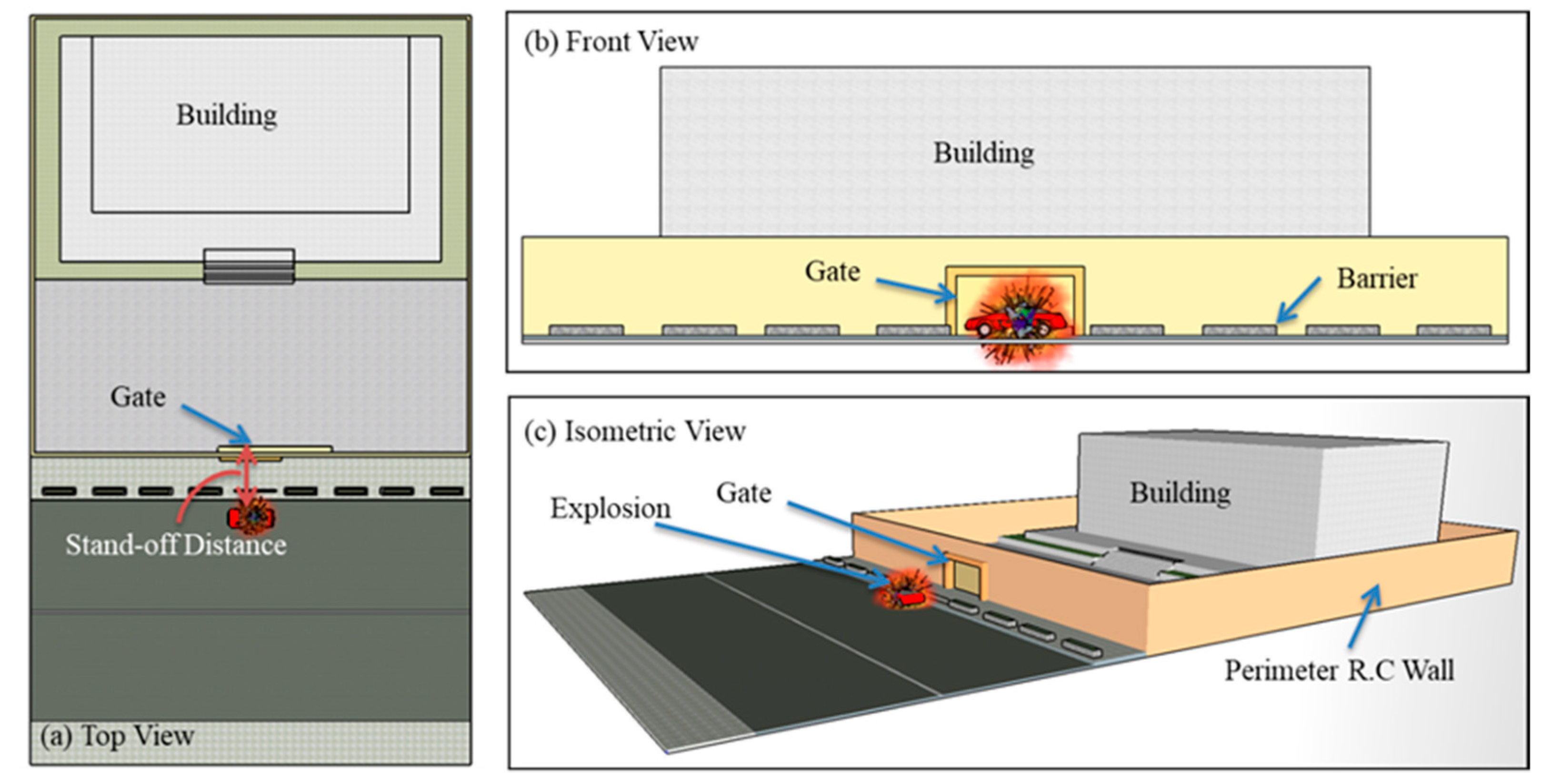
2. Site Plan and Assumptions
- The gate is outside the explosion fireball. In other words, the interaction with the produced gases can be neglected and there is no afterburning effect. Afterburning (combustion of the detonation products following an explosion) can increase the duration of the positive phase and thus the impulse on near field structure.
- As a blast wave propagates in the air, atmospheric pressure is an important factor which varies with the altitude of the location. Therefore, it is assumed here that the blast occurs at sea level.
- The charge was uncased with no additional loading from fragmentation (for more information about fragmentation, refer to Szymczyk et al. [34].
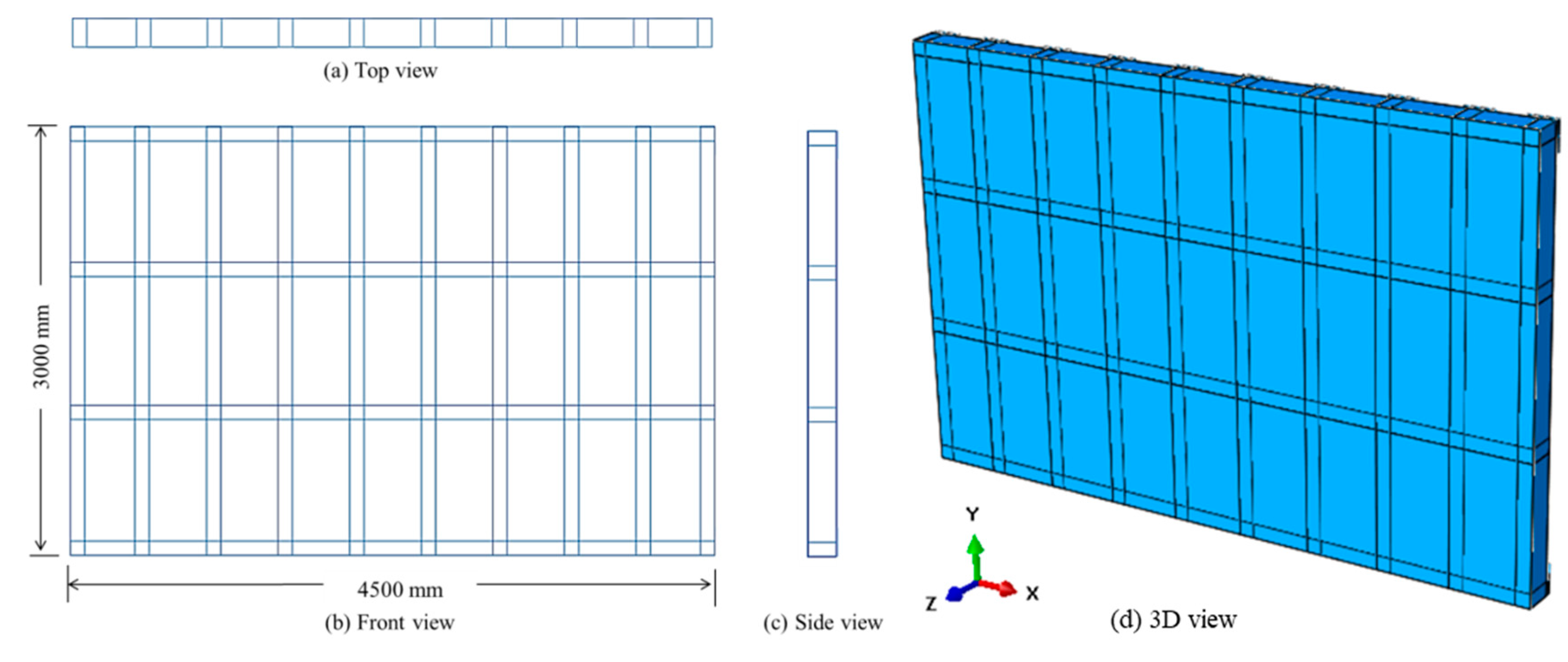
3. Geometrical and Material Properties of the Gate
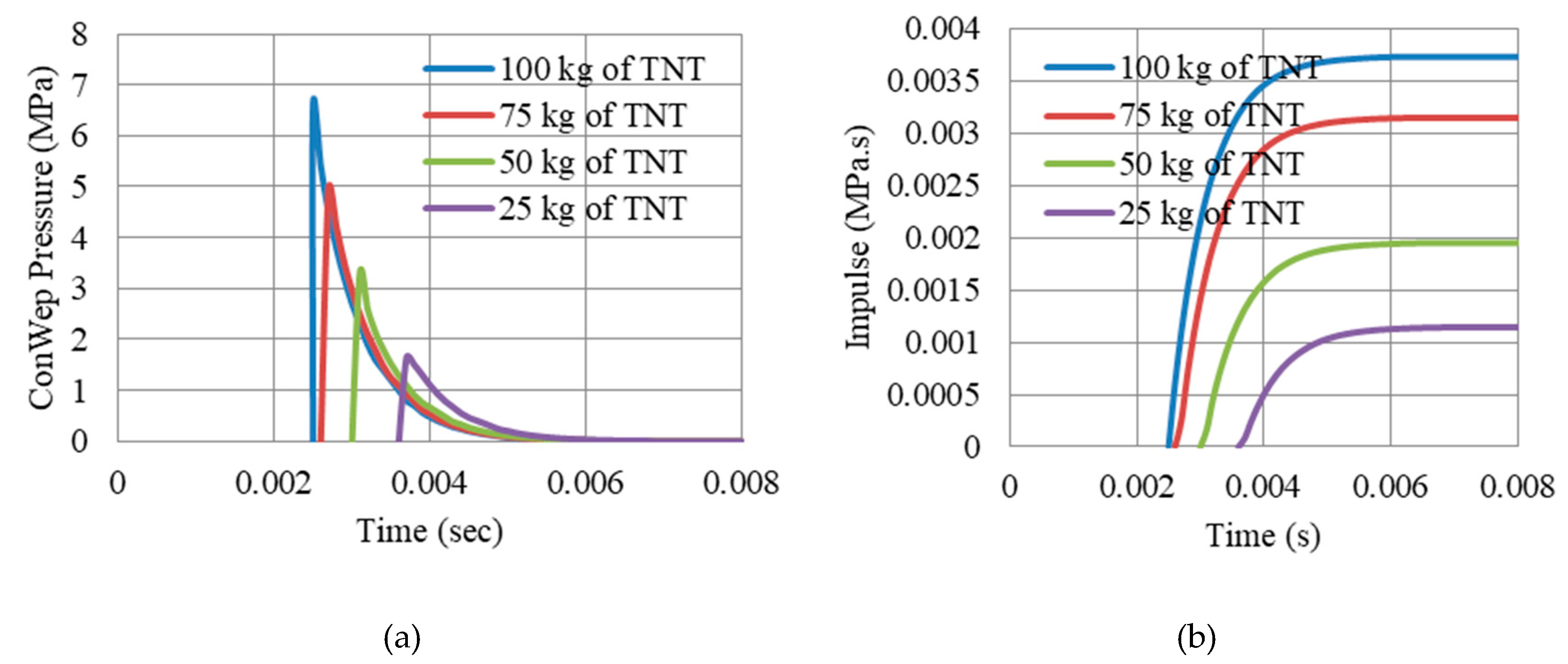
4. Threat Assessment and Blast Loading
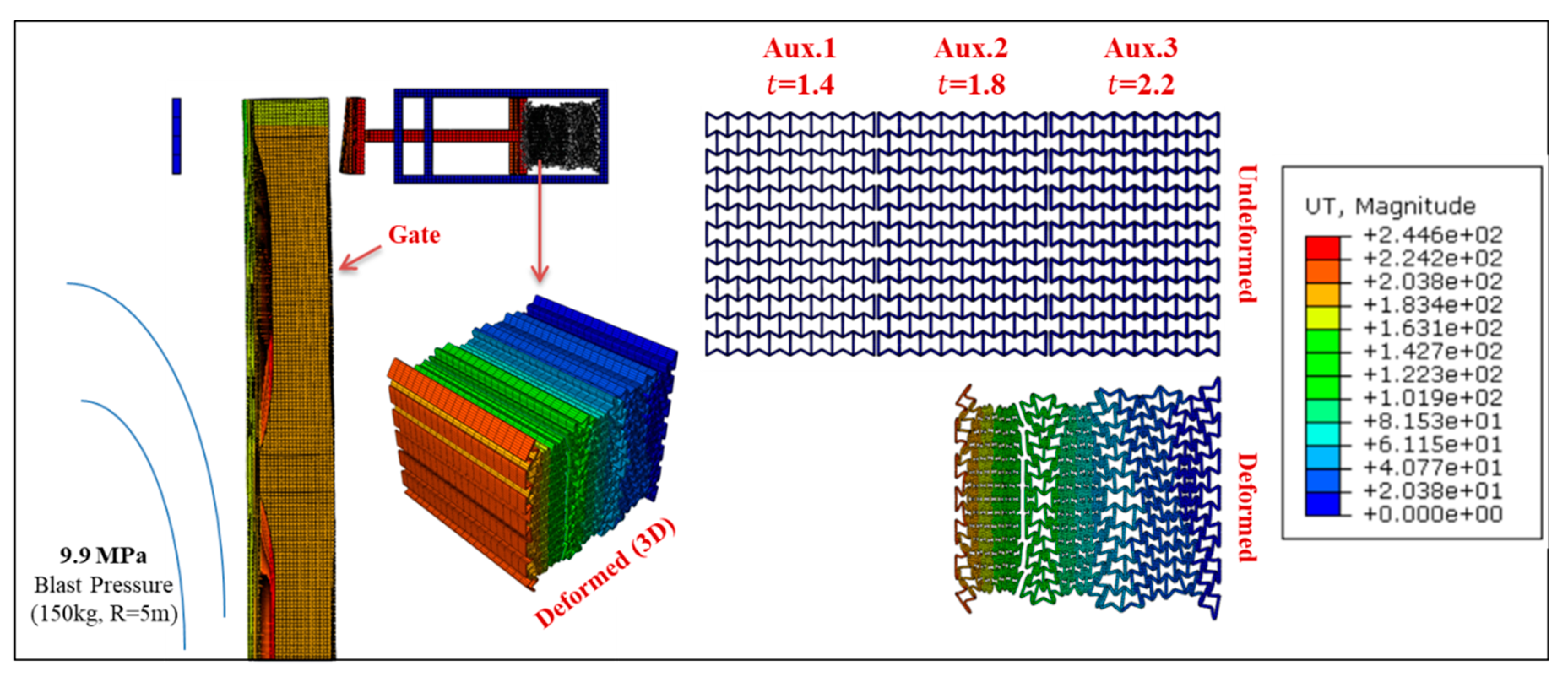
5. Numerical Modelling
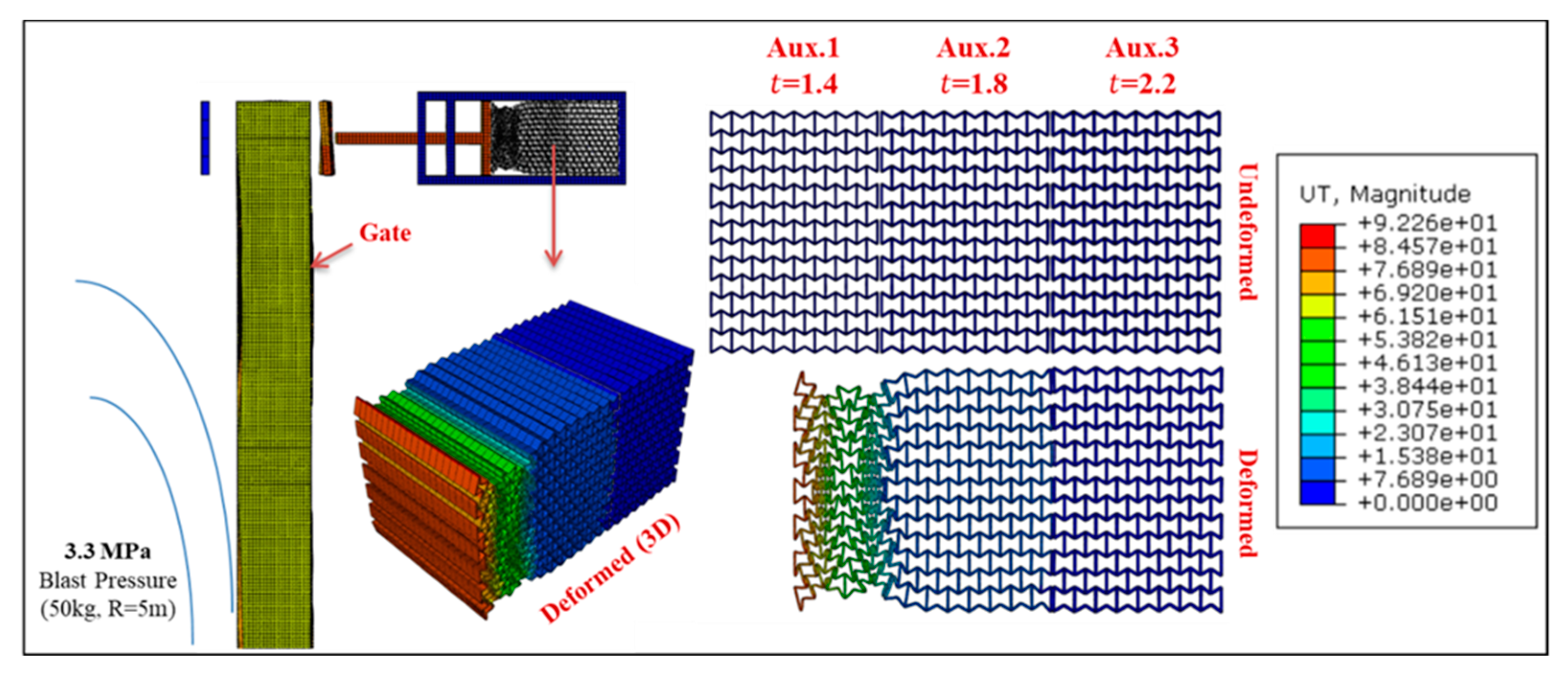
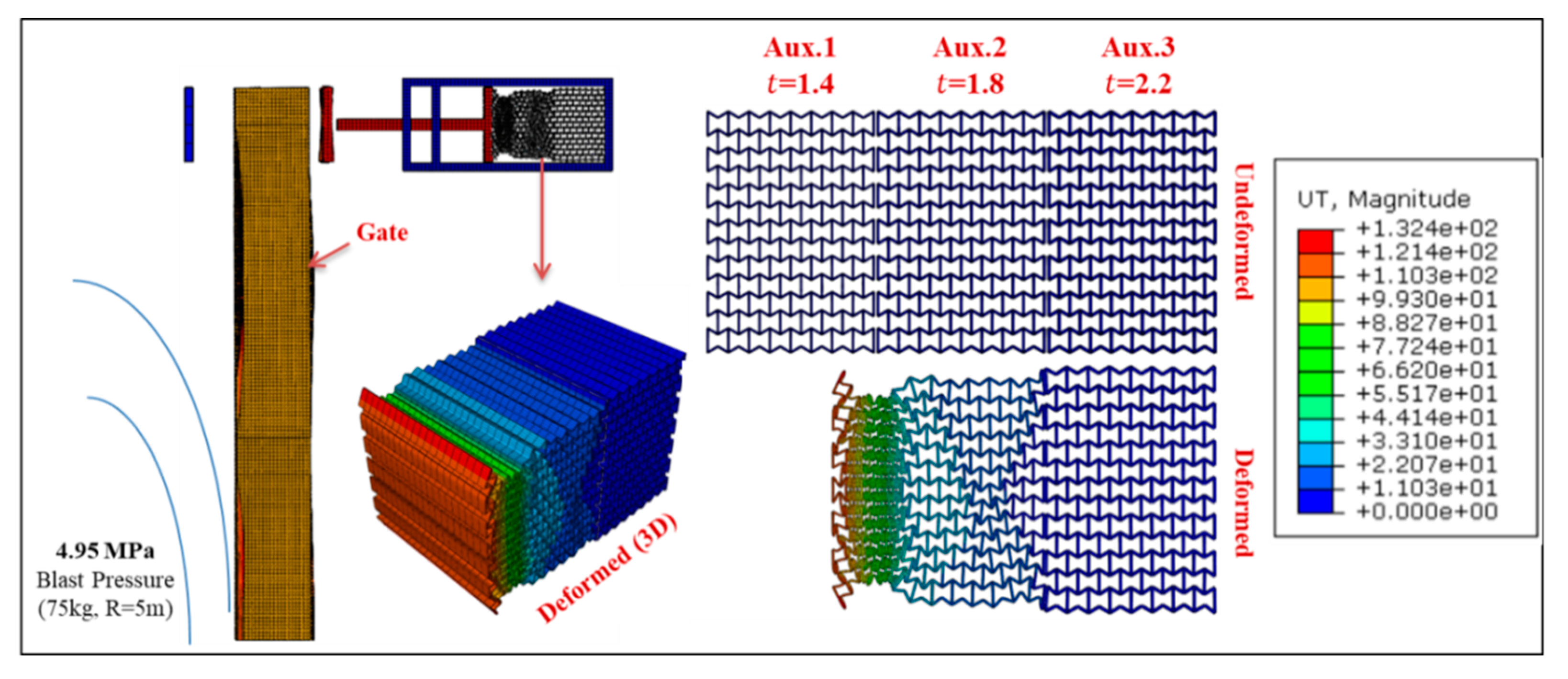
6. Uniaxial Graded Auxetic Damper (UGAD)
7. Gate Response (without UGAD)
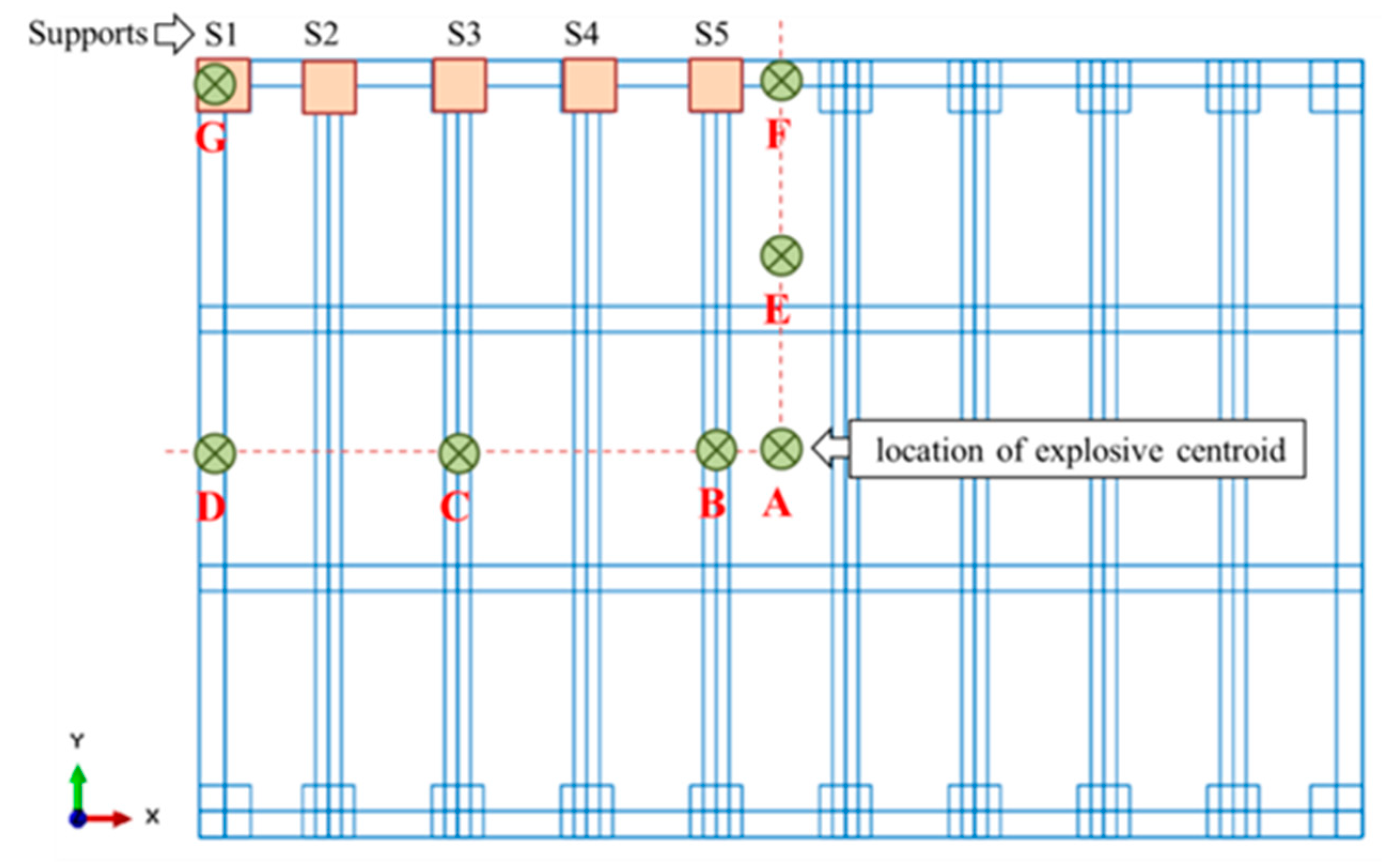
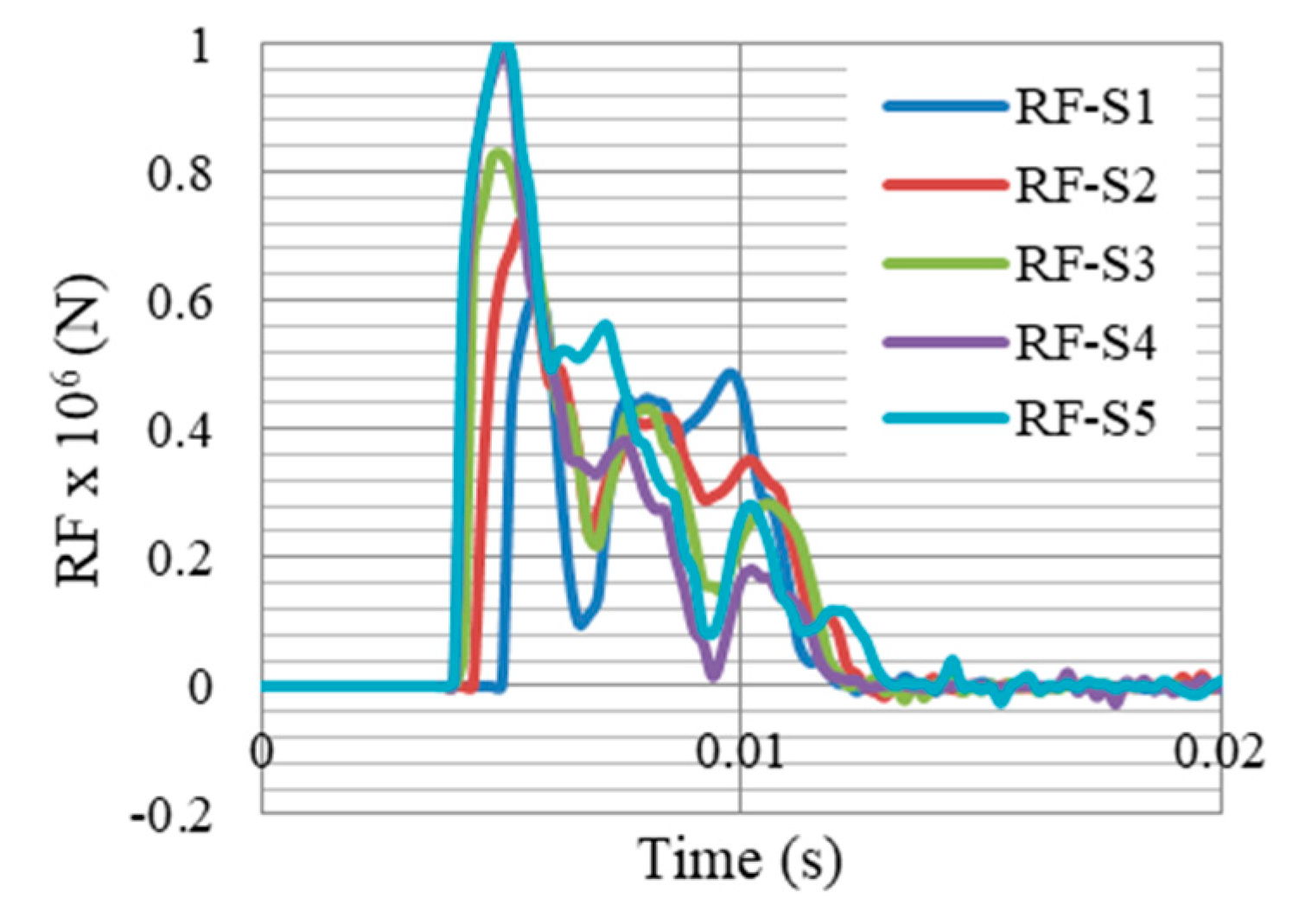
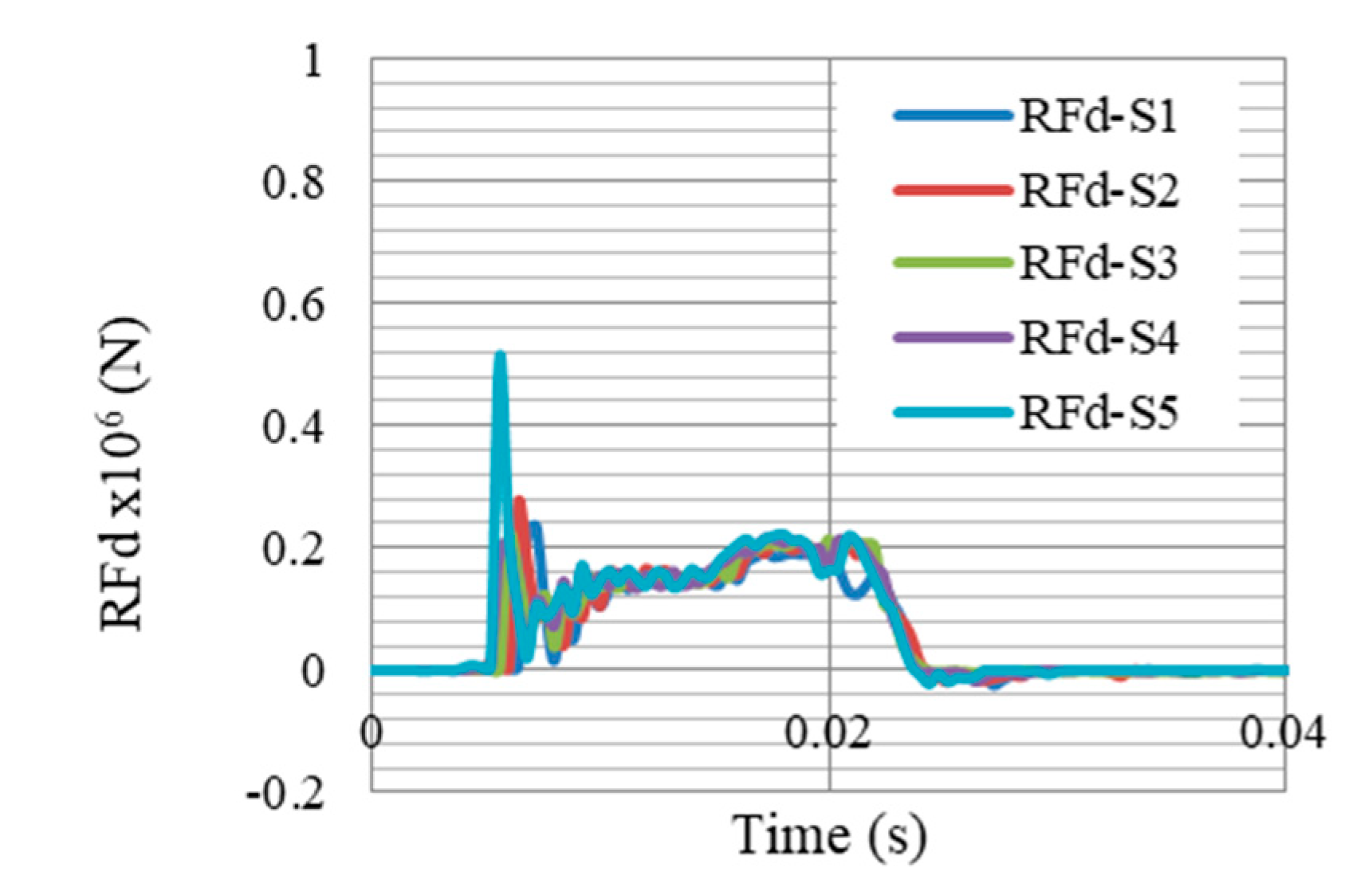
7.1. Peak Nodal Reaction Forces
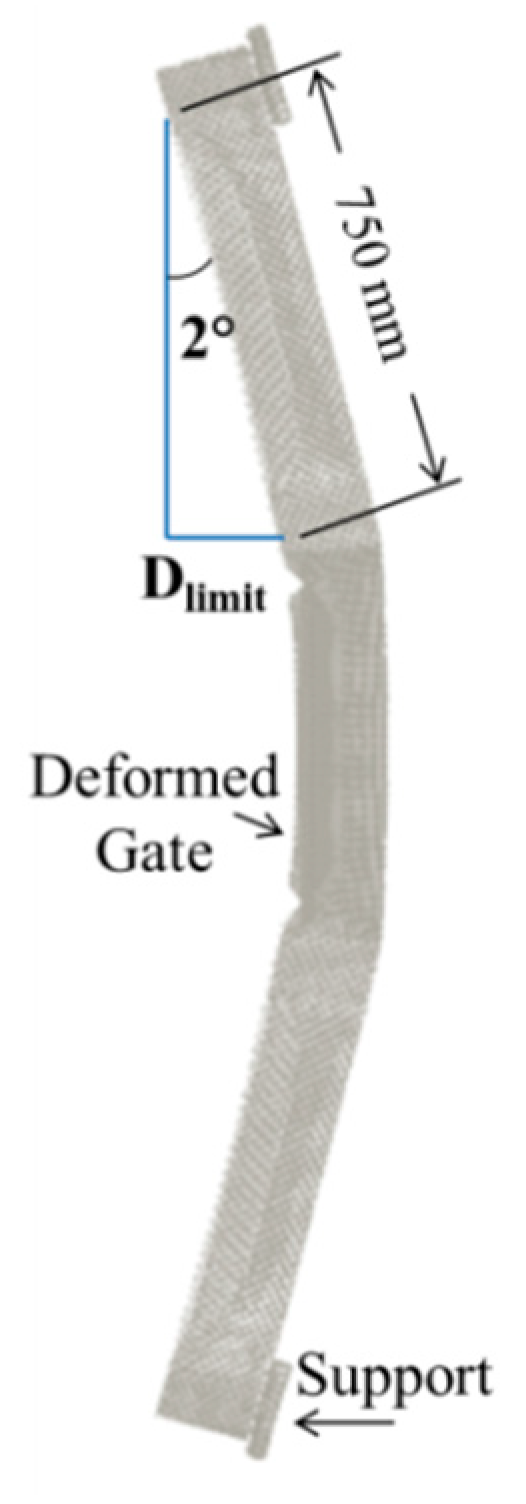
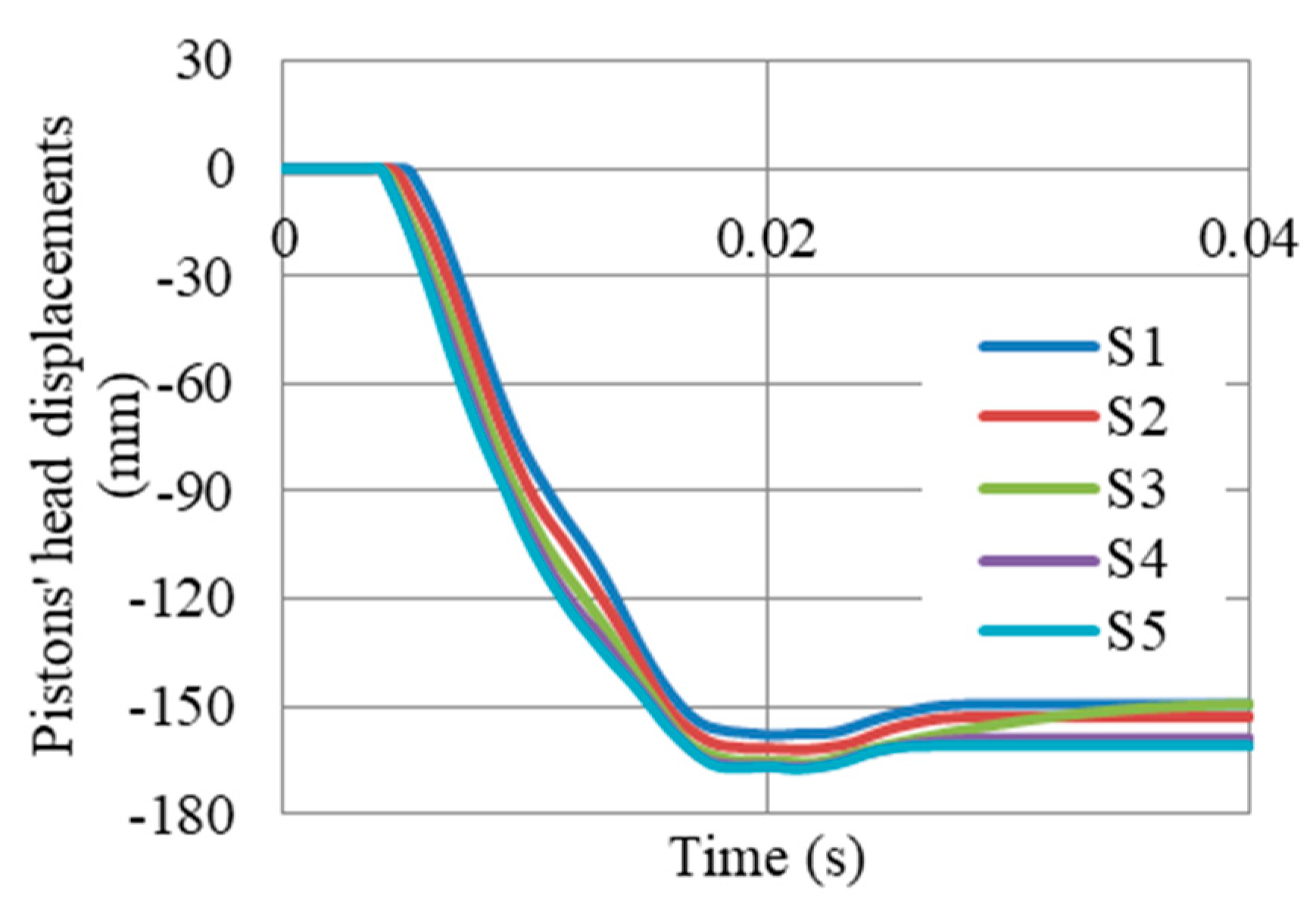
7.2. Deformation and Operability Analysis
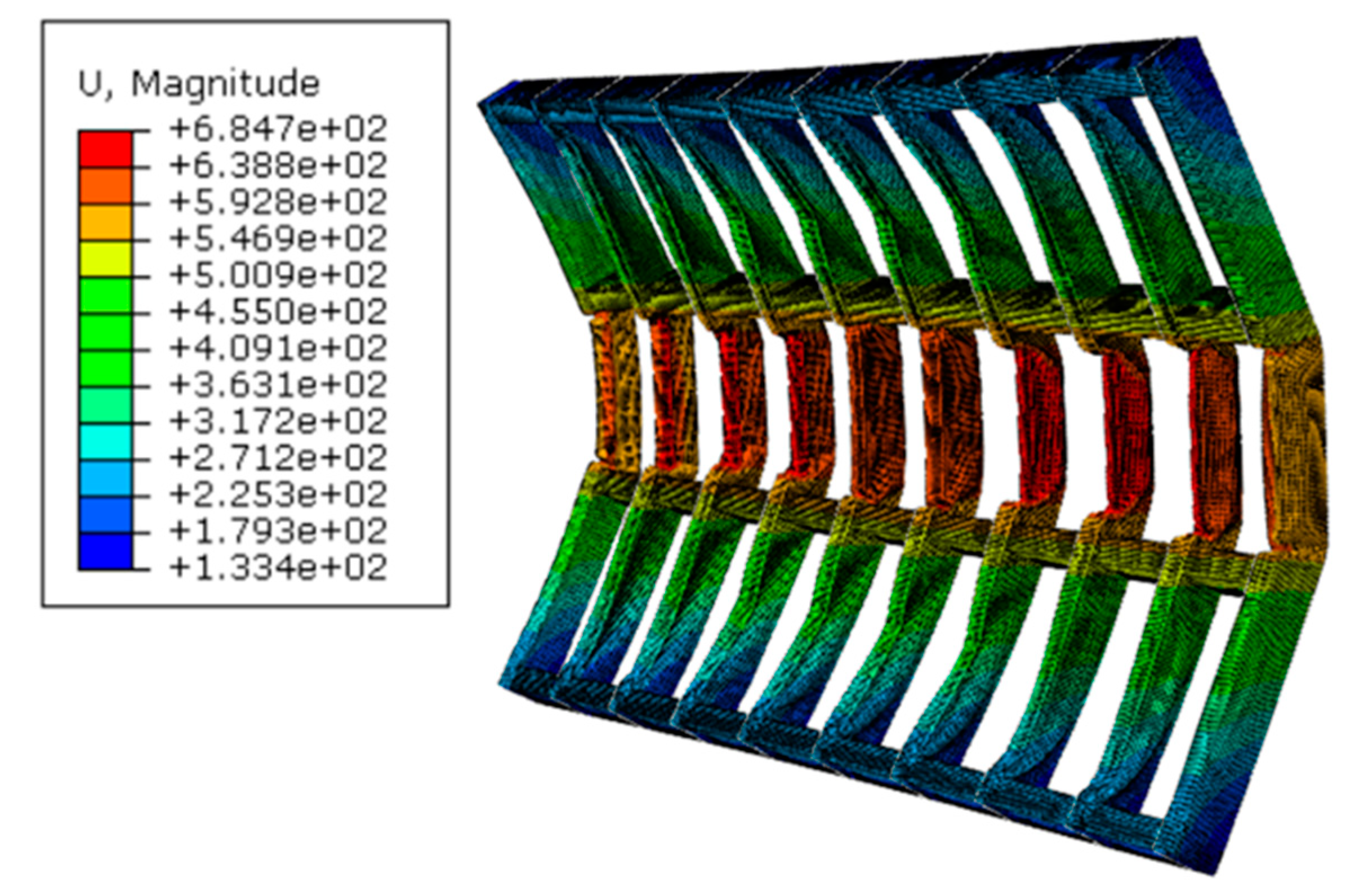
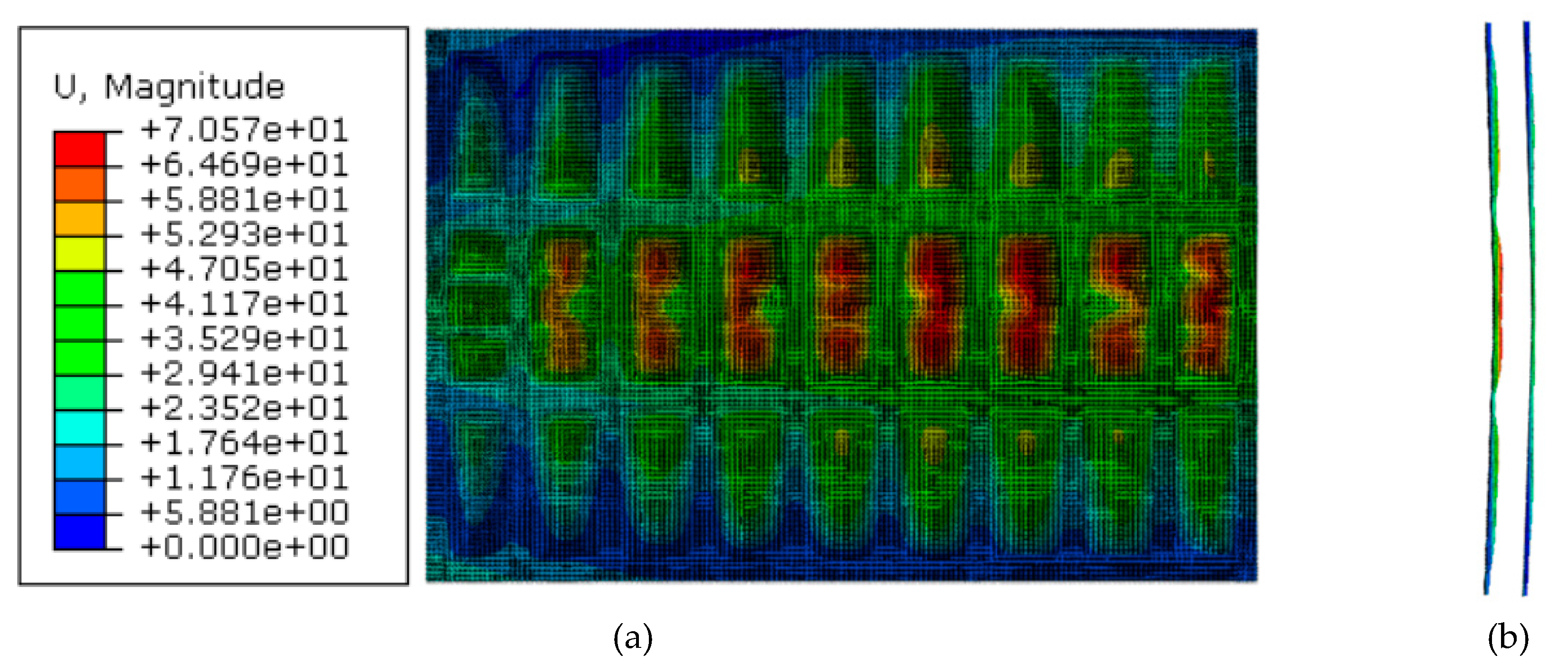
8. Gate Behavior with the Proposed Auxetic Damper
9. Conclusions
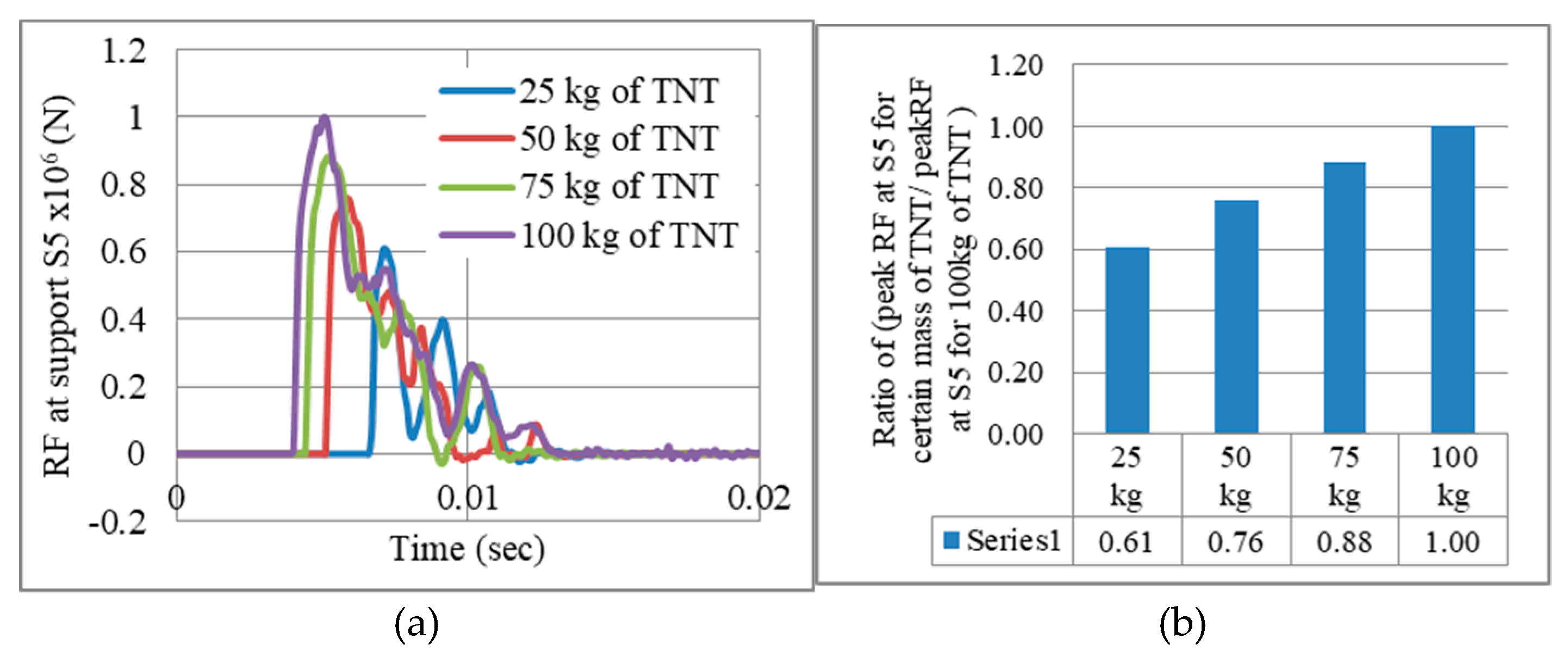
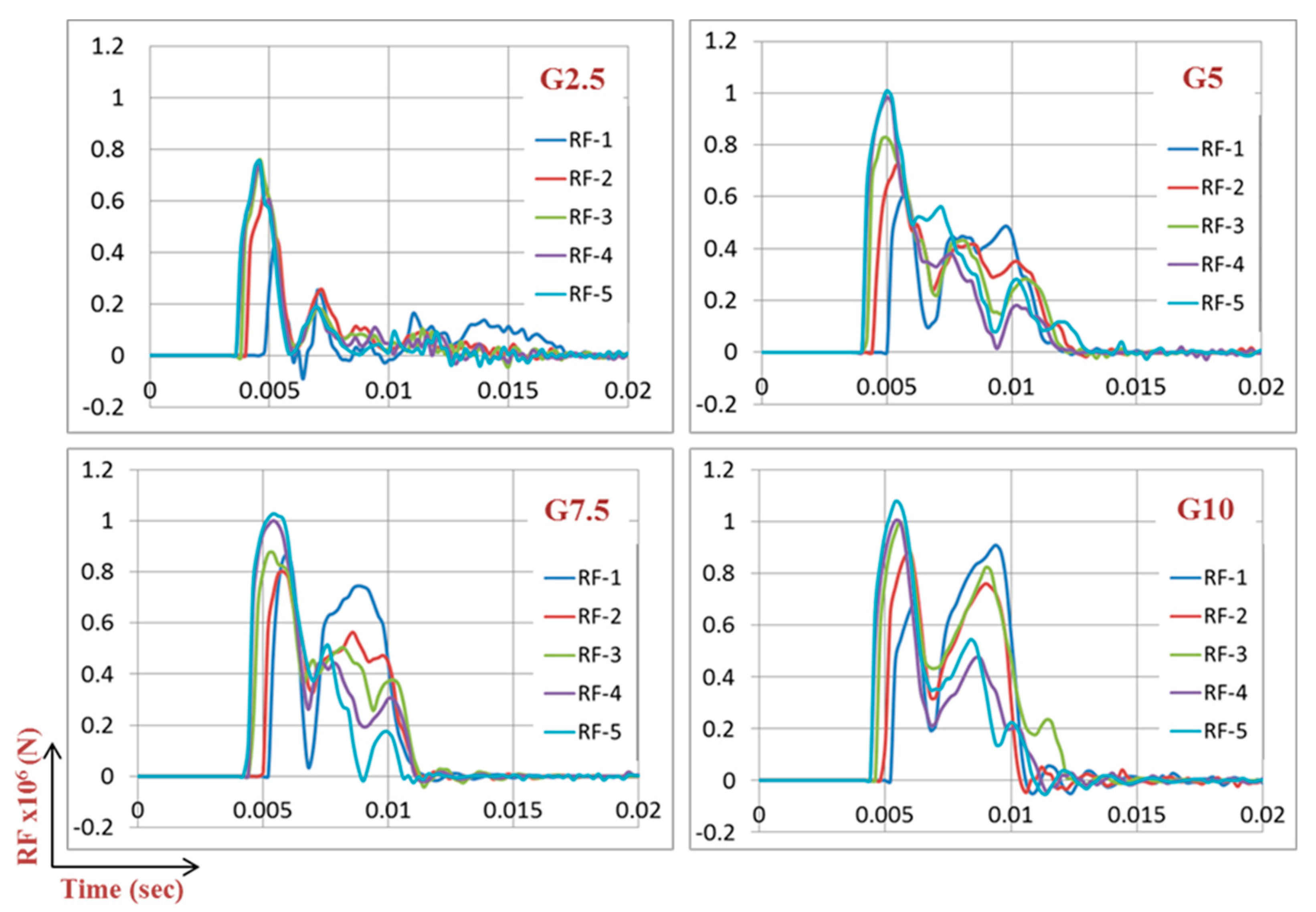
- In-plane reaction forces are very small compared to those out-of-plane (direction of blast). Therefore, RFz is the considered component in this paper as it is the prominent one.
- The UGAD dampers may work for G5, G7.5, or G10 in the same efficiency, as the mass shown to have slight effect on RFs (Figure 11).
- G10 was the only gate (without external damping systems) that satisfied operability condition after the blast event, with peak permanent deformation, dframe = 4.4 mm.
- With the application of the proposed UGAD, both G7.5 and G5 passed the operability requirement. The frame permanent deformation of G5 decreased from 40.5 to 22 mm, making G5 the lightest-operable option that can withstand the peak reflected overpressure target of 6.6 MPa. In addition, a 49% reduction in peak reaction forces was recorded which can reduce the required cross section and strength of the concrete supports.
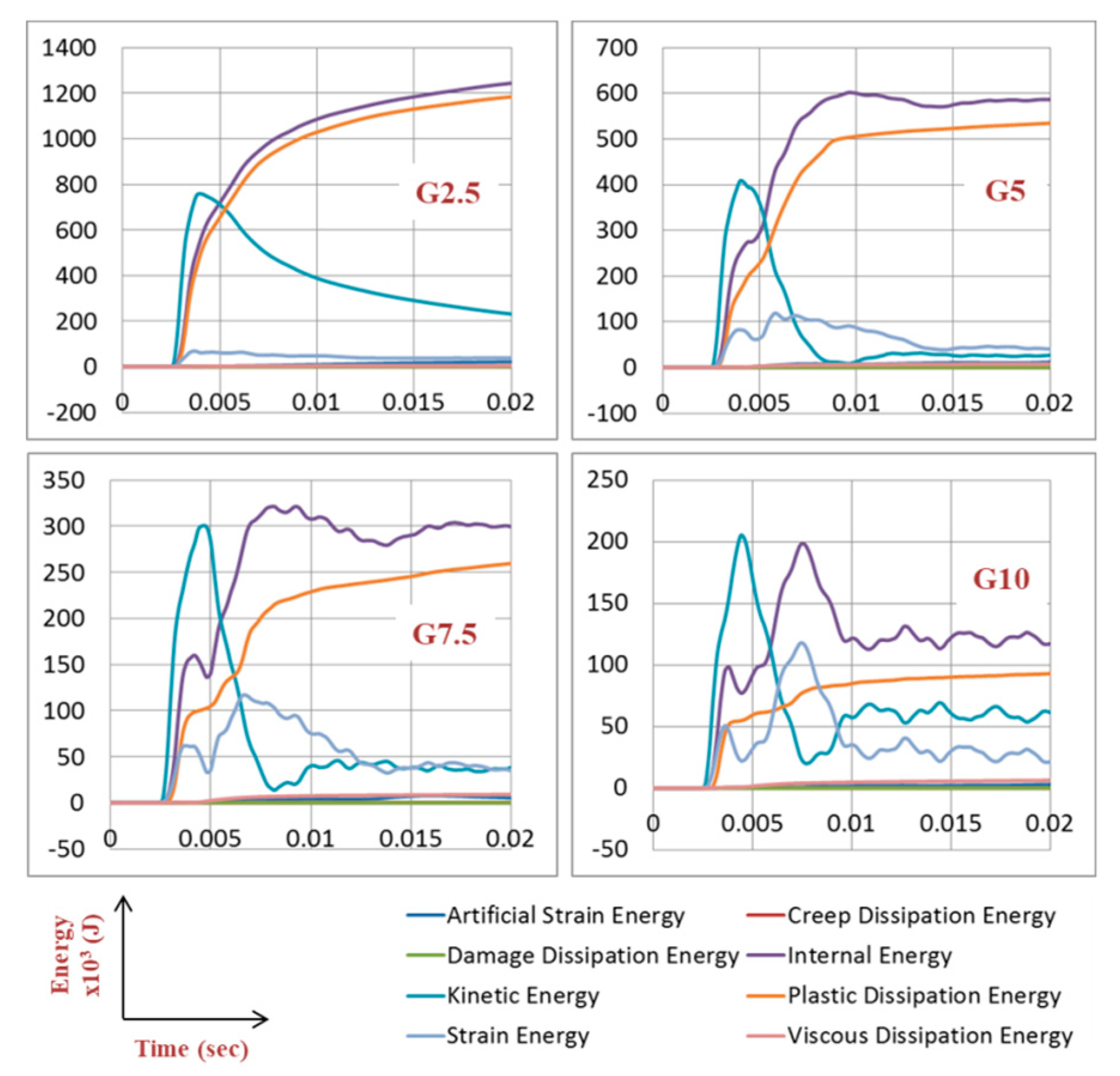
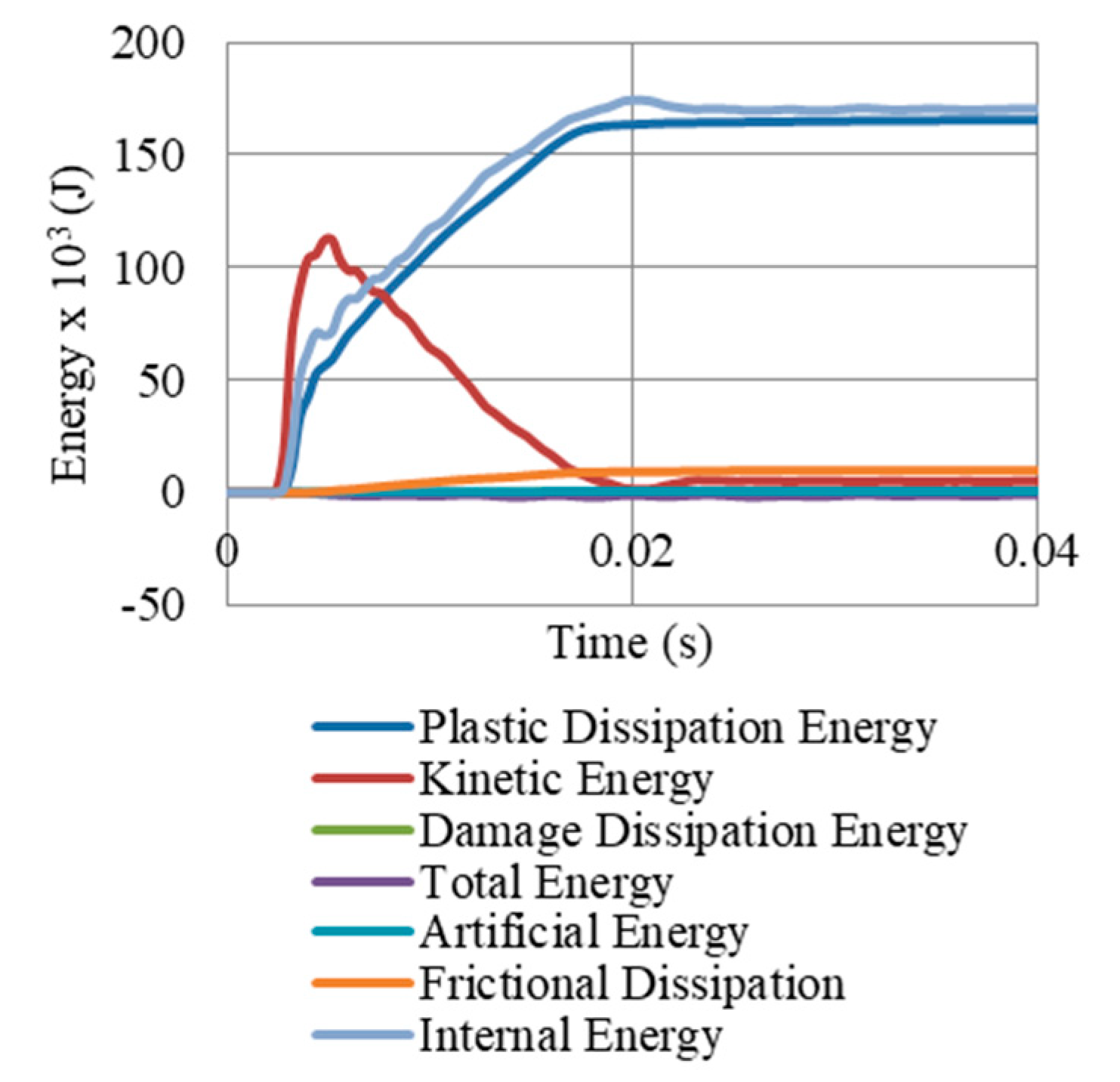
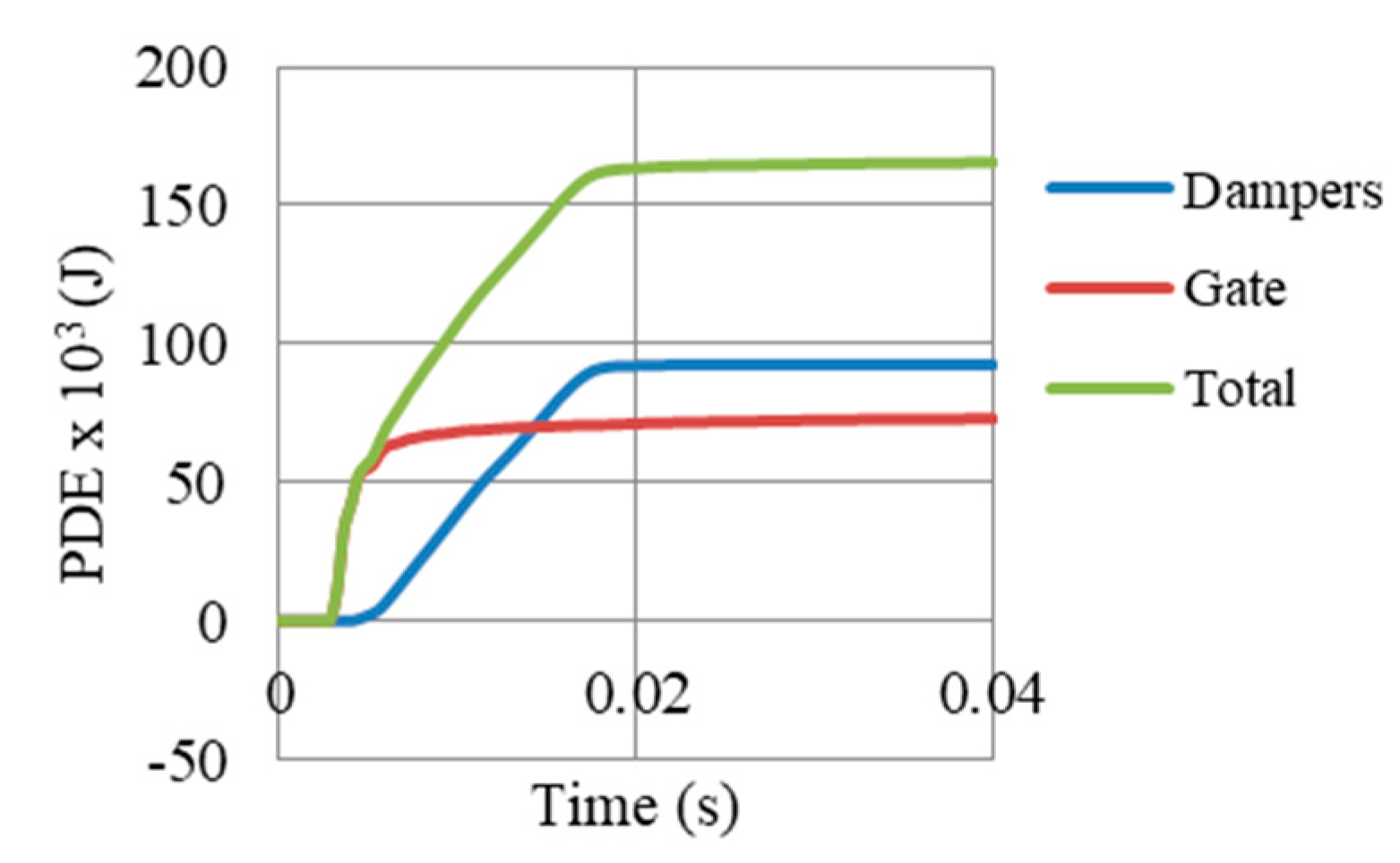
- Internal energy in the whole model composed mainly of plastic dissipation, small frictional dissipation, and no dissipation due to damage. Moreover, 56% of the total plastic dissipation energy in the system was achieved from the UGADs, while 44% from the gate. Based on that successful energy dissipation, the kinetic energy was mitigated.
Author Contributions
Funding
Conflicts of Interest
References
- Mazek, S.A. Performance of sandwich structure strengthened by pyramid cover under blast effect. Struct. Eng. Mech. 2014, 50, 471–486. [Google Scholar] [CrossRef]
- Lotfi1a, S.; Zahrai, S.M. Blast behavior of steel infill panels with various thickness and stiffener arrangement. Struct. Eng. Mech. 2018, 65, 587–600. [Google Scholar]
- Koh, C.; Ang, K.; Chan, P. Dynamic analysis of shell structures with application to blast resistant doors. Shock Vib. 2003, 10, 269–279. [Google Scholar] [CrossRef]
- US DoD. United Facilities Criteria UFC 3-340-02, Structures to Resist the Effects of Accidental Explosions; US Government Printing Office: Washington, DC, USA, 2008.
- Meng, F.; Zhang, B.; Zhao, Z.; Xu, Y.; Fan, H.; Jin, F. A novel all-composite blast-resistant door structure with hierarchical stiffeners. Compos. Struct. 2016, 148, 113–126. [Google Scholar] [CrossRef]
- Meng, F.; Xu, Y.; Gong, H.; MA, S.-N.; Wu, X.-Y. Review on Design and Research of Protective Door. J. Sichuan Ordnance 2015, 10, 161–164. [Google Scholar]
- Al-Rifaie, H.; Sumelka, W. Numerical assessment of a blast-protective steel gate with a new damping system. In Proceedings of the 22nd International Conference on Computer Methods in Mechanics, Lublin, Poland, 13–16 September 2017; pp. 15–16. [Google Scholar]
- Sielicki, P.; Łodygowski, T.; Al-Rifaie, H.; Sumelka, W. Designing of Blast Resistant Lightweight Elevation System-Numerical Study. Procedia Eng. 2017, 172, 991–998. [Google Scholar] [CrossRef]
- Hsieh, M.; Hung, J.; Chen, D. Investigation on the blast resistance of a stiffened door structure. J. Mar. Sci. Technol. 2008, 16, 149–157. [Google Scholar]
- Mohammed, A.; Rao, K.; Abdulkader, H. Analysis of Plates Subjected to Blast Loads. Int. J. Sci. Eng. Technol. Res. 2013, 2, 927–934. [Google Scholar]
- Goel, M.D.; Matsagar, V.A.; Gupta, A.K. Dynamic response of stiffened plates under air blast. Int. J. Prot. Struct. 2011, 2, 139–155. [Google Scholar] [CrossRef]
- Veeredhi, L.S.B.; Rao, N.R. Studies on the Impact of Explosion on Blast Resistant Stiffened Door Structures. J. Inst. Eng. Ser. A 2015, 96, 11–20. [Google Scholar] [CrossRef]
- TM5-1300. Structures to Resist the Effects of Accedental Explosions; US Departments of Army, US Navy, Air Force: Washington, DC, USA, 1990.
- Zhang, B.; Chen, H.; Li, M.; Zhao, Z.; Zhou, Y.; Fan, H. Equivalent static load method for hierarchical stiffened composite panel subjected to blast loading. Eng. Struct. 2018, 171, 569–582. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, B.; Jin, F.; Zhou, J.; Chen, H.; Fan, H. BFRP reinforcing hierarchical stiffened SMC protective structure. Compos. Part B Eng. 2019, 168, 195–203. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, L.; Fan, H. Energy absorption mechanisms of hierarchical woven lattice composites. Compos. Part B Eng. 2012, 43, 1516–1522. [Google Scholar] [CrossRef]
- Broekel, J.; Prusty, B.G. Experimental and theoretical investigations on stiffened and unstiffened composite panels under uniform transverse loading. Compos. Struct. 2004, 63, 293–304. [Google Scholar] [CrossRef]
- Fatt, M.S.H.; Pothula, S.G. Dynamic pulse buckling of composite shells subjected to external blast. Compos. Struct. 2010, 92, 1716–1727. [Google Scholar] [CrossRef]
- Paschero, M.; Hyer, M.W. Axial buckling of an orthotropic circular cylinder: Application to orthogrid concept. Int. J. Solids Struct. 2009, 46, 2151–2171. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, F.; Fan, H.; Fang, D. Fabrication and testing of composite orthogrid sandwich cylinder. Compos. Sci. Technol. 2017, 142, 171–179. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, F.; Zhang, X.; Fan, H. Interlocking orthogrid: An efficient way to construct lightweight lattice-core sandwich composite structure. Compos. Struct. 2017, 176, 55–71. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, B.; Zhou, J.; Chen, H.; Wang, B.; Zhou, Y.; Xu, Y.; Jin, F.; Fan, H. Quasi-far-field blast responses of hierarchical orthogrid-stiffened sheet molding compound (SMC) protective door structures. Eng. Struct. 2018, 168, 431–446. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Wang, Z.; Zhao, L. Experiments on curved sandwich panels under blast loading. Int. J. Impact Eng. 2010, 37, 960–970. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Zhao, L.; Qu, Z. Response of curved sandwich panels subjected to blast loading. J. Performa. Constr. Facil. 2011, 25, 382–393. [Google Scholar] [CrossRef]
- Chen, L.; Qin, F.; Ya-Dong, Z.; Yi, Z.; Jun-Yu, F. Numerical and Experimental Investigations on the blast-resistant properties of arched RC blast doors. Int. J. Prot. Struct. 2010, 1, 425–441. [Google Scholar]
- Chen, L.; Fang, Q.; Zhang, Y.; Zhang, Y. Rate-sensitive numerical analysis of dynamic responses of arched blast doors subjected to blast loading. Trans. Tianjin Univ. 2008, 14, 348–352. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H. Numerical study of a new multi-arch double-layered blast-resistance door panel. Int. J. Impact Eng. 2012, 43, 16–28. [Google Scholar] [CrossRef]
- Anderson, M.; Dover, D. Lightweight, blast-resistant doors for retrofit protection against the terrorist threat. In Proceedings of the 2nd International Conference on Innovation in Architecture, Engineering and Construction (AEC), Loughborough, UK, 25–27 June 2003. [Google Scholar]
- Morgan, T.W. Lightweight Armored Panels and Doors. U.S. Patent No. 6,568,310, 27 May 2003. [Google Scholar]
- Mandall, M.C. Ablative Blast Resistant Security Door Panel. U.S. Patent No. 7,000,550, 21 February 2006. [Google Scholar]
- Al-Rifaie, H.; Sumelka, W. The development of a new shock absorbing Uniaxial Graded Auxetic Damper (UGAD). Materials 2019, 12, 2573. [Google Scholar] [CrossRef] [PubMed]
- Børvik, T.; Hopperstad, O.; Berstad, T.; Langseth, M. A computational model of viscoplasticity and ductile damage for impact and penetration. Eur. J. Mech. A/Solids 2001, 20, 685–712. [Google Scholar] [CrossRef]
- Dusenberry, D. Handbook for Blast Resistant Design of Buildings; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Szymczyk, M.; Sumelka, W.; Łodygowski, T. Numerical investigation on ballistic resistance of aluminium multi-layered panels impacted by improvised projectiles. Arch. Appl. Mech. 2018, 88, 51–63. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Sumelka, W. Numerical analysis of reaction forces in blast resistant gates. Struct. Eng. Mech. 2017, 63, 347–359. [Google Scholar]
- Chipley, M.; Lyon, W.; Smilowitz, R.; Williams, P.; Arnold, C.; Blewett, W.; Hazen, L.; Krimgold, F. Primer to Design Safe School Projects in Case of Terrorist Attacks and School Shootings. Buildings and Infrastructure Protection Series. FEMA-428/BIPS-07/January 2012, 2nd ed.; US Department of Homeland Security: Washington, DC, USA, 2012.
- Yuen, S.C.K.; Nurick, G.; Langdon, G.; Iyer, Y. Deformation of thin plates subjected to impulsive load: Part III—An update 25 years on. Int. J. Impact Eng. 2016, 107, 108–117. [Google Scholar]
- Rigby, S.E.; Tyas, A.; Clarke, S.D.; Fay, S.D.; Reay, J.J.; Warren, J.A.; Gant, M.; Elgy, I. Observations from preliminary experiments on spatial and temporal pressure measurements from near-field free air explosions. Int. J. Prot. Struct. 2015, 6, 175–190. [Google Scholar] [CrossRef]
- Shin, J.; Whittaker, A.S.; Cormie, D. TNT Equivalency for Overpressure and Impulse for Detonations of Spherical Charges of High Explosives. Int. J. Prot. Struct. 2015, 6, 567–579. [Google Scholar] [CrossRef]
- Hong, X.; Li, W.; Cheng, W.; Li, W.; Xu, H. Numerical simulation of the blast wave of a multilayer composite charge. Def. Technol. 2019, 16, 96–106. [Google Scholar] [CrossRef]
- Cullis, I.; Dunsmore, P.; Harrison, A.; Lewtas, I.; Townsley, R. Numerical simulation of the natural fragmentation of explosively loaded thick walled cylinders. Def. Technol. 2014, 10, 198–210. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Grazka, M.; Janiszewski, J. Identification of Johnson-Cook Equation Constants using Finite Element Method. Eng. Trans. 2012, 60, 215–223. [Google Scholar]
- Shrot, A.; Bäker, M. Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus Documentation; Dassault Systemes Simulia Corporation: Johnston, RI, USA, 2016. [Google Scholar]
- Wisniewski, K.; Turska, E. Improved nine-node shell element MITC9i with reduced distortion sensitivity. Comput. Mech. 2017, 62, 488–523. [Google Scholar] [CrossRef]
- Wisniewski, K.; Kowalczyk, P.; Turska, E. Analytical DSA for explicit dynamics of elastic-plastic shells. Comput. Mech. 2007, 39, 761–785. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Sumelka, W. Numerical Analysis of a Reinforced Concrete Supporting Structure for Blast Resistant Gates. In Proceedings of the 23rd International Conference on Computer Methods in Mechanics PCM-CMM, Krakow, Poland, 8–12 September 2019. [Google Scholar]
- Al-Rifaie, H. Application of Passive Damping Systems in Blast Resistant Gates. Ph.D. Thesis, Poznan University of Technology, Poznan, Poland, 2019. [Google Scholar]






| Category | Constant | Description | Unit | Value |
|---|---|---|---|---|
| Elastic Constants | E | Modulus of Elasticity | MPa | 200 × 103 |
| ν | Poisson’s ratio | - | 0.33 | |
| Density | ρ | Mass density | t/mm3 | 7.85 × 10−9 |
| Yield stress and strain hardening | A | Yield Strength | MPa | 490 |
| B | Ultimate Strength | MPa | 807 | |
| n | Work-hardening exponent | - | 0.73 | |
| Strain-rate hardening | Reference Strain rate | S−1 | 5 × 10−4 | |
| C | Strain rate factor | - | 0.0114 | |
| Damage evolution | Critical Damage | - | 0.3 | |
| Damage threshold | - | 0 | ||
| Adiabatic heating and temperature softening | Specific heat | mm2K/S2 | 452 × 106 | |
| χ | Taylor Quinney empirical constant/inelastic heat fraction | - | 0.9 | |
| α | Coefficient of thermal expansion | K−1 | 1.1 × 10−5 | |
| Melting Temperature | K | 1800 | ||
| Room Temperature | K | 293 | ||
| m | Thermal-softening exponent | - | 0.94 | |
| K | - | - | 0.74 | |
| Fracture Strain Constants | - | - | 0.0705 | |
| - | - | 1.732 | ||
| - | - | −0.54 | ||
| - | - | −0.015 | ||
| - | - | 0 |
| Mesh = 50 mm | Mesh = 20 mm | Mesh = 10 mm | |
|---|---|---|---|
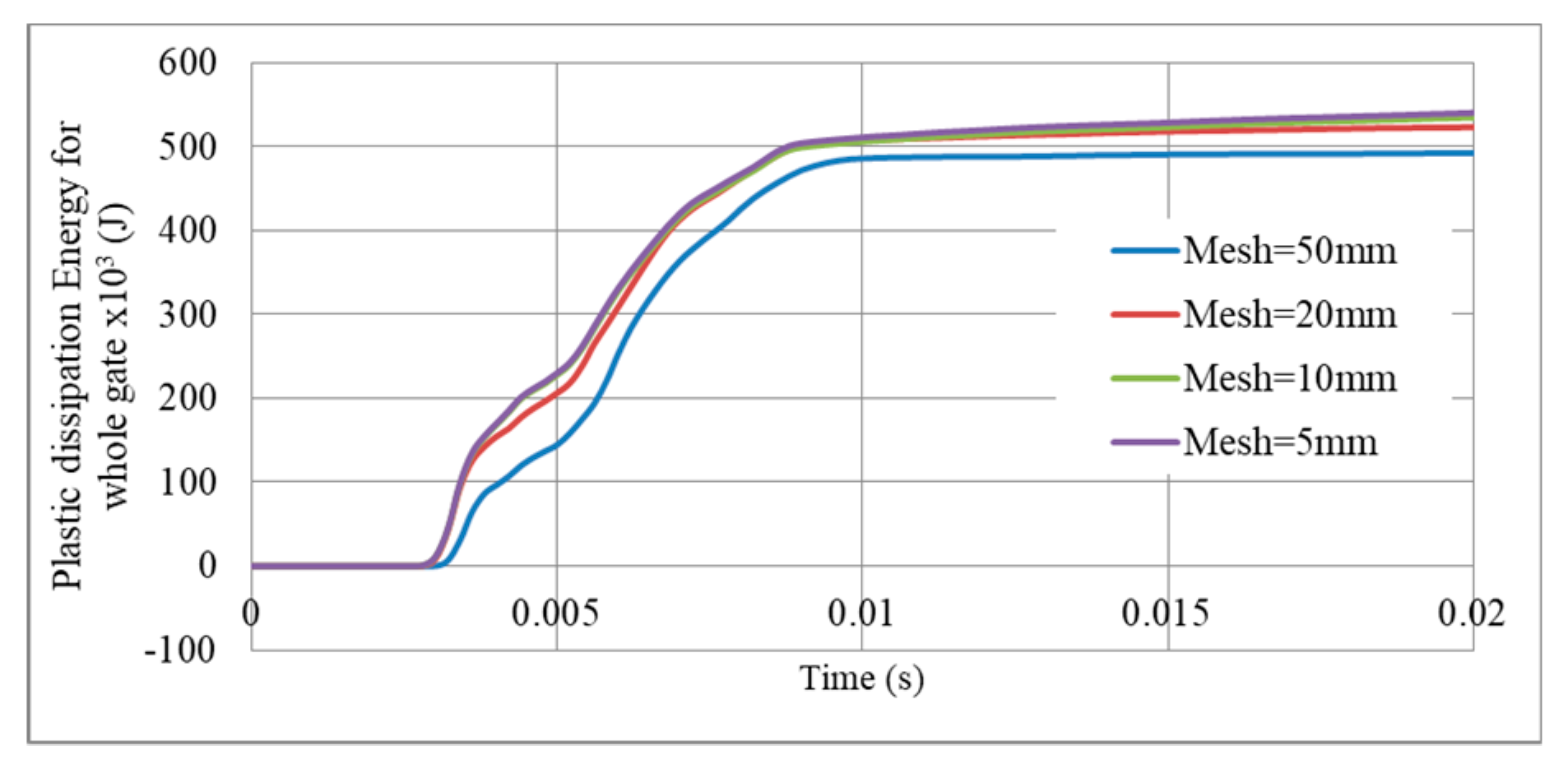
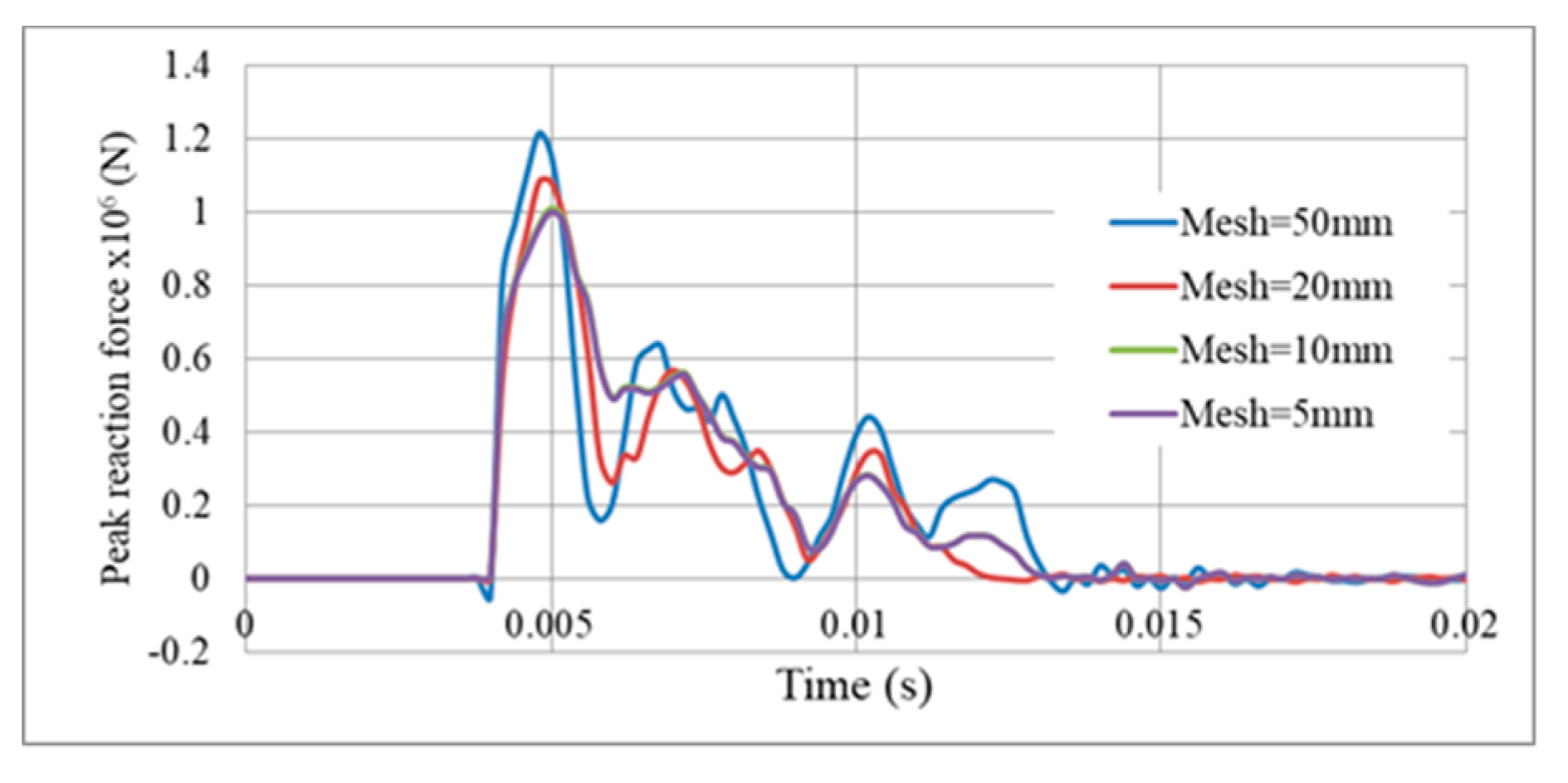
| Plastic dissipation Energy | 12.84 | 2.85 | 0.84 |
| Peak reaction force | 46.79 | 32.52 | 0.80 |
| Aux.1 | Aux.2 | Aux.3 | |
|---|---|---|---|
| Shape |  |  |  |
| Shared parameters | L = 10 mm, cell angle = 60°, Grade AL3 ( = 2.703 × 10−9 t/mm3), Size = 140 mm × 200 mm × 200 mm, volume of one core V = 5.6 × 106 mm3 | ||
| (mm) | 1.4 | 1.8 | 2.2 |
| t/L | 0.14 | 0.18 | 0.22 |
| Mass (ton) | 0.00338 | 0.00434 | 0.00530 |
| Mass (kg) | 3.38 | 4.34 | 5.30 |
| Density (t/mm3) | 6.036 × 10−10 | 7.75 × 10−10 | 9.46 × 10−10 |
| Relative Density | 0.223 | 0.287 | 0.35 |
| Void ratio % | 77.7 | 71.3 | 65 |
| Gate | G2.5 | G5 | G7.5 | G10 |
|---|---|---|---|---|
| Total Mass (ton) | 1.10 | 2.19 | 3.29 | 4.38 |
| Mass/Area (kg/m2) | 81.12 | 162.23 | 243.35 | 324.47 |
| Peak Plastic Strain | Permanent Deformation d (mm) | Operable | ||||||
|---|---|---|---|---|---|---|---|---|
| Gate | t (mm) | Frame | Front Plate | Back Plate | Frame | Front Plate | Back Plate | (Yes/No) |
| G2.5 | 2.5 | 0.89 | 0.82 | 0.17 | 551.0 | 489.0 | 490.0 | No |
| G5 | 5 | 0.29 | 0.17 | 0.25 | 40.5 | 65.6 | 40.0 | No |
| G7.5 | 7.5 | 0.20 | 0.13 | 0.17 | 28.4 | 30.0 | 28.0 | No |
| G10 | 10 | 0.02 | 0.07 | 0.05 | 4.4 | 11.6 | 10.5 | Yes |
| Peak Plastic Strain | Permanent Deformation d (mm) | Operable | ||||||
|---|---|---|---|---|---|---|---|---|
| Gate | t (mm) | Frame | Front Plate | Back Plate | Frame | Front Plate | Back Plate | (Yes/No) |
| G2.5 | 2.5 | 0.93 | 0.89 | 0.19 | 676 | 613 | 609 | No |
| G5 | 5 | 0.1 | 0.17 | 0.156 | 22 | 51 | 24 | Yes |
| G7.5 | 7.5 | 0.03 | 0.16 | 0.1 | 4 | 19 | 8 | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Rifaie, H.; Sumelka, W. Improving the Blast Resistance of Large Steel Gates—Numerical Study. Materials 2020, 13, 2121. https://doi.org/10.3390/ma13092121
Al-Rifaie H, Sumelka W. Improving the Blast Resistance of Large Steel Gates—Numerical Study. Materials. 2020; 13(9):2121. https://doi.org/10.3390/ma13092121
Chicago/Turabian StyleAl-Rifaie, Hasan, and Wojciech Sumelka. 2020. "Improving the Blast Resistance of Large Steel Gates—Numerical Study" Materials 13, no. 9: 2121. https://doi.org/10.3390/ma13092121
APA StyleAl-Rifaie, H., & Sumelka, W. (2020). Improving the Blast Resistance of Large Steel Gates—Numerical Study. Materials, 13(9), 2121. https://doi.org/10.3390/ma13092121






