The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis

Abstract

The comparison of shear stress determination methods in tubular specimens under torsion is presented in this paper. Four methods were analyzed: purely elastic solutions, purely plastic solutions, the midsection approach, and the Chaboche nonlinear kinematic hardening model. Using experimental data from self-designed and conducted fatigue experiments, an interesting insight on this problem was obtained that is not often tackled in the literature. It was shown that there are differences in determined shear stress values, and their level depends on a few factors. The midsection approach and purely plastic solution gave values of surface shear stress very close to the values obtained using the Chaboche nonlinear kinematic hardening model for high strain levels. The purely elastic solution gave proper results for the low strain ranges, close to the cyclic yield limit. Since none of the methods can be trusted in the full range of loading, an important conclusion from these analyses regards the formulated ranges of their applicability. It was also shown that the calculated values of shear stress and plastic and elastic strain energy density determined on this basis have a strong impact on fatigue life predictions. Finally, the influence of predicted values of shear stresses on the interpretation of cyclic hardening phenomena was also presented.

1. Introduction

Usually, fatigue cracks originate on a free surface due to the stress concentration on a micro and macro scale. Given polycrystalline materials, plastic deformation is also higher on a surface as a result of lower constraints from neighboring grains [1]. In the case of elements that are loaded with bending moment or torque, stresses are additionally higher on a surface due to their gradient [2,3]. These types of loading are often studied [4,5], also in an elastic–plastic strain range [6,7]. Considering this, it is clear that the proper analysis of stress and strain on the surface of elements undergoing fatigue loading is an important issue. On the other hand, a compromise between the accuracy and simplicity of the solution is usually desired.

In the present study, the focus is placed on the analysis of shear stress in thin-walled tubular specimens, which are most often used in strain-controlled multiaxial fatigue tests [8,9]. The problem of elastic–plastic torsion has already been studied by other authors. Usually, some advanced mathematical models are made regarding this issue, together with proposals of numerical solutions devoted to the determination of the twist angle or accumulated energy [10,11,12,13,14,15,16]. Other papers concern an application of the Finite Elements Method or the Finite Differences Method to model the torsion of different profiles [17,18,19]. Sometimes, the topic of the study is very narrow, e.g., it concerns only a selected issue related to the yield point, which the authors term the “small corrugations of the elastic–plastic boundary” [20]. Unfortunately, quite often such works do not provide practical solutions and explanations on how to correctly determine the surface shear stress for tubular specimens subjected to cyclic torsion, based on experimental data like torque and shear strain on the surface of the specimen. If any cyclic plasticity models are involved, they assume perfectly elastic or perfectly plastic material behavior. More practical considerations regarding the cyclic torsion of cylindrical specimens have previously been performed by Miller and Chandler [21] and Brown [22].

In fatigue analysis, authors use various approaches to solve the problem of shear stress determination in tubular specimens under torsion. Shamsaei and Fatemi [23] used midsection shear stress values, which were further fitted with a Ramberg–Osgood-type function and extrapolated on the surface. However, this method can be used only for materials that exhibit Masing behavior (the upper branches of hysteresis loops form one common curve) and do not show significant differences in stress history depending on the loading level. Furthermore, the fit and extrapolation procedure must be separately repeated for each loading case. The midsection approach was also used by Socie [24], Zhong et al. [25], Wu et al. [26], Zhang and Jiang [27,28], and in other works by Fatemi and coauthors [29,30]. Dey et al. used an elastic solution, even though they applied relatively high strain values [31]. There are also several papers where the shear stress determination method was not mentioned [32,33,34,35].

In the present paper, three different approaches based on the measured value of torque were applied to determine shear stress in tubular specimens made of PA38-T6 (AW-6060) aluminum alloy subjected to torsion. They were further compared to values calculated using the Chaboche kinematic hardening model. This thorough approach to the problem makes it possible to become aware of differences in shear stress values obtained using various methods and to find their dependence on factors such as specimen size and loading level. The results of this work also give an idea of the order of magnitude of these differences, the impact on the interpretation of cyclic hardening, and on the prediction of fatigue life. Considering these factors, the guidance was provided according to the applicability of these methods. Furthermore, it is worth noting that all analyses were conducted based on a self-designed and conducted experiment. The adopted research methodology of the experiment assumed continuous recording of all signals from the testing system with a high sampling frequency. This enabled accurate calculations and detailed analyses.

2. Theoretical Background

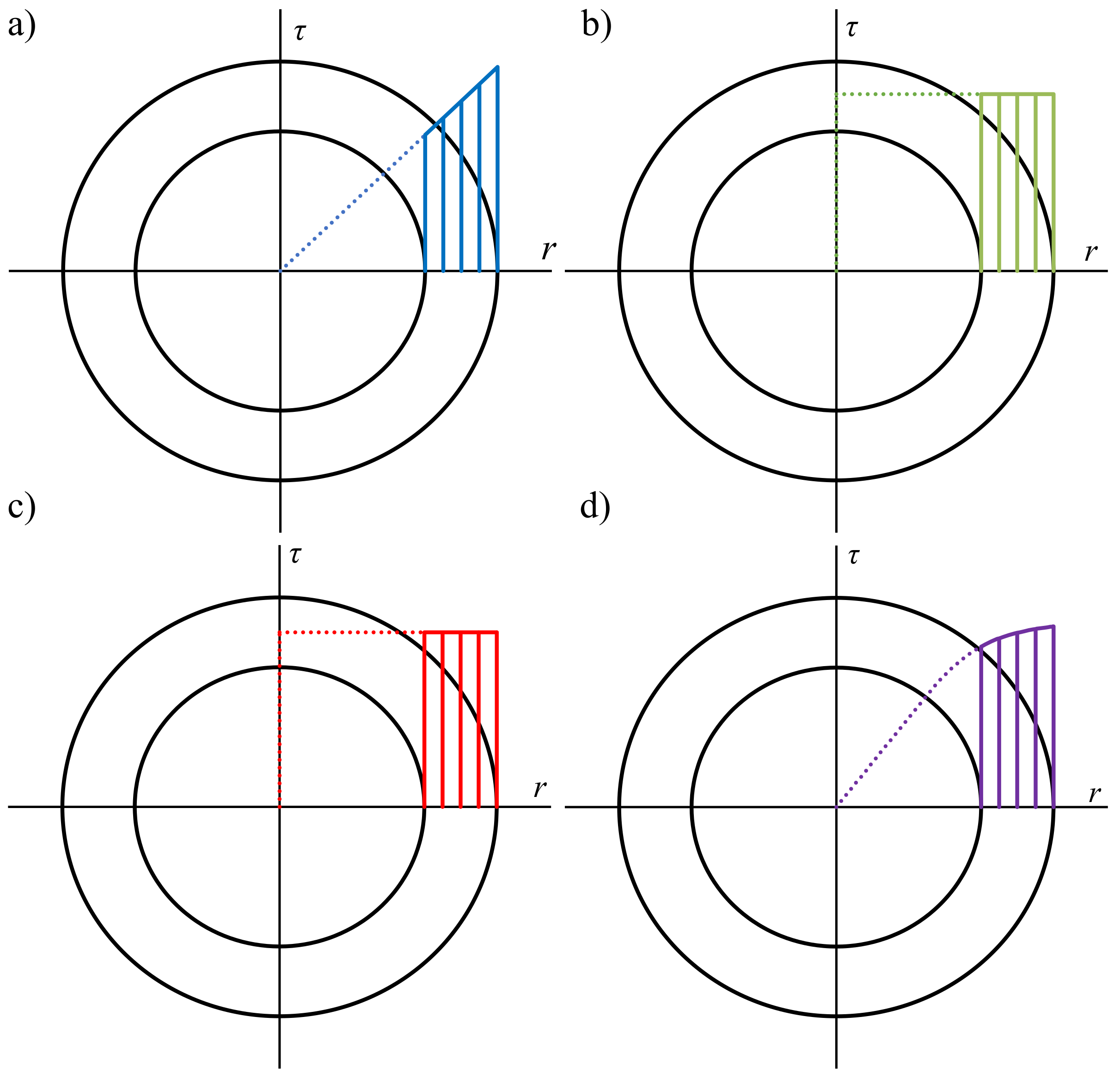
2.1. Shear Stress Distribution under Elastic–Plastic Torsion

Nonuniform shear stress distribution occurs in every specimen subjected to torsion if the stress is higher than the yield limit [19]. Such distributions make it dubious to apply simple elastic solutions for accurate determination of shear stress since they assume a linear relationship between stress and strain. Furthermore, several other phenomena influence the shear stress value on the surface of the specimen. For example, the torque can be high enough to induce yielding of the outer layers of the material, but at the same time small enough to remain elastic at internal layers [12]. The boundary between elastic and elastic–plastic deformation also moves along the radius during the cyclic loading and unloading processes [21]. The torque, which is a measured quantity, depends on the stresses acting in the whole cross-section of the specimen; thus, the stress–strain and torque–twist angle relationship differ (Figure 1). These relationships become even more complicated when considering cyclic loadings [36]. When twisting right (conventionally) and subsequent unloading, the stress in the outer layer is not yet zero, while the stress in the internal layer exceeds zero, so it is already compressed (stressed left) [18] (Figure 2). Therefore, when the torque being measured equals zero, the value of shear stress in the external layer differs from zero (points 3 and 7). This influences the shape of the hysteresis loop and the calculated plastic strain energy density. If the material hardens or softens cyclically, the amount of hardening/softening depending on strain level varies for different layers (in the radial direction) of the specimen. This hardening or softening is difficult to consider during the analysis of data that is only recorded from the testing system. All the abovementioned phenomena depend further on the level of loading, on internal and external diameters of the specimen, and on the specimen’s thickness.

2.2. Selected Methods of the Shear Stress Determination in Case of Tubular Specimens

The first of the considered approaches for determining shear stress in tubular specimens is based on a purely elastic solution. The relationship between torque T and shear stress $\tau$ is given by [37]

$$T={\int }_A\tau \left(r\right)rdA=2\pi {\int }_r\tau \left(r\right)rdr=2\pi {\int }_{r_i}^{r_o}\tau \left(r\right)·r^{2}dr,$$

(1)

where $r_i$ and $r_o$ are internal and outer radii of the specimen, respectively. By the assumption that the shear stress is a linear function of radius, $\tau \left(r\right)=ar$, where a is the slope of function, after integration and substitution of a by ${\tau }_o$, we get

$$T=\frac{\pi {\tau }_o(r_o^4-r_i^4)}{2}.$$

(2)

The shear stress on the surface is then given by

$${\tau }_o=\frac{T}{J_0}{r}_o=\frac{2r_{o}T}{\pi (r_o^4-r_i^4)},$$

(3)

where $J_0$ is the polar moment of inertia. The resulting distribution of shear stress along the radial direction is presented in Figure 3a.

The second method is recommended by the ASTM standard [57] for the low-cycle fatigue regime. It is assumed that the shear stress distribution is uniform through the wall thickness (Figure 3b) and is equal to the midsection value ${\tau }_m$. The torque is given by the following simplified Equation (1):

$$T={\tau }_m{r}_{m}A,$$

(4)

and ${\tau }_m$ by

$${\tau }_m=\frac{T}{A{r}_m}=\frac{16T}{\pi (d_o^2-d_i^2)(d_o+d_i)},$$

(5)

where $r_m$ is the mean radius. The standard also specifies the criterion for a thin wall, for which the shear stress variation in the radial direction is negligible. Specimens that do not meet the criterion of a thin wall are examined in the work of Brown [22].

The next approach is based on a purely plastic solution. The assumption is the same as in the case of the midsection method (Figure 3c), and the relationship between shear stress and the radius of the specimen is given by

$$\tau \left(r\right)=\mathrm{const}.$$

(6)

After substituting (6) into (1) and integration, the following formula is obtained:

$$T=\frac{2}{3}\pi \tau (r_o^3-r_i^3),$$

(7)

and after conversion, the shear stress on the surface is then given by

$${\tau }_o=\frac{3T}{2\pi (r_o^3-r_i^3)}.$$

(8)

The shear stress distributions and values obtained by the previously presented approaches were compared to the values calculated using the Chaboche nonlinear kinematic hardening model [38,39]. The set of applied equations is listed below. The yield surface according to Huber–Mises yield criterion describes the formula:

$$f=\sqrt{\frac{3}{2}(s-\alpha ):(s-\alpha )}-R,$$

(9)

where s is a deviatoric stress tensor, R is cyclic yield stress, and $\alpha$ is a backstress tensor given by

$$d\alpha =\sum _{i=1}^m\frac{2}{3}{C}^{\left(i\right)}d{\epsilon }^p-{\gamma }^{\left(i\right)}{\alpha }^{\left(i\right)}dp,$$

(10)

where $C^{\left(i\right)}$ and ${\gamma }^{\left(i\right)}$ (not to be confused with the shear strain) are material parameters and $d{\epsilon }^p$ is a plastic strain tensor rate, given by the associated plastic flow rule:

$$d{\epsilon }^p=\frac{3}{2}\frac{ds:n}{H}n,$$

(11)

where n is an outward unit tensor determining the direction normal to the yield surface:

$$n=\frac{\frac{\partial f}{\partial s}}{\sqrt{\frac{\partial f}{\partial s}:\frac{\partial f}{\partial s}}}.$$

(12)

H is a plastic hardening modulus and $dp$ is the accumulated equivalent plastic strain rate:

$$dp=\sqrt{\frac{2}{3}d{\epsilon }^p:d{\epsilon }^p}.$$

(13)

The value of H can be determined from the yield surface consistency condition:

$$\frac{\partial f}{\partial s}:ds+\frac{\partial f}{\partial \alpha }:d\alpha =0.$$

(14)

Using the Chaboche model, a nonlinear distribution of the shear stress along the specimen’s radius is achieved (Figure 3d).

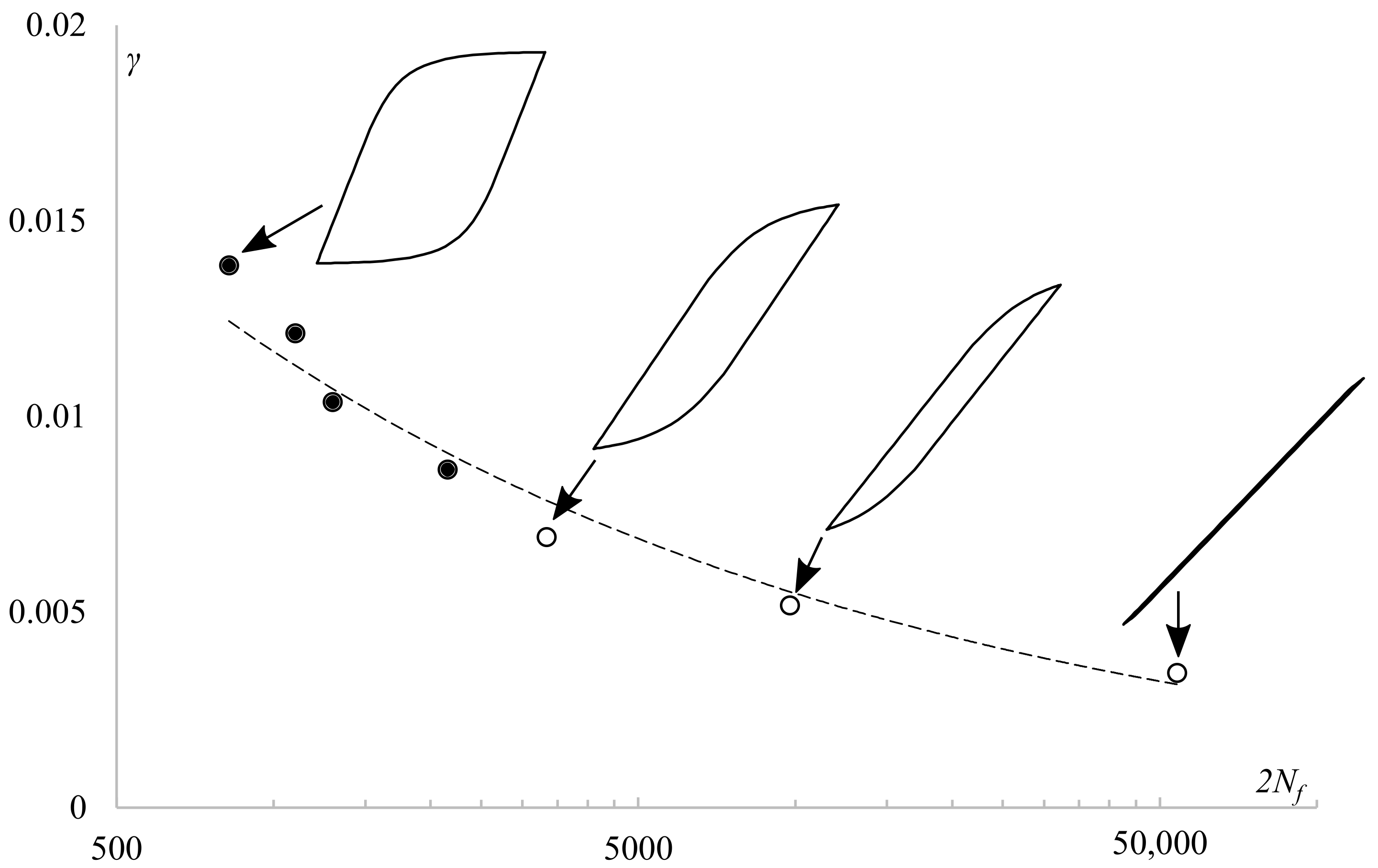
2.3. Influence of Shear Stress on Fatigue Life Prediction

For fatigue of materials, the ability to determine the correct shear stress value is crucial. The most popular multiaxial fatigue damage parameters, like Fatemi–Socie [40], generalized Smith–Watson–Topper [24,41], Łagoda–Macha [42], Ince–Glinka [43], or Garud [44], depend directly or indirectly on the determined value of this stress. Such a fatigue damage parameter is proposed by Gołoś and Ellyin [45,46]:

$$\frac{\Delta W^p}{\rho }+\Delta W^{e+},$$

(15)

where $\Delta W^p$ and $\Delta W^{e+}$ are total plastic and positive elastic strain energy densities and $\rho$ is a multiaxiality coefficient given by

$$\rho =(1+{\nu }_{eq})\frac{{\epsilon }_1}{{\gamma }_{max}},$$

(16)

where ${\nu }_{eq}$ is an equivalent Poisson ratio, ${\epsilon }_1$ is maximum principal strain, and ${\gamma }_{max}$ is the maximum shear strain. The Gołoś–Ellyin parameter was further employed in the present work to analyze the influence of the shear stress value on fatigue life prediction in an energy-based approach.

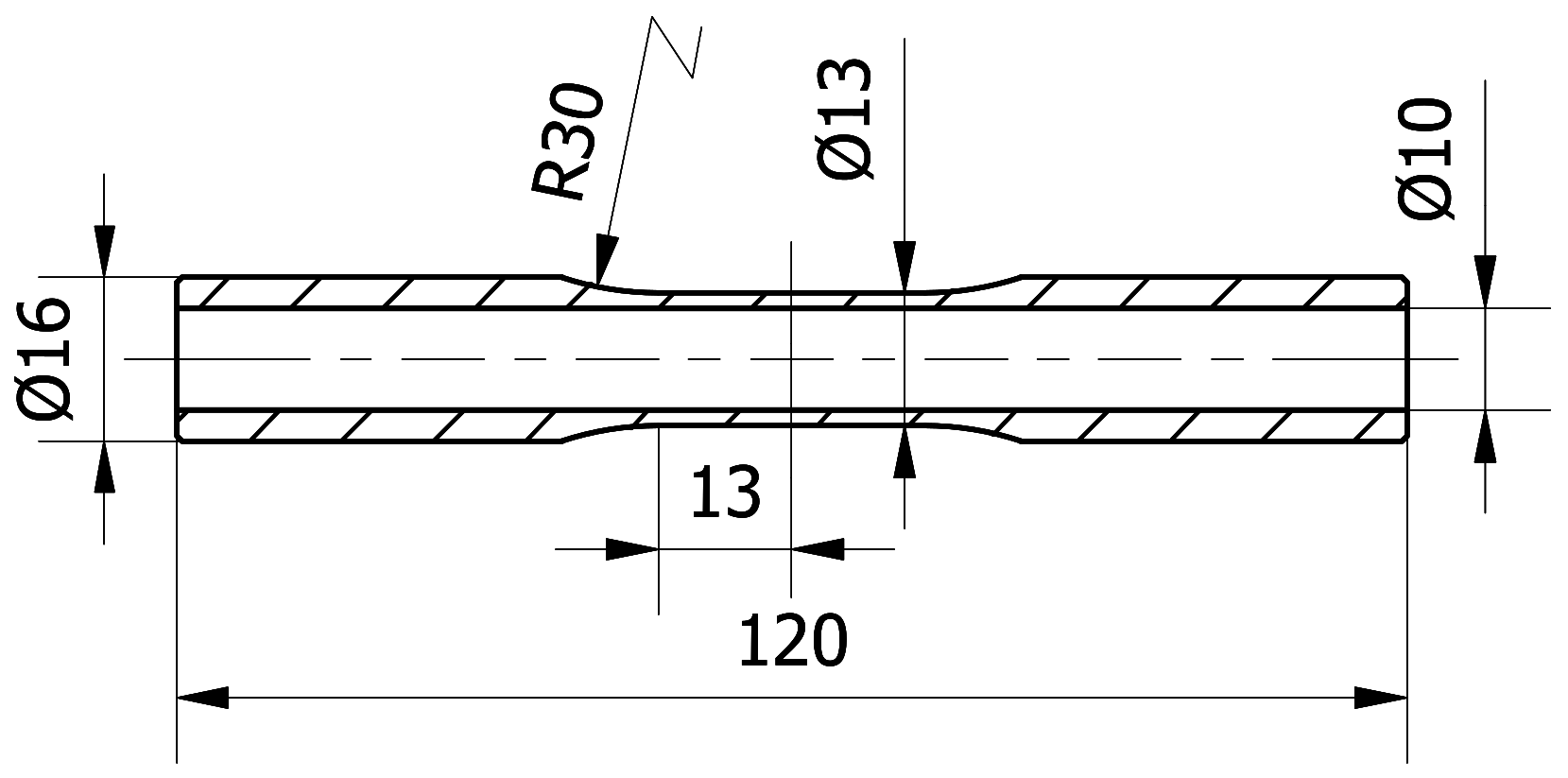
3. Materials and Methods

The experimental data used in this work comes from a broader research program [47,48]. The present work considers previous research regarding the cyclic torsion and axial loading of tubular specimens made of PA38-T6 (AW-6060) aluminum alloy. The chemical composition of this material is given in

Table 1. Chemical composition of PA38-T6 aluminum alloy according to EN 573-3 standard.

Element	Si	Fe	Cu	Mn	Mg	Cr	Zn	Ti	Other	Al
Share (%)	0.3–0.6	0.1–0.3	0.1	0.1	0.35–0.6	0.05	0.15	0.1	0.15	Balance

. Basic mechanical properties, Young’s modulus E, 0.2% offset yield stress ${\sigma }_{y02}$, ultimate tensile strength ${\sigma }_u$ and corresponding strain ${\epsilon }_{{\sigma }_u}$, elastic Poisson ratio ${\nu }_e$, cyclic strength coefficient $K^{\prime }$, and cyclic strain hardening exponent $n^{\prime }$ are given in

Table 2. Basic mechanical properties of PA38-T6 aluminum alloy determined experimentally.

E, GPa	${\mathit{\sigma }}_{\mathit{y}02}$, MPa	${\mathit{\sigma }}_{\mathit{u}}$, MPa	${\mathit{\epsilon }}_{{\mathit{\sigma }}_{\mathit{u}}}$, mm/mm	${\mathit{\nu }}_{\mathit{e}}$, -	${\mathit{K}}^{\prime }$, MPa	${\mathit{n}}^{\prime }$, -
68.3	191.5	229.1	0.094	0.35	288.1	0.051

. The dimensions of the specimens are presented in Figure 4. All fatigue tests were performed on an Instron 8874 servohydraulic axial/torsional testing system. Axial and shear strains were measured and controlled using an Epsilon 3550 biaxial extensometer, and the axial force and torque were measured by the system’s load cell. For further details of the experiment, the reader is referred to [47,48].

The values of the Chaboche model material parameters were determined by using the Interior-Point optimization algorithm to find the best fit of the plastic strain–stress curve for the experimental data recorded for axial loading at midlife [49]. The value of $m=3$ decomposition parts of the backstress tensor was found to be optimal. Determined material parameters are given in

Table 3. Chaboche model material parameters determined for PA38-T6 aluminum alloy.

${\mathit{C}}^1$, MPa	${\mathit{C}}^2$, MPa	${\mathit{C}}^3$, MPa	${\mathit{\gamma }}^1$, -	${\mathit{\gamma }}^2$, -	${\mathit{\gamma }}^3$, -	R, MPa
$1.3723\times {10}^5$	$5.3704\times {10}^4$	$1.6667\times {10}^4$	$7.8078\times {10}^3$	$1.9759\times {10}^3$	$459.3$	$141.1$

. All the calculations were further performed analytically, using own-developed Matlab code, employing the tensor algebra. The strain tensor was used as a controlled quantity and the stress tensor increments were determined for the corresponding strain tensor increments.

The results of the cyclic stress–strain response calculations for fully reversed axial straining are shown in Figure 5. The Chaboche model with correctly determined parameters resulted in accurate modeling of the stress response for several strain amplitudes.

4. Results

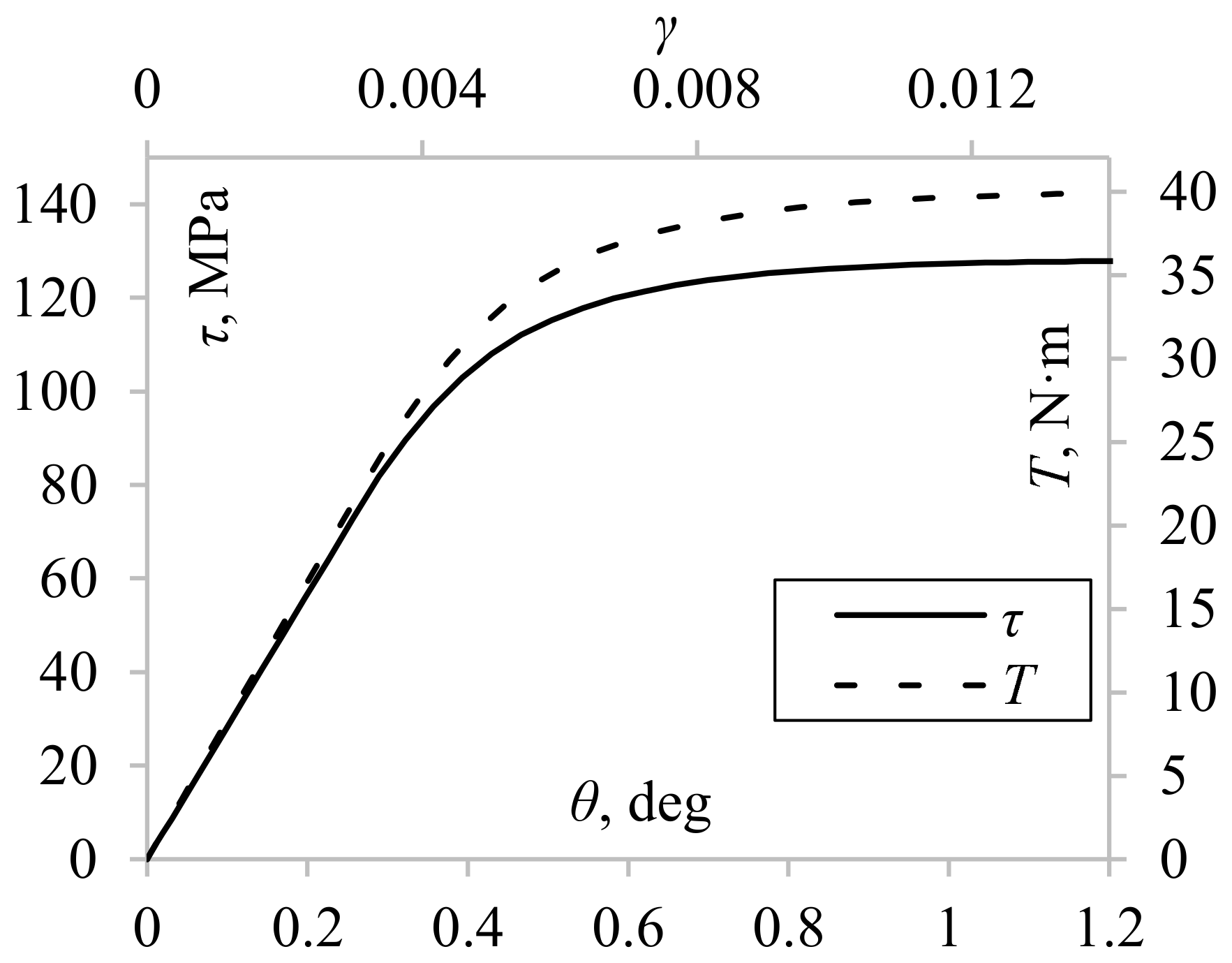
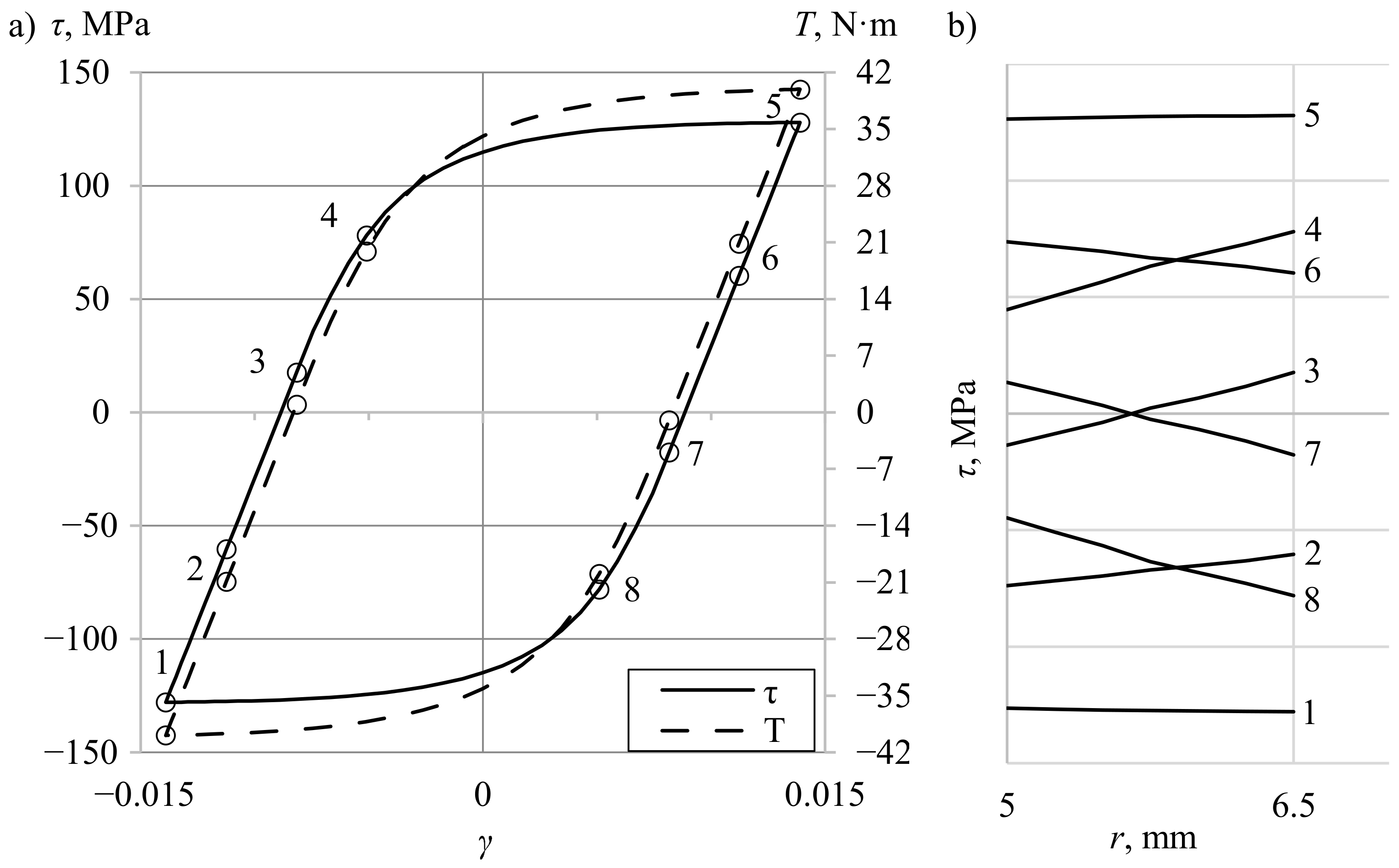
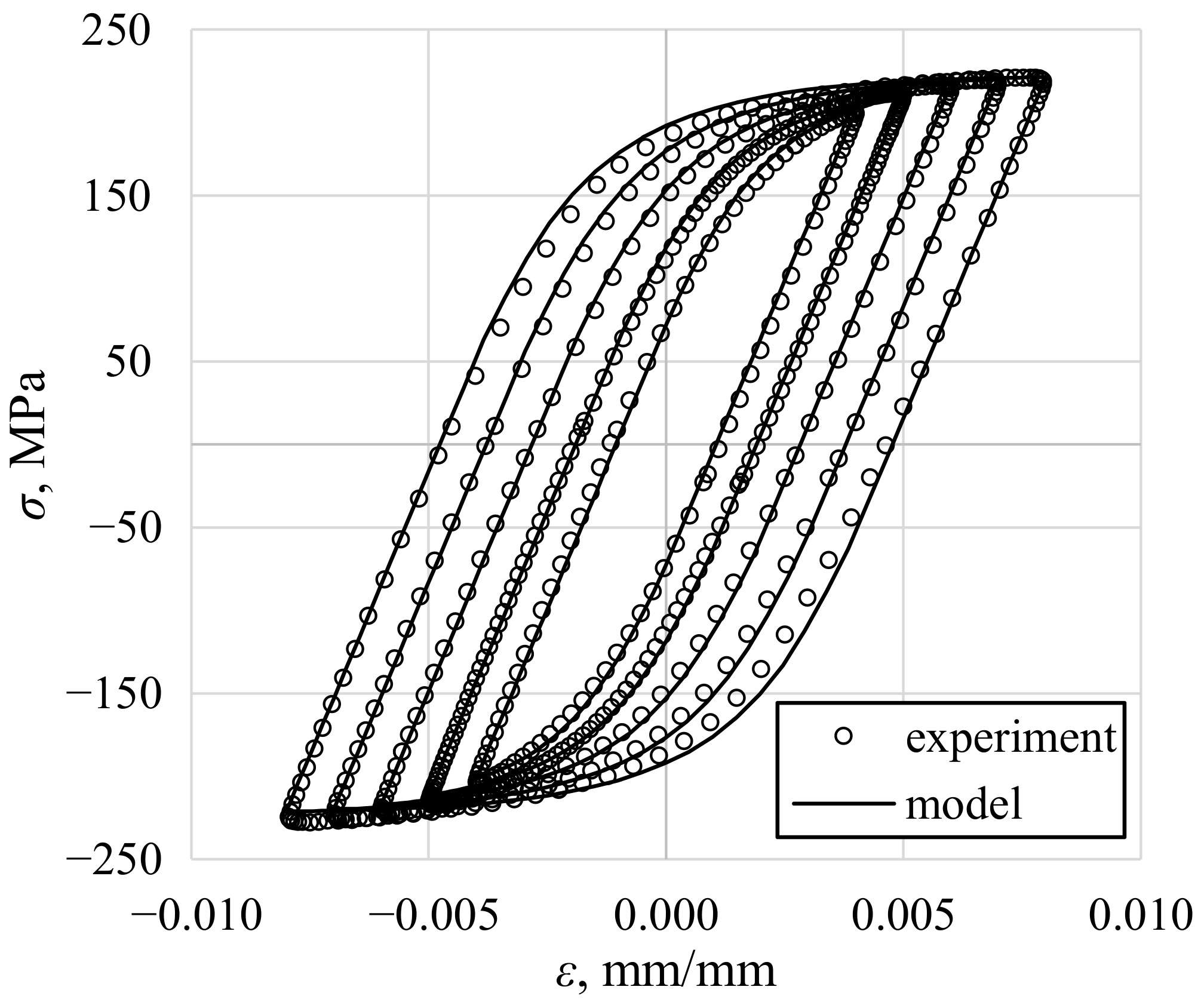
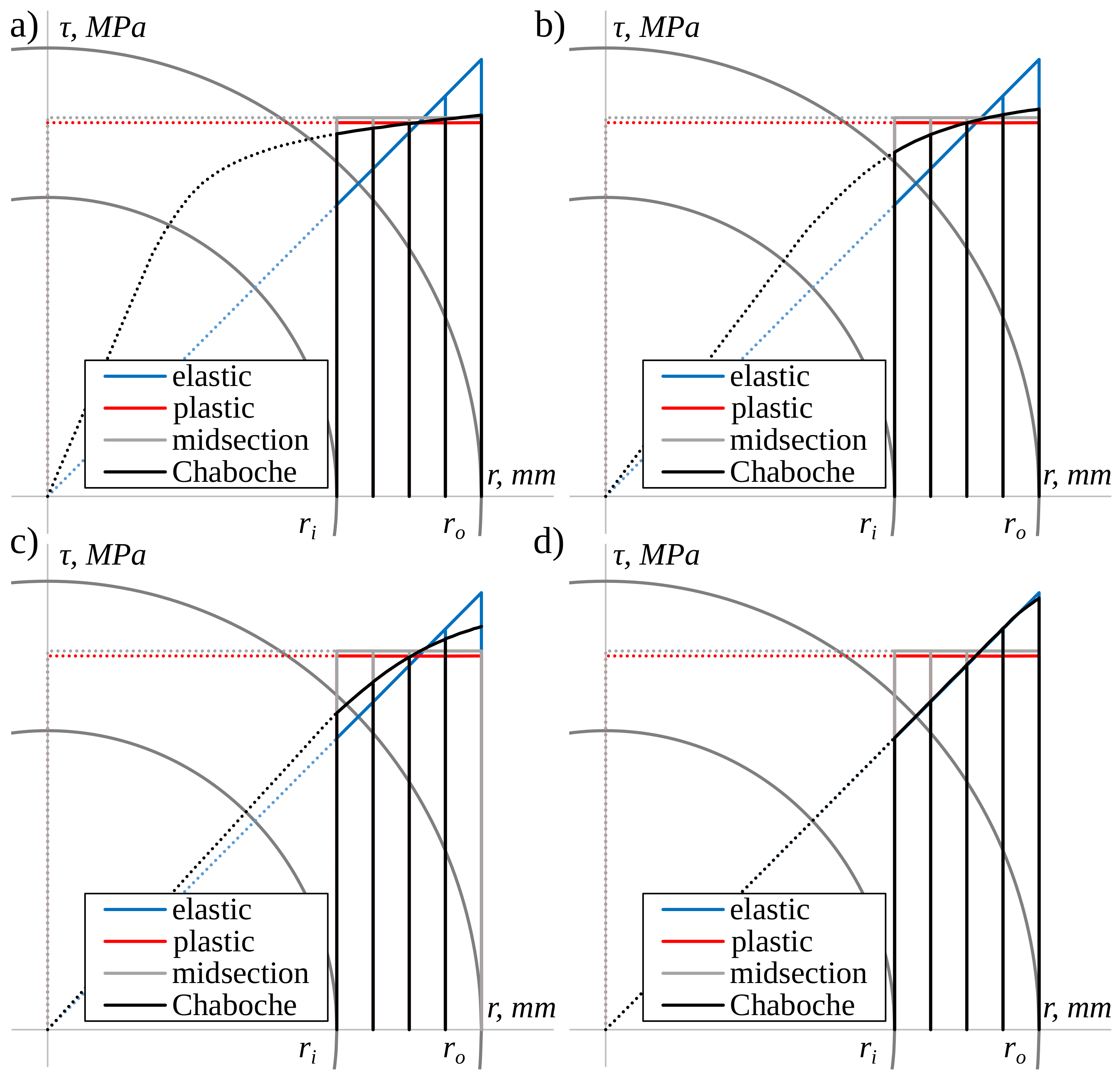
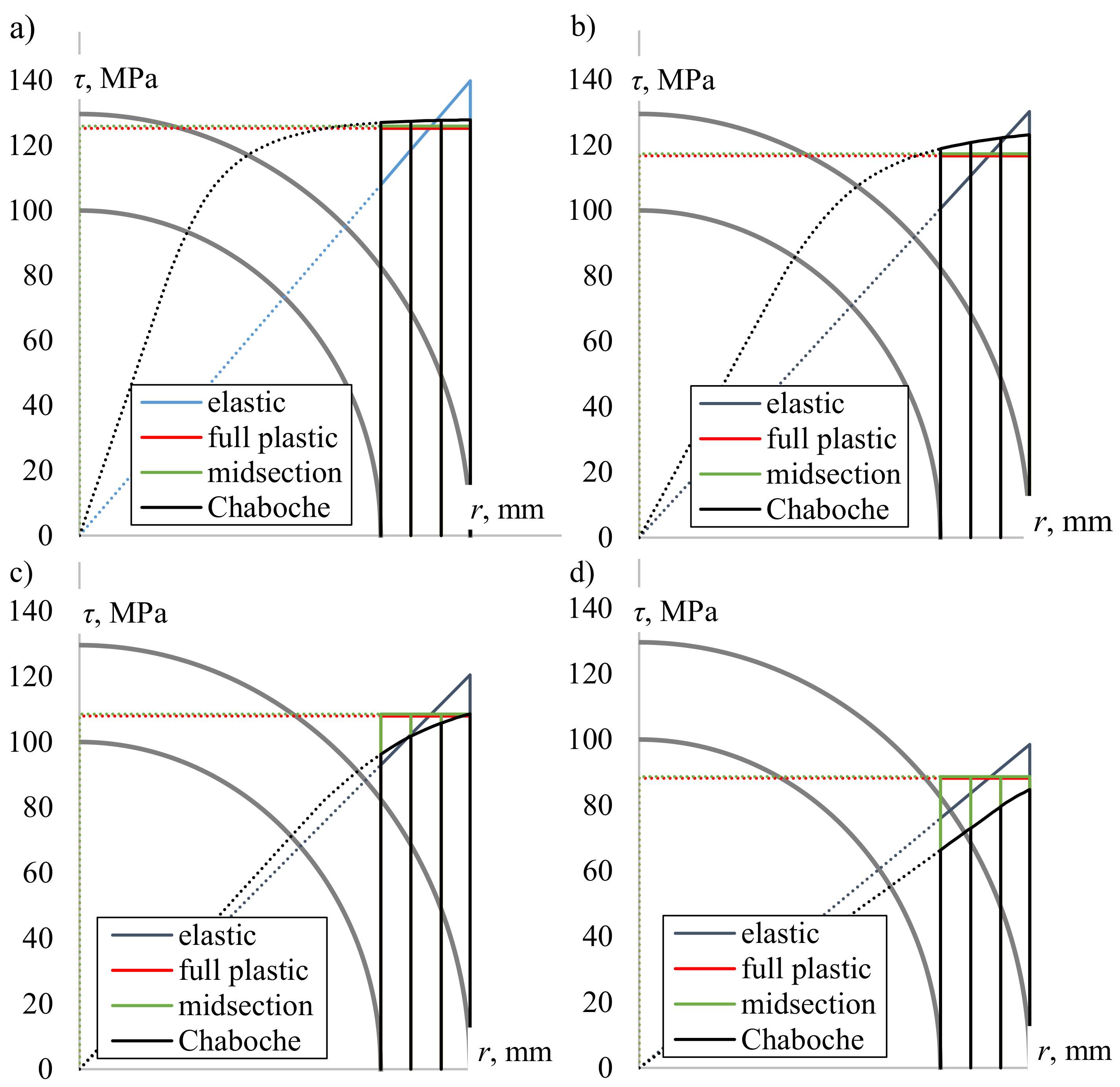
4.1. Shear Stress Distribution Comparison

The shear stress distributions along the radial direction, according to the different shear strain levels determined by the aforementioned approaches, are shown in Figure 6. For this purpose, twice the theoretical thickness of the real specimen (Figure 4) was assumed to best show the differences in shear stress distribution. In the first step, the shear stress distribution for a given shear strain level on the surface was calculated using the Chaboche model. Based on this distribution, the torque was calculated using Equation (1), and then the shear stress distribution was determined using other approaches for the same torque value. This procedure was applied since, in the case of the Chaboche model, the shear stress value is calculated based on the shear strain. With other methods, the shear stress value is determined based on torque. It should be noted that the most important quantity is the shear stress on the specimen’s surface. In reality, it falls between the values resulting from purely elastic and purely plastic solutions.

Based on the similarity between experimental values of stress under axial loading and values calculated using the Chaboche model (Figure 5), it was assumed that when torsion occurs, the shear stress determined using the Chaboche model is closer to the actual values than when it is obtained using other selected approaches. It was then concluded that for high levels of plastic strain, the midsection approach and the purely plastic solution reflect the real values of the shear stress quite well (Figure 6a,b). However, as the strain level decreases and approaches the purely elastic state of deformation, the elastic solution gives better results (Figure 6c,d). Generally, the elastic solution overestimates shear stress with higher strain levels. On the contrary, the midsection approach and the purely plastic solution underestimate shear stress. The underestimation is very small for high levels of strain (Figure 6a,b), while it is higher for small strain levels (Figure 6c,d).

4.2. Application of the Selected Methods to Experimental Data Analysis

In Figure 7, experimental fatigue life was presented against applied shear strain amplitudes. Results were fitted with a power curve. Shear stress was calculated using the midsection method for the purpose of the presentation only. For four selected levels of strain, midlife hysteresis loops were presented to show the plastic-to-total strain ratio with respect to loading level. The applied loading ranges resulted in various stress–strain responses, from almost perfectly elastic to having a high share of plastic strain.

Figure 8 presents the shear stress distribution along the specimen radius obtained using the selected methods for different shear strain levels. The difference compared to the data shown in Figure 6 is that in the case of elastic, plastic, and midsection solutions, the shear stress was calculated directly from the torque measured during the fatigue tests using a load cell. The actual specimens’ diameters were considered as well. Using the Chaboche model, the shear stress was calculated based on the measured shear strain, regardless of the real torque value. It can be seen that for the highest level of loading, i.e., $\gamma =0.0139$ (Figure 8a), the surface shear stress determined from torque using the midsection and a perfectly plastic solution was very close to the surface shear stress calculated using the plasticity model. The elastic solution gave higher values. The same observation was made for other relatively high levels of loading, namely, $\gamma =0.0121,0.0104$, and 0.0087 (black dots in Figure 7). A noticeable discrepancy between the results obtained from the plasticity model, midsection and the plastic solution began from $\gamma =0.0069$ (Figure 8b). For that level of shear strain amplitude, the surface shear stresses determined using the Chaboche model were higher than those calculated using the midsection and plastic methods. Similarly, so was the stress obtained from using the elastic solution. In the case of $\gamma =0.0052$, the surface shear stress calculated from the plasticity model, midsection, and plastic solution was nearly the same (Figure 8c). However, the whole shear stress distribution curve based on the Chaboche model is below the midsection and plastic solution. Again, the elastic approach gave higher values. For the lowest examined level of loading ($\gamma =0.0035$), the surface shear stress from the midsection and purely plastic solution is considerably higher than the stress calculated by the Chaboche model (Figure 8d).

In general, it is worth noting that if the shear stress distribution curve resulting from the application of the Chaboche model lies above the midsection and plastic values (Figure 8a,b), the experimental torque value was lower than expected from the plasticity model and vice versa. The purely elastic approach always resulted in surface shear stress higher than stress obtained using other applied methods, which seems to be obvious. Although the PA38-T6 aluminum alloy was found to be isotropic, quite cyclically stable, and to follow the Masing behavior, the application of the plasticity model did not offer a significantly better solution than other, much simpler methods. Stress evolution during the experiments can be given here as an explanation.

In Figure 9, the Huber–Mises midsection equivalent stress histories are presented. Stresses from the beginning of the test to midlife were more stable for high strain amplitudes. The least stability can be seen in the loading levels that result in stress values close to the cyclic yield stress (the curves with black dots). The consequence of this instability is differences in midlife stress values for low levels of loading, as shown in Figure 10 (black hysteresis loops). Similar behavior was also found by other authors [50,51]. A much more sophisticated and complicated cyclic plasticity model would have to be used to describe this phenomenon, which would make its application less practical.

Two quantities often used in fatigue analysis were further evaluated and compared, based on selected approaches to shear stress determination. The first was the maximum surface shear stress. The best-fit power-law shear-stress–fatigue life curves are presented in Figure 11. The curves for the midsection approach and perfectly plastic solution are almost identical. The data points for the Chaboche model are also very close, except for the lowest level of loading. In the case of an elastic solution, the curve is located significantly above the others. If only stress values are considered, about a 10% difference exists between plastic or midsection and elastic solutions. However, due to quite small slopes of the curves, that difference results in fatigue lives eight times higher. In the same figure, a ”hybrid“ curve was also presented. It was fitted for midsection value points corresponding to the six highest levels of strain and one elastic value point corresponding to the lowest level of strain, for which an almost perfectly elastic response was observed. Such a curve seems to be the most adequate.

The second selected quantity was a sum of plastic and positive elastic strain energy density, similar to the case of the Gołoś–Ellyin energy parameter (compare (15)). Calculated values of energy are presented in Figure 12. This quantity turned out to be less sensitive for the shear stress determination approach, even for the elastic solution. Differences between the best-fit curves for the midsection approach or the plastic and elastic solutions in terms of fatigue life were approximately 15%. The explanation can be seen in Figure 13, where shear strain hysteresis loops according to different stress determination methods were plotted for $\gamma =0.0139$. Compared to the hysteresis loop obtained using the plasticity model, the hysteresis loop based on the elastic solution has stress underestimated for the lower strain range and overestimated for the higher range. However, these differences even each other out and the resulting energies are quite similar.

Cyclic hardening is another phenomenon often investigated by researchers [52,53,54]. The interpretation of the experimental results is strongly related to the applied method of shear stress determination. To support this conclusion, the midlife Huber–Mises equivalent peak stresses from axial and torsional fatigue tests are presented in Figure 14 with a superimposed fragment of the monotonic tension stress–strain curve. For torsion, the equivalent stress was calculated based on the surface shear stress determined using the selected methods. A moderate cyclic axial hardening can be observed. If the elastic solution was applied for the shear stress determination, a higher amount of cyclic hardening under torsion could be found. This observation may be further interpreted as anisotropy in yield stress and hardening [55,56]. However, if the midsection or plastic solution were applied, the equivalent stresses under axial and torsional loading would be quite similar.

5. Summary

Based on the performed analyses of the experimental results of fatigue tests on thin-walled tubular specimens of PA38-T6 aluminum alloy, the following conclusions can be drawn:

• None of the considered approximate solutions can determine the exact value of surface shear stress for tubular specimens under elastic–plastic cyclic torsional loading.
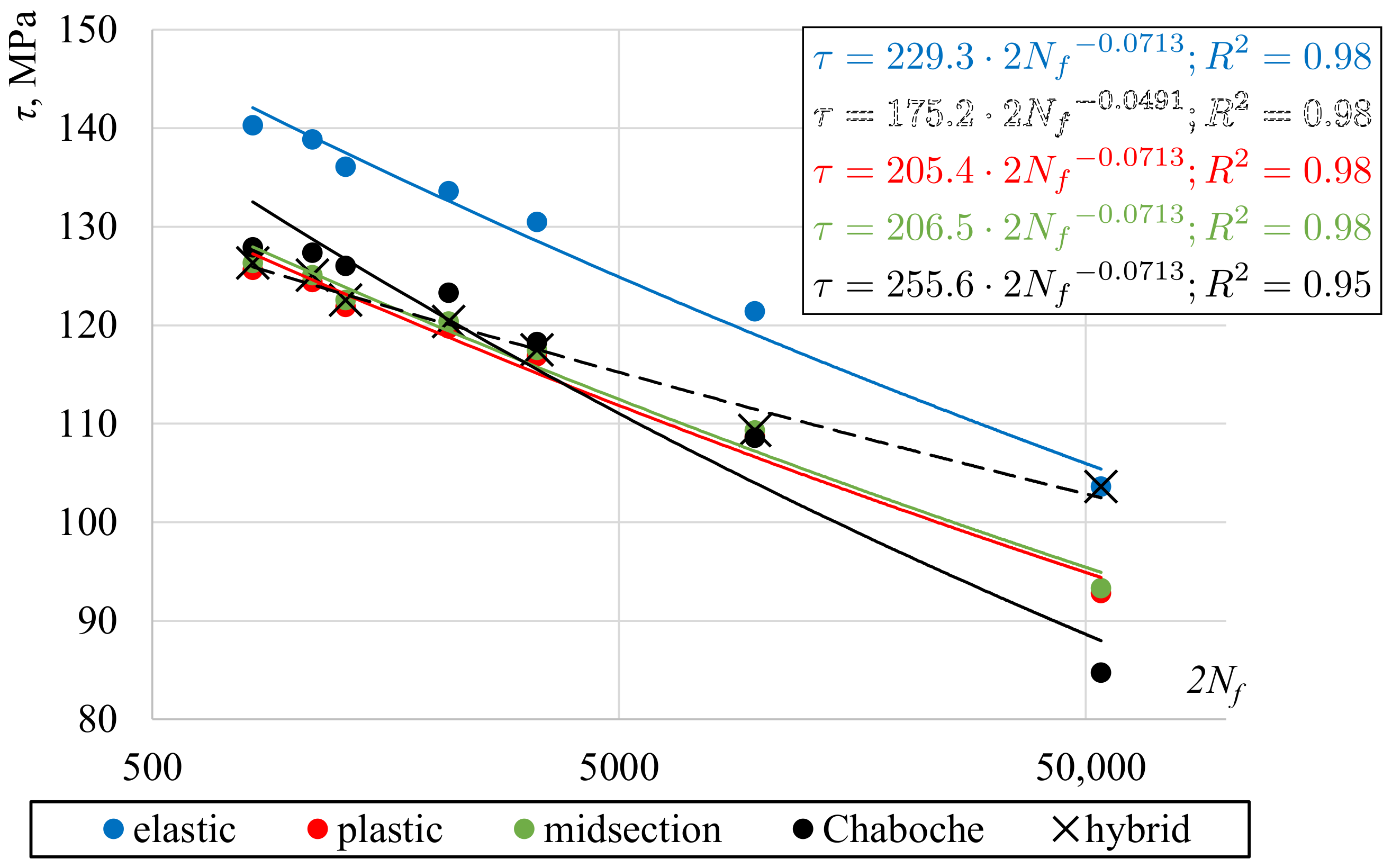
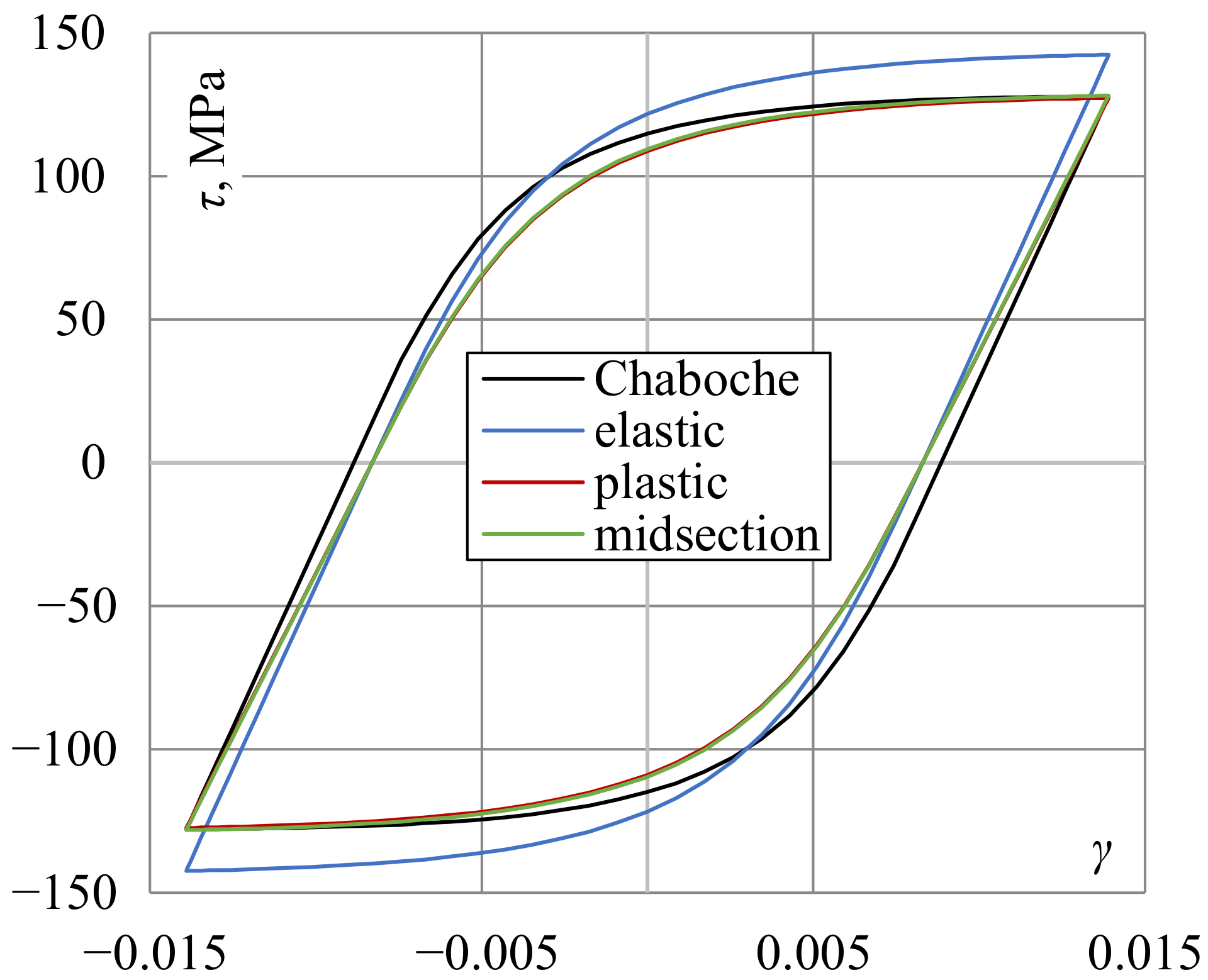
• Using the midsection approach and purely plastic solution for high strain levels, it was found that values of surface shear stress were very close to the values obtained using the Chaboche nonlinear kinematic model, calibrated using the experimental data for the axial loading.
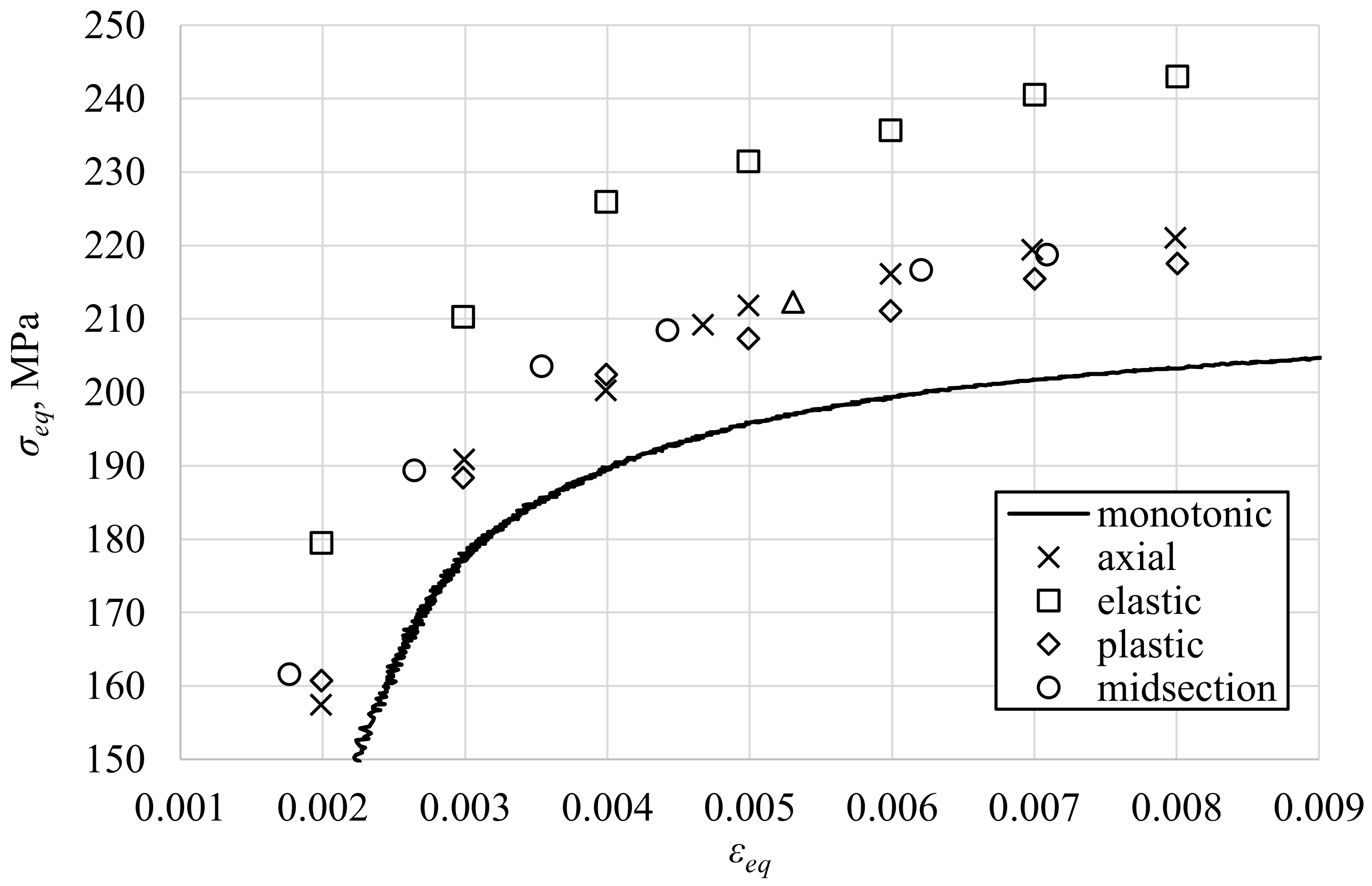
• The largest differences between shear stress values calculated using the plasticity model and other methods were found for the low strain ranges, close to the cyclic yield limit.
• When the ratio of inner and outer diameters of tubular specimens is close to 1, the effect of the nonuniform shear stress distribution through wall thickness is less pronounced.
• It was confirmed that the recommendations of the ASTM standard can be successfully implemented to approximately determine the surface shear stress under torsion; however, if the applied loading levels cover the boundary between elastic and elastic–plastic deformation, it should be carefully considered which loading levels justify choosing a purely elastic or midsection approach.
• The methods discussed are not valid for the full range of loadings. The selection of the approach should be based on the applied loading level and observed material response.
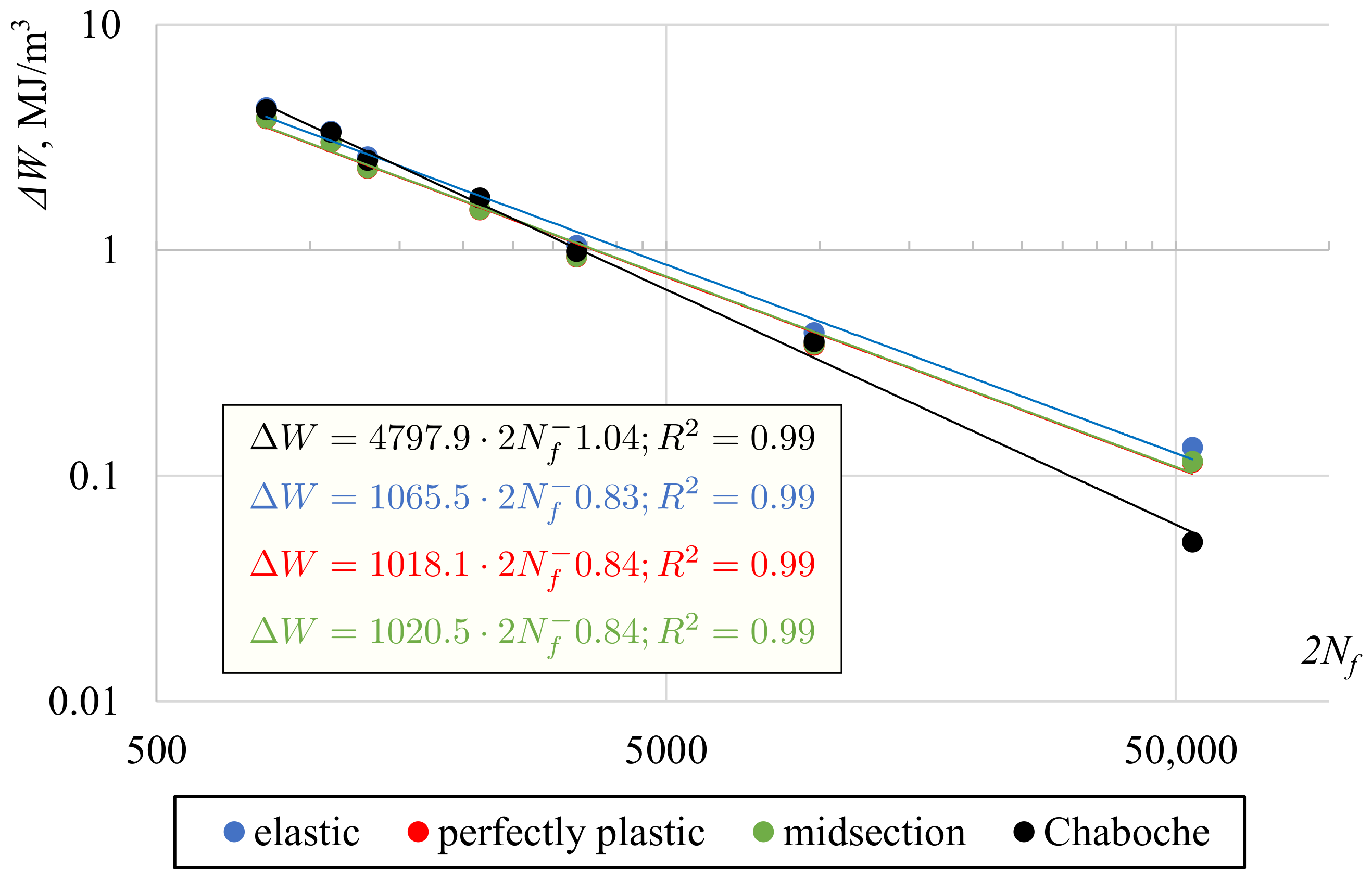
• The calculated values of shear stress can have a strong impact on the fatigue life prediction, depending on the selected fatigue damage parameter. Thus, it is recommended to clearly indicate how the shear stress values are determined in a study when presenting the results of an experiment.