The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis
Abstract
1. Introduction
2. Theoretical Background
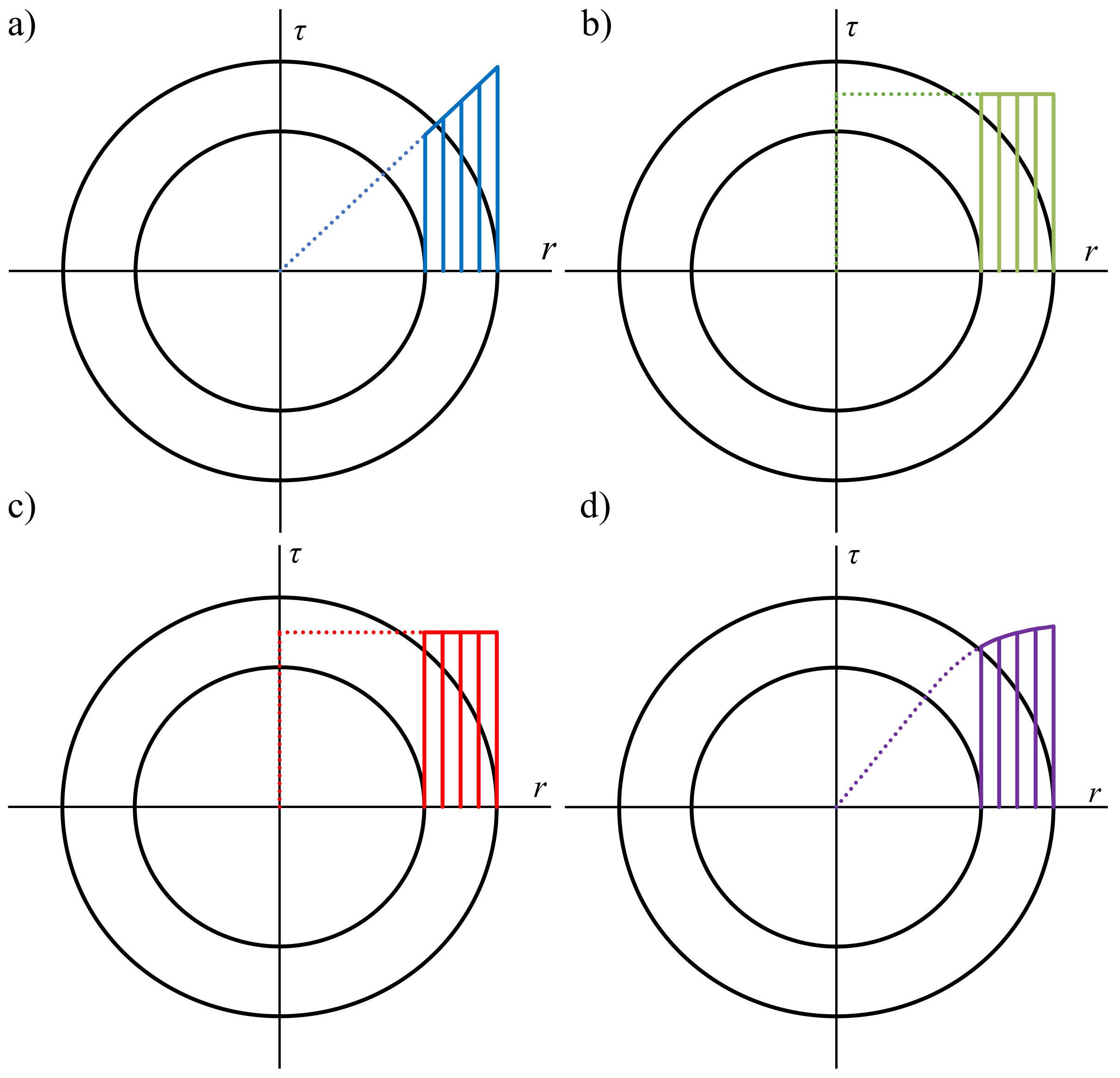
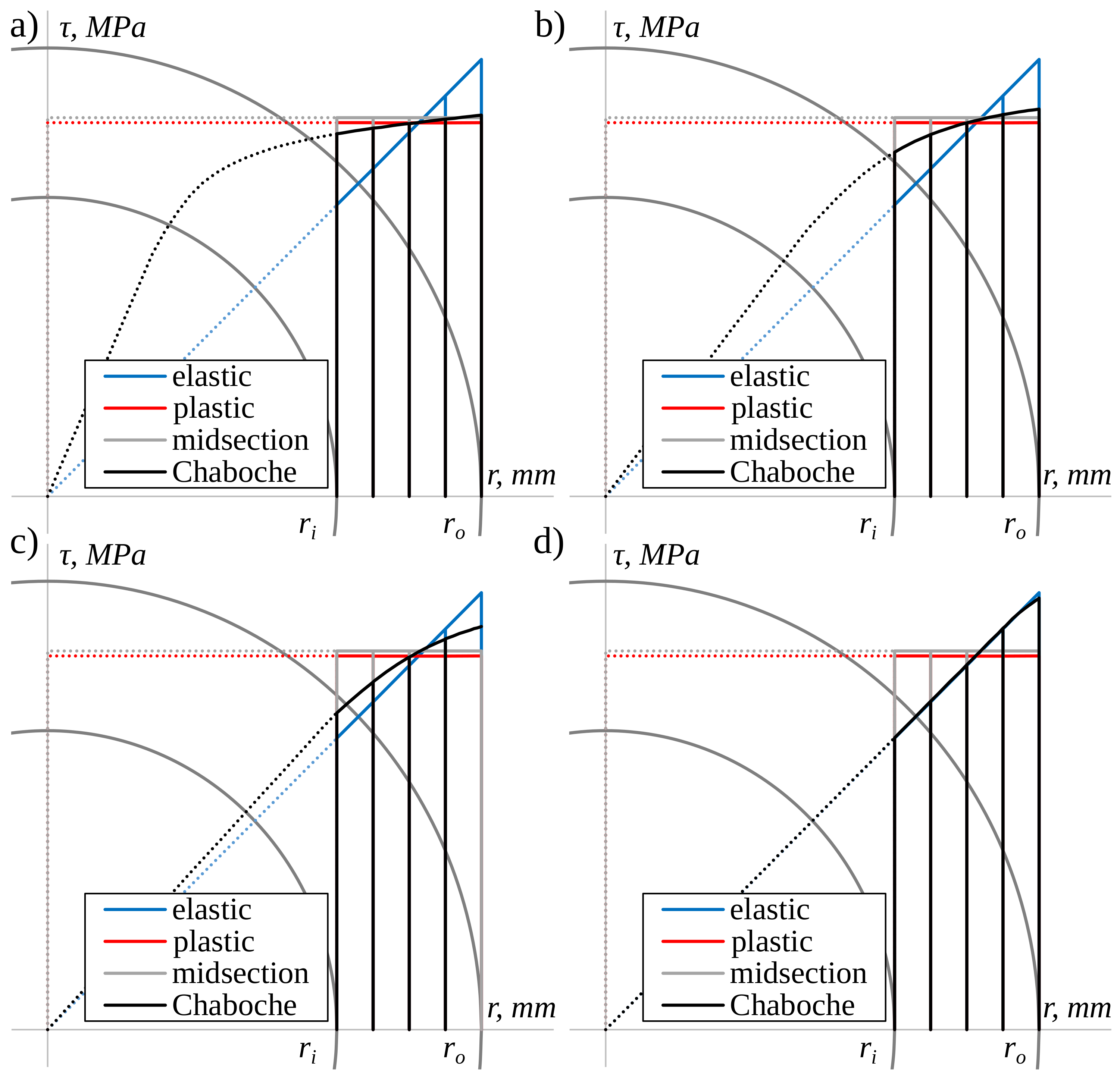
2.1. Shear Stress Distribution under Elastic–Plastic Torsion
2.2. Selected Methods of the Shear Stress Determination in Case of Tubular Specimens
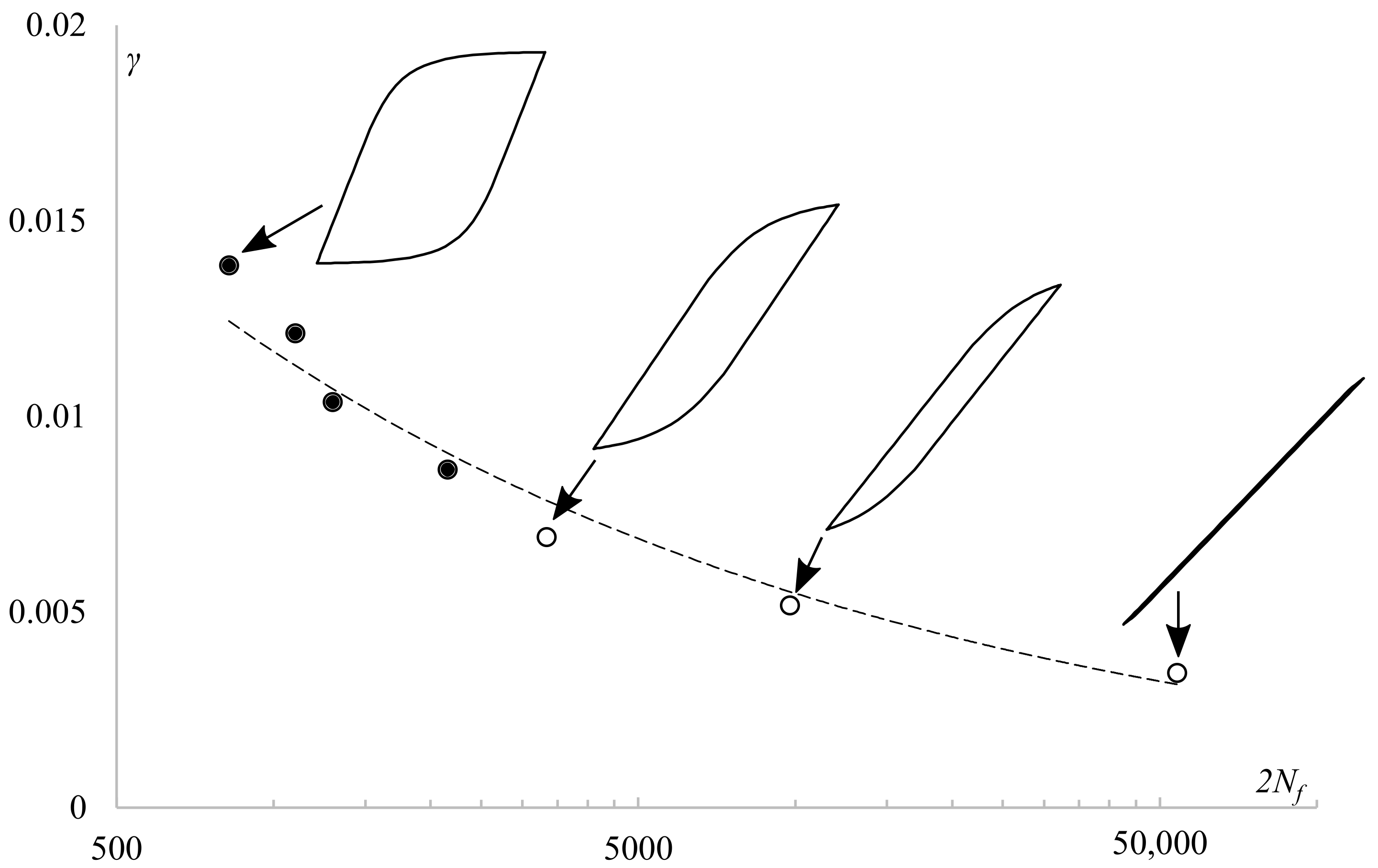
2.3. Influence of Shear Stress on Fatigue Life Prediction
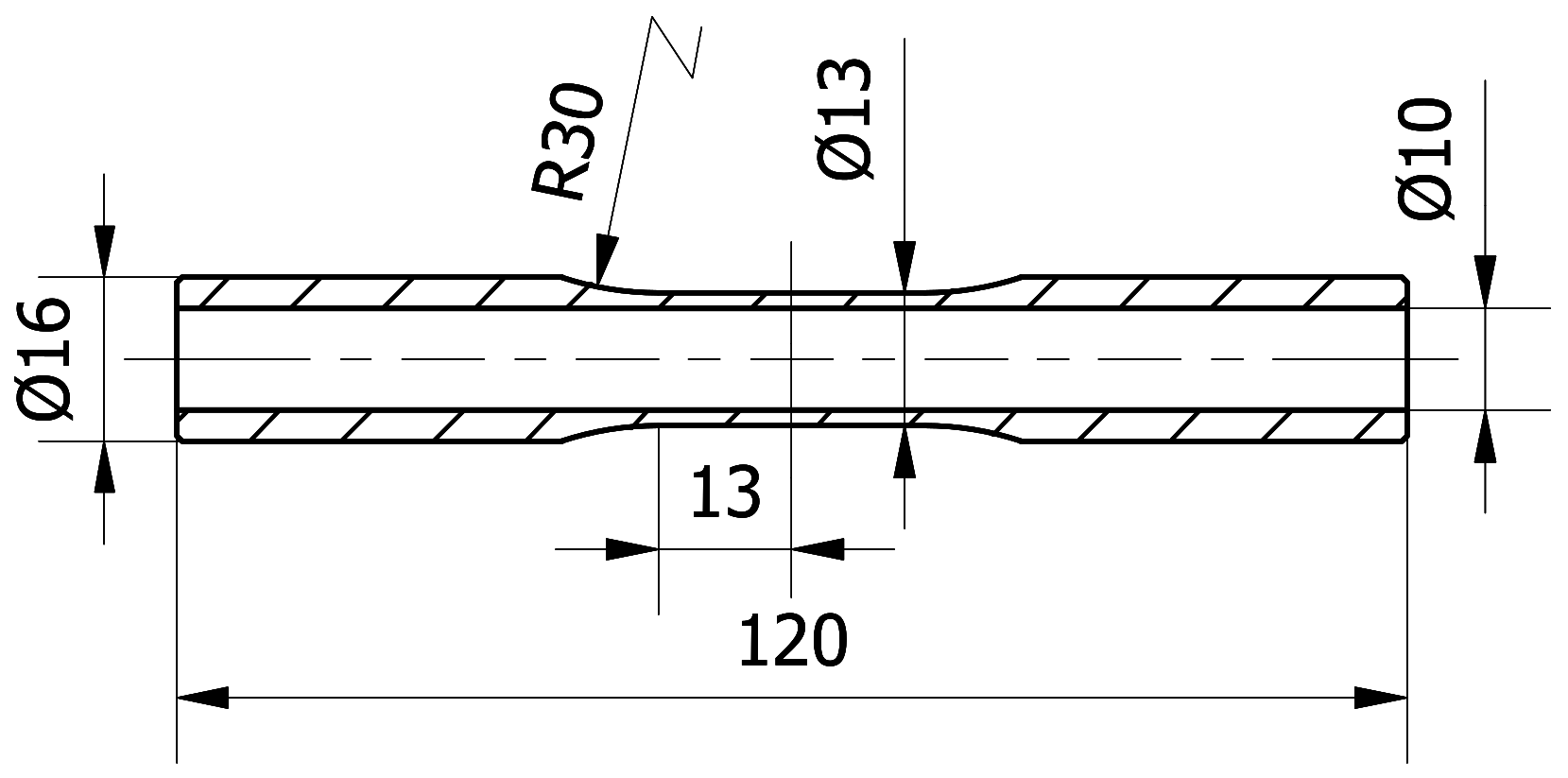
3. Materials and Methods
4. Results
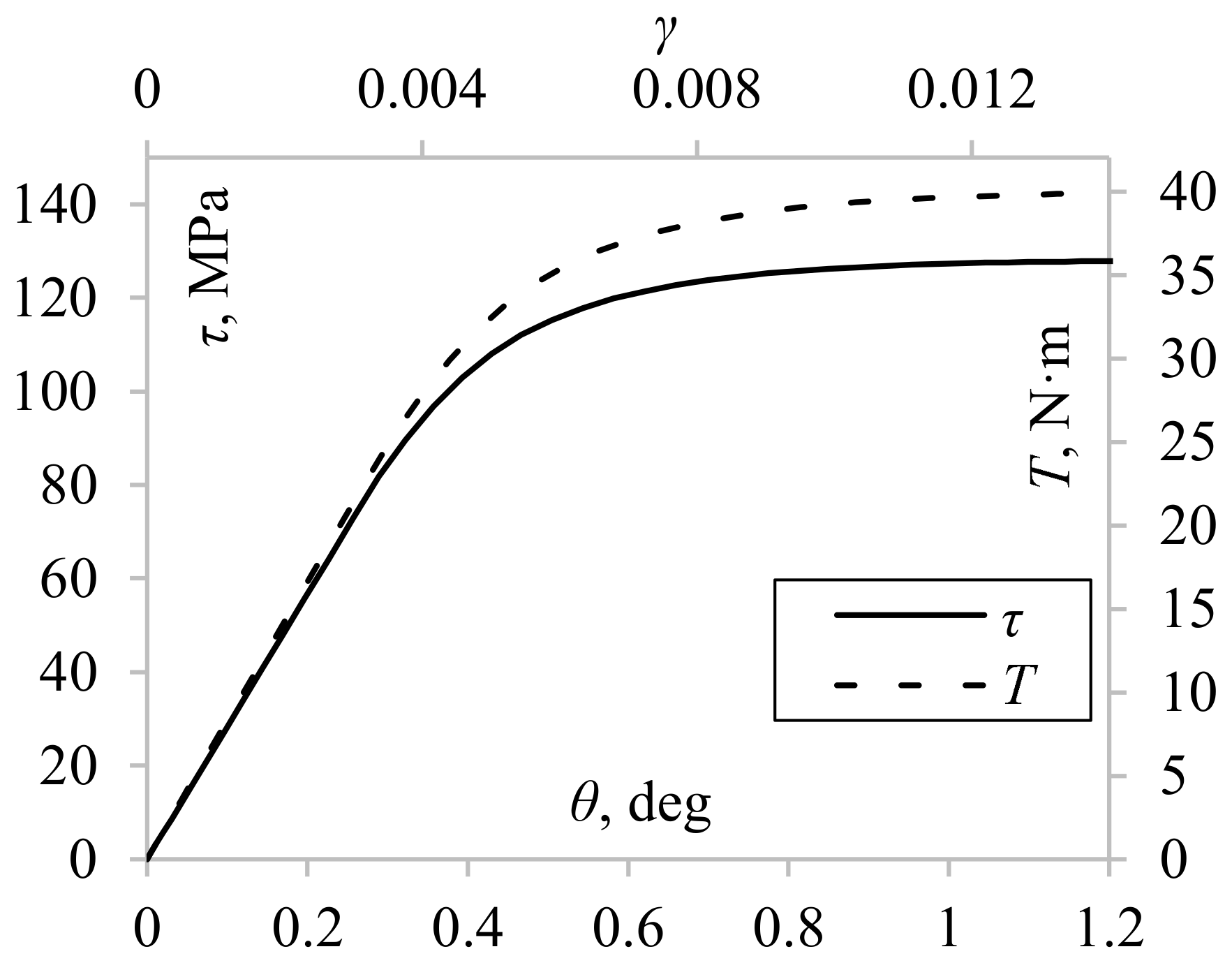
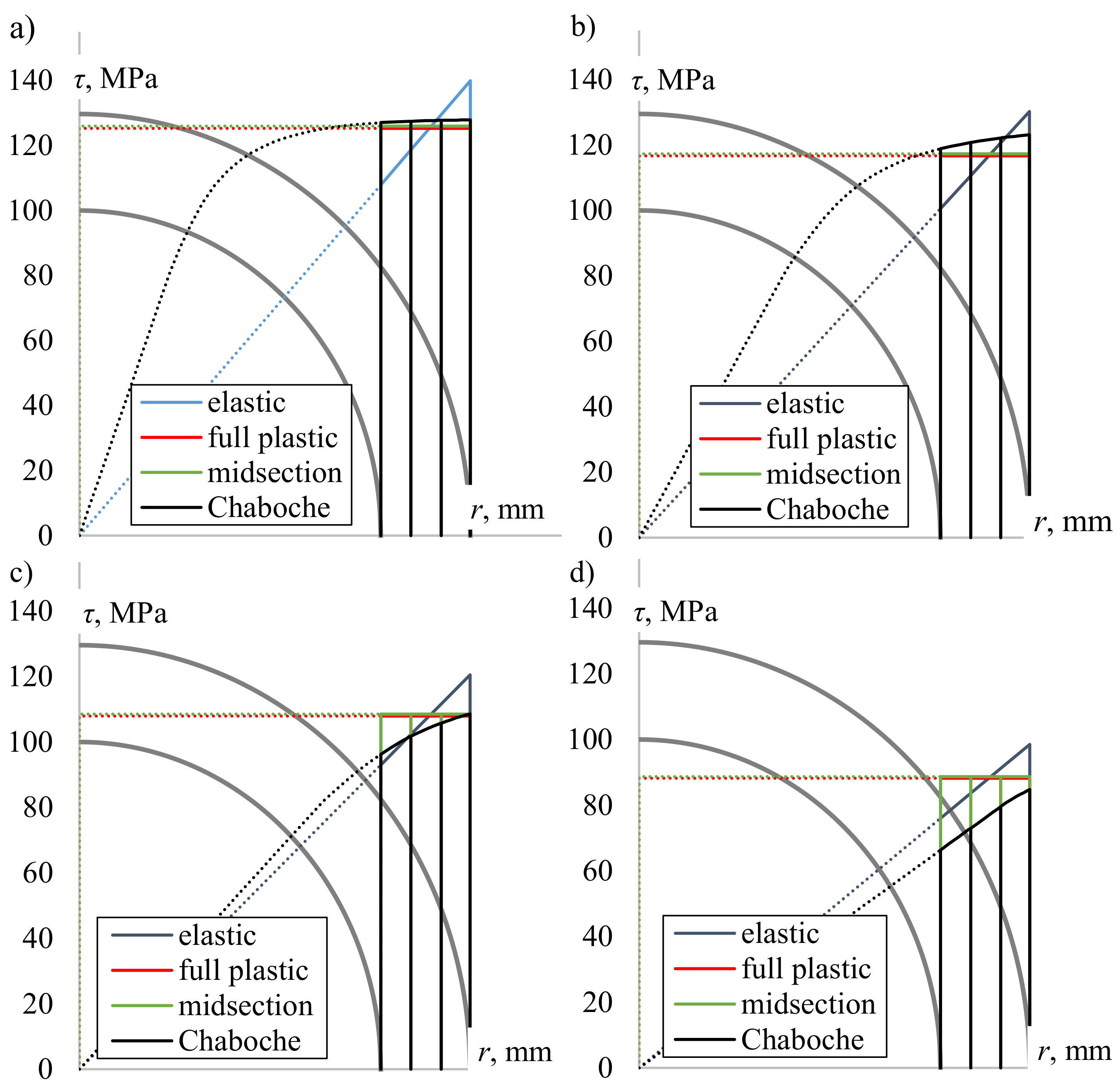
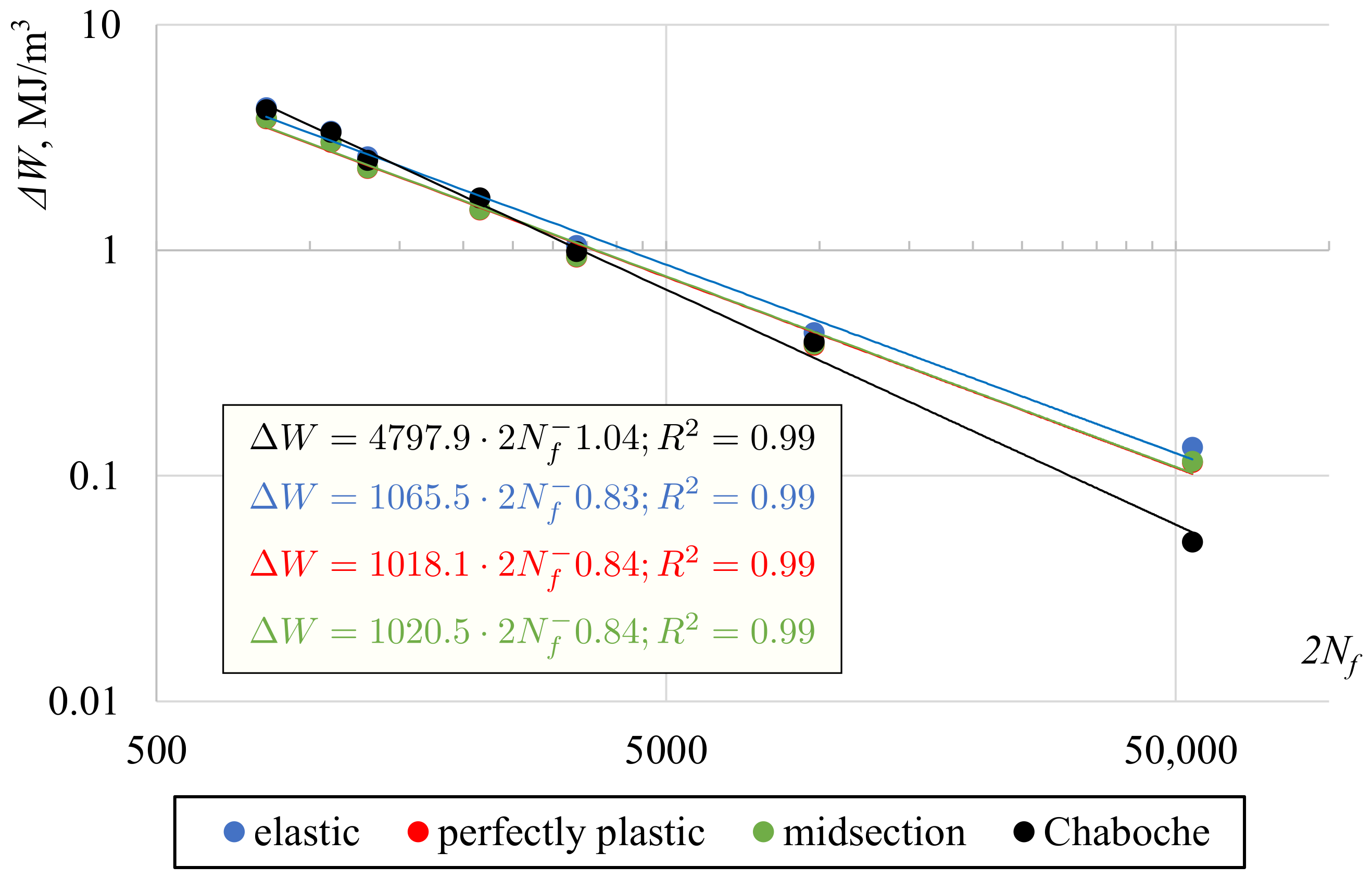
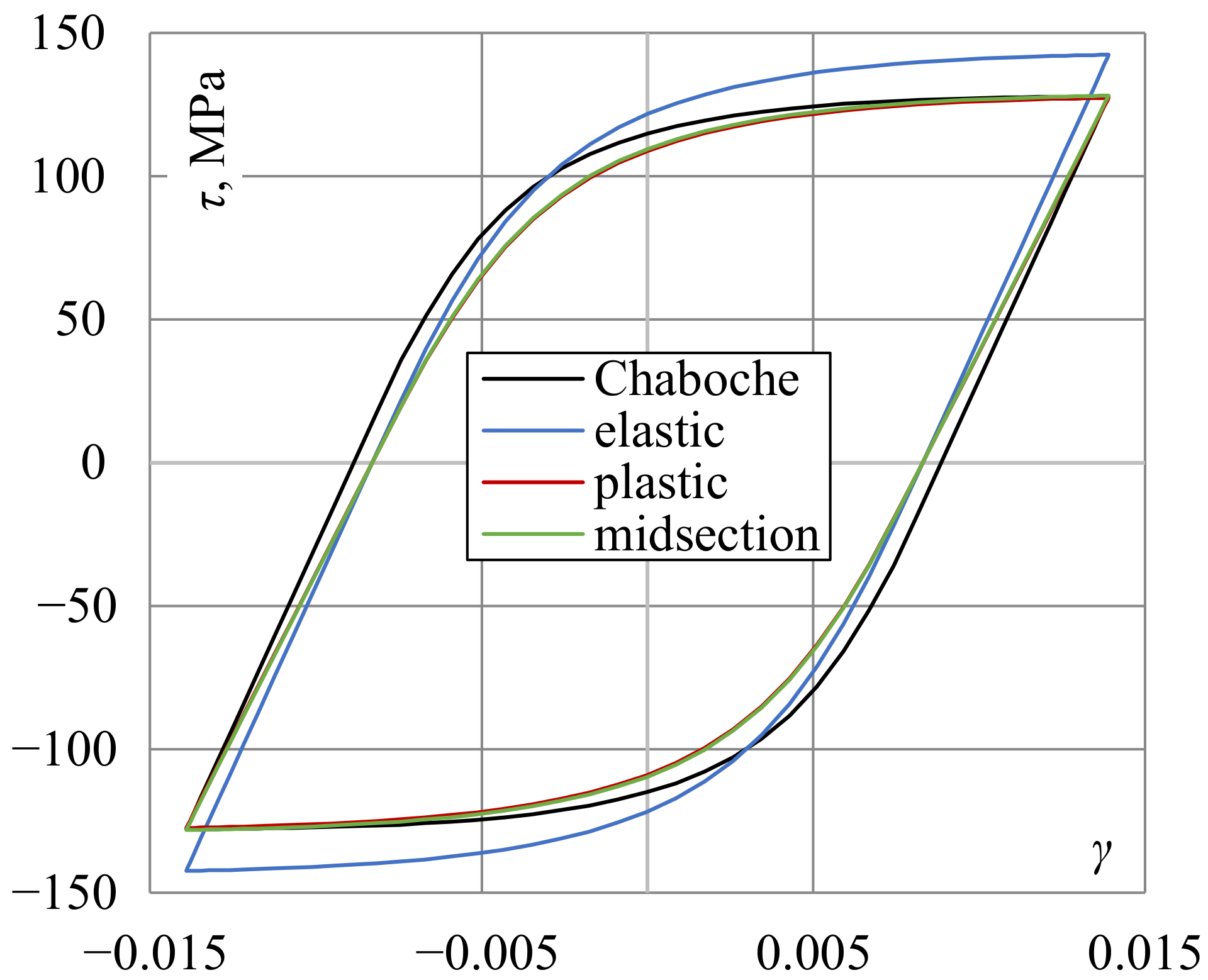
4.1. Shear Stress Distribution Comparison
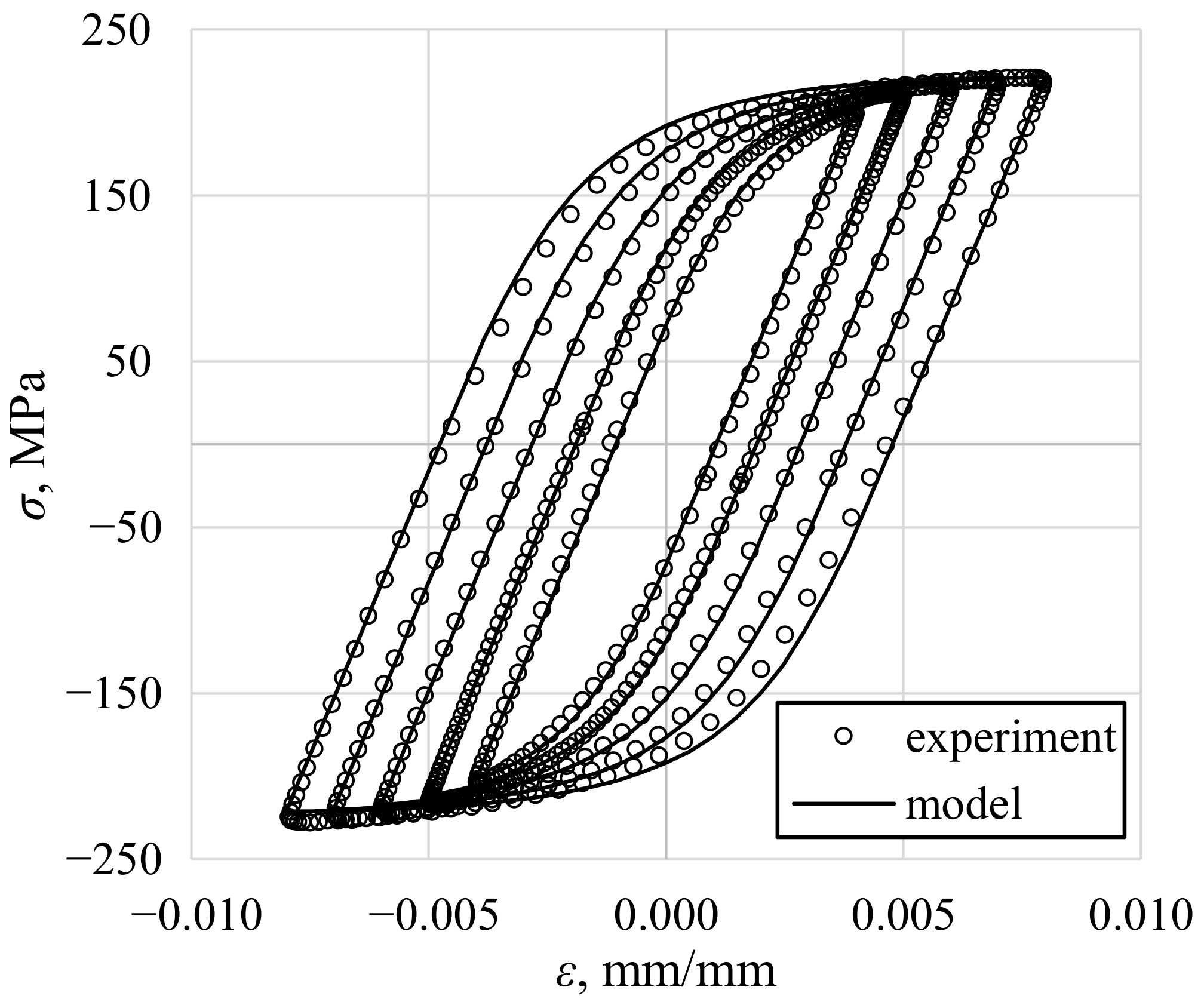
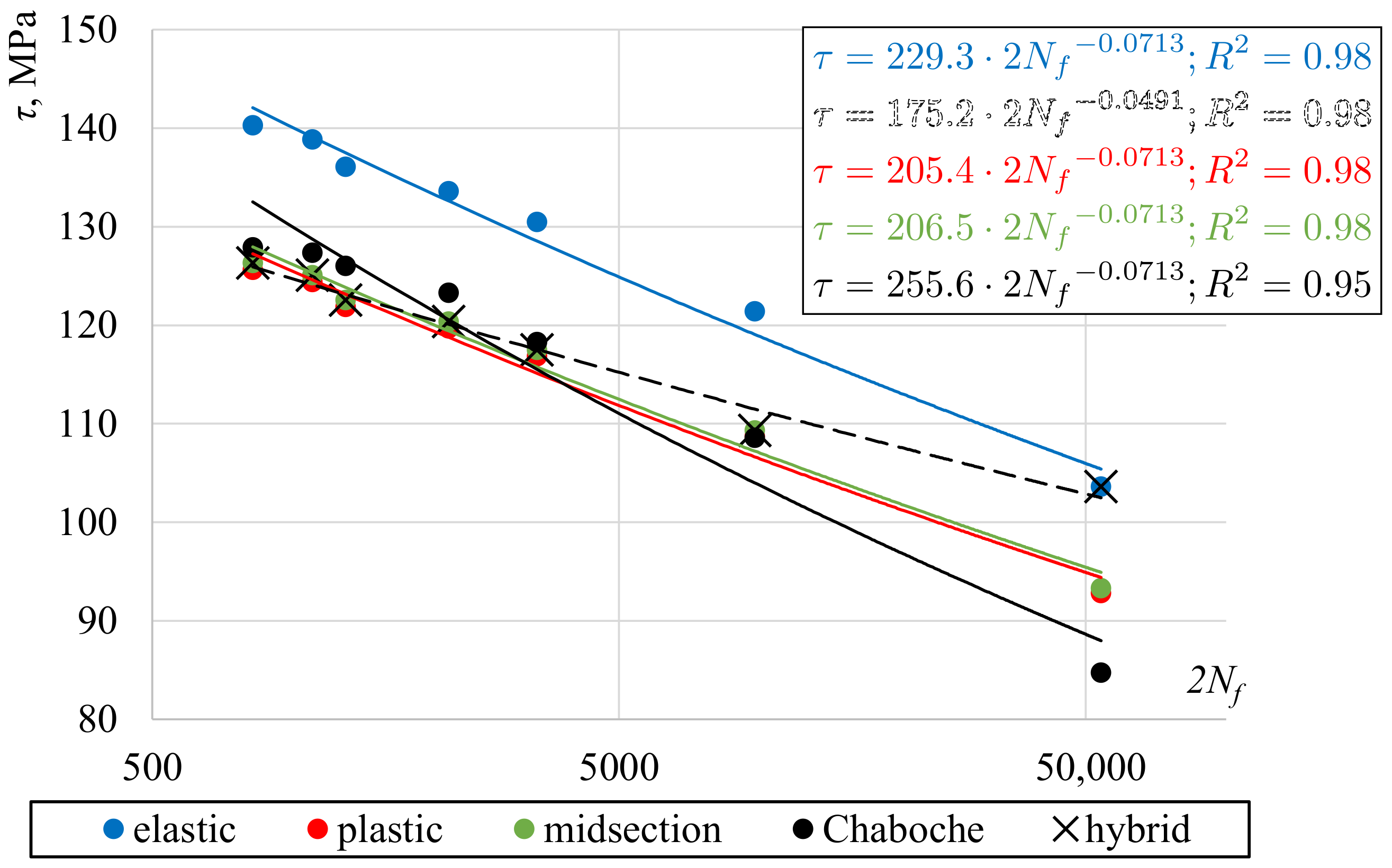
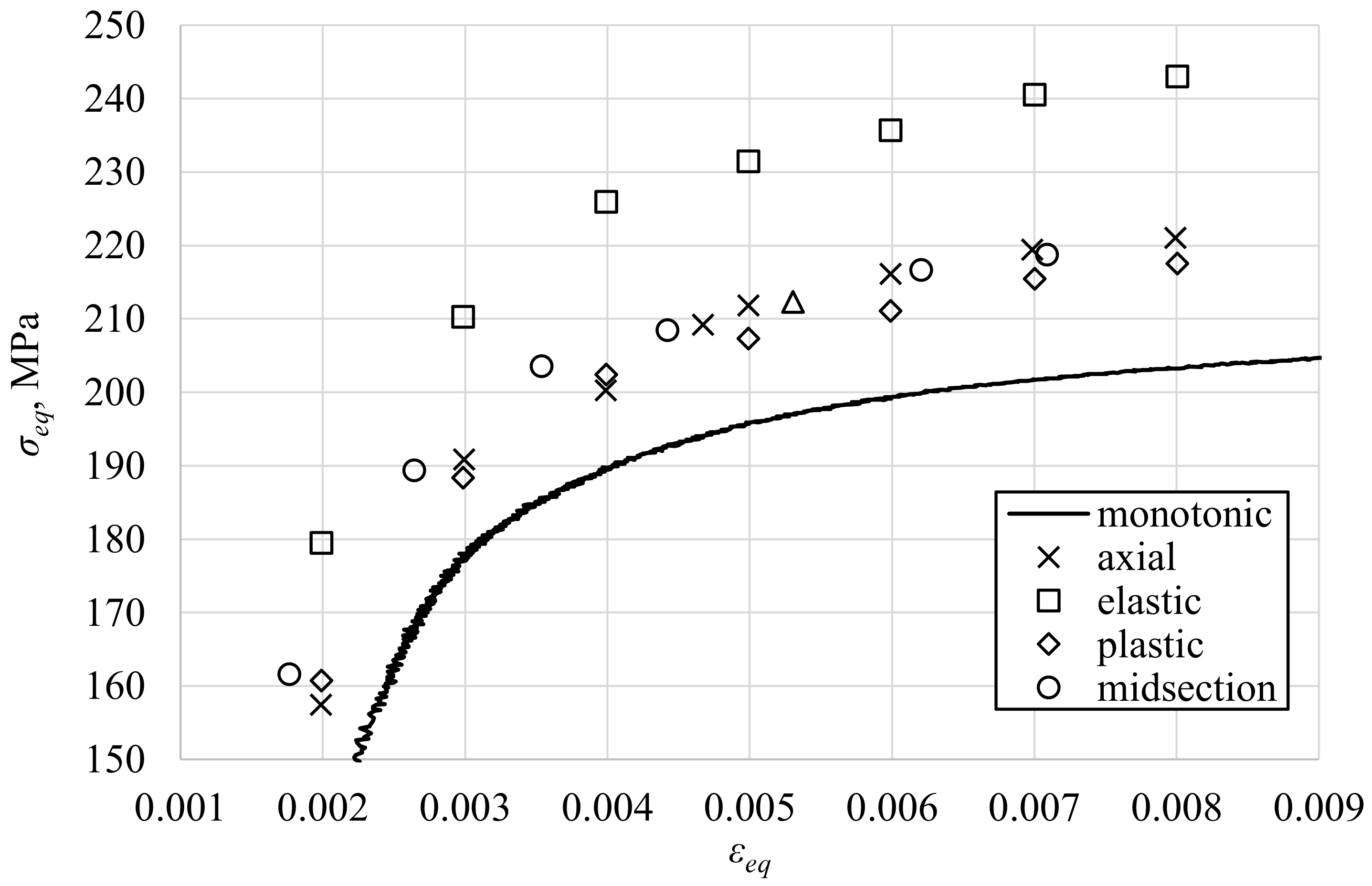
4.2. Application of the Selected Methods to Experimental Data Analysis
5. Summary
- None of the considered approximate solutions can determine the exact value of surface shear stress for tubular specimens under elastic–plastic cyclic torsional loading.
- Using the midsection approach and purely plastic solution for high strain levels, it was found that values of surface shear stress were very close to the values obtained using the Chaboche nonlinear kinematic model, calibrated using the experimental data for the axial loading.
- The largest differences between shear stress values calculated using the plasticity model and other methods were found for the low strain ranges, close to the cyclic yield limit.
- When the ratio of inner and outer diameters of tubular specimens is close to 1, the effect of the nonuniform shear stress distribution through wall thickness is less pronounced.
- It was confirmed that the recommendations of the ASTM standard can be successfully implemented to approximately determine the surface shear stress under torsion; however, if the applied loading levels cover the boundary between elastic and elastic–plastic deformation, it should be carefully considered which loading levels justify choosing a purely elastic or midsection approach.
- The methods discussed are not valid for the full range of loadings. The selection of the approach should be based on the applied loading level and observed material response.
- The calculated values of shear stress can have a strong impact on the fatigue life prediction, depending on the selected fatigue damage parameter. Thus, it is recommended to clearly indicate how the shear stress values are determined in a study when presenting the results of an experiment.
Author Contributions
Funding
Conflicts of Interest
References
- Tu, S.T.; Zhang, X.C. Fatigue Crack Initiation Mechanisms. Ref. Modul. Mater. Sci. Mater. Eng. 2016, 1–23. [Google Scholar] [CrossRef]
- Rozumek, D.; Marciniak, Z. The investigation of crack growth in specimens with rectangular cross-sections under out-of-phase bending and torsional loading. Int. J. Fatigue 2012, 39, 81–87. [Google Scholar] [CrossRef]
- Macek, W. Fractal analysis of the bending-torsion fatigue fracture of aluminium alloy. Eng. Fail. Anal. 2019, 99, 97–107. [Google Scholar] [CrossRef]
- Karolczuk, A.; Kluger, K.; Łagoda, T. A correction in the algorithm of fatigue life calculation based on the critical plane approach. Int. J. Fatigue 2016, 83, 174–183. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, P. A generalized cycle counting criterion for arbitrary multi-axial fatigue loading conditions. J. Strain Anal. Eng. Des. 2014, 49, 325–341. [Google Scholar] [CrossRef]
- Macek, W.; Łagoda, T.; Mucha, N. Energy-based fatigue failure characteristics of materials under random bending loading in elastic-plastic range. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 249–259. [Google Scholar] [CrossRef]
- Krzyżak, D.; Kurek, M.; Łagoda, T.; Sówka, D. Influence of changes of the bending plane position on the fatigue life. Mater. Werkst. 2014, 45, 1018–1029. [Google Scholar] [CrossRef]
- Arora, P.; Gupta, S.K.; Bhasin, V.; Singh, R.; Sivaprasad, S.; Tarafder, S. Testing and assessment of fatigue life prediction models for Indian PHWRs piping material under multi-axial load cycling. Int. J. Fatigue 2016, 85, 98–113. [Google Scholar] [CrossRef]
- Skibicki, D.; Pejkowski, Ł.; Stopel, M. Finite element analysis of ventilation system fire damper dynamic time-history. Pol. Marit. Res. 2017, 24, 116–123. [Google Scholar] [CrossRef][Green Version]
- Bildhauer, M.; Fuchs, M.; Repin, S. The elastic-plastic torsion problem: A posteriori error estimates for approximate solutions. Numer. Funct. Anal. Optim. 2009, 30, 653–664. [Google Scholar] [CrossRef][Green Version]
- Idone, G.; Maugeri, A.; Vitanza, C. Variational inequalities and the elastic-plastic torsion problem. J. Optim. Theory Appl. 2003, 117, 489–501. [Google Scholar] [CrossRef]
- Hout, J.W.; Benedict, R.L. The Elastic-Plastic Torsion Problem: A Direct Boundary Approach. J. Struct. Mech. 1984, 12, 447–463. [Google Scholar] [CrossRef]
- Annin, B.D. Existence and uniqueness of the solution of the elastic-plastic torsion problem for a cylindrical bar of oval cross-section. J. Appl. Math. Mech. 1965, 29, 1038–1047. [Google Scholar] [CrossRef]
- Caffarelli, L.A.; Friedman, A. Unloading in the elastic-plastic torsion problem. J. Differ. Equations 1981, 41, 186–217. [Google Scholar] [CrossRef][Green Version]
- Rubinstein, R. On the elastic-plastic torsion problem. J. Eng. Math. 1977, 11, 319–323. [Google Scholar] [CrossRef]
- Wu, P.D.; Van der Giessen, E. Analysis of elastic-plastic torsion of circular bars at large strains. Arch. Appl. Mech. 1991, 61, 89–103. [Google Scholar] [CrossRef]
- May, I.M.; Al-Shaarbaf, I.A. Elasto-plastic analysis of torsion using a three-dimensional finite element model. Comput. Struct. 1989, 33, 667–678. [Google Scholar] [CrossRef]
- Stout, R.B.; Hodge, P.G. Elastic/plastic torsion of hollow cylinders. Int. J. Mech. Sci. 1970, 12, 91–108. [Google Scholar] [CrossRef]
- Wagner, W.; Gruttmann, F. Finite element analysis of Saint-Venant torsion problem with exact integration of the elastic-plastic constitutive equations. Comput. Methods Appl. Mech. Eng. 2001, 190, 3831–3848. [Google Scholar] [CrossRef]
- Shoemaker, E.M. Second order effects in the elastic-plastic torsion problem. Meccanica 1973, 8, 125–128. [Google Scholar] [CrossRef]
- Miller, K.; Chandler, D.C. High Strain Torsion Fatigue of Solid and Tubular Specimens. Proc. Inst. Mech. Eng. 1969, 184, 433–448. [Google Scholar] [CrossRef]
- Brown, M.W. Torsional stresses in tubular specimens. J. Strain Anal. Eng. Des. 1978, 13, 23–28. [Google Scholar] [CrossRef]
- Shamsaei, N.; Fatemi, A. Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 631–646. [Google Scholar] [CrossRef]
- Socie, D.F. Multiaxial Fatigue Damage Models. J. Eng. Mater. Technol. Trans. ASME 1987, 109, 293–298. [Google Scholar] [CrossRef]
- Zhong, B.; Wang, Y.; Wei, D.; Zhang, K.; Wang, J. Multiaxial fatigue life prediction for powder metallurgy superalloy FGH96 based on stress gradient effect. Int. J. Fatigue 2018, 109, 26–36. [Google Scholar] [CrossRef]
- Wu, Z.R.; Li, X.; Fang, L.; Song, Y.D. Evaluation of multiaxial fatigue life prediction criteria for Ni-based superalloy GH4169. Proc. Inst. Mech. Eng. Part J Mech. Eng. Sci. 2018, 232, 1823–1837. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y. Constitutive modeling of cyclic plasticity deformation of a pure polycrystalline copper. Int. J. Plast. 2008, 24, 1890–1915. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y. An experimental investigation on cyclic plastic deformation and substructures of polycrystalline copper. Int. J. Plast. 2005, 21, 2191–2211. [Google Scholar] [CrossRef]
- Sharifimehr, S.; Fatemi, A. Fatigue analysis of ductile and brittle behaving steels under variable amplitude multiaxial loading. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1722–1742. [Google Scholar] [CrossRef]
- McClaflin, D.; Fatemi, A. Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effects. Int. J. Fatigue 2004, 26, 773–784. [Google Scholar] [CrossRef]
- Dey, R.; Tarafder, S.; Sivaprasad, S. Influence of proportional and non-proportional loading on deformation behaviour of austenitic stainless steel-macro and micro analysis. Theor. Appl. Fract. Mech. 2019, 100, 342–353. [Google Scholar] [CrossRef]
- Gryguć, A.; Behravesh, S.; Shaha, S.; Jahed, H.; Wells, M.; Williams, B.; Su, X. Multiaxial cyclic behaviour of extruded and forged AZ80 Mg alloy. Int. J. Fatigue 2019, 127, 324–337. [Google Scholar] [CrossRef]
- Han, Q.; Wang, P.; Lu, Y. Low-cycle multiaxial fatigue behavior and life prediction of Q235B steel welded material. Int. J. Fatigue 2019, 127, 417–430. [Google Scholar] [CrossRef]
- Albinmousa, J.; Adinoyi, M.J.; Merah, N. Multiaxial fatigue of extruded ZK60 magnesium alloy. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2276–2289. [Google Scholar] [CrossRef]
- Ogawa, F.; Itoh, T.; Yamamoto, T. Evaluation of multiaxial low cycle fatigue cracks in Sn-8Zn-3Bi solder under non-proportional loading. Int. J. Fatigue 2018, 110, 215–224. [Google Scholar] [CrossRef]
- Ting, T.W. The repeated loading-unloading processes of elastic-plastic torsion of solid bars. Ann. Mat. Pura Appl. 1979, 119, 333–378. [Google Scholar] [CrossRef]
- Bruhns, O.T. Advanced Mechanics of Solids; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Chaboche, J.L. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Chaboche, J. Constitutive equations for cyclic plasticty and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Fatemi, A.; Socie, D.F. A Critical Plane Approach To Multiaxial Fatigue Damage Including Out-of-Phase Loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Smith, K.; Watson, P.; Topper, T. Stress-Strain Function for the Fatigue of Metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Walat, K.; Kurek, M.; Ogonowski, P.; Łagoda, T. The multiaxial random fatigue criteria based on strain and energy damage parameters on the critical plane for the low-cycle range. Int. J. Fatigue 2012, 37, 100–111. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2014, 62, 34–41. [Google Scholar] [CrossRef]
- Garud, Y.S. A New Approach to the Evaluation of Fatigue Under Multiaxial Loadings. J. Eng. Mater. Technol. 1981, 103, 118. [Google Scholar] [CrossRef]
- Ellyin, F.; Golos, K.; Xia, Z. In-Phase and Out-of-Phase Multiaxial Fatigue. J. Eng. Mater. Technol. 1991, 113, 112. [Google Scholar] [CrossRef]
- Ellyin, F. Fatigue Damage, Crack Growth and Life Prediction; Chapman & Hall: London, UK, 1997. [Google Scholar] [CrossRef]
- Skibicki, D.; Pejkowski, Ł. The relationship between additional non-proportional hardening coefficient and fatigue life. Int. J. Fatigue 2019, 123, 66–78. [Google Scholar] [CrossRef]
- Pejkowski, Ł.; Skibicki, D. Stress-strain response and fatigue life of four metallic materials under asynchronous loadings: Experimental observations. Int. J. Fatigue 2019, 128, 105202. [Google Scholar] [CrossRef]
- Karolczuk, A.; Skibicki, D.; Pejkowski, Ł. Evaluation of the Fatemi-Socie damage parameter for the fatigue life calculation with application of the Chaboche plasticity model. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 197–208. [Google Scholar] [CrossRef]
- Li, H.; Lv, F.; Xiao, Z.; Liang, X.; Sang, F.; Li, P. Low-cycle fatigue behavior of a cast Mg–Y–Nd–Zr alloy by T6 heat treatment. Mater. Sci. Eng. A 2016, 676, 377–384. [Google Scholar] [CrossRef]
- Wu, D.L.; Xuan, F.Z.; Guo, S.J.; Zhao, P. Uniaxial mean stress relaxation of 9–12% Cr steel at high temperature: Experiments and viscoplastic constitutive modeling. Int. J. Plast. 2016, 77, 156–173. [Google Scholar] [CrossRef]
- Li, Y.; Yu, D.; Li, B.; Chen, X. Martensitic transformation of an austenitic stainless steel under non-proportional cyclic loading. Int. J. Fatigue 2019, 124, 338–347. [Google Scholar] [CrossRef]
- Molaei, R.; Fatemi, A.; Phan, N. Significance of hot isostatic pressing (HIP) on multiaxial deformation and fatigue behaviors of additive manufactured Ti-6Al-4V including build orientation and surface roughness effects. Int. J. Fatigue 2018, 117, 352–370. [Google Scholar] [CrossRef]
- Fu, Y.S.S.; Chen, S.S.X. Torsional fatigue with axial constant stress of oligo-crystalline 316L stainless steel thin wire. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1929–1937. [Google Scholar] [CrossRef]
- Lin, H.; Nayeb-Hashemi, H.; Pelloux, R.M. Constitutive relations and fatigue life prediction for anisotropic Al-6061-T6 rods under biaxial proportional loadings. Int. J. Fatigue 1992, 14, 249–259. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Q.; Jiang, Y.; Li, Q. An experimental study of cyclic deformation of extruded AZ61A magnesium alloy. Int. J. Plast. 2011, 27, 768–787. [Google Scholar] [CrossRef]
- Standard Practice for Strain-Controlled Axial-Torsional Fatigue Testing with Thin-Walled Tubular Specimens; ASTM E2207-02; STM International: West Conshohocken, PA, USA, 2002.



| Element | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Other | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| Share (%) | 0.3–0.6 | 0.1–0.3 | 0.1 | 0.1 | 0.35–0.6 | 0.05 | 0.15 | 0.1 | 0.15 | Balance |
| E, GPa | , MPa | , MPa | , mm/mm | , - | , MPa | , - |
|---|---|---|---|---|---|---|
| 68.3 | 191.5 | 229.1 | 0.094 | 0.35 | 288.1 | 0.051 |
| , MPa | , MPa | , MPa | , - | , - | , - | R, MPa |
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyda, J.; Pejkowski, Ł.; Skibicki, D. The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis. Materials 2020, 13, 5583. https://doi.org/10.3390/ma13235583
Seyda J, Pejkowski Ł, Skibicki D. The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis. Materials. 2020; 13(23):5583. https://doi.org/10.3390/ma13235583
Chicago/Turabian StyleSeyda, Jan, Łukasz Pejkowski, and Dariusz Skibicki. 2020. "The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis" Materials 13, no. 23: 5583. https://doi.org/10.3390/ma13235583
APA StyleSeyda, J., Pejkowski, Ł., & Skibicki, D. (2020). The Shear Stress Determination in Tubular Specimens under Torsion in the Elastic–Plastic Strain Range from the Perspective of Fatigue Analysis. Materials, 13(23), 5583. https://doi.org/10.3390/ma13235583






