Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks
Abstract
1. Introduction
2. Background
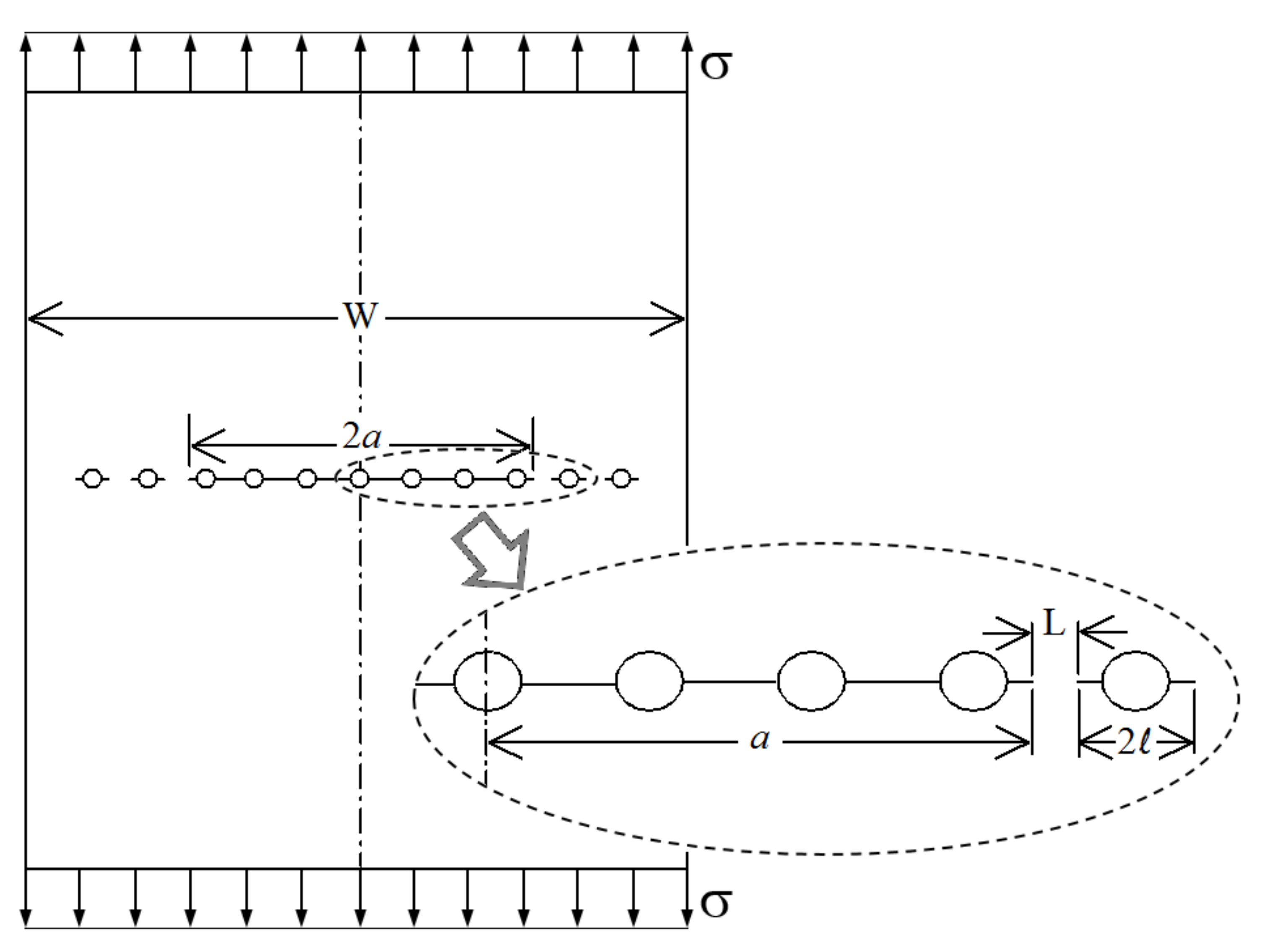
2.1. Residual Strength of Panels with MSD
- σy: The yield strength of the material.
- L: Length of the ligament between the lead crack and MSD crack.
- a: Lead crack half-length.
- : MSD crack half-length.
- : The overall SIF correction factor for the lead crack tip.
- : The overal SIF correction factor for the adjacent MSD crack tip.
2.2. Applications of ANN in Fracture Mechanics
3. Experimental Data
3.1. Unstiffened Panels
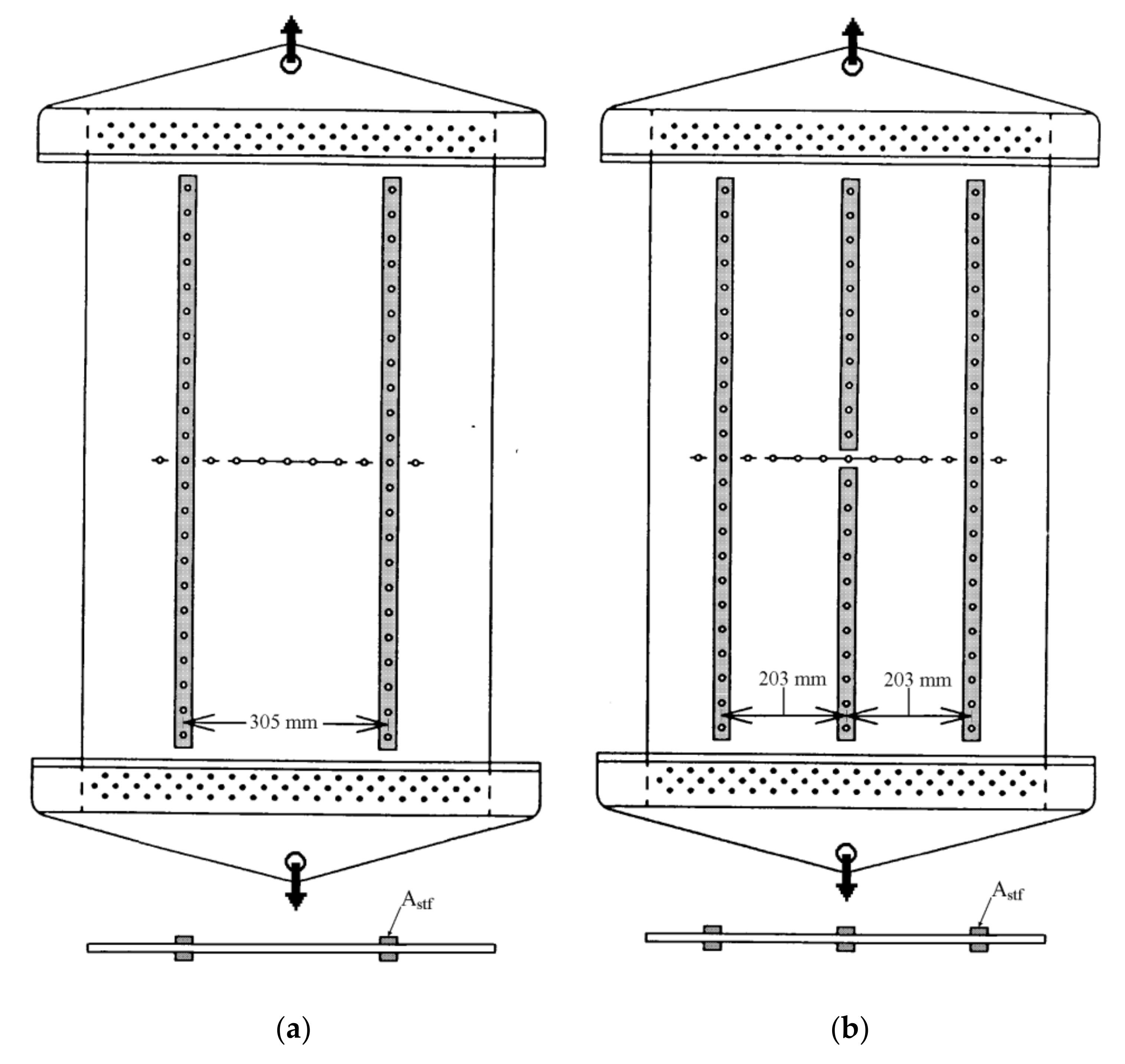
3.2. Stiffened Panels
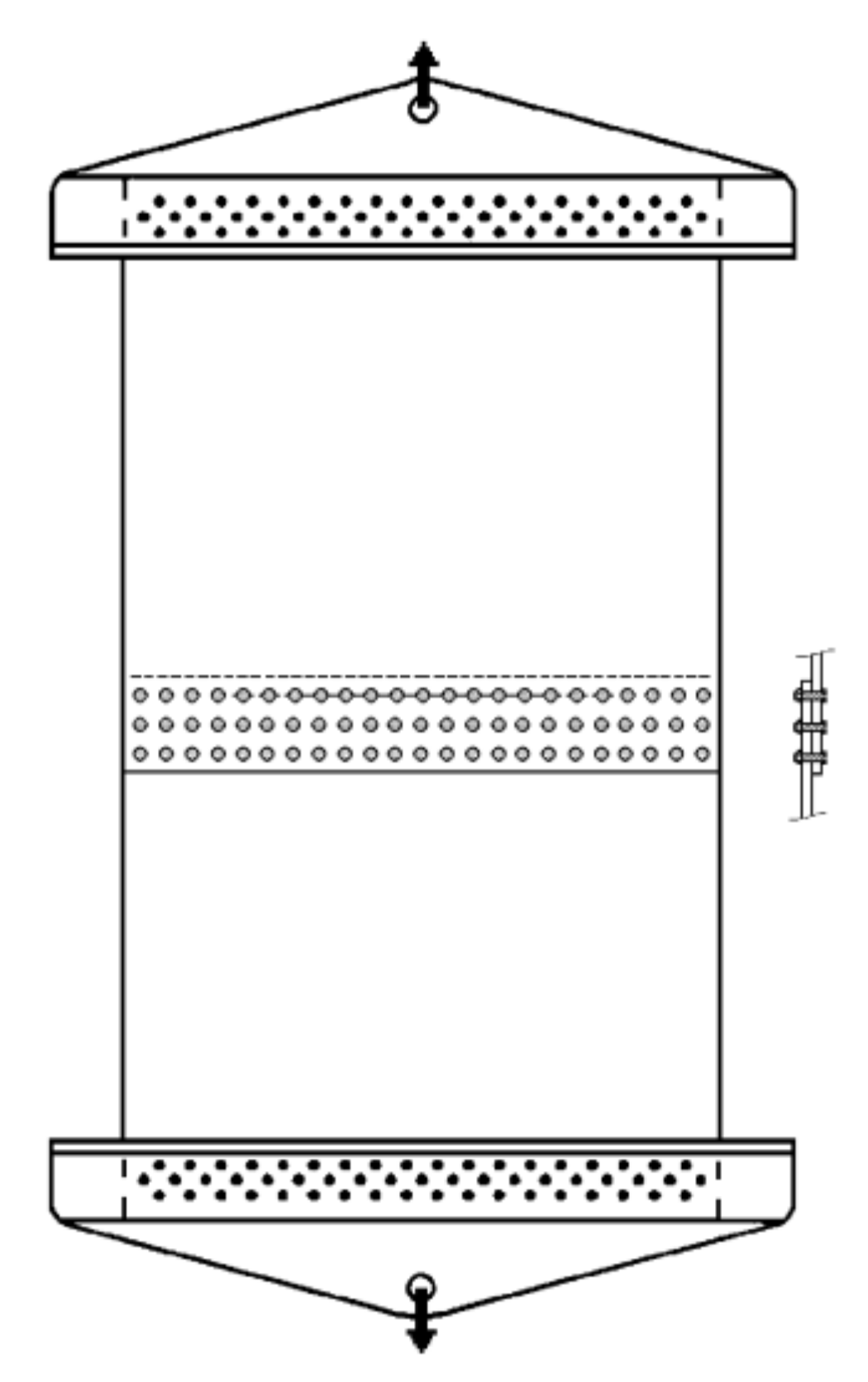
3.3. Lap-Joint Panels
4. ANN Modeling Procedure
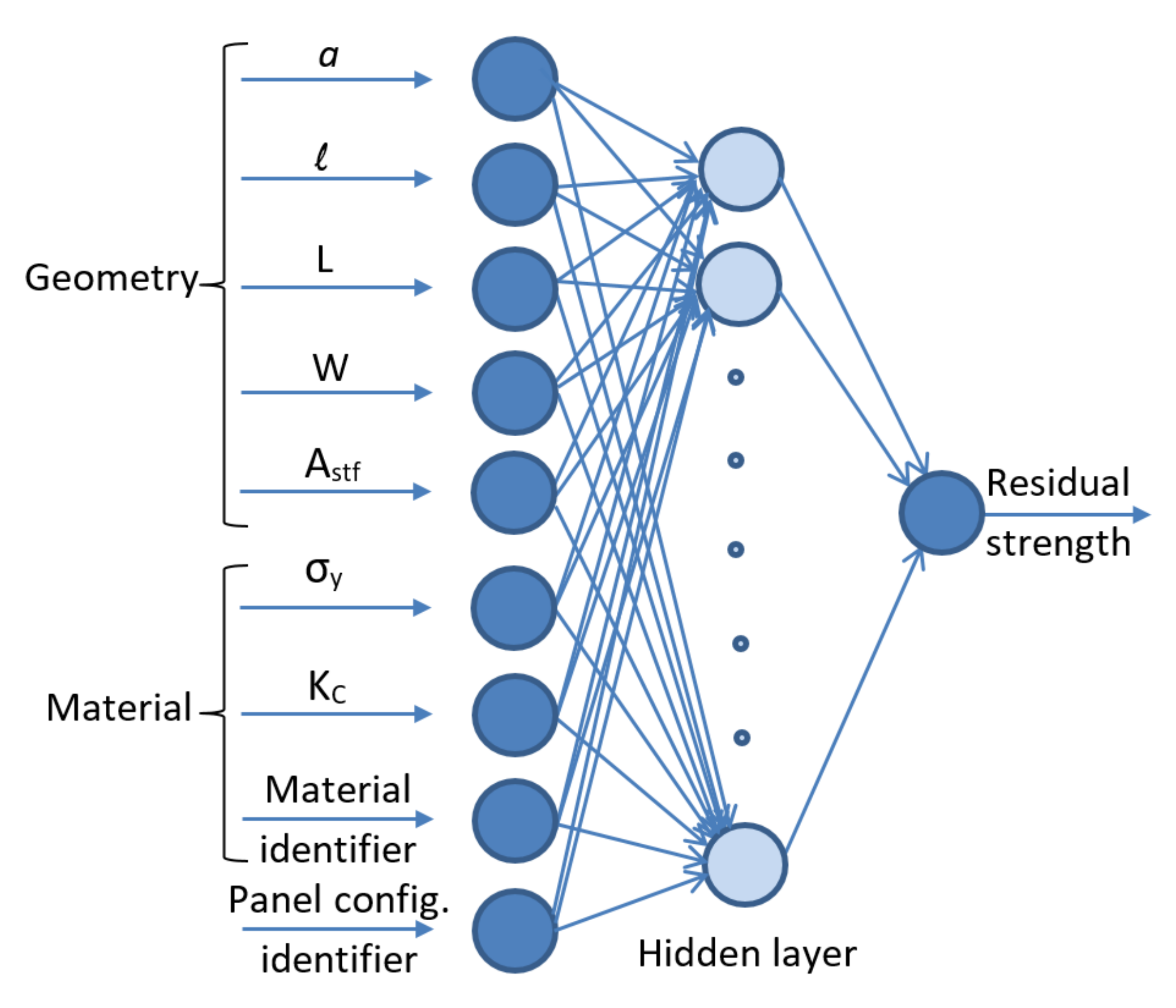
4.1. Ann Inputs and Structure
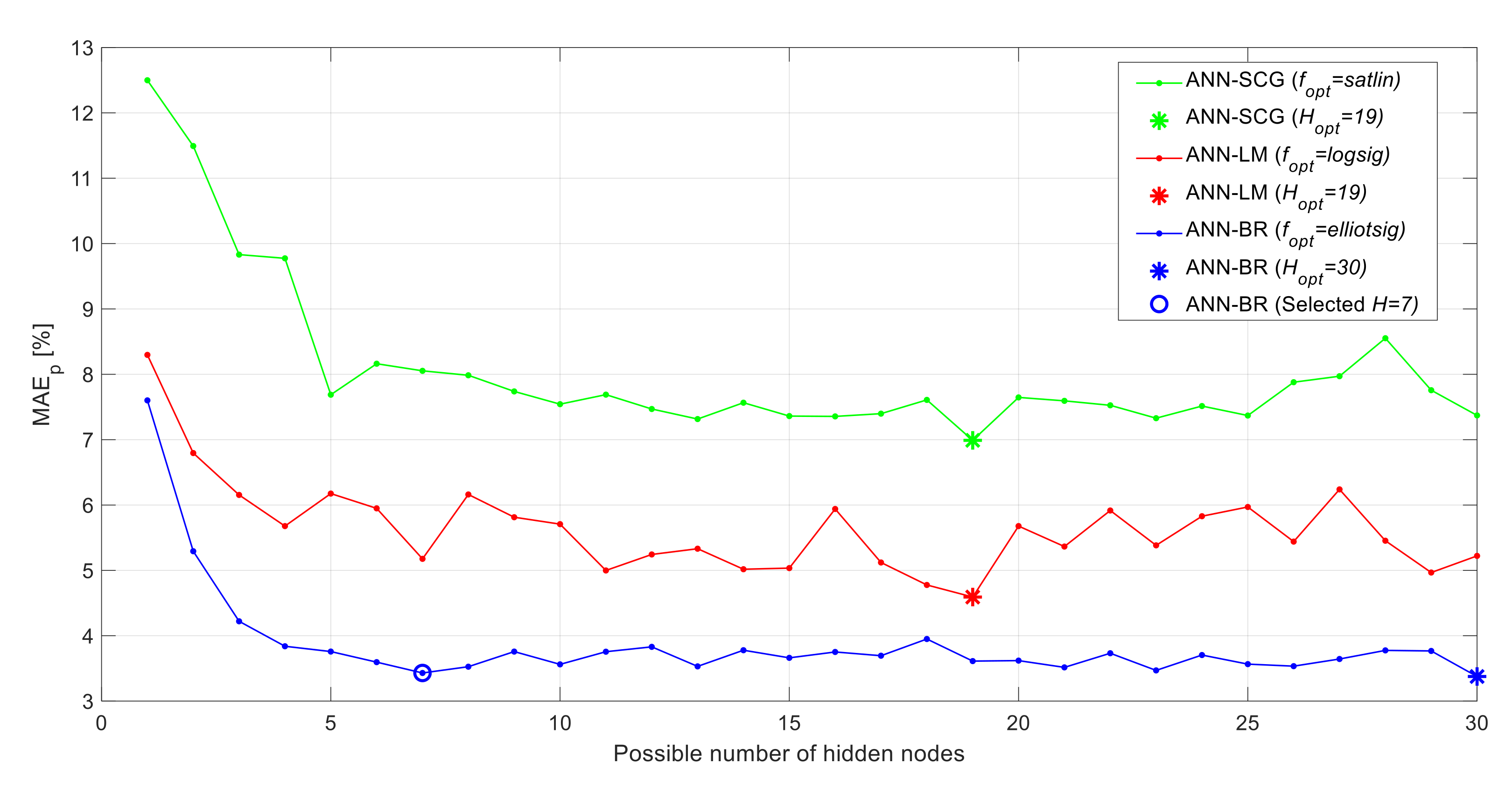
4.2. ANN Optimization
- (1)
- The adopted back-propagation learning algorithm () used to optimally define the ANN’s internal parameters (i.e., weights and biases). Basically, the weights and biases of the ANN are initially set randomly and then updated iteratively by calculating the error on the training outputs and distributing it back to the ANN layers.
- (2)
- The hidden nodes activation function () used to process the ANN’s inputs.
- (3)
- The number of nodes () in the hidden layer.
- Three different possible learning algorithms; = Bayesian Regularization (BR), Levenberg– Marquardt (LM), and Scaled Conjugate Gradient (SCG).
- Twelve different possible activation functions; = ‘logsig’, ‘tansig’, ‘purelin’, ‘tribas’, ‘radbas’, ‘elliotsig’, ‘hardlims’, ‘hardlim’, ‘poslin’, ‘radbasn’, ‘satlin’, ‘satlins’.
- Up to 30 possible number of hidden nodes; = [1–30].
5. Results and Discussion
5.1. Training Datasets Selection
5.2. Optimum ANN Configuration
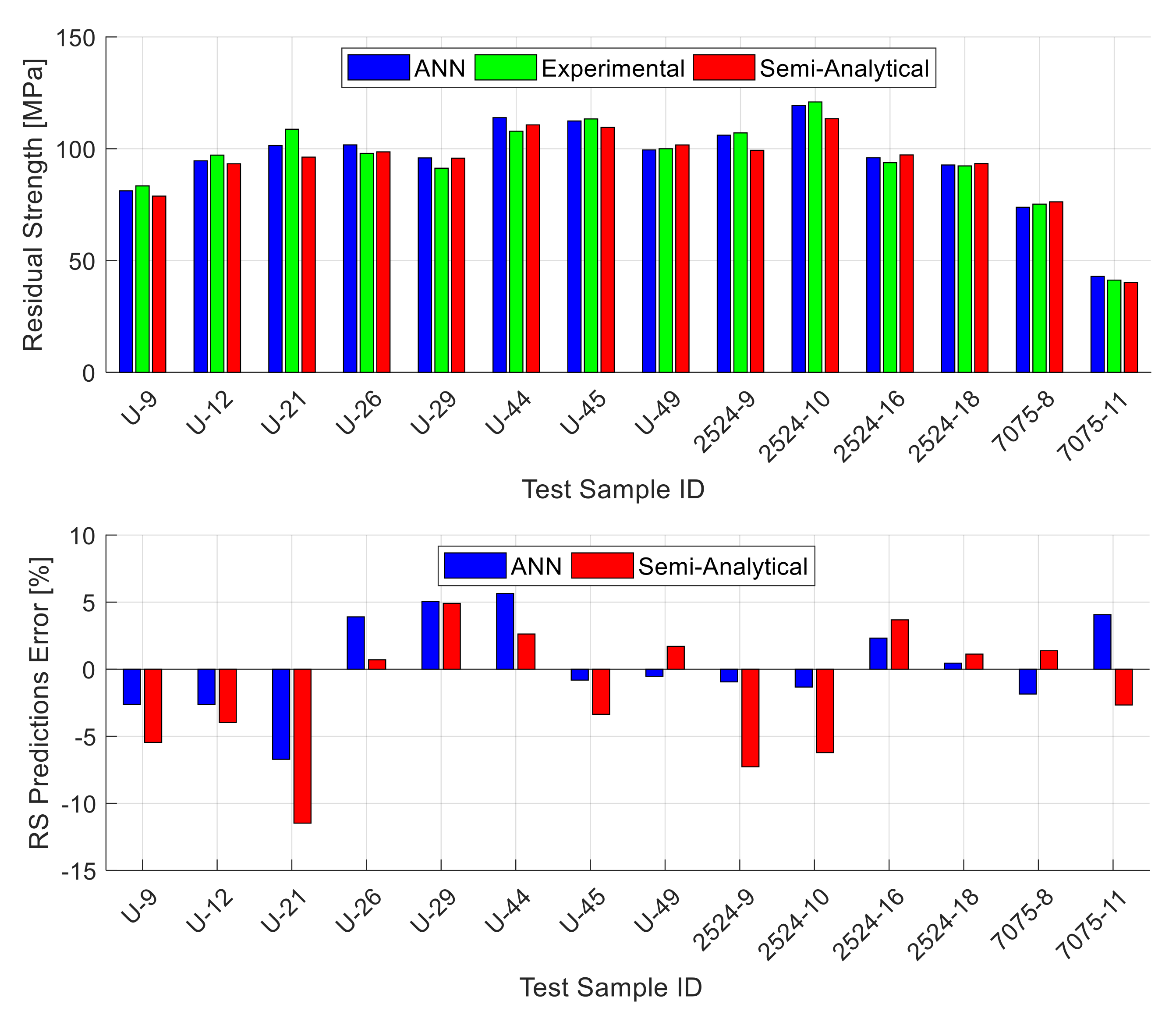
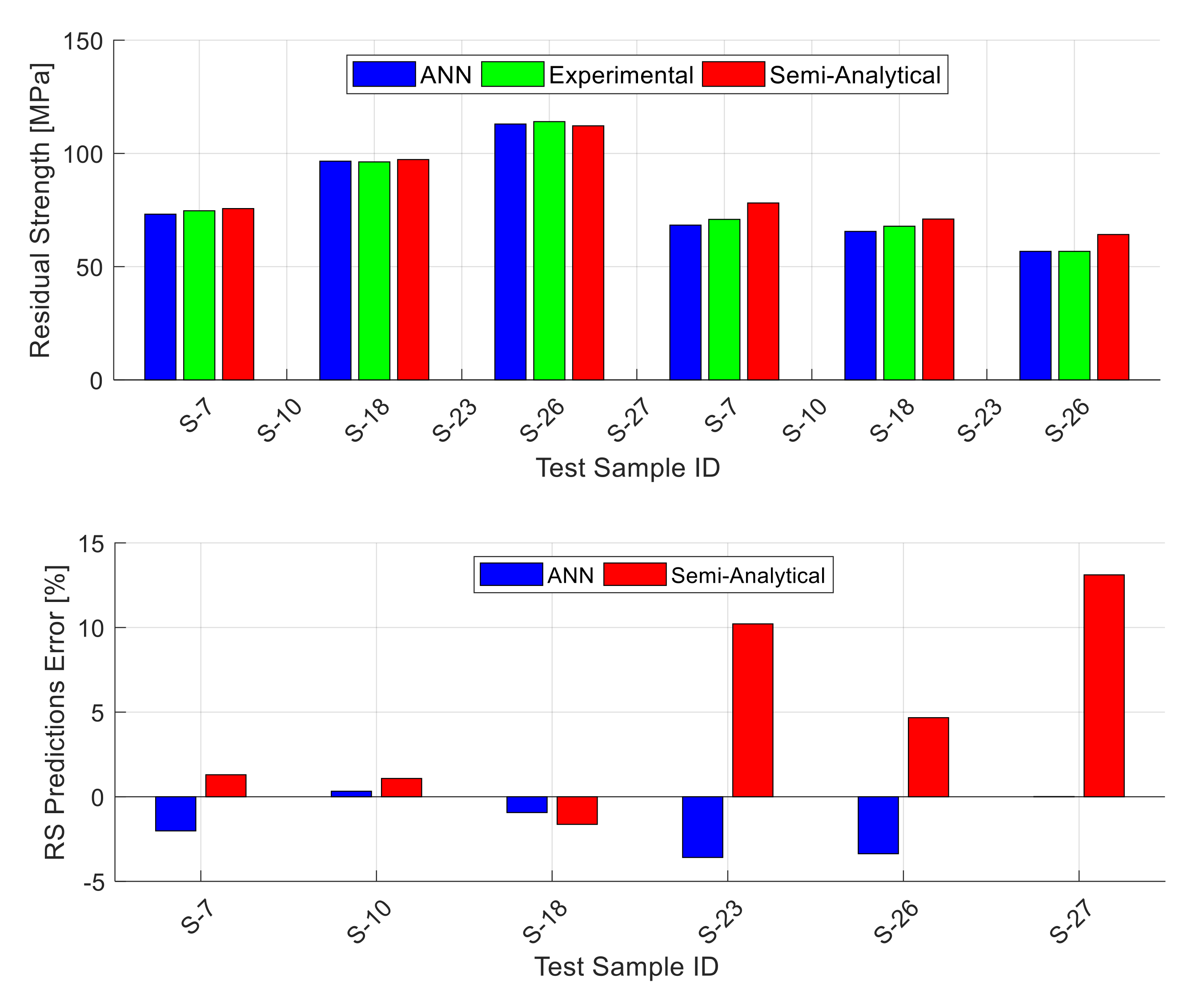
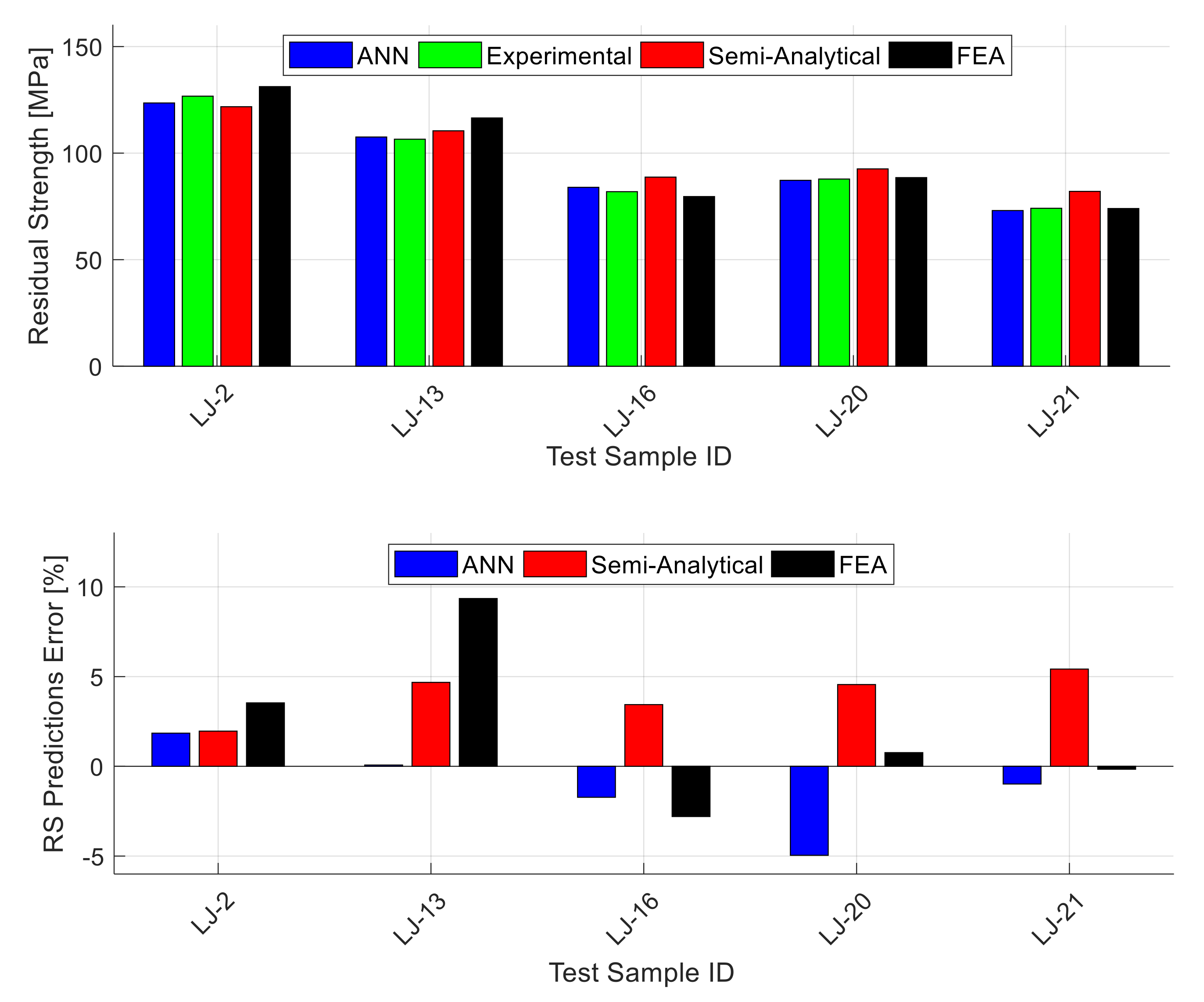
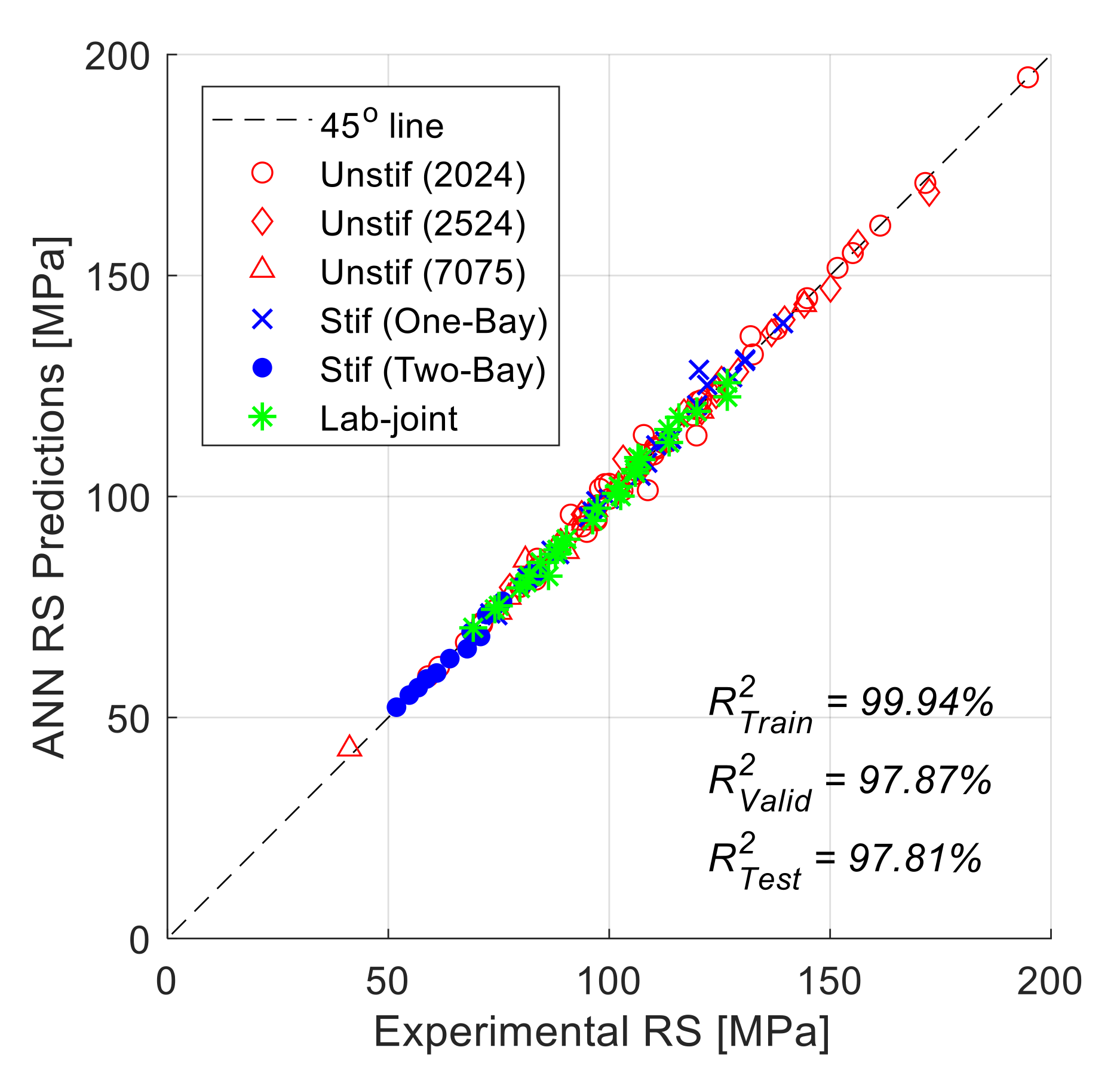
5.3. ANN Residual Strength Predictions
6. Concluding Remarks
- Proper selection of the input parameters for representing the different materials and the geometric and panel configurations is essential for obtaining good results using ANN. For instance, two fracture-related material properties (yield strength and fracture toughness) and a designation number are used as inputs to account for the three different materials being used here. The material properties also "indirectly" account for sheet thickness, material condition, and grain orientation, and this eliminates the need for some inputs. In addition, using the standard handbook values of the material properties (instead of the actual properties obtained from testing) makes the ANN modeling approach being used here simpler and more convenient for engineering use.
- Optimizing the ANN model is essential for obtaining high-accuracy predictions. The ANN optimization carried out here showed that there could be quite a significant difference in the prediction accuracy when using different learning algorithms, hidden node activation functions, and numbers of hidden nodes. In this investigation, the best ANN performance was obtained using the Bayesian Regularization learning algorithm with the Elliot symmetric sigmoid activation function and seven hidden nodes.
- In order to avoid bias and get more reliable results, it is essential to implement a randomized selection procedure for the data points used in the training, validation, and testing datasets; also, the randomized selection needs to be repeated several times (cross-validation). Additionally, it is beneficial to include some fixed, manually selected data points that cover the upper and lower limit values of the different inputs within the training group. This will avoid the extrapolation in the ANN predictions and thus improve the accuracy.
- There are some differences (relatively small yet noticeable) in the average residual strength prediction error values between the different materials and panel configurations. These differences in the error values can be attributed to two factors: (i) the different number of data points available for training the ANN for the different materials and configurations and (ii) the amount of variation in the different inputs parameters within the different materials and configurations. For instance, the highest error is observed for the 7075-T6 material (MAEP = 8.2%) since only eight data points are used for training. In fact, eight data points is a very small number, and it is definitely not sufficient for training an ANN; however, the error level is still reasonable, since this material is not used alone for developing an ANN model but rather among a larger group of data points that share many common geometric and configuration inputs, although the materials are different. On the other hand, the best accuracy (MAEP = 1.81%) is observed for the lap-joint panels, since they all share the same sheet thickness, material condition, and grain orientation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Swift, T. Widespread fatigue damage monitoring: Issues and concerns. In Proceedings of the 5th International Conference on Structural Airworthiness of New and Ageing Aircraft, Hamburg, Germany, 16–18 June 1993; pp. 113–150. [Google Scholar]
- Broek, D. The Effects of Multi-Site Damage on The Arrest Capability of Aircraft Fuselage Structures; FractuREsearch Report No. TR9302; Foster Miller Inc.: Waltham, MA, USA, 1993. [Google Scholar]
- Schijve, J. Multiple-site damage in aircraft fuselage structures. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 329–344. [Google Scholar] [CrossRef]
- Dawicke, D.S.; Newman, J.C. Evaluation of Various Fracture Parameters for Predictions of Residual Strength in Sheets with Multi-Site Damage. In Proceedings of the 1st Joint NASA/FAA/DOD Conference on Aging Aircraft, Ogden, UT, USA, 8–10 July 1997. [Google Scholar]
- Ingram, J.E.; Kwon, Y.S.; Duffie, K.J.; Irby, W.D. Residual strength analysis of skin splices with multiple site damage. In Proceedings of the 2nd Joint NASA/FAA/DOD Conference on Aging Aircraft, Williamsburg, VA, USA, 31 August–3 September 1998; Langley Research Center: Hampton, VA, USA, 1999; pp. 427–436. [Google Scholar]
- Kuang, J.H.; Chen, C.K. The failure of ligaments due to multiple-site damage using interactions of dugdale-type cracks. Fatigue Fract. Eng. Mater. Struct. 1998, 21, 1147–1156. [Google Scholar] [CrossRef]
- Thomson, D.; Hoadley, D.; McHatton, J. Load Tests of Flat and Curved Panels with Multiple Cracks; Foster-Miller Draft Final Report to the FAA Technical Center; Foster Miller Inc.: Waltham, MA, USA, 1993. [Google Scholar]
- Dewit, R.; Fields, R.J.; Mordfin, L.; Low, S.R.; Harne, D. Fracture Behavior of Large-Scale Thin-Sheet Aluminum Alloy. In 1995 National Fracture Symposium; American Society for Testing and Materials: West Conshohocken, PA, USA, 1995. [Google Scholar]
- Smith, B.L.; Saville, P.A.; Mouak, A.; Myose, R.Y. Strength of 2024-T3 aluminum panels with multiple site damage. J. Aircr. 2000, 37, 325–331. [Google Scholar] [CrossRef]
- Smith, B.L.; Hijazi, A.L.; Haque, A.K.M.; Myose, R.Y. Strength of stiffened 2024-T3 aluminum panels with multiple site damage. J. Aircr. 2001, 38, 764–768. [Google Scholar] [CrossRef]
- Hijazi, A.L.; Smith, B.L.; Lacy, T.E. Linkup Strength of 2024-T3 Bolted Lap Joint Panels with Multiple Site Damage. J. Aircr. 2004, 41, 359–364. [Google Scholar] [CrossRef]
- Hijazi, A.L.; Lacy, T.E.; Smith, B.L. Comparison of residual strength estimates for bolted lap-joint panels. J. Aircr. 2004, 41, 657–664. [Google Scholar] [CrossRef]
- Smith, B.L.; Hijazi, A.L.; Myose, R.Y. Strength of 7075-T6 and 2024-T3 aluminum panels with multiple-site damage. J. Aircr. 2002, 39, 354–358. [Google Scholar] [CrossRef]
- Smith, B.L.; Flores, T.L.; Hijazi, A.L. Link-up strength of 2524-T3 and 2024-T3 aluminum panels with multiple site damage. J. Aircr. 2005, 42, 535–541. [Google Scholar] [CrossRef]
- Hijazi, A.L. Residual Strength of Thin-Sheet Aluminum Panels with Multiple Site Damage. Ph.D. Thesis, Wichita State University, Wichita, KS, USA, 2002. [Google Scholar]
- Labeas, G.; Diamantakos, J. Analytical prediction of crack coalesce in Multiple Site Damaged structures. Int. J. Fract. 2005, 134, 161–174. [Google Scholar] [CrossRef]
- Pidaparti, R.M.V.; Palakal, M.J.; Rahman, Z.A. Simulation of structural integrity predictions for panels with multiple site damage. Adv. Eng. Softw. 2000, 31, 127–135. [Google Scholar] [CrossRef]
- Dawicke, D.S.; Newman, J.C. Residual strength predictions for multiple site damage cracking using a three-dimensional finite element analysis and a CTOA criterion. In Fatigue and Fracture Mechanics; ASTM International: West Conshohocken, PA, USA, 1999; Volume 29. [Google Scholar]
- Xu, W.; Wang, H.; Wu, X.; Zhang, X.; Bai, G.; Huang, X. A novel method for residual strength prediction for sheets with multiple site damage: Methodology and experimental validation. Int. J. Solids Struct. 2014, 51, 551–565. [Google Scholar] [CrossRef]
- Wu, N.; Xie, L.; Zhao, F.; Chen, B. Residual strength assessment to panels with multiple site damage by method of system reliability. In Proceedings of the 9th International Conference on Reliability Maintainability and Safety IEEE, Guiyang, China, 12–15 June 2011; pp. 74–79. [Google Scholar]
- Pidaparti, R.M.; Jayanti, S.; Palakal, M.J. Residual strength and corrosion rate predictions of aging aircraft panels: Neural network study. J. Aircr. 2002, 39, 175–180. [Google Scholar] [CrossRef]
- Pidaparti, R. Aircraft structural integrity assessment through computational intelligence techniques. Struct. Durab. Health Monit. 2006, 2, 131–148. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-learning-based control for a constrained robotic manipulator with flexible joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5993–6003. [Google Scholar] [CrossRef] [PubMed]
- Al-Dahidi, S.; Ayadi, O.; Alrbai, M.; Adeeb, J. Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction. IEEE Access 2019, 7, 81741–81758. [Google Scholar] [CrossRef]
- Cao, J.; Fang, Z.; Qu, G.; Sun, H.; Zhang, D. An accurate traffic classification model based on support vector machines. Int. J. Netw. Manag. 2017, 27, e1962. [Google Scholar] [CrossRef]
- Mehdy, M.M.; Ng, P.Y.; Shair, E.F.; Saleh, N.I.; Gomes, C. Artificial neural networks in image processing for early detection of breast cancer. Comput. Math. Methods Med. 2017, 2017, 2610628. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A. Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 2020, 237, 106283. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2020, 136, 102852. [Google Scholar] [CrossRef]
- Szklarek, K.; Gajewski, J. Optimisation of the Thin-Walled Composite Structures in Terms of Critical Buckling Force. Materials 2020, 13, 3881. [Google Scholar] [CrossRef]
- Altarazi, S.; Ammouri, M.; Hijazi, A. Artificial neural network modeling to evaluate polyvinylchloride composites’ properties. Comput. Mater Sci. 2018, 153, 1–9. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Kharmanda, G.; Mahdi, E. Constitutive models for the prediction of the hot deformation behavior of the 10% Cr steel alloy. Materials 2019, 12, 2873. [Google Scholar] [CrossRef] [PubMed]
- Dagli, C.H. (Ed.) Artificial Neural Networks for Intelligent Manufacturing; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Nasiri, S.; Khosravani, M.R.; Weinberg, K. Fracture mechanics and mechanical fault detection by artificial intelligence methods: A review. Eng. Fail. Anal. 2017, 81, 270–293. [Google Scholar] [CrossRef]
- Balcıoğlu, H.E.; Seçkin, A.Ç.; Aktaş, M. Failure load prediction of adhesively bonded pultruded composites using artificial neural network. J. Compos. Mater. 2016, 50, 3267–3281. [Google Scholar] [CrossRef]
- Hakim, S.J.S.; Razak, H.A. Structural damage detection of steel bridge girder using artificial neural networks and finite element models. Steel Compos. Struct. 2013, 14, 367–377. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Shu, J.; Zhang, Z.; Gonzalez, I.; Karoumi, R. The application of a damage detection method using Artificial Neural Network and train-induced vibrations on a simplified railway bridge model. Eng. Struct. 2013, 52, 408–421. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, H.; Dong, H. Using deep neural network with small dataset to predict material defects. Mater. Des. 2019, 162, 300–310. [Google Scholar] [CrossRef]
- Nechval, K.N.; Nechval, N.A.; Bausova, I.; Skiltere, D.; Strelchonok, V.F. Prediction of fatigue crack growth process via artificial neural network technique. Int. J. Comput. 2006, 5, 21–32. [Google Scholar]
- Gajewski, J.; Sadowski, T. Sensitivity analysis of crack propagation in pavement bituminous layered structures using a hybrid system integrating Artificial Neural Networks and Finite Element Method. Comput. Mater. Sci. 2014, 82, 114–117. [Google Scholar] [CrossRef]
- Lee, J.A.; Almond, D.P.; Harris, B. The use of neural networks for the prediction of fatigue lives of composite materials. Compos. Part A Appl. Sci. Manuf. 1999, 30, 1159–1169. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Lahmer, T.; Nguyen-Thoi, T.; Rabczuk, T. Predicting the fracture toughness of PNCs: A stochastic approach based on ANN and ANFIS. Comput. Mater. Sci. 2015, 102, 304–313. [Google Scholar] [CrossRef]
- Mohanty, J.R.; Verma, B.B.; Ray, P.K.; Parhi, D.K. Application of artificial neural network for fatigue life prediction under interspersed mode-I spike overload. J. Test. Eval. 2010, 38, 177–187. [Google Scholar]
- Mortazavi, S.M.; Ince, A. An artificial neural network modeling approach for short and long fatigue crack propagation. Comput. Mater. Sci. 2020, 185, 109962. [Google Scholar] [CrossRef]
- Seibi, A.; Al-Alawi, S.M. Prediction of fracture toughness using artificial neural networks (ANNs). Eng. Fract. Mech. 1997, 56, 311–319. [Google Scholar] [CrossRef]
- Ince, R. Prediction of fracture parameters of concrete by artificial neural networks. Eng. Fract. Mech. 2004, 71, 2143–2159. [Google Scholar] [CrossRef]
- Pidaparti, R.M.V.; Palakal, M.J. Neural network approach to fatigue-crack-growth predictions under aircraft spectrum loadings. J. Aircr. 1995, 32, 825–831. [Google Scholar] [CrossRef]
- Pidaparti, R.M.V.; Palakal, M.J. Fatigue crack growth predictions in aging aircraft panels using optimization neural network. AIAA J. 1998, 36, 1300–1304. [Google Scholar] [CrossRef]
- Spear, A.D.; Priest, A.R.; Veilleux, M.G.; Ingraffea, A.R.; Hochhalter, J.D. Surrogate modeling of high-fidelity fracture simulations for real-time residual strength predictions. AIAA J. 2011, 49, 2770–2782. [Google Scholar] [CrossRef]
- Candelieri, A.; Sormani, R.; Arosio, G.; Giordani, I.; Archetti, F. Assessing structural health of helicopter fuselage panels through artificial neural networks hierarchies. Int. J. Reliab. Saf. 2013, 7, 216–234. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Handbook, M. Metallic Materials and Elements for Aerospace Vehicle Structures; Military Handbook No. MIL-HDBK-5H, Section 5; Defense Standardization Program: Riverside, OH, USA, 1998. [Google Scholar]
- Dawicke, D.S.; Newman, J.C., Jr.; Starnes, J.H., Jr.; Rose, C.A.; Young, R.D.; Seshadri, B.R. Residual strength analysis methodology: Laboratory coupons to structural components. In Proceedings of the 3rd Joint NASA/FAA/DOD Conference on Aging Aircraft; NASA Langley Technical Report Server, Hampton, VA, USA; 2000. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 729. [Google Scholar]
- Pearson’s Correlation Coefficient. In Encyclopedia of Public Health; Kirch, W., Ed.; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network ToolboxTM 6 User’s Guide; MathWorks: Natick, MA, USA, 2015. [Google Scholar]
- Baghirli, O. Comparison of Lavenberg-Marquardt, Scaled Conjugate Gradient and Bayesian Regularization Backpropagation Algorithms for Multistep Ahead Wind Speed Forecasting Using Multilayer Perceptron Feedforward Neural Network. Master’s Thesis, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
- Peters, S.O.; Sinecen, M.; Gallagher, G.R.; Pebworth, L.A.; Hatfield, J.S.; Kizilkaya, K. Comparison of linear model and artificial neural network using antler beam diameter and beam length of white-tailed deer (Odocoileus virginianus). J. Anim. Sci. 2016, 94, 823–824. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Louzazni, M. Assessment of Artificial Neural Networks Learning Algorithms and Training Datasets for Solar Photovoltaic Power Production Prediction. Front. Energy Res. 2019, 7, 130. [Google Scholar] [CrossRef]
- Arora, M.; Ashraf, F.; Saxena, V.; Mahendru, G.; Kaushik, M.; Shubham, P. A Neural Network-Based Comparative Analysis of BR, LM, and SCG Algorithms for the Detection of Particulate Matter. In Advances in Interdisciplinary Engineering; Springer: Singapore, 2019; pp. 619–634. [Google Scholar]
- Heaton, J. Deep Learning and Neural Networks; Artificial Intelligence for Humans; Heaton Research: St. Louis, MO, USA, 2015; Volume 3. [Google Scholar]
| Panel ID | Source | Mat. Cond. | Grain Orient. | σy MPa | KC MPa.m1/2 | t mm | W mm | a mm | ℓ mm | L mm | σExp MPa |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U-1 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 93.35 | 4.45 | 3.81 | 79.84 |
| U-2 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 90.81 | 4.45 | 6.35 | 97.15 |
| U-3 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 88.27 | 4.45 | 8.89 | 112.18 |
| U-4 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 84.46 | 8.26 | 8.89 | 94.25 |
| U-5 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 83.19 | 6.99 | 11.43 | 110.04 |
| U-6 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 81.92 | 5.72 | 13.97 | 120.04 |
| U-7 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 80.65 | 4.45 | 16.51 | 132.52 |
| U-8 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 118.75 | 4.45 | 3.81 | 67.57 |
| U-9 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 116.21 | 4.45 | 6.35 | 83.36 |
| U-10 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 113.67 | 4.45 | 8.89 | 94.94 |
| U-11 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 109.86 | 8.26 | 8.89 | 82.33 |
| U-12 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 108.59 | 6.99 | 11.43 | 97.15 |
| U-13 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 105.7 |
| U-14 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 106.05 | 4.45 | 16.51 | 119.77 |
| U-15 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 144.15 | 4.45 | 3.81 | 59.02 |
| U-16 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 141.61 | 4.45 | 6.35 | 73.98 |
| U-17 | WSU | Clad | L-T | 310.3 | 114.3 | 1.6 | 610 | 139.07 | 4.45 | 8.89 | 83.71 |
| U-18 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 135.26 | 8.26 | 8.89 | 71.23 |
| U-19 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 133.99 | 6.99 | 11.43 | 83.50 |
| U-20 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 93.91 |
| U-21 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 131.45 | 4.45 | 16.51 | 108.73 |
| U-22 | WSU | Clad | T-L | 275.8 | 109.9 | 1.6 | 610 | 160.66 | 8.26 | 8.89 | 71.23 |
| U-23 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 254 | 6.35 | 6.35 | 61.50 |
| U-24 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 177.8 | 5.08 | 7.62 | 84.12 |
| U-25 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 71.12 | 7.62 | 10.16 | 137.9 |
| U-26 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 195.58 | 5.08 | 15.24 | 97.91 |
| U-27 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 241.3 | 6.35 | 19.05 | 88.95 |
| U-28 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 96.52 | 7.62 | 22.86 | 161.34 |
| U-29 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 273.05 | 6.35 | 25.4 | 91.29 |
| U-30 | NIST | Bare | L-T | 324.1 | 111.0 | 1.02 | 2286 | 127 | 5.08 | 33.02 | 151.69 |
| U-31 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 101.6 | 3.81 | 8.89 | 97.43 |
| U-32 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 96.52 | 6.35 | 11.43 | 99.98 |
| U-33 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 40.64 | 10.16 | 12.7 | 144.8 |
| U-34 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 63.5 | 12.7 | 12.7 | 106.05 |
| U-35 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 93.98 | 6.35 | 13.97 | 110.32 |
| U-36 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 40.64 | 6.35 | 16.51 | 171.55 |
| U-37 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 91.44 | 6.35 | 16.51 | 118.94 |
| U-38 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 76.2 | 6.35 | 31.75 | 155.14 |
| U-39 | FM * | Clad | T-L | 268.9 | 113.2 | 1.02 | 508 | 38.1 | 12.7 | 38.1 | 194.78 |
| U-40 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 90 | 7.5 | 8 | 106.83 |
| U-41 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 90 | 7.5 | 12 | 120.83 |
| U-42 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 90 | 7.5 | 18 | 132 |
| U-43 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 111 | 7.5 | 10 | 103 |
| U-44 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 111 | 7.5 | 15 | 107.83 |
| U-45 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 113 | 7.5 | 15 | 113.33 |
| U-46 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 113 | 7.5 | 20 | 119.67 |
| U-47 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 136 | 7.5 | 20 | 99 |
| U-48 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 138 | 7.5 | 30 | 110.67 |
| U-49 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 143 | 7.5 | 20 | 100 |
| U-50 | SJTU * | Clad | L-T | 303.4 | 117.6 | 1 | 600 | 148 | 7.5 | 30 | 106.67 |
| Panel ID | Grain Orient. | σy MPa | KC MPa.m1/2 | t mm | W mm | a mm | ℓ mm | L mm | σExp MPa |
|---|---|---|---|---|---|---|---|---|---|
| 2524-1 | L-T | 310.3 | 204.4 | 1.6 | 610 | 93.35 | 4.45 | 3.81 | 102.11 |
| 2524-2 | L-T | 310.3 | 204.4 | 1.6 | 610 | 90.81 | 4.45 | 6.35 | 124.18 |
| 2524-3 | L-T | 310.3 | 204.4 | 1.6 | 610 | 88.27 | 4.45 | 8.89 | 139.69 |
| 2524-4 | T-L | 275.8 | 180.2 | 1.6 | 610 | 84.46 | 8.26 | 8.89 | 125.42 |
| 2524-5 | T-L | 275.8 | 180.2 | 1.6 | 610 | 83.19 | 6.99 | 11.43 | 144.17 |
| 2524-6 | T-L | 275.8 | 180.2 | 1.6 | 610 | 81.92 | 5.72 | 13.97 | 156.31 |
| 2524-7 | T-L | 275.8 | 180.2 | 1.6 | 610 | 80.65 | 4.45 | 16.51 | 172.44 |
| 2524-8 | T-L | 275.8 | 180.2 | 1.6 | 610 | 118.75 | 4.45 | 3.81 | 89.01 |
| 2524-9 | T-L | 275.8 | 180.2 | 1.6 | 610 | 116.21 | 4.45 | 6.35 | 107.08 |
| 2524-10 | T-L | 275.8 | 180.2 | 1.6 | 610 | 113.67 | 4.45 | 8.89 | 120.94 |
| 2524-11 | T-L | 275.8 | 180.2 | 1.6 | 610 | 109.86 | 8.26 | 8.89 | 108.67 |
| 2524-12 | T-L | 275.8 | 180.2 | 1.6 | 610 | 108.59 | 6.99 | 11.43 | 124.32 |
| 2524-13 | T-L | 275.8 | 180.2 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 136.73 |
| 2524-14 | T-L | 275.8 | 180.2 | 1.6 | 610 | 106.05 | 4.45 | 16.51 | 150.1 |
| 2524-15 | L-T | 310.3 | 204.4 | 1.6 | 610 | 144.15 | 4.45 | 3.81 | 77.5 |
| 2524-16 | L-T | 310.3 | 204.4 | 1.6 | 610 | 141.61 | 4.45 | 6.35 | 93.77 |
| 2524-17 | L-T | 310.3 | 204.4 | 1.6 | 610 | 139.07 | 4.45 | 8.89 | 103.15 |
| 2524-18 | T-L | 275.8 | 180.2 | 1.6 | 610 | 135.26 | 8.26 | 8.89 | 92.32 |
| 2524-19 | T-L | 275.8 | 180.2 | 1.6 | 610 | 133.99 | 6.99 | 11.43 | 107.63 |
| 2524-20 | T-L | 275.8 | 180.2 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 116.94 |
| 2524-21 | T-L | 275.8 | 180.2 | 1.6 | 610 | 131.45 | 4.45 | 16.51 | 129.21 |
| 2524-22 | T-L | 275.8 | 180.2 | 1.6 | 610 | 160.66 | 8.26 | 8.89 | 80.67 |
| Panel ID | Grain Orient. | σy MPa | KC MPa.m1/2 | t mm | W mm | a mm | ℓ mm | L mm | σExp MPa |
|---|---|---|---|---|---|---|---|---|---|
| 7075-1 | T-L | 468.9 | 76.9 | 1.8 | 610 | 84.46 | 6.99 | 10.16 | 100.6 |
| 7075-2 | T-L | 468.9 | 76.9 | 1.8 | 610 | 109.86 | 8.26 | 8.89 | 81.02 |
| 7075-3 | T-L | 468.9 | 76.9 | 1.8 | 610 | 108.59 | 6.99 | 11.43 | 94.25 |
| 7075-4 | T-L | 468.9 | 76.9 | 1.8 | 610 | 108.59 | 5.72 | 12.7 | 96.94 |
| 7075-5 | T-L | 468.9 | 76.9 | 1.8 | 610 | 107.32 | 4.45 | 15.24 | 105.36 |
| 7075-6 | T-L | 468.9 | 76.9 | 1.8 | 610 | 133.99 | 5.72 | 12.7 | 81.22 |
| 7075-7 | T-L | 468.9 | 76.9 | 1.8 | 610 | 132.72 | 5.72 | 13.97 | 90.46 |
| 7075-8 | T-L | 468.9 | 76.9 | 1.8 | 610 | 135.26 | 6.99 | 10.16 | 75.22 |
| 7075-9 | T-L | 468.9 | 76.9 | 1.8 | 610 | 158.12 | 5.72 | 13.97 | 77.29 |
| 7075-10 | T-L | 468.9 | 76.9 | 1.8 | 610 | 191.14 | 8.26 | 3.81 | 32.61 |
| 7075-11 | T-L | 468.9 | 76.9 | 1.8 | 610 | 189.87 | 8.26 | 5.08 | 41.23 |
| 7075-12 | T-L | 468.9 | 76.9 | 1.8 | 610 | 188.60 | 8.26 | 6.35 | 46.68 |
| Panel ID | Stiff. Config. | Grain Orient. | σy MPa | KC MPa.m1/2 | Astf mm2 | t mm | W mm | a mm | ℓ mm | L mm | σExp MPa |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S-1 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 118.75 | 4.45 | 3.81 | 73.09 |
| S-2 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 116.21 | 4.45 | 6.35 | 86.95 |
| S-3 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 113.67 | 4.45 | 8.89 | 99.91 |
| S-4 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 108.59 | 6.99 | 11.43 | 95.43 |
| S-5 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 110.66 |
| S-6 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 106.05 | 4.45 | 16.51 | 122.18 |
| S-7 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 144.15 | 4.45 | 3.81 | 74.67 |
| S-8 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 141.61 | 4.45 | 6.35 | 88.67 |
| S-9 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 139.07 | 4.45 | 8.89 | 97.08 |
| S-10 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 133.99 | 6.99 | 11.43 | 96.25 |
| S-11 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 112.66 |
| S-12 | One-Bay | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 131.45 | 4.45 | 16.51 | 127.83 |
| S-13 | One-Bay | L-T | 310.3 | 114.3 | 161.3 | 1.6 | 610 | 113.67 | 4.45 | 8.89 | 107.08 |
| S-14 | One-Bay | L-T | 310.3 | 114.3 | 151.6 | 1.6 | 610 | 108.59 | 6.99 | 11.43 | 108.6 |
| S-15 | One-Bay | L-T | 310.3 | 114.3 | 151.6 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 119.9 |
| S-16 | One-Bay | L-T | 310.3 | 114.3 | 151.6 | 1.6 | 610 | 106.05 | 4.45 | 16.51 | 130.8 |
| S-17 | One-Bay | L-T | 310.3 | 114.3 | 161.3 | 1.6 | 610 | 144.15 | 4.45 | 3.81 | 81.5 |
| S-18 | One-Bay | L-T | 310.3 | 114.3 | 151.6 | 1.6 | 610 | 133.99 | 6.99 | 11.43 | 114.04 |
| S-19 | One-Bay | L-T | 310.3 | 114.3 | 161.3 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 120.32 |
| S-20 | One-Bay | L-T | 310.3 | 114.3 | 161.3 | 1.6 | 610 | 131.45 | 4.45 | 16.51 | 139.35 |
| S-21 | One-Bay | L-T | 303.4 | 117.6 | 105 | 1.02 | 610 | 81.92 | 5.72 | 13.97 | 130.73 |
| S-22 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 80.53 |
| S-23 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 108.59 | 6.99 | 11.43 | 70.88 |
| S-24 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 109.86 | 8.26 | 8.89 | 58.68 |
| S-25 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 75.85 |
| S-26 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 133.99 | 6.99 | 11.43 | 67.85 |
| S-27 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 135.26 | 8.26 | 8.89 | 56.75 |
| S-28 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 158.12 | 5.72 | 13.97 | 72.26 |
| S-29 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 159.39 | 6.99 | 11.43 | 63.92 |
| S-30 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 160.66 | 8.26 | 8.89 | 54.75 |
| S-31 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 183.52 | 5.72 | 13.97 | 68.74 |
| S-32 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 184.79 | 6.99 | 11.43 | 60.95 |
| S-33 | Two-Bay * | T-L | 275.8 | 109.9 | 105 | 1.6 | 610 | 186.06 | 8.26 | 8.89 | 51.85 |
| S-34 | Two-Bay * | L-T | 310.3 | 114.3 | 105 | 1.6 | 610 | 107.32 | 5.72 | 13.97 | 97.01 |
| S-35 | Two-Bay * | L-T | 310.3 | 114.3 | 105 | 1.6 | 610 | 132.72 | 5.72 | 13.97 | 84.26 |
| S-36 | Two-Bay * | L-T | 310.3 | 114.3 | 105 | 1.6 | 610 | 158.12 | 5.72 | 13.97 | 82.33 |
| Panel ID | Grain Orient. | σy MPa | KC MPa.m1/2 | t mm | W mm | a mm | ℓ mm | L mm | σExp MPa |
|---|---|---|---|---|---|---|---|---|---|
| LJ-1 | T-L | 268.9 | 109.9 | 1.42 | 610 | 106.52 | 3.65 | 16.83 | 126.73 |
| LJ-2 | T-L | 268.9 | 109.9 | 1.42 | 610 | 106.52 | 4.92 | 15.56 | 115.77 |
| LJ-3 | T-L | 268.9 | 109.9 | 1.42 | 610 | 107.79 | 3.65 | 15.56 | 126.73 |
| LJ-4 | T-L | 268.9 | 109.9 | 1.42 | 610 | 107.79 | 4.92 | 14.29 | 113.35 |
| LJ-5 | T-L | 268.9 | 109.9 | 1.42 | 610 | 107.79 | 6.19 | 13.02 | 106.53 |
| LJ-6 | T-L | 268.9 | 109.9 | 1.42 | 610 | 109.06 | 3.65 | 14.29 | 119.84 |
| LJ-7 | T-L | 268.9 | 109.9 | 1.42 | 610 | 109.06 | 4.92 | 13.02 | 113.56 |
| LJ-8 | T-L | 268.9 | 109.9 | 1.42 | 610 | 109.06 | 6.19 | 11.75 | 105.77 |
| LJ-9 | T-L | 268.9 | 109.9 | 1.42 | 610 | 109.06 | 7.46 | 10.48 | 101.49 |
| LJ-10 | T-L | 268.9 | 109.9 | 1.42 | 610 | 131.92 | 3.65 | 16.83 | 107.29 |
| LJ-11 | T-L | 268.9 | 109.9 | 1.42 | 610 | 131.92 | 4.92 | 15.56 | 102.6 |
| LJ-12 | T-L | 268.9 | 109.9 | 1.42 | 610 | 133.19 | 3.65 | 15.56 | 105.91 |
| LJ-13 | T-L | 268.9 | 109.9 | 1.42 | 610 | 133.19 | 4.92 | 14.29 | 97.29 |
| LJ-14 | T-L | 268.9 | 109.9 | 1.42 | 610 | 133.19 | 6.19 | 13.02 | 90.32 |
| LJ-15 | T-L | 268.9 | 109.9 | 1.42 | 610 | 134.46 | 3.65 | 14.29 | 102.18 |
| LJ-16 | T-L | 268.9 | 109.9 | 1.42 | 610 | 134.46 | 4.92 | 13.02 | 96.25 |
| LJ-17 | T-L | 268.9 | 109.9 | 1.42 | 610 | 134.46 | 6.19 | 11.75 | 88.26 |
| LJ-18 | T-L | 268.9 | 109.9 | 1.42 | 610 | 134.46 | 7.46 | 10.48 | 81.91 |
| LJ-19 | T-L | 268.9 | 109.9 | 1.42 | 610 | 157.32 | 3.65 | 16.83 | 89.29 |
| LJ-20 | T-L | 268.9 | 109.9 | 1.42 | 610 | 157.32 | 4.92 | 15.56 | 86.26 |
| LJ-21 | T-L | 268.9 | 109.9 | 1.42 | 610 | 158.59 | 3.65 | 15.56 | 87.84 |
| LJ-22 | T-L | 268.9 | 109.9 | 1.42 | 610 | 158.59 | 4.92 | 14.29 | 81.29 |
| LJ-23 | T-L | 268.9 | 109.9 | 1.42 | 610 | 158.59 | 6.19 | 13.02 | 75.02 |
| LJ-24 | T-L | 268.9 | 109.9 | 1.42 | 610 | 159.86 | 3.65 | 14.29 | 84.46 |
| LJ-25 | T-L | 268.9 | 109.9 | 1.42 | 610 | 159.86 | 4.92 | 13.02 | 79.78 |
| LJ-26 | T-L | 268.9 | 109.9 | 1.42 | 610 | 159.86 | 6.19 | 11.75 | 74.12 |
| LJ-27 | T-L | 268.9 | 109.9 | 1.42 | 610 | 159.86 | 7.46 | 10.48 | 69.23 |
| SCG | LM | BR | |
|---|---|---|---|
| satlin | logsig | elliotsig | |
| 19 | 19 | 30 | |
| MAEP [%] | 6.99 | 4.59 | 3.38 |
| RSMEP [%] | 9.61 | 7.22 | 4.9 |
| R2 [%] | 85.77 | 91.27 | 96 |
| Unstif (2024) | Unstif (2524) | Unstif (7075) | Stif | Lab-joint | All | |
|---|---|---|---|---|---|---|
| MAEP [%] | 4.61 | 2.86 | 8.2 | 3.62 | 1.81 | 3.82 |
| RMSEP [%] | 6.36 | 3.38 | 9.96 | 4.49 | 2.21 | 5.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hijazi, A.; Al-Dahidi, S.; Altarazi, S. Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks. Materials 2020, 13, 5216. https://doi.org/10.3390/ma13225216
Hijazi A, Al-Dahidi S, Altarazi S. Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks. Materials. 2020; 13(22):5216. https://doi.org/10.3390/ma13225216
Chicago/Turabian StyleHijazi, Ala, Sameer Al-Dahidi, and Safwan Altarazi. 2020. "Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks" Materials 13, no. 22: 5216. https://doi.org/10.3390/ma13225216
APA StyleHijazi, A., Al-Dahidi, S., & Altarazi, S. (2020). Residual Strength Prediction of Aluminum Panels with Multiple Site Damage Using Artificial Neural Networks. Materials, 13(22), 5216. https://doi.org/10.3390/ma13225216






