Young’s Modulus of Different Illitic Clays during Heating and Cooling Stage of Firing
Abstract
1. Introduction
1.1. Quartz and Illite
1.2. Illite-Based Ceramics
2. Materials and Methods
3. Results and Discussion
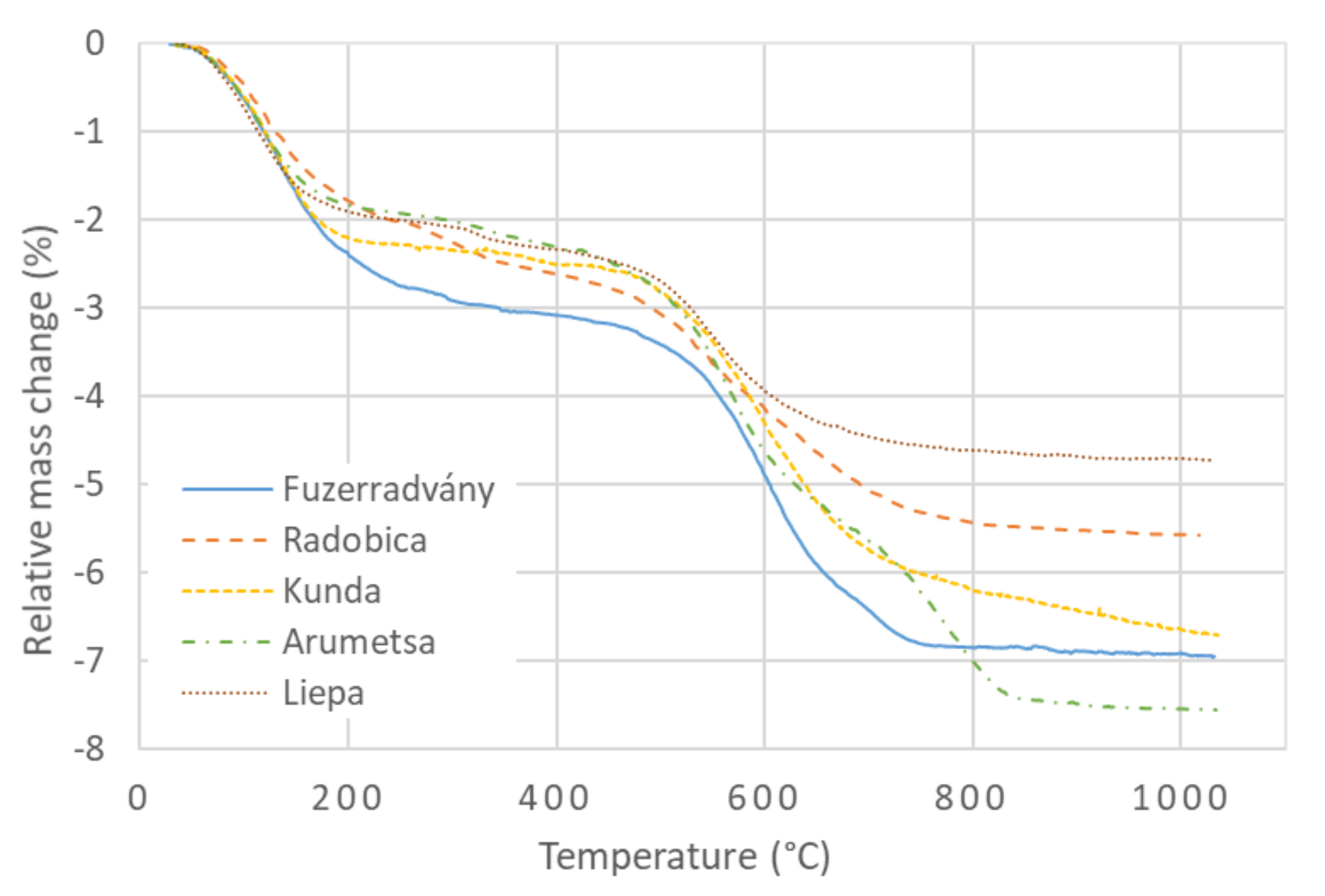
3.1. Mass Changes
3.2. Volume Changes
3.3. Bulk Density
3.4. Young’s Modulus during Heating
3.5. Young’s Modulus during Cooling
4. Conclusions
- The release of the physically bound water increases Young’s modulus by ∼70%.
- The influence of the α → β quartz transition and dehydroxylation of illite on Young’s modulus is negligible during heating.
- The intensive sintering, which takes place at ∼800 °C → 1100 °C → 800 °C increases Young’s modulus.
- Solidification of the glassy phase is finished at ∼750 °C. Cooling from this temperature, the creation of cracks begins due to differences between the thermal expansions of quartz, glassy phase, and other mineral phases.
- At around the β → α quartz transition, a partial recovery of Young’s modulus occurs as the result of the thermal stresses reversal.
- Young’s modulus lowers its values down to the room temperature as the consequence of cracking.
- The results of Young’s modulus indicate that the mineral composition and character of the clay particles, determined by the clay’s origin, play an important role for Young’s modulus, with the final values varying between 15 GPa to 68 GPa.
- Only the Kunda clay from Estonia keeps its Young’s modulus values after the β → α quartz transition. To explain this anomalous behavior, a new set of experiments should focus on studying the microstructure, composition, and granulometry of the Kunda clay.
Author Contributions
Funding
Conflicts of Interest
References
- Shishkin, A.; Laksa, A.; Shidlovska, V.; Timermane, Z.; Aguedal, H.; Mironov, V.; Ozolins, J. Illite clay ceramic hollow sphere—Obtaining and properties. Key Eng. Mater. 2016, 721, 316–321. [Google Scholar] [CrossRef]
- Shishkin, A.; Bumanis, G.; Irtiseva, K.; Ozolins, J.; Korjakins, A. Clay ceramic hollow sphere–cement syntactic foam composite for building applications. Key Eng. Mater. 2019, 800, 228–234. [Google Scholar] [CrossRef]
- Rugele, K.; Lehmhus, D.; Hussainova, I.; Peculevica, J.; Lisnanskis, M.; Shishkin, A. Effect of fly-ash cenospheres on properties of clay-ceramic syntactic foams. Materials 2017, 10, 828. [Google Scholar] [CrossRef] [PubMed]
- Shishkin, A.; Mironov, V.; Zemchenkov, V.; Antonov, M.; Hussainova, I. Hybrid syntactic foams of metal–fly ash cenosphere–clay. Key Eng. Mater. 2016, 674, 35–40. [Google Scholar] [CrossRef]
- Štubňa, I.; Trník, A.; Vozár, L. Thermomechanical analysis of quartz porcelain in temperature cycles. Ceram. Int. 2007, 33, 1287–1291. [Google Scholar] [CrossRef]
- Chmelík, F.; Trník, A.; Pešička, J.; Štubňa, I. Creation of microcracks in porcelain during firing. J. Eur. Ceram. Soc. 2011, 31, 2205–2209. [Google Scholar] [CrossRef]
- Jankula, M.; Húlan, T.; Štubňa, I.; Ondruška, J.; Podoba, R.; Šín, P.; Bačík, P.; Trník, A. The influence of heat on elastic properties of illitic clay Radobica. J. Ceram. Soc. Jpn. 2015, 123, 874–879. [Google Scholar] [CrossRef]
- Knapek, M.; Húlan, T.; Dobroň, P.; Chmelík, F.; Trník, A.; Štubňa, I. Acoustic emission during firing of the illite-based ceramics with fly ash addition. Acta Phys. Pol. A 2015, 128, 783–786. [Google Scholar] [CrossRef]
- Knapek, M.; Húlan, T.; Minárik, P.; Dobroň, P.; Štubňa, I.; Stráská, J.; Chmelík, F. Study of microcracking in illite-based ceramics during firing. J. Eur. Ceram. Soc. 2016, 36, 221–226. [Google Scholar] [CrossRef]
- Húlan, T.; Trník, A.; Štubňa, I.; Bačík, P.; Kaljuvee, T.; Vozár, L. Development of Young’s modulus of illitic clay during heating up to 1100 °C. Mater. Sci. Medzg. 2015, 21, 429–434. [Google Scholar] [CrossRef][Green Version]
- Húlan, T.; Kaljuvee, T.; Štubňa, I.; Trník, A. Investigation of elastic and inelastic properties of Estonian clay from a locality in Kunda during thermal treatment. J. Therm. Anal. Calorim. 2016, 124, 1153–1159. [Google Scholar] [CrossRef]
- Húlan, T.; Štubňa, I.; Shishkin, A.; Ozolins, J.; Csáki, Š.; Bačík, P.; Fridrichová, J. Development of Young’s modulus of natural illitic clay during heating and cooling stage of firing. Clay Min. 2019, 54, 229–233. [Google Scholar] [CrossRef]
- Štubňa, I.; Húlan, T.; Kaljuvee, T.; Vozár, L. Investigation of dynamic mechanical properties of Estonian clay Arumetsa. Appl. Clay Sci. 2018, 153, 23–28. [Google Scholar] [CrossRef]
- Pánek, Z. Konštrukčná Keramika; R&D Print: Bratislava, Slovakia, 1992. (In Slovak) [Google Scholar]
- Štubňa, I.; Trník, A.; Šín, P.; Sokolář, R.; Medveď, I. Relationship between mechanical strength and Young’s modulus in traditional ceramics. Mater. Tehnol. 2011, 45, 375–378. [Google Scholar]
- Pytlík, P.; Sokolář, R. Stavební Keramika–Technologie, Vlastnosti a Využití; Akademické nakladatelství CERM: Brno, Czech Republic, 2002. (In Czech) [Google Scholar]
- Prjanishnikov, V.P. Sistema Kremnezema; Izdatelstvo Literatury po Stroitelstvu: Leningrad, Russia, 1971. (In Russian) [Google Scholar]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorová, E. Elastic properties of silica polymorphs—A review. Ceram. Silik. 2013, 57, 167–184. [Google Scholar]
- Hosieni, K.R.; Howald, R.A.; Scanlon, M.W. Thermodynamics of the lambda transition and the equation of state of quartz. Am. Miner. 1985, 70, 782–793. [Google Scholar]
- Stixrude, L.; Peacor, D.R. First-principles study of illite-smectite and implications for clay mineral systems. Nature 2002, 420, 165–168. [Google Scholar] [CrossRef]
- Ferrari, S.; Gualtieri, A.F.; Grathoff, G.H.; Leoni, M. Model of structure disorder of illite: Preliminary results. Z. Kristall. Suppl. 2006, 23, 493–498. [Google Scholar] [CrossRef]
- Drits, V.A.; McCarty, D.K. The nature of structure-bonded H2O in illite and leucophyllite from dehydration and dehydroxylation experiments. Clay Clay Min. 2007, 55, 45–58. [Google Scholar] [CrossRef]
- Gualtieri, A.F.; Ferrari, S.; Leoni, M.; Grathoff, G.H.; Hugo, R.; Shatnawi, M.T.M.; Paglia, G.; Billinge, S.J.L. Structural characterization of the clay mineral illite-1M. J. Appl. Crystallogr. 2008, 41, 402–415. [Google Scholar] [CrossRef]
- Schomburg, J.; Zwar, H. Thermal differential diagnosis of mica mineral group. J. Therm. Anal. 1997, 48, 135–139. [Google Scholar] [CrossRef]
- Gualtieri, A.F.; Ferrari, S. Kinetics of illite dehydroxylation. Phys. Chem. Miner. 2006, 33, 490–501. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Hu, Y.; Danging, Y.; Wang, J. Phase changes during heating of illite. In Proceedings of the TMS Annual Meeting, San Antonio, TX, USA, 12–16 March 2006; pp. 309–316. [Google Scholar]
- ČSN 72 1083. Termické Rozbory Keramických Surovin; Czech Technical Standard: Prague, Czech Republic, 2015. (In Czech) [Google Scholar]
- Venturelli, C.; Paganelli, M. Sintering behaviour of clays for the production of ceramics. CGF Ceram. Forum Int. 2007, 84, E32. [Google Scholar]
- Ori, R. The Mineralogical and Technological Characterization of Illite from Füzérradvány (Hungary) as a Raw Material for Traditional Ceramics. PhD Thesis, University of Modena and Emilia Region, Modena, Italy, 2003. (In Italian). [Google Scholar]
- Escalera, E.; Antti, M.L.; Odén, M. Thermal treatment and phase formation in kaolinite and illite based clays from tropical regions of Bolivia. IOP Conf. Ser. Mater. Sci. Eng. 2012, 31, 012017. [Google Scholar] [CrossRef]
- Aras, A. The change of phase composition in kaolinite- and illite-rich clay-based ceramic bodies. Appl. Clay Sci. 2004, 24, 257–269. [Google Scholar] [CrossRef]
- Pécskay, Z.; Molnár, F.; Itaya, T.; Zelenka, T. Geology and K-Ar geochronology of illite from the clay deposit at Fuzérradvány, Tokaj Mts., Hungary. Acta Mineral.-Petrogr. 2005, 46, 1–7. [Google Scholar]
- Kockal, N.U. Utilisation of different types of coal fly ash in the production of ceramic tiles. Bol. Soc. Esp. Ceram. Vidr. 2012, 51, 297–304. [Google Scholar] [CrossRef]
- Kockal, N.U. Properties and microstructure of porous ceramic bodies containing fly ash. J. Build Phys. 2012, 35, 338–352. [Google Scholar] [CrossRef]
- Sedmale, G.; Stinkulis, Ģ.; Sedmalis, U.; Juhnevica, I.; Klavins, J. Characteristics of illite clay and its use for high-and low temperature ceramics. Mater. Sci. Appl. Chem. 2012, 26, 60–63. [Google Scholar]
- Eppler, R. Glazes and glass coatings. Am. Ceram. Soc. Bull. 1999, 78, 69–71. [Google Scholar]
- Schreiber, E.; Anderson, O.; Soga, N. Elastic Constants and Their Measurement; McGraw-Hill Book, Co.: New York, NY, USA, 1973. [Google Scholar]
- ASTM E 1875-13. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus and Poisson’s Ratio for Advanced Ceramics by Sonic Resonance; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM C 1259-15. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus and Poisson’s Ratio for Advanced Ceramics by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Štubňa, I.; Trník, A.; Vozár, L. Determination of Young’s modulus of ceramics from flexural vibration at elevated temperatures. Acta Acust. United Acust. 2011, 97, 1–7. [Google Scholar] [CrossRef]
- Štubňa, I.; Húlan, T.; Trník, A.; Vozár, L. Uncertainty in the determination of Young’s modulus of ceramics using the impulse excitation technique at elevated temperatures. Acta Acust. United Acust. 2018, 104, 269–276. [Google Scholar] [CrossRef]
- Podoba, R.; Trník, A.; Podobník, Ľ. Upgrading of TGA/DTA analyzer derivatograph. Építőanyag 2012, 64, 28–29. [Google Scholar] [CrossRef]
- Jankula, M.; Šín, P.; Podoba, R.; Ondruška, J. Typical problems in push-rod dilatometry analysis. Építőanyag 2013, 65, 11–14. [Google Scholar] [CrossRef]
- Pelovski, Y.; Petkova, V. Investigation on thermal decomposition of pyrite. Part I. J. Therm. Anal. Calorim. 1999, 56, 95–99. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Willey & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Freud, F. Kaolinite-metakaolinite, a model of a solid with extremely high lattice defect concentration. Ber. Deutsche. Keram. Ges. 1967, 44, 5–13. [Google Scholar]
- Kang, S.J.L. Sintering: Densification, Grain Growth and Microstructure; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Ferarri, S.; Gualtieri, A.F. The use of illitic clays in the production of stoneware tile ceramics. Appl. Clay Sci. 2006, 32, 73–81. [Google Scholar] [CrossRef]
- Wattanasiriwech, D.; Srijan, K.; Wattanasiriwech, S. Vitrification of illitic clay from Malaysia. Appl. Clay Sci. 2009, 43, 57–62. [Google Scholar] [CrossRef]
- Martín-Márquez, J.; Rincón, J.M.; Romero, M. Effect of microstructure on mechanical properties of porcelain stoneware. J. Eur. Ceram. Soc. 2010, 30, 3063–3069. [Google Scholar] [CrossRef]
- Liebermann, J. Reliability of materials for high-voltage insulators. Am. Ceram. Soc. Bull. 2000, 5, 55–58. [Google Scholar]
- Liebermann, J. Avoiding quartz in alumina porcelain for high-voltage insulators. Keramische Z. 2001, 53, 683–686. [Google Scholar]
- Štubňa, I.; Mánik, M.; Húlan, T.; Trník, A. Development of stress on quartz grain in illite ceramics during cooling stage of firing. J. Ceram. Soc. Jpn. 2020, 128, 1–7. [Google Scholar] [CrossRef]
- Nigay, P.M.; Cutard, T.; Nzihou, A. The impact of heat treatment on the microstructure of a clay ceramics and its thermal and mechanical properties. Ceram. Int. 2017, 43, 1747–1754. [Google Scholar] [CrossRef]
- Oliveira, A.; Vilches, E.; Soler, V.; Villegas, F. Relationship between Young’s modulus and temperature in porcelain tiles. J. Eur. Ceram. Soc. 2012, 32, 2853–2858. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorová, E.; Kutzendorfer, J. Elastic anomalies in tridymite- and cristobalite-based silica materials. Ceram. Int. 2014, 40, 4207–4211. [Google Scholar] [CrossRef]
- Štubňa, I.; Kozík, T.; Hanic, F. Young’s modulus and mechanical strength of porcelain at the firing cooling stage. Ceram. Int. 1992, 18, 353–354. [Google Scholar] [CrossRef]






| Minerals | Füzérradvány | Radobica | Kunda | Arumetsa | Liepa |
|---|---|---|---|---|---|
| Illite | 80 | 51 | 54 | 43 | 37 |
| Kaolinite | – | – | 8 | 18 | 15 |
| Montmorillonite | 4 | – | – | – | – |
| Chlorite | – | – | 5 | – | – |
| Quartz | 12 | 34 | 28 | 25 | 35 |
| Feldspar | 4 | 13 | 5 | 11 | 13 |
| Calcite | – | 2 | – | 3 | – |
| Oxides | Füzérradvány | Radobica | Kunda | Arumetsa | Liepa |
|---|---|---|---|---|---|
| SiO2 | 58.4 | 56.7 | 61.4 | 57.8 | 62.7 |
| Al2O3 | 23.9 | 23.1 | 17.8 | 18.7 | 15.9 |
| Fe2O3 | 0.6 | 6.3 | 5.7 | 7.0 | 7.2 |
| TiO2 | – | 0.5 | – | – | 1.9 |
| CaO | 0.4 | 0.4 | 0.4 | 1.6 | 0.9 |
| MgO | 1.7 | 2.4 | 2.3 | 2.6 | 1.5 |
| K2O | 7.7 | 5.0 | 5.6 | 4.8 | 4.3 |
| Na2O | 0.1 | – | 0.1 | 0.6 | 0.1 |
| SO2 | – | – | 1.7 | – | – |
| L.O.I | 7.2 | 5.6 | 5.0 | 6.9 | 5.5 |
| Minerals | Füzérradvány | Radobica | Kunda | Arumetsa | Liepa |
|---|---|---|---|---|---|
| Quartz | 11 | 34 | 23 | 24.3 | 35 |
| Feldspar | 6 | 10 | 7 | 4.6 | 5 |
| Hematite | – | 4 | 2 | 3.0 | 4 |
| Spinel | 4 | 7 | – | 2.8 | – |
| Amorphous | 79 | 45 | 68 | 62.0 | 56 |
| Quantity | Füzérradvány | Radobica | Kunda | Arumetsa | Liepa |
|---|---|---|---|---|---|
| Efinal (GPa) | 39 | 17 | 68 | 30 | 15 |
| ρfinal (g/cm3) | 1.84 | 1.95 | 2.27 | 2.17 | 1.94 |
| Δρ (g/cm3) | 0.18 | 0.1 | 0.44 | 0.28 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Húlan, T.; Štubňa, I.; Ondruška, J.; Csáki, Š.; Lukáč, F.; Mánik, M.; Vozár, L.; Ozolins, J.; Kaljuvee, T.; Trník, A. Young’s Modulus of Different Illitic Clays during Heating and Cooling Stage of Firing. Materials 2020, 13, 4968. https://doi.org/10.3390/ma13214968
Húlan T, Štubňa I, Ondruška J, Csáki Š, Lukáč F, Mánik M, Vozár L, Ozolins J, Kaljuvee T, Trník A. Young’s Modulus of Different Illitic Clays during Heating and Cooling Stage of Firing. Materials. 2020; 13(21):4968. https://doi.org/10.3390/ma13214968
Chicago/Turabian StyleHúlan, Tomáš, Igor Štubňa, Ján Ondruška, Štefan Csáki, František Lukáč, Marek Mánik, Libor Vozár, Jurijs Ozolins, Tiit Kaljuvee, and Anton Trník. 2020. "Young’s Modulus of Different Illitic Clays during Heating and Cooling Stage of Firing" Materials 13, no. 21: 4968. https://doi.org/10.3390/ma13214968
APA StyleHúlan, T., Štubňa, I., Ondruška, J., Csáki, Š., Lukáč, F., Mánik, M., Vozár, L., Ozolins, J., Kaljuvee, T., & Trník, A. (2020). Young’s Modulus of Different Illitic Clays during Heating and Cooling Stage of Firing. Materials, 13(21), 4968. https://doi.org/10.3390/ma13214968






