Robust Metallic Nanolaminates Having Phonon-Glass Thermal Conductivity
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ARB | accumulative roll bonding |
| SPD | severe plastic deformation |
| EDMM | electron diffusive mismatch model |
| k | thermal conductivity |
| N | number of interfaces |
| n | number of ARB passes |
| HRTEM | high-resolution transmission electron microscopy |
| Q | heat |
| kCu | copper thermal conductivity |
| kNb | niobium thermal conductivity |
| kslab | two-segment bimetallic thermal conductivity |
| RITR | interfacial thermal resistance |
| RTCR | thermal contact resistance |
| AMM | acoustic mismatch model |
| DMM | diffusive mismatch model |
| ki | thermal conductivity of the metals forming the interface |
| i | subscript to refer to either metal 1 or 2 |
| kf | thermal conductivity of the fluid in the void |
| α | squared root of the ratio of the real area of contact to the contact area |
| Ac | real area of contact |
| A | total contact area |
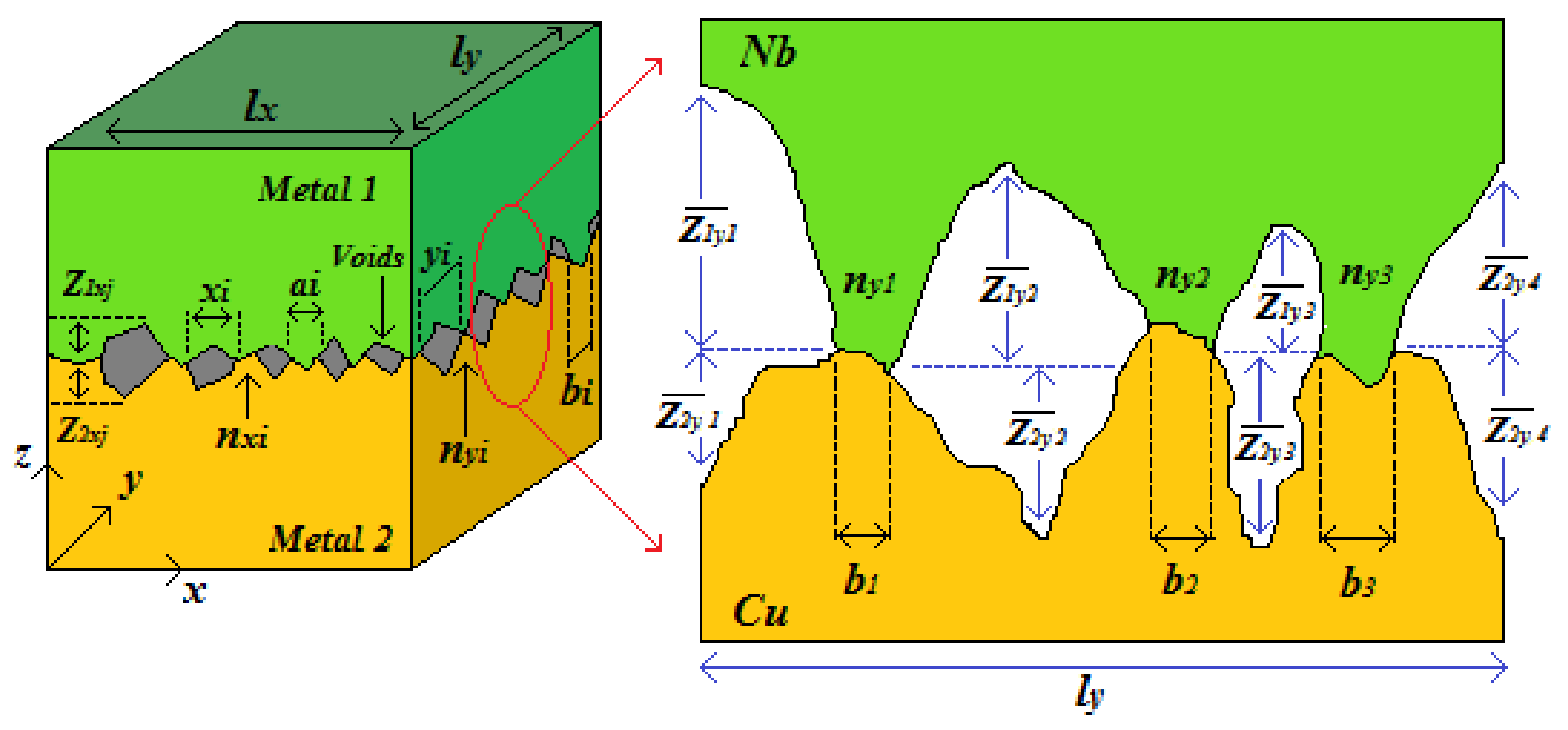
| δi | equivalent idealized gap thickness in terms of average height |
| , | average height of voids |
| j | subscript index for void number |
| np | number of contact points per unit area |
| Cei | electronic heat capacity of metal i |
| vFi | electron Fermi velocity of metal i |
| β | term describing the exponential decay of heat flux across the interface |
| RITR-B | ballistic ITR contribution |
| RITR-D | diffusive ITR contribution |
| kmin | thermal conductivity lower limit |
| νT | transversal speed of sound |
| νL | longitudinal speed of sound |
| na | number of density of atoms |
| kB | constant of Boltzmann |
| ReITR | effective interfacial thermal resistance |
| λe | effective mean free path of electrons |
| d | half metallic lamellae thickness |
References
- Chen, G. Thermal conductivity and ballistic-phonon transport in the cross-plane direction of superlattices. Phys. Rev. B 1998, 57, 14958–14973. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Koh, Y.K.; Bae, M.-H.; Cahill, D.G.; Pop, E. Heat Conduction across Monolayer and Few-Layer Graphenes. Nano Lett. 2010, 10, 4363–4368. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.; Poudel, N.; Cronin, S.B.; Shi, L. Effects of basal-plane thermal conductivity and interface thermal conductance on the hot spot temperature in graphene electronic devices. Appl. Phys. Lett. 2017, 110, 073104. [Google Scholar] [CrossRef]
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Yang, J.; Ziade, E.; Maragliano, C.; Crowder, R.; Wang, X.; Stefancich, M.; Chiesa, M.; Swan, A.K.; Schmidt, A.J. Thermal conductance imaging of graphene contacts. J. Appl. Phys. 2014, 116, 023515. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, L.-D. Promising Thermoelectric Bulk Materials with 2D Structures. Adv. Mater. 2017, 29, 1702676. [Google Scholar] [CrossRef]
- Zhao, L.-D.; Lo, S.-H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.M.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nat. Cell Biol. 2014, 508, 373–377. [Google Scholar] [CrossRef]
- Cao, Y.Q.; Zhao, X.B.; Zhu, T.J.; Zhang, X.B.; Tu, J.P. Syntheses and thermoelectric properties of Bi2Te3/Sb2Te3 bulk nanocomposites with laminated nanostructure. Appl. Phys. Lett. 2008, 92, 143106. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef]
- Ma, Y.; Hao, Q.; Poudel, B.; Lan, Y.; Yu, B.; Wang, D.; Chen, G.; Ren, Z. Enhanced Thermoelectric Figure-of-Merit in p-Type Nanostructured Bismuth Antimony Tellurium Alloys Made from Elemental Chunks. Nano Lett. 2008, 8, 2580–2584. [Google Scholar] [CrossRef]
- Costescu, R.M.; Cahill, D.G.; Fabreguette, F.H.; Sechrist, Z.A.; George, S.M. Ultra-Low Thermal Conductivity in W/Al2O3 Nanolaminates. Science 2004, 303, 989–990. [Google Scholar] [CrossRef]
- Kim, E.-K.; Kwun, S.-I.; Lee, S.-M.; Seo, H.; Yoon, J.-G. Thermal boundary resistance at Ge2Sb2Te5/ZnS:SiO2Ge2Sb2Te5/ZnS:SiO2 interface. Appl. Phys. Lett. 2000, 76, 3864–3866. [Google Scholar] [CrossRef]
- Dechaumphai, E.; Lu, D.; Kan, J.J.; Moon, J.; Fullerton, E.E.; Liu, Z.; Chen, R. Ultralow Thermal Conductivity of Multilayers with Highly Dissimilar Debye Temperatures. Nano Lett. 2014, 14, 2448–2455. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Tan, S.; Bozorg-Grayeli, E.; Kodama, T.; Asheghi, M.; Delgado, G.; Panzer, M.; Pokrovsky, A.; Wack, D.; Goodson, K.E. Phonon Dominated Heat Conduction Normal to Mo/Si Multilayers with Period below 10 nm. Nano Lett. 2012, 12, 3121–3126. [Google Scholar] [CrossRef]
- Dalkilic, A.S.; Celen, A.; Çebi, A.; Wongwises, S. Effect of Refrigerant Type and Insulation Thickness on Refrigeration Systems of Land and Sea Vehicles. Strojniški Vestnik J. Mech. Eng. 2016, 62, 252. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef]
- Okamoto, H. Cu-Nb (Copper-Niobium). J. Phase Equilibria Diffus. 2012, 33, 344. [Google Scholar] [CrossRef]
- Saito, Y.; Utsunomiya, H.; Tsuji, N.; Sakai, T. Novel ultra-high straining process for bulk materials—development of the accumulative roll-bonding (ARB) process. Acta Mater. 1999, 47, 579–583. [Google Scholar] [CrossRef]
- Yasuna, K.; Terauchi, M.; Otsuki, A.; Ishihara, K.; Shingu, P. Formation of nanoscale Fe/Ag multilayer by repeated press-rolling and its layer thickness dependence of magnetoresistance. Mater. Sci. Eng. A 2000, 285, 412–417. [Google Scholar] [CrossRef]
- Knezevic, M.; Nizolek, T.; Ardeljan, M.; Beyerlein, I.J.; Mara, N.A.; Pollock, T.M. Texture evolution in two-phase Zr/Nb lamellar composites during accumulative roll bonding. Int. J. Plast. 2014, 57, 16–28. [Google Scholar] [CrossRef]
- Chang, H.; Zheng, M.; Gan, W.; Wu, K.; Maawad, E.; Brokmeier, H. Texture evolution of the Mg/Al laminated composite fabricated by the accumulative roll bonding. Scr. Mater. 2009, 61, 717–720. [Google Scholar] [CrossRef]
- Hosseini, M.; Pardis, N.; Manesh, H.D.; Abbasi, M.; Kim, D.-I. Structural characteristics of Cu/Ti bimetal composite produced by accumulative roll-bonding (ARB). Mater. Des. 2017, 113, 128–136. [Google Scholar] [CrossRef]
- Mara, N.A.; Beyerlein, I.J. Review: Effect of bimetal interface structure on the mechanical behavior of Cu–Nb fcc–bcc nanolayered composites. J. Mater. Sci. 2014, 49, 6497–6516. [Google Scholar] [CrossRef]
- Carpenter, J.; Zheng, S.; Zhang, R.; Vogel, S.; Beyerlein, I.; Mara, N. Thermal stability of Cu–Nb nanolamellar composites fabricated via accumulative roll bonding. Philos. Mag. 2013, 93, 718–735. [Google Scholar] [CrossRef]
- Kang, K.; Wang, J.; Zheng, S.J.; Beyerlein, I.J. Minimum energy structures of faceted, incoherent interfaces. J. Appl. Phys. 2012, 112, 73501. [Google Scholar] [CrossRef]
- Clemens, B.M.; Eesley, G.L.; Paddock, C.A. Time-resolved thermal transport in compositionally modulated metal films. Phys. Rev. B 1988, 37, 1085–1096. [Google Scholar] [CrossRef]
- Wang, J.; Hoagland, R.; Misra, A. Mechanics of nanoscale metallic multilayers: From atomic-scale to micro-scale. Scr. Mater. 2009, 60, 1067–1072. [Google Scholar] [CrossRef]
- Wilson, R.B.; Cahill, D.G. Experimental Validation of the Interfacial Form of the Wiedemann-Franz Law. Phys. Rev. Lett. 2012, 108, 255901. [Google Scholar] [CrossRef]
- Gundrum, B.C.; Cahill, D.G.; Averback, R.S. Thermal conductance of metal-metal interfaces. Phys. Rev. B 2005, 72, 245426. [Google Scholar] [CrossRef]
- Savija, I.; Culham, J.R.; Yovanovich, M.M.; Marotta, E.E. Review of Thermal Conductance Models for Joints Incorporating Enhancement Materials. J. Thermophys. Heat Transf. 2003, 17, 43–52. [Google Scholar] [CrossRef]
- Little, W.A. The Transport of Heat between Dissimilar Solids at Low Temperatures. Can. J. Phys. 1959, 37, 334–349. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Reddy, P.; Castelino, K.; Majumdar, A. Diffuse mismatch model of thermal boundary conductance using exact phonon dispersion. Appl. Phys. Lett. 2005, 87, 211908. [Google Scholar] [CrossRef]
- Fenech, H.; Rohsenow, W.M. Prediction of Thermal Conductance of Metallic Surfaces in Contact. J. Heat Transf. 1963, 85, 15–24. [Google Scholar] [CrossRef]
- Gang, C. Ballistic-Diffusive Heat-Conduction Equations. Phys. Rev. Lett. 2001, 86, 2297–2300. [Google Scholar] [CrossRef]
- Fletcher, L.S.; Blanchard, D.G.; Kinnear, K.P. Thermal conductance of multilayered metallic sheets. J. Thermophys. Heat Transf. 1993, 7, 120–126. [Google Scholar] [CrossRef]
- Mayadas, A.F.; Shatzkes, M. Electrical-Resistivity Model for Polycrystalline Films: The Case of Arbitrary Reflection at External Surfaces. Phys. Rev. B 1970, 1, 1382. [Google Scholar] [CrossRef]
- Jin, J.S.; Lee, J.S.; Kwon, O. Electron effective mean free path and thermal conductivity predictions of metallic thin films. Appl. Phys. Lett. 2008, 92, 171910. [Google Scholar] [CrossRef]
- Nath, P.; Chopra, K.L. Thermal conductivity of copper films. Thin Solid Films 1974, 20, 53–62. [Google Scholar] [CrossRef]
- Kelemen, F. Pulse method for the measurement of the thermal conductivity of thin films. Thin Solid Films 1976, 36, 199–203. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]

| Sample | n (1028 m−3) | vT (m/s) | vL (m/s) | Kmin (W/mK) | Kexp (W/mK) |
|---|---|---|---|---|---|
| SiO2 | 6.63 | 3740 | 5980 | 1.21 | 1.35 |
| Al2O3 | 10.89 | 5800 | 9900 | 2.71 | 2.76 |
| Cu | 8.47 | 3720 | 4720 | 1.3 | - |
| Nb | 5.56 | 2092 | 5068 | 0.76 | - |
| a-Cu/Nb System | - | - | - | 0.95 | |
| Cu-Nb (n = 0) | - | - | - | - | 92.5 |
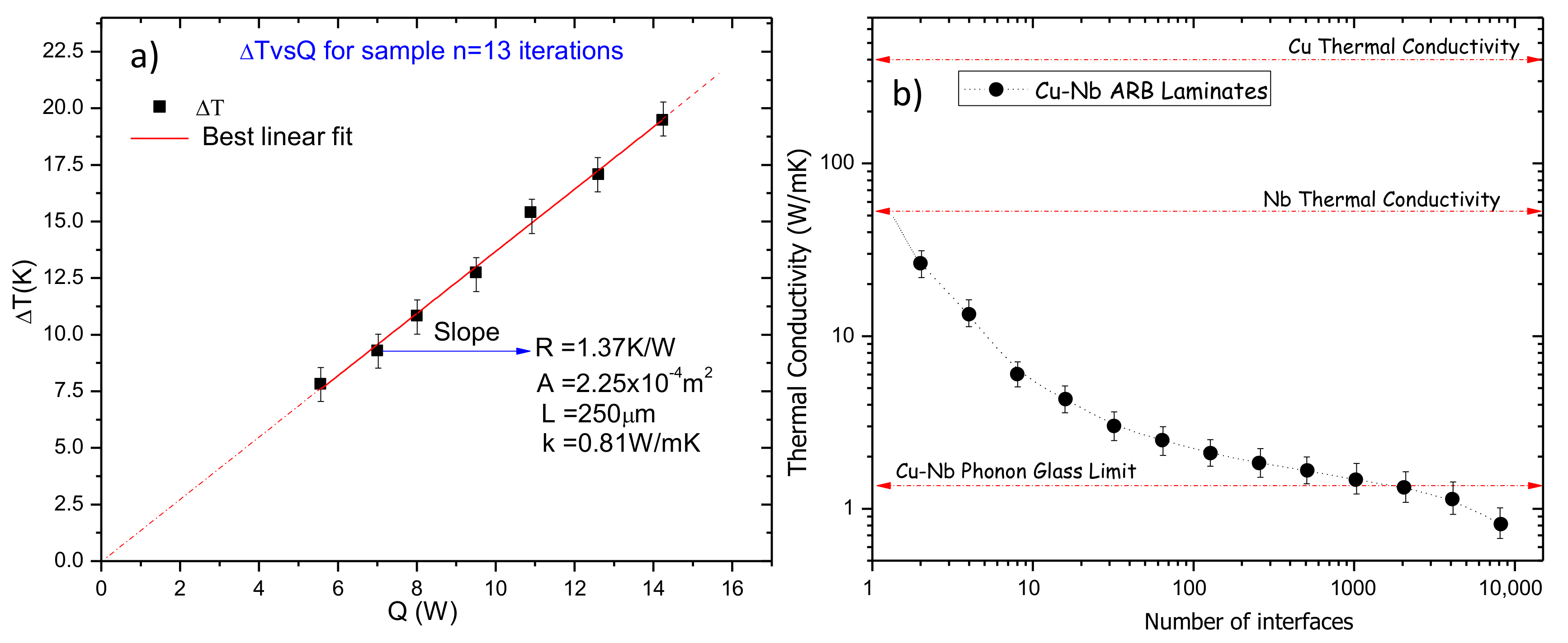
| Cu-Nb (n = 13) | - | - | - | - | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Pastor, F.A.; Montelongo-Vega, J.B.; Tovar-Padilla, M.V.; Cardona-Castro, M.A.; Alvarez-Quintana, J. Robust Metallic Nanolaminates Having Phonon-Glass Thermal Conductivity. Materials 2020, 13, 4954. https://doi.org/10.3390/ma13214954
García-Pastor FA, Montelongo-Vega JB, Tovar-Padilla MV, Cardona-Castro MA, Alvarez-Quintana J. Robust Metallic Nanolaminates Having Phonon-Glass Thermal Conductivity. Materials. 2020; 13(21):4954. https://doi.org/10.3390/ma13214954
Chicago/Turabian StyleGarcía-Pastor, Francisco Alfredo, Josué Benjamín Montelongo-Vega, Marco Vinicio Tovar-Padilla, María Antonia Cardona-Castro, and Jaime Alvarez-Quintana. 2020. "Robust Metallic Nanolaminates Having Phonon-Glass Thermal Conductivity" Materials 13, no. 21: 4954. https://doi.org/10.3390/ma13214954
APA StyleGarcía-Pastor, F. A., Montelongo-Vega, J. B., Tovar-Padilla, M. V., Cardona-Castro, M. A., & Alvarez-Quintana, J. (2020). Robust Metallic Nanolaminates Having Phonon-Glass Thermal Conductivity. Materials, 13(21), 4954. https://doi.org/10.3390/ma13214954





