Simulation and Experimental Study of Dynamical Recrystallization Kinetics of TB8 Titanium Alloys
Abstract
1. Introduction
2. Experiment
3. Results and Discussion
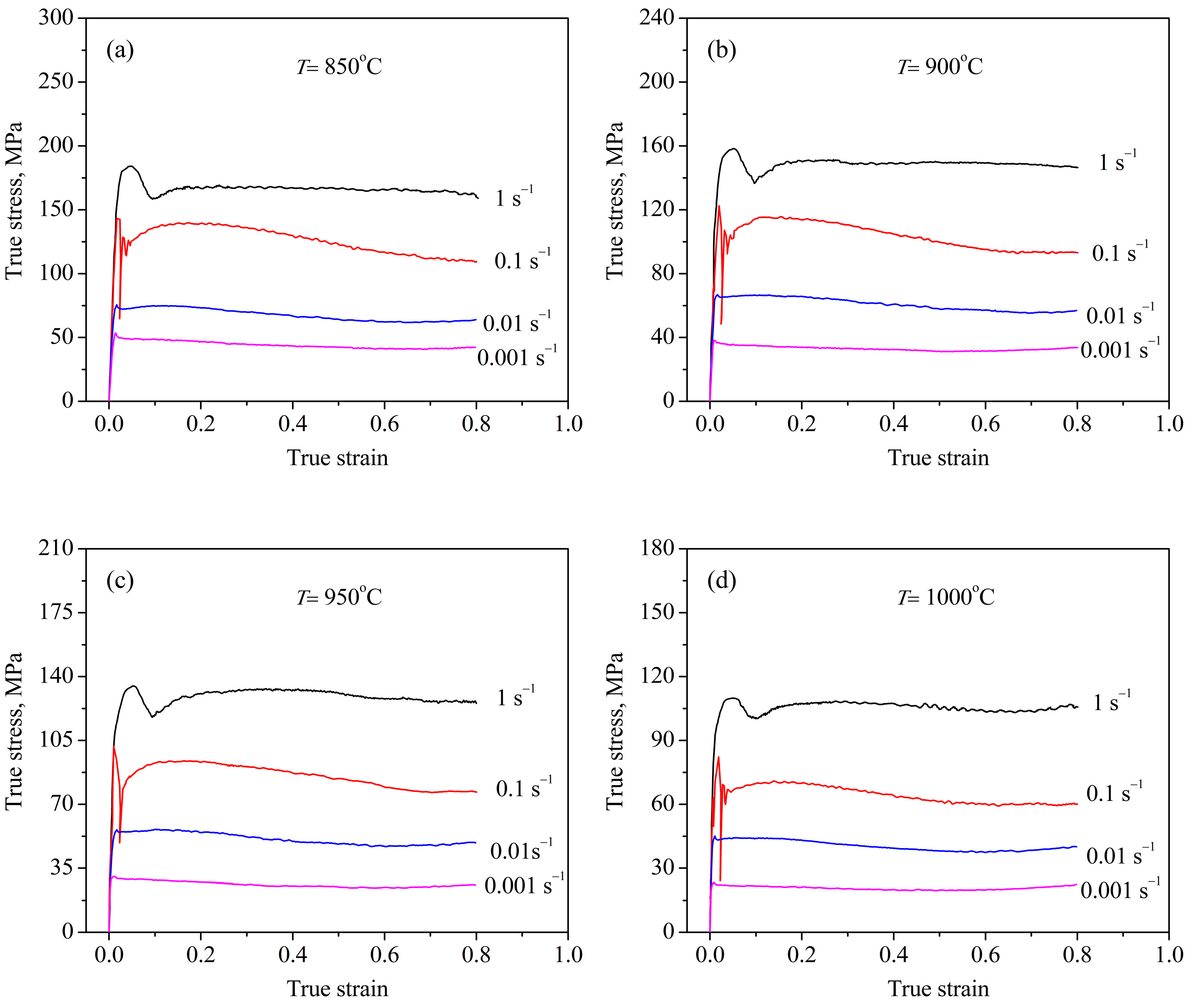
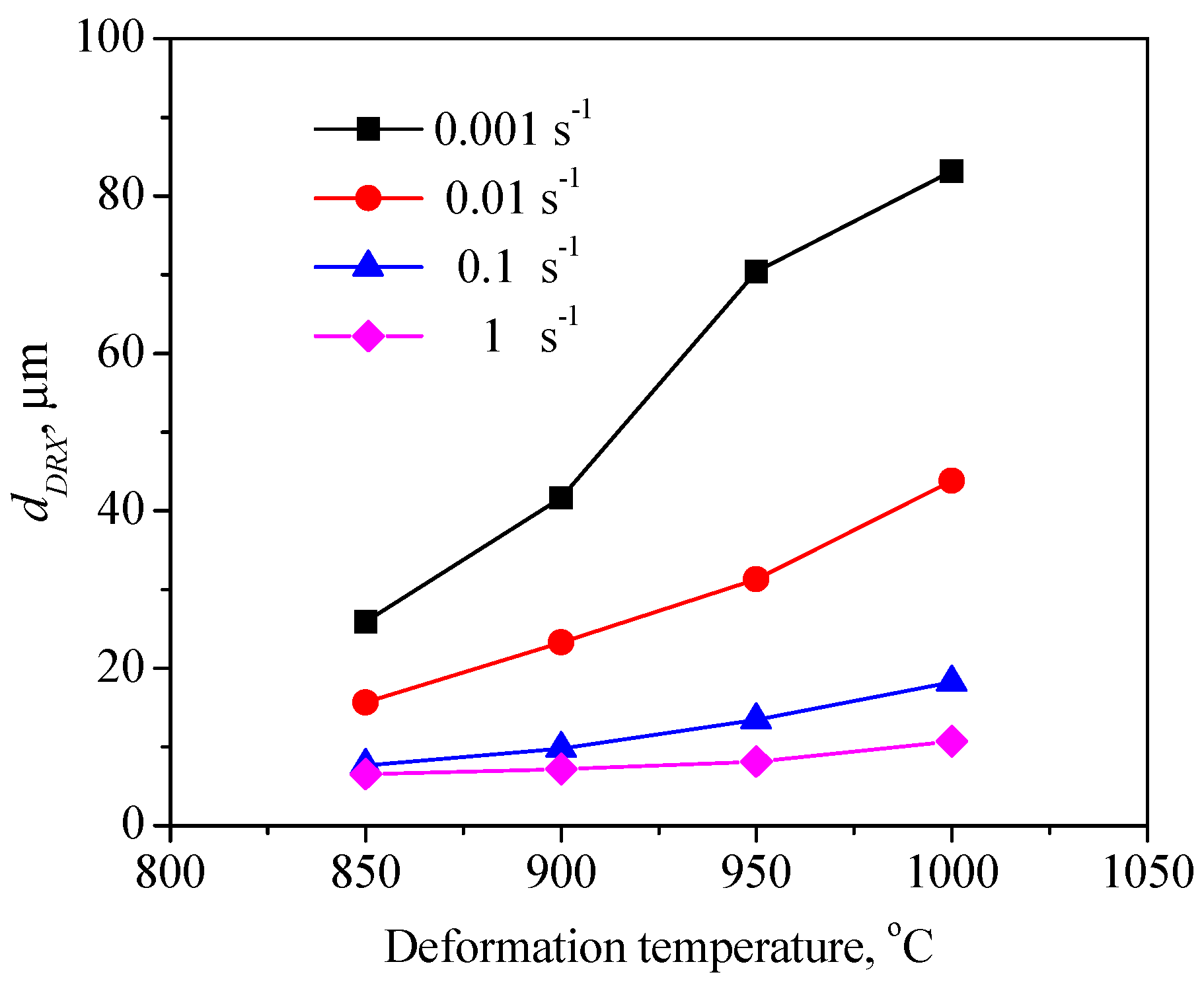
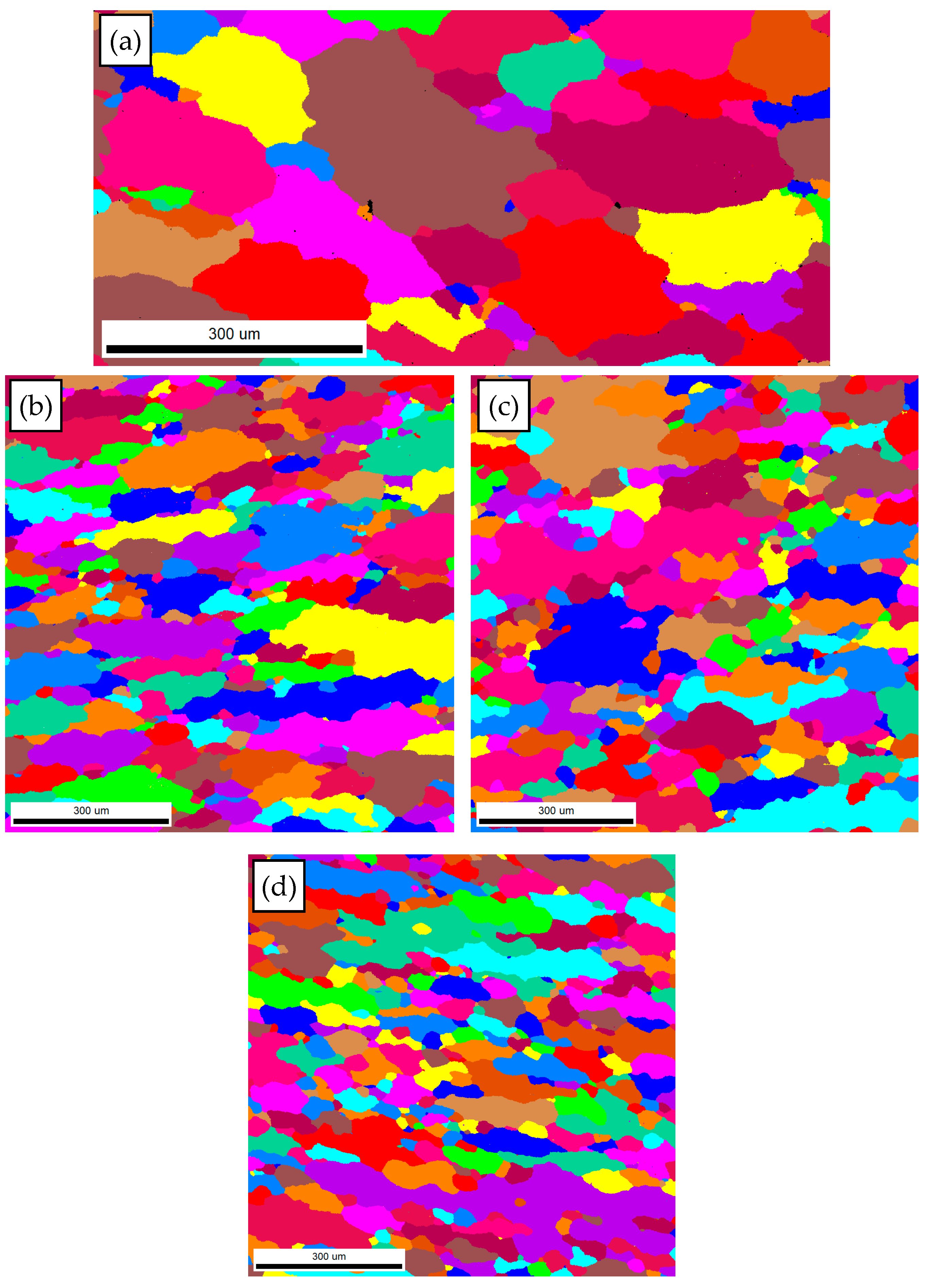
3.1. The Flow Behavior and Deformed Microstructure
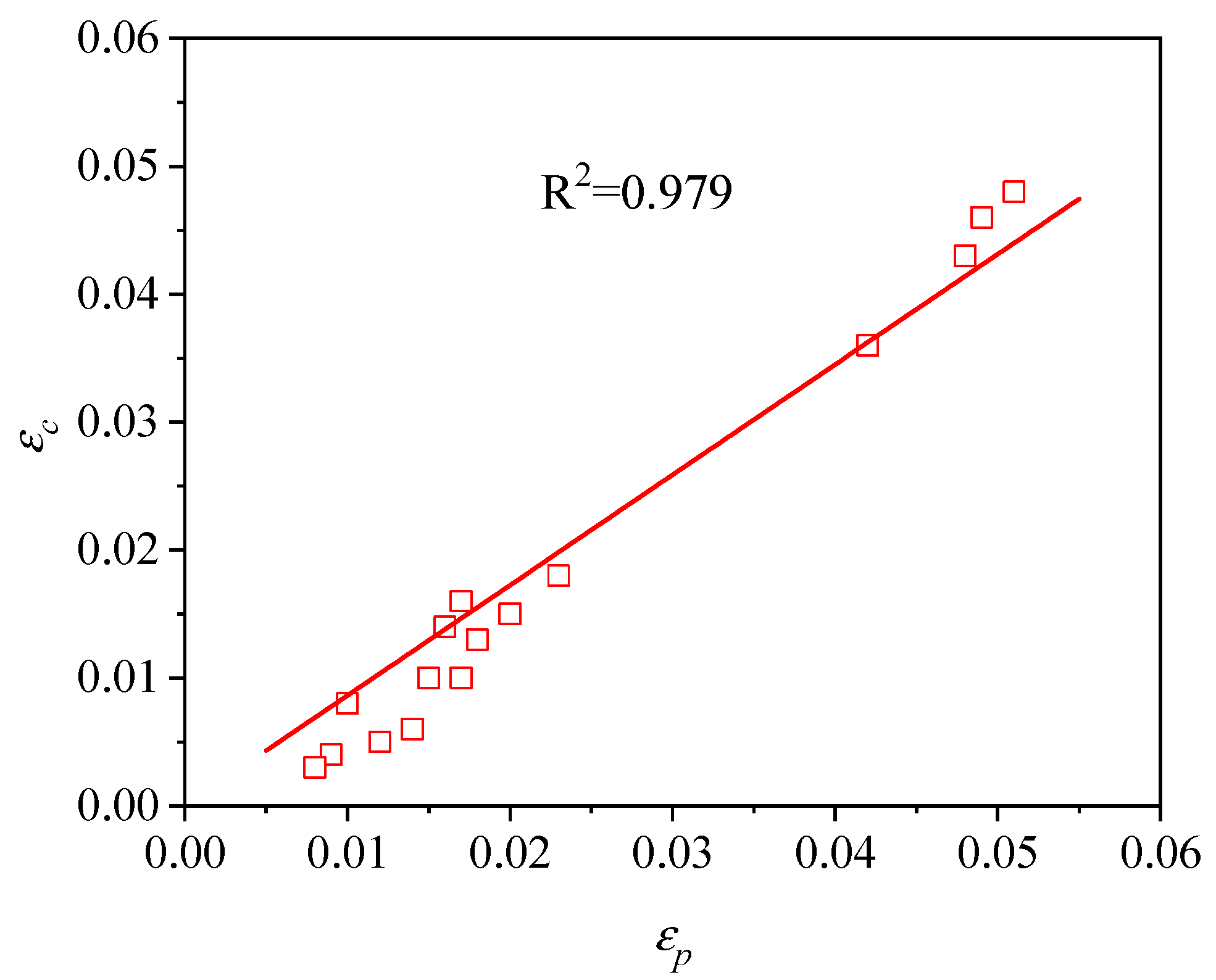
3.2. Peak Strain and Critical Strain
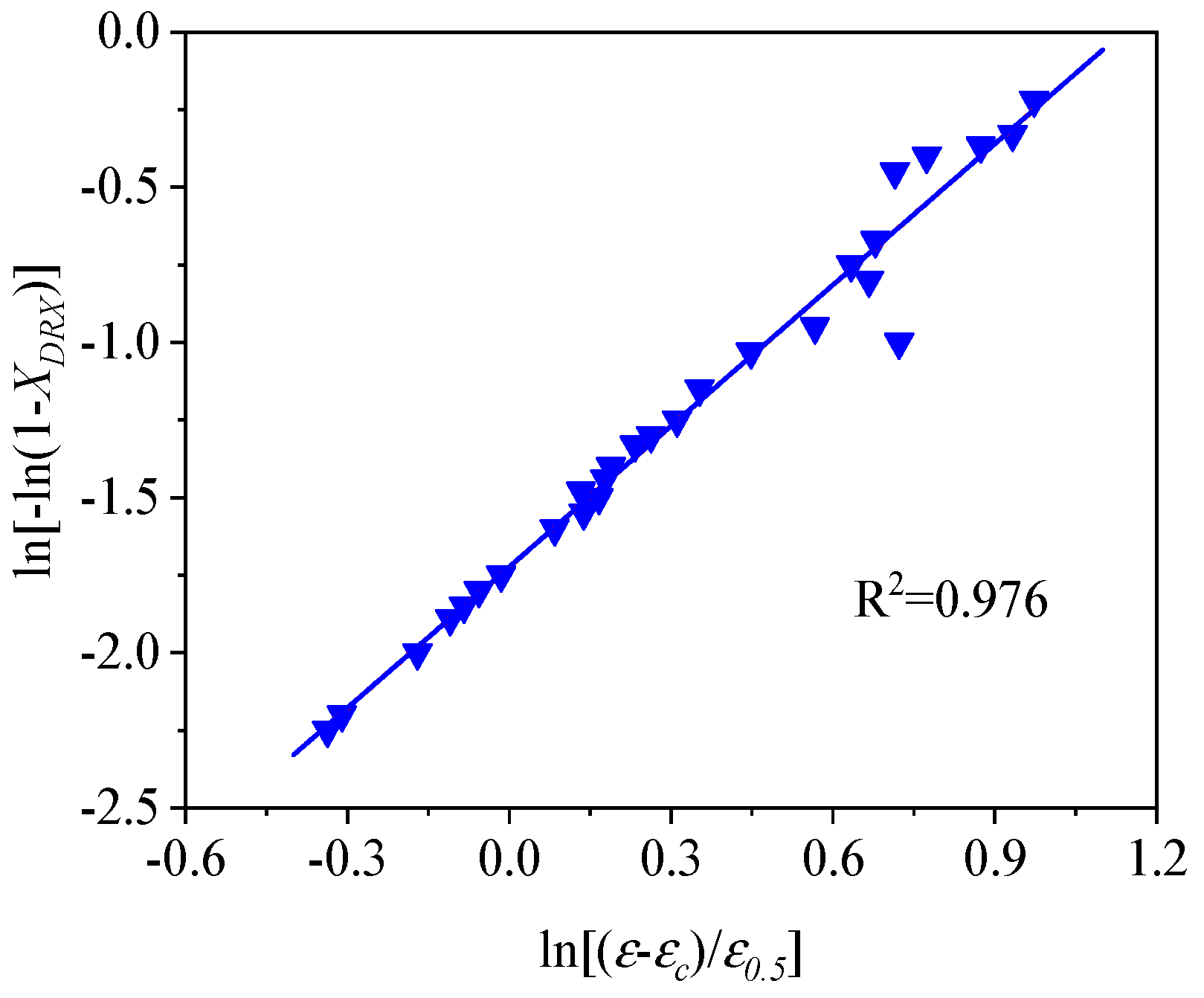
3.3. Kinetics Model of DRX
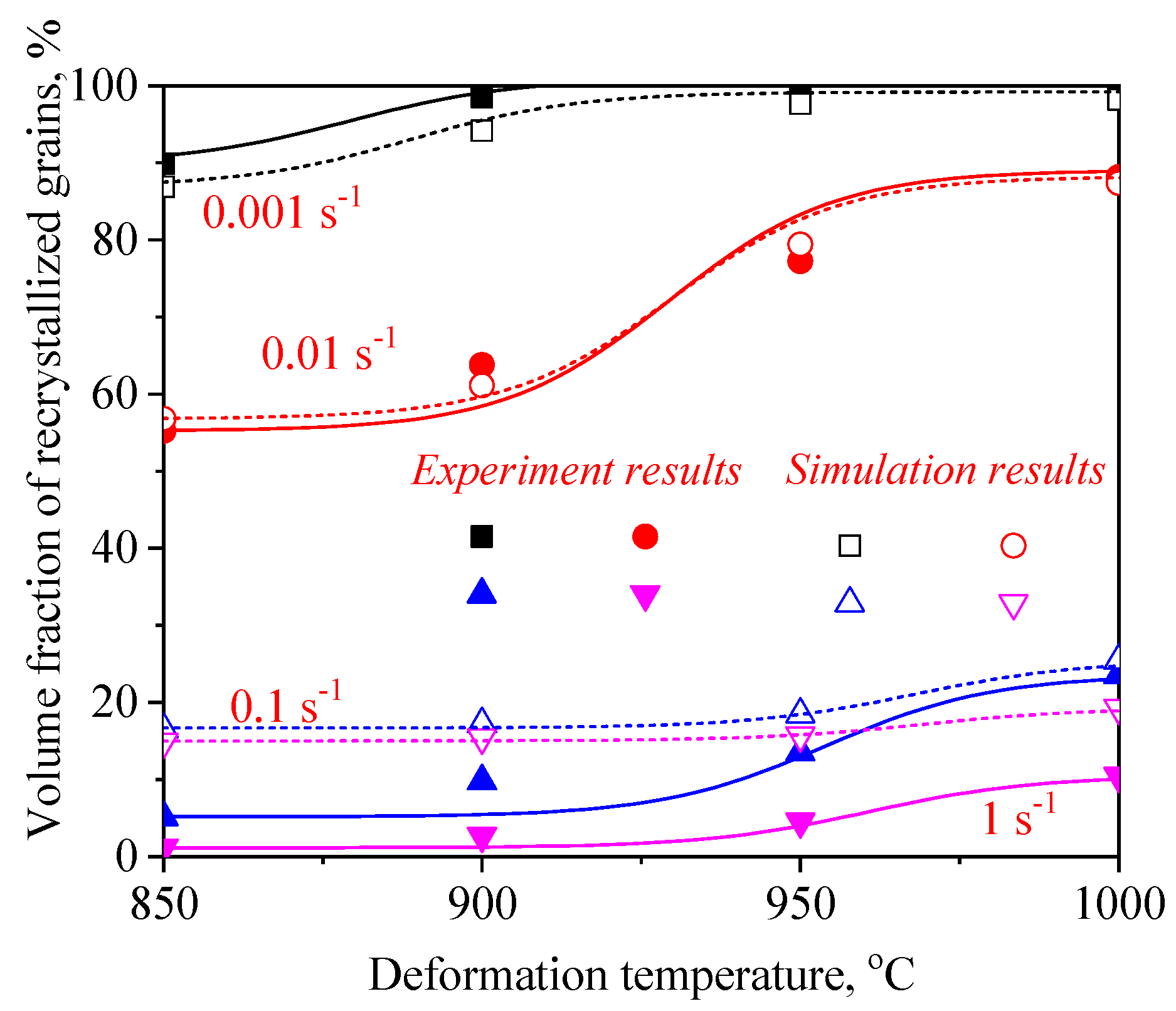
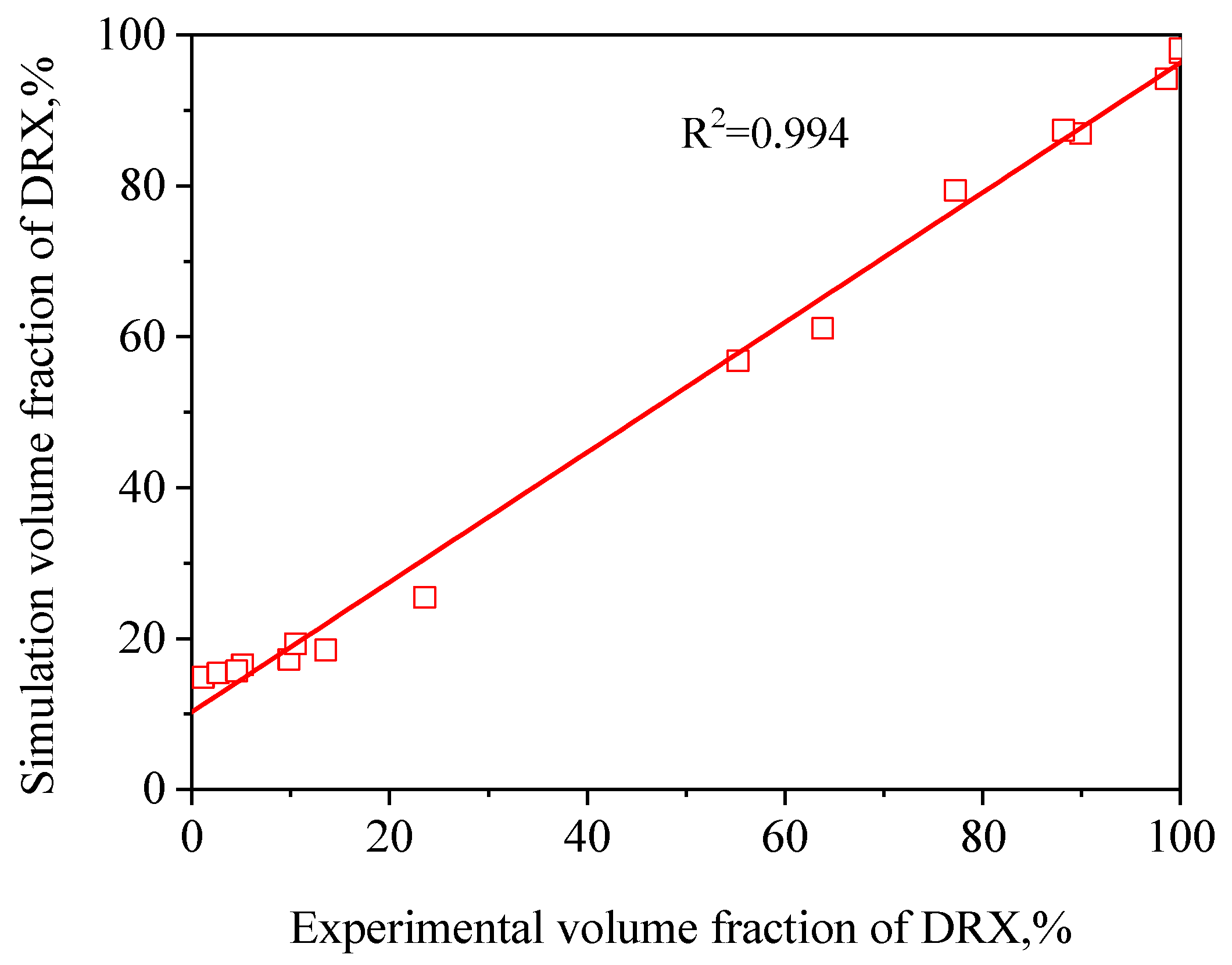
3.4. FE Simulation of DRX Behavior
4. Conclusions
- (1)
- The DRX behavior of TB8 titanium alloys was drastically influenced by the processing parameters. The rising deformation temperature and reducing strain rate resulted in an increase in the and ;
- (2)
- Based on the true stress–strain curves obtained from experimental tests, the and kinetics models of DRX were established, which were expressed as
- (3)
- In terms of the true stress–strain curve gained from isothermal tests and the developed models for the DRX of TB8 titanium alloy, the isothermal forging process of the cylindrical samples was simulated by the DEFORM-3D software. The distributions of effective strain and DRX volume fraction were analyzed for TB8 titanium alloys during hot deformation. The maximum values of the effective strain and were distributed in the center of the section of samples along the forging axis under a given deformation condition;
- (4)
- The value of the correlation coefficient was respectively 0.973 and 0.994 for the and between the experimental and FE simulation results, while the average absolute relative error value for the and was respectively 3.2% and 17.0%, which presents the good prediction capabilities of the established FEM model for TB8 titanium alloy during hot working.
Author Contributions
Funding
Conflicts of Interest
References
- Chen, X.F.; Tang, B.; Liu, Y.; Xue, X.Y.; Li, L.; Kou, H.C.; Li, J.S. Dynamic recrystallization behavior of the Ti-48Al-2Cr-2Nb alloy during isothermal hot deformation. Prog. Nat. Sci. Mater. Int. 2019, 29, 587–594. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, H.; Wan, Z.P.; Ren, L.L.; Hu, L.X. Establishment of a novel constitutive model considering dynamic recrystallization behavior of Ti-22Al-25Nb alloy during hot deformation. Trans. Nonferrous Met. Soc. China 2019, 29, 546–557. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Hot Deformation and Dynamic Restoration. In Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2004; Chapter 13; pp. 415–450. [Google Scholar]
- Ouyang, D.L.; Fu, M.W.; Lu, S.Q. Study on the dynamic recrystallization behavior of Ti-alloy Ti-10V-2Fe-3V in β processing via experiment and simulation. Mater. Sci. Eng. A 2014, 619, 26–34. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, L.; Dong, J.X.; Zhang, M.C.; Yao, Z.H. The recrystallization model and microstructure prediction of alloy 690 during hot deformation. Mater. Des. 2016, 104, 162–173. [Google Scholar] [CrossRef]
- Li, X.L.; Li, X.L.; Zhou, H.T.; Zhou, X.; Li, F.B.; Liu, Q. Simulation of dynamic recrystallization in AZ80 magnesium alloy using cellular automaton. Comput. Mater. Sci. 2017, 140, 95–104. [Google Scholar] [CrossRef]
- Irani, M.; Joun, M. Determination of JMAK dynamic recrystallization parameters through FEM optimization techniques. Comput. Mater. Sci. 2018, 142, 178–184. [Google Scholar] [CrossRef]
- Sun, Y.; Feng, X.Y.; Hu, L.X.; Zhang, H.; Zhang, H.Z. Characterization on hot deformation behavior of Ti-22Al-25Nb alloy using a combination of 3D processing maps and finite element simulation method. J. Alloys Compd. 2018, 753, 256–271. [Google Scholar] [CrossRef]
- Donati, L.; Bandini, C.; Reggiani, B.; Tomesani, L. Prediction and validation of grain shape evolution by 3D FEM simulations of a real industrial profile. Mater. Today 2019, 10, 255–262. [Google Scholar] [CrossRef]
- Quan, G.Z.; Shi, R.J.; Zhao, J.; Liu, Q.; Xiong, W.; Qiu, H.M. Modeling of dynamic recrystallization volume fraction evolution for AlCu4SiMg alloy and its application in FEM. Trans. Nonferrous Met. Soc. China 2019, 29, 1138–1151. [Google Scholar] [CrossRef]
- Wu, H.; Xu, W.C.; Wang, S.B.; Yang, Z.Z.; Chen, Y.; Teng, B.G.; Shan, D.B.; Guo, B. A cellular automaton coupled FEA model for hot deformation behavior of AZ61 magnesium alloys. J. Alloys Compd. 2020, 816, 152562. [Google Scholar] [CrossRef]
- Xu, T.W.; Li, J.S.; Zhang, F.S.; Wang, F.Y.; Liu, X.H.; Feng, Y. Microstructure evolution during cold-deformation and aging response after annealing of TB8 titanium alloy. Rare Metal Mater. Eng. 2016, 45, 575–580. [Google Scholar] [CrossRef]
- Bo, T.; Bin, T.; Han, F.B.; Yang, G.J.; Li, J.S. Influence of strain rate on stress induced martensitic transformation in β solution treated TB8 alloy. J. Alloys Compd. 2013, 565, 1–5. [Google Scholar] [CrossRef]
- Duan, Y.P.; Li, P.; Xue, K.M.; Zhang, Q.; Wang, X.X. Flow behavior and microstructure evolution of TB8 alloy during hot deformation process. Trans. Nonferrous Met. Soc. China 2007, 17, 1199–1204. [Google Scholar] [CrossRef]
- Liu, Q. A simple and rapid method for determining orientations and misorientations of crystalline specimens in TEM. Ultramicroscopy 1995, 60, 81–89. [Google Scholar] [CrossRef]
- Sachtleber, M.; Zhao, Z.; Raabe, D. Experimental investigation of plastic grain interaction. Mater. Sci. Eng. A 2002, 336, 81–87. [Google Scholar] [CrossRef]
- Tan, Y.B.; Wang, X.M.; Ma, M.; Zhang, J.X.; Liu, W.C.; Fu, R.D.; Xiang, S. A study on microstructure and mechanical properties of AA 3003 aluminum alloy joints by underwater friction stir welding. Mater. Charact. 2017, 127, 41–52. [Google Scholar] [CrossRef]
- Mcqueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of dynamic recrystallization in constant strain rate hot deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Prediction of the critical conditions for initiation of dynamic recrystallization. Mater. Des. 2010, 31, 1174–1179. [Google Scholar] [CrossRef]
- Wang, K.L.; Fu, M.W.; Lu, S.Q.; Li, X. Study of the dynamic recrystallization of Ti-6.5Al-3.5Mo-1.5Zr-0.3Si alloy in β-forging process via Finite Element Method modeling and microstructure characterization. Mater. Des. 2011, 32, 1283–1291. [Google Scholar] [CrossRef]
- Devadas, C.; Samarasekera, I.V.; Hawbolt, E.B. The thermal and metallurgical state of steel strip during hot rolling, Part III. Microstructural evolution. Metall. Trans. A 1991, 22, 335–349. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wu, X.Y.; Chen, X.M.; Chen, J.; Wen, D.X.; Zhang, J.L.; Li, L.T. EBSD study of a hot deformed nickel-based superalloy. J. Alloys Compd. 2015, 640, 101–113. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization of single-phase alloys. In Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2004; Chapter 7; pp. 251–257. [Google Scholar]
- Wan, Z.P.; Sun, Y.; Hu, L.X.; Yu, H. Experimental study and numerical simulation of dynamic recrystallization behavior of TiAl-based alloy. Mater. Des. 2017, 122, 11–20. [Google Scholar] [CrossRef]
- Li, X.C.; Duan, L.L.; Li, J.W.; Wu, X.C. Experimental study and numerical simulation of dynamic recrystallization behavior of a micro-alloyed plastic mold steel. Mater. Des. 2015, 66, 309–320. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, F.G.; Li, Q.H.; Li, H.Q.; Li, Z. Research on the dynamic recrystallization kinetics of Aermet100 steel. Mater. Sci. Eng. A 2010, 527, 2350–2355. [Google Scholar] [CrossRef]
- Sellars, C.M. Modelling microstructural development during hot rolling. J. Mater. Sci. Technol. 1990, 6, 1072–1081. [Google Scholar] [CrossRef]
- Wu, H.; Liu, M.X.; Wang, Y.; Huang, Z.Q.; Tan, G.; Yang, L. Experimental study and numerical simulation of dynamic recrystallization for a FGH96 superalloy during isothermal compression. J. Mater. Res. Technol. 2020, 9, 5090–5104. [Google Scholar] [CrossRef]
- Luo, S.Y.; Wang, Q.; Zhang, P.; Li, J.; Liu, Q.L. Effect of friction conditions on phase transformation characteristics in hot forging process of Ti-6Al-4V turbine blade. J. Mater. Res. Technol. 2020, 9, 2107–2115. [Google Scholar] [CrossRef]
- Meng, Q.G.; Bai, C.G.; Xu, D.S. Flow behavior and processing map for hot deformation of ATI425 titanium alloy. J. Mater. Sci. Technol. 2018, 34, 679–688. [Google Scholar] [CrossRef]





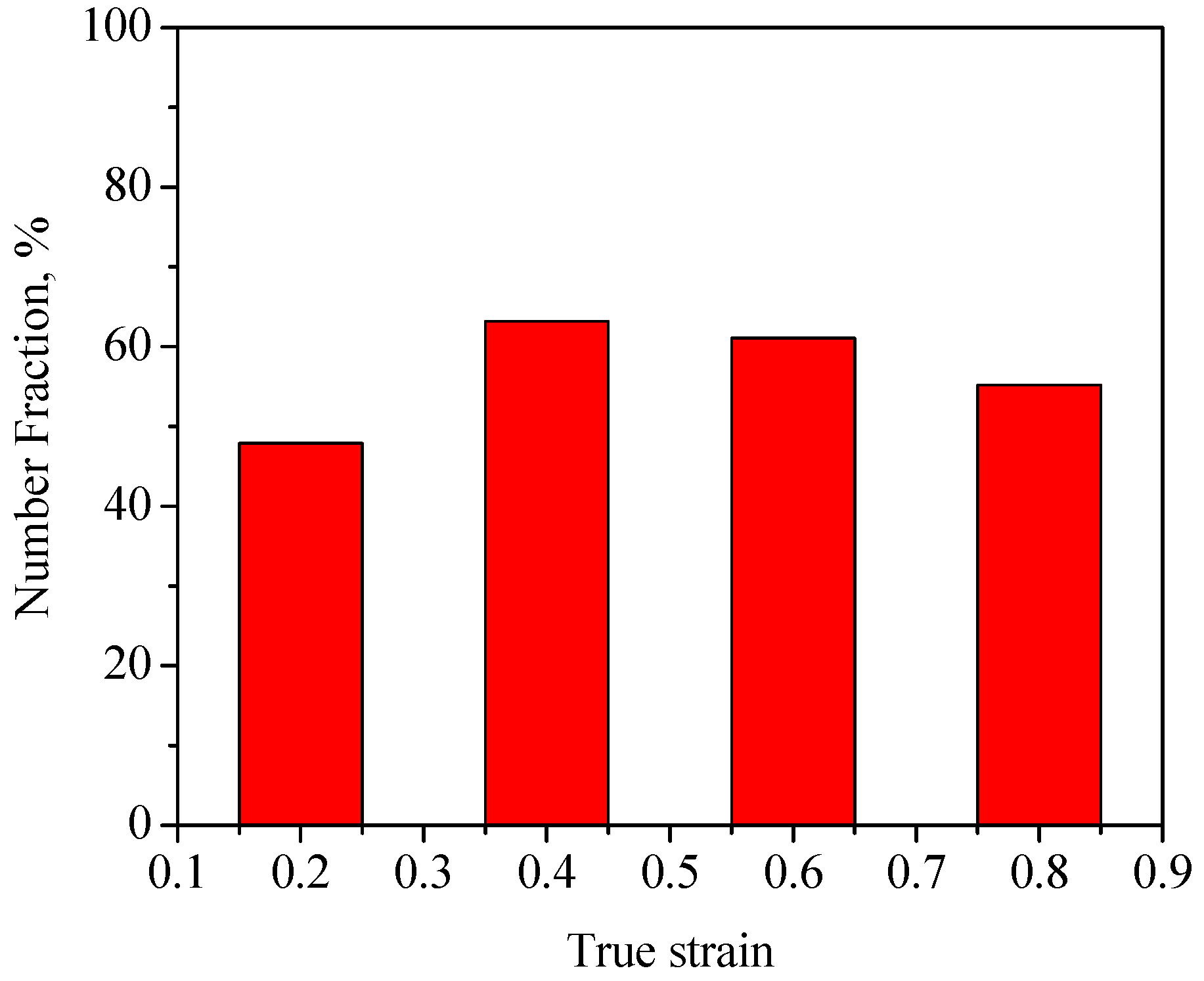
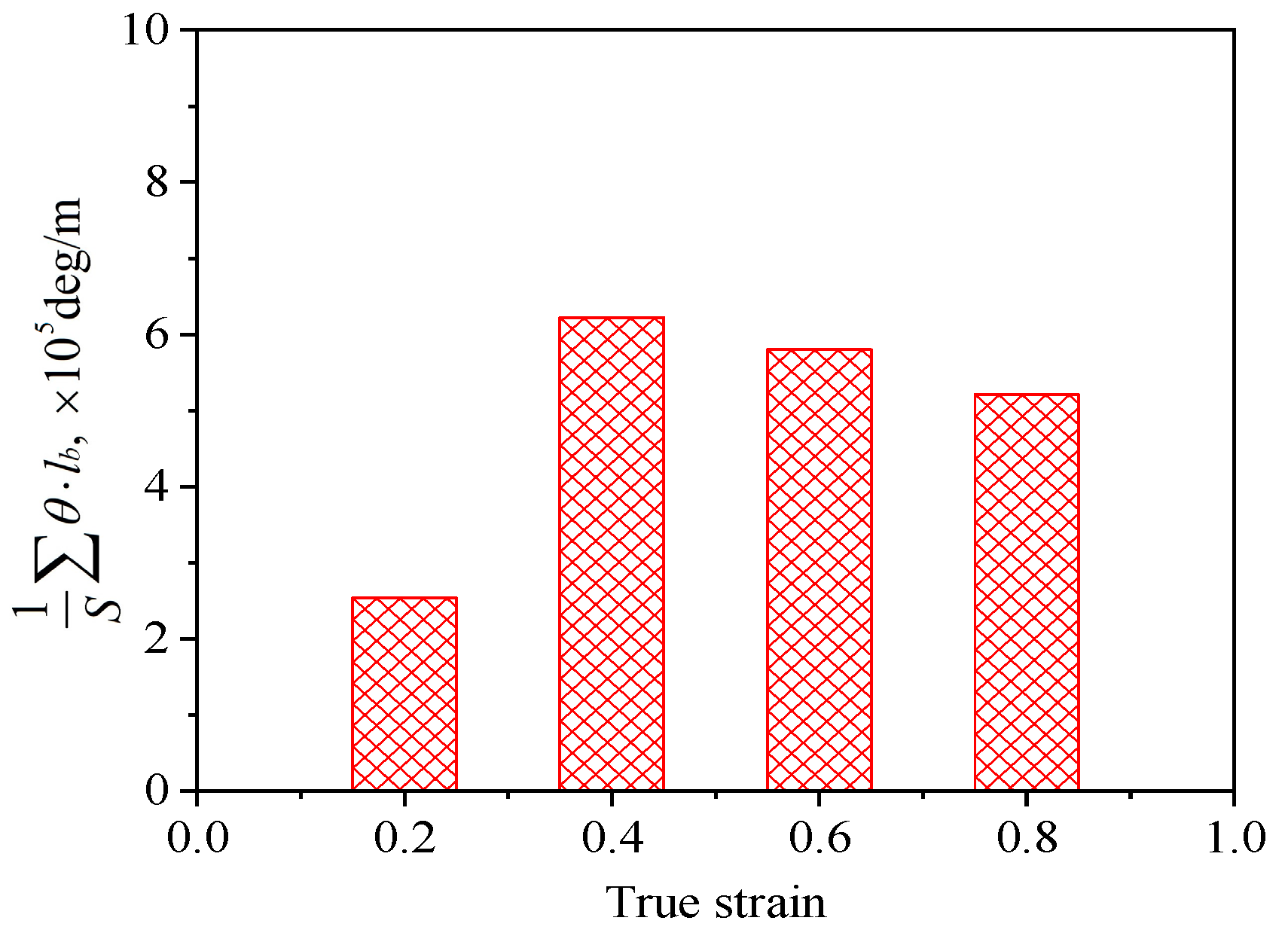
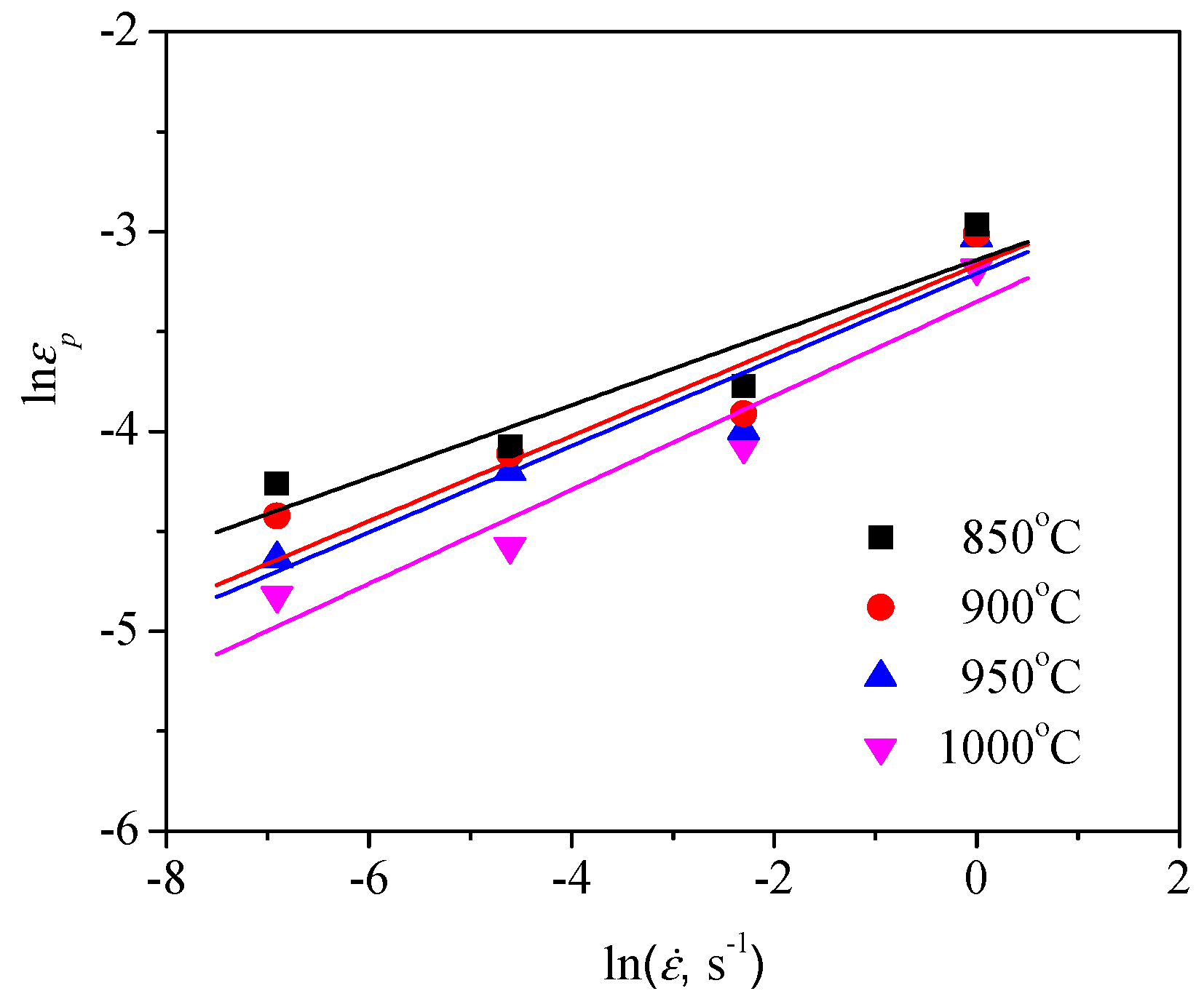
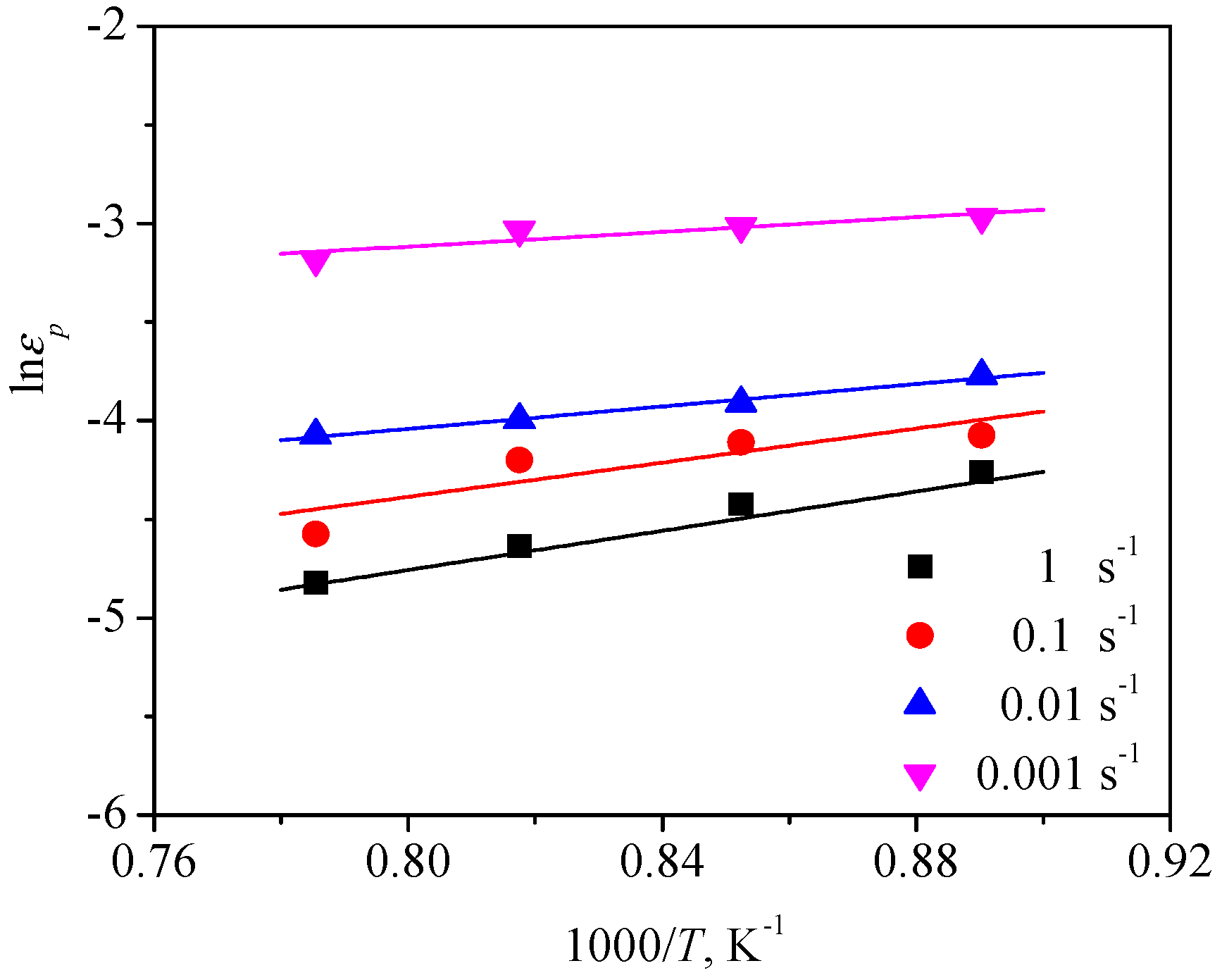




| Mo | Al | Nb | Si | Fe | C | N | O | H | Ti |
|---|---|---|---|---|---|---|---|---|---|
| 14.5 | 2.9 | 2.85 | 0.19 | 0.07 | 0.02 | 0.02 | 0.09 | 0.002 | Bal |
| Temperature | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 s−1 | 0.1 s−1 | 0.01 s−1 | 0.001 s−1 | 1 s−1 | 0.1 s−1 | 0.01 s−1 | 0.001 s−1 | |
| 850 °C | 0.051 | 0.023 | 0.017 | 0.014 | 0.048 | 0.018 | 0.016 | 0.006 |
| 900 °C | 0.049 | 0.02 | 0.016 | 0.012 | 0.046 | 0.015 | 0.014 | 0.005 |
| 950 °C | 0.048 | 0.018 | 0.015 | 0.009 | 0.043 | 0.013 | 0.010 | 0.004 |
| 1000 °C | 0.042 | 0.017 | 0.010 | 0.008 | 0.036 | 0.01 | 0.008 | 0.003 |
| Strain Rate/s−1 | Temperature/°C | Effective Strain | |||
|---|---|---|---|---|---|
| 850 | 900 | 950 | 1000 | ||
| 0.001 |  | 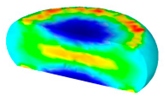 | 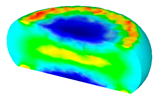 | 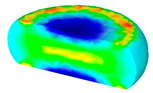 |  |
| 0.01 | 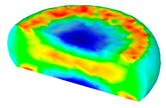 | 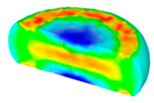 |  | 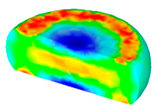 | |
| 0.1 | 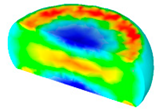 | 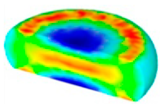 | 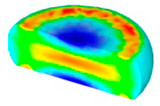 |  | |
| 1 |  | 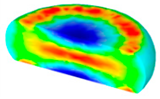 |  |  | |
| Strain Rate/s−1 | Temperature/°C | XDRX | |||
|---|---|---|---|---|---|
| 850 | 900 | 950 | 1000 | ||
| 0.001 |  | 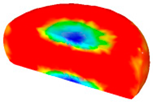 | 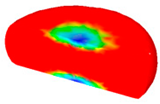 | 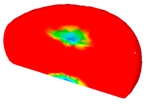 |  |
| 0.01 | 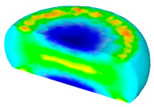 | 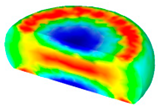 |  | 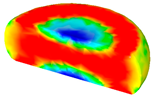 | |
| 0.1 |  |  |  | 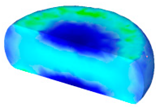 | |
| 1 |  |  | 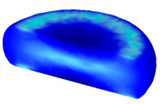 | 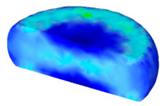 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Yang, Q.; Tan, Y.; Ma, M.; Xiang, S.; Zhao, F. Simulation and Experimental Study of Dynamical Recrystallization Kinetics of TB8 Titanium Alloys. Materials 2020, 13, 4429. https://doi.org/10.3390/ma13194429
Zhang W, Yang Q, Tan Y, Ma M, Xiang S, Zhao F. Simulation and Experimental Study of Dynamical Recrystallization Kinetics of TB8 Titanium Alloys. Materials. 2020; 13(19):4429. https://doi.org/10.3390/ma13194429
Chicago/Turabian StyleZhang, Wenwei, Qiuyue Yang, Yuanbiao Tan, Min Ma, Song Xiang, and Fei Zhao. 2020. "Simulation and Experimental Study of Dynamical Recrystallization Kinetics of TB8 Titanium Alloys" Materials 13, no. 19: 4429. https://doi.org/10.3390/ma13194429
APA StyleZhang, W., Yang, Q., Tan, Y., Ma, M., Xiang, S., & Zhao, F. (2020). Simulation and Experimental Study of Dynamical Recrystallization Kinetics of TB8 Titanium Alloys. Materials, 13(19), 4429. https://doi.org/10.3390/ma13194429






