Nonlinear Analysis of Compressed Concrete Elements Reinforced with FRP Bars
Abstract
:1. Introduction
- Glass fibers—glass fiber reinforced polymer (GFRP);
- Carbon fibers—carbon fiber reinforced polymer (CFRP);
- Aramid fibers—aramid fiber reinforced polymer (AFRP);
- Basalt fibers—basalt fiber reinforced polymer (BFRP);
- Hybrid (e.g., carbon/basalt) fibers—hybrid fiber reinforced polymer (HFRP).
2. Materials and Preparation of the Specimens
3. Methods
3.1. Experimental Investigation
3.2. Analytical Method
- fcm—compressive strength of concrete (32.8 MPa);
- n—2 for concrete not higher class than C50/60;
- εc2—minimum value of strain, for which the stresses gain compressive strength value, 2‰ for concrete not higher class than C50/60;
- εcu2—maximum value of concrete strain, 3.5‰ for concrete not higher class than C50/60.
- N—normal force;
- M—bending moment;
- Asi—area of singular bar;
- σsi—stress value in a singular bar;
- n—quantity of bars;
- σc—stress value in concrete;
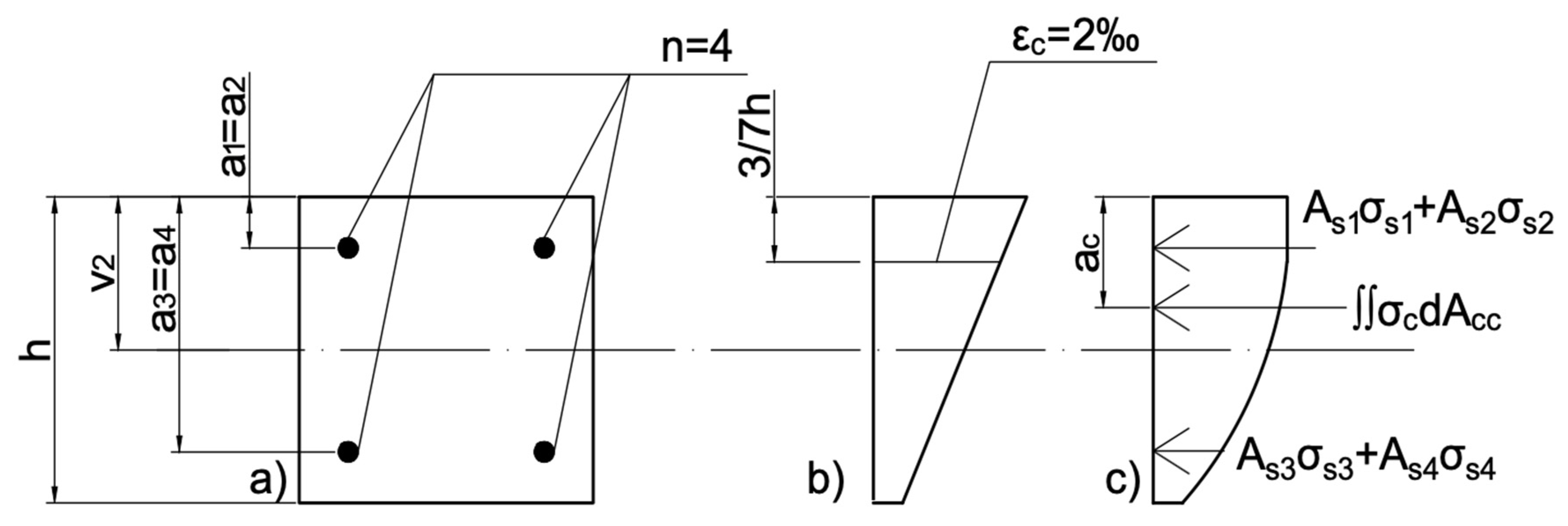
- Acc—compressed concrete area;
- ν2—the distance from the center of gravity of the concrete cross-section to the most compressed edge;
- ai—spacing of reinforcement from the most compressed section edge;
- ac—the location of the resultant force of the compressive stress block taken from the area Acc, measured from the compressed edge of the cross-section.
- without considering the influence of composite bars (cross-section in the calculations consisting of concrete only—values given in brackets in Table 3);
- considering the influence of composite bars (assuming the value of stresses in the bars on the basis of their modulus of elasticity—as for metallic bars before gaining yield strength).
- x—distance from the point on the height of the cross-section to the most compressed section edge;
- h—height of the cross-section;
- εc2 = 2‰;
- εcu2 = 3.5‰;
- a—calibrating parameter.
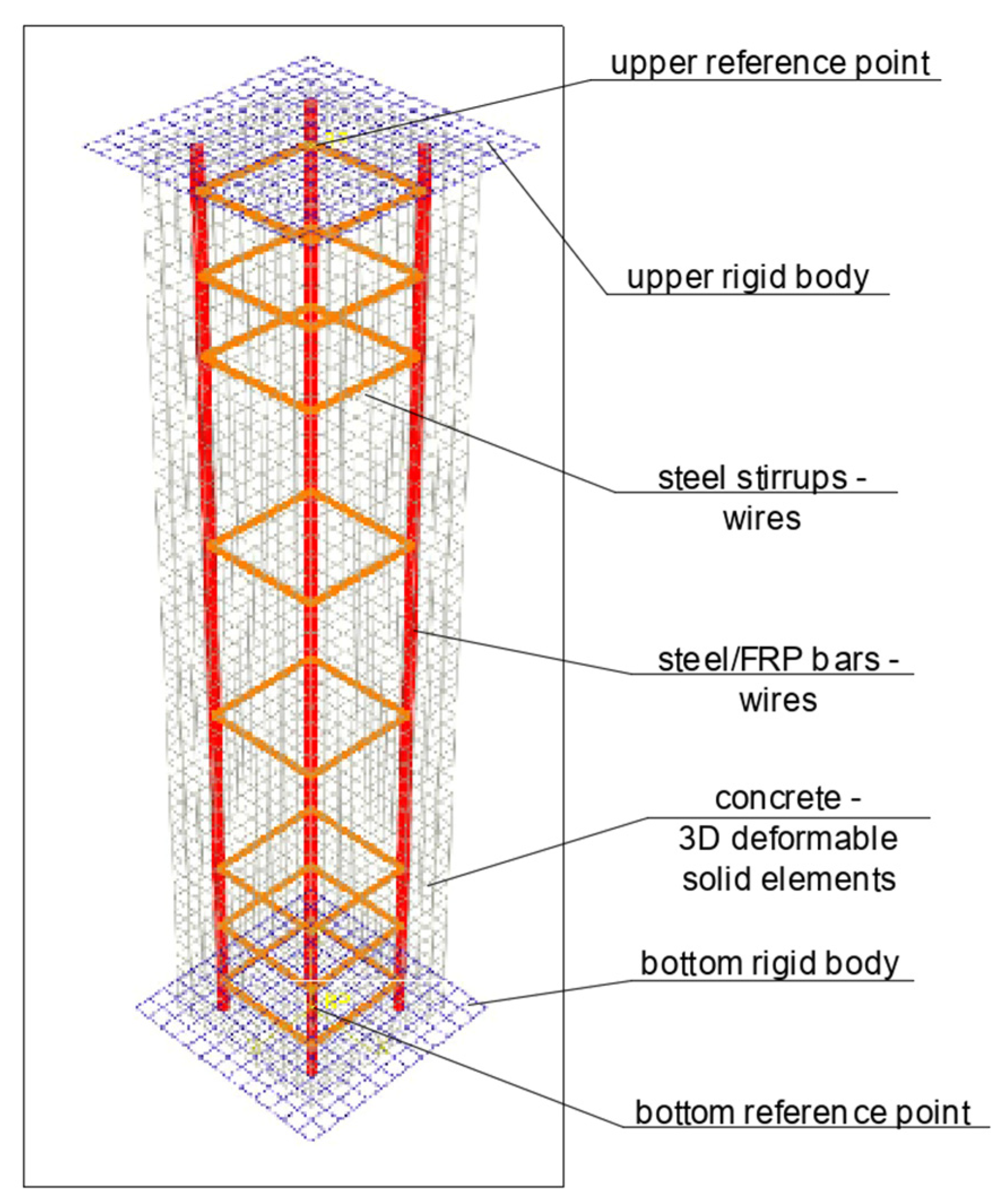
3.3. Numerical Analysis
- ;
- —value of strain, for which the maximum value of stress occurs (2.1‰ for the concrete with the medium value of strength ~33 MPa);
- —maximum value of a concrete strain (3.5‰ for concrete not higher class than C50/60);
- .
- Dilatation angle—assumed value in following FEM analysis: 36;
- Eccentricity—0.1;
- fb0/fc0—1.16;
- κ—0.667;
- Viscosity parameter—0.
- E0—undamaged modulus of deformation;
- —compression strain;
- —tensile strain;
- —plastic compression strain;
- —plastic tensile strain.
- Values of reaction force as a function of displacement in upper reference point;
- Values of stresses in the middle of the longitudinal reinforcement bar as a function of reaction in upper reference point;
- Location of damaged zones through the test duration.
4. Results
4.1. Failure Load
- Achieved during the experimental investigation—Nexp;
- Calculated with the use of analytical method NR (values in brackets assume no additional positive influence of the FRP bars on the overall capacity of the element);
- Obtained from FEM analysis in ABAQUS NFEM.
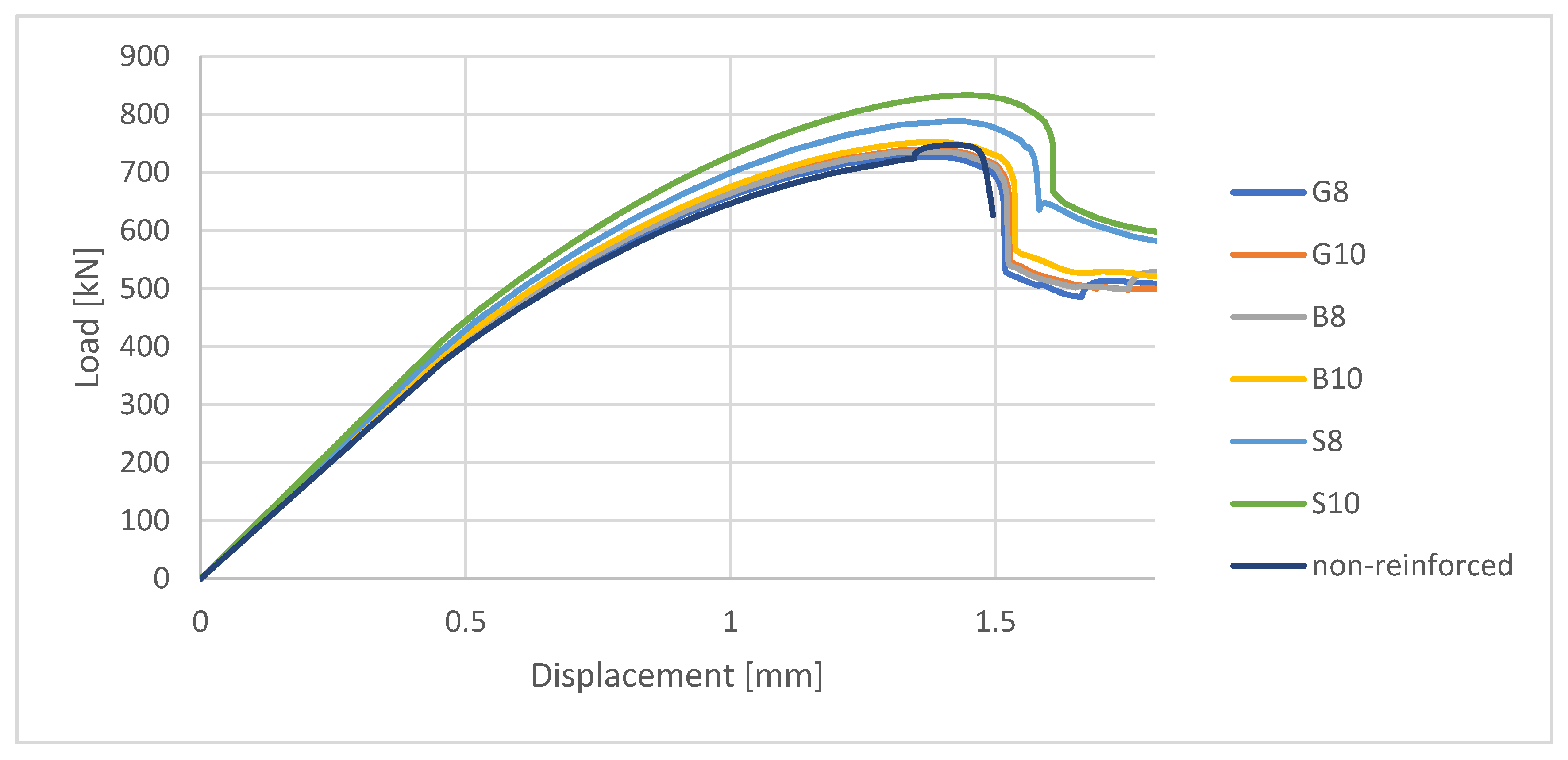
4.2. Load–Displacement Analysis
4.3. Damage Evolution and Failure Mode
- Corners of the specimen (it may correspond to the detaching of the concrete cover observed in experimental investigations);
- Medium height of the specimen—most significant in the failure stadium (also revealed in the experimental test).
4.4. Stress Values in Longitudinal Reinforcement
5. Discussion and Conclusions
- (1)
- A good agreement between calculated failure loads and experimental results has been proven for most of the analyzed specimens. The difference (up to 10%, apart from specimen S10) in the maximum value of load might be influenced by geometric tolerances (for example eccentricity of load, tolerances of dimensions or concrete cover thickness, etc.). When designing axially compressed elements, the influence of unintentional load eccentricity (not less than 2 cm [27]) should be taken into consideration. The above-presented analysis has proven that all the calculated values are higher than achieved in the experiment, only when eccentricity is assumed to be 0 cm. Considering eccentricity proves to give lower values of loads than established experimentally, even if the eccentricity equals only 1 cm, which seems to give a safety reserve.
- (2)
- When comparing values of loads calculated with the use of FEM analysis for non-reinforced and FRP-reinforced elements, FRP compressed elements have in some cases lower values of load. The potential negative influence of FRP reinforcement on the compressive capacity of the reinforced element should not be neglected. A positive influence on the compressive capacity for other specimens has been calculated as not higher than 5%. On the basis of the load–displacement curve (Figure 5), it should be pointed out that post-critical stadium proves some residual capacity for FRP-reinforced elements (same for steel-reinforced ones), while non-reinforced elements crush rapidly after gaining a maximum load value.
- (3)
- Nonlinear FEM analysis has appeared to be useful in predicting the maximum value of load as far as damage zones, in which plasticity processes and cracking might start and propagate for FRP- and metallic-reinforced compressed elements.
- (4)
- Stress values of only about 100 MPa-much lower than FRPs’ compressive strength, have been obtained in bars for above-described analyses. Therefore, the benefits of using non-metallic reinforcement in compressed concrete elements should be seen in their high corrosive resistance, electrical indifference, or ecological friendliness rather than in their high strength. However, analyses of interaction between FRP bars and different types of concrete (with various values of elasticity modulus) are also recommended.
Author Contributions
Funding
Conflicts of Interest
References
- Thiyagarajan, P.; Pavalan, V.; Sivagamasundari, R. Mechanical characterization of basalt fibre reinforced polymer bars for reinforced concrete structures. Int. J. Appl. Eng. Res. 2018, 13, 5858–5862. [Google Scholar]
- Szumigała, M.; Pawłowski, D. Zastosowanie kompozytowych prętów zbrojeniowych w konstrukcjach budowlanych. Przegląd Bud. 2014, 3, 47–50. [Google Scholar]
- Rduch, A.; Rduch, Ł. Właściwości i zastosowanie kompozytowych prętów zbrojeniowych. Przegląd Bud. 2017, 11, 43–46. [Google Scholar]
- Drzazga, M. Pręty zbrojeniowe FRP jako główne zbrojenie zginanych elementów betonowych—przegląd zaleceń i efektywność projektowania. Przegląd Bud. 2015, 3, 22–28. [Google Scholar]
- Brózda, K.; Selejdak, J. Analysis of FRP bars used as reinforcement in concrete structures. Prod. Eng. Arch. 2016, 12, 2–4. [Google Scholar] [CrossRef]
- Inman, M.; Thorhallsson, E.R.; Azrague, K. A mechanical and environmental assessment and comparison of Basalt Fibre Reinforced Polymer (BFRP) rebar and steel rebar in concrete beams. Energy Proc. 2017, 111, 31–40. [Google Scholar] [CrossRef]
- El-Salasakawy, E.; Kassem, C.; Benmokrane, B. Field application of FRP composite bars as reinforcement for bridge decks. In Proceedings of the 4th Structural Specialty Conference of the Canadian Society for Civil Engineering, Montreal, QC, Canada, 5–8 June 2002; pp. 1–10. [Google Scholar]
- Kosior-Kazberuk, M. Application of basalt-FRP bars for reinforcing geotechnical concrete structures. In MATEC Web of Conferences GCCETS 2018; EDP Sciences: Les Ulis, France, 2019; Volume 265, p. 05011. [Google Scholar]
- JSCE. Recommendation for Design and Construction of Concrete Structures Using Continous Fiber Reinforcing Materials; Tokyo: Research Comittee on Continous Fiber Reinforcin Mateials; Japan Society of Civil Engineers: Tokyo, Japan, 1997. [Google Scholar]
- CSA-S806-02. Design and Construction of Building Components with Fibre-Reinforced Polymers; Canadian Standards Association: Toronto, ON, Cannada, 2002. [Google Scholar]
- CAN/CSA. Canadian Highway Bridge Design Code; Canadian Standards Association: Toronto, ON, Cannada, 2006. [Google Scholar]
- ACI 440.1R-06. Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI Comittee 440, American Concrete Institute (ACI): Farmington Hills, MI, USA, 2006. [Google Scholar]
- CNR-DT 203/2006. Guide for the Design and Construction of Concrete Structures Reinforced with Fiber-Reinforced Polymer Bars; National Research Council: Rome, Italy, 2006. [Google Scholar]
- Wiater, A.; Siwowski, T. Nośność na ścinanie zginanych elementów betonowych zbrojonych prętami kompozytowymi FRP w świetle wybranych procedur obliczeniowych. J. Civ. Eng. Environ. Archit. 2017, 64, 267–297. [Google Scholar] [CrossRef] [Green Version]
- Al-Hamrani, A.; Alnahhal, W.; Alnuaimi, N. Shear behavior of fiber reinforced concrete beams reinforced with basalt FRP bars. In Proceedings of the Sixth International Conference on Advances in Civil, Structural and Environmental Engineering—ACSEE 2017, Rome, Italy, 9–10 December 2017; pp. 50–53. [Google Scholar]
- Kassem, C.; Farghaly, A.S.; Benmokrane, B. Evaluation of flexural behavior and serviceability performance of concrete beams reinforced with FRP bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- Urbanski, M.; Lapko, A.; Garbacz, A. Investigation on concrete beams reinforced with basalt rebars as an effective alternative of conventional R/C structures. Proc. Eng. 2013, 57, 1183–1191. [Google Scholar] [CrossRef] [Green Version]
- Włodarczyk, M.; Markowski, H. Analiza pracy zginania belki ze zbrojeniem niemetalicznym. TTS Tech. Transp. Szyn. 2016, 12, 277–282. [Google Scholar]
- Elmessalami, N.; el Refai, A.; Abed, F. Fiber-reinforced polymers bars for compression reinforcement: A promising alternative to steel bars. Constr. Build. Mater. 2019, 209, 725–737. [Google Scholar] [CrossRef]
- Park, K.T.; Kim, H.Y.; You, Y.J.; Lee, S.Y.; Seo, D.W. Basalt FRP reinforcing bars for concrete structures. In Proceedings of the 4th Asia-Pacific Conference on FRP in structures, Melbourne, Australia, 11–13 December 2013; p. 440. [Google Scholar]
- Elgabbas, F.; Ahmed, E.A.; Benmokrane, B. Physical and mechanical characteristics of new basalt-FRP bars for reinforcing concrete structures. Constr. Build. Mater. 2015, 95, 623–635. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Ma, H.; Xu, X. Properties and applications of basalt fiber and its composites. IOP Conf. Ser. Earth Environ. Sci. 2018, 186, 2. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part. B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Włodarczyk, M. The strength capacity of compression members reinforced with FRP bars. The results of structural testing. AUTOBUSY Tech. Eksploat. Syst. Transp. 2018, 19, 715–719. [Google Scholar] [CrossRef]
- Włodarczyk, M.; Trofimczuk, D. Prediction of ultimate capacity of FRP reinforced concrete compression members. In Proceedings of the Concrete Innovations in Materials, Design and Structures Book of Abstracts for the 2019 fib International Symposium, Krakow, Poland, 27–29 May 2019. [Google Scholar]
- PN-EN 12390-3:2019-07 Badania Betonu—Część 3: Wytrzymałość na Ściskanie Próbek do Badań; Testing Hardened Concrete—Part. 3: Compressive Strength of Test Specimens; Polish Committee for Standardization: Warszawa, Poland, 2019.
- PN-EN 1992-1-1:2008 Eurocode 2: Design of Concrete Structures—Part. 1-1 General Rules and Rules for Buildings; Polish Committee for Standardization: Warszawa, Poland, 2008.
- ISO 6935-2:2019 Steel for the Reinforcement of Concrete—Part. 2: Ribbed Bars; ISO: Geneva, Switzerland, 2019.
- Kmiecik, P.; Kamiński, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef] [Green Version]




| Reinforcement Material | Diameter of the Bars [mm] | Quantity of Reinforcement Bars | Designation of the Specimens | Reinforcement Ratio [%] |
|---|---|---|---|---|
| GFRP | 8 | 4 | G8 | 0.89 |
| GFRP | 10 | 4 | G10 | 1.40 |
| BFRP | 8 | 4 | B8 | 0.89 |
| BFRP | 10 | 4 | B10 1 | 1.40 |
| steel | 8 | 4 | S8 | 0.89 |
| steel | 10 | 4 | S10 | 1.40 |
| Reinforcement Material | Poisson’s Ratio | Modulus of Elasticity E [GPa] | Yield Strength fy [MPa] | Ultimate Tensile Strength fut [MPa] |
|---|---|---|---|---|
| GFRP | 0.25 | 50 | - | up to 1600 |
| BFRP | 0.25 | 70 | - | 1100 |
| steel | 0.3 | 200 | 500 | 550 |
| Reinforcement Type | Designation of the Specimen | Experimental Value Nexp [kN] | Analytical Failure Load NR [kN] | Nexp/NR | FEM Failure Load NFEM [kN] | Nexp/NFEM |
|---|---|---|---|---|---|---|
| 4#8 GFRP | G8 | 699.1 | 753.2 (742.9) 2 | 0.928 (0.941) 2 | 727.9 | 0.960 |
| 4#10 GFRP | G10 | 733.2 | 764.5 (742.9) 2 | 0.959 (0.987) 2 | 738.3 | 0.993 |
| 4#8 BFRP | B8 | 727.2 | 761.2 (742.9) 2 | 0.955 (0.979)2 | 735.2 | 0.989 |
| 4#10 BFRP | B101 | -1 | 777.1 (742.9) 2 | -1 | 752.2 | -1 |
| 4#8 steel | S8 | 740.0 | 813.5 | 0.910 | 789.0 | 0.938 |
| 4#10 steel | S10 | 580.0 | 858.7 | 0.657 | 833.1 | 0.696 |
| Designation of the Specimen | Load Eccentricity e | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| e = 0 cm | e = 1 cm | e = 2 cm | ||||||||
| Nexp [kN] | NR [kN] | NRc [kN] | NFEM [kN] | NR [kN] | NRc [kN] | NFEM [kN] | NR [kN] | NRc [kN] | NFEM [kN] | |
| G8 | 699.1 | 753.2 (742.9) 2 | 578.9 (566.3) 2 | 727.9 | 654.8 | 503.9 | 629.2 | 576.1 | 443.9 | 543.5 |
| G10 | 733.2 | 764.5 (742.9) 2 | 590.2 (566.3) 2 | 738.3 | 666.1 | 515.2 | 630.3 | 587.4 | 455.2 | 538.4 |
| B8 | 727.2 | 761.2 (742.9) 2 | 586.9 (566.3)2 | 735.2 | 662.8 | 511.9 | 630.0 | 584.1 | 451.9 | 540.4 |
| B10 1 | -1 | 777.1 (742.9) 2 | 602.07 (566.3) 2 | 752.2 | 678.7 | 527.7 | 631.5 | 599.9 | 460.2 | 558.0 |
| S8 | 740.0 | 813.5 | 639.2 | 789.0 | 705.3 | 556.7 | 705.0 | 616.7 | 489.2 | 607.1 |
| S10 | 580.0 | 858.7 | 684.4 | 833.1 | 750.5 | 594.4 | 745.0 | 652.1 | 519.4 | 645.0 |
| Part of the Testing Process | G8 Specimen (GFRP Bars) | S8 Specimen (Steel Bars) | ||
|---|---|---|---|---|
| Compression Damage Zones | Tension Damage Zones | Compression Damage Zones | Tension Damage Zones | |
| First occurrence of visible damage zones |  Load value F = 422.4 kN |  Load value F = 422.4 kN |  Load value F = 442.0 kN |  Load value F = 442.0 kN |
| Failure |  Load value F = 727.9 kN |  Load value F = 727.9 kN |  Load value F = 789.0 kN |  Load value F = 789.0 kN |
| Post - failure |  Load value F = 500.0 kN |  Load value F = 500.0 kN |  Load value F = 550.8 kN |  Load value F = 550.8 kN |
| Load Eccentricity | e = 0 cm (F = 735.2 kN) | e = 1 cm (F = 630.0 kN) | e = 2 cm (F = 540.4 kN) |
|---|---|---|---|
| Compression damage zones |  |  |  |
| Tension damage zones |  |  |  |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wydra, M.; Włodarczyk, M.; Fangrat, J. Nonlinear Analysis of Compressed Concrete Elements Reinforced with FRP Bars. Materials 2020, 13, 4410. https://doi.org/10.3390/ma13194410
Wydra M, Włodarczyk M, Fangrat J. Nonlinear Analysis of Compressed Concrete Elements Reinforced with FRP Bars. Materials. 2020; 13(19):4410. https://doi.org/10.3390/ma13194410
Chicago/Turabian StyleWydra, Małgorzata, Maria Włodarczyk, and Jadwiga Fangrat. 2020. "Nonlinear Analysis of Compressed Concrete Elements Reinforced with FRP Bars" Materials 13, no. 19: 4410. https://doi.org/10.3390/ma13194410
APA StyleWydra, M., Włodarczyk, M., & Fangrat, J. (2020). Nonlinear Analysis of Compressed Concrete Elements Reinforced with FRP Bars. Materials, 13(19), 4410. https://doi.org/10.3390/ma13194410






