Numerical Mesoscale Analysis of Textile Reinforced Concrete
Abstract
:1. Introduction
2. Construction of a Representative Volume Element for Textile Reinforced Concrete
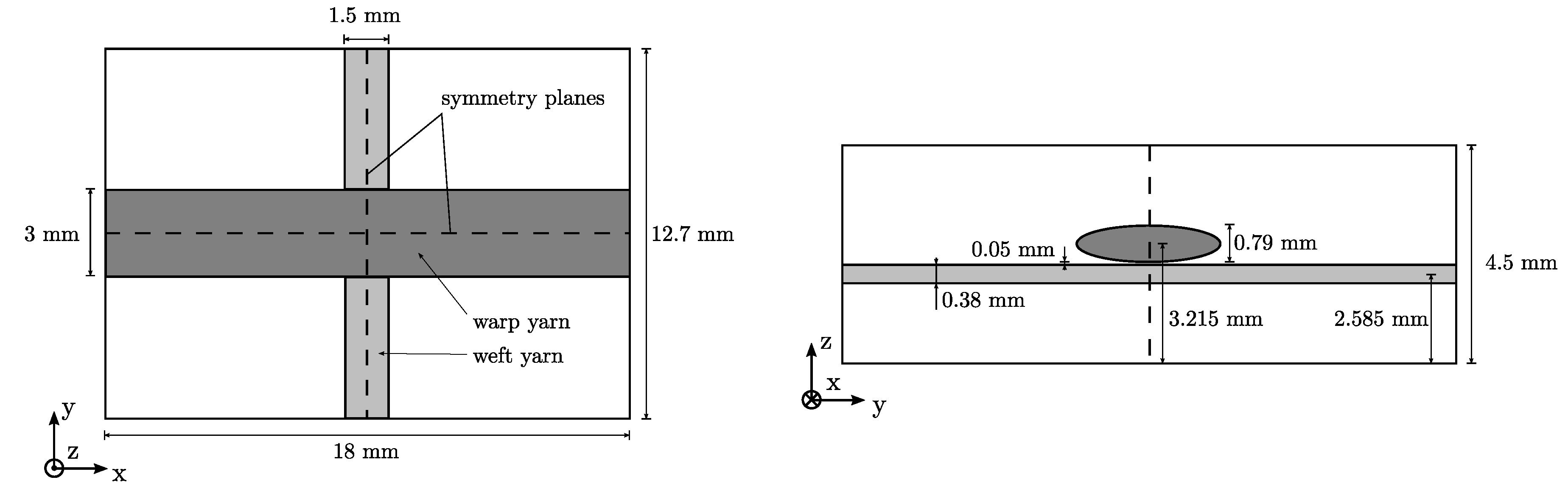
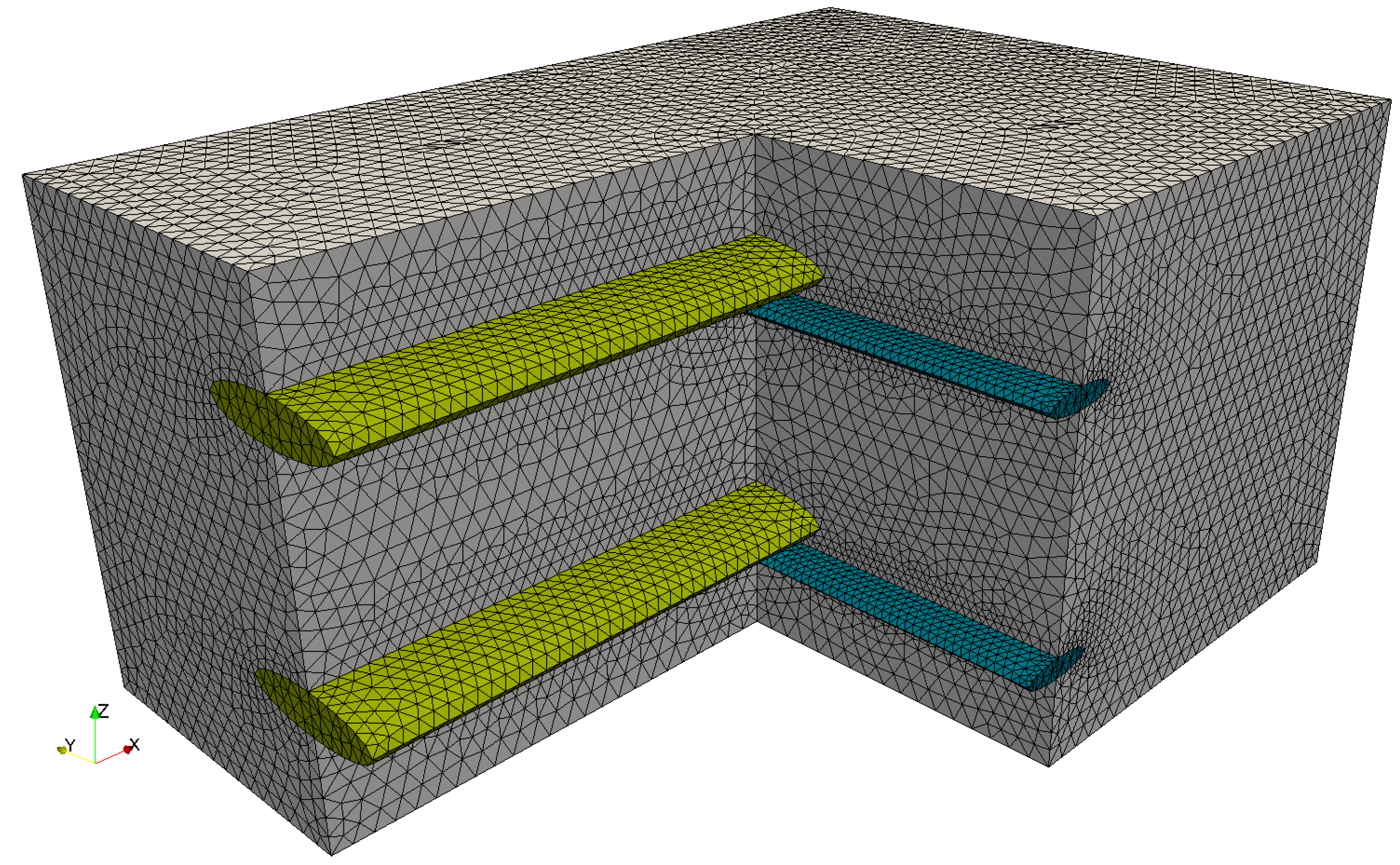
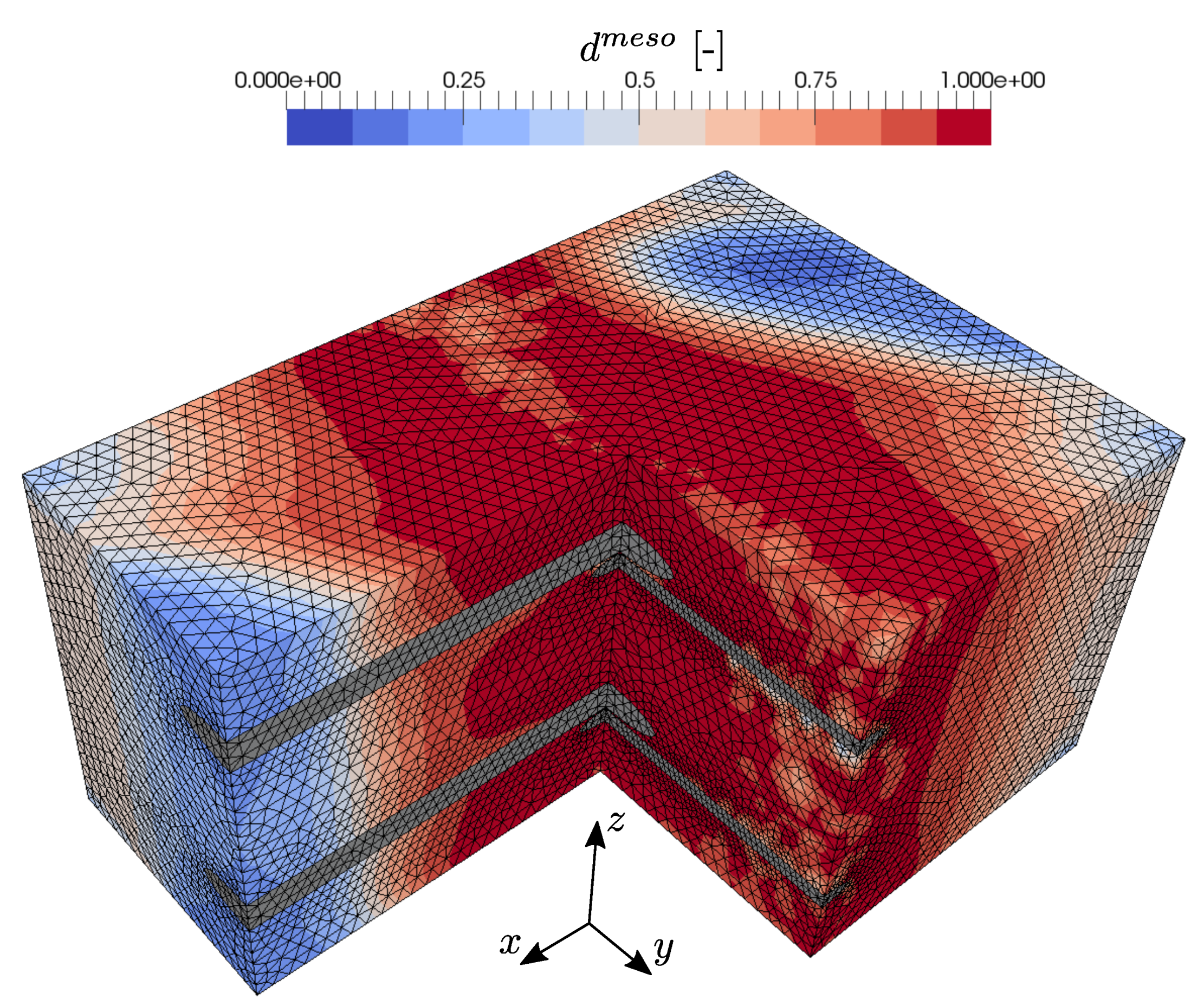
2.1. Geometry and Finite-Element Discretization
2.2. Constitutive Modeling of Composite Constituents
2.2.1. Textile Yarns
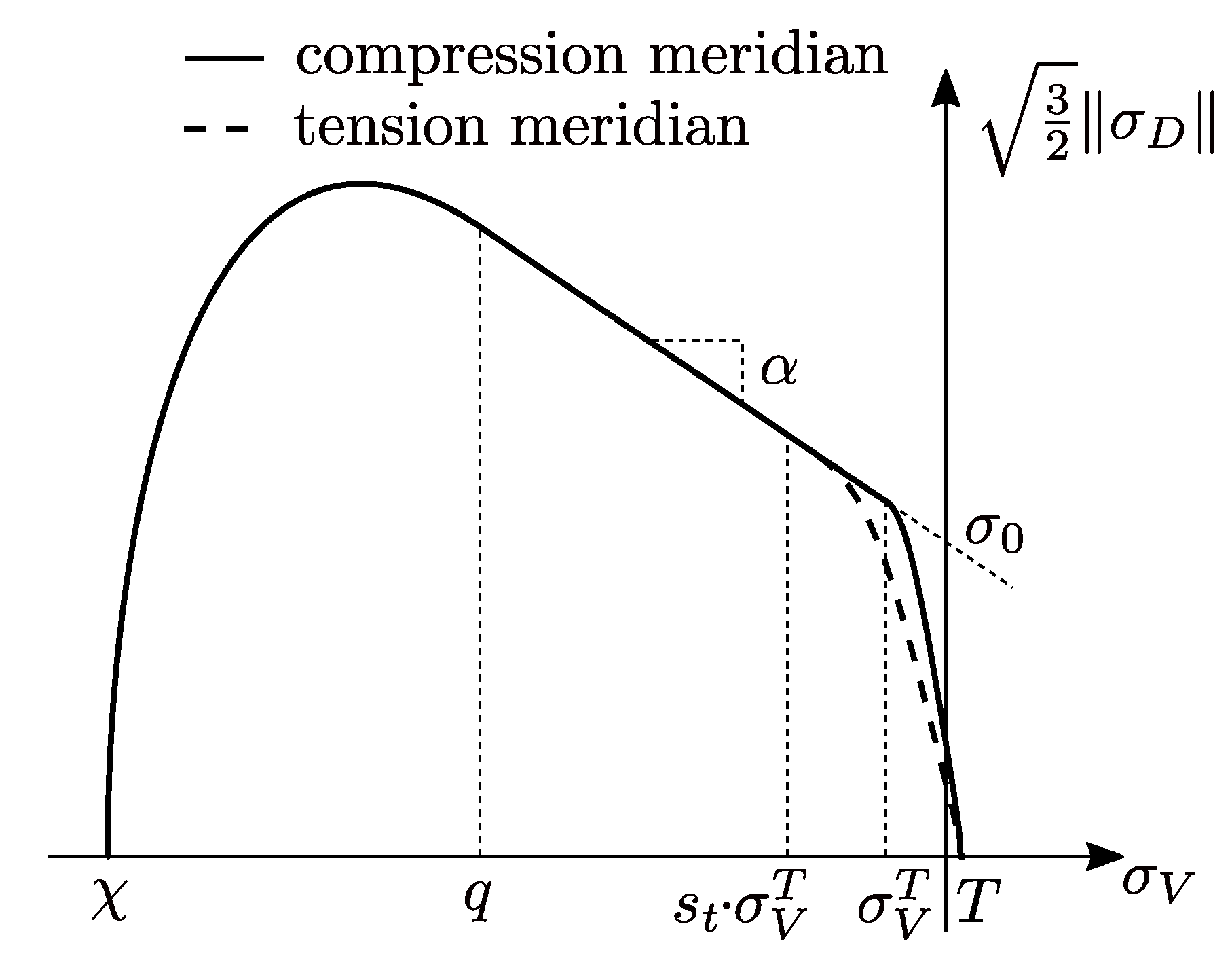
2.2.2. Concrete
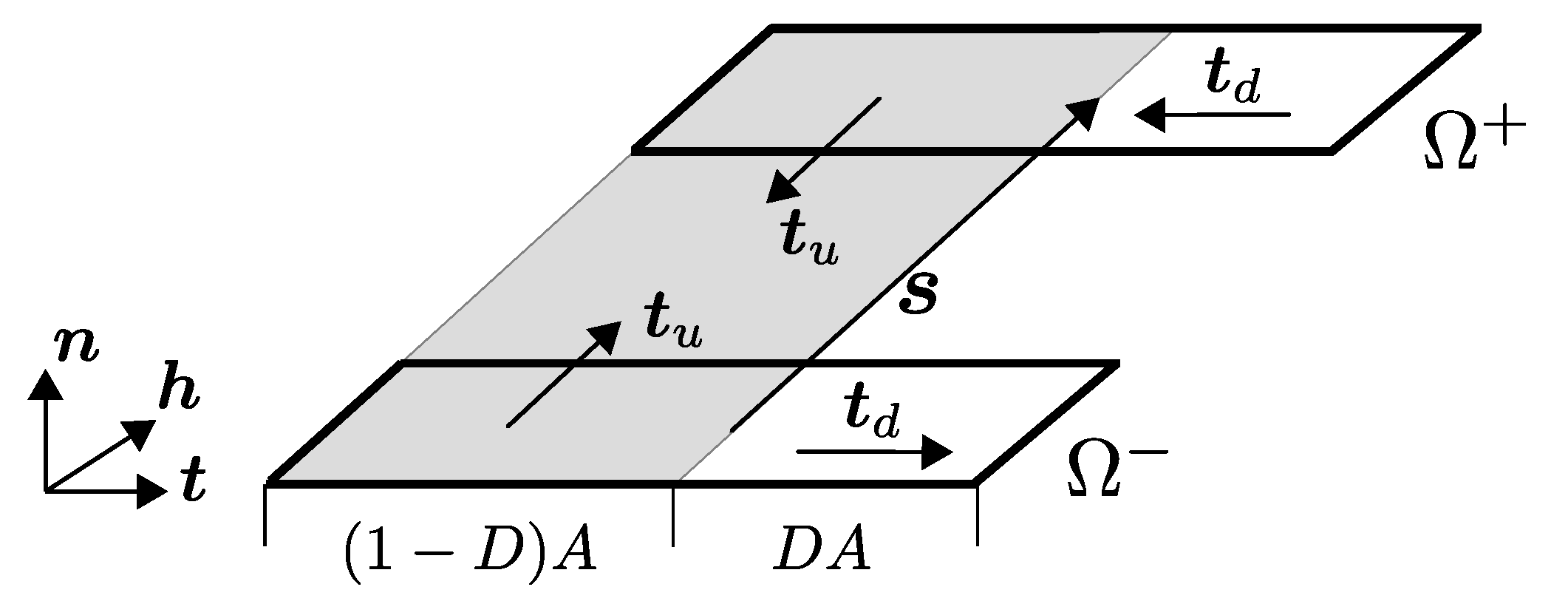
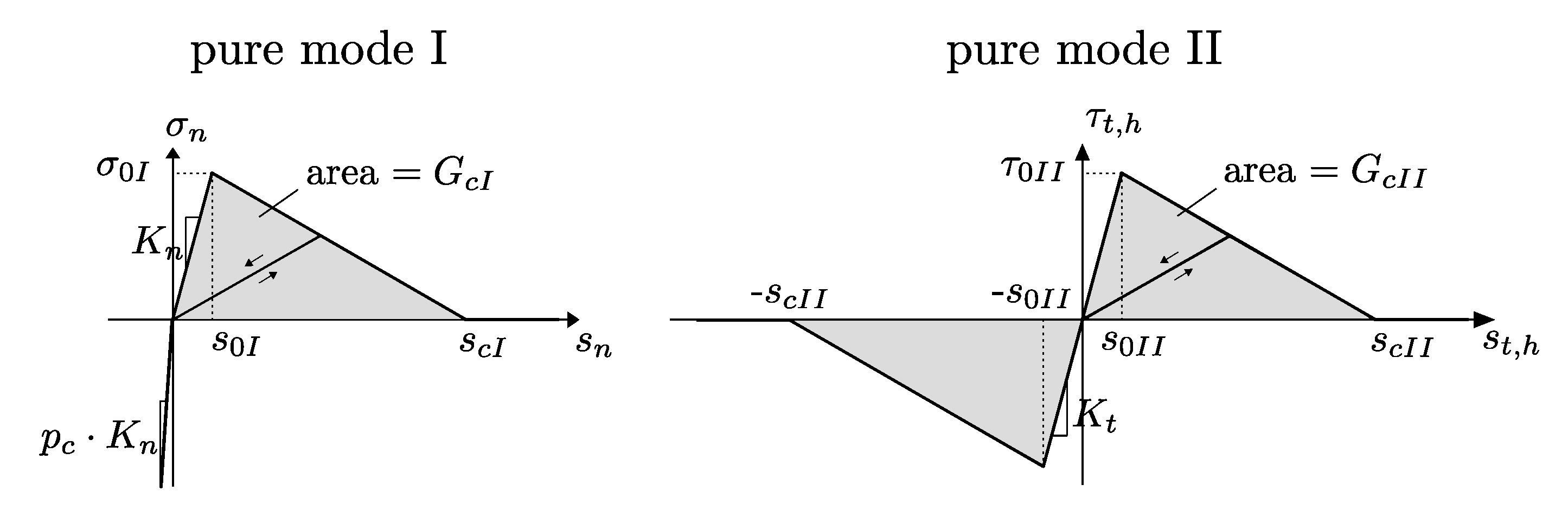
2.2.3. Yarn–Concrete Interface
2.3. Calibration of Model Parameters
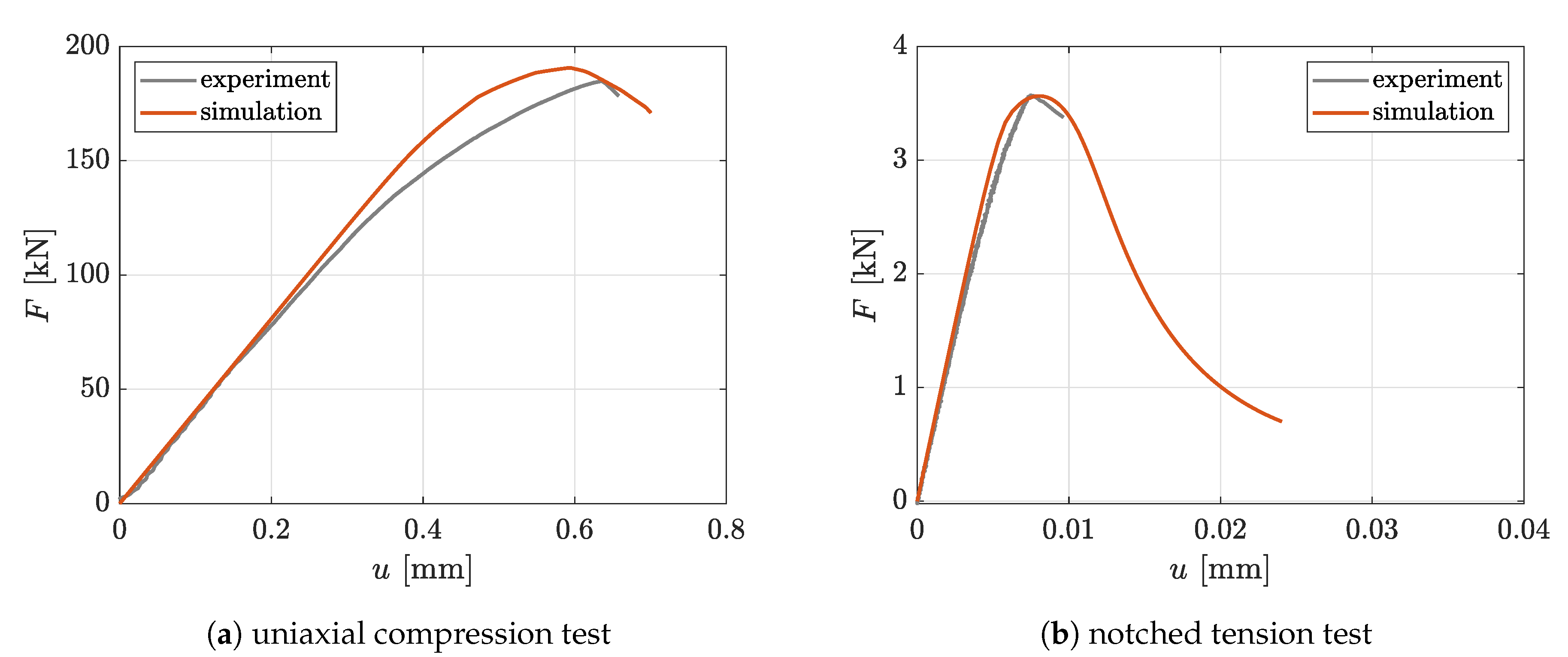
2.3.1. Identification of Yarn Material Parameters
2.3.2. Identification of Concrete Material Parameters
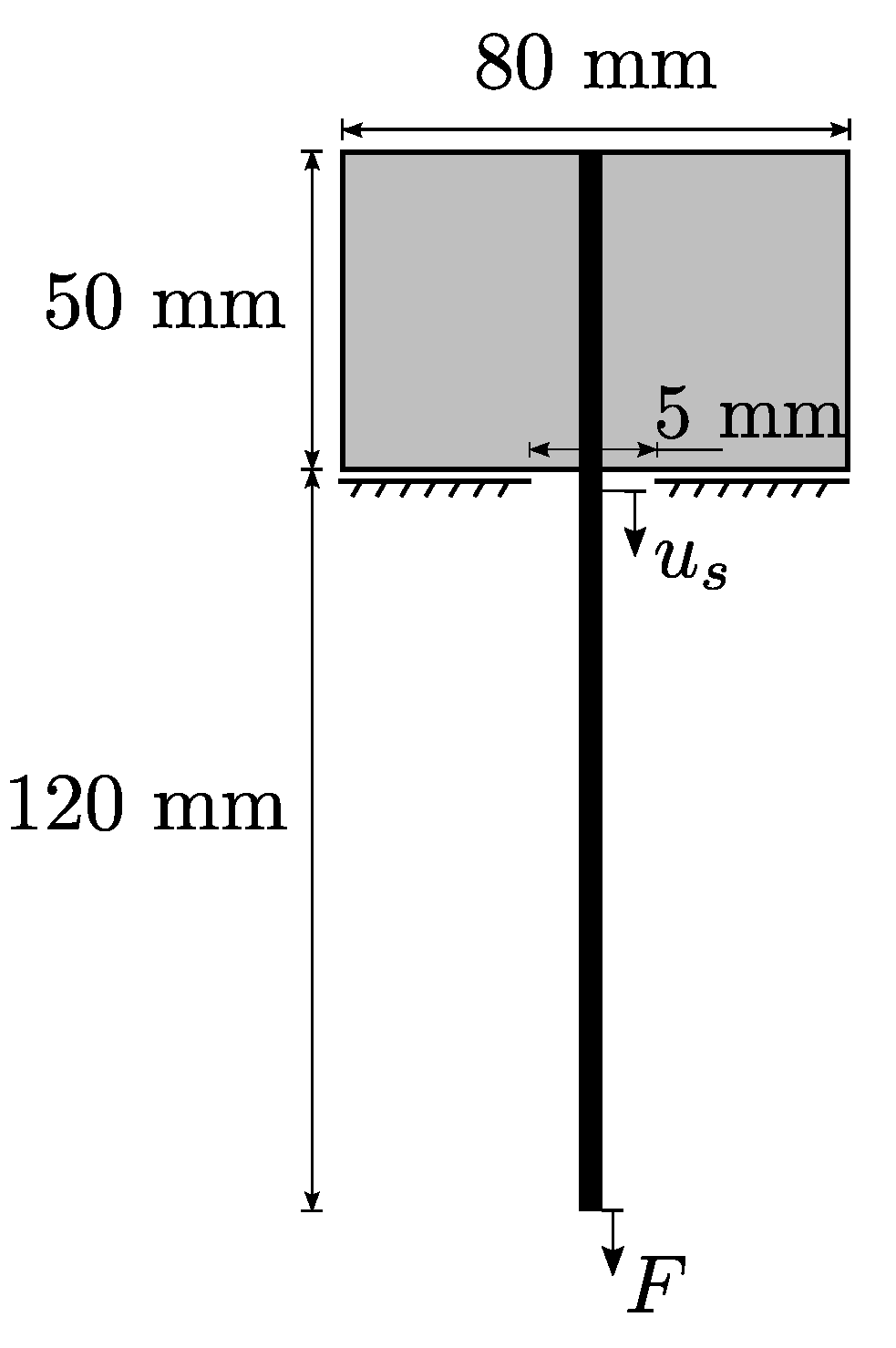
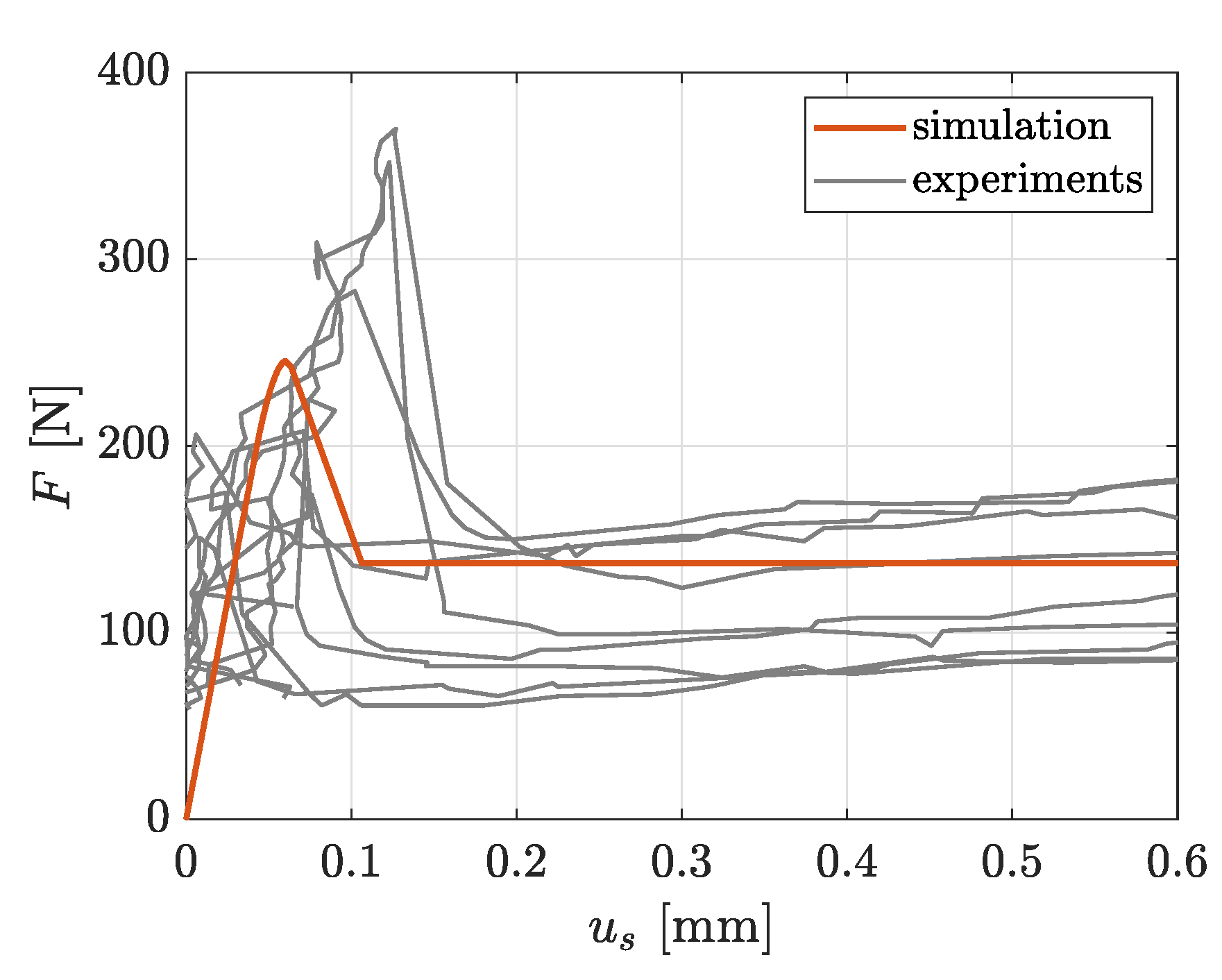
2.3.3. Identification of Interface Parameters
3. Numerical Material Testing
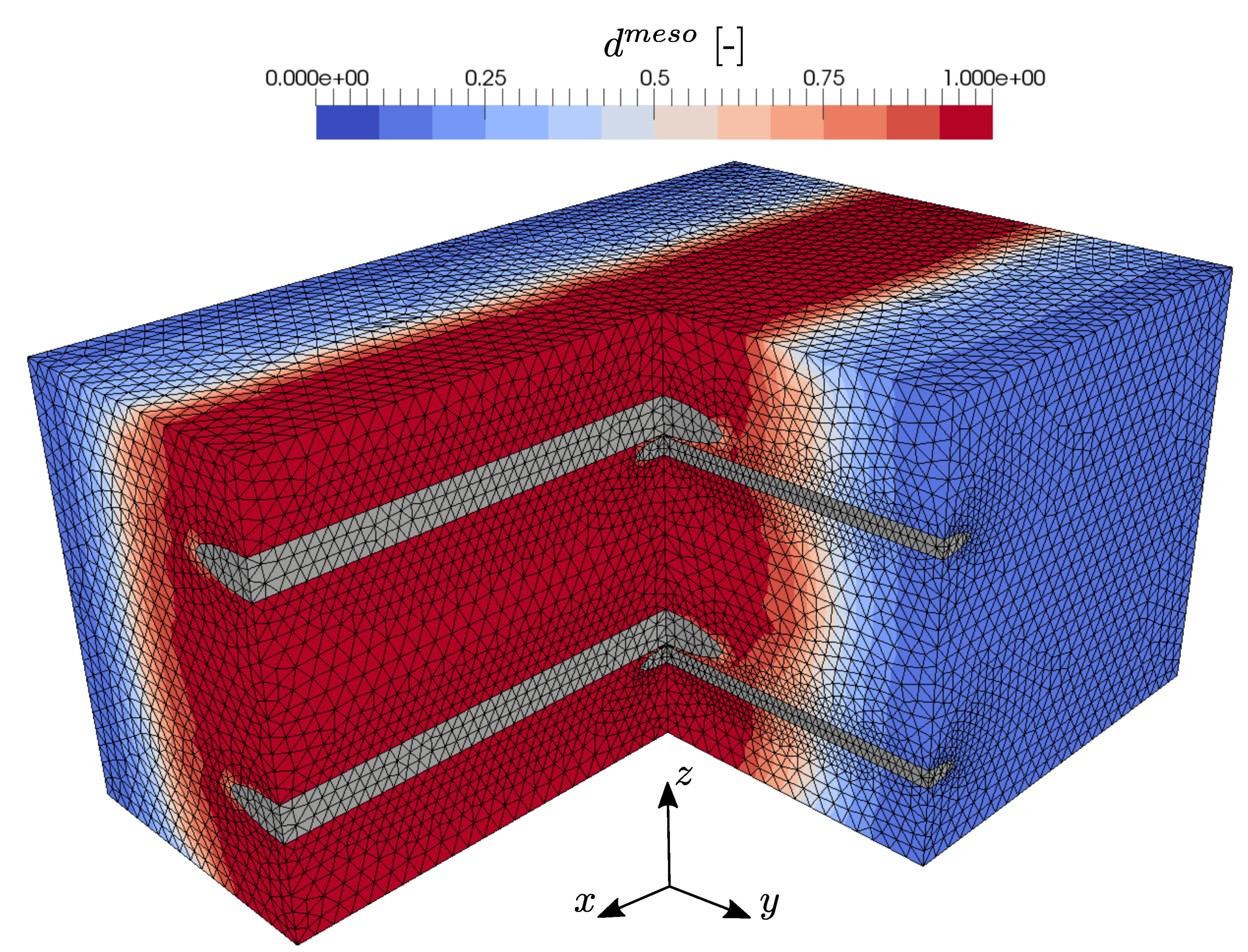
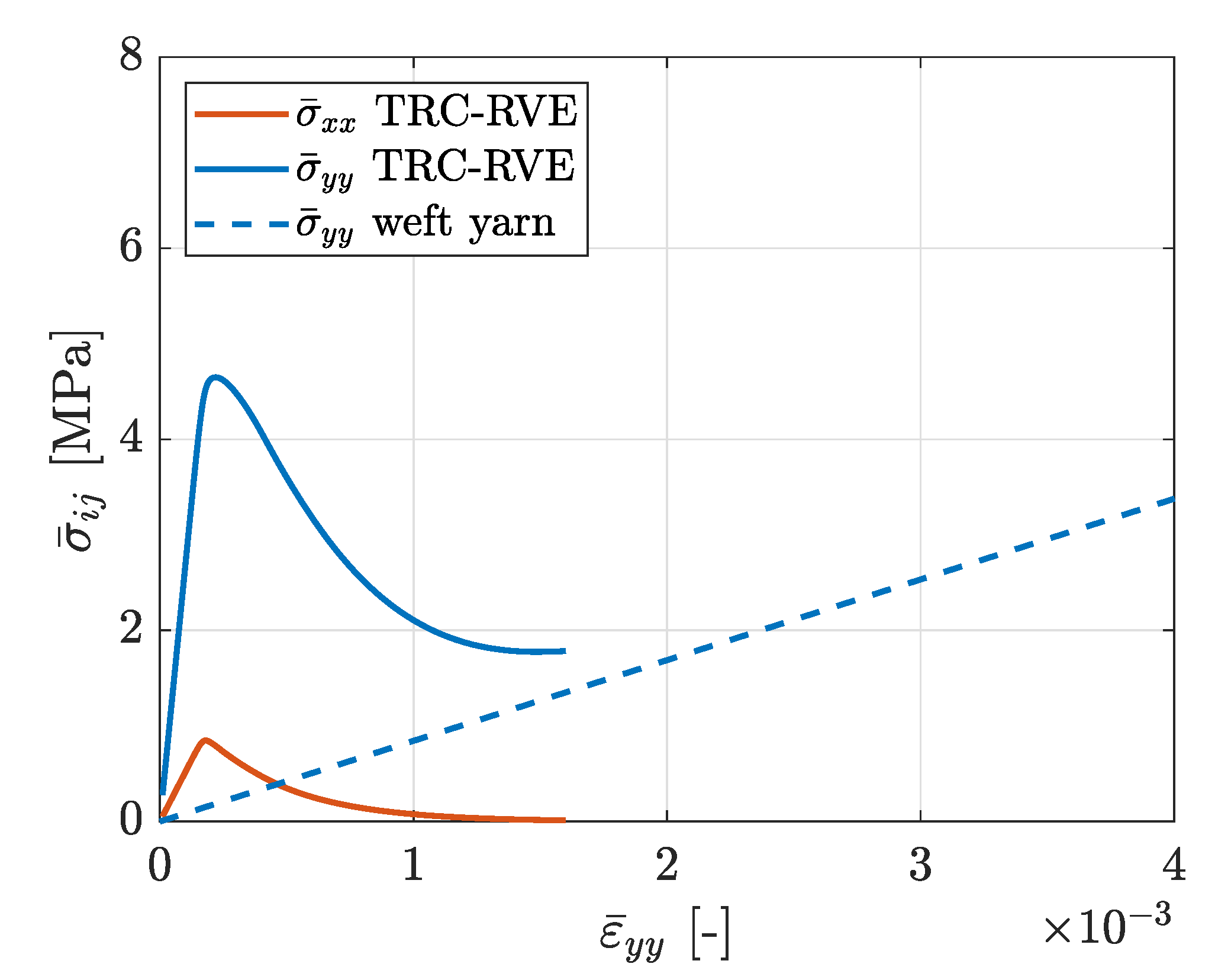
3.1. Tensile Loading in Warp and Weft Direction
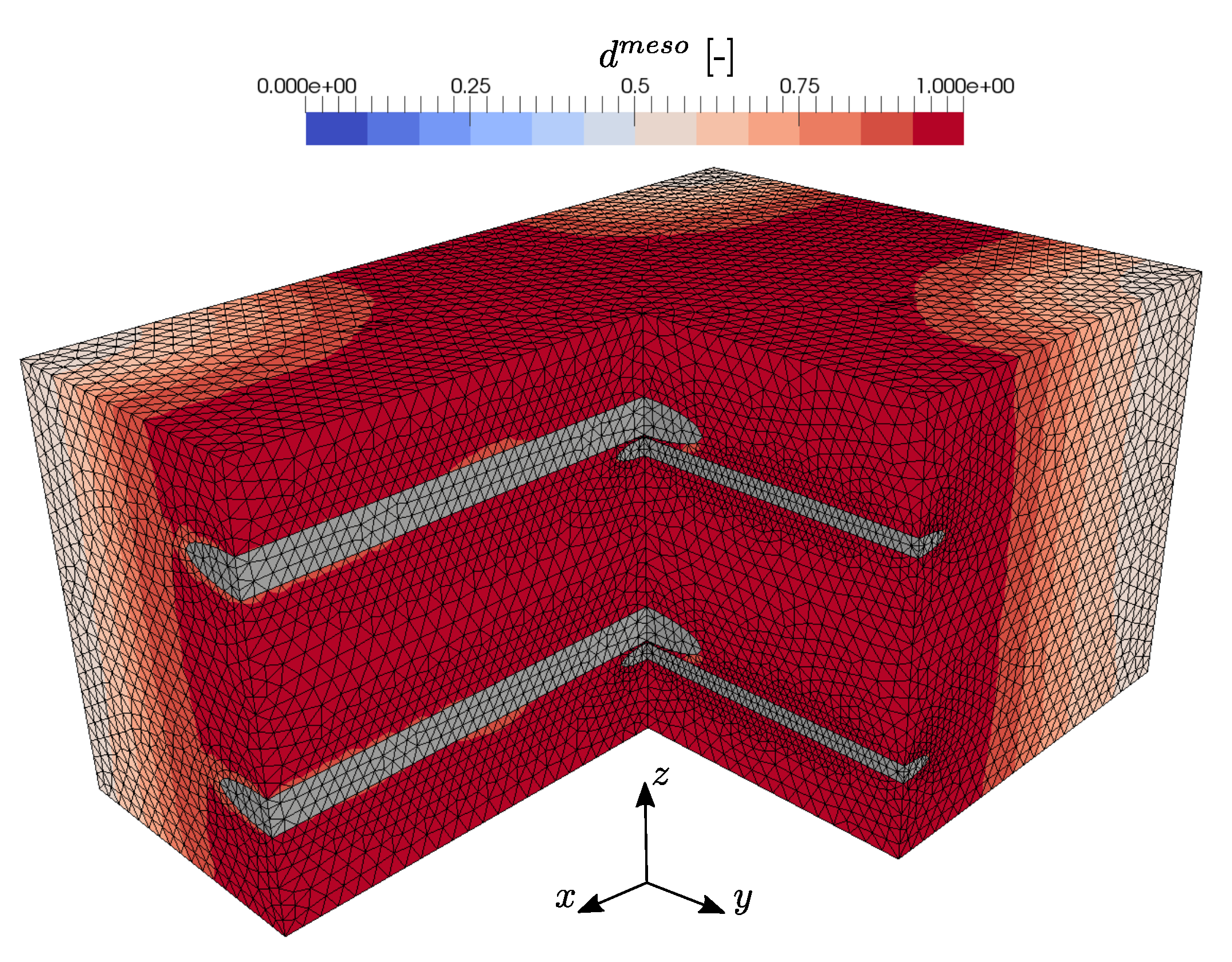
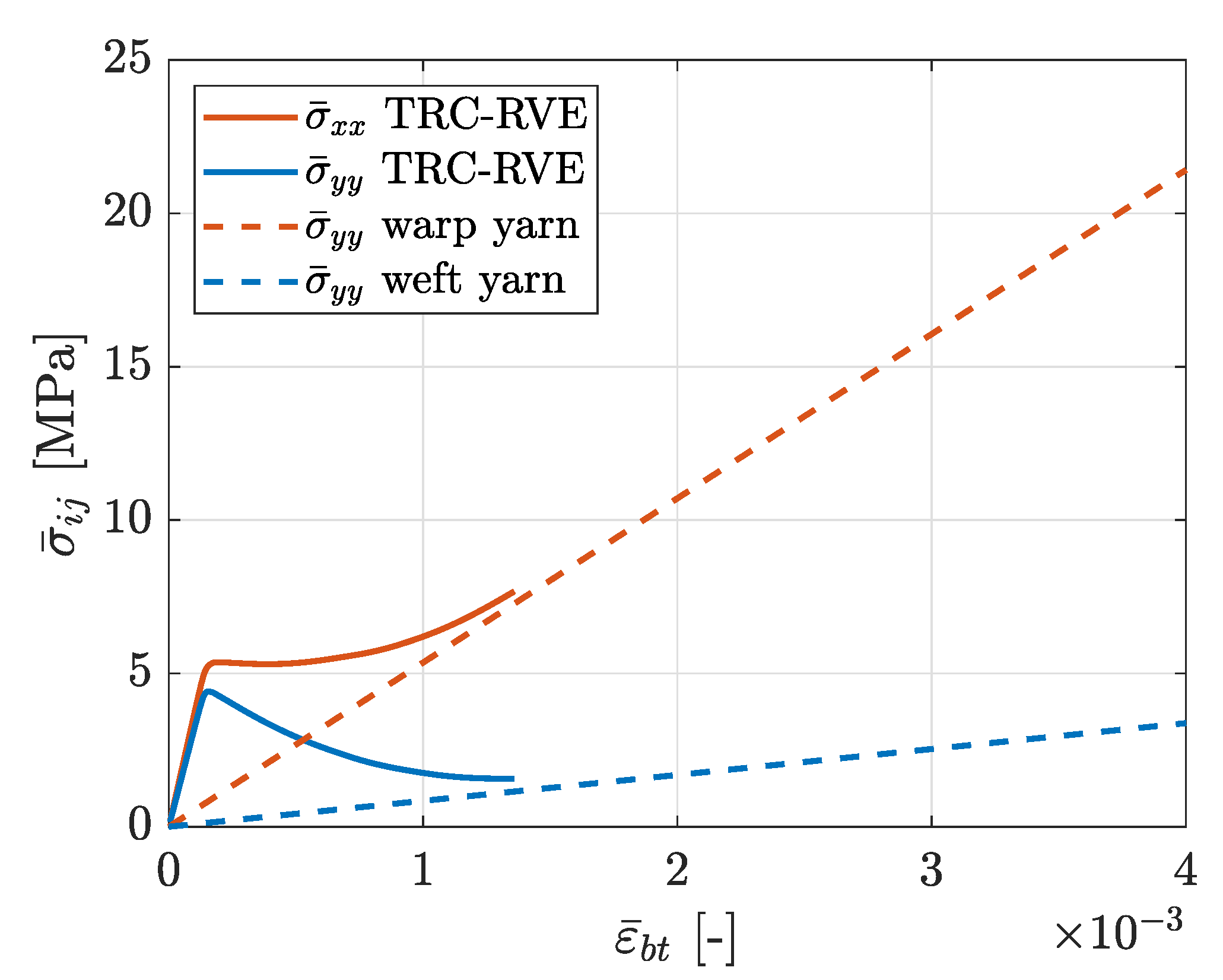
3.2. Biaxial Tensile Loading
3.3. In-Plane Shear Loading
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scheerer, S.; Chudoba, R.; Garibaldi, M.P.; Curbach, M. Shells made of textile reinforced concrete–applications in Germany. J. Int. Assoc. Shell Spat. Struct. 2017, 58, 79–93. [Google Scholar]
- Brückner, A.; Ortlepp, R.; Curbach, M. Textile reinforced concrete for strengthening in bending and shear. Mater. Struct. 2006, 39, 741–748. [Google Scholar] [CrossRef]
- Bösche, A.; Jesse, F.; Ortlepp, R.; Weiland, S.; Curbach, M. Textile-reinforced Concrete for Flexural Strengthening of RC-structures-Part 1: Structural Behavior and Design Model. Am. Concr. Inst. ACI Spec. Publ. 2008, 251, 19–40. [Google Scholar]
- Weiland, S.; Ortlepp, R.; Hauptenbuchner, B.; Curbach, M. Textile Reinforced Concrete for Flexural Strengthening of RC-Structures-Part 2: Application on a Concrete Shell. Am. Concr. Inst. ACI Spec. Publ. 2008, 251, 41–58. [Google Scholar]
- Chudoba, R.; Sharei, E.; Scholzen, A. A strain-hardening microplane damage model for thin-walled textile-reinforced concrete shells, calibration procedure, and experimental validation. Compos. Struct. 2016, 152, 913–928. [Google Scholar] [CrossRef]
- Möller, B.; Graf, W.; Hoffmann, A.; Steinigen, F. Numerical simulation of RC structures with textile reinforcement. Comput. Struct. 2005, 83, 1659–1688. [Google Scholar] [CrossRef]
- Graf, W.; Hoffmann, A.; Möller, B.; Sickert, J.U.; Steinigen, F. Analysis of textile-reinforced concrete structures under consideration of non-traditional uncertainty models. Eng. Struct. 2007, 29, 3420–3431. [Google Scholar] [CrossRef]
- Häußler-Combe, U.; Hartig, J. Bond and failure mechanisms of textile reinforced concrete (TRC) under uniaxial tensile loading. Cem. Concr. Compos. 2007, 29, 279–289. [Google Scholar]
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K. Influence of bond properties on the tensile behaviour of Textile Reinforced Concrete. Cem. Concr. Compos. 2008, 30, 898–906. [Google Scholar] [CrossRef]
- Rypl, R.; Chudoba, R.; Scholzen, A.; Vořechovskỳ, M. Brittle matrix composites with heterogeneous reinforcement: Multi-scale model of a crack bridge with rigid matrix. Compos. Sci. Technol. 2013, 89, 98–109. [Google Scholar] [CrossRef]
- Cox, H. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Xia, Z.; Okabe, T.; Curtin, W. Shear-lag versus finite element models for stress transfer in fiber-reinforced composites. Compos. Sci. Technol. 2002, 62, 1141–1149. [Google Scholar] [CrossRef]
- Zastrau, B.; Richter, M.; Lepenies, I. On the analytical solution of pullout phenomena in textile reinforced concrete. J. Eng. Mater. Technol. 2003, 125, 38–43. [Google Scholar] [CrossRef]
- Richter, M.; Zastrau, B.W. On the nonlinear elastic properties of textile reinforced concrete under tensile loading including damage and cracking. Mater. Sci. Eng. A 2006, 422, 278–284. [Google Scholar] [CrossRef]
- Lepenies, I.G. Zur Hierarchischen und Simultanen Multi-Skalen-Analyse von Textilbeton. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2007. [Google Scholar]
- Djamai, Z.I.; Bahrar, M.; Salvatore, F.; Larbi, A.S.; El Mankibi, M. Textile reinforced concrete multiscale mechanical modelling: Application to TRC sandwich panels. Finite Elem. Anal. Des. 2017, 135, 22–35. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Kröner, E. Bounds for effective elastic moduli of disordered materials. J. Mech. Phys. Solids 1977, 25, 137–155. [Google Scholar] [CrossRef]
- Milton, G.W.; Sawicki, A. Theory of composites. Cambridge monographs on applied and computational mathematics. Appl. Mech. Rev. 2003, 56, B27–B28. [Google Scholar] [CrossRef]
- Hill, R. On constitutive macro-variables for heterogeneous solids at finite strain. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 131–147. [Google Scholar]
- Miehe, C. Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Int. J. Numer. Methods Eng. 2002, 55, 1285–1322. [Google Scholar] [CrossRef]
- Kouznetsova, V. Computational Homogenization for the Multi-Scale Analysis of Multi-Phase Materials. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Massart, T.J.; Kouznetsova, V.; Peerlings, R.H.; Geers, M.G. Computational homogenization for localization and damage. Adv. Comput. Mater. Model. Class. Multi-Scale Tech. 2010, 111–164. [Google Scholar] [CrossRef]
- De Souza Neto, E.A.; Feijóo, R.A.; Novotny, A. Variational foundations of large strain multiscale solid constitutive models: Kinematical formulation. Adv. Comput. Mater. Model. Class. Multi-Scale Tech. 2011. [Google Scholar] [CrossRef]
- Miehe, C. Computational micro-to-macro transitions for discretized micro-structures of heterogeneous materials at finite strains based on the minimization of averaged incremental energy. Comput. Methods Appl. Mech. Eng. 2003, 192, 559–591. [Google Scholar] [CrossRef]
- Terada, K.; Kato, J.; Hirayama, N.; Inugai, T.; Yamamoto, K. A method of two-scale analysis with micro-macro decoupling scheme: Application to hyperelastic composite materials. Comput. Mech. 2013, 52, 1199–1219. [Google Scholar] [CrossRef]
- Terada, K.; Hirayama, N.; Yamamoto, K.; Kato, J.; Kyoya, T.; Matsubara, S.; Arakawa, Y.; Ueno, Y.; Miyanaga, N. Applicability of micro–macro decoupling scheme to two-scale analysis of fiber-reinforced plastics. Adv. Compos. Mater. 2014, 23, 421–450. [Google Scholar] [CrossRef]
- Fleischhauer, R.; Thomas, T.; Kato, J.; Terada, K.; Kaliske, M. Finite thermo-elastic decoupled two-scale analysis. Int. J. Numer. Methods Eng. 2020, 121, 355–392. [Google Scholar] [CrossRef]
- Häfner, S.; Eckardt, S.; Luther, T.; Könke, C. Mesoscale modeling of concrete: Geometry and numerics. Comput. Struct. 2006, 84, 450–461. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Stroeven, M.; Sluys, L.J. Multiscale failure modeling of concrete: Micromechanical modeling, discontinuous homogenization and parallel computations. Comput. Methods Appl. Mech. Eng. 2012, 201, 139–156. [Google Scholar] [CrossRef]
- Trawiński, W.; Tejchman, J.; Bobiński, J. A three-dimensional meso-scale modelling of concrete fracture, based on cohesive elements and X-ray μCT images. Eng. Fract. Mech. 2018, 189, 27–50. [Google Scholar] [CrossRef]
- Gal, E.; Kryvoruk, R. Meso-scale analysis of FRC using a two-step homogenization approach. Comput. Struct. 2011, 89, 921–929. [Google Scholar] [CrossRef]
- Sun, B.; Wang, X.; Li, Z. Meso-scale image-based modeling of reinforced concrete and adaptive multi-scale analyses on damage evolution in concrete structures. Comput. Mater. Sci. 2015, 110, 39–53. [Google Scholar] [CrossRef]
- Xu, Z.; Hao, H.; Li, H. Mesoscale modelling of fibre reinforced concrete material under compressive impact loading. Constr. Build. Mater. 2012, 26, 274–288. [Google Scholar] [CrossRef]
- Verfahren zur Verstärkung von Stahlbeton mit TUDALIT (Textilbewehrter Beton); Allgemeine bauaufsichtliche Zulassung Z-31.10-182; Deutsches Institut für Bautechnik DIBt: Berlin, Germany, 2015.
- Interner Versuchsbericht zur Erlangung der Zulassung Z-31.10-182-Verfahren zur Verstärkung von Stahlbeton mit TUDALIT (Textilbewehrter Beton); Internal report: Unpublished; Institut für Massivbau TU Dresden: Dresden, Germany, 2015.
- Nguyen, V.D.; Béchet, E.; Geuzaine, C.; Noels, L. Imposing periodic boundary condition on arbitrary meshes by polynomial interpolation. Comput. Mater. Sci. 2012, 55, 390–406. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Bessa, M.A.; Melro, A.R.; Camanho, P.P.; Guo, L.; Liu, W.K. High-fidelity micro-scale modeling of the thermo-visco-plastic behavior of carbon fiber polymer matrix composites. Compos. Struct. 2015, 134, 132–141. [Google Scholar] [CrossRef] [Green Version]
- Schürmann, H. Konstruieren mit Faser-Kunststoff-Verbunden; Springer: Berlin, Germany, 2007. [Google Scholar]
- Gong, T.; Hamza, A.A.; Curosu, I.; Mechtcherine, V. On the Synergetic Action between Strain-Hardening Cement-based Composites (SHCC) and Carbon Textile Reinforcement under Tensile Loading. In Proceedings of the 10th International Conference on Fracture Mechanics of Concrete and Concrete Structures, FraMCoS-X, Bayonne, France, 23–26 June 2019. [Google Scholar] [CrossRef]
- Fuchs, A.; Kaliske, M. A gradient enhanced viscoplasticity-damage microplane model for concrete at static and transient loading. In Proceedings of the 10th International Conference on Fracture Mechanics of Concrete and Concrete Structures, FraMCoS-X, Bayonne, France, 23–26 June 2019. [Google Scholar] [CrossRef]
- Zreid, I.; Kaliske, M. A gradient enhanced plasticity–damage microplane model for concrete. Comput. Mech. 2018, 62, 1239–1257. [Google Scholar] [CrossRef]
- Willam, K.J.; Warnke, E. Constitutive model for the triaxial behaviour of concrete. Proc. Int. Assoc. Bridge Struct. Eng. 1975, 19, 1–30. [Google Scholar]
- Fleischhauer, R.; Qinami, A.; Hickmann, R.; Diestel, O.; Götze, T.; Cherif, C.; Heinrich, G.; Kaliske, M. A thermomechanical interface description and its application to yarn pullout tests. Int. J. Solids Struct. 2015, 69, 531–543. [Google Scholar] [CrossRef]
- Albarella, M.; Serpieri, R.; Alfano, G.; Sacco, E. A 3D multiscale cohesive zone model for quasi-brittle materials accounting for friction, damage and interlocking. Eur. J. Comput. Mech. 2015, 24, 144–170. [Google Scholar] [CrossRef]
- Alfano, G.; Sacco, E. Combining interface damage and friction in a cohesive-zone model. Int. J. Numer. Methods Eng. 2006, 68, 542–582. [Google Scholar] [CrossRef]
- Serpieri, R.; Alfano, G. Bond-slip analysis via a thermodynamically consistent interface model combining interlocking, damage and friction. Int. J. Numer. Methods Eng. 2011, 85, 164–186. [Google Scholar] [CrossRef]
- Serpieri, R.; Sacco, E.; Alfano, G. A thermodynamically consistent derivation of a frictional-damage cohesive-zone model with different mode I and mode II fracture energies. Eur. J. Mech.-A/Solids 2015, 49, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Engelen, R.A.; Geers, M.G.; Baaijens, F.P. Nonlocal implicit gradient-enhanced elasto-plasticity for the modelling of softening behaviour. Int. J. Plast. 2003, 19, 403–433. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Pijaudier-Cabot, G. Measurement of characteristic length of nonlocal continuum. J. Eng. Mech. 1989, 115, 755–767. [Google Scholar] [CrossRef] [Green Version]
- Ožbolt, J.; Bažant, Z. Numerical smeared fracture analysis: Nonlocal microcrack interaction approach. Int. J. Numer. Methods Eng. 1996, 39, 635–661. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef] [Green Version]
- Kruppke, I.; Butler, M.; Schneider, K.; Hund, R.D.; Mechtcherine, V.; Cherif, C. Carbon Fibre Reinforced Concrete: Dependency of Bond Strength on Tg of Yarn Impregnating Polymer. Mater. Sci. Appl. 2019, 10, 328–348. [Google Scholar]
- Sun, C.; Vaidya, R. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Hassani, B. A direct method to derive the boundary conditions of the homogenization equation for symmetric cells. Commun. Numer. Methods Eng. 1996, 12, 185–196. [Google Scholar] [CrossRef]
- Yang, Q.S.; Becker, W. Numerical investigation for stress, strain and energy homogenization of orthotropic composite with periodic microstructure and non-symmetric inclusions. Comput. Mater. Sci. 2004, 31, 169–180. [Google Scholar] [CrossRef]
- Serafinska, A.; Kaliske, M.; Zopf, C.; Graf, W. A multi-objective optimization approach with consideration of fuzzy variables applied to structural tire design. Comput. Struct. 2013, 116, 7–19. [Google Scholar] [CrossRef]
- Pham, K.; Kouznetsova, V.G.; Geers, M.G. Transient computational homogenization for heterogeneous materials under dynamic excitation. J. Mech. Phys. Solids 2013, 61, 2125–2146. [Google Scholar] [CrossRef]
- Tamsen, E.; Weber, W.; Balzani, D. First, Steps Towards the Direct Micro-Macro Simulation of Reinforced Concrete Under Impact Loading. Proc. Appl. Math. Mech. 2018, 18, e201800181. [Google Scholar] [CrossRef]






| Carbon Filaments | Lefasol VLT-1 Coating |
|---|---|
| = 230,000 MPa | = 1802.9 MPa |
| = 28,000 MPa | |
| = 50,000 MPa | = 605 MPa |
| = 0.23 | = 0.49 |
| = 0.259 |
| E [GPa] | [-] | [MPa] | [MPa] | [-] | [MPa] | R [-] | W [-] | [1/MPa] | e [-] | [-] | [-] | [-] | [-] | [-] | c [mm] | m [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 35 | 105 | 72,500 | 1 | 0 | 4000 | 3500 | 1 | 2 |
| [MPa] | [N/mm] | [MPa] | [N/mm] | [-] | [-] | [MPa] |
|---|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuchs, A.; Curosu, I.; Kaliske, M. Numerical Mesoscale Analysis of Textile Reinforced Concrete. Materials 2020, 13, 3944. https://doi.org/10.3390/ma13183944
Fuchs A, Curosu I, Kaliske M. Numerical Mesoscale Analysis of Textile Reinforced Concrete. Materials. 2020; 13(18):3944. https://doi.org/10.3390/ma13183944
Chicago/Turabian StyleFuchs, Alexander, Iurie Curosu, and Michael Kaliske. 2020. "Numerical Mesoscale Analysis of Textile Reinforced Concrete" Materials 13, no. 18: 3944. https://doi.org/10.3390/ma13183944
APA StyleFuchs, A., Curosu, I., & Kaliske, M. (2020). Numerical Mesoscale Analysis of Textile Reinforced Concrete. Materials, 13(18), 3944. https://doi.org/10.3390/ma13183944





