Abstract
The main purpose of this paper is to establish an analysis model of laminated composite rectangular plate with/without cutouts on the basis of three-dimensional elasticity theory and provide the exact three-dimensional solution. In the present work, the effect of the cutout is considered by subtracting the energies of cutouts from the total energy of the entire plate. The standard three-dimensional trigonometric cosine Fourier series and auxiliary Fourier series are chosen as admissible functions, and the Hamilton’s principle and Rayleigh-Ritz procedure are used to obtain the exact solution. In order to verify the effectiveness and reliability of the proposed method, some numerical results are obtained, and the results are compared with the ones available in the literature or finite element analysis. Finally, the effects of some key parameters which will affect the vibration characteristics are analyzed, and the non-dimensional frequency parameters are obtained, which can serve as benchmark data for the future research.
1. Introduction
A composite material is a heterogeneous material formed by combining two or more constituent materials with different properties integrated together to achieve enhanced structural performance. Owing to the high specific strength and stiffness, high fatigue resistance, light weight, and good thermal stability compared with conventional heterogeneous materials, applications of composite structures are employed in diverse fields that include vehicles, aircraft, turbines, architecture, submarines, and so on. [,]. With the continuous development of composite material manufacturing technology, composite materials have developed into one of the four major material systems in parallel with metal materials, polymer materials, inorganic non-metal materials, and laminated composite plates have become the basic structural components of most engineering structures. Therefore, it is necessary for engineers to have a thorough understanding of the vibration characteristics of laminated composite plates to ensure the reliability of structural performance.
In recent decades, the prediction of vibration characteristics of composite structure has attracted great interest from engineers and experts, and significant research advances have been achieved. Furthermore, a large amount of analytical theories have been established, such as the classical laminated plate theory (CLPT), first-order shear deformation theory (FSDT), higher-order shear deformation theory (HSDT), zigzag theory (ZZT), and three-dimensional elasticity theory (3DT).
The classical laminated plate theory is the simplest theory of all plate theories, Love [] proposed this theory which is based on the Kirchhoff’s hypothesis in the late 19th century. According to the theory, the displacement field is expressed as three displacement components along the x, y, z coordinate directions of a point on the midplane, thus the three-dimensional structures are reduced to two-dimensional structures. The simple form of displacement fields and reduction of variables result in simple equations and high calculation efficiency, it is applicable to the thin multi-layer composite structures. By neglecting the influence of the transverse shear deformation and rotational inertia, the vibration characteristics of the rather thick plates obtained by this theory are inaccurate, which will lead to smaller displacement and stress and higher natural frequency of the plates. Even for thin laminated composite plates, when the Young’s modulus of the material is small, the transverse shear deformation cannot be neglected, and the resultant deviation of the theory increases sharply. CLPT remains a popular approach to solving the vibration problems of thin structures, and many research groups have proposed some theories in order to achieve better results based on CLPT. Gorman and Ding [,] exploited the superposition method and Galerkin method to obtain the exact analytical solution of laminated composite plates under free boundary conditions. Nallim et al. [,,] used the Ritz method in conjunction with natural coordinates to express the geometry of general plates by using a set of beam characteristic orthogonal polynomials. Vibration characteristics of general quadrilateral plates, trapezoidal plates, skew plates, and rhomboidal plates with angle-ply layers have been studied. Secgin et al. [] proposed a discrete singular convolution (DSC) approach by using a grid discretization based on distribution theory and wavelets. Cosentino and Weaver [] developed a mixed theory by means of Reissner’s variational approach based on Castigliano’s principle of least work in conjunction with a Lagrange multiplier method to assess the effect of transverse shear stresses of thick composite laminates and sandwich plates.
In order to obtain more accurate vibration characteristics of laminated composite structures, Reissner [] and Mindlin [] proposed the first-order shear deformation theory by including the transverse shear deformation, and assumed that the shear force and strain are constant in the thickness coordinate direction, which is not consistent with the parabola distribution of shear force and strain. Therefore, the shear correction factor has been introduced into this theory to correct the shear strain and stress [,,], which is related to the material, geometry, loads, boundary conditions, and laminations. The results obtained by the first-order shear deformation theory largely depend on the shear correction factor which is generally selected as 5/6 or . Subsequently, the higher-order shear deformation theory was proposed by Reddy [,] to overcome the shortcomings of CLPT or FSDT. Liew et al. [] adopted the first-order shear deformation theory in the moving least squares differential quadrature procedure by using the moving least squares shape functions and their partial derivatives to obtain the weighting coefficients to predict the free vibration behavior of moderately thick symmetrically laminated composite plates. Karami et al. [] applied the differential quadrature method (DQM) for free vibration analysis of moderately thick composite plates with edges elastically restrained against translation and rotation. The governing differential equations with their boundary conditions are transformed into algebraic equations by using differential quadrature rules in order to establish the eigenvalue equations, and the results showed that the DQM can yield an accurate solution using few grid points. Ngo-Cong et al. [] employed one-dimensional integrated RBF networks instead of conventional differentiated RBF networks to approximate the field variables, and the rectangular or non-rectangular plates are discretized by means of Cartesian grids. Carrera [] reduced the third-order model from five displacement variables to three by imposing homogeneous stress conditions with correspondence to the plate top-surface, and then modified it to apply to non-homogeneous stress conditions. Closed form solution has been obtained for both stresses and displacements in the case of harmonic loadings and simply supported boundary conditions. Chen et al. [] employed the p-Ritz method by using the polynomials as the admissible trial displacement and rotation functions to study the vibration of laminated plates. Aydogdu [] chose different types of shape functions to determine the distribution of the transverse shear strains and stresses along the thickness according to 3-D results to present a new higher order shear deformation theory. The new shear model was used to analyze bending, free vibration, and bulking of laminated composite plates. Ferreira et al. [] applied a multi-quadrics radial basis function method and a third-order shear deformation theory to solve the analysis of isotropic and symmetric laminated composite thick beams and plates. Liu et al. [] used the radial basis functions with polynomial reproduction to present the problem domain by a set of scattered nodes in its support domain. The static deflection, free vibration, and bulking analysis of laminated composite plates were presented.
Generally, the solution of higher-order shear deformation theory is more accurate than that obtained by using the first-order shear deformation theory due to the shear strain being distributed as a cubic function in the thickness direction; however, they introduce rather sophisticated formulations and boundary terms that are not easily applicable or yet understood []. All of the above methods belong to the equivalent two-dimensional methods, and the two-dimensional methods cannot satisfy the piecewise continuous displacement requirement and insufficient considerations for the transverse stress fields between layers. Murakami [] developed the zigzag theory by including a zigzag shaped function to approximate the thickness variation of in-plane displacement. Sciuva [,] proposed a piecewise linear zigzag theory and then a non-linear third-order zigzag theory which accounts for continuous inter-laminar transverse shearing stresses at the interfaces between any two adjacent layers. Kapuria et al. [,,,] applied a new zigzag theory to analyze the static, dynamic, bulking, and thermal problems of laminated composite beams or plates. Pandit et al. [] proposed an improved higher order zigzag theory for the static analysis of laminated sandwich plates with soft compressible core. The variation of in-plane displacements is assumed to be cubic for both the face sheets and the core, the transverse displacement is assumed to vary quadratically within the core while it remains constant through the faces. Khandelwal et al. [] developed an improved FE plate model based on refined higher order shear deformation theory (RHSDT) and a least square error method (LSE) to accurately predict the deflections and stresses of composite and sandwich laminates. The zigzag theory was proposed based on the nine node element which satisfies the inter-laminar shear stress continuity conditions at the layer interfaces and zero transverse shear stress conditions at the top and bottom of the plate. The development of zigzag theory can be found in []. Generally, there are many variables in the zigzag theory and the displacement field functions are relatively complicated.
The three-dimensional elasticity theory does not rely on any hypothesis, each sublayer of the structure is regarded as a three-dimensional entity which is described as an independent function, and it satisfies the continuity of interlaminar displacement and stress requirement. Liew et al. [] presented a continuum three-dimensional Ritz formulation by selecting sets of orthogonally generated polynomial functions as shape functions. The frequency parameters and mode shapes of thick plates have been solved with five practical groups of boundary conditions. Senthil et al. [] presented a three-dimensional exact analytical solution and benchmark results for the free and forced vibrations of simply supported functionally graded rectangular plates by using suitable displacement functions in order to reduce the governing partial differential equations to a set of coupled ordinary differential equations in the thickness direction, which are solved by the power series method. Zhou et al. [,,,,] used Chebyshev polynomials and static beam functions as admissible functions in conjunction with Rayleigh-Ritz method to study the three-dimensional vibrations of rectangular, skew, elliptical, and circular annular plates, as well as solid and hollow circular cylinders with different boundary conditions. Qu et al. [] employed a multilevel partitioning hierarchy, viz., multilayered parallelepiped, individual layer and layer segment, which are based on the exact three-dimensional elasticity theory to analyze the free and transverse vibrations of multilayered laminated composite and sandwich beams, plates, and solids with various boundary conditions. The displacement components of each layer segment are approximated as the product of orthogonal polynomials and/or trigonometric functions.
The structure with cutouts is common in the practical engineering, the cutouts are used to reduce the weight or provide operational and maintenance access. The existence of cutouts changes the dynamic characteristics of the structure and damages the service life of the structures. It is necessary to study the effect of the cutouts on the vibration response of the structures. Liew et al. [] employed a domain decomposition method by using a basic L-shaped element which is divided into appropriate sub-domains that are dependent upon the location of the cutouts as the basic element to solve the free vibration of plates with central cutouts. Kumar et al. [] developed a finite element formulation based on higher-order shear deformation theory and Hamilton’s principle to study the vibration response of thick square composite plates with a central rectangular cutout. The effect of material orthotropy, boundary conditions, side-to-thickness ratio, delamination size, and location around the cutout is investigated. Sakiyama et al. [] proposed an approximate method and transformed the problem into an equivalent square plate with non-uniform thickness by considering the cutout as an extremely thin part of the equivalent plate. The Green function is used to obtain the discrete solution and characteristic equation of the plate. Laura et al. [,,,] have made some achievements in the vibration characteristics of plates with cutouts by applying the Rayleigh-Ritz variational method. Shufrin et al. [] presented a new semi-analytical variational extended the Kantorovich method to model rectangular plates with variable thickness and cutouts. The plate thickness and deflections are represented as a finite sum of multiplications of one-dimensional functions. Kwak et al. [] developed an independent coordinated coupling method (ICCM) in which the energies of the plate domain and the cutout domain are derived independently and the two independent coordinates are coupled by imposing kinematic relations. The vibration analysis of a rectangular plate with a rectangular cutout or a circular cutout is investigated. Huang [,] then applied this method to solve the problem of orthotropic composite laminated plate and functionally graded carbon nanotube-reinforced plate. The existing literature surveys show that most of the studies on the vibration of rectangular plates with cutouts are based on the traditional two-dimensional theories, and that three-dimensional exact solutions are very rare.
In this paper, a unified analysis model of the vibration characteristics of the laminated composite plates with/without cutouts is established, and the three-dimensional exact solution is provided with different boundary conditions. According to the energy principle, the Lagrangian energy functions of the plate and the cutout are obtained, and then a standard three-dimensional trigonometric cosine function and auxiliary Fourier series are selected as the admissible functions. The basic idea of solving the free vibration of a plate with a cutout is to subtract the energy of the cutout part from the total energy of the plate. The governing equations are solved by using the Hamilton’s principle and Rayleigh-Ritz method. In order to verify the reliability of the method, some numerical examples are carried out to compare with those available in the literature and the finite element analysis. Furthermore, the effect of some key parameters which may affect the vibration characteristics is conducted, including the position of the cutouts, the size of the cutouts, the laminations, the boundary conditions, and the layer fiber direction angle. The non-dimensional frequency parameters are shown which can serve as a benchmark solution for future research.
2. Theoretical Formulations
2.1. Description of the Model
Consider a multilayered laminated composite rectangular plate with a rectangular cutout, as shown in Figure 1. The global coordinate system (x, y, z) which located in the middle surface of the structure is considered to present the dimensions. The length, width, and thickness of the plate are assumed as a, b, and h, the dimensions of the rectangular cutout in the x and y directions are c and d, the distances of the cutout in the x and y directions with respect to the coordinated point O are xa and yb, the coordinates of the cutout center are xh and yh, whereas xh = xa + c/2 and yh = yb + d/2, respectively. The middle surface displacements of the plate in the x, y, and z directions are denoted by u, v, and w, respectively. The number of the layers of the laminated composite plate is assumed to be N, and the kth layer has a thickness of hk, where the hk = zk+1 − zk, and the zk+1 and zk are the distances from the top surface and the bottom surface of the layer to the referenced middle surface. The principal coordinates of the laminated composite plate in the kth layer are denoted as 1, 2, and 3, the angle between the material axis and x coordinate is denoted by . The artificial springs are introduced in order to simulate different kinds of boundary conditions, three groups of springs ku, kv, and kw, which are distributed uniformly along the edges. The stiffness of the springs can take any value from zero to infinity to model the classical boundary conditions or elastic boundary conditions.
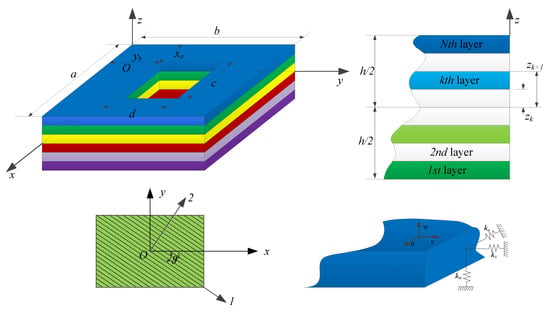
Figure 1.
Model of laminated composite rectangular plate with a rectangular cutout.
2.2. Stress-Strain Relations and Stress Resultants
Based on the three-dimensional elasticity theory and small deformation theory, the strain—displacement relations of the kth layer for the plate are of the form
where the uk, vk, and wk are the middle surface displacement components of an arbitrary point of the plate in the x, y, and z directions, respectively. , , , , , and are the normal and shear strain components in the x, y, and z coordinate system.
According to the generalized Hooke’s law, the corresponding stress-strain relations in the kth layer of the plate are obtained as
where the , , , , , and are the normal and shear stress components of the kth layer of the plate. The constants are elastic stiffness coefficients of the layer, which can be expressed as
where are material constants in the principal coordinate system (1, 2, and 3), which are expressed as
where ,, and are moduli of elasticity of the kth layer in the principle directions, , , and are shear moduli and are Poisson’s ratios. According to the symmetry of coefficients in the stress-strain relationship, the constants satisfy the following
An isotropic model can be obtained by letting: , , and , where and are elastic modulus and Poisson’s ratio of the isotropic material, respectively.
2.3. Energy Functions
As shown in Figure 1, according to the three-dimensional elasticity theory, the energy functions of the plate and the cutouts are established independently in the global coordinate system, which can be expressed as
where is the kinetic energy of the entire plate, is the kinetic energy of the cutout part, is the strain energy of the entire plate, is the strain energy of the cutout part, is the potential energy stored in the boundary springs, and is the work done by the external force.
The basic idea to solve the vibration of a plate with cutouts is to subtract the energies of the cutouts part from the total energy of the plate without cutouts. In that sense, the total energy of a plate with a cutout is express as Equation (38), a plate without cutouts can be seen as a special case of a plate with cutouts, the total energy of a plate without cutouts is expressed as Equation (39)
2.4. Admissible Displacement Functions
The selection of the admissible displacement functions has a significant effect on the convergence and efficiency of the results. According to [], the author expressed the displacement field functions as Fourier series with auxiliary polynomials, the integration process is complicated due to the non-orthogonality between Fourier series and polynomials. With the increase of the cutout number, the solution process will become more and more complex, therefore, the selection of the admissible displacement functions is significant to reduce the complexity of the calculation. In this paper, the admissible displacement functions are expressed in the form of complete trigonometric Fourier series expansions due to the orthogonality and completeness, as well as the excellent stability in numerical calculations when using the Rayleigh-Ritz method. The admissible functions are expressed as the component segment standard cosine Fourier series functions, and the potential derivative discontinuities of the displacements at the boundary are transferred to the added auxiliary trigonometric terms. The admissible displacement functions are expressed as three variables separated along the x, y, and z directions.
where , , , and , , and are the unknown Fourier coefficients of the three-dimensional Fourier series expansions for the admissible displacement functions, M, N, and Q are the truncation numbers with respect to variables x, y, and z, respectively. The supplementary functions are defined as
It is easy to verify that
, , and have the same expression as and . The six supplementary functions are introduced to solve the potential discontinuities of displacement functions of three-dimensional plate structure at the boundary conditions. The displacement functions can satisfy arbitrary boundary conditions and will significantly improve the convergence of the solution compared with the polynomials and reduce the calculation time due to the orthogonality of the trigonometric Fourier series.
2.5. Solution Procedure
In order to obtain the exact solution of the governing equations and boundary conditions of the plate with a cutout, the Hamilton’s principle is applied. Substituting the admissible displacement functions Equation (40) to Equation (43) into the Lagrangian energy functions Equation (32) to Equation (39), and minimizing the function L with respect to the unknown Fourier coefficients of the admissible displacement functions, one can easily obtain
The Equations of motion for the plate with a cutout can be yielded and are summed up in the matrix form as
where K is the stiffness matrix of the plate and M is the mass matrix. The stiffness matrix and the mass matrix both are symmetric and they can be expressed as
X is the column vector which contains the unknown Fourier coefficients. The natural frequencies and mode shapes of laminated composite rectangular plate with cutouts can be obtained by solving the eigenvalues of Equation (47). Due to the large number of formula terms of K and M, the detailed calculation expressions are not given here.
3. Results and Discussion
In this part, numerical examples pertaining to the free vibration analysis of multilayered laminated composite rectangular or square plates with/without cutouts are presented in order to demonstrate the validity and efficiency of the described method. The results are compared with the solutions available in the existing literature and the finite element analysis. The effect of eccentricity of cutout positions and cutout sizes are studied for free vibration behavior with different boundary conditions. Numerical results are obtained with different layered laminations of symmetric and antisymmetric cross-ply and angle-ply.
Four groups of springs are introduced to simulate different kinds of boundary conditions, including free (F), simply supported (S), clamped supported (C), and elastic supported (E) boundary conditions, the stiffness of the springs are given in Table 1. Unless other stated, all layers of the plate have equal thickness and the same material parameters. The geometrical dimensions and material properties of the plate are given as follows: m, , ; , GPa, , , , kg/m3. The non-dimensional frequency parameters are expressed as .

Table 1.
Values of spring stiffness taken by different boundary conditions
3.1. Validity and Convergence of The Method
In this section, some numerical examples are carried out to verify the validity and the convergence of the proposed method in terms of thickness, boundary conditions, and cutout sizes. The accuracy of the method is confirmed by a comparison study with the data published in the literature of rectangular plate with/without considering cutouts, the data are given in Table 2 and Table 3. The symbol ‘-’ in Table 2 and Table 3 indicate that the frequencies were not considered in the reference work.

Table 2.
The first six natural frequencies (Hz) of simply supported cross-ply (0°/90°/0°) laminated square plate with different thickness-length ratios.

Table 3.
First six natural frequencies (Hz) of angle-ply (45°/−45°/45°/−45°) laminated square plate with different thickness-length ratios and different boundary conditions.
First, for the case of plate without cutouts, the first six natural frequencies of a three-layered, cross-ply (0°/90°/0°) laminated square plate without cutouts under simply supported boundary conditions are presented in Table 2. Three kinds of thickness-length ratios, i.e., = 0.01, 0.1, 1 corresponding to thin, moderately thick, and thick plates are performed, whereas represents a solid cube, respectively. From Table 2, it is obvious that the proposed method has fast convergence behavior. The maximum error of the 9 × 9 × 9 truncated configuration compared with [] is 0.086%, which proves the validity and accuracy of this method. In the following examples, the Fourier series is truncated to M × N × Q = 9 × 9 × 9. In Table 3, the first six natural frequencies of a four-layered, angle-ply (45°/−45°/45°/−45°) laminated square plate without cutouts are presented, and the FFFF, SFSF, FFCF boundary conditions with different thickness-length ratios are performed in the comparison. The geometrical dimensions and material properties are the same as for Table 2. It can be seen from the table that the maximum error with the first-four natural frequencies provided by Qu et al. [] is 0.155%, and the present results are in good agreement with those results of Ref. [].
Second, in order to verify the reliability of solving the vibration characteristics of a plate with cutouts, a two-layered, cross-ply (0°/90°) laminated square plate with central square cutouts or rectangular cutouts under simply supported boundary condition has been considered, and the first six natural frequency parameters are performed in Table 4. The results of the proposed method are compared with those obtained by Sheikh et al. []. The geometrical dimensions and material properties of the plate are given as follows: m, , ; , GPa, , , , kg/m3. From the table, it can be seen that the difference between the data of the proposed method and Sheikh et al. [] is less than 0.556%, which shows that the present method is able to accurately predict the frequency parameters of a rectangular plate with cutouts. The small differences are related to different laminated plate theory and solution program methods.

Table 4.
First six frequency parameters Ω of cross-ply (0°/90°) laminated square plate with different cutout sizes under simply supported boundary condition
3.2. Effect of Eccentricity of Cutout Position
In this section, the effect of eccentricity of cutout positions is studied for antisymmetric cross-ply (0°/90°/0°/90°) laminated rectangular plate with CCCC (four edges clamped) boundary condition. The geometry dimensions are: , m, , , . The coordinates of the cutout center ratio, thus eccentricity ratio, xh/a and yh/b are varied from 0.2 to 0.8 along the x direction and y direction, separately. Table 5 and Table 6 show some of the first 20 non-dimensional frequency parameters compared with the solution of finite element method. The finite element method results are obtained from 3D model by using the software ANSYS Workbench, and the element size is selected as 5 × 5 mm. The present solution agrees well with the results of finite element method, and the data obtained by finite element method are slightly larger than the data obtained by the present method because of the finite element method needs to refine mesh to obtain enough accuracy. The data are symmetric about the geometric centers due to the symmetry of the geometry.

Table 5.
Some of the first 20 frequency parameters Ω of cross-ply (0°/90°/0°/90°) laminated rectangular plate with different cutout positions in the x direction under CCCC boundary condition.

Table 6.
Some of the first 20 frequency parameters Ω of cross-ply (0°/90°/0°/90°) laminated rectangular plate with different cutout positions in the y direction under CCCC boundary condition.
In Figure 2, variation of the lowest four order frequency parameters against the cutout position ratio are shown for the eccentricity in both x and y directions. From Figure 2a, we can see that the frequency firstly increases and then decreases for the first and second order frequency parameters when the eccentricity in the x direction goes from 0.2 to 0.5, while the third and fourth orders have reverse behavior, respectively. From Figure 2b, there is little variation in the second and third orders with the eccentricity ratio varied in the y direction. However, for the fourth order, the frequency parameter has gone through the process of decrease after going up for yh/b in the range of 0.2–0.5. For the first order, the fundamental frequency increases and then declines both in the x direction and y direction, and reaches its wave crest at 0.5. It can conclude that, for a rectangular plate with different aspect ratios, the cutout positions have different effects on the vibration characteristics. Nevertheless, for a square plate with a square cutout, it is conceivable that the frequency parameter variation is consistent in the x direction and y direction.
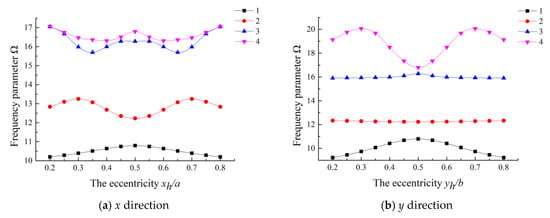
Figure 2.
Variation of the frequency parameters for a (0°/90°/0°/90°) laminated rectangular plate with different cutout eccentricity ratios.
3.3. Effect of Cutout Size
Three examples are selected to demonstrate the effect of the cutout size with different boundary conditions, the cutout size ratio is varied from 0 to 0.8. In Table 7, some of the first 20 non-dimensional frequency parameters for the symmetric cross-ply (0°/90°/0°/90°) lamination with different cutout sizes under CCCC boundary conditions are examined. From Table 7, it can be seen that increasing of the cutout size of the plate increases the fundamental frequency parameters. The increasing trend is due to the introduction of the cutout; however, the loss of mass gets more significance over the loss of stiffness and hence the frequency parameters increase. Table 8 shows the data of antisymmetric cross-ply (0°/90°/90°/0°) laminated square plate with different cutout sizes under CSCS boundary condition, and Table 9 for angle-ply (45°/−45°/45°/−45°) laminated square plate with different cutout sizes under CFCF boundary condition. It is evident that from Table 8 and Table 9, the fundamental frequency parameters increase and then decrease when the cutout size ratio is varied from 0 to 0.8. The typical mode shapes corresponding to the first four orders of vibration for the plate compared with those obtained from the finite element method are given in Figure 3, Figure 4 and Figure 5.

Table 7.
Some of the first 20 frequency parameters Ω of cross-ply (0°/90°/0°/90°) laminated square plate with different cutout sizes under CCCC boundary condition.

Table 8.
Some of the first 20 frequency parameters Ω of cross-ply (0°/90°/90°/0°) laminated square plate with different cutout sizes under CSCS boundary condition.

Table 9.
Some of the first 20 frequency parameters Ω of angle-ply (45°/−45°/45°/−45°) laminated square plate with different cutout sizes under CFCF boundary condition.
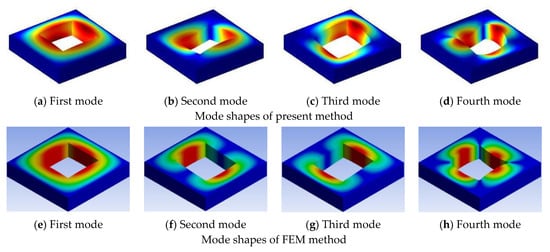
Figure 3.
First four mode shapes of (0°/90°/0°/90°) laminated square plate with CCCC boundary condition for a cutout size ratio of 0.5.
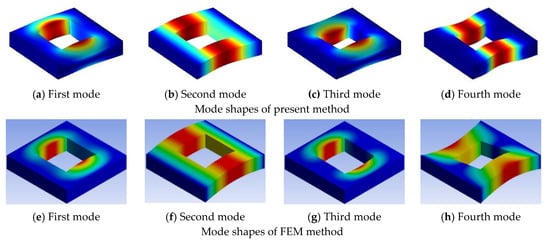
Figure 4.
First four mode shapes of (0°/90°/90°/0°) laminated square plate with CSCS boundary condition for a cutout size ratio of 0.5.
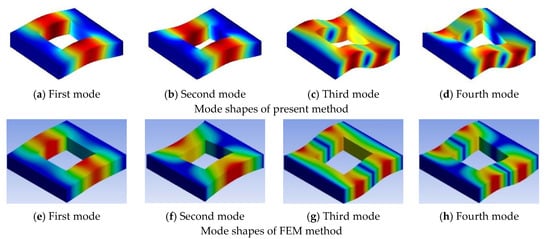
Figure 5.
First four mode shapes of (45°/−45°/45°/−45°) laminated square plate with CFCF boundary condition for a cutout size ratio of 0.5.
3.4. Effect of Lamination
To further study the effect of the number of layers on the frequency characteristic, the fundamental frequency parameters of two-layered, three-layered, four-layered, six-layered, and eight-layered, cross-ply and angle-ply plates with different cutout sizes are presented, the data are given in Table A1. Figure 6 shows the fundamental frequency parameters of cross-ply and angle-ply laminations with even numbers of layers under CCCC and SSSS boundary conditions. From Figure 6, it can be noticed that the frequency parameters increase with the increase of the number of the layers for both cross-ply and angle-ply. From Figure 6a,b, it is obvious that for CCCC boundary condition, the frequency parameters increase with the increase of cutout size ratio, and when the cutout size ratio exceeds 0.6, the frequency parameters increase sharply. However, it is somewhat complicated for SSSS boundary condition. From Figure 6c, for cross-ply lamination, the trend of frequency parameters declines first and then rises, when the cutout size ratio reaches a certain value which is respectively equal to 0.7, the frequency parameter decreases sharply. For angle-ply lamination, there is only a little bit of an upward trend when the cutout size ratio is less than 0.3, while after that, the frequency parameter trend declines with the increase of cutout sizes.
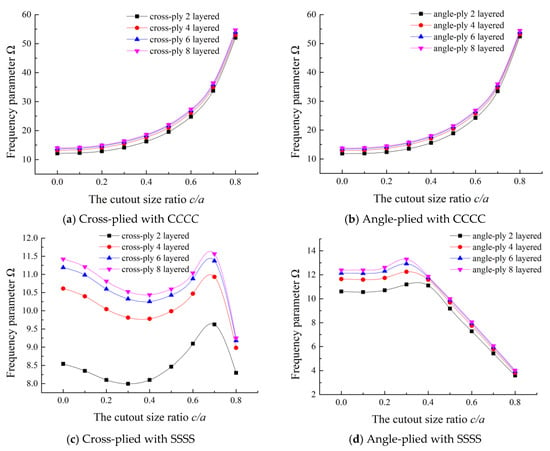
Figure 6.
Fundamental frequency parameters of different laminations with various cutout sizes.
3.5. Effect of Boundary Condition
Next, to research the effect of boundary conditions, a four-layered, symmetric, and antisymmetric composite plate under six groups of boundary conditions, i.e., CCCC, CSCC, CSSC, CSCS, CSSS, and SSSS are considered. The fundamental frequency parameters are calculated for various cutout sizes and the data are detailed in Table 10.

Table 10.
Fundamental frequency parameters Ω of square plate for various cutout size ratio with different boundary conditions.
It can be seen that the fundamental frequency parameters of antisymmetric structures are slightly larger than those of symmetric structures and the maximum frequency parameters are under the CCCC boundary conditions. Comparing the boundary conditions of CCCC and CSCC, for the same cutout size ratios, the boundary constrain is released from clamp supported to simply supported, the stiffness becomes smaller and the mass remains unchanged, thus the frequency parameter decreases both for symmetric and antisymmetric structures, cross-ply and angle-ply laminations. For different boundary conditions, with the increase of the cutout sizes, both of the mass matrix and the stiffness matrix get smaller, the frequency parameters tend to rise or drop. When the frequency parameters increase, mainly because the loss mass is more significant than the loss of stiffness, whereas the reason is reverse for the frequency parameters decreasing.
3.6. Effect of Layer Fiber Direction Angle
The effect of layer fiber direction angle on the frequency parameters of laminated composite plate with cutouts is studied in the following section. The detailed data are given in Table A2. The first six frequency parameters of a three-layered angle-ply (0°/°/0°) square plate with a center cutout under CFCF boundary condition are investigated, where is the fiber angle in the range of 0°–90°. In Figure 7, the curves of frequency parameters changing with the fiber orientations under various cutout sizes are plotted. The fiber direction angle is varied from 0° to 180° with a step of 15°. All of the curves are symmetric about = 90°, and the trend of frequency parameters is not changing in the same way with the increase of cutout size ratio. The fundamental frequency parameters increase and then decrease with the increase of the cutout size ratio. The trend can be regrouped in three groups according to the performance: Group I, a smaller cutout size ratio, where 0 ≤ c/a ≤ 0.2; Group II, 0.2 < c/a ≤ 0.5; Group III, a larger cutout size ratio, where 0.5 < c/a ≤ 0.8. The trend in each group is generally consistent. It can be observed that the increment of the fiber direction angle from 0° to 90° results in the increase of the lowest two frequency parameters of the plate. For Group III, the frequency parameters climb up with the fiber direction angle changed from 0° to 90°. When the cutout size ratio is small, the trend of the lower-order modal is simpler, but for higher-order modal, the trend is more complex. This is mainly because the bending stiffness plays a dominant role for the lower-order modal, while for the higher-order modal, the bending and shear deformation are coupled with each other, which make the vibration behavior more complex.
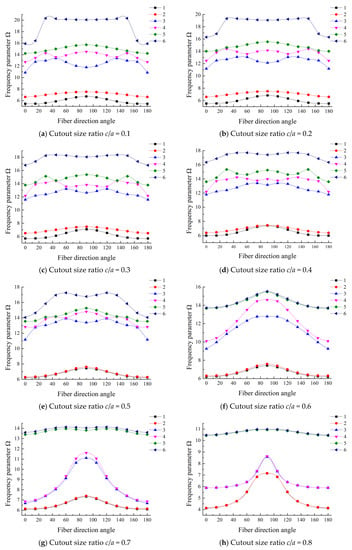
Figure 7.
The first six frequency parameters of different fiber orientations with various cutout sizes.
4. Conclusions
In this paper, a unified three-dimensional solution is provided to study the free vibration characteristics of laminated composite rectangular plate with/without cutouts by using the energy principles in conjunction with Rayleigh-Ritz method. The energy equations of the plate and the cutouts which are based on the three-dimensional elasticity theory are established independently. The governing equation was obtained by subtracting the energies of cutouts from the total energies of the entire plate. The displacement field is represented as a standard three-dimensional trigonometric cosine Fourier series and modified auxiliary Fourier series which can satisfy the boundary conditions and reduce the computational complexity. The three-dimensional solution is obtained by using the Hamilton’s principle to solve the unknown Fourier coefficients. The advantage of this method is that the unified model can simulate the different boundary conditions by changing the values of spring stiffness and there is no need to establish various models separately. For the free vibration characteristics of laminated composite rectangular plate with/without cutouts under various boundary conditions, the accuracy of this method is better than the results of the literature and finite element analysis. Furthermore, some numerical examples are carried out to show the performance of the proposed method and we can arrive at the following conclusions:
First, the frequency parameters of laminated composite square plate with/without cutouts under various boundary conditions are calculated and compared with those available in the literature. It can be seen from the comparison that the proposed method is accurate in predicting the vibration characteristics of plates with cutouts.
Second, the influence of some key parameters, such as the cutout positions, the cutout sizes, the boundary conditions, the laminations, and the fiber orientations on the frequency parameters are discussed. The cutout positions have a significant effect on the frequency parameters, and the maximum fundamental frequency occurs when the cutout is located in the center of plate. From the variations of the cutout size ratio, it can be concluded that with the increase of cutout size ratio under various boundary conditions, the loss of mass and stiffness play a different role in determining the frequency parameters. When the total thickness is constant, the frequency parameter grows as the number of the layers increases. The fundamental frequency parameters climb up as the fiber direction angle varies from 0°–90°.
Author Contributions
Conceptualization, K.X., W.H., and Q.L.; Methodology, W.H. and Q.L.; Programming, W.H.; Validation, K.X., W.H., and Q.L.; Writing—original draft preparation, W.H.; Writing—review and editing, K.X., W.H., and Q.L.; Visualization, W.H.; Supervision, K.X. and Q.L.; Project administration, K.X., W.H., and Q.L.; Funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 51405096) and the Fundamental Research Funds for the Central Universities (HEU3072019CF0706).
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
Appendix A

Table A1.
Fundamental frequency parameters Ω of square plate with different cutout sizes under different laminations.
Table A1.
Fundamental frequency parameters Ω of square plate with different cutout sizes under different laminations.
| BC | Laminations | Cutout Size Ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | ||
| CCCC | 0°/90° | 12.150 | 12.275 | 12.876 | 14.142 | 16.251 | 19.543 | 24.769 | 33.761 | 52.051 |
| 0°/90°/0° | 12.730 | 12.907 | 13.606 | 14.918 | 16.886 | 19.624 | 23.752 | 31.375 | 48.357 | |
| (0°/90°)2 | 13.234 | 13.419 | 14.140 | 15.514 | 17.688 | 20.997 | 26.177 | 35.012 | 52.924 | |
| 0°/90°/90°/0° | 13.198 | 13.383 | 14.105 | 15.464 | 17.563 | 20.618 | 25.186 | 33.058 | 49.937 | |
| (0°/90°)3 | 13.743 | 13.941 | 14.683 | 16.091 | 18.310 | 21.678 | 26.941 | 35.889 | 53.979 | |
| (0°/90°)4 | 14.003 | 14.204 | 14.954 | 16.380 | 18.626 | 22.033 | 27.356 | 36.402 | 54.685 | |
| 45°/−45° | 11.888 | 11.928 | 12.390 | 13.543 | 15.590 | 18.888 | 24.216 | 33.469 | 52.450 | |
| 45°/−45°/45° | 12.359 | 12.454 | 13.030 | 14.304 | 16.439 | 19.770 | 25.059 | 34.169 | 52.794 | |
| (45°/−45°)2 | 13.008 | 13.100 | 13.680 | 14.969 | 17.120 | 20.458 | 25.727 | 34.761 | 53.203 | |
| 45°/−45°/−45°/45° | 12.898 | 12.992 | 13.576 | 14.870 | 17.028 | 20.379 | 25.670 | 34.731 | 53.196 | |
| (45°/−45°)3 | 13.512 | 13.621 | 14.214 | 15.532 | 17.723 | 21.115 | 26.444 | 35.521 | 53.974 | |
| (45°/−45°)4 | 13.765 | 13.875 | 14.473 | 15.805 | 18.021 | 21.447 | 26.823 | 35.964 | 54.498 | |
| SSSS | 0°/90° | 8.539 | 8.351 | 8.100 | 7.994 | 8.101 | 8.463 | 9.093 | 9.624 | 8.297 |
| 0°/90°/0° | 10.234 | 10.082 | 9.806 | 9.630 | 9.653 | 9.935 | 10.534 | 11.404 | 8.723 | |
| (0°/90°)2 | 10.612 | 10.399 | 10.046 | 9.811 | 9.778 | 9.987 | 10.471 | 10.934 | 8.979 | |
| 0°/90°/90°/0° | 10.683 | 10.498 | 10.177 | 9.960 | 9.942 | 10.175 | 10.716 | 11.576 | 8.896 | |
| (0°/90°)3 | 11.192 | 10.984 | 10.600 | 10.327 | 10.255 | 10.429 | 10.883 | 11.374 | 9.178 | |
| (0°/90°)4 | 11.422 | 11.210 | 10.814 | 10.525 | 10.438 | 10.596 | 11.038 | 11.566 | 9.249 | |
| 45°/−45° | 10.607 | 10.560 | 10.704 | 11.196 | 11.108 | 9.178 | 7.278 | 5.420 | 3.592 | |
| 45°/−45°/45° | 10.986 | 10.935 | 11.009 | 11.382 | 11.431 | 9.515 | 7.577 | 5.645 | 3.725 | |
| (45°/−45°)2 | 11.641 | 11.595 | 11.736 | 12.250 | 11.596 | 9.695 | 7.746 | 5.782 | 3.814 | |
| 45°/−45°/−45°/45° | 11.502 | 11.453 | 11.565 | 12.030 | 11.472 | 9.557 | 7.611 | 5.666 | 3.732 | |
| (45°/−45°)3 | 12.134 | 12.119 | 12.309 | 12.926 | 11.774 | 9.898 | 7.951 | 5.958 | 3.942 | |
| (45°/−45°)4 | 12.393 | 12.390 | 12.617 | 13.305 | 11.858 | 9.994 | 8.052 | 6.052 | 4.016 | |

Table A2.
First six frequency parameters Ω of angle-ply (0°/°/0°) square plate with various fiber direction angle varied from 0° to 180° under CFCF boundary condition.
Table A2.
First six frequency parameters Ω of angle-ply (0°/°/0°) square plate with various fiber direction angle varied from 0° to 180° under CFCF boundary condition.
| Fiber Angle | Modes | Cutout Size Ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | ||
| 0° | 1 | 5.444 | 5.448 | 5.516 | 5.700 | 5.987 | 6.254 | 6.205 | 6.093 | 4.115 |
| 2 | 6.639 | 6.631 | 6.588 | 6.500 | 6.385 | 6.284 | 6.313 | 6.145 | 4.134 | |
| 3 | 10.757 | 10.866 | 11.170 | 11.575 | 11.792 | 11.162 | 9.260 | 6.685 | 5.892 | |
| 4 | 12.773 | 12.716 | 12.467 | 12.156 | 12.183 | 12.817 | 10.098 | 6.855 | 5.897 | |
| 5 | 14.310 | 14.214 | 14.010 | 13.787 | 13.603 | 13.542 | 13.667 | 13.396 | 10.426 | |
| 6 | 15.756 | 15.907 | 16.302 | 16.787 | 16.345 | 14.047 | 13.726 | 13.606 | 10.473 | |
| 15° | 1 | 5.459 | 5.464 | 5.532 | 5.715 | 6.003 | 6.272 | 6.241 | 6.115 | 4.186 |
| 2 | 6.758 | 6.747 | 6.697 | 6.593 | 6.459 | 6.338 | 6.332 | 6.162 | 4.195 | |
| 3 | 12.809 | 12.752 | 12.504 | 12.196 | 12.223 | 12.747 | 9.975 | 6.937 | 5.905 | |
| 4 | 13.304 | 13.437 | 13.794 | 13.885 | 13.689 | 12.852 | 10.434 | 7.015 | 5.909 | |
| 5 | 14.466 | 14.354 | 14.127 | 14.209 | 14.176 | 13.616 | 13.727 | 13.496 | 10.472 | |
| 6 | 16.252 | 16.415 | 16.845 | 17.361 | 16.861 | 14.634 | 13.757 | 13.694 | 10.513 | |
| 30° | 1 | 5.576 | 5.579 | 5.646 | 5.831 | 6.119 | 6.383 | 6.355 | 6.202 | 4.367 |
| 2 | 7.006 | 6.991 | 6.925 | 6.794 | 6.630 | 6.479 | 6.428 | 6.240 | 4.372 | |
| 3 | 13.014 | 12.954 | 12.697 | 12.382 | 12.409 | 13.038 | 10.869 | 7.379 | 5.965 | |
| 4 | 14.116 | 14.252 | 14.406 | 14.138 | 13.913 | 13.815 | 11.234 | 7.434 | 5.967 | |
| 5 | 14.785 | 14.658 | 14.625 | 15.118 | 15.332 | 14.087 | 13.902 | 13.705 | 10.576 | |
| 6 | 20.766 | 20.317 | 19.311 | 18.237 | 17.450 | 15.837 | 13.918 | 13.887 | 10.614 | |
| 45° | 1 | 5.858 | 5.859 | 5.929 | 6.122 | 6.410 | 6.649 | 6.576 | 6.393 | 4.722 |
| 2 | 7.224 | 7.208 | 7.141 | 7.011 | 6.851 | 6.706 | 6.653 | 6.428 | 4.729 | |
| 3 | 13.444 | 13.371 | 13.083 | 12.749 | 12.793 | 13.440 | 11.628 | 8.043 | 6.109 | |
| 4 | 13.445 | 13.575 | 13.930 | 14.415 | 14.231 | 14.119 | 12.280 | 8.136 | 6.111 | |
| 5 | 15.106 | 14.991 | 14.752 | 14.476 | 14.759 | 14.164 | 14.197 | 13.891 | 10.704 | |
| 6 | 20.674 | 20.252 | 19.324 | 18.354 | 17.682 | 16.945 | 14.261 | 14.050 | 10.744 | |
| 60° | 1 | 6.238 | 6.240 | 6.324 | 6.536 | 6.829 | 7.008 | 6.901 | 6.713 | 5.526 |
| 2 | 7.374 | 7.363 | 7.314 | 7.220 | 7.108 | 7.042 | 7.007 | 6.752 | 5.541 | |
| 3 | 12.586 | 12.712 | 13.064 | 13.215 | 13.297 | 13.903 | 12.317 | 9.137 | 6.391 | |
| 4 | 13.980 | 13.888 | 13.560 | 13.567 | 14.020 | 13.985 | 13.510 | 9.340 | 6.393 | |
| 5 | 15.408 | 15.313 | 15.103 | 14.849 | 14.617 | 14.522 | 14.600 | 13.966 | 10.835 | |
| 6 | 20.574 | 20.151 | 19.221 | 18.279 | 17.700 | 17.250 | 14.730 | 14.132 | 10.879 | |
| 75° | 1 | 6.569 | 6.578 | 6.679 | 6.913 | 7.218 | 7.295 | 7.244 | 7.110 | 6.841 |
| 2 | 7.477 | 7.471 | 7.443 | 7.391 | 7.335 | 7.427 | 7.391 | 7.162 | 6.845 | |
| 3 | 11.921 | 12.040 | 12.380 | 12.884 | 13.405 | 13.566 | 12.768 | 10.645 | 7.320 | |
| 4 | 14.428 | 14.324 | 13.971 | 13.632 | 13.766 | 14.517 | 14.446 | 11.051 | 7.359 | |
| 5 | 15.661 | 15.582 | 15.407 | 15.197 | 15.017 | 14.976 | 15.076 | 13.904 | 10.926 | |
| 6 | 20.511 | 20.078 | 19.107 | 18.125 | 17.531 | 16.961 | 15.196 | 14.104 | 10.976 | |
| 90° | 1 | 6.709 | 6.722 | 6.834 | 7.081 | 7.397 | 7.436 | 7.422 | 7.335 | 7.148 |
| 2 | 7.529 | 7.525 | 7.506 | 7.473 | 7.444 | 7.613 | 7.592 | 7.397 | 7.155 | |
| 3 | 11.681 | 11.797 | 12.130 | 12.631 | 13.165 | 13.390 | 12.777 | 11.108 | 8.569 | |
| 4 | 14.615 | 14.505 | 14.145 | 13.816 | 13.983 | 14.793 | 14.595 | 11.606 | 8.637 | |
| 5 | 15.781 | 15.710 | 15.552 | 15.372 | 15.238 | 15.256 | 15.468 | 13.813 | 10.926 | |
| 6 | 20.495 | 20.059 | 19.065 | 18.050 | 17.412 | 16.764 | 15.527 | 14.041 | 10.980 | |
References
- Liew, K.M.; Pan, Z.Z.; Zhang, L.W. An overview of layerwise theories for composite laminates and structures: Development, numerical implementation and application. Compos. Struct. 2019, 216, 240–259. [Google Scholar] [CrossRef]
- Kulkarni, P.A.; Dhoble, A.S.; Padole, P.M. A review of research and recent trends in analysis of composite plates. Sadhana-Acad. Proc. Eng. Sci. 2018, 43. [Google Scholar] [CrossRef]
- Love, A.E.I. The small free vibrations and deformation of a thin elastic shell. Proc. R. Soc. Lond. 1887, 43, 352–353. [Google Scholar]
- Gorman, D.J. Accurate Free Vibration Analysis of the Completely Free Orthotropic Rectangular Plate by the Method of Superposition. J. Sound Vib. 1993, 165, 409–420. [Google Scholar] [CrossRef]
- Gorman, D.J.; Ding, W. Accurate free vibration analysis of completely free symmetric cross-ply rectangular laminated plates. Compos. Struct. 2003, 60, 359–365. [Google Scholar] [CrossRef]
- Nallim, L.G.; Martinez, S.H.; Grossi, R.O. Statical and dynamical behaviour of thin fibre reinforced composite laminates with different shapes. Comput. Methods Appl. Mech. Eng. 2005, 194, 1797–1822. [Google Scholar] [CrossRef]
- Nallim, L.G.; Oller, S. An analytical-numerical approach to simulate the dynamic behaviour of arbitrarily laminated composite plates. Compos. Struct. 2008, 85, 311–325. [Google Scholar] [CrossRef]
- Nallim, L.G.; Grossi, R.O. Vibration of angle-ply symmetric laminated composite plates with edges elastically restrained. Compos. Struct. 2007, 81, 80–83. [Google Scholar] [CrossRef]
- Secgin, A.; Sarigul, A.S. Free vibration analysis of symmetrically laminated thin composite plates by using discrete singular convolution (DSC) approach: Algorithm and verification. J. Sound Vib. 2008, 315, 197–211. [Google Scholar] [CrossRef]
- Cosentino, E.; Weaver, P.M. An Enhanced Single-layer Variational Formulation for the Effect of Transverse Shear on Laminated Orthotropic Plates. Eur. J. Mech. A-Solids 2010, 29, 567–590. [Google Scholar] [CrossRef]
- Reissner, E. The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 1945, 12, 69–77. [Google Scholar]
- Mindlin, R.D. Influence of rotary inertia and shear on flexural motions of isotropic elastic plates. J. Appl. Mech.-Trans. Asme 1951, 18, 31–38. [Google Scholar]
- Whitney, J.M. Shear Correction Factors for Orthotropic Laminates under Static Load. J. Appl. Mech. 1973, 40, 302–304. [Google Scholar] [CrossRef]
- Bert, C.W. Simplified Analysis of Static Shear Factors for Beams of NonHomogeneous Cross Section. J. Compos. Mater. 1973, 7, 525–529. [Google Scholar] [CrossRef]
- Srinivas, S.; Rao, C.V.; Rao, A.K. An exact analysis for vibration of simply-supported homogeneous and laminated thick rectangular plates. J. Sound Vib. 1970, 12, 187–199. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Reddy, J.N. A general non-linear third-order theory of plates with moderate thickness. Int. J. Non-Linear Mech. 1990, 25, 677–686. [Google Scholar] [CrossRef]
- Liew, K.M.; Huang, Y.Q.; Reddy, J.N. Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadrature method. Comput. Meth. Appl. Mech. Eng. 2003, 192, 2203–2222. [Google Scholar] [CrossRef]
- Karami, G.; Malekzadeh, P.; Mohebpour, S.R. DQM free vibration analysis of moderately thick symmetric laminated plates with elastically restrained edges. Compos. Struct. 2006, 74, 115–125. [Google Scholar] [CrossRef]
- Ngocong, D.; Maiduy, N.; Karunasena, W.; Tran-Cong, T. Free vibration analysis of laminated composite plates based on FSDT using one-dimensional IRBFN method. Comput. Struct. 2011, 89, 1–13. [Google Scholar] [CrossRef]
- Carrera, E. On the use of transverse shear stress homogeneous and non-homogeneous conditions in third-order orthotropic plate theory. Compos. Struct. 2007, 77, 341–352. [Google Scholar] [CrossRef]
- Chen, C.C.; Liew, K.M.; Lim, C.W. Vibration analysis of symmetrically laminated thick rectangular plates using the higher-order theory and p-Ritz method. J. Acoust. Soc. Am. 1997, 102, 1600–1611. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Roque, C.M.; Martins, P. Radial basis functions and higher-order shear deformation theories in the analysis of laminated composite beams and plates. Compos. Struct. 2004, 66, 287–293. [Google Scholar] [CrossRef]
- Liu, L.; Chua, L.P.; Ghista, D.N. Mesh-free radial basis function method for static, free vibration and buckling analysis of shear deformable composite laminates. Compos. Struct. 2007, 78, 58–69. [Google Scholar] [CrossRef]
- Qu, Y.; Long, X.; Yuan, G.; Meng, G. A unified formulation for vibration analysis of functionally graded shells of revolution with arbitrary boundary conditions. Compos. Part B-Eng. 2013, 50, 381–402. [Google Scholar] [CrossRef]
- Murakami, H. Laminated composite plate theory with improved in-plane responses. J. Appl. Mech. 1986, 53, 661–666. [Google Scholar] [CrossRef]
- Sciuva, M.D. Bending, vibration and buckling of simply supported thick multilayered orthotropic plates: An evaluation of a new displacement model. J. Sound Vib. 1986, 105, 425–442. [Google Scholar] [CrossRef]
- Sciuva, M.D. Multilayered anisotropic plate models with continuous interlaminar stresses. Compos. Struct. 1992, 22, 149–167. [Google Scholar] [CrossRef]
- Kapuria, S.; Dumir, P.C.; Ahmed, A. An efficient higher order zigzag theory for composite and sandwich beams subjected to thermal loading. Int. J. Solids Struct. 2003, 40, 6613–6631. [Google Scholar] [CrossRef]
- Kapuria, S.; Achary, G.G. An efficient higher order zigzag theory for laminated plates subjected to thermal loading. Int. J. Solids Struct. 2004, 41, 4661–4684. [Google Scholar] [CrossRef]
- Kapuria, S.; Dumir, P.C.; Jain, N.K. Assessment of zigzag theory for static loading, buckling, free and forced response of composite and sandwich beams. Compos. Struct. 2004, 64, 317–327. [Google Scholar] [CrossRef]
- Kapuria, S.; Kulkarni, S.D. An improved discrete Kirchhoff quadrilateral element based on third-order zigzag theory for static analysis of composite and sandwich plates. Int. J. Numer. Methods Eng. 2007, 69, 1948–1981. [Google Scholar] [CrossRef]
- Pandit, M.K.; Sheikh, A.H.; Singh, B.N. An improved higher order zigzag theory for the static analysis of laminated sandwich plate with soft core. Finite Elem. Anal. Des. 2008, 44, 602–610. [Google Scholar] [CrossRef]
- Khandelwal, R.P.; Chakrabarti, A.; Bhargava, P. An efficient FE model and Least Square Error method for accurate calculation of transverse shear stresses in composites and sandwich laminates. Compos. Part B-Eng. 2012, 43, 1695–1704. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of Zig-Zag theories for multilayered plates and shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Liew, K.M.; Hung, K.C.; Lim, M.K. A continuum three-dimensional vibration analysis of thick rectangular plates. Int. J. Solids Struct. 1993, 30, 3357–3379. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K.; Au, F.T.; Lo, S. Three-dimensional vibration analysis of thick rectangular plates using Chebyshev polynomial and Ritz method. Int. J. Solids Struct. 2002, 39, 6339–6353. [Google Scholar] [CrossRef]
- Zhou, D.; Au, F.T.; Cheung, Y.K.; Lo, S. Three-dimensional vibration analysis of circular and annular plates via the Chebyshev-Ritz method. Int. J. Solids Struct. 2003, 40, 3089–3105. [Google Scholar] [CrossRef]
- Zhou, D.; Lo, S.H.; Cheung, Y.K.; Au, F. 3-D vibration analysis of generalized super elliptical plates using Chebyshev-Ritz method. Int. J. Solids Struct. 2004, 41, 4697–4712. [Google Scholar] [CrossRef]
- Zhou, D.; Lo, S.H.; Au, F.T.; Cheung, Y.; Liu, W. 3-D vibration analysis of skew thick plates using Chebyshev-Ritz method. Int. J. Mech. Sci. 2006, 48, 1481–1493. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K.; Lo, S.H.; Au, F. 3D vibration analysis of solid and hollow circular cylinders via Chebyshev-Ritz method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1575–1589. [Google Scholar] [CrossRef]
- Qu, Y.; Wu, S.; Li, H.; Meng, G. Three-dimensional free and transient vibration analysis of composite laminated and sandwich rectangular parallelepipeds: Beams, plates and solids. Compos. Part B-Eng. 2015, 73, 96–110. [Google Scholar] [CrossRef]
- Liew, K.M.; Kitipornchai, S.; Leung, A.Y.; Lim, C.W. Analysis of the free vibration of rectangular plates with central cut-outs using the discrete Ritz method. Int. J. Mech. Sci. 2003, 45, 941–959. [Google Scholar] [CrossRef]
- Kumar, A.; Shrivastava, R.P. Free vibration of square laminates with delamination around a central cutout using HSDT. Compos. Struct. 2005, 70, 317–333. [Google Scholar] [CrossRef]
- Sakiyama, T.; Huang, M.; Matsuda, H.; Morita, C. Free vibration of orthotropic square plates with a square hole. J. Sound Vib. 2003, 259, 63–80. [Google Scholar] [CrossRef]
- Gutierrez, R.H.; Laura, P.A.; Rossit, C.A. Fundamental frequency of transverse vibration of a clamped rectangular orthotropic plate with a free-edge hole. J. Sound Vib. 2000, 235, 697–701. [Google Scholar] [CrossRef]
- Larrondo, H.A.; Avalos, D.R.; Laura, P.A.; Rossi, R. Vibrations of simply supported rectangular plates with varying thickness and same aspect ratio cutouts. J. Sound Vib. 2001, 244, 738–745. [Google Scholar] [CrossRef]
- Avalos, D.R.; Laura, P.A. Transverse vibrations of simply supported rectangular plates with two rectangular cutouts. J. Sound Vib. 2003, 267, 967–977. [Google Scholar] [CrossRef]
- Laura, P.A.; Avalos, D.R. Small amplitude, transverse vibrations of circular plates with an eccentric rectangular perforation elastically restrained against rotation and translation on both edges. J. Sound Vib. 2008, 312, 906–914. [Google Scholar] [CrossRef]
- Shufrin, I.; Eisenberger, M. Semi-analytical modeling of cutouts in rectangular plates with variable thickness–Free vibration analysis. Appl. Math. Modeling 2016, 40, 6983–7000. [Google Scholar] [CrossRef]
- Kwak, M.K.; Han, S. Free vibration analysis of rectangular plate with a hole by means of independent coordinate coupling method. J. Sound Vib. 2007, 306, 12–30. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J.; Du, J.; Ma, T.; Guo, Y.; Qian, Z. Vibration analysis of a specially orthotropic composite laminate with rectangular cutout using independent coordinate coupling method. Composite Structures 2016, 150, 53–61. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, Y.; Huang, B. Independent coordinate coupling method for vibration analysis of a functionally graded carbon nanotube-reinforced plate with central hole. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Du, J.T.; Li, W.L.; Liu, Z.G.; Xu, H.A.; Ji, Z.L.; Li, W.L. Acoustic analysis of a rectangular cavity with general impedance boundary conditions. J. Acoust. Soc. Am. 2011, 130, 807–817. [Google Scholar] [CrossRef]
- Sheikh, A.H.; Haldar, S.; Sengupta, D. Free Flexural Vibration of Composite Plates in Different Situations Using a High Precision Triangular Element. J. Vib. Control 2004, 10, 371–386. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).