Reliability-Based Low Fatigue Life Analysis of Turbine Blisk with Generalized Regression Extreme Neural Network Method
Abstract
1. Introduction
2. Basic Theory
2.1. Mathematical Model of Low Cycle Fatigue Life
2.2. Mathematical Model of Extremum Response Surface Method
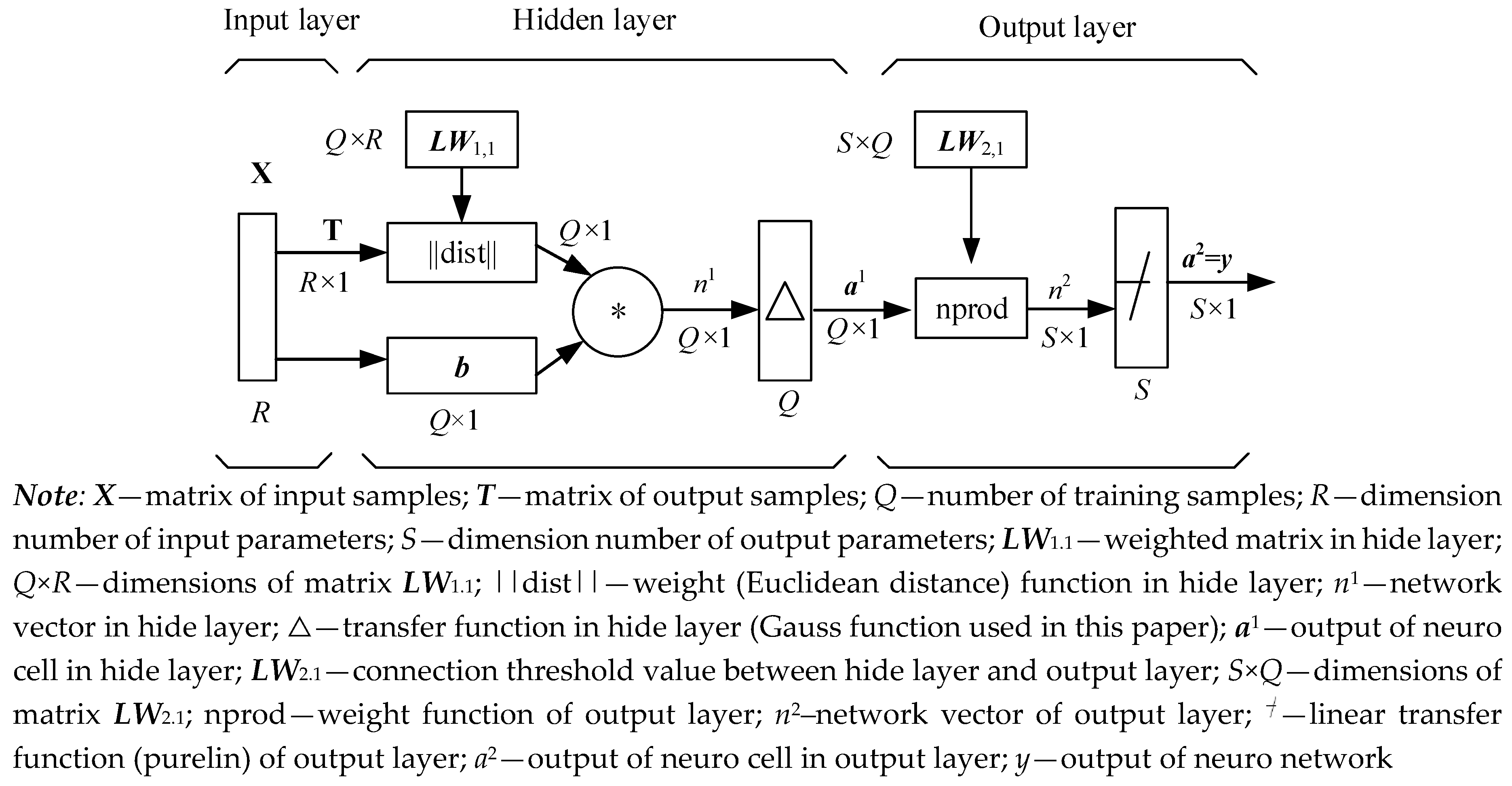
2.3. Mathematical Model of Generated Regression Extremum Neural Network Method
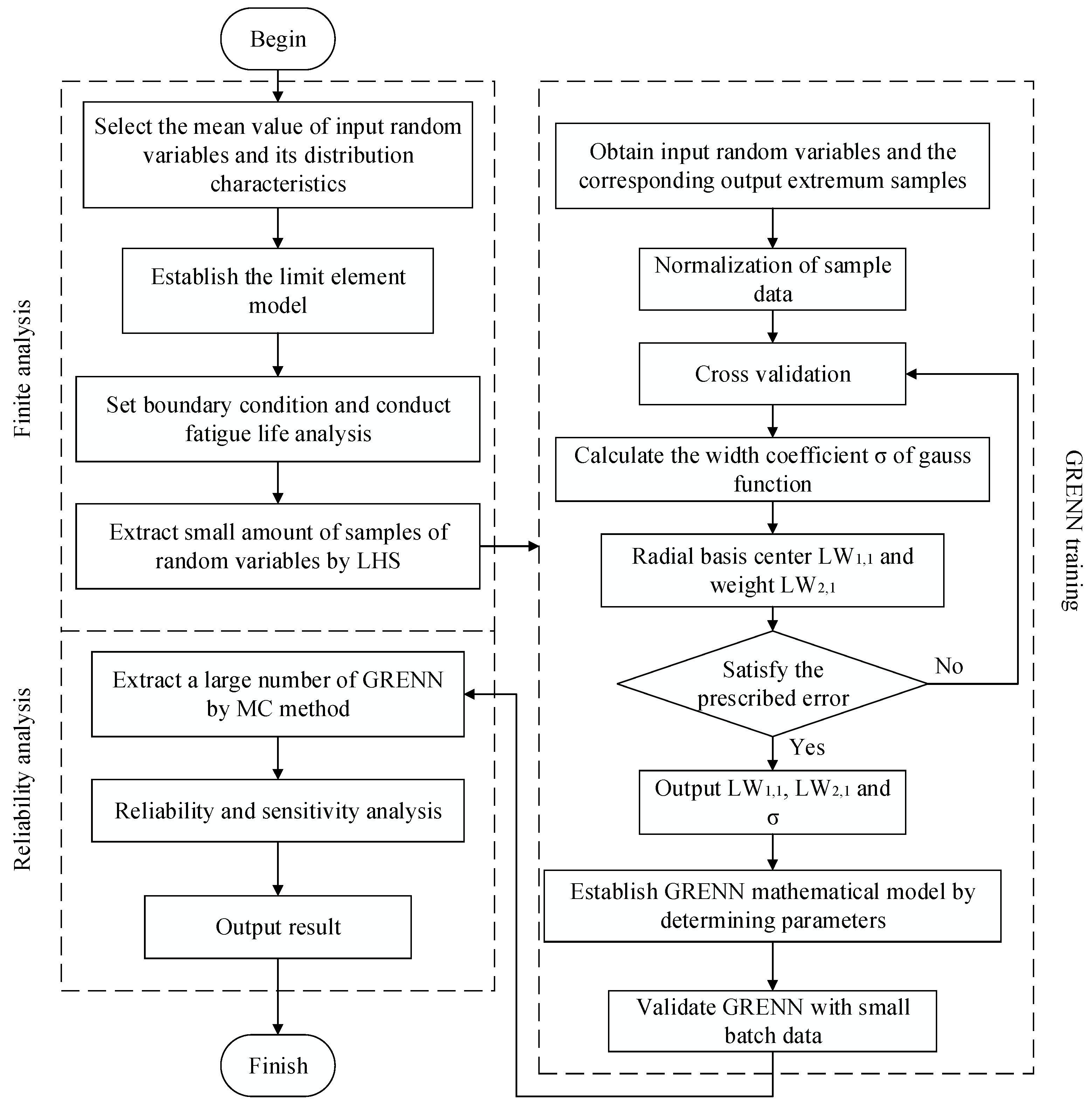
2.4. Reliability Sensitivity Analyses Approaches with GRENN Model
- Step 1:
- Build the finite element (FE) model of blisk in a workbench environment;
- Step 2:
- Consider the means of the input random variables (i.e., gas temperature, rotation speed, material parameters and fatigue performance parameters) and set boundary conditions to conduct the blisk FE analysis under the interaction of heat load, centrifugal load and then gain the minimum fatigue point as the design point of the blisk reliability design.
- Step 3:
- Extract small samples of the input random variables using the Latin hypercube sampling (LHS) method and perform FE analyses for each group of samples to gain the output responses (blisk LCF life) and extract the minimum values of the responses as a training sample set by combining the input samples.
- Step 4:
- Training the GRENN model by computing the optimal smooth factors, radial basis function and connection weights with the cross validation method [26], through the normalization of training samples.
- Step 5:
- Structure of the limit state function of blisk LCF life with the established GRENN model.
- Step 6:
- Check the precision of the GRENN model. If unacceptable, return to Step 4; if acceptable, conduct Step 7.
- Step 7:
- Calculate the reliability degree and sensitivity degree of the fatigue life and input variables, by conducting the reliability and sensitivity analyses of blisk LCF life with thermal-structure coupling, through a large number of samples extracted by the MC method.
3. Reliability and Sensitivity Analyses of Blisk Low Cycle Fatigue Life
3.1. Random Variables Selection
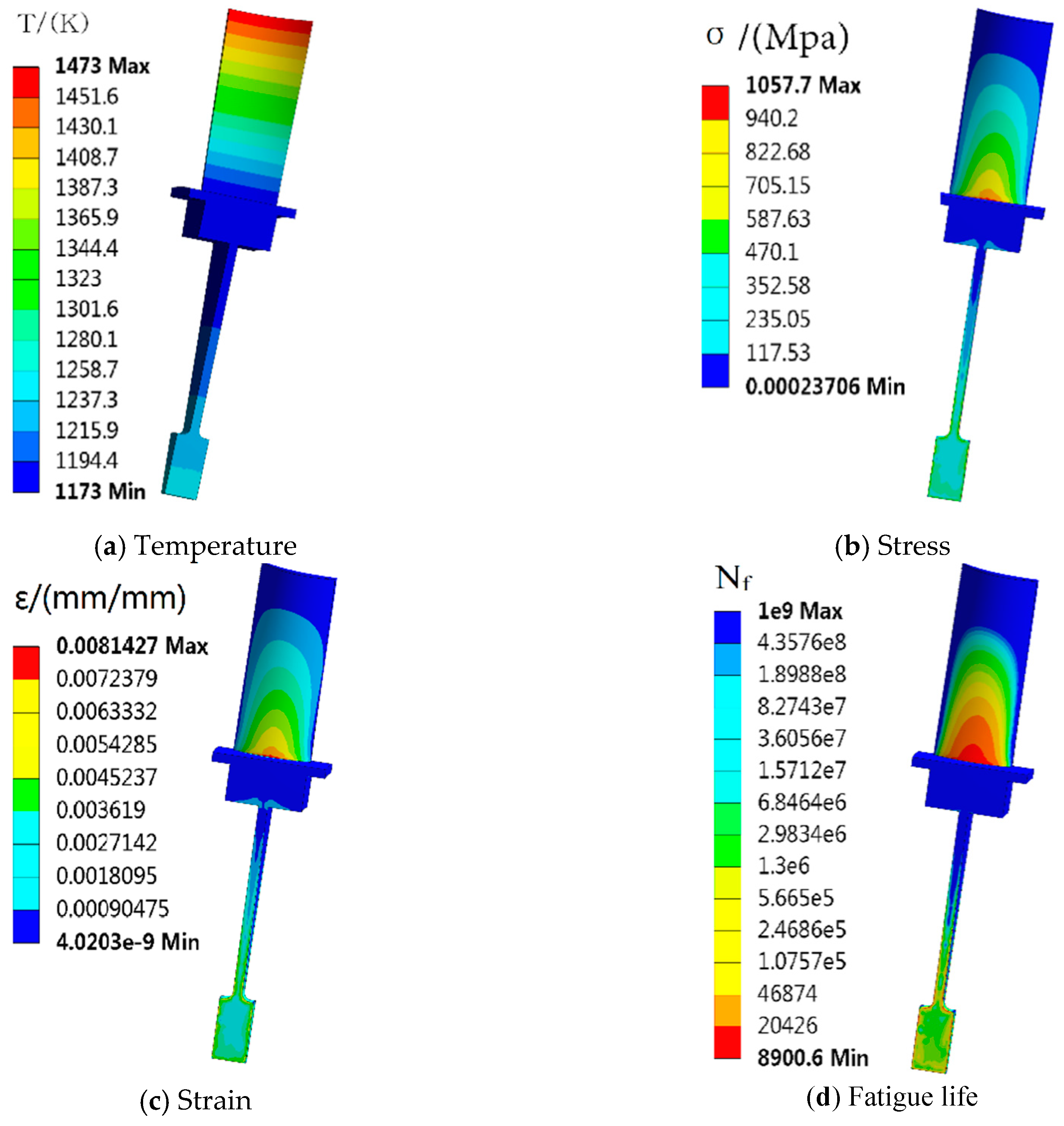
3.2. Deterministic Analysis of Blisk Low Cycle Fatigue Life
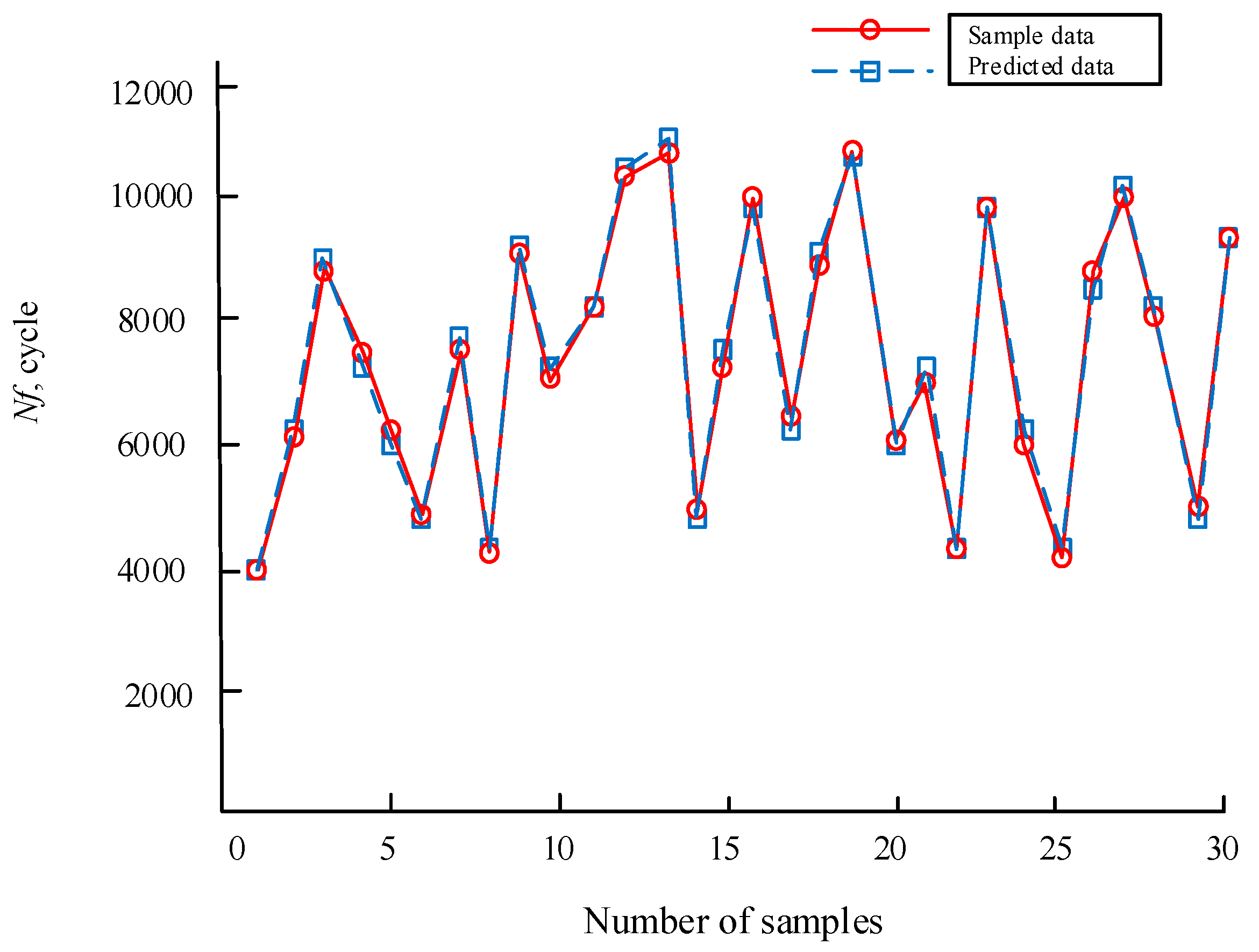
3.3. Low Cycle Fatigue Life Models of Blisk with GRENN Method
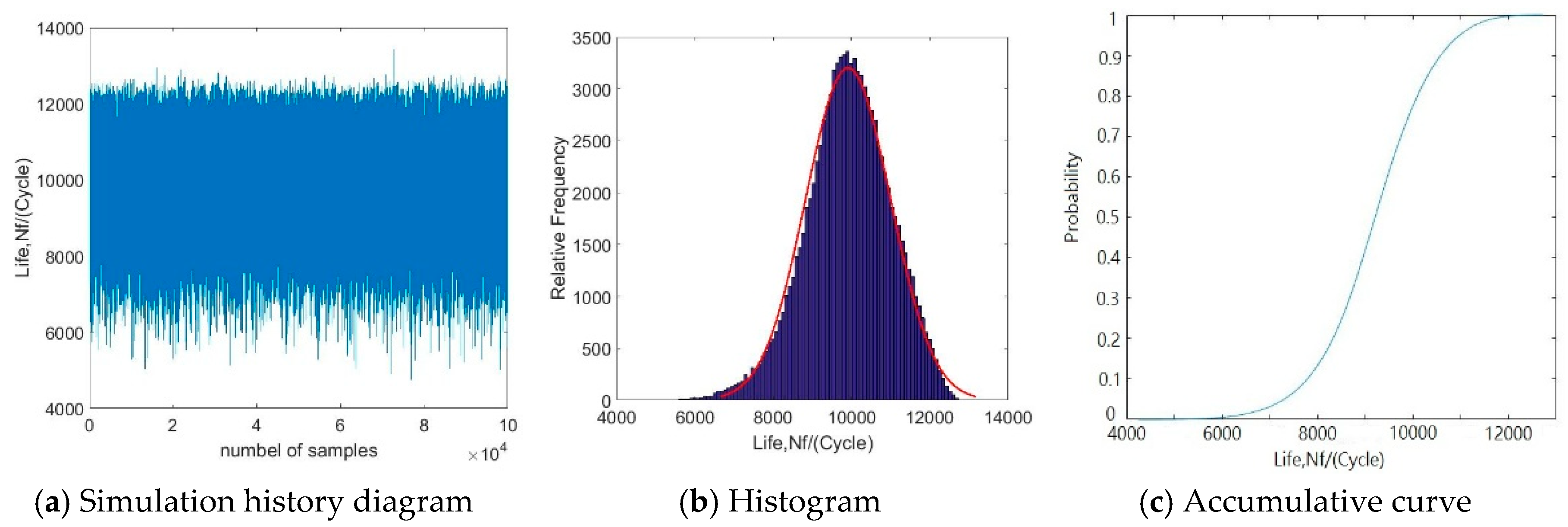
3.4. Reliability Analysis of Blisk Low Cycle Fatigue Life with GRENN Model
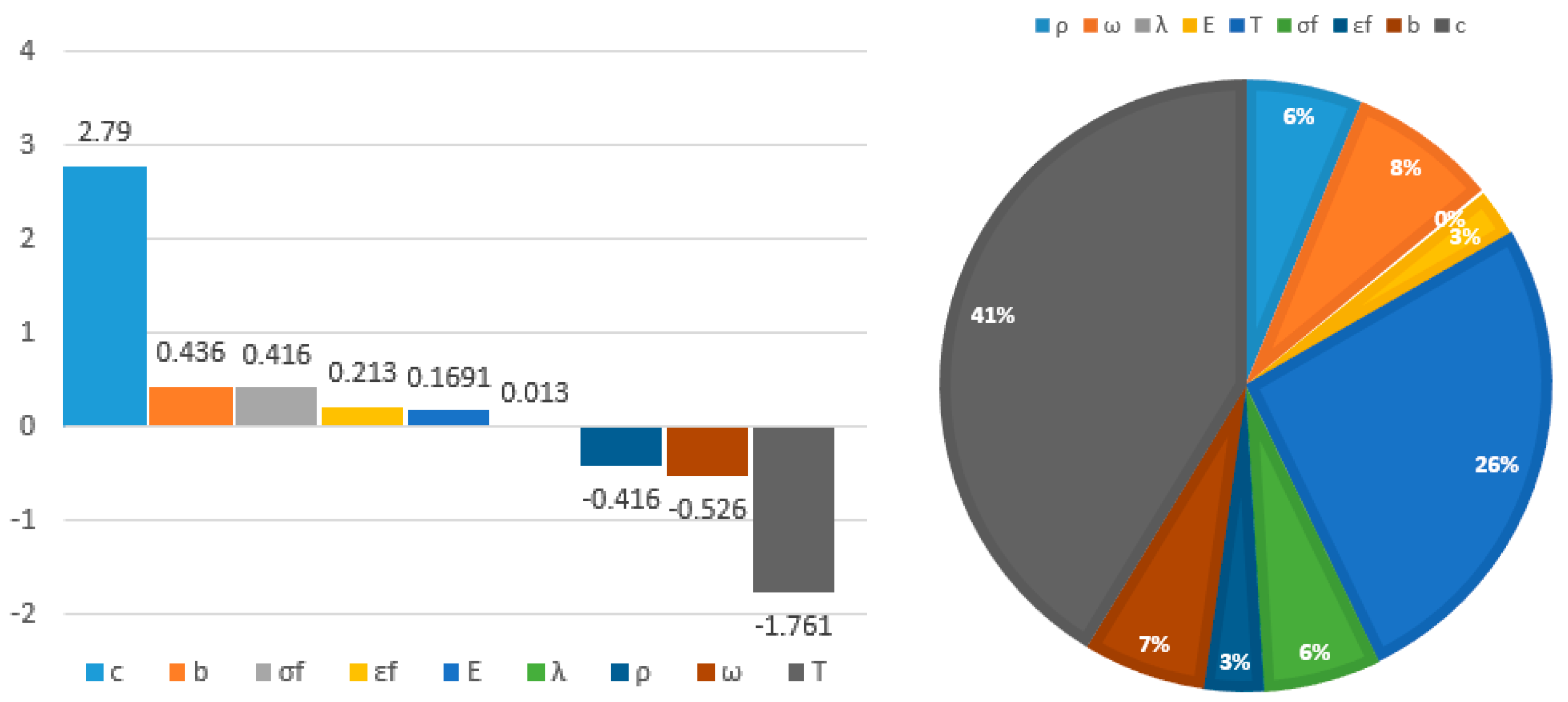
3.5. Sensitivity Analysis of Blisk Low Cycle Fatigue Life with GRENN Method
3.6. Validation of GRENN
4. Conclusions
- (1)
- The reliability degree of blisk LCF life was 0.99848 when the life allowable value was 6000 cycles. Relative to 4450 cycles acquired from the deterministic analysis after considering the double coefficient of a safe life, the LCF (6000 cycles to ensure a reliability degree of 0.99848) of the blisk obtained from the reliability design had enough life margin (about 1550 cycles) to ensure the operation of the blisk structure.
- (2)
- From the sensitivity analysis of a blisk, the fatigue ductility index c and gas temperature T played key roles in blisk LCF life evaluation and design. T and c were positively and negatively correlated with blisk life, respectively. The conclusions can significantly guide the optimization and design of blisk LCF life.
- (3)
- Through the comparison of the methods, it is demonstrated that the developed GRENN method is far better than ERSM in modeling precision and computing efficiency and is basically consistent with the MC method. Moreover, the strengths of the GRENN method become more obvious with the increasing number of simulations. It is fully supported that the proposed GRENN method is a high-accuracy and high-efficiency method to address the key questions of nonlinearity, transients and large sample-based modeling.
Author Contributions
Funding
Conflicts of Interest
References
- Bin, B.; Bai, G.C. Dynamic probabilistic analysis of stress and deformation for bladed disk assemblies of aeroengine. J. Cent. South Univ. 2014, 21, 3722–3735. [Google Scholar]
- Gao, H.F.; Wang, A.; Bai, G.C.; Wei, C.M.; Fei, C.W. Substructure-based distributed collaborative probabilistic analysis method for low-cycle fatigue damage assessment of turbine blade-disk. Aerosp. Sci. Technol. 2018, 79, 636–646. [Google Scholar] [CrossRef]
- Scott-Emuakpor, O.; George, T.; Cross, C.; Shen, M. Multi-axial fatigue-life prediction via a strain-energy method. AIAA J. 2010, 48, 63–72. [Google Scholar] [CrossRef]
- Hou, N.X.; Wen, Z.X.; Yu, Q.M.; Yue, Z.Y. Application of a combined high and low cycle fatigue life model on life prediction of SC blade. Int. J. Fatigue 2009, 31, 616–619. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Peng, W.; Zhang, X.C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142–143, 502–517. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Zhou, J.; Yu, Z.Y. Fatigue reliability assessment of turbine discs under multi-source uncertainties. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1291–1305. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Lei, Q.; Wang, Q.Y. Probabilistic fatigue life prediction and reliability assessment of a high pressure turbine disc considering load variations. Int. J. Damage Mech. 2018, 27, 1569–1588. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Smith, R.; Ontiveros, V.; He, L.P.; Modarres, M. Bayesian framework for probabilistic low cycle fatigue life prediction and uncertainty modeling of aircraft turbine disk alloys. Probab. Eng. Mech. 2013, 34, 114–122. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, L.S. Low cycle fatigue life prediction of a 300MW steam turbine rotor using a new nonlinear accumulation approach. In Proceedings of the 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 3913–3918. [Google Scholar]
- Letcher, T.; Shen, M.H.H.; Scott-Emuakpor, O.; George, T.; Cross, C. An energy-based critical fatigue life prediction method for AL6061-T6. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 861–870. [Google Scholar] [CrossRef]
- Bargmann, H.; Rüstenberg, I.; Devlukia, J. Reliability of metal components in fatigue: A simple algorithm for the exact solution. Fatigue Fract. Eng. Mater. Struct. 2010, 17, 1445–1457. [Google Scholar] [CrossRef]
- Zhu, S.P.; Foletti, S.; Beretta, S. Probabilistic framework for multiaxial LCF assessment under material variability. Int. J. Fatigue 2017, 103, 371–385. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Peng, W.; Wang, H.K.; Mahadevan, S. Probabilistic Physics of Failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Viadero, F.; Bueno, J.I.; de Lacalle, L.L.; Sancibrian, R. Reliability computation on stiffened bending plates. Adv. Eng. Softw. 1995, 20, 43–48. [Google Scholar] [CrossRef]
- Pagnini, L.; Repetto, M.P. The role of parameter uncertainties in the damage prediction of the alongwind-induced fatigue. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 227–238. [Google Scholar] [CrossRef]
- Repetto, M.P.; Torrielli, A. Long term simulation of wind-induced fatigue loadings. Eng. Struct. 2017, 132, 551–561. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E. The cell-to-boundary method in Monte Carlo-based dynamic PSA. Reliab. Eng. Syst. Saf. 1995, 48, 199–204. [Google Scholar] [CrossRef]
- Melchers, R.E.; Ahammed, M. A fast-approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput. Struct. 2004, 82, 55–61. [Google Scholar] [CrossRef]
- Puatatsananon, W.; Saouma, V.E. Reliability analysis in fracture mechanics using the first-order reliability method and Monte Carlo simulation. Fatigue Fract. Eng. Mater. Struct. 2010, 29, 959–975. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. An efficient reliability method combining adaptive support vector machine and Monte Carlo simulation. Struct. Saf. 2017, 67, 85–95. [Google Scholar] [CrossRef]
- Fei, C.W.; Bai, G.C.; Tian, C. Extremum response surface method for casing radial deformation probabilistic analysis. AIAA J. Aerosp. Inf. Syst. 2013, 10, 47–52. [Google Scholar]
- Tvedt, L. Distribution of quadratic forms in normal space—Application to structural reliability. J. Eng. Mech. 1990, 116, 1183–1197. [Google Scholar] [CrossRef]
- Fei, C.W.; Bai, G.C. Distributed collaborative extremum response surface method for mechanical dynamic assembly reliability analysis. J. Cent. South Univ. 2013, 20, 2414–2422. [Google Scholar] [CrossRef]
- Kaymaz, I.; Marti, K. Reliability-based design optimization for elastoplastic mechanical structures. Comput. Struct. 2007, 85, 615–625. [Google Scholar] [CrossRef]
- Fei, C.W.; Tang, W.Z.; Bai, G.C.; Shuang, M. Dynamic probabilistic design for blade deformation with SVM-ERSM. Aircr. Eng. Aerosp. Technol. 2015, 87, 312–321. [Google Scholar] [CrossRef]
- Wei, Z.; Feng, F.; Wei, W. Non-linear partial least squares response surface method for structural reliability analysis. Reliab. Eng. Syst. Saf. 2017, 161, 69–77. [Google Scholar]
- Fei, C.W.; Bai, G.C. Distributed collaborative probabilistic design for turbine blade-tip radial running clearance using support vector machine of regression. Mech. Syst. Signal Process. 2014, 49, 196–208. [Google Scholar] [CrossRef]
- Fei, C.W.; Choy, Y.S.; Hu, D.Y.; Bai, G.C.; Tang, W.Z. Dynamic probabilistic design approach of high-pressure turbine blade-tip radial running clearance. Nonlinear Dyn. 2016, 86, 205–223. [Google Scholar] [CrossRef]
- Goswami, S.; Ghosh, S.; Chakraborty, S. Reliability analysis of structures by iterative improved response surface method. Struct. Saf. 2016, 60, 56–66. [Google Scholar] [CrossRef]
- Bai, G.C.; Fei, C.W. Distributed collaborative response surface method for mechanical dynamic assembly reliability design. Chin. J. Mech. Eng. 2013, 26, 1160–1168. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Alvarez, D.A. An optimization method for learning statistical classifiers in structural reliability. Probab. Eng. Mech. 2010, 25, 26–34. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Bai, G.C. Extremum response surface method of reliability analysis on two-link flexible robot manipulator. J. Cent. South Univ. 2012, 19, 101–107. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Liem, R.P.; Fei, C.W. Improved kriging with extremum response surface method for structural dynamic reliability and sensitivity analyses. Aerosp. Sci. Technol. 2018, 76, 164–175. [Google Scholar] [CrossRef]
- Nose-Filho, K.; Lotufo, A.D.P.; Minussi, C.R. Short-term multinodal load forecasting using a modified general regression neural network. IEEE Trans. Power Deliv. 2011, 26, 2862–2869. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, K.; Li, D.S. Freight volume forecast based on GRNN. J. China Railw. Soc. 2004, 26, 12–15. [Google Scholar]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl. Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Sun, G.; Hoff, S.J.; Zelle, B.C.; Smith, M.A. Development and comparison of backpropagation and generalized regression neural network models to predict diurnal and seasonal gas and PM 10 concentrations and emissions from swine buildings. Trans. Asabe 2008, 51, 685–694. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, H. Underwater acoustic source localization using generalized regression neural network. J. Acoust. Soc. Am. 2018, 143, 2321–2331. [Google Scholar] [CrossRef]
- Gao, H.; Fei, C.; Bai, G.; Ding, L. Reliability-based low-cycle fatigue damage analysis for turbine blade with thermo-structural interaction. Aerosp. Sci. Technol. 2016, 49, 289–300. [Google Scholar] [CrossRef]
- Liu, C.L.; Lu, Z.Z.; Xu, Y.L.; Yue, Z.F. Reliability analysis for low cycle fatigue life of the aeronautical engine turbine disc structure under random environment. Mater. Sci. Eng. A 2005, 395, 218–225. [Google Scholar] [CrossRef]
- Vubac, N.; Lahmer, T.; Keitel, H.; Zhao, J.; Zhuang, X.; Rabczuk, T. Stochastic predictions of bulk properties of amorphous polyethylene based on molecular dynamics simulations. Mech. Mater. 2014, 68, 70–84. [Google Scholar] [CrossRef]
- Zhai, X.; Fei, C.W.; Zhai, Q.G.; Bai, G.C.; Ding, L. Reliability and sensitivity analyses of HPT blade-tip radial running clearance using multiply response surface model. J. Cent. South Univ. 2014, 21, 4368–4377. [Google Scholar] [CrossRef]
- Shu, M.A.; Wang, K.M.; Hui, M.; Shuai, Z. Research on turbine blade vibration characteristic under steady state temperature field. J. Shenyang Aerosp. Univ. 2011, 28, 18–21. [Google Scholar]
- Zhang, C.Y.; Lu, C.; Fei, C.W.; Liu, L.J. Multiobject reliability analysis of turbine blisk with multidiscipline under multiphysical field interaction. Adv. Mater. Sci. Eng. 2015, 2015, 519–520. [Google Scholar] [CrossRef]
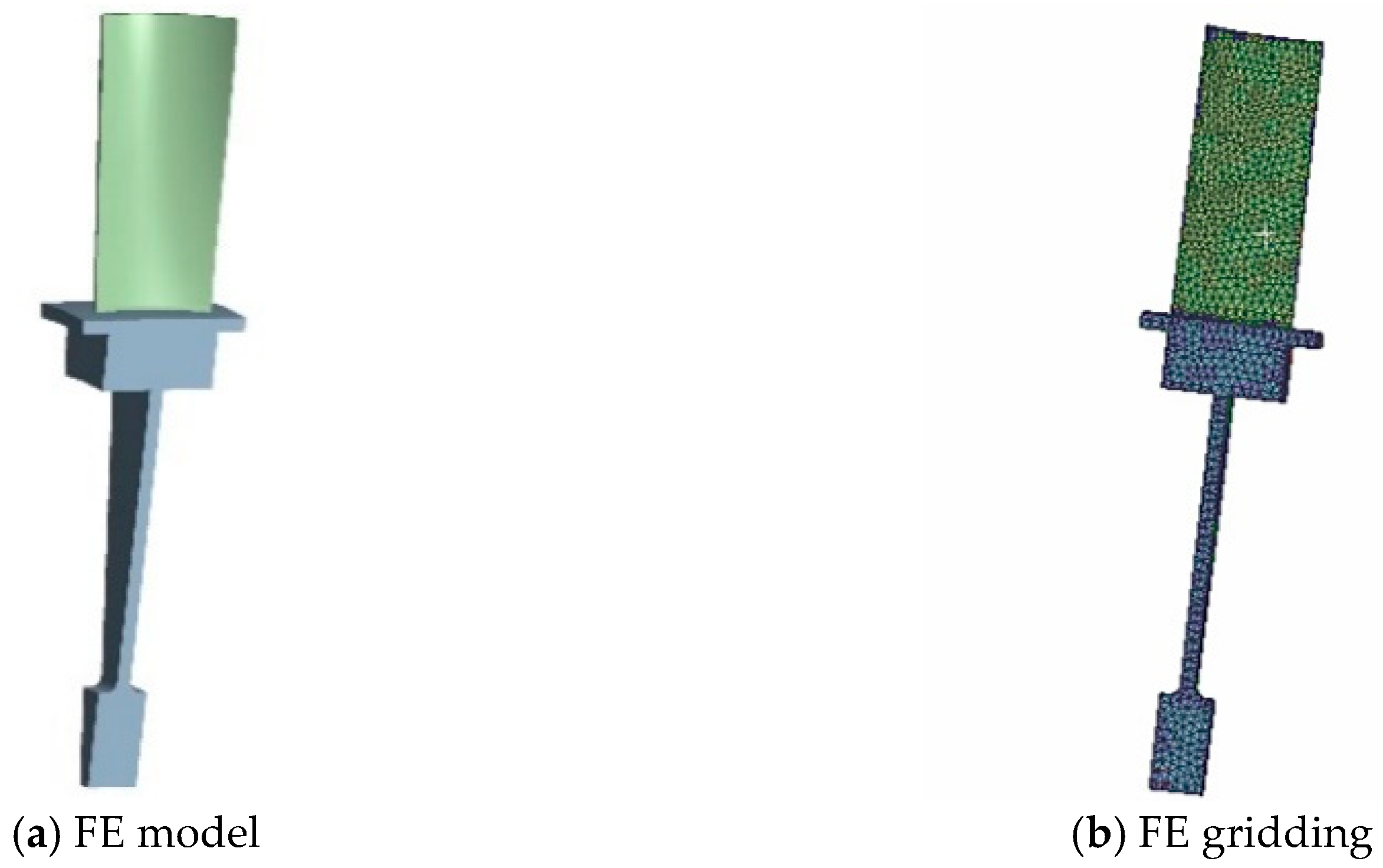
| Random Variables | Mean μ | Standard Deviation δ | Distribution |
|---|---|---|---|
| Density ρ, kg.m−3 | 8210 | 328.4 | Normal |
| Rotate speed ω, rad·s−1 | 1168 | 35 | Normal |
| Heat conductivity λ, W·m−1·°C−1 | 23 | 0.005 | Normal |
| Modulus of elasticity, E, MPa | 163000 | 4890 | Normal |
| Blade-root temperature Ta , k | 1173.15 | 35.2 | Normal |
| Blade-tip temperature Tb, k | 1473.15 | 47 | Normal |
| Fatigue strength efficient σ′f | 1419 | 42.5 | Normal |
| Fatigue ductility coefficient ε′f | 50.5 | 1.53 | Normal |
| Fatigue strength index b | −0.1 | 0.005 | Normal |
| Fatigue ductility index c | −0.84 | 0.042 | Normal |
| Random Parameters | Sensitivity Degree, ×10−3 | Effect Probability, % |
|---|---|---|
| ρ | −0.41586 | 6.18 |
| ω | −0.52565 | 7.81 |
| +0.0132 | 0.20 | |
| E | +0.16948 | 2.52 |
| T | −1.76022 | 26.16 |
| σ′f | +0.41615 | 6.18 |
| ε′f | +0.21311 | 3.17 |
| b | +0.43585 | 6.48 |
| c | +2.7929 | 41.30 |
| Number of Samples | Computing Time under Different Simulations, s | Reduced Time, s | Improved Efficiency, % | ||
|---|---|---|---|---|---|
| MC Method | ERSM | GRENN | |||
| 102 | 5400 | 1.249 | 1.201 | 0.048 | 3.843 |
| 103 | 14400 | 1.266 | 1.201 | 0.065 | 5.134 |
| 104 | 432000 | 1.681 | 1.311 | 0.370 | 15.18 |
| 105 | — | 2.437 | 1.342 | 1.095 | 44.93 |
| 106 | — | 4.312 | 2.138 | 2.174 | 50.42 |
| Samples | Reliability Degree | Precision/% | Improved Precision/% | |||
|---|---|---|---|---|---|---|
| MC Method | ERSM | GRENN | ERSM | GRENN | ||
| 102 | 0.85 | 0.76 | 0.79 | 76.24 | 79.25 | 3.01 |
| 103 | 0.976 | 0.947 | 0.968 | 95.00 | 97.11 | 2.11 |
| 104 | 0.9968 | 0.9824 | 0.9973 | 98.56 | 99.95 | 1.39 |
| 105 | — | 0.98181 | 0.99848 | 98.49 | 99.83 | 1.34 |
| 106 | — | 0.98262 | 0.99587 | 98.58 | 99.91 | 1.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wei, J.; Jing, H.; Fei, C.; Tang, W. Reliability-Based Low Fatigue Life Analysis of Turbine Blisk with Generalized Regression Extreme Neural Network Method. Materials 2019, 12, 1545. https://doi.org/10.3390/ma12091545
Zhang C, Wei J, Jing H, Fei C, Tang W. Reliability-Based Low Fatigue Life Analysis of Turbine Blisk with Generalized Regression Extreme Neural Network Method. Materials. 2019; 12(9):1545. https://doi.org/10.3390/ma12091545
Chicago/Turabian StyleZhang, Chunyi, Jingshan Wei, Huizhe Jing, Chengwei Fei, and Wenzhong Tang. 2019. "Reliability-Based Low Fatigue Life Analysis of Turbine Blisk with Generalized Regression Extreme Neural Network Method" Materials 12, no. 9: 1545. https://doi.org/10.3390/ma12091545
APA StyleZhang, C., Wei, J., Jing, H., Fei, C., & Tang, W. (2019). Reliability-Based Low Fatigue Life Analysis of Turbine Blisk with Generalized Regression Extreme Neural Network Method. Materials, 12(9), 1545. https://doi.org/10.3390/ma12091545






