Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications
Abstract
1. Introduction
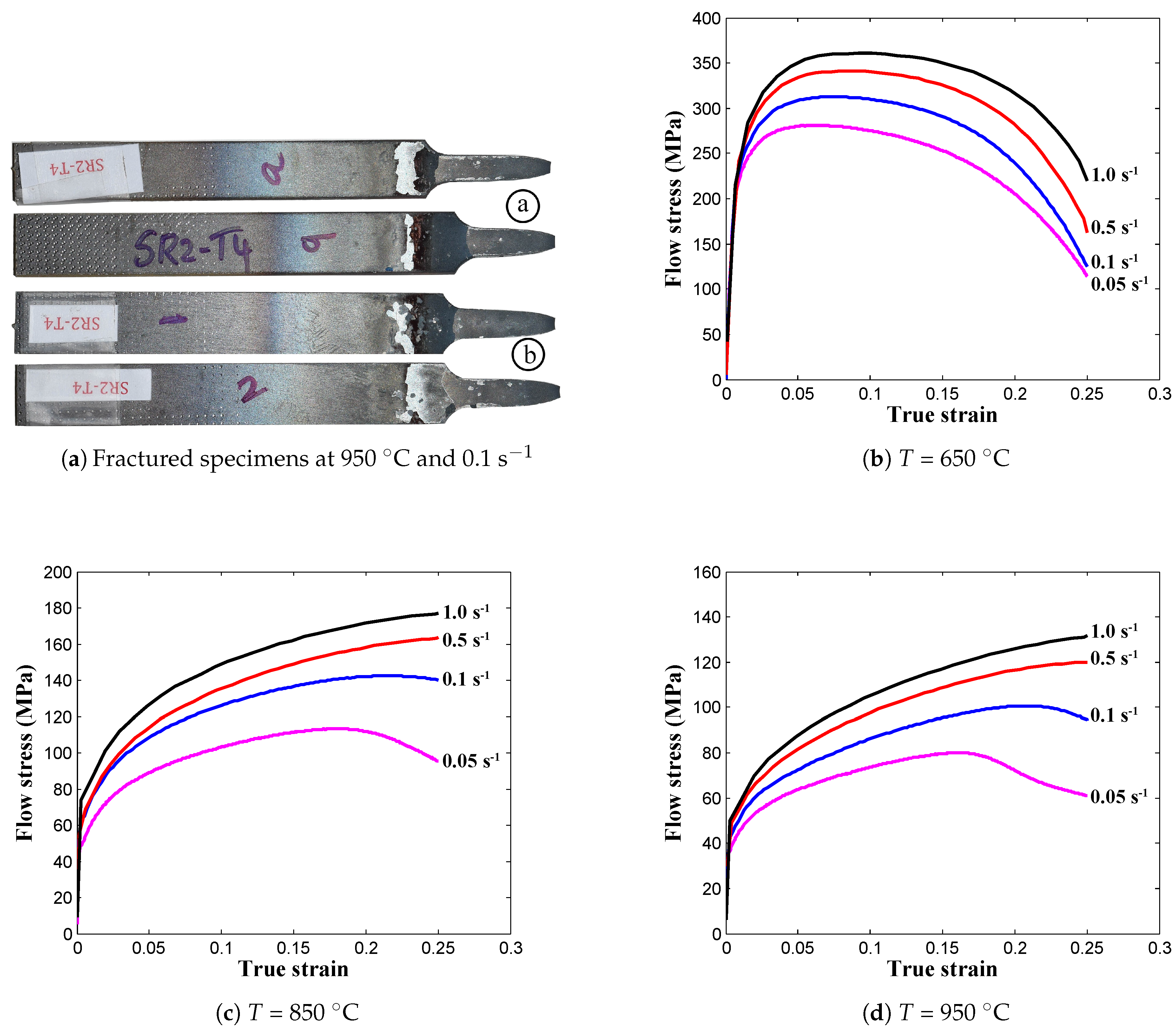
2. Experimental Procedures
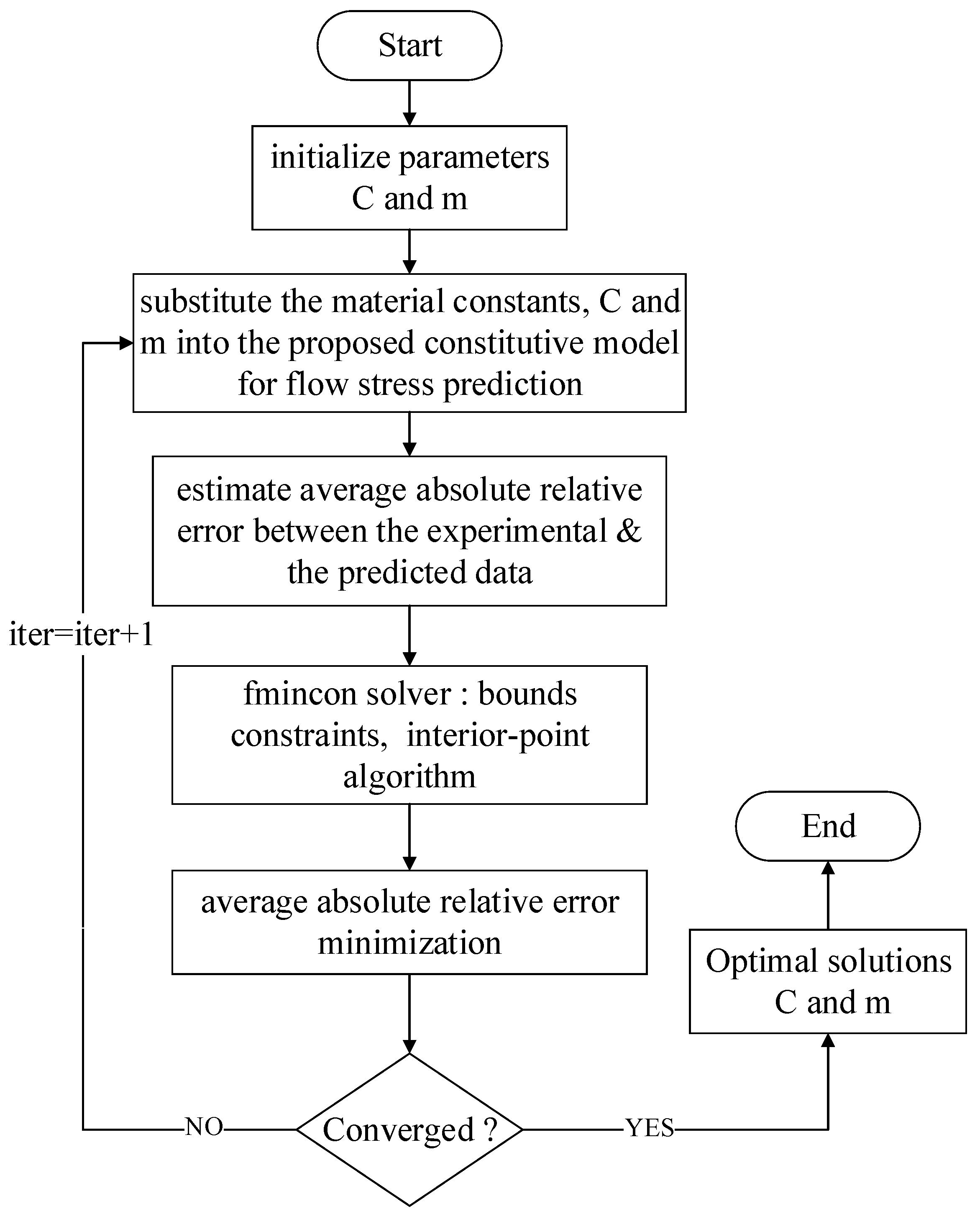
3. Johnson-Cook Model
3.1. Determination of Material Constants B and n
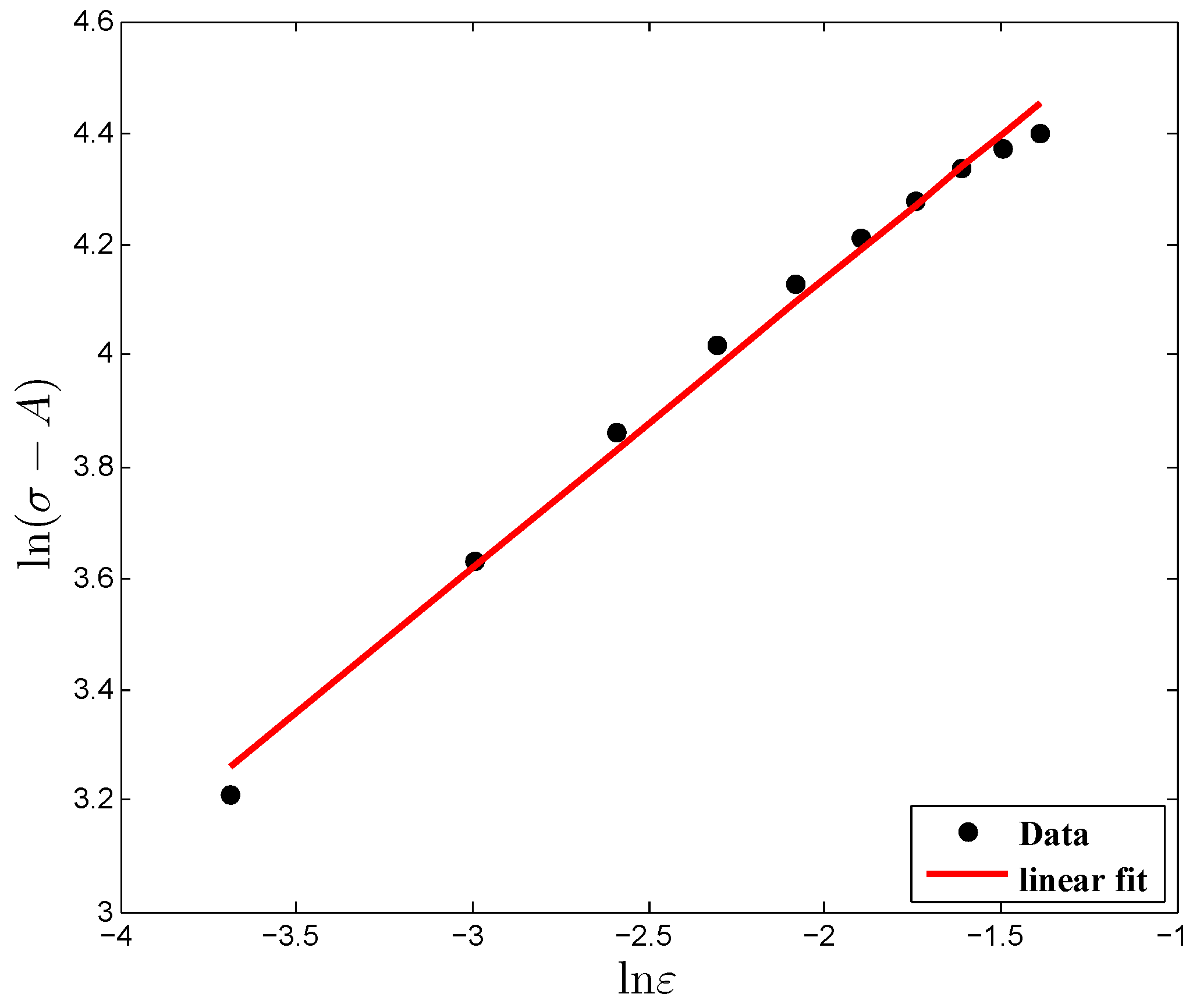
3.2. Determination of Material Constant C
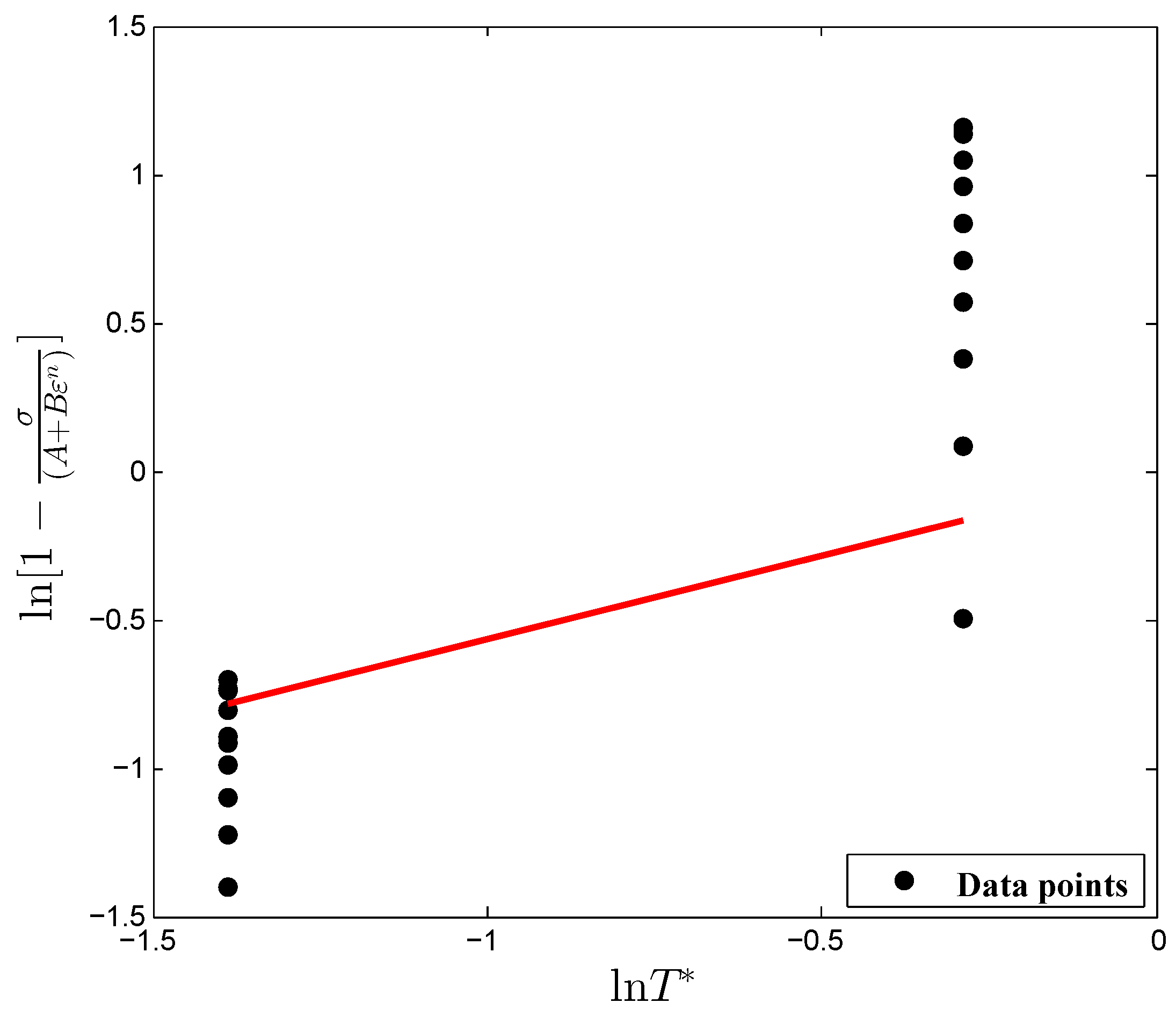
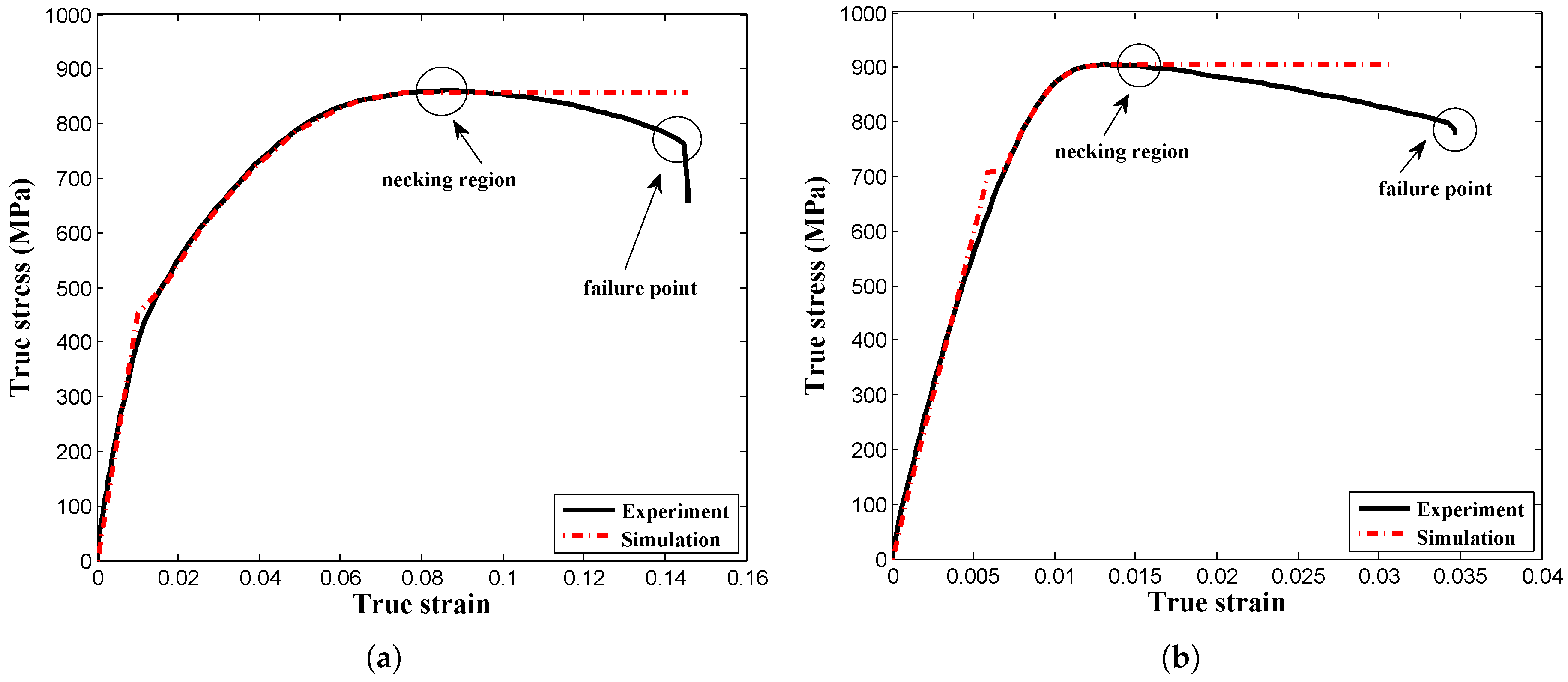
3.3. Determination of the Material Constant, m
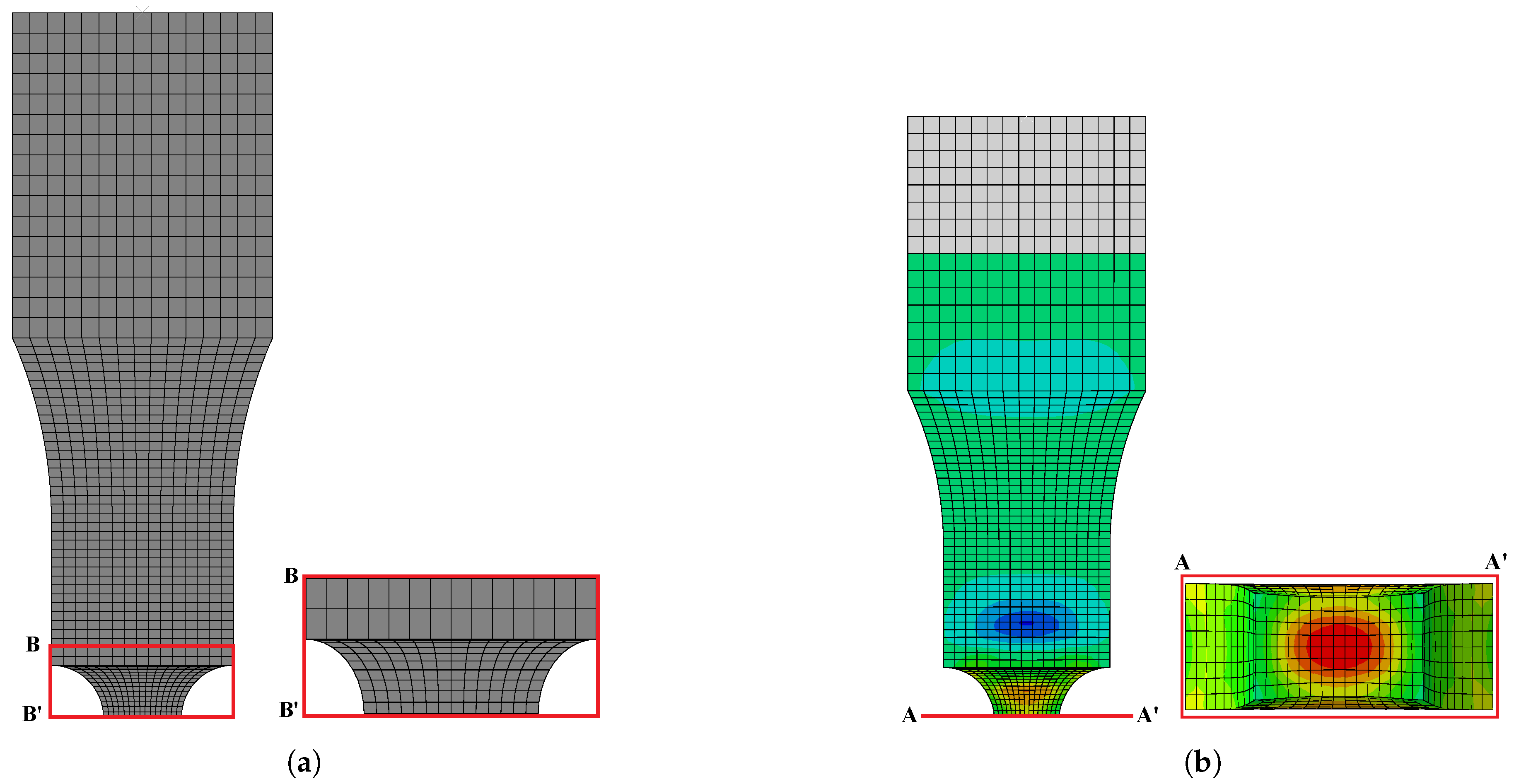
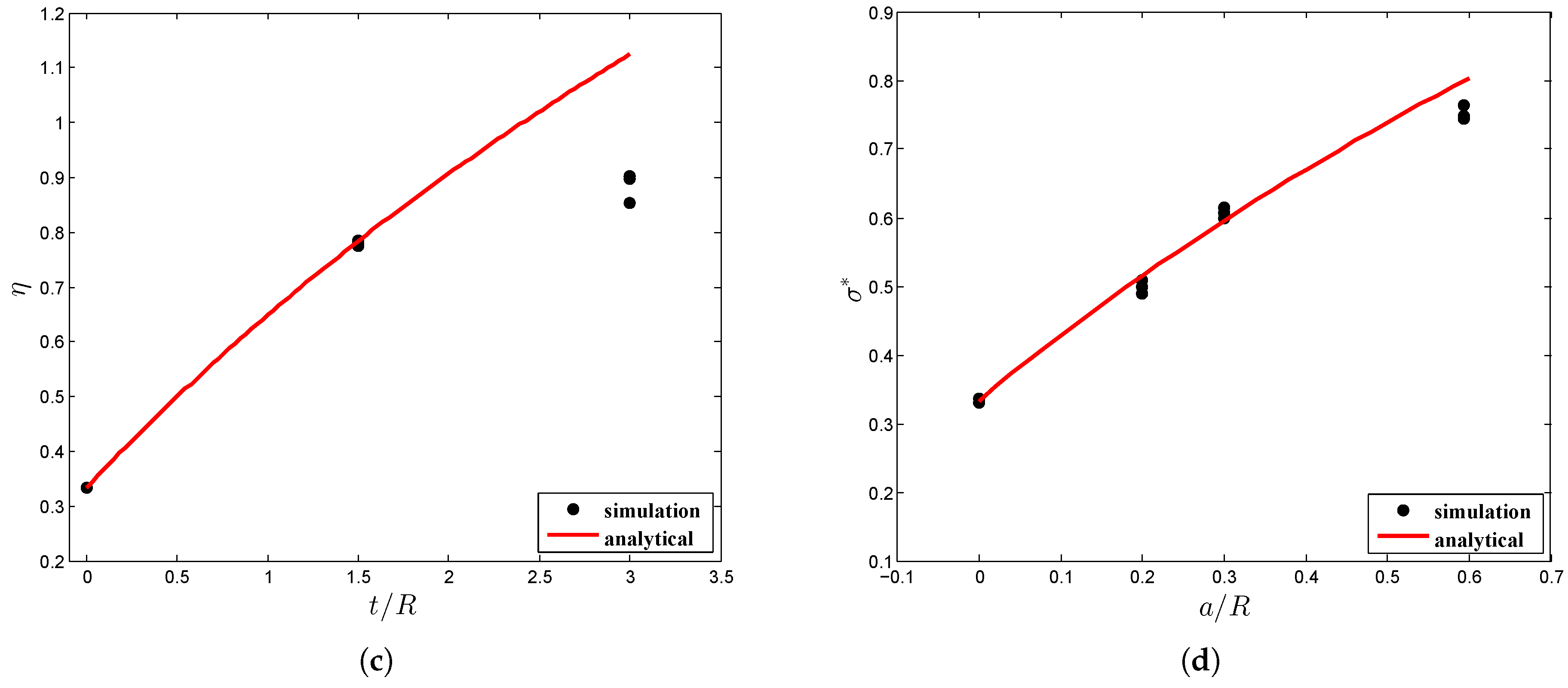
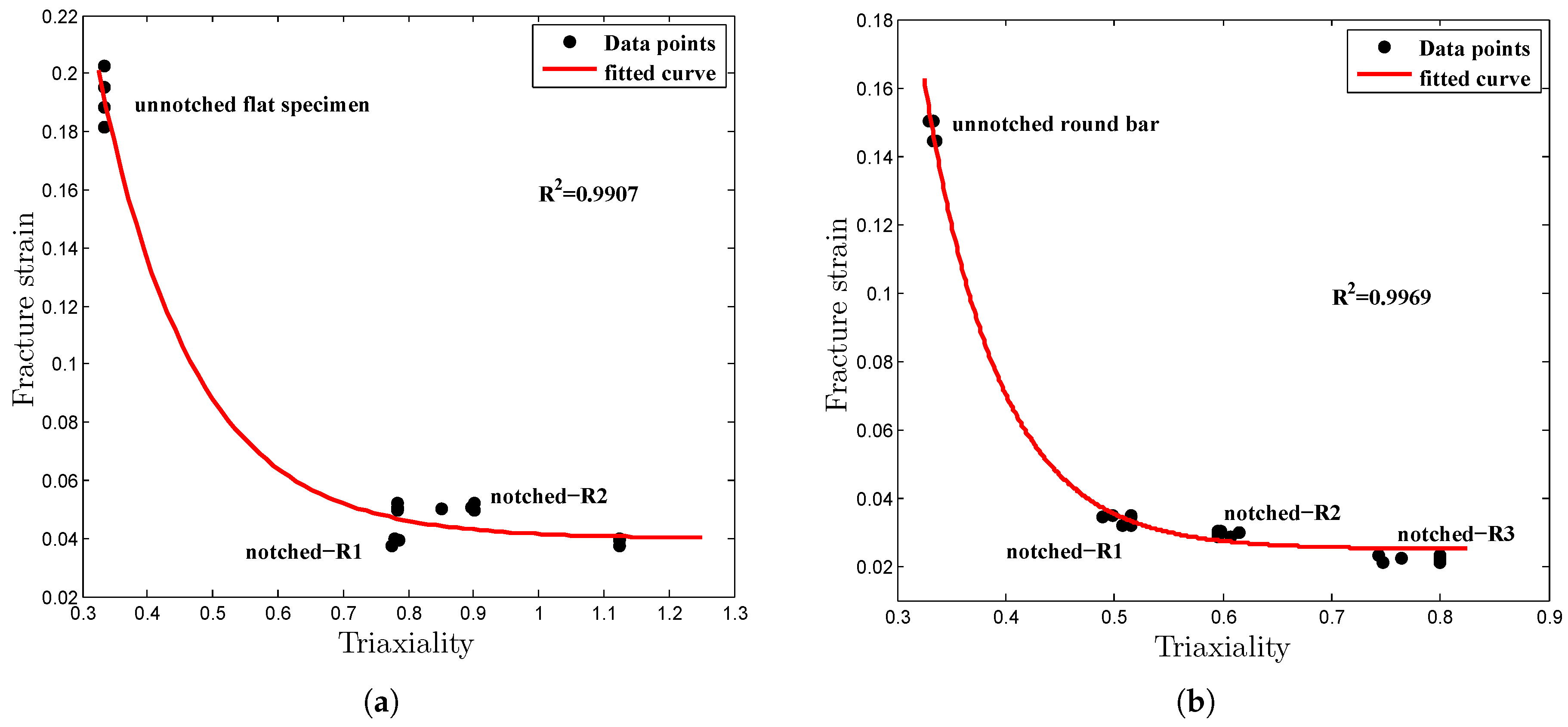
3.4. Johnson-Cook Damage Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, J.; Chen, F.; Wang, B.; Zhu, L.B. A modified Johnson-Cook model for 10% Cr steel at elevated temperatures and a wide range of strain rates. Mater. Sci. Eng. A 2018, 715, 1–9. [Google Scholar] [CrossRef]
- Shrot, A.; Bäker, M. Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Gambirasio, L.; Rizzi, E. On the calibration strategies of the Johnson-Cook strength model: Discussion and applications to experimental data. Mater. Sci. Eng. A 2015, 610, 220–228. [Google Scholar] [CrossRef]
- Gambirasio, L.; Rizzi, E. An enhanced Johnson–Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow. Comput. Mater. Sci. 2016, 113, 231–265. [Google Scholar] [CrossRef]
- Bobbili, R.; Ramakrishna, B.; Madhu, V.; Gogia, A.K. Prediction of flow stress of 7017 aluminium alloy under high strain rate compression at elevated temperatures. Def. Technol. 2015, 11, 93–98. [Google Scholar] [CrossRef]
- Milani, A.S.; Dabboussi, W.; Nemes, J.A.; Abeyaratne, R.C. An improved multi-objective identification of Johnson–Cook material parameters. Int. J. Impact Eng. 2009, 36, 294–302. [Google Scholar] [CrossRef]
- Majzoobia, G.H.; Dehgolan, F.R. Determination of the constants of damage models. Procedia Eng. 2011, 10, 764–773. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson cook material and failure model constants and numerical modelling of Charpy impact test of armour steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Buzyurkina, A.E.; Gladkyb, I.L.; Krausa, E.I. Determination and verification of Johnson-Cook model parameters athigh-speed deformation of titanium alloys. Aerosp. Sci. Technol. 2015, 45, 121–127. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, S.; Wang, H.; Liu, C.R. Predicting the Effects of Cutting Parameters and Tool Geometry on Hard Turning Process Using Finite Element Method. J. Manuf. Sci. Eng. 2011, 133. [Google Scholar] [CrossRef]
- Liu, J.; Bai, Y.; Xu, C. Evaluation of Ductile Fracture Models in Finite Element Simulation of Metal Cutting Processes. J. Manuf. Sci. Eng. 2014, 136. [Google Scholar] [CrossRef]
- Abbasi-Bani, A.; Zarei-Hanzaki, A.; Pishbin, M.H.; Haghdadi, N. A comparative study on the capability of Johnson-Cook and Arrhenius-type constitutive equations to describe the flow behavior of Mg-6Al-1Zn alloy. Mech. Mater. 2014, 71, 52–61. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Maheshwari, A.K. Prediction of flow stress for hot deformation processing. Comput. Mater. Sci. 2013, 69, 350–358. [Google Scholar] [CrossRef]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, G.; Kent, D.; Dargusch, M. Constitutive modelling of the flow behaviour of a beta titanium alloy at high strain rates and elevated temperatures using the Johnson-Cook and modified Zerilli-Armstrong models. Mater. Sci. Eng. A 2014, 612, 71–79. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. A comparative study on Johnson Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr-1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Cao, Y.; Di, H.S.; Misra, R.D.K.; Zhang, J. Hot Deformation Behavior of Alloy 800 H at Intermediate Temperatures: Constitutive Models and Microstructure Analysis. J. Mater. Eng. Perform. 2014, 23, 4298–4308. [Google Scholar] [CrossRef]
- Murugesan, M.; Lee, S.; Kim, D.; Kang, Y.H.; Kim, N. A Comparative Study of Ductile Damage Models Approaches for Joint Strength Prediction in Hot Shear Joining Process. Procedia Eng. 2017, 207, 1689–1694. [Google Scholar] [CrossRef]
- Zhanga, Y.; Outeirob, J.C.; Mabroukic, T. On the selection of Johnson-Cook constitutive model parameters for Ti-6Al-4V using three types of numerical models of orthogonal cutting. In Proceedings of the 15th CIRP Conference on Modelling of Machining Operations, Karlsruhe, Germany, 11–12 June 2015; pp. 112–117. [Google Scholar]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Brunig, M.; Chyra, O.; Albrecht, D.; Driemeier, L.; Alves, M. A ductile damage criterion at various stress triaxialities. Int. J. Plast. 2008, 24, 1731–1755. [Google Scholar] [CrossRef]
- Mirone, G.; Corallo, D. A local viewpoint for evaluating the influence of stress triaxiality and Lode angle on ductile failure and hardening. Int. J. Plast. 2010, 26, 348–371. [Google Scholar] [CrossRef]
- Cao, T.S.; Gachet, J.M.; Montmitonnet, P.; Bouchard, P.O. A Lode-dependent enhanced Lemaitre model for ductile fracture prediction at low stress triaxiality. Eng. Fract. Mech. 2014, 124–125, 80–96. [Google Scholar] [CrossRef]
- Bao, Y. Dependence of ductile crack formation in tensile tests on stress triaxiality, stress and strain ratios. Eng. Fract. Mech. 2005, 72, 505–522. [Google Scholar] [CrossRef]
- Bao, Y. Prediciton of Ductile Crack Formation in Uncracked Bodies. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1952. [Google Scholar]
- Lee, K.; Murugesan, M.; Lee, S.M.; Kang, B.S. A Comparative Study on Arrhenius-Type Constitutive Models with Regression Methods. Trans. Mater. Process. 2017, 26, 18–27. [Google Scholar] [CrossRef]
- Murugesan, M.; Kang, B.S.; Lee, K. Multi-Objective Design Optimization of Composite Stiffened Panel Using Response Surface Methodology. J. Compos. Res. 2015, 28, 297–310. [Google Scholar] [CrossRef]



| C | Fe | Mn | P | S |
|---|---|---|---|---|
| 0.42–0.50 | 98.51–98.98 | 0.60–0.90 | ≤0.04 | ≤0.05 |
| Regular JC Model | Optimized JC Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A (MPa) | B (MPa) | n | C | m | A (MPa) | B (MPa) | n | C | m |
| 50.103 | 176.091 | 0.5176 | 0.1056 | 0.5655 | 50.103 | 176.091 | 0.5176 | 0.095 | 0.6622 |
| T | (s) | Flat 6w | N-R0 | N-R1 | N-R2 | N-R3 |
|---|---|---|---|---|---|---|
| 27 C | 0.001 | 0.3345 | – | 0.8523 | 0.7756 | – |
| 0.005 | 0.3337 | – | 0.9017 | 0.7782 | – | |
| 0.010 | 0.3332 | – | 0.8961 | 0.7852 | – | |
| 0.050 | 0.3333 | – | 0.9015 | 0.7829 | – | |
| 0.0001 | – | 0.3359 | 0.5082 | 0.6070 | 0.7473 | |
| 0.001 | – | 0.3299 | 0.4989 | 0.6152 | 0.7641 | |
| 0.010 | – | – | 0.4897 | 0.5983 | 0.7438 |
| Round Bar and Notched Specimens | Flat and Notched Specimens | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | D1 | D2 | D3 | D4 | D5 |
| 0.025 | 16.93 | -14.8 | 0.0214 | 0 | 0.04 | 1.519 | -6.905 | -0.023 | 1.302 |
| Conditions | Overall- | AARE (%) | Overall-AARE (%) | |
|---|---|---|---|---|
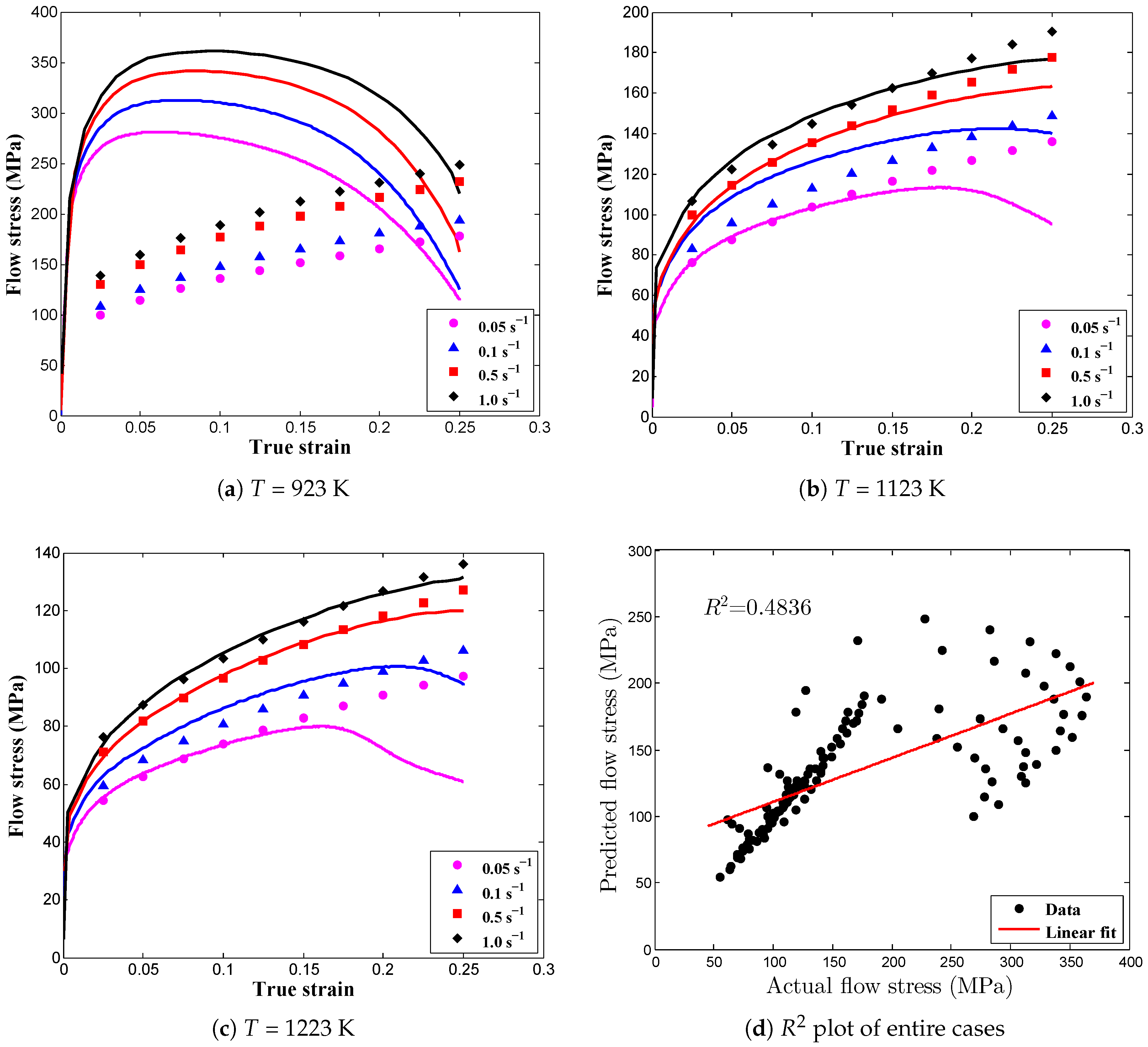
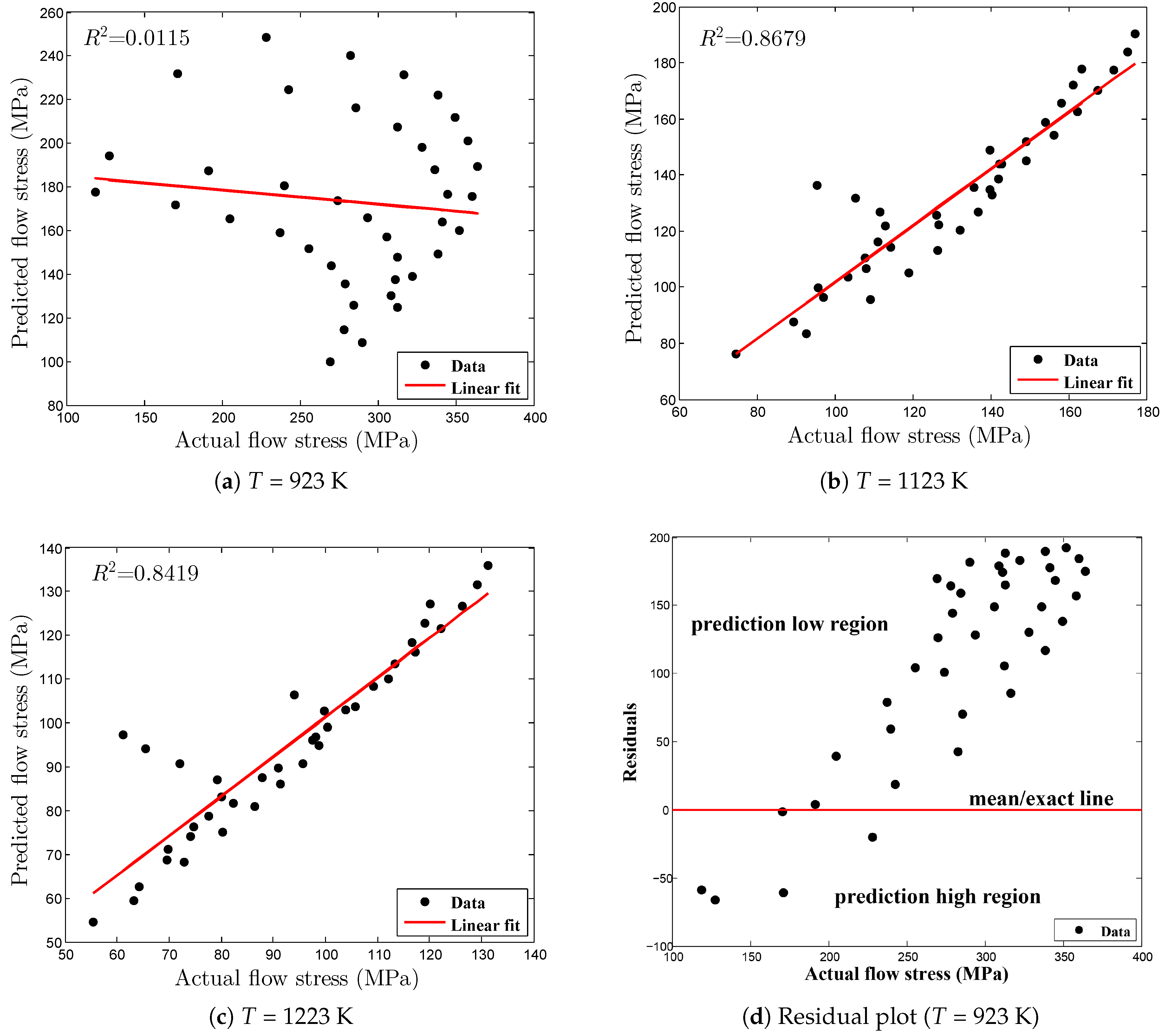
| 923 K | 0.0115 | 0.4836 | 40.9341 | 17.6112 |
| 1123 K | 0.8679 | 5.9313 | ||
| 1223 K | 0.8419 | 5.9689 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murugesan, M.; Jung, D.W. Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications. Materials 2019, 12, 609. https://doi.org/10.3390/ma12040609
Murugesan M, Jung DW. Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications. Materials. 2019; 12(4):609. https://doi.org/10.3390/ma12040609
Chicago/Turabian StyleMurugesan, Mohanraj, and Dong Won Jung. 2019. "Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications" Materials 12, no. 4: 609. https://doi.org/10.3390/ma12040609
APA StyleMurugesan, M., & Jung, D. W. (2019). Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications. Materials, 12(4), 609. https://doi.org/10.3390/ma12040609






