Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models
Abstract
:1. Introduction
2. Control Equation
2.1. Heat Transfer Equation
2.2. Chemical Reaction
2.3. Thermo-Physical Properties
2.4. Modified CHILE Model
3. Numerical Formulation
4. Material Model Verification
5. Results and Discussion
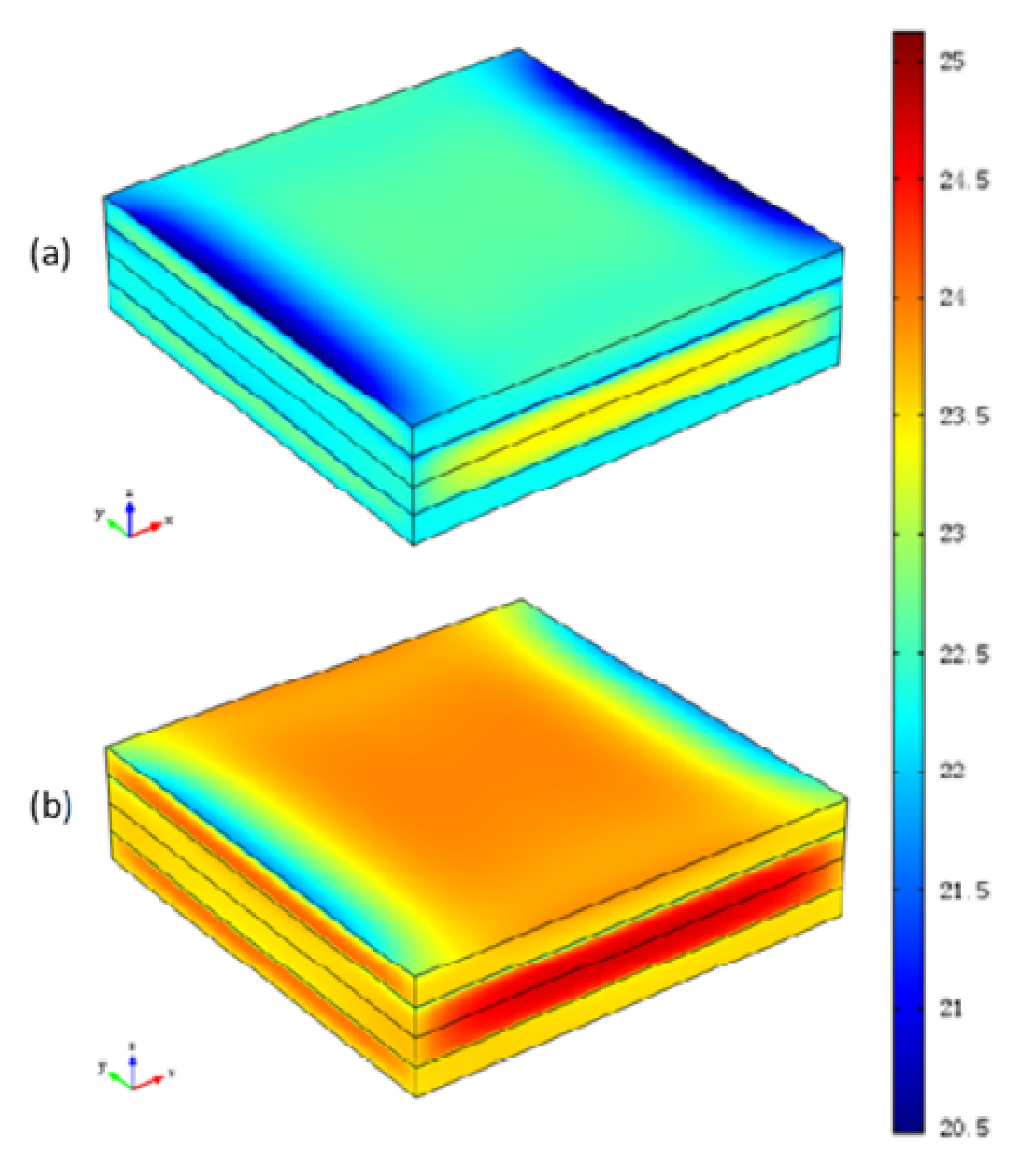
5.1. Thermo-Chemical Analysis
5.2. Residual Stress Analysis
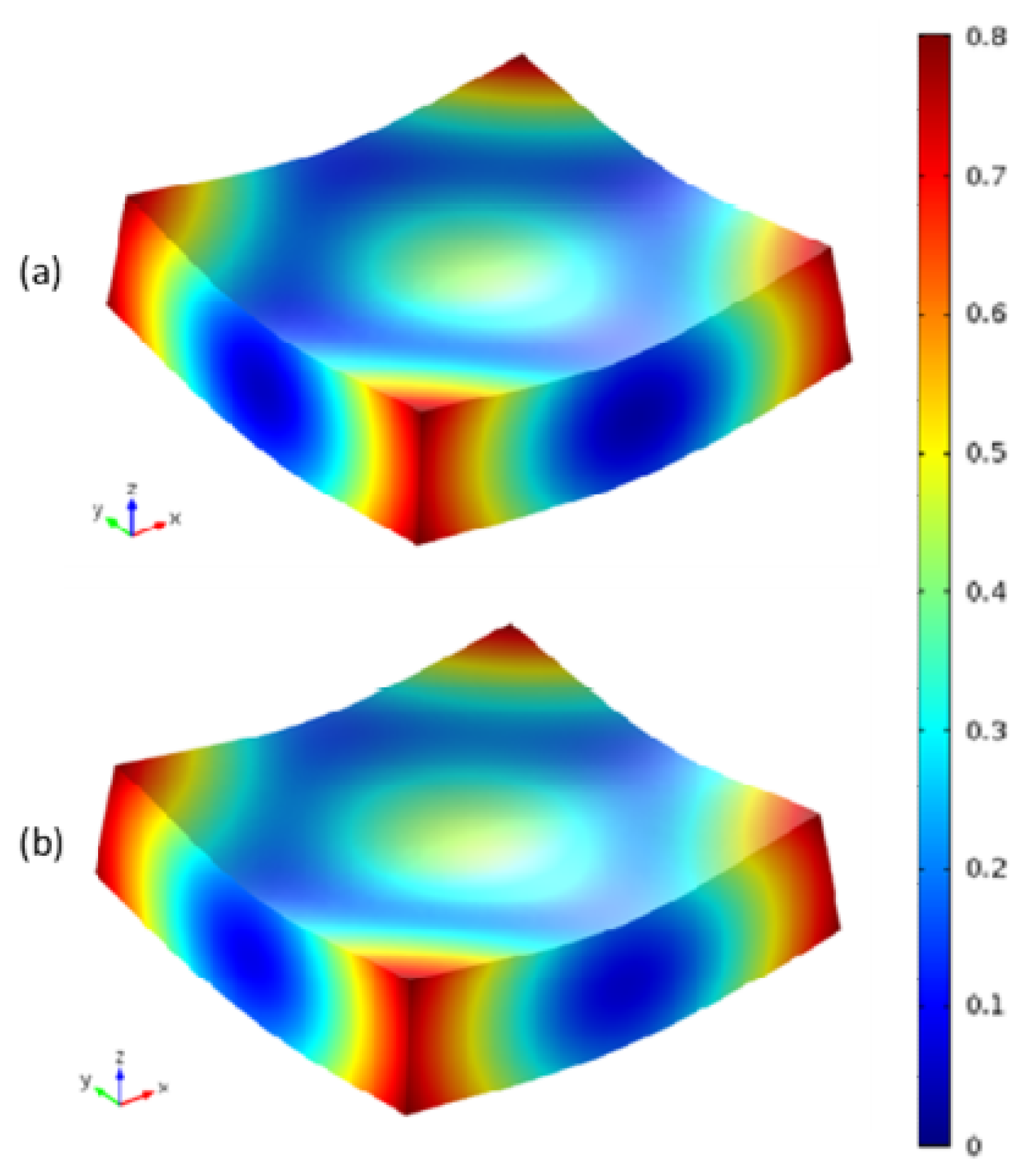
5.3. Curing Deformation Analysis
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bogetti, T.A.; Gillespie, J.W. Process-induced stress and deformation in thick-section thermoset composite laminates. J. Compos. Mater. 1992, 26, 626–660. [Google Scholar] [CrossRef]
- Griffin, O.H. Three-dimensional curing stresses in symmetric cross-ply laminates with temperature-dependent properties. J. Compos. Mater. 1983, 17, 449–463. [Google Scholar] [CrossRef]
- Hahn, H.T. Residual stresses in polymer matrix composite laminates. J. Compos. Mater. 1976, 10, 266–277. [Google Scholar] [CrossRef]
- Chao, L.; Yaoyao, S. An improved analytical solution for process-induced residual stresses and deformations in flat composite laminates considering thermo-viscoelastic effects. Materials 2018, 11, 2506. [Google Scholar]
- Shin, D.D.; Hahn, H.T. Compaction of thick composites: Simulation and experiment. Polym. Compos. 2004, 25, 49–59. [Google Scholar] [CrossRef]
- Fragassa, C.; de Camargo, F.V.; Pavlovic, A.; Minak, G. Explicit numerical modeling assessment of basalt reinforced composites for low-velocity impact. Compos. Part B Eng. 2019, 163, 522–535. [Google Scholar] [CrossRef]
- Adolf, D.B.; Chambers, R.S. A thermodynamically consistent, nonlinear viscoelastic approach for modelling thermosets during cure. J. Rheol. 2007, 51, 23–50. [Google Scholar] [CrossRef]
- Ganapathi, A.S.; Joshi, S.C.; Chen, Z. Simulation of Bleeder flow and curing of thick composites with pressure and temperature dependent properties. Simul. Model. Pract. Theory 2013, 32, 64–82. [Google Scholar] [CrossRef]
- Abdelal, G.F.; Robotham, A.; Cantwell, W. Autoclave cure simulation of composites structures applying implicit and explicit FE techniques. Int. J. Mech. Mater. Des. 2013, 9, 55–63. [Google Scholar] [CrossRef]
- Vautard, F.; Ozcan, S.; Poland, L. Influence of thermal history on the mechanical properties of carbon fiber-acrylate composites cured by electron beam and thermal processes. Compos. Part A Appl. Sci. Manuf. 2013, 45, 162–172. [Google Scholar] [CrossRef]
- Curiel, T.; Fernlund, G. Deformation and stress build-up in bi-material beam specimens with a curing FM 300 adhesive interlayer. Compos. Part A Appl. Sci. Manuf. 2008, 39, 252–261. [Google Scholar] [CrossRef]
- Maria, B.; Lionel, M.; Alice, C.; Martin, L.; Edu, R. Numerical analysis of viscoelastic process-induced residual distortions during manufacturing and post-curing. Compos. Part A Appl. Sci. Manuf. 2018, 107, 205–216. [Google Scholar]
- Ruiz, E.; Trochu, F. Numerical analysis of cure temperature and internal residual stresses in thin and thick RTM parts. Compos. Part A Appl. Sci. Manuf. 2005, 36, 806–826. [Google Scholar] [CrossRef]
- Jansen, K.M.B.; De Vreugd, J.; Ernst, L.J. Analytical estimate for curing-induced stress and warpage in coating layers. J. Appl. Polym. Sci. 2012, 126, 1623–1630. [Google Scholar] [CrossRef]
- Tavakol, B.; Roozbehjavan, P.; Ahmed, A.; Das, R.; Joven, R.; Koushyar, H. Prediction of Residual Stresses and Distortion in Carbon Fiber-Epoxy Composite Parts Due to Curing Process Using Finite Element. J. Appl. Polym. Sci. 2013, 128, 941–950. [Google Scholar] [CrossRef]
- White, S.R.; Hahn, H.T. Process modeling of composite materials: Residual stress development during cure. Part II. Experimental validation. J. Compos. Mater. 1992, 26, 2423–2453. [Google Scholar] [CrossRef]
- Prasatya, R.; McKenna, G.B.; Simon, S.L. A viscoelastic model for predicting isotropic residual stresses in thermosetting materials: Effects of processing parameters. J. Compos. Mater. 2001, 35, 826–849. [Google Scholar] [CrossRef]
- Khoun, L.; Hubert, P. Investigation of the dimensional stability of carbon epoxy cylinders manufactured by resin transfer moulding. Compos. Part A Appl. Sci. Manuf. 2013, 41, 116–124. [Google Scholar] [CrossRef]
- Toudeshky, H.H.; Sadighi, M.; Vojdani, A. Effects of curing thermal residual stresses on fatigue crack propagation of aluminum plates repaired by FML patches. Compos. Struct. 2013, 100, 154–162. [Google Scholar] [CrossRef]
- Wang, X.X.; Zhao, Y.R.; Su, H.; Jia, Y.X. Curing process-induced internal stress and deformation of fiber reinforced resin matrix composites: Numerical comparison between elastic and viscoelastic models. Polym. Polym. Compos. 2016, 24, 155–160. [Google Scholar] [CrossRef]
- Stango, R.J.; Wang, S.S. Process-induced residual thermal stresses in advanced fiber-reinforced composite laminates. J. Manuf. Sci. Eng. 1984, 106, 48–54. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Kamali, S.M. Theoretical and experimental studies on residual stresses in laminated polymer composites. J. Compos. Mater. 2005, 39, 2213–2225. [Google Scholar] [CrossRef]
- Johnston, A.; Vaziri, R.; Poursartip, A. A plane strain model for process-induced deformation of laminated composite structures. J. Compos. Mater. 2001, 35, 1435–1469. [Google Scholar] [CrossRef]
- Fernlund, G.; Osooly, A.; Poursartip, A.; Vaziri, R.; Courdji, R.; Nelson, K.; George, P.; Hendrickson, L.; Griffiith, J. Finite element based prediction of process-induced deformation of autoclaved composite structures using 2D process analysis and 3D structural analysis. Compos. Struct. 2003, 62, 223–234. [Google Scholar] [CrossRef]
- Baran, I.; Tutum, C.C.; Nielsen, M.W.; Hattel, J.H. Process induced residual stresses and distortions in pultrusion. Compos. Part B Eng. 2013, 51, 148–161. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Stress relaxation behavior of 3501-6 epoxy resin during cure. Polym. Eng. Sci. 1996, 36, 2852–2862. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Mather, P.T.; White, S.R. Viscoelastic properties of an epoxy resin during cure. J. Compos. Mater. 2001, 35, 883–904. [Google Scholar] [CrossRef]
- Patham, B. Multiphysics simulations of cure residual stresses and springback in a thermoset resin using a viscoelastic model with cure-temperature-time superposition. J. Appl. Polym. Sci. 2013, 129, 983–998. [Google Scholar] [CrossRef]
- Taylor, R.L.; Pister, K.S.; Goudreau, G.L. Thermo-mechanical analysis of viscoelastic solids. Int. J. Numer. Methods Eng. 1970, 2, 45–59. [Google Scholar] [CrossRef]
- Nima, Z.; Reza, V.; Anoush, P. Computationally efficient pseudo-viscoelastic models for evaluation of residual stresses in thermoset polymer composites during cure. Compos. Part A Appl. Sci. Manuf. 2010, 41, 247–256. [Google Scholar]
- Salla, J.M.; Ramis, X. Comparative study of the cure kinetics of an unsaturated polyester resin using different procedures. Polym. Eng. Sci. 1996, 36, 835–850. [Google Scholar] [CrossRef]
- Chu, F.; Mckenna, T.; Lu, S. Curing kinetics of an acrylic/epoxy resin system using dynamic scanning calorimetry. Eur. Polym. J. 1997, 33, 837–840. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Process-Induced stress relaxation analysis of AS4/3501-6 laminate. J. Reinf. Plast. Compos. 1997, 26, 2–16. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Viscoelastic analysis of processing-induced residual stresses in thick composite laminates. Mech. Compos. Mater. Struct. 1997, 4, 361–387. [Google Scholar] [CrossRef]
- White, S.R.; Kim, Y.K. Process-induced residual stress analysis of AS4/3501-6 composite material. Mech. Compos. Mater. Struct. 1998, 5, 153–186. [Google Scholar] [CrossRef]
- Huang, X.; Gillespie, J.W.; Boghetti, T.A. Process-induced stress for woven fabric thick section composite structures. Compos. Struct. 2000, 49, 303–312. [Google Scholar] [CrossRef]
- Ma, Y.R.; He, J.L.; Li, D.; Tan, Y.; Xu, L. Numerical simulation of curing deformation of resin matrix composite curved structure. Acta Mater. Compos. Sin. 2015, 32, 874–880. [Google Scholar]
- Tavman, I.; Akinci, H. Transverse thermal conductivity of fiber reinforced polymer composites. Int. Commun. Heat Mass Transf. 2000, 27, 253–261. [Google Scholar] [CrossRef]











| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (min−1) | 2.102 × 109 | (J/mol) | 8.07 × 104 |
| (min−1) | −2.014 × 109 | (J/mol) | 7.78 × 104 |
| (min−1) | 1.96 × 105 | (J/mol) | 5.66 × 104 |
| (J/Kg) | 1.989 × 105 | (J·mol−1·K−1) | 8.3143 |
| Property | Value |
|---|---|
| Resin density (mg·m−3) | |
| Fiber density (mg·m−3) | 1790 |
| Resin specific heat capacity (J·mol−1·K−1) | 4184[0.468 + 5.975 × 10−4T − 0.141] |
| Fiber specific heat capacity (J·mol−1·K−1) | 1390 + 4.50T |
| Thermal conductivity of resin (W·m−1·K−1) | 0.04184[3.85 + (0.035T − 0.141)] |
| Thermal conductivity of fiber (W·m−1·K−1) | 0.742 + 9.02 × 10−4T |
| Property | AS4 Carbon Fiber | 3501-6 Epoxy Resin |
|---|---|---|
| Longitudinal elastic modulus (Gpa) | 206.8 | 3.2 |
| Transverse elastic modulus (Gpa) | 17.2 | 3.2 |
| In-plane shear modulus (Gpa) | 27.58 | 1.185 |
| Transverse shear modulus (Gpa) | 6.894 | 1.185 |
| In-plane Poisson’s ratio | 0.2 | 0.35 |
| Transverse Poisson’s ratio | 0.3 | 0.35 |
| Longitudinal CTE () | −9 × 10−7 | 5.76 × 10−5 |
| Transverse CTE () | 7.2 × 10−6 | 5.76 × 10−5 |
| Longitudinal CSE | 0 | −0.01695 |
| Transverse CSE | 0 | −0.01695 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Xi, S.; Li, D. Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models. Materials 2019, 12, 572. https://doi.org/10.3390/ma12040572
Dai J, Xi S, Li D. Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models. Materials. 2019; 12(4):572. https://doi.org/10.3390/ma12040572
Chicago/Turabian StyleDai, Jianfeng, Shangbin Xi, and Dongna Li. 2019. "Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models" Materials 12, no. 4: 572. https://doi.org/10.3390/ma12040572
APA StyleDai, J., Xi, S., & Li, D. (2019). Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models. Materials, 12(4), 572. https://doi.org/10.3390/ma12040572




