A Mechanical Sensor Using Hybridized Metamolecules
Abstract
1. Introduction
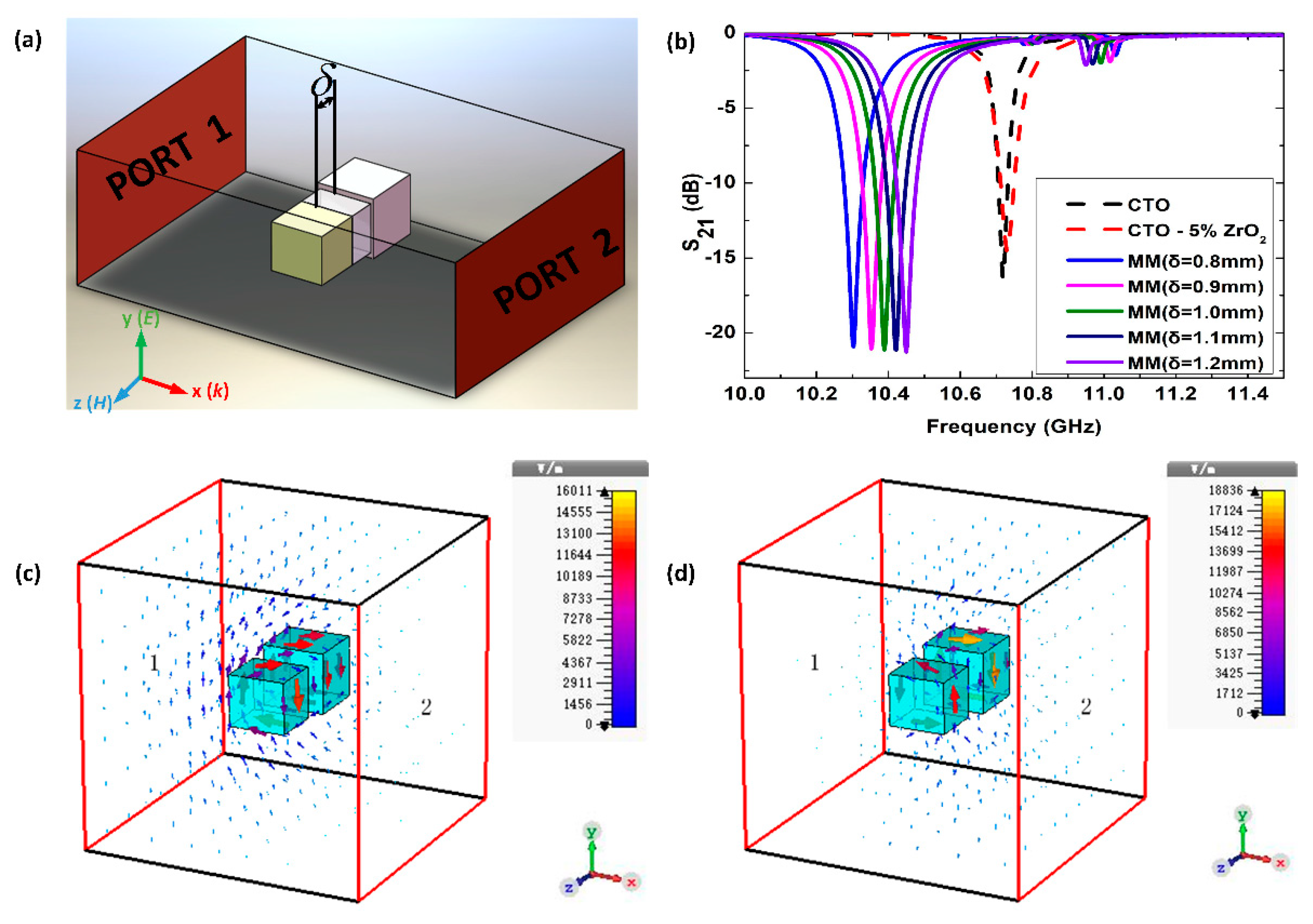
2. Materials and Simulation
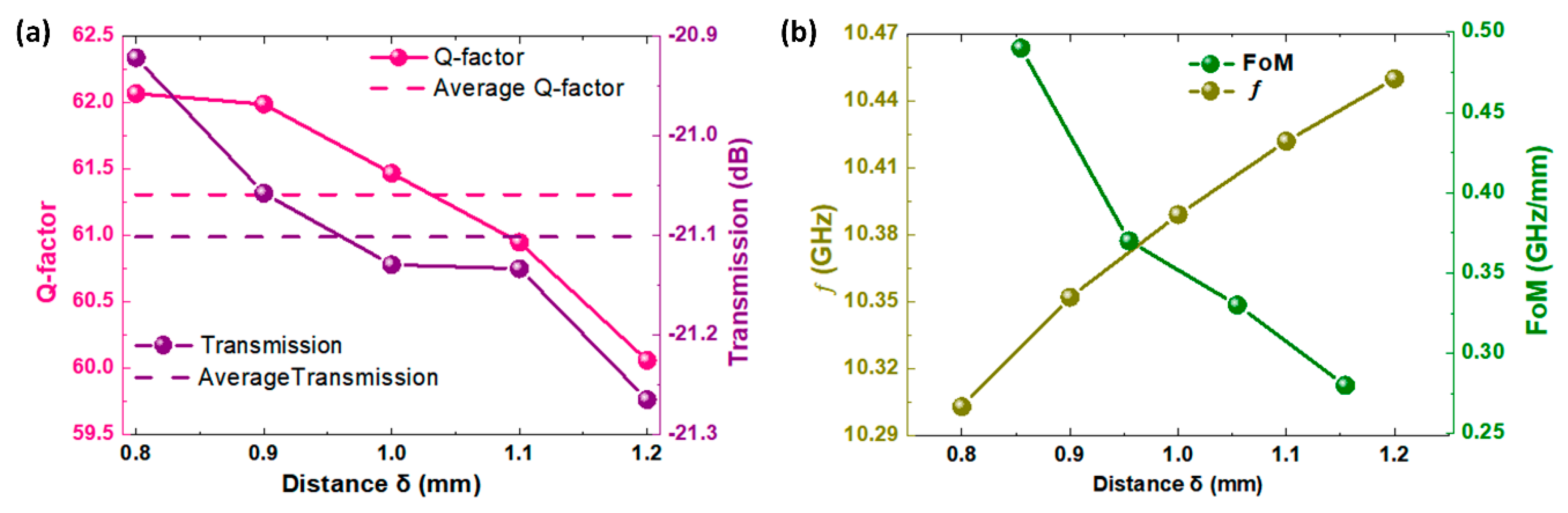
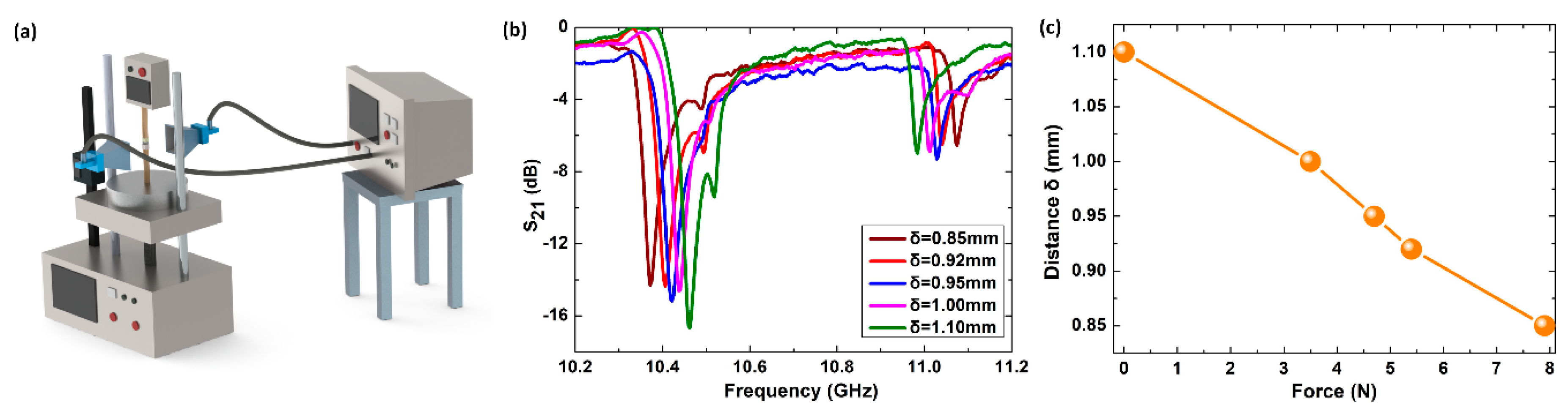
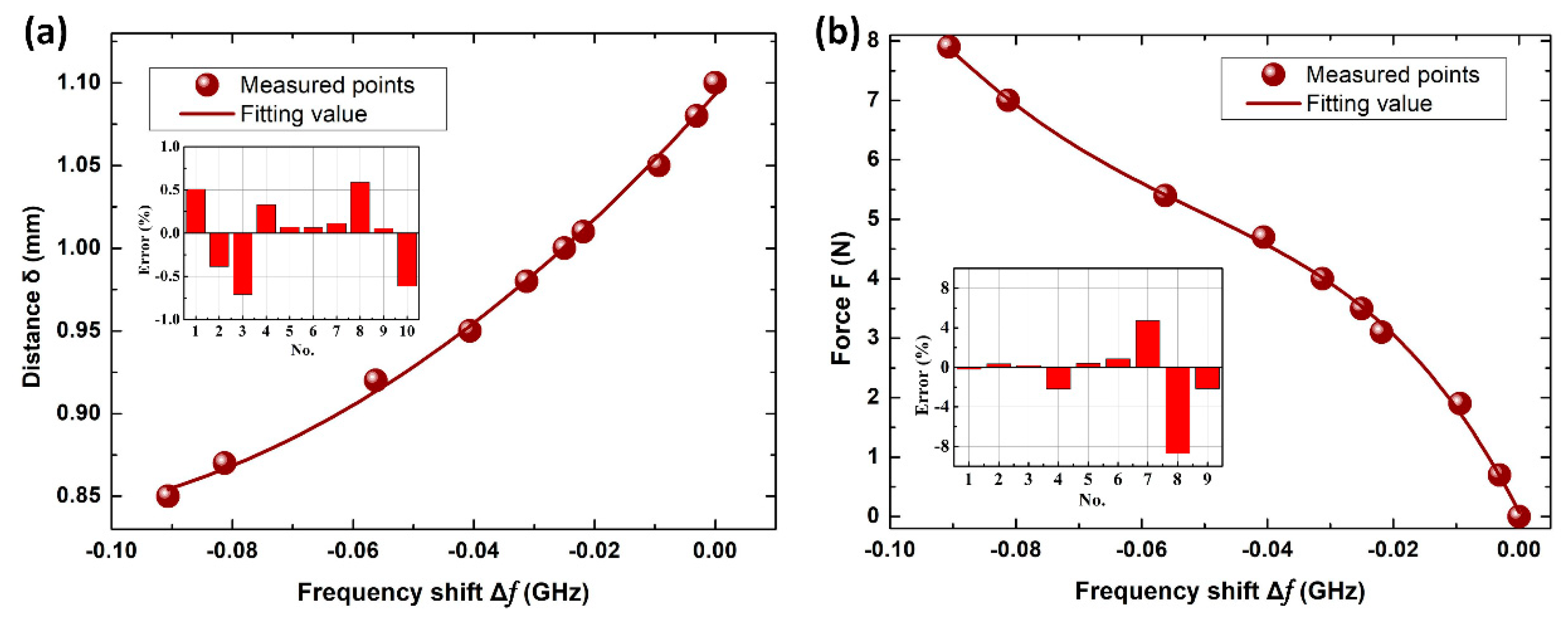
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nordlander, P.; Oubre, C.; Prodan, E.; Li, K.; Stockman, M.I. Plasmon hybridizaton in nanoparticle dimers. Nano Lett. 2004, 4, 899–903. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.J.; Liu, X.J. Tunable near-infrared optical properties of three-layered gold-silica-gold manoparticles. Appl. Phys. B Lasers Opt. 2009, 97, 193–197. [Google Scholar] [CrossRef]
- Hu, Y.; Noelck, S.J.; Drezek, R.A. Symmetry breaking in gold-silica-gold multilayer nanoshells. Acs Nano 2010, 4, 1521–1528. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Chen, Z.; Wang, W.; Li, Y.; Xu, J.; Sun, Q. Dual symmetry breaking in gold-silica-gold multilayer nanoshells. Plasmonics 2014, 9, 1361–1369. [Google Scholar] [CrossRef]
- Wu, D.J.; Cheng, Y.; Wu, X.W.; Liu, X.J. An active metallic nanomatryushka with two similar super-resonances. J. Appl. Phys. 2014, 116, 013502. [Google Scholar] [CrossRef]
- Weis, P.; Garcia-Pomar, J.L.; Beigang, R.; Rahm, M. Hybridization induced transparency in composites of metamaterials and atomic media. Opt. Express 2011, 19, 23573–23580. [Google Scholar] [CrossRef]
- Shelton, D.J.; Brener, I.; Ginn, J.C.; Sinclair, M.B.; Peters, D.W.; Coffey, K.R.; Boreman, G.D. Strong coupling between nanoscale metamaterials and phonons. Nano Lett. 2011, 11, 2104–2108. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Y.; Zhang, Y.; Wang, Y.; Aba, T.; Li, H.; Wang, L.; Zhang, Z. Asymmetric transmission of a planar metamaterial induced by symmetry breaking. J. Phys. Condens. Matter 2018, 30, 114001. [Google Scholar] [CrossRef]
- Huo, Y.; Jia, T.; Zhang, Y.; Zhao, H.; Zhang, S.; Feng, D.; Sun, Z. Narrow and deep fano resonances in a rod and concentric square ring-disk nanostructures. Sensors 2013, 13, 11350–11361. [Google Scholar] [CrossRef]
- Sharac, N.; Giles, A.J.; Perkins, K.; Tischler, J.; Bezares, F.; Prokes, S.M.; Folland, T.G.; Glembocki, O.J.; Caldwell, J.D. Implementation of plasmonic band structure to understand polariton hybridization within metamaterials. Opt. Express 2018, 26, 29363–29374. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Fan, C.; He, J.; Ding, P.; Liang, E.; Xue, Q. Double fano resonances due to interplay of electric and magnetic plasmon modes in planar plasmonic structure with high sensing sensitivity. Opt. Express 2013, 21, 2236–2244. [Google Scholar] [CrossRef] [PubMed]
- Rana, G.; Deshmukh, P.; Palkhivala, S.; Gupta, A.; Duttagupta, S.P.; Prabhu, S.S.; Achanta, V.G.; Agarwal, G.S. Quadrupole-quadrupole interactions to control plasmon-induced transparency. Phys. Rev. Appl. 2018, 9, 064015. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, Z. Spoof surface plasmon based planar antennas for the realization of terahertz hotspots. Sci. Rep. 2015, 5, 18606. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.Q.; Luxmoore, I.J.; Mikhailov, S.A.; Savostianova, N.A.; Valmorra, F.; Faist, J.; Nash, G.R. Highly tunable hybrid metamaterials employing split-ring resonators strongly coupled to graphene surface plasmons. Nat. Commun. 2015, 6, 8969. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.; Huang, Z.; Singh, A.; Yao, Y.; Azad, A.K.; Mohite, A.D.; Taylor, A.J.; Smith, D.R.; Chen, H.T. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light Sci. Appl. 2018, 7, 51. [Google Scholar] [CrossRef]
- Xu, R.J.; Luo, J.; Sha, J.S.; Zhong, J.T.; Xu, Z.F.; Tong, Y.L.; Lin, Y.S. Stretchable IR metamaterial with ultra-narrowband perfect absorption. Appl. Phys. Lett. 2018, 113, 101907. [Google Scholar] [CrossRef]
- Kipfstuhl, L.; Guldner, F.; Riedrich-Moeller, J.; Becher, C. Modeling of optomechanical coupling in a phoxonic crystal cavity in diamond. Opt. Express 2014, 22, 12410–12423. [Google Scholar] [CrossRef]
- Goltcman, L.; Hadad, Y. Scattering from artificial piezoelectriclike meta-atoms and molecules. Phys. Rev. Lett. 2018, 120, 054301. [Google Scholar] [CrossRef]
- Vallet, G.; Bookjans, E.; Eismann, U.; Bilicki, S.; Le Targat, R.; Lodewyck, J. A noise-immune cavity-assisted non-destructive detection for an optical lattice clock in the quantum regime. New J. Phys. 2017, 19, 083002. [Google Scholar] [CrossRef]
- Pryce, I.M.; Aydin, K.; Kelaita, Y.A.; Briggs, R.M.; Atwater, H.A. Highly strained compliant optical metamaterials with large frequency tunability. Nano Lett. 2010, 10, 4222–4227. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.R.; Sun, X.Y.; Xu, H.; Lu, Y.H.; Lee, Y.; Rhee, J.Y.; Song, W.J. Strain sensitivity of electric-magnetic coupling in flexible terahertz metamaterials. Plasmonics 2015, 10, 1331–1335. [Google Scholar] [CrossRef]
- Christ, A.; Martin, O.J.F.; Ekinci, Y.; Gippius, N.A.; Tikhodeev, S.G. Symmetry breaking in a plasmonic metamaterial at optical wavelength. Nano Lett. 2008, 8, 2171–2175. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Soennichsen, C.; Giessen, H. Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. 2010, 10, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Verellen, N.; Sonnefraud, Y.; Sobhani, H.; Hao, F.; Moshchalkov, V.V.; Van Dorpe, P.; Nordlander, P.; Maier, S.A. Fano resonances in individual coherent plasmonic nanocavities. Nano Lett. 2009, 9, 1663–1667. [Google Scholar] [CrossRef]
- Fan, J.A.; Bao, K.; Wu, C.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Shvets, G.; Nordlander, P.; Capasso, F. Fano-like interference in self-assembled plasmonic quadrumer clusters. Nano Lett. 2010, 10, 4680–4685. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; You, C.L.; Mahigir, A.; Liu, T.T.; Xia, F.; Kong, W.J.; Veronis, G.; Dowling, J.P.; Dong, L.F.; Yun, M.J. Graphene-based dual-band independently tunable infrared absorber. Nanoscale 2018, 10, 15564–15570. [Google Scholar] [CrossRef]
- Zhao, Q.; Kang, L.; Du, B.; Zhao, H.; Xie, Q.; Huang, X.; Li, B.; Zhou, J.; Li, L. Experimental demonstration of isotropic negative permeability in a three-dimensional dielectric composite. Phys. Rev. Lett. 2008, 101, 027402. [Google Scholar] [CrossRef]
- Liu, X.; Lan, C.; Bi, K.; Li, B.; Zhao, Q.; Zhou, J. Dual band metamaterial perfect absorber based on mie resonances. Appl. Phys. Lett. 2016, 109, 062902. [Google Scholar] [CrossRef]
- Lan, C.; Bi, K.; Li, B.; Cui, X.; Zhou, J.; Zhao, Q. Hyperbolic metamaterial based on anisotropic mie-type resonance. Opt. Express 2013, 21, 29592–29600. [Google Scholar] [CrossRef]
- Bi, K.; Guo, Y.S.; Liu, X.M.; Zhao, Q.; Xiao, J.H.; Lei, M.; Zhou, J. Magnetically tunable Mie resonance-based dielectric metamaterials. Sci. Rep. 2014, 4, 7001. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.S.; Zhou, J.; Lan, C.W.; Wu, H.Y.; Bi, K. Mie-resonance-coupled total broadband transmission through a single subwavelength aperture. Appl. Phys. Lett. 2014, 104, 204103. [Google Scholar]
- Wu, L.; Xi, X.; Li, B.; Zhou, J. A Mie resonant antenna with high sensitivity for force and strain measurement. Sci. Rep. 2017, 7, 4615. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.Y.; Wu, Q.; Erni, D.; Wu, K.; Lee, J.C. Polarization-independent metamaterial analog of electromagnetically induced transparency for a refractive-index-based sensor. IEEE Trans. Microw. Theory Tech. 2012, 60, 3013–3022. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Zhou, J. Adjustment of Electric Field Intensity by Dielectric Metamolecule Hybridization Model. Available online: https://arxiv.org/abs/1901.08757 (accessed on 25th January 2019).
- Zhao, Q.; Zhou, J.; Zhang, F.; Lippens, D. Mie resonance-based dielectric metamaterials. Mater. Today 2009, 12, 60–69. [Google Scholar] [CrossRef]
| Q-Factors | ||||||
|---|---|---|---|---|---|---|
| Diatomic Molecule | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | Average |
| CTO–CTO | 76.50 | 75.69 | 75.40 | 74.55 | 73.70 | 75.168 |
| (CTO–5%ZrO2)–(CTO–5%ZrO2) | 50.46 | 49.56 | 49.26 | 48.72 | 48.18 | 49.236 |
| Metamolecule | 62.07 | 61.99 | 61.47 | 60.95 | 60.06 | 61.308 |
| FoM | ||||||
|---|---|---|---|---|---|---|
| Diatomic Molecule | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | Average |
| CTO–CTO | 0.42 | 0.36 | 0.32 | 0.28 | \ | 0.345 |
| (CTO–5%ZrO2)–(CTO–5%ZrO2) | 0.64 | 0.37 | 0.32 | 0.30 | \ | 0.4075 |
| Metamolecule | 0.49 | 0.37 | 0.33 | 0.28 | \ | 0.3675 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, X.; Yang, T.; Zhou, J. A Mechanical Sensor Using Hybridized Metamolecules. Materials 2019, 12, 466. https://doi.org/10.3390/ma12030466
Li H, Wang X, Yang T, Zhou J. A Mechanical Sensor Using Hybridized Metamolecules. Materials. 2019; 12(3):466. https://doi.org/10.3390/ma12030466
Chicago/Turabian StyleLi, Haohua, Xiaobo Wang, Tian Yang, and Ji Zhou. 2019. "A Mechanical Sensor Using Hybridized Metamolecules" Materials 12, no. 3: 466. https://doi.org/10.3390/ma12030466
APA StyleLi, H., Wang, X., Yang, T., & Zhou, J. (2019). A Mechanical Sensor Using Hybridized Metamolecules. Materials, 12(3), 466. https://doi.org/10.3390/ma12030466





