Modelling and Analysis of the Corrosion Characteristics of Ferritic-Martensitic Steels in Supercritical Water
Abstract
:1. Introduction
2. ANN and ‘Fuzzy Logic’ Analyses
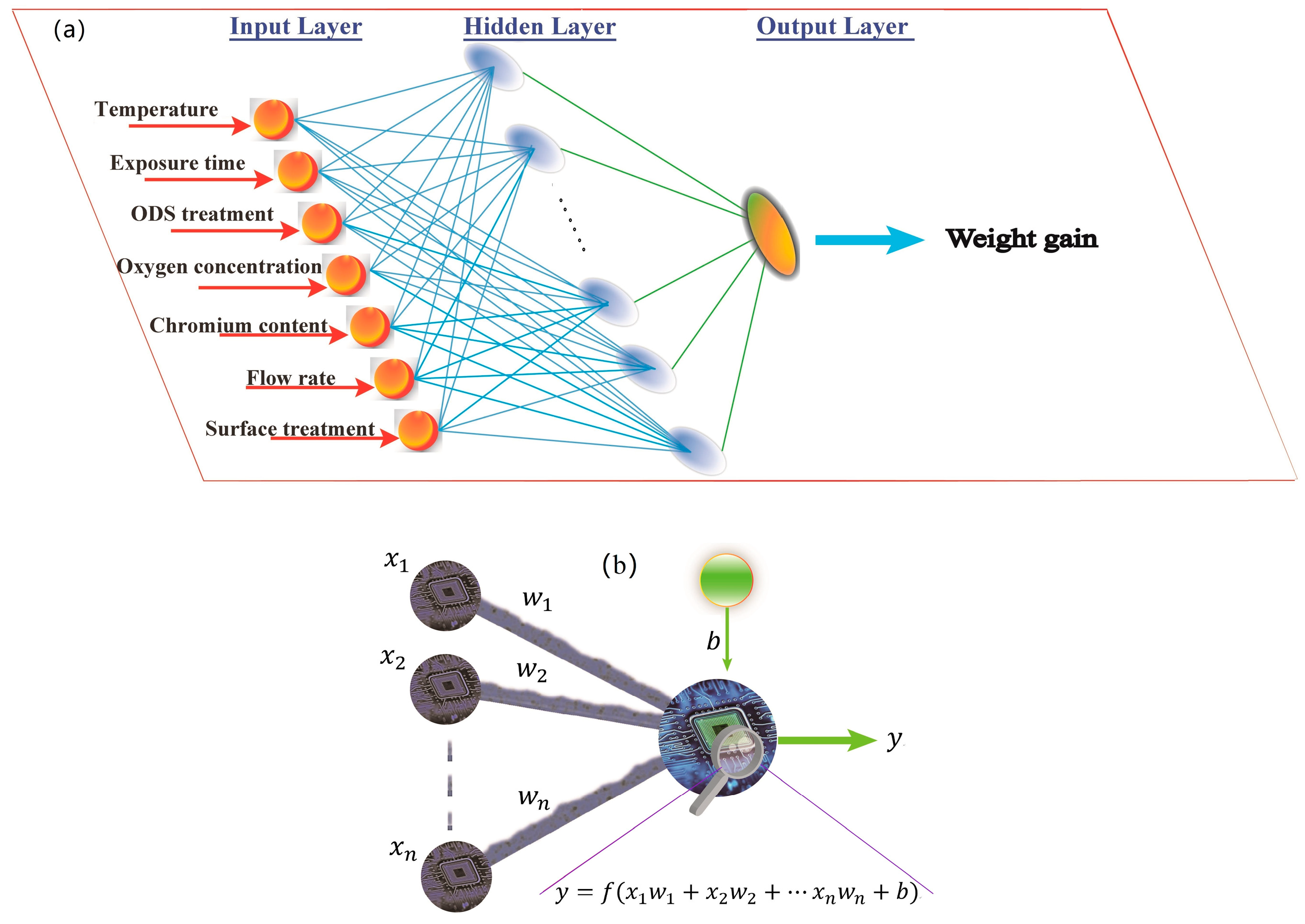
2.1. Neural Network Backpropagation Method
2.2. Data Collection and Preprocessing
2.3. Model Formulation
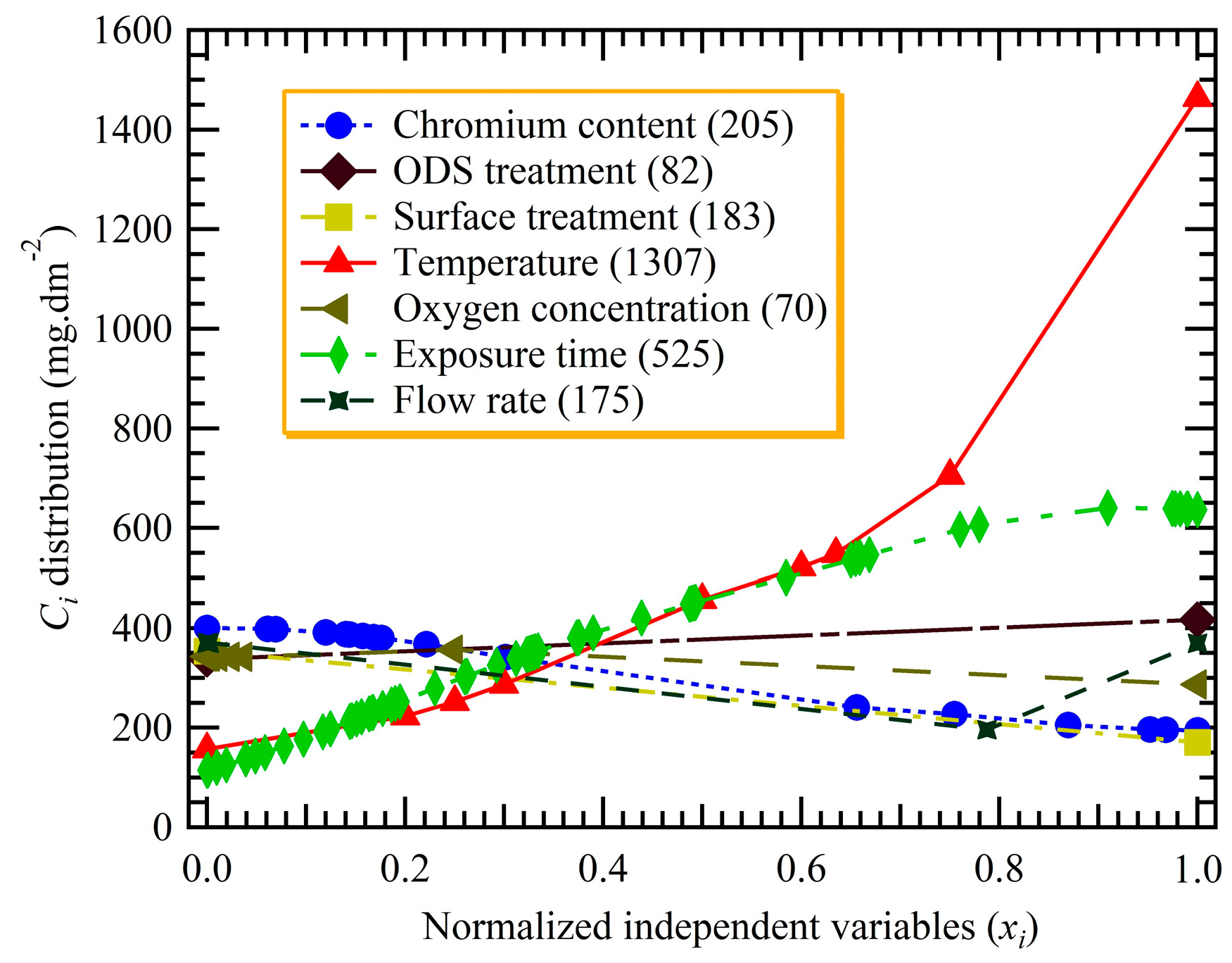
2.4. Fuzzy Curve Analysis
3. Results and Discussion
3.1. Significance of Variables
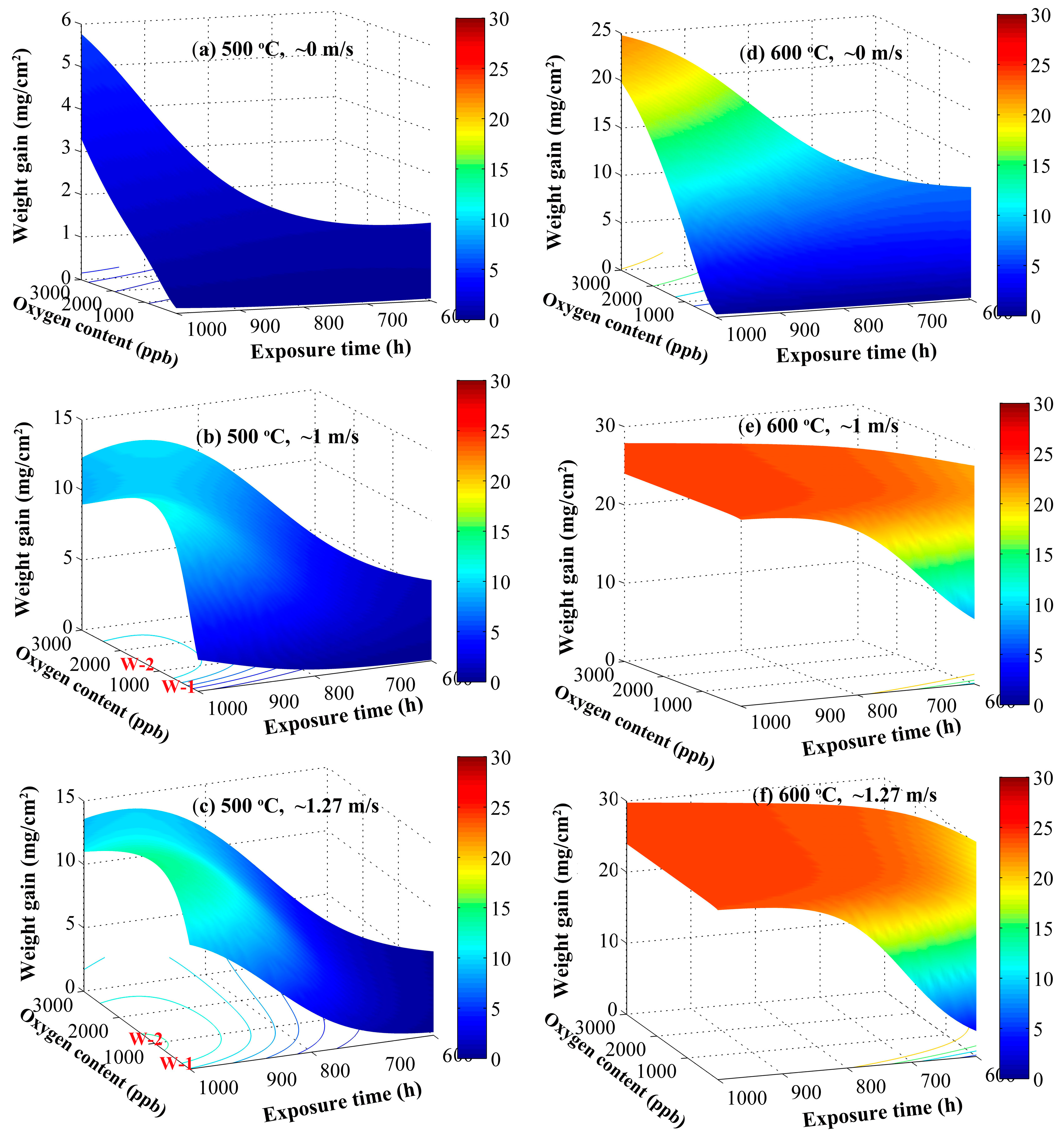
3.2. Temperature and Exposure Time
3.3. Effect of Cr Content
3.4. Oxygen Content and Flow Rate
4. Conclusions
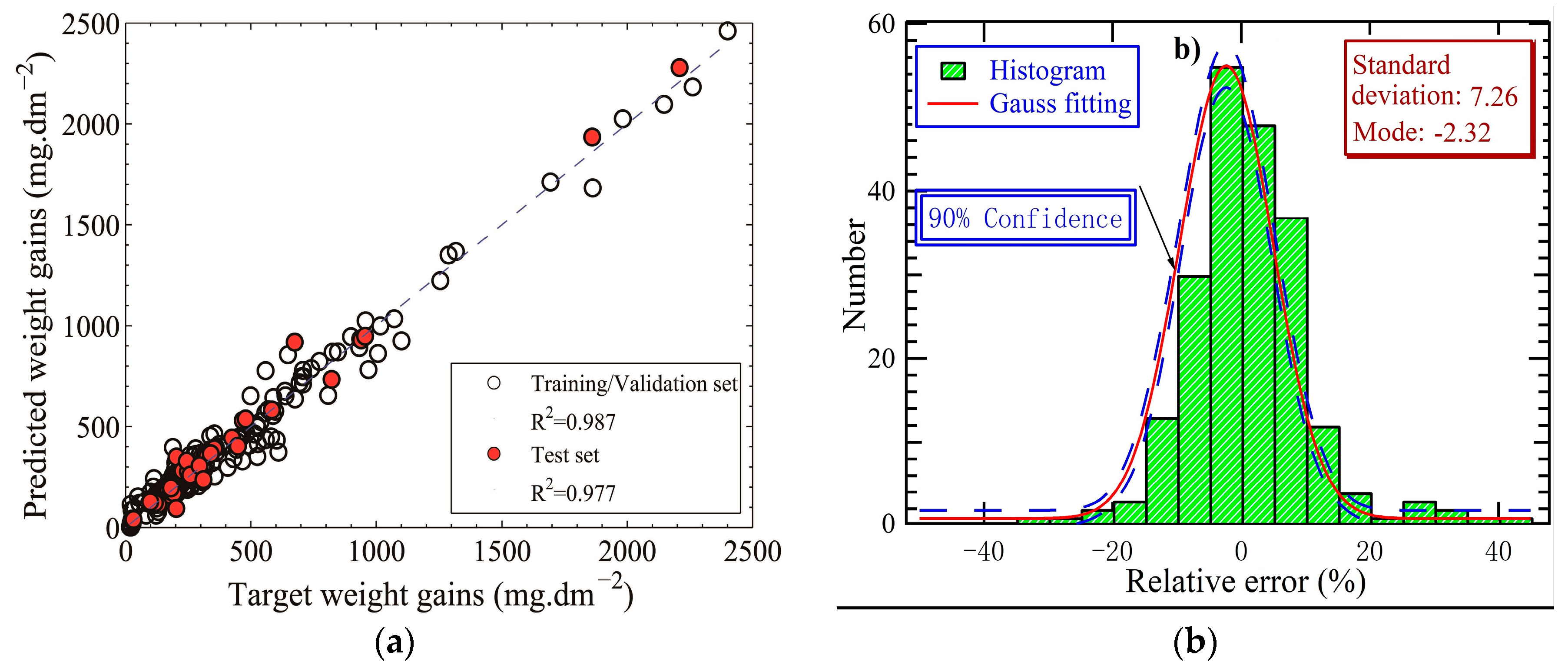
- Fuzzy curve analysis ranks temperature and exposure time as the most important. However, the importance of the oxygen concentration comes in the last place. The obtained three-layer ANN architecture of 7:30:1 exhibits a satisfying performance with an R-squared value of more than 0.98.
- Predicted weight gain increases with temperature and exposure time, being in good consistence with experimentally measured data. The departure of oxidation kinetics from the parabolic law may be due to the dependence of the effective diffusivities of cations and anions through the oxide scale on short-circuit transport paths, such as the oxide grain boundaries. The dependence decreases with the temperature from 500 °C to 600 °C, because of the reduction of density of the short-circuit transport paths, due to the enlargement of oxide grain size. However, this dependence enhances with an increase in temperature up to 700 °C, deriving from the local formation of chromia within the scales at the high temperature. Additionally, high temperature delays the occurrence of the steady-state oxidation stage of 9-12Cr F-M steels in SCW.
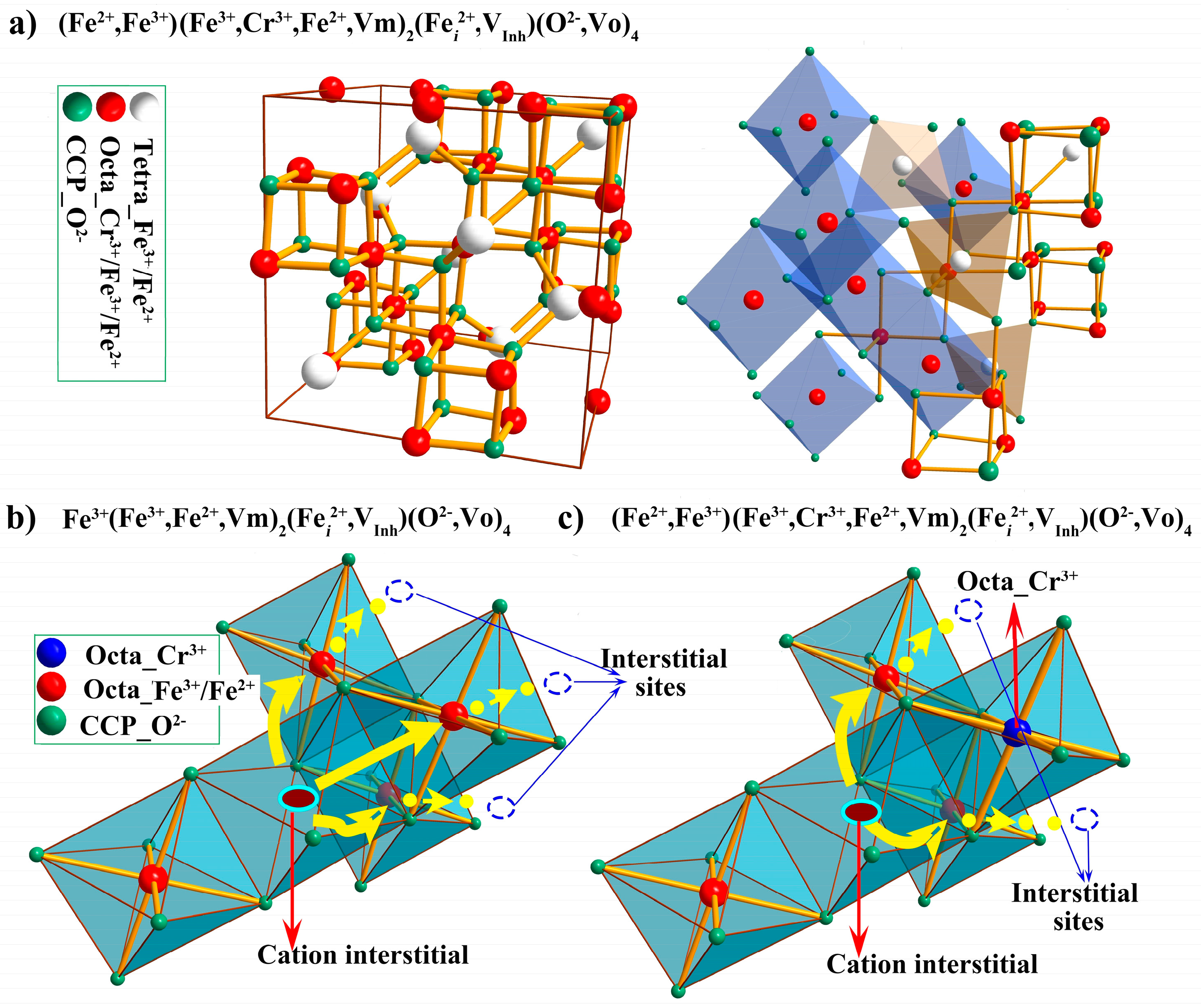
- Influence of the chromium content (~9–12 wt.%) in the substrate on the weight gain is negligible at 500 °C, but becomes marked at 600 °C and above, due to the additional local formation of chromia. The certain amount of Cr restricted in the inner layer, can “block” some transport paths of cation defects (predominant cation interstitials) and thus inhibits the generation kinetics of cation defects, to decrease the diffusion flux of cations outward, finally improving the oxidation resistance of steels.
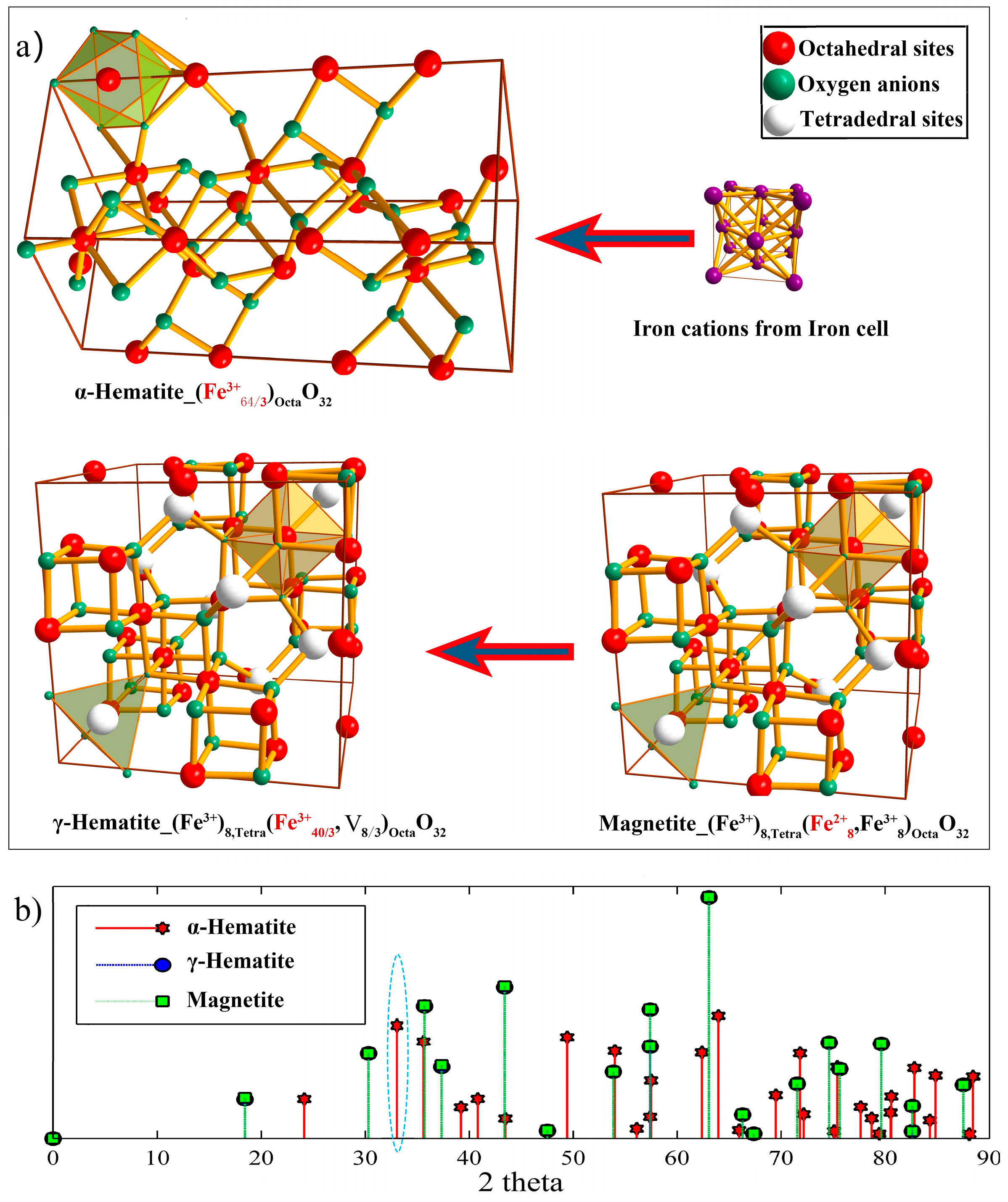
- At 500 °C, the oxygen content at which there is a maximum weight gain decreases with increasing SCW flow rate. The effective oxygen potential at the scale/SCW interface, being synergistically determined by oxygen concentration, flow rate of SCW and temperature, plays a key role in influencing the oxidation rate of steels. Higher oxygen potentials at the scale/SCW interface can promote the secondary oxidation of magnetite, accelerating the occurrence of hematite on the outmost surface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Viswanathan, R.; Sarver, J.; Tanzosh, J.M. Boiler materials for ultra-supercritical coal power plants-stearnside oxidation. J. Mater. Eng. Perform. 2006, 15, 255–274. [Google Scholar] [CrossRef]
- A Technology Roadmap for Generation IV Nuclear Energy Systems. Available online: http://130.88.20.21/uknuclear/pdfs/GenIV_Roadmap_September_2002.pdf (accessed on 3 December2016).
- Tan, L.; Yang, Y.; Allen, T.R. Oxidation behavior of iron-based alloy HCM12A exposed in supercritical water. Corros. Sci. 2006, 48, 3123–3138. [Google Scholar] [CrossRef]
- Ampornrat, P.; Was, G.S. Oxidation of ferritic-martensitic alloys T91, HCM12A and HT-9 in supercritical water. J. Nucl. Mater. 2007, 371, 1–17. [Google Scholar] [CrossRef]
- Zhang, N.Q.; Zhu, Z.L.; Xu, H.; Mao, X.P.; Li, J. Oxidation of ferritic and ferritic-martensitic steels in flowing and static supercritical water. Corros. Sci. 2016, 103, 124–131. [Google Scholar] [CrossRef]
- Allen, T.R.; Chen, Y.; Ren, X.; Sridharan, K.; Tan, L.; Was, G.S.; West, E.; Guzonas, D. Material Performance in Supercritical Water. In Comprehensive Nuclear Materials; Elsevier: Oxford, UK, 2012; pp. 279–326. [Google Scholar]
- Tan, L.; Ren, X.; Allen, T.R. Corrosion behavior of 9–12% Cr ferritic-martensitic steels in supercritical water. Corros. Sci. 2010, 52, 1520–1528. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Sun, P.; Yang, J.; Tang, X.; Xu, D.; Guo, Y.; Yang, J.; Macdonald, D.D. Investigation on early formation and evolution of oxide scales on ferritic–martensitic steels in supercritical water. Corros. Sci. 2018, 135, 136–146. [Google Scholar] [CrossRef]
- Bischoff, J.; Motta, A.T.; Eichfeld, C.; Comstock, R.J.; Cao, G.; Allen, T.R. Corrosion of ferritic-martensitic steels in steam and supercritical water. J. Nucl. Mater. 2013, 441, 604–611. [Google Scholar] [CrossRef]
- Bischoff, J.; Motta, A.T. Oxidation behavior of ferritic-martensitic and ODS steels in supercritical water. J. Nucl. Mater. 2012, 424, 261–276. [Google Scholar] [CrossRef]
- Sun, L.; Yan, W.P. Estimation of oxidation kinetics and oxide scale void position of ferritic-martensitic steels in supercritical water. Adv. Mater. Sci. Eng. 2017, 2017, 9154934. [Google Scholar] [CrossRef]
- Tan, L.; Machut, M.T.; Sridharan, K.; Allen, T.R. Corrosion behavior of a ferritic/martensitic steel HCM12A exposed to harsh environments. J. Nucl. Mater. 2007, 371, 161–170. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Xu, H.; Jiang, D.F.; Zhang, N.Q. Temperature dependence of oxidation behaviour of a ferritic-martensitic steel in supercritical water at 600–700 degrees C. Oxid. Met. 2016, 86, 483–496. [Google Scholar] [CrossRef]
- Zhang, N.; Xu, H.; Li, B.; Bai, Y.; Liu, D. Influence of the dissolved oxygen content on corrosion of the ferritic-martensitic steel P92 in supercritical water. Corros. Sci. 2012, 56, 123–128. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Macdonald, D.D. Prediction of crack growth rate in Type 304 stainless steel using artificial neural networks and the coupled environment fracture model. Corros. Sci. 2014, 89, 69–80. [Google Scholar] [CrossRef]
- Kamrunnahar, M.; Urquidi-Macdonald, M. Prediction of corrosion behaviour of Alloy 22 using neural network as a data mining tool. Corros. Sci. 2011, 53, 961–967. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Macdonald, D.D. Prediction of primary water stress corrosion crack growth rates in Alloy 600 using artificial neural networks. Corros. Sci. 2015, 92, 217–227. [Google Scholar] [CrossRef]
- Cavanaugh, M.K.; Buchheit, R.G.; Birbilis, N. Modeling the environmental dependence of pit growth using neural network approaches. Corros. Sci. 2010, 52, 3070–3077. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer: New York, NY, USA, 1996. [Google Scholar]
- Yin, K.; Qiu, S.; Tang, R.; Zhang, Q.; Zhang, L. Corrosion behavior of ferritic/martensitic steel P92 in supercritical water. J. Supercrit. Fluid 2009, 50, 235–239. [Google Scholar] [CrossRef]
- Sagaradze, V.V.; Shalaev, V.I.; Arbuzov, V.L.; Goshchitskii, B.N.; Yun, T.; Wan, Q.; Sun, J.G. Radiation resistance and thermal creep of ODS ferritic steels. J. Nucl. Mater. 2001, 295, 265–272. [Google Scholar] [CrossRef]
- Was, G.S.; Ampornrata, P.; Guptaa, G.; Teysseyre, S.; West, E.A.; Allen, T.R.; Sridharan, K.; Tan, L.; Chen, Y.; Ren, X.; et al. Corrosion and stress corrosion cracking in supercritical water. J. Nucl. Mater. 2007, 371, 176–201. [Google Scholar] [CrossRef]
- Bischoff, J.; Motta, A.T.; Comstock, R.J. Evolution of the oxide structure of 9CrODS steel exposed to supercritical water. J. Nucl. Mater. 2009, 392, 272–279. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signal 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Lin, Y.; Cunningham, G.A. A new approach to fuzzy-neural system modeling. IEEE Trans. Fuzzy Syst. 1995, 3, 190–198. [Google Scholar]
- Sung, A.H. Ranking importance of input parameters of neural networks. Expert Syst. Appl. 1998, 15, 405–411. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Sun, P.; Tong, Z.; Xu, D.; Guo, Y.; Yang, J. Early oxidation of Super304H stainless steel and its scales stability in supercritical water environments. Int. J. Hydrogen Energy 2016, 41, 15764–15771. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Sun, P.; Xu, D.; Ren, M.; Guo, Y.; Lin, G. Early oxidation mechanism of austenitic stainless steel TP347H in supercritical water. Corros. Sci. 2017, 128, 241–252. [Google Scholar] [CrossRef]
- Briceno, D.G.; Blazquez, F.; Maderuelo, A.S. Oxidation of austenitic and ferritic/martensitic alloys in supercritical water. J. Supercrit. Fluid 2013, 78, 103–113. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Yang, J.; Xu, D.; Guo, Y.; Qian, L.; Song, W. Corrosion characteristics of a nickel-base alloy C-276 in harsh environments. Int. J. Hydrogen Energy 2017, 42, 19829–19835. [Google Scholar] [CrossRef]
- Li, Y.H.; Wang, S.Z.; Li, X.D.; Lu, J.M. Corrosion of an austenitic heat-resistant steel HR3C in high-temperature steam and supercritical water. J. Adv. Res. 2014, 908, 67–71. [Google Scholar] [CrossRef]
- Guan, X.; Macdonald, D.D. Determination of corrosion mechanisms and estimation of electrochemical kinetics of metal corrosion in high subcritical and supercritical aqueous systems. Corrosion 2009, 65, 376–387. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, H.; Jiang, D.; Mao, X.; Zhang, N. Influence of temperature on the oxidation behaviour of a ferritic-martensitic steel in supercritical water. Corros. Sci. 2016, 113, 172–179. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Rifaie, M.A.; Engelhardt, G.R. New rate laws for the growth and reduction of passive films. J. Electrochem. Soc. 2001, 148, B343–B347. [Google Scholar] [CrossRef]
- Fromhold, A.T.; Fromhold, R.G. An Overview of Metal Oxidation Theory. In Comprehensive Chemical Kinetics; Bamford, C.H., Tipper, C.F.H., Compton, R.G., Eds.; Elsevier: Oxford, UK, 1984; Volume 21, pp. 1–117. [Google Scholar]
- Atkinson, A. Transport processes during the growth of oxide films at elevated temperature. Rev. Mod. Phys. 1985, 57, 437–470. [Google Scholar] [CrossRef]
- Macdonald, D.D.; Sikora, E.; Sikora, J. The point defect model vs. the high field model for describing the growth of passive films. In Proceedings of the 7th International Symposium on Oxide Films on Metals and Alloys, Clausthal, Germany, 21–26 August 1994; pp. 139–151. [Google Scholar]
- Young, L. Anodic Oxide Films; Academic Press: New York, NY, USA, 1961. [Google Scholar]
- Li, Y.H.; Macdonald, D.D.; Yang, J.; Wang, S.Z. Point defect model for the corrosion of steels and alloys in supercritical water I. film growth kinetics. 2019; Unpublished work. [Google Scholar]
- Gibbs, G.B. The influence of oxide grain boundaries on diffusion-controlled oxidation. Corros. Sci. 1967, 7, 165–169. [Google Scholar] [CrossRef]
- Gao, W.H.; Guo, X.L.; Shen, Z.; Zhang, L.F. Corrosion behavior of oxide dispersion strengthened ferritic steels in supercritical water. J. Nucl. Mater. 2017, 486, 1–10. [Google Scholar] [CrossRef]
- Chen, Y.; Sridharan, K.; Ukai, S.; Allen, T.R. Oxidation of 9Cr oxide dispersion strengthened steel exposed in supercritical water. J. Nucl. Mater. 2007, 371, 118–128. [Google Scholar] [CrossRef]
- Čermák, J.; Růžičková, J.; Pokorná, A. Low-temperature tracer diffusion of chromium in Fe-Cr ferritic alloys. Scr. Mater. 1996, 35, 411–416. [Google Scholar] [CrossRef]
- Ampornrat, P.; Gupta, G.; Was, G.S. Tensile and stress corrosion cracking behavior of ferritic-martensitic steels in supercritical water. J. Nucl. Mater. 2009, 395, 30–36. [Google Scholar] [CrossRef]
- Robertson, J. The mechanism of high temperature aqueous corrosion of steel. Corros. Sci. 1989, 29, 1275–1291. [Google Scholar] [CrossRef]
- Hallström, S.; Höglund, L.; Ågren, J. Modeling of iron diffusion in the iron oxides magnetite and hematite with variable stoichiometry. Scr. Mater. 2011, 59, 53–60. [Google Scholar] [CrossRef]
- Backhaus-Ricoult, M.; Dieckmann, R. Defects and cation diffusion in magnetite (VII): Diffusion controlled formation of magnetite during reactions in the iron-oxygen system. Phys. Chem. 1986, 90, 690–698. [Google Scholar] [CrossRef]
- Töpfer, J.; Aggarwal, S.; Dieckmann, R. Point defects and cation tracer diffusion in (CrxFe1−x)3−δO4 spinels. Solid State Ionics 1995, 81, 251–266. [Google Scholar] [CrossRef]
- Macdonald, D.D. The point defect model for the passive state. J. Electrochem. Soc. 1992, 139, 3434–3449. [Google Scholar] [CrossRef]
- Macdonald, D.D. The history of the point defect model for the passive state: A brief review of film growth aspects. Electrochim. Acta 2011, 56, 1761–1772. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Tang, X.; Xu, D.; Guo, Y.; Zhang, J.; Qian, L. Effects of sulfides on the corrosion behavior of Inconel 600 and Incoloy 825 in supercritical water. Oxid. Met. 2015, 84, 509–526. [Google Scholar] [CrossRef]
- Robertson, J. The mechanism of high-temperature aqueous corrosion of stainless-steels. Corros. Sci. 1991, 32, 443–465. [Google Scholar] [CrossRef]
- Payet, M. Mechanism Study of c.f.c Fe-Ni-Cr Alloy Corrosion in Supercritical Water. Ph.D. Thesis, Conservatoire National des Arts et Metiers, Paris, France, 2011. [Google Scholar]
- Tan, L.; Yang, Y.; Allen, T.R. Porosity prediction in supercritical water exposed ferritic/martensitic steel HCM12A. Corros. Sci. 2006, 48, 4234–4242. [Google Scholar] [CrossRef]
- Gillot, B.; Ferriot, J.-F.; Dupré, G.; Rousset, A. Study of the oxidation kinetics of finely-divided magnetites. Mater. Res. Bull. 1976, 11, 843–849. [Google Scholar] [CrossRef]
- Nakagawa, K.; Yanagisawa, T.; Sato, M.; Abet, M. Study of corrosion resistance of newly developed 9–12% Cr steels for advanced units. In Advanced Heat Resistant Steels for Power Generation; Viswanathan, R., Nutting, J., Eds.; IOM Communications Ltd.: San Sebastian, Spain, 1999. [Google Scholar]
- Holcomb, G.R. High pressure steam oxidation of alloys for advanced ultra-supercritical conditions. Oxid. Met. 2014, 82, 271–295. [Google Scholar] [CrossRef]
- Choudhry, K.I.; Mahboubi, S.; Botton, G.A.; Kish, J.R.; Svishchev, I.M. Corrosion of engineering materials in a supercritical water cooled reactor: Characterization of oxide scales on Alloy 800H and stainless steel 316. Corros. Sci. 2015, 100, 222–230. [Google Scholar] [CrossRef]
- Macdonald, D.D. Viability of hydrogen water chemistry for protecting in-vessel components of boiling water reactors. Corrosion 1992, 48, 194–205. [Google Scholar] [CrossRef]
- Gorman, D.M.; Higginson, R.L.; Du, H.; McColvin, G.; Fry, A.T.; Thomson, R.C. Microstructural analysis of IN617 and IN625 oxidised in the presence of steam for use in ultra-supercritical power plant. Oxid. Met. 2013, 79, 553–566. [Google Scholar] [CrossRef]
- Sarrade, S.; Féron, D.; Rouillard, F.; Perrin, S.; Robin, R.; Ruiz, J.-C.; Turc, H.-A. Overview on corrosion in supercritical fluids. J. Supercrit. Fluid 2017, 120, 335–344. [Google Scholar] [CrossRef]
- Zhang, N.Q.; Zhu, Z.L.; Lv, F.B.; Jiang, D.F.; Xu, H. Influence of exposure pressure on oxidation behavior of the ferritic-martensitic steel in steam and supercritical water. Oxid. Met. 2016, 86, 113–124. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Z.L.; Zhang, N.Q. Oxidation of ferritic steel T24 in supercritical water. Oxid. Met. 2014, 82, 21–31. [Google Scholar] [CrossRef]
- Yang, J.Q.; Wang, S.Z.; Li, Y.H.; Zhang, T.; Wang, L.S.; Wang, M. Study on corrosion behavior of stainless steel 316 in low oxygen concentration supercritical water. In Proceedings of the 2nd Technical Congress on Resources, Environment and Engineering, CREE 2015, Hong Kong, China, 25–26 September 2015; Xie, L., Ed.; CRC Press/Balkema: Hong Kong, China, 2015; pp. 437–440. [Google Scholar]
- Hansson, A.N.; Danielsen, H.; Grumsen, F.B.; Montgomery, M. Microstructural investigation of the oxide formed on TP 347H FG during long-term steam oxidation. Mater. Corros. 2010, 61, 665–675. [Google Scholar] [CrossRef]
- Yasumasa, G. The effect of squeezing on the phase transformation and magnetic properties of γ-Fe2O3. Jpn. J. Appl. Phys. 1964, 3, 739. [Google Scholar]
- Tang, X.Y.; Wang, S.Z.; Qian, L.L.; Li, Y.H.; Lin, Z.H.; Xu, D.H.; Zhang, Y.P. Corrosion behavior of nickel base alloys, stainless steel and titanium alloy in supercritical water containing chloride, phosphate and oxygen. Chem. Eng. Res. Des. 2015, 100, 530–541. [Google Scholar] [CrossRef]
- Yang, J.; Wang, S.; Tang, X.; Wang, Y.; Li, Y. Effect of low oxygen concentration on the oxidation behavior of Ni-based alloys 625 and 825 in supercritical water. J. Supercrit. Fluid 2018, 131, 1–10. [Google Scholar] [CrossRef]


| Input variables | Range |
|---|---|
| temperature, °C | 500–700 |
| Chromium content, wt.% | 8.37–12.12 |
| ODS treatment | exists(1) or not(0) |
| surface treatment | exists(1) or not(0) |
| oxygen concentration, ppb | 10–8000 |
| exposure time, h | 1–1000 |
| flow rate, m·s−1 | 0–1.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, T.; Wang, S.; Fekete, B.; Yang, J.; Yang, J.; Qiu, J.; Xu, A.; Wang, J.; Xu, Y.; et al. Modelling and Analysis of the Corrosion Characteristics of Ferritic-Martensitic Steels in Supercritical Water. Materials 2019, 12, 409. https://doi.org/10.3390/ma12030409
Li Y, Xu T, Wang S, Fekete B, Yang J, Yang J, Qiu J, Xu A, Wang J, Xu Y, et al. Modelling and Analysis of the Corrosion Characteristics of Ferritic-Martensitic Steels in Supercritical Water. Materials. 2019; 12(3):409. https://doi.org/10.3390/ma12030409
Chicago/Turabian StyleLi, Yanhui, Tongtong Xu, Shuzhong Wang, Balazs Fekete, Jie Yang, Jianqiao Yang, Jie Qiu, Aoni Xu, Jiaming Wang, Yi Xu, and et al. 2019. "Modelling and Analysis of the Corrosion Characteristics of Ferritic-Martensitic Steels in Supercritical Water" Materials 12, no. 3: 409. https://doi.org/10.3390/ma12030409
APA StyleLi, Y., Xu, T., Wang, S., Fekete, B., Yang, J., Yang, J., Qiu, J., Xu, A., Wang, J., Xu, Y., & Macdonald, D. D. (2019). Modelling and Analysis of the Corrosion Characteristics of Ferritic-Martensitic Steels in Supercritical Water. Materials, 12(3), 409. https://doi.org/10.3390/ma12030409






