Next Article in Journal
Self-Healing Concrete by Biological Substrate
Previous Article in Journal
A Parasitic Resistance-Adapted Programming Scheme for Memristor Crossbar-Based Neuromorphic Computing Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 12
Issue 24
10.3390/ma12244098
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

312 MAX Phases: Elastic Properties and Lithiation

by
P.P. Filippatos
1,2,
M.A. Hadi
3,
S.-R.G. Christopoulos
1,
A. Kordatos
1,
N. Kelaidis
1,
M.E. Fitzpatrick
1,
M. Vasilopoulou
2 and
A. Chroneos
1,4,*
1
Faculty of Engineering, Environment and Computing, Coventry University, Priory Street, Coventry CV1 5FB, UK
2
Institute of Nanoscience and Nanotechnology (INN), National Center for Scientific Research “Demokritos”, AgiaParaskevi, 15341 Athens, Greece
3
Department of Physics, University of Rajshahi, Rajshahi 6205, Bangladesh
4
Department of Materials, Imperial College London, London SW7 2BP, UK
*
Author to whom correspondence should be addressed.
Materials 2019, 12(24), 4098; https://doi.org/10.3390/ma12244098
Submission received: 25 October 2019 / Revised: 26 November 2019 / Accepted: 3 December 2019 / Published: 8 December 2019
Browse Figures
Review Reports Versions Notes

Abstract

:
Interest in the Mn+1AXn phases (M = early transition metal; A = group 13–16 elements, and X = C or N) is driven by their ceramic and metallic properties, which make them attractive candidates for numerous applications. In the present study, we use the density functional theory to calculate the elastic properties and the incorporation of lithium atoms in the 312 MAX phases. It is shown that the energy to incorporate one Li atom in Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2 is particularly low, and thus, theoretically, these materials should be considered for battery applications.

1. Introduction

MAX phases are a class of ternary nitrides and carbides that we can categorize into families of M(n+1)AXn, with n = 1, 2, 3, 4, and other MAX phase-related structures like the 321 MAX phases or the iMAX phases [1,2,3,4]. A family of 211 of these materials was discovered in powder form in 1960, with the name H-phases from Nowotny et al. [5], but, after many years, Barsoum and El-Taghy synthesized the first bulk MAX phase, Ti3SiC2 [6], with enough purity to enable them to characterize its properties. Since then, there interest has grown regarding MAX compounds, due to their unusual properties, which are a result of their bonding characteristics and their structures [7,8,9,10,11,12,13,14]. Just like MXenes, which are the corresponding binary carbides and nitrides that are created from MAX phases after an exfoliation process that removes the A layer [7], the MAX compounds have a high elastic stiffness and are good electrical conductors [8]. Regarding their mechanical behavior, MAX phases are machinable and have high thermal and damage resistance [11,12]. These properties have constituted the 312 MAX phases as important materials for numerous high-end applications, including space, electronic, and nuclear [13,14,15,16,17,18,19,20,21,22,23,24,25].
A schematic of the crystal structure (P63/mmc, space group no. 194) [5] of the 312 MAX phases is given in Figure 1. The “metallic” layers (A) are positioned between the n “ceramic” layers (M3AX2 for n = 2) along the c-direction. The M and X layers effectively form M2X slabs, with face-centered cubic-type stacking. In the present research, we have examined the potential application of the 312 MAX phases as anode materials in Li-ion batteries or supercapacitors. Modern battery technology uses the 3D carbon structure, graphite, as an anode material, and there are reports that graphene batteries that could have better performances [26]. Etching the A from the MAX compounds leads to the 2D material MXenes, which, from a theoretical point, could become the future Li-ion battery anode material, as it exhibits better cycles than graphite [27,28]. However, in order to create the MXenes, the method of hydrofluoric acid (HF) etching is used, and although it removes the A layer, it also affects the bonding between the M and X layers. This creates some unwanted characteristic changes, as it sometimes affects the elastic properties of the material. Moreover, although in most cases MXenes have unique electrical characteristics, sometimes when the etching removes the A layer, the resulting structure becomes a semiconductor [29], and as a result, this MXene cannot be used as an anode material. Recently, the first 2D MAX phases (MAXenes) were demonstrated that consist of a 2D structure, which, unlike the 2D MXenes, keeps the A layer [30]. In order to examine the application of MAXenes in Li-ion batteries, it is evident that the interactions of Li in the MAX phases should be examined first in order to predict how the lithiation is affected by the A layer. Lastly, as has been indicated in previous studies, the creation of MXenes is a high-cost method [29]. From all of the above, we believe that our research is important, as the Li-doped MAX phases could have better performances in the Li-ion batteries technology than MXenes, and moreover, they have never been investigated before.
The aim of the present work is to study the elastic properties and Li formation in the M3AX2 phases (M = Hf, Nb, Ta, Ti, V, Zr, and Mo; A = Si, Al, Sn, Ga, and In; X = C) using the density functional theory (DFT), and to compare our results with other related experimental and theoretical studies. Although Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2 are of interest, it should be noted that not all of these compounds have been synthesized yet, although there are many reports that provide some of them in stable forms. Specifically, Zhou et al. [31] have synthesized an Zr3AlC2 together with Solvas-Zapata et al. [32], who synthesized Zr3(Al1−xSix)C2. Regarding Mo3SiC2, there are many theoretical reports [33] about its properties, like self-healing. However, it has not been synthesized. There are also experimental reports on stable forms of Zr3SnC2 and Hf3AlC2 from Lapauw et al. [34]. There are also some trends in thin film MAX phases [35], as well as in sol-gel methods of creating the MAX phases compounds [36], that are examined by experimentalists for the synthesis of new MAX phases. To conclude, of the four 312 materials that we propose should be examined for potential lithiation, two of them have already been synthesized in stable forms (Zr3SnC2 and Hf3AlC2) and one has been synthesized as part of a mixed structure (Zr3SiC2); accordingly, we believe that their lithiation abilities could be investigated both experimentally and theoretically. We will then propose some experimental works with the stable synthesized forms of the 312 MAX phases that could be examined, in order to see their performances as Li-ion battery anodes.

2. Computational Methods

CASTEP, a plane-wave DFT code, was employed for all the calculations [37,38]. The generalized gradient approximation, ultra-soft pseudopotentials [39], and the Purdew, Burke, and Ernzerhof (PBE) [40] exchange-correlation function were used. To optimize the geometry, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimizer was employed and implemented in the CASTEP. The supercells contained 108 atomic sites, with a plane-wave basis set cut-off of 450 eV, 3 × 3 × 1 Monkhorst–Pack (MP) [41]. The Li interstitial was placed at all possible sites. After an extensive search for all the possible sites, we found all the minimum energy positions of the Li interstitials. The minimum energy sites are presented in Figure 2. For the elastic properties, a unit cell was considered, with a plane-wave energy cut-off of 550 eV and with 18 × 18 × 2k-point mesh.

3. Results

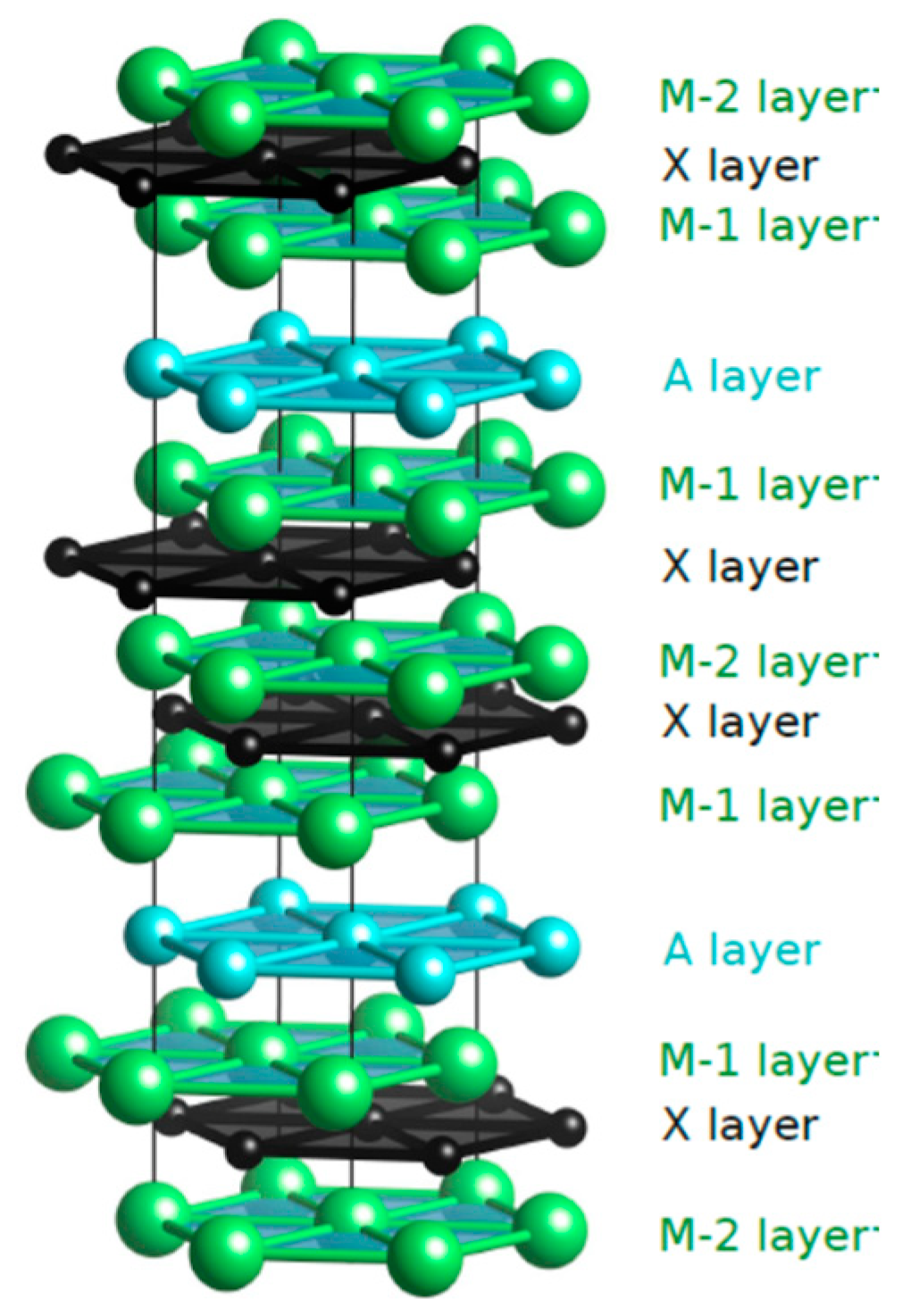
3.1. Elastic Properties

The mechanical behavior of materials is dependent on their elastic constants. Moreover, the elastic properties of the materials are linked to the bonding characteristics, so the information that the elastic constants provide is also connected to the chemical bonds of the atoms of the solid. The MAX compounds have hexagonal crystal structures [5,42]. Therefore, the 312 MAX phases have six different elastic constants: c11, c12, c13, c33, c44, and c66. Only the first five of them are independent, taking into account that c66 = (c11 − c12)/2. In order for the MAX compounds to be dynamically stable, the following conditions must be met [43]:
c11 > 0, c33 > 0, c44 > 0, (c11 + c12) c33 > 2(c13)2, and (c11 − c12) > 0
The calculated results for the selected 312 MAX phases have been investigated in previous studies [44,45]. In Table 1, we present the elastic properties of the 312 MAX phases. It is seen that the above conditions are met, and so the studied MAX phases are mechanically stable.
The elastic stiffness of a solid, regarding the (100) <100> strain, is calculated by the c11 constant. Thus, V3AlC2 is the stiffest. On the other hand, Zr3AlC2 and Ti3InC2 are the least stiff. The c12 elastic constant is a measure of the deformation of the material in the (110) plane along the <100> direction. Therefore, Ti3AlC2 is the most easily deformed. The c12 and c13 values indicate that when force is applied along the a- crystallographic axis, Ti3AlC2, Ti3InC2, Ti3GaC2, and V3AlC2 are easier to shear along the b and c axes than the other MAX compounds in Table 1. Lastly, the lower value of c33 for Zr3SnC2 results in the conclusion that it is easiest to deform via <001> compression under uniaxial stress.
Focusing on the bulk elastic parameters, in Table 1, the bulk modulus B, Young’s modulus Y, and the shear modulus G have been calculated. It is evident that the Zr3SnC2 has the lowest value of B, and, as a consequence, it has the lowest resistance under compression. Conversely, Mo3SiC2, which has the highest value, has the highest resistance to compression. The shear modulus G has the lowest value in Zr3SnC2, and so this MAX phase is more prone to shape change than the others. The Young’s modulus Y, which is a measure of the stress required for deformation, has the lowest value in the Zr3SnC2 MAX phase, compared to the other MAX phases in Table 1 (also refer to [44,45,46,47,48,49,50,51,52]).
In order to gain information about the brittle or ductile failure of the MAX phases, the Pugh’s modulus (B/G) is used [53]. More analytically, when the Pugh’s modulus exceeds 1.75, the material is characterized as ductile, which means that a crack progresses slowly when plastic deformation occurs. Conversely, in brittle materials, cracks extend rapidly with little applied stress. According to the results of Table 1, all of the MAX phases studied are brittle, except for Mo3SiC2 and Ta3SiC2. Another important parameter is the anisotropy factor kc/ka = (c11 + c12 − 2c13)/(c33 − c13), which indicates whether the MAX phase is more compressible along the a- or c-axis. It is obvious that Ti3SiC2, Mo3SiC2, Hf3SnC2, Hf3SiC2, V3AlC2, and Ta3SiC2 are the only MAX compounds of those studied where compression on the a-axis has almost the same value as on the c-axis.
The Poisson’s ratio is another important constant that informs us if the material is a central-force solid or a non-central-force solid [48], and also classifies the materials as brittle or ductile [54,55]. If the Poisson’s ratio is between 0.25 and 0.50, then the material is a central-force solid. Otherwise, it is a non-central-force solid. Furthermore, if the Poisson’s ratio is more than 0.26, then the solid is ductile, and if it has a lower value, it is brittle. The calculated results show that all the studied MAX phases in Table 1 are non-central-force and brittle, except for Mo3SiC2 and Ta3SiC2, which are central-force.
The elastic anisotropy, A, is an important description meaning that a body cannot develop the same strain independently of the direction in which the stress is applied. The elastic anisotropy factor indicates how the elastic properties of a solid are dependent on the direction of the stress. Additionally, the elastic anisotropy is connected with the thermal expansion and the crystal microcracks [56]. For the MAX phase systems that are hexagonal, the elastic anisotropy factor is calculated from the equation A = 4c44/(c11 + c33 − 2c13), and if A = 1, the crystal is isotropic. The results of Table 1 characterize Mo3SiC2 and Ta3SiC2 as being more elastically anisotropic than the other MAX phases, and because the value of the elastic anisotropy factor of Hf3SnC2 is almost 1, this MAX phase is elastically isotropic.
As regards the elastic properties of the MXenes, focusing on the research of Ge et al. [57] on the superconducting and high hardness of Mo3C2, it has been proved that it is a brittle material with a B/G of 2.35. We calculated that the hypothetical Mo3SiC2 is a brittle material, and we found that the B/G is slightly lower than the similar MXene, with a value of 2.11. As a result, it is seen that the Mo3SiC2 is not as brittle as Mo3C2, which makes it more difficult to crack during “diffusion”. As regards the Ti3C2, Borysiuk et al. [58] used the molecular dynamics method in order to predict the elastic properties of the Tin+1Cn MXenes, and they calculated, in the case of Ti3C2, a value of 502 GPa for the Young’s modulus, while Bai calculated a c11 constant equal to 523 GPa [59]. Compared to our results, it is evident that for every one of the Ti3AC2 MAX compounds, the Young modulus and the elastic constant c11 have much lower values. Focusing on the Zr3C2 MXene, Xie et al. [60] made a theoretical study on the elastic properties of that MXene, and compared to our 312 MAX phases with Zr-A-C, it is seen that only the Zr3SnC2 is less stiff. As a result, it will be softer and more easily machinable than the Zr3C2. From all of the above, it is evident that the majority of our MAX phases are performing with better elasticity characteristics and can be more easily manipulated than the similar MXenes, in order to be used as anodes in Li-ion batteries (LIBs).

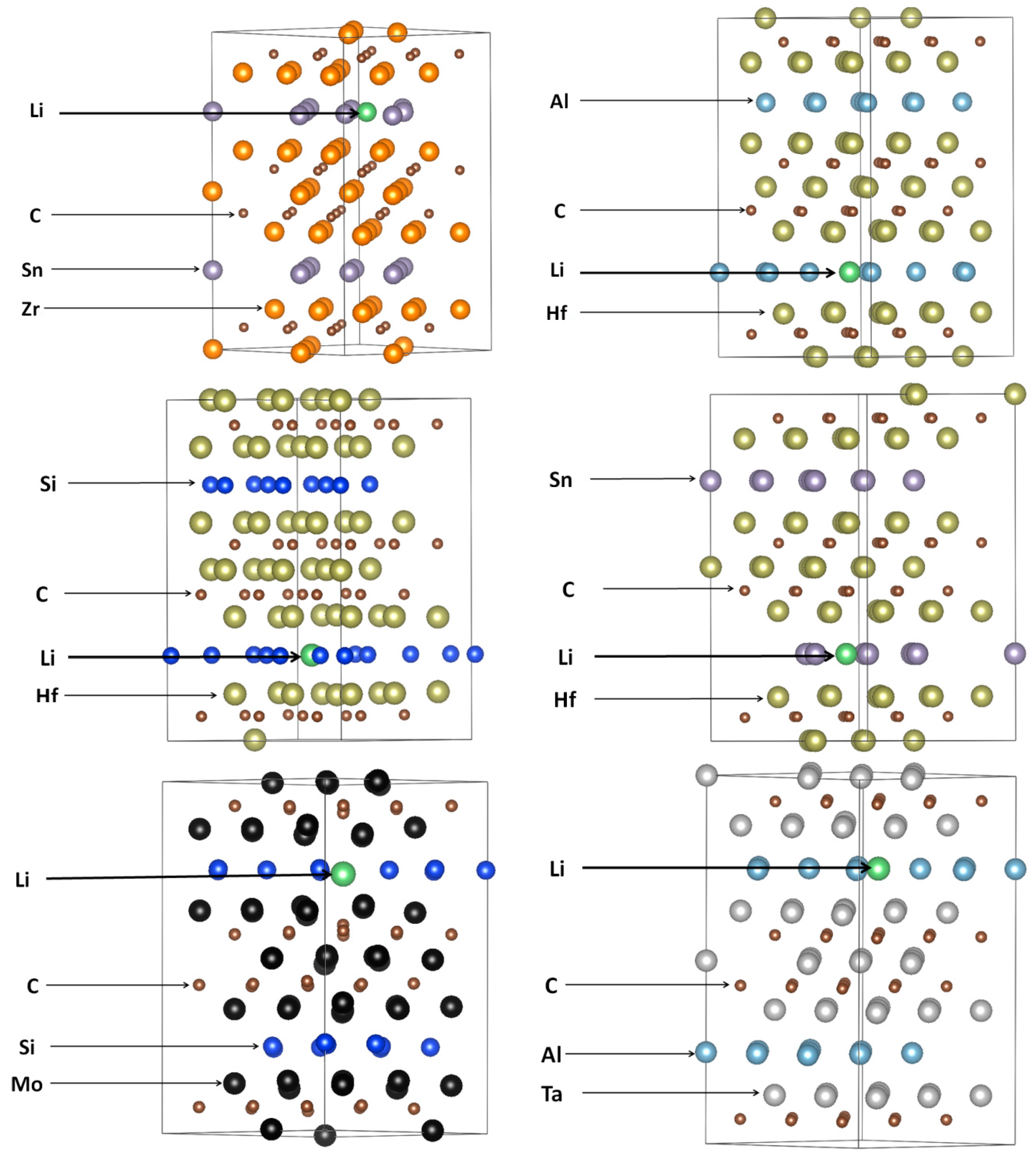
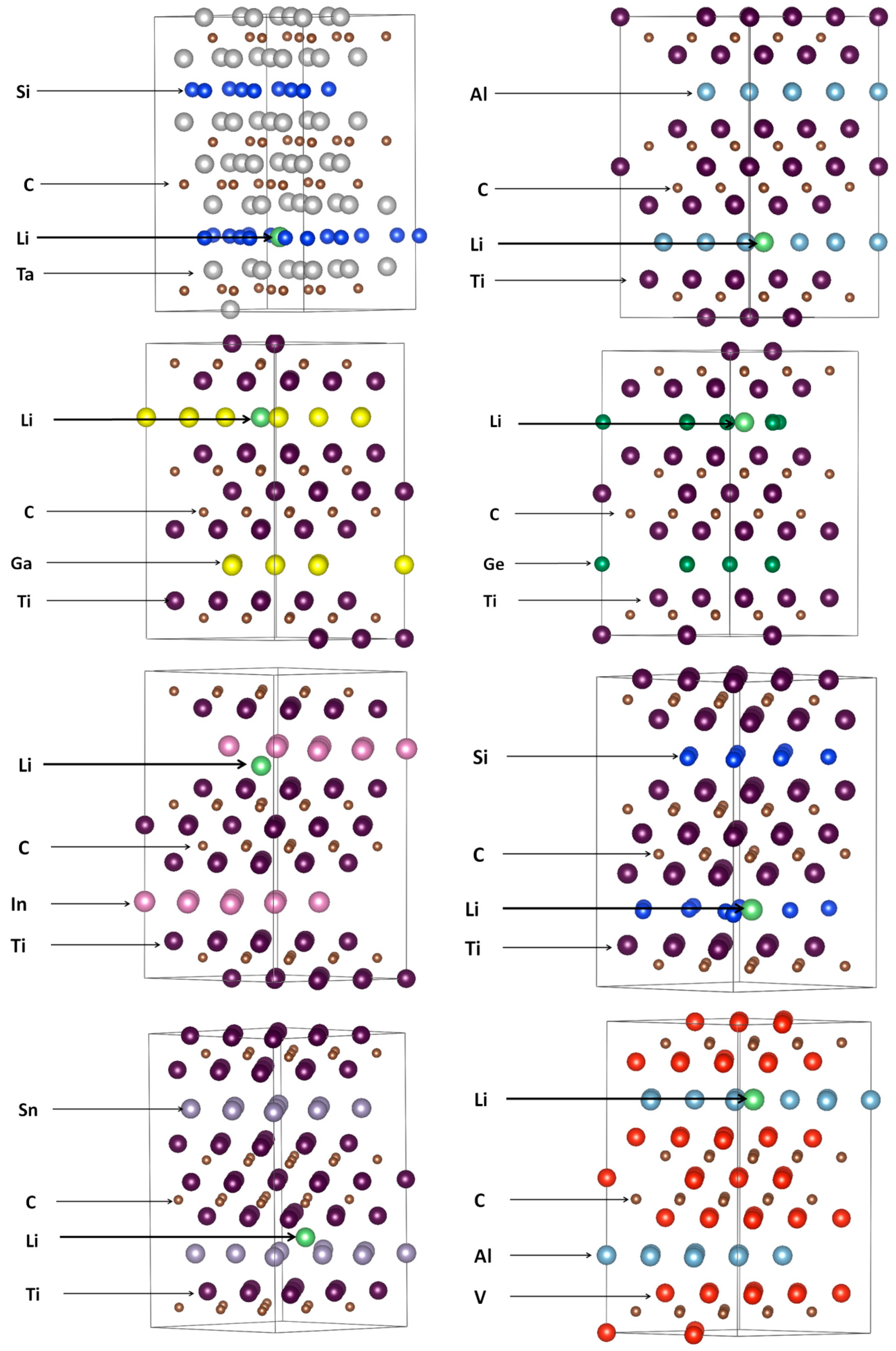
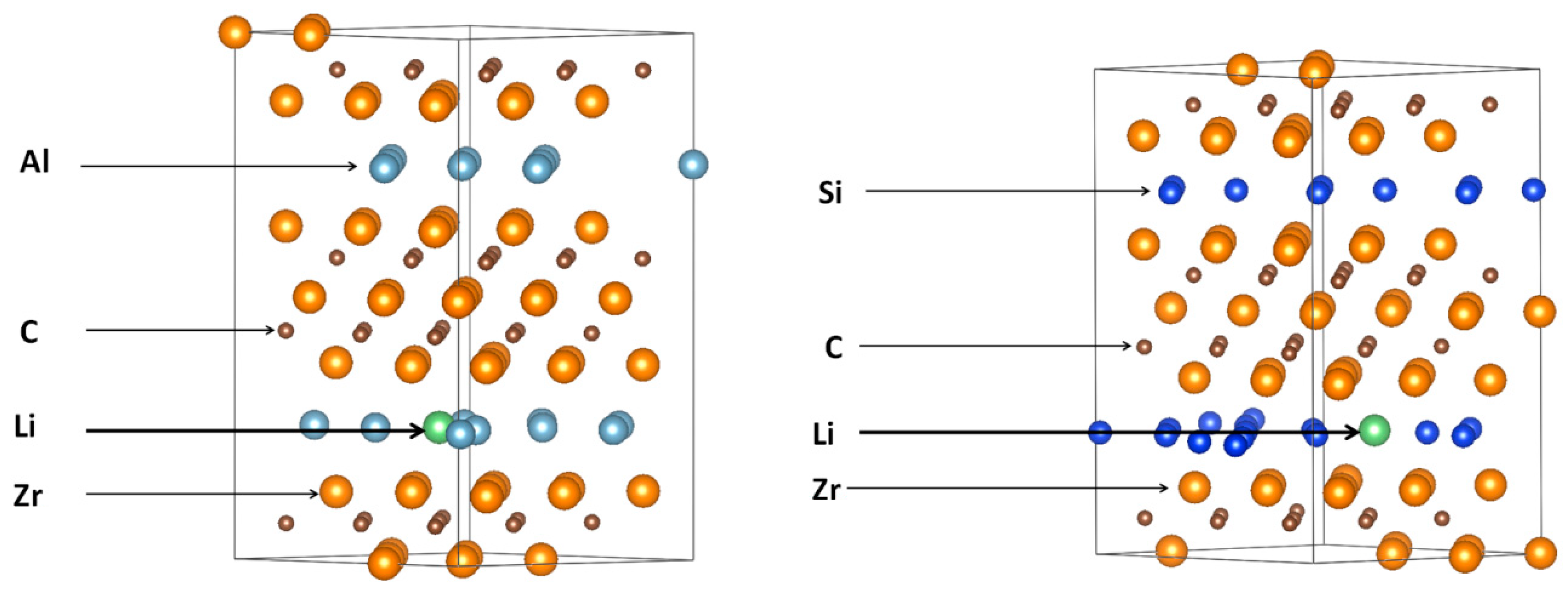
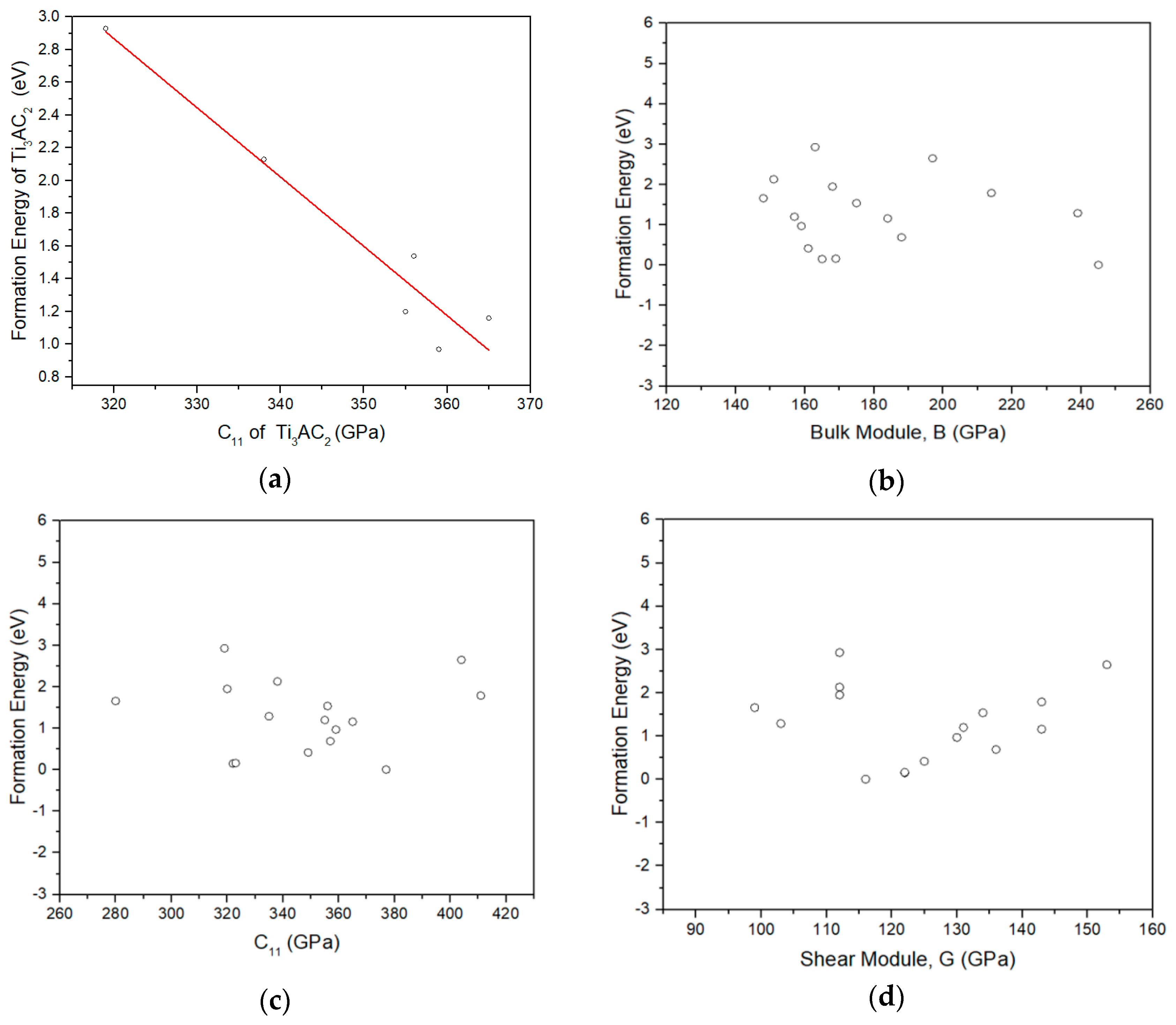
3.2. Lithiation

The formation energy to incorporate a Li atom in the MAX phase, with ΔH for Li-intercalated systems, is defined by the following equation:
Δ H = E ( with xLi ) − E ( without Li ) − x E ( Li )
where E (with xLi) and E (without Li) are the energies of the system with and without Li atoms. Herein, we used one Li atom as an interstitial, and in result, x = 1. Also, E (Li) is the total energy of a single Li atom (here, it is 192.029 eV). In order to calculate the energy of the one Li atom, we performed a calculation for a supercell consisting of 67 Li atoms, and we performed geometry relaxation. We thus calculated the energy of the supercell, and we divided it with 67 in order to find the energy of the one atom. In Table 2, the formation energies of the lithiated 312 MAX phases are provided.
From Table 2, it is evident that the lithiation of the 312 MAX phases studied here is endothermic, which reflects instability. However, Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2 exhibit Li formation energies less than 0.5 Ev, making the incorporation of Li in the MAX lattice feasible, and they are even lower than those of MAX materials considered in previous works [61,62,63]. This is extremely important, as MXenes are generally considered better candidates for battery applications, compared to the MAX phases. Nevertheless, the present work identifies four materials (Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2) that are potentially important for such applications. It should be stressed that previous experimental works have only identified oxygen-doped Ti3SiC2 as having high Li-ion storage capacity, and hence, as being potentially important as an anode material for Li-ion batteries [64]. In the present study, though, we found that Ti3SiC2 has a high formation energy for lithiation (refer to Table 2). This implies that doping could further decrease the Li-intercalation formation energy of Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2, thus making them appropriate candidates for battery applications. MAX phases present potential advantages over MXenes, exhibiting better material properties (high thermal-shock resistance, elastic stiffness, melting temperatures, and electrical and thermal conductivity). They are less-complicated structures, as they do not need functional groups to be stabilized [61]. We searched the literature about the formation energy of similar lithiated MXene structures, but we could only find a report about Ti3C2 where the formation energy for the lithiated structure was calculated at 4.40 eV [65]. It is obvious that this value is higher than our theoretical results, so the lithiation in the 312 MAX phases needs less energy than the above-mentioned MXene.
In an effort to link the elastic properties with the Li formation energies in the 312 MAX phases, we considered Figure 3. This was motivated by initial work on the Ti3AC2 (A = Sn, Si, Ge, Ga, Al, and In) MAX phases where there is a decrease of Li formation energy with respect to the C11 elastic constant (refer to Figure 3a). Nevertheless, when considering the whole range of the 312 MAX phases, there is no specific trend (refer to Figure 3b–d). Future theoretical work should include thermodynamic models to investigate further if the bulk properties impact the formation energies of Li in these systems [66,67,68].

4. Conclusions

To summarize, the mechanical behavior and the formation energy for the lithiation of the 312 MAX phases has been calculated using the density functional theory. From our calculations, it is evident that Zr3SnC2 is more prone to shape change along the b- and c-axes when stress along the a-axis is applied. Moreover, Zr3SnC2 does not need high stress in order to deform, and has low resistance to deformation under compression.
The energy to incorporate Li-ions in the 312 MAX phases is considerably high, with the exception of Mo3SiC2, Hf3AlC2, Zr3AlC2, and Zr3SiC2, for which formation energies of Li intercalation less than 0.5 eV were calculated. The Li formation energies in Mo3SiC2 and Zr3SiC2 are particularly low. However, they have not yet been synthesized. Regarding the other compounds, it could be proposed that their potential as LIBs or supercapacitor anodes should be examined.
To conclude, from the four 312 materials that we propose should be examined for potential lithiation, two of them have already been synthesized in stable forms (Zr3SnC2 and Hf3AlC2) and one has been synthesized as part of a mixed structure (Zr3SiC2), and so we believe that their lithiation ability could be investigated both experimentally and theoretically. There have been, compared to the MXenes, very few studies of the MAX phases for battery applications. Obviously, the incorporation of Li is only part of the picture, and future studies should focus on the diffusion of Li from both an experimental and theoretical viewpoint. Doping strategies should also be employed to lower the formation and migration energies of Li in the MAX phases.

Author Contributions

Conceptualization, A.C.; formal analysis, P.P.F. and M.A.H.; investigation, P.P.F., S.-R.G.C., A.K. and N.K.; writing—original draft preparation, P.P.F. and A.C.; writing—review and editing, M.E.F. and M.V.; supervision, M.V. and A.C.

Funding

This research received no external funding.

Acknowledgments

P.P.F., S.-R.G.C., A.C., N.K. and M.E.F. are grateful for funding from the Lloyd’s Register Foundation, a charitable foundation helping to protect life and property by supporting engineering-related education, public engagement, and the application of research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Barsoum, M.W.; El-Raghy, T. The MAX phases: Unique new carbide and nitride materials: Ternary ceramics turn out to be surprisingly soft and machinable, yet also heat-tolerant, strong and lightweight. Am. Sci. 2001, 89, 334–343. [Google Scholar] [CrossRef]
  2. Barsoum, M.W. The MN+1AXN phases: A new class of solids: Thermodynamically stable nanolaminates. Prog. Solid State Chem. 2000, 28, 201–281. [Google Scholar] [CrossRef]
  3. Chen, H.; Yang, D.; Zhang, Q.; Jin, S.; Guo, L.; Deng, J.; Chen, X. A series of MAX phases with MA-triangular-prism bilayers and elastic properties. Angew. Chem. 2019, 131, 4624–4628. [Google Scholar] [CrossRef]
  4. Thore, A.; Rosén, J. An investigation of the in-plane chemically ordered atomic laminates (Mo2/3 Sc 1/3)2 AlC and (Mo2/3 Y1/3)2 AlC from first principles. Phys. Chem. Chem. Phys. 2017, 19, 21595–21603. [Google Scholar] [CrossRef]
  5. Nowotny, H. Strukturchemieeinigerverbindungen der übergangsmetallemit den elementen C, Si, Ge, Sn. Prog. Solid State Chem. 1971, 5, 27–70. [Google Scholar] [CrossRef]
  6. Barsoum, M.W.; El-Raghy, T. Synthesis and characterization of a remarkable ceramic. J. Am. Ceram. Soc. 1996, 79, 1953. [Google Scholar] [CrossRef]
  7. Khazaei, M.; Ranjbar, A.; Esfarjani, K.; Bogdanovski, D.; Dronskowski, R.; Yunoki, S. Insights into exfoliation possibility of MAX phases to MXenes. Phys. Chem. Chem. Phys. 2018, 20, 8579–8592. [Google Scholar] [CrossRef] [Green Version]
  8. Barsoum, M.W. MAX Phases: Properties of Machinable Ternary Carbides and Nitrides; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
  9. Eklund, P.; Rosen, J.; Persson, P.O.Å. Layered ternary Mn+1AXn phases and their 2D derivative MXene: An overview from a thin-film perspective. J. Phys. D Appl. Phys. 2017, 50, 113001. [Google Scholar] [CrossRef] [Green Version]
  10. Buschow, K.J.; Cahn, R.W.; Flemings, M.C.; Ilschner, B.; Kramer, E.J.; Mahajan, S. Encyclopedia of Materials Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
  11. Sun, Z.M. Progress in research and development on MAX phases: A family of layered ternary compounds. Int. Mater. Rev. 2011, 56, 143–166. [Google Scholar] [CrossRef]
  12. Wang, X.H.; Zhou, Y.C. Layered machinable and electrically conductive Ti2AlC and Ti3AlC2 ceramics: A review. J. Mater. Sci. Tehnol. 2011, 26, 385–416. [Google Scholar] [CrossRef]
  13. Middleburgh, S.C.; Lumpkin, G.R.; Riley, D. Accommodation, accumulation, and migration of defects in Ti3SiC2 and Ti3AlC2 MAX phases. J. Am. Ceram. Soc. 2013, 96, 3196–3201. [Google Scholar]
  14. Sokol, M.; Natu, V.; Kota, S.; Barsoum, M.W. On the chemical diversity of the MAX phases. Trends Chem. 2019, 1, 210. [Google Scholar] [CrossRef]
  15. Horlait, D.; Grasso, S.; Chroneos, A.; Lee, W.E. Attempts to synthesise quaternary MAX phases (Zr,M)2AlC and Zr2(Al,A)C as a way to approach Zr2AlC. Mater. Res. Lett. 2016, 4, 137–144. [Google Scholar] [CrossRef] [Green Version]
  16. Horlait, D.; Grasso, S.; Al Nasiri, N.; Burr, P.A.; Lee, W.E. Synthesis and high-temperature oxidation of MAX phases in the Cr-Ti-Al-C quaternary system. J. Am. Ceram. Soc. 2016, 99, 682–690. [Google Scholar] [CrossRef]
  17. Saltas, V.; Horlait, D.; Sgourou, E.N.; Vallianatos, F.; Chroneos, A. Modelling solid solutions with cluster expansion, special quasirandom structures, and thermodynamic approaches. Appl. Phys. Rev. 2017, 4, 041301. [Google Scholar] [CrossRef]
  18. Horlait, D.; Middleburgh, S.C.; Chroneos, A.; Lee, W.E. Synthesis and DFT investigation of new bismuth-containing MAX phases. Sci. Rep. 2016, 6, 18829. [Google Scholar] [CrossRef] [Green Version]
  19. Lapauw, T.; Halim, J.; Lu, J.; Cabioc’h, T.; Hultman, L.; Barsoum, M.W.; Lambrinou, K.; Vleugels, J. Synthesis of the novel Zr3AlC2 MAX phase. J. Eur. Ceram. Soc. 2016, 36, 943–947. [Google Scholar] [CrossRef]
  20. Talapatra, A.; Duong, T.; Son, W.; Gao, H.; Radovic, M.; Arróyave, R. High-throughput combinatorial study of the effect of M site alloying on the solid solution behavior of M2AlC MAX phases. Phys. Rev. B 2016, 94, 104106. [Google Scholar] [CrossRef] [Green Version]
  21. Tunca, B.; Lapauw, T.; Karakulina, O.M.; Batuk, M.; Cabioc’h, T.; Hadermann, J.; Delville, R.; Lambrinou, K.; Vleugels, J. Synthesis of MAX phases in the Zr-Ti-Al-C system. Inorg. Chem. 2017, 56, 3489–3498. [Google Scholar] [CrossRef]
  22. Arróyave, R.; Talapatra, A.; Duong, T.; Son, W.; Gao, H.; Radovic, M. Does aluminium play well with others? Intrinsic Al-A alloying behavior in 211/312 MAX phases. Mater. Res. Lett. 2017, 5, 170–178. [Google Scholar]
  23. Hadi, M.A.; Panayiotatos, Y.; Chroneos, A. Structural and optical properties of the recently synthesized (Zr3-xTix)AlC2 MAX phases. J. Mater. Sci. Mater. Electron. 2017, 28, 3386–3393. [Google Scholar] [CrossRef] [Green Version]
  24. Lei, J.C.; Zhang, X.; Zhou, Z. Recent advances in MXene: Preparation, properties, and applications. Front. Phys. 2015, 10, 276–286. [Google Scholar] [CrossRef]
  25. Zapata-Solvas, E.; Hadi, M.A.; Horlait, D.; Parfitt, D.C.; Thibaud, A.; Chroneos, A.; Lee, W.E. Synthesis and physical properties of (Zr1-xTix)AlC2 MAX phases. J. Am. Ceram. Soc. 2017, 100, 3393–3401. [Google Scholar] [CrossRef]
  26. Kim, H.; Park, K.Y.; Hong, J.; Kang, K. All-graphene-battery: Bridging the gap between supercapacitors and lithium ion batteries. Sci. Rep. 2014, 4, 5278. [Google Scholar] [CrossRef]
  27. Naguib, M.; Come, J.; Dyatkin, B.; Presser, V.; Taberna, P.L.; Simon, P.; Barsoum, M.W.; Gogotsi, Y. MXene: A promising transition metal carbide anode for lithium-ion batteries. Electrochem. Commun. 2012, 16, 61–64. [Google Scholar] [CrossRef] [Green Version]
  28. Liang, X.; Garsuch, A.; Nazar, L.F. Sulfur cathodes based on conductive MXene nanosheets for high-performance lithium–sulfur batteries. Angew. Chem. 2015, 54, 3907–3911. [Google Scholar] [CrossRef]
  29. Khazaei, M.; Arai, M.; Sasaki, T.; Chung, C.Y.; Venkataramanan, N.S.; Estili, M.; Sakka, Y.; Kawazoe, Y. Novel electronic and magnetic properties of two-dimensional transition metal carbides and nitrides. Adv. Funct. Mater. 2013, 23, 2185–2192. [Google Scholar] [CrossRef]
  30. Peer Mohamed, A. Shear induced micromechanical synthesis of Ti3SiC2 MAXene nanosheets for functional applications. RSC Adv. 2015, 5, 51242–51247. [Google Scholar]
  31. Zhou, J.; Zha, X.; Chen, F.Y.; Ye, Q.; Eklund, P.; Du, S.; Huang, Q. A two-dimensional zirconium carbide by Selective etching of Al3C3 from nanolaminated Zr3Al3C5. Angew. Chem. 2016, 55, 5008–5013. [Google Scholar] [CrossRef] [Green Version]
  32. Zapata-Solvas, E.; Christopoulos, S.R.G.; Ni, N.; Parfitt, D.C.; Horlait, D.; Fitzpatrick, M.E.; Chroneos, A.; Lee, W.E. Experimental synthesis and density functional theory investigation of radiation tolerance of Zr3 (Al1-xS ix) C2 MAX phases. J. Am. Ceram. Soc. 2017, 100, 1377–1387. [Google Scholar] [CrossRef] [Green Version]
  33. Farle, A.M.; Van der Zwaag, S.; Sloof, W.G. A conceptual study into the potential of max-phase ceramics for self-healing of crack damage. In Proceedings of the 4th International Conference on Self-Healing Materials, ICSHM 2013, Ghent, Belgium, 16–20 June 2013. [Google Scholar]
  34. Lapauw, T.; Tunca, B.; Cabioc’h, T.; Lu, J.; Persson, P.O.A.; Lambrinou, K.; Vleugels, J. Synthesis of MAX phases in the Hf–Al–C system. Inorg. Chem. 2016, 55, 10922–10927. [Google Scholar] [CrossRef]
  35. Pshyk, A.V.; Coy, E.; Kempiński, M.; Scheibe, B.; Jurga, S. Low-temperature growth of epitaxial Ti2AlC MAX phase thin films by low-rate layer-by-layer PVD. Mater. Res. Let. 2019, 7, 244–250. [Google Scholar] [CrossRef] [Green Version]
  36. Siebert, J.P.; Bischoff, L.; Lepple, M.; Zintler, A.; Molina-Luna, L.; Wiedwald, U.; Birkel, C.S. Sol–gel based synthesis and enhanced processability of MAX phase Cr 2 GaC. J. Mater. Chem. C 2019, 7, 6034–6040. [Google Scholar] [CrossRef]
  37. Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef] [Green Version]
  38. Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter. 2002, 14, 2717. [Google Scholar] [CrossRef]
  39. Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
  40. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef]
  41. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
  42. Barsoum, M.W. The Mn+1AXn phases and their properties. In Ceramics Science and Technology; Riedel, R.R., Chen, I.W., Eds.; Wiley-VCH Verlag GmbH & Co: Weinheim, Germany, 2010; Volume 2. [Google Scholar]
  43. Born, M. On the stability of crystal lattices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1940; Volume 36, pp. 160–172. [Google Scholar]
  44. Christopoulos, S.R.; Filippatos, P.P.; Hadi, M.A.; Kelaidis, N.; Fitzpatrick, M.E.; Chroneos, A. Intrinsic defect processes and elastic properties of Ti3AC2 (A= Al, Si, Ga, Ge, In, Sn) MAX phases. J. Appl. Phys. 2018, 123, 025103. [Google Scholar] [CrossRef]
  45. Hadi, M.A.; Christopoulos, S.R.; Naqib, S.H.; Chroneos, A.; Fitzpatrick, M.E.; Islam, A.K.M.A. Physical properties and defect processes of M3SnC2 (M = Ti, Zr, Hf) MAX phases: Effect of M-elements. J. Alloy. Comp. 2018, 748, 804–813. [Google Scholar] [CrossRef]
  46. Aryal, S.; Sakidja, R.; Barsoum, M.W.; Ching, W.Y. A genomic approach to the stability, elastic, and electronic properties of the MAX phases. Phys. Status Solidi B 2014, 251, 1480–1497. [Google Scholar] [CrossRef]
  47. Ali, M.S.; Islam, A.K.M.A.; Hossain, M.M.; Parvin, F. Phase stability, elastic, electronic, thermal and optical properties of Ti3Al1 − xSixC2 (0 ≤ × ≤ 1): First principle study. Phys. B 2012, 407, 4221–4228. [Google Scholar] [CrossRef] [Green Version]
  48. Wang, W.; Sun, L.; Yang, Y.; Dong, J.; Gu, Z.; Jin, H. Pressure effects on electronic, anisotropic elastic and thermal properties of Ti3AC2 (Si, Ge and Sn) by ab initio calculations. Results Phys. 2017, 7, 1055–1065. [Google Scholar] [CrossRef]
  49. Finkel, P.; Barsoum, M.W.; El-Raghy, T. Low temperature dependencies of the elastic properties of Ti4AlN3, Ti3 Al1.1 C1.8, and Ti3SiC2. J. Appl. Phys. 2000, 87, 1701–1703. [Google Scholar] [CrossRef]
  50. Roknuzzaman, M.; Hadi, M.A.; Ali, M.A.; Hossain, M.M.; Jahan, N.; Uddin, M.M.; Alarco, J.A.; Ostrikov, K. First hafnium-based MAX phase in the 312 family, Hf3AlC2: A first principles study. J. Alloy Compd. 2017, 727, 616–626. [Google Scholar] [CrossRef] [Green Version]
  51. He, X.; Bai, Y.; Zhu, C.; Sun, Y.; Li, M.; Barsoum, M.W. General trends in the structural, electronic and elastic properties of the M3AlC2 phases (M¼ transition metal): A first-principle study. Comput. Mater. Sci. 2010, 49, 691–698. [Google Scholar] [CrossRef]
  52. Radovic, M.; Barsoum, M.W.; Ganguly, A.; Zhen, T.; Finkel, P.; Kalidindi, S.R.; Lara-Curzio, E. On the elastic properties and mechanical damping of Ti3SiC2, Ti3GeC2, Ti3Si0.5Al0.5C2 and Ti2AlC in the 300–1573 K temperature range. Acta Mater. 2006, 54, 2757–2767. [Google Scholar] [CrossRef]
  53. Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
  54. Anderson, O.L.; Demarest, H.H., Jr. Elastic constants of the central force model for cubic structures: Polycrystalline aggregates and instabilities. J. Geophy. Res. 1971, 76, 1349–1369. [Google Scholar] [CrossRef]
  55. Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators; Frantsevich, I.N., Ed.; NaukovaDumka: Kiev, Ukraine, 1983; Volume 60, p. 180. [Google Scholar]
  56. Vaitheeswaran, G.; Kanchana, V.; Svane, A.; Delin, A. Elastic properties of MgCNi3—A superconducting perovskite. J. Phys. Condens. Matter. 2007, 19, 326214. [Google Scholar] [CrossRef]
  57. Ge, Y.; Ma, S.; Bao, K.; Tao, Q.; Zhao, X.; Feng, X.; Li, L.; Liu, B.; Zhu, P.; Cui, T. Superconductivity with high hardness in Mo3 C2. Inorg. Chem. Front. 2019, 6, 1282–1288. [Google Scholar] [CrossRef]
  58. Borysiuk, V.N.; Mochalin, V.N.; Gogotsi, Y. Molecular dynamic study of the mechanical properties of two-dimensional titanium carbides Tin+1Cn (MXenes). Nanotechnology 2015, 26, 265705. [Google Scholar] [CrossRef] [Green Version]
  59. Bai, Y.; Zhou, K.; Srikanth, N.; Pang, J.H.; He, X.; Wang, R. Dependence of elastic and optical properties on surface terminated groups in two-dimensional MXene monolayers: A first-principles study. RSC Adv. 2016, 6, 35731–35739. [Google Scholar] [CrossRef]
  60. Xie, C.; Oganov, A.R.; Li, D.; Debela, T.T.; Liu, N.; Dong, D.; Zeng, Q. Effects of carbon vacancies on the structures, mechanical properties, and chemical bonding of zirconium carbides: A first-principles study. Phys. Chem. Chem. Phys. 2016, 18, 12299–12306. [Google Scholar] [CrossRef] [Green Version]
  61. Zhu, J.J.; Chroneos, A.; Eppinger, J.; Schwingenschlögl, U. S-functionalized MXenes as electrode materials for Li-ion batteries. Appl. Mater. Today 2016, 5, 19–24. [Google Scholar] [CrossRef]
  62. Zhu, J.; Chroneos, A.; Wang, L.; Rao, F.; Schwingenschloegl, U. Stress-enhanced lithiation in MAX compounds for battery applications. Appl. Mater. Today 2017, 9, 192–195. [Google Scholar] [CrossRef]
  63. Pang, J.B.; Mendes, R.G.; Bachmatiuk, A.; Zhao, L.; Ta, H.Q.; Gemming, T.; Liu, H.; Liu, Z.F.; Rummeli, M.H. Applications of 2D MXenes in energy conversion and storage systems. Chem. Soc. Rev. 2019, 48, 72–133. [Google Scholar] [CrossRef]
  64. Luan, S.R.; Zhou, J.S.; Xi, Y.K.; Han, M.Z.; Wang, D.; Gao, J.J.; Hou, L.; Gao, F.M. High lithium-ion storage performance of Ti3SiC2 MAX by oxygen doping. Chem. Sel. 2019, 4, 5319–5321. [Google Scholar]
  65. Er, D.; Li, J.; Naguib, M.; Gogotsi, Y.; Shenoy, V.B. Ti3C2 MXene as a high capacity electrode material for metal (Li, Na, K., Ca) ion batteries. ACS Appl. Mater. Interfaces 2014, 6, 11173–11179. [Google Scholar] [CrossRef]
  66. Varotsos, P. Point defect parameters in β-PbF2 revisited. Solid State Ion. 2008, 179, 438–441. [Google Scholar] [CrossRef]
  67. Chroneos, A.; Vovk, R.V. Modeling self-diffusion in UO2 and ThO2 by connecting point defect parameters with bulk properties. Solid State Ion. 2015, 274, 1–3. [Google Scholar] [CrossRef]
  68. Cooper, M.W.D.; Grimes, R.W.; Fitzpatrick, M.E.; Chroneos, A. Modeling oxygen self-diffusion in UO2 under pressure. Solid State Ion. 2015, 282, 26–30. [Google Scholar] [CrossRef]
Materials 12 04098 g001 550
Figure 1. Crystal structure of the 312 MAX phase.
Figure 1. Crystal structure of the 312 MAX phase.
Materials 12 04098 g001
Materials 12 04098 g002a 550Materials 12 04098 g002b 550Materials 12 04098 g002c 550
Figure 2. The Li interstitial positions (green atoms) in the 312 MAX phases.
Figure 2. The Li interstitial positions (green atoms) in the 312 MAX phases.
Materials 12 04098 g002aMaterials 12 04098 g002bMaterials 12 04098 g002c
Materials 12 04098 g003 550
Figure 3. (a) The dependence of the Li MAX phases formation energy (eV), with respect to the c11 (GPa) elastic constant for the Ti3AC2 (A = Sn, Si, Ge, Ga, Al, In) MAX phases. (b) The dependence of the formation energy (eV) of lithiated 312 MAX phases from the bulk modulus (GPa). (c) The dependence of the formation energy (eV) of the lithiated 312 MAX phases from the C11 (GPa) elastic constant. (d) The dependence of the formation energy (eV) of the lithiated 312 MAX phases from the shear modulus G (GPa).
Figure 3. (a) The dependence of the Li MAX phases formation energy (eV), with respect to the c11 (GPa) elastic constant for the Ti3AC2 (A = Sn, Si, Ge, Ga, Al, In) MAX phases. (b) The dependence of the formation energy (eV) of lithiated 312 MAX phases from the bulk modulus (GPa). (c) The dependence of the formation energy (eV) of the lithiated 312 MAX phases from the C11 (GPa) elastic constant. (d) The dependence of the formation energy (eV) of the lithiated 312 MAX phases from the shear modulus G (GPa).
Materials 12 04098 g003
Table
Table 1. Calculated elastic constants Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus Y (GPa), Poisson’s ratio v, Pugh’s ratio B/G, elastic anisotropy factor A, and shear anisotropy factor (kc/ka) for the 312 MAX phases *. Comparison with previous studies [44,45,46,47,48,49,50,51,52].
Table 1. Calculated elastic constants Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus Y (GPa), Poisson’s ratio v, Pugh’s ratio B/G, elastic anisotropy factor A, and shear anisotropy factor (kc/ka) for the 312 MAX phases *. Comparison with previous studies [44,45,46,47,48,49,50,51,52].
Phasec11c12c13c33c44Akc/kaBGYB/GvRef.
Ti3AlC235574662951250.9711.3141571313071.1990.174[44]
35884752931220.9741.3431631273031.2790.190[47]
36175702991240.9541.2971601313091.2210.178[47]
36881763131300.9831.2531681353201.2450.183[46]
-------1651242971.3310.20[49]
Zr3AlC232284972871381.3301.1161651222941.3530.203This
31478792621071.0241.2791511102661.3730.207[46]
V3AlC2404841083611581.1511.0751971533641.2880.191This
390821163581581.2250.9911961473541.3330.200[46]
Hf3AlC234979792831230.9631.3241611252981.2880.192This
34777802911270.9411.2511621273021.2760.189[50]
35782832831260.9401.3651661283051.2970.193[51]
34879822901121.0581.2641631212911.3470.203[52]
Ta3AlC24111131363431560.7721.2172141433511.4970.227This
4411321383821750.7811.2172311573841.4710.223[46]
Ti3SiC236589993521561.2021.0121841433411.2870.191[44]
370991113491511.2091.0381921383341.3920.210[46]
37288983531671.2671.0361851493521.2450.183[48]
-------1851393331.3310.20[49]
-------1861443431.2910.192[48]
Hf3SiC2357931153341571.3621.0051881363291.3820.209This
3481011203351441.3000.9721901273121.4960.227[46]
Ta3SiC23351452213251793.2840.3652391032702.3200.317This
3522202103451822.6281.1262561022702.5090.324[46]
Zr3SiC232385993041350.7941.0241691222951.3850.209This
3201001072961250.8041.090174113279-0.233[46]
Mo3SiC23771751863641511.6371.0112451163012.1120.300This
Hf3SnC232095963001151.0751.0931681122751.5000.227[45]
32696973001070.9911.1231701102721.5500.234[46]
Ti3SnC2319103803041130.9761.1701631122731.4550.221[44]
33196802851080.9431.3021611132741.4360.217[46]
33191812991291.1031.1931621222851.3280.208[48]
Zr3SnC228092842571101.1921.179148992431.4950.227[45]
2979087268950.9721.177154982441.5710.237[46]
Ti3InC23388063276920.7541.3711511112671.3600.205[44]
3408567263970.8261.4781521112671.3620.205[46]
Ti3GaC235978692921230.9591.3411591303061.2230.179[44]
35686752851130.9201.3901621222931.3240.198[46]
Ti3GeC235688913241401.1251.1251751343201.3060.195[44]
357100973251291.0511.1521801263071.4260.216[46]
35585943381481.1711.0321771383121.2830.207[48]
* Elastic constants and moduli are shown in round figures.
Table
Table 2. The formation energy of 312 MAX phases when one Li atom is inserted.
Table 2. The formation energy of 312 MAX phases when one Li atom is inserted.
312 MAX PhasesFormation Energy/eV
Ti3AlC21.1966
Zr3AlC20.1499
V3AlC22.6507
Hf3AlC20.4172
Ta3AlC21.7890
Ti3SiC21.1597
Hf3SiC20.6902
Ta3SiC21.2943
Mo3SiC20.0056
Zr3SiC20.1608
Hf3SnC21.9508
Ti3SnC22.9303
Zr3SnC21.6645
Ti3InC22.1320
Ti3GaC20.9735
Ti3GeC21.5416

Share and Cite

MDPI and ACS Style

Filippatos, P.P.; Hadi, M.A.; Christopoulos, S.-R.G.; Kordatos, A.; Kelaidis, N.; Fitzpatrick, M.E.; Vasilopoulou, M.; Chroneos, A. 312 MAX Phases: Elastic Properties and Lithiation. Materials 2019, 12, 4098. https://doi.org/10.3390/ma12244098

AMA Style

Filippatos PP, Hadi MA, Christopoulos S-RG, Kordatos A, Kelaidis N, Fitzpatrick ME, Vasilopoulou M, Chroneos A. 312 MAX Phases: Elastic Properties and Lithiation. Materials. 2019; 12(24):4098. https://doi.org/10.3390/ma12244098

Chicago/Turabian Style

Filippatos, P.P., M.A. Hadi, S.-R.G. Christopoulos, A. Kordatos, N. Kelaidis, M.E. Fitzpatrick, M. Vasilopoulou, and A. Chroneos. 2019. "312 MAX Phases: Elastic Properties and Lithiation" Materials 12, no. 24: 4098. https://doi.org/10.3390/ma12244098

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop