Novel Semi-Analytical Solutions for the Transient Behaviors of Functionally Graded Material Plates in the Thermal Environment
Abstract
1. Introduction
2. Theoretical Formulation
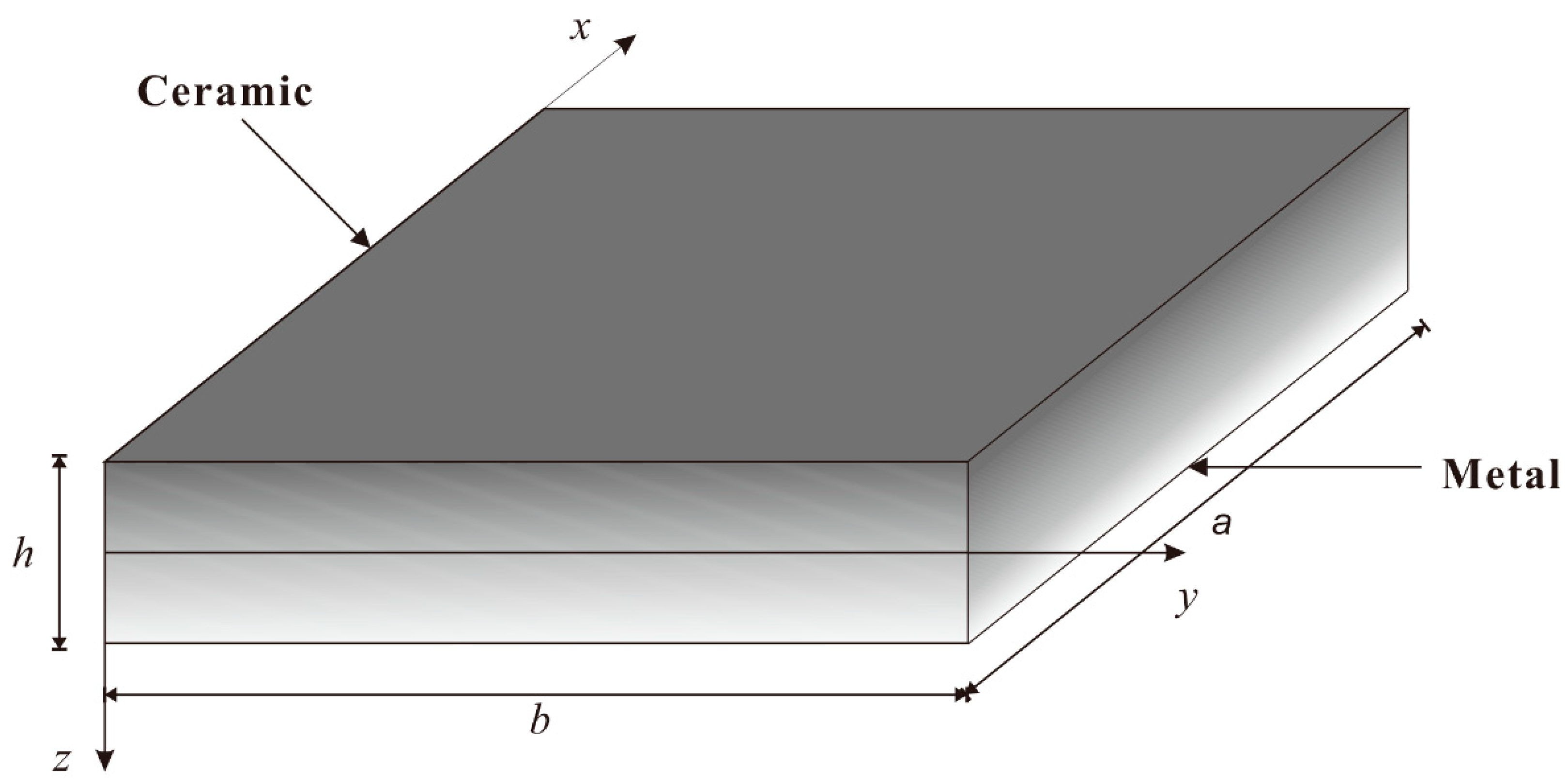
2.1. Material Properties
2.2. Mathematical Model
3. Solution Procedure
3.1. Differential Quadrature Method and Laplace Transform
3.1.1. Differential Quadrature Method
3.1.2. Laplace Numerical Inversion
3.2. Dynamic Response Calculation
4. Numerical Results
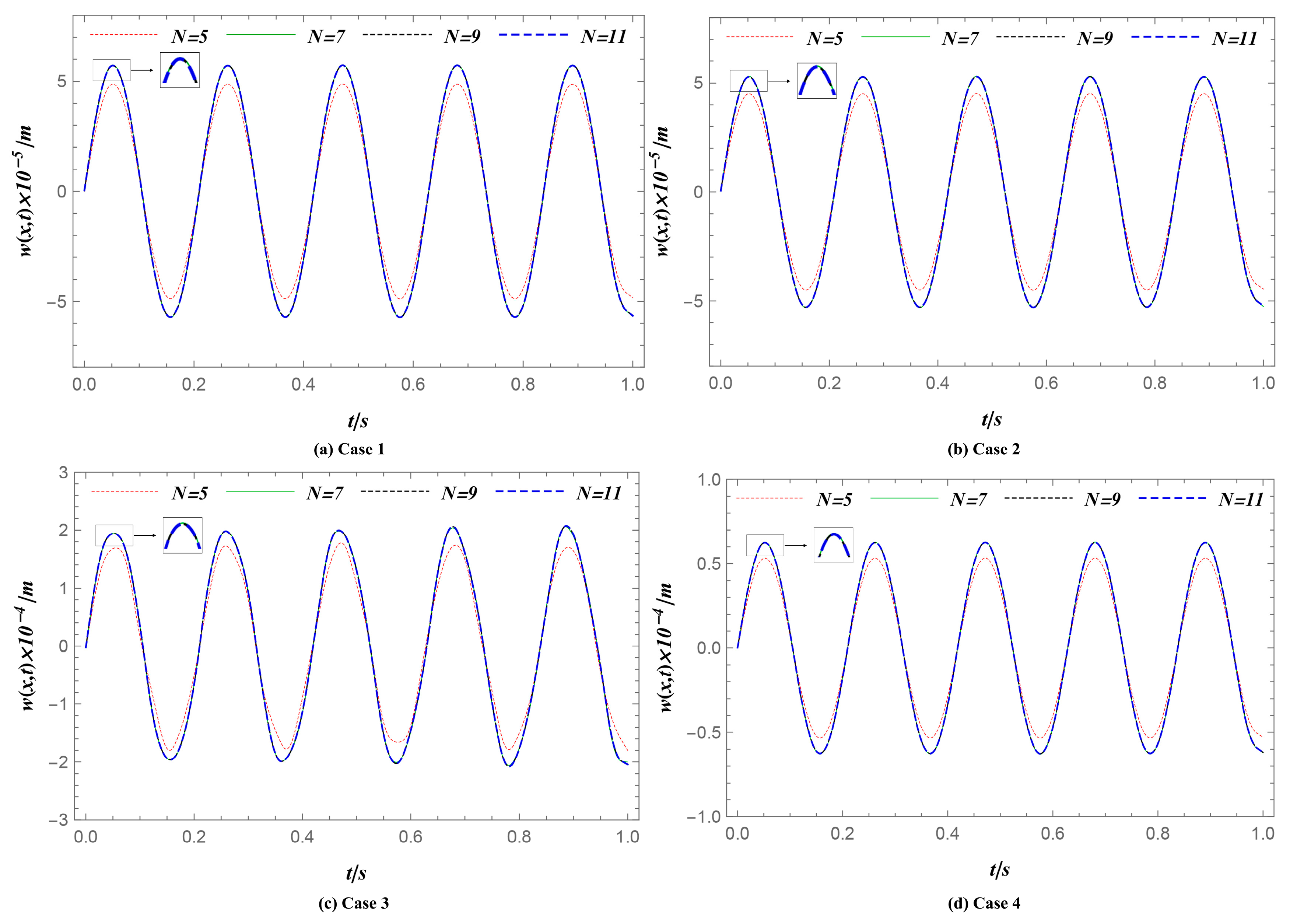
4.1. Convergence Studies
4.2. Validation of the Proposed Method
4.2.1. Validation by Comparison with Natural Frequencies Results
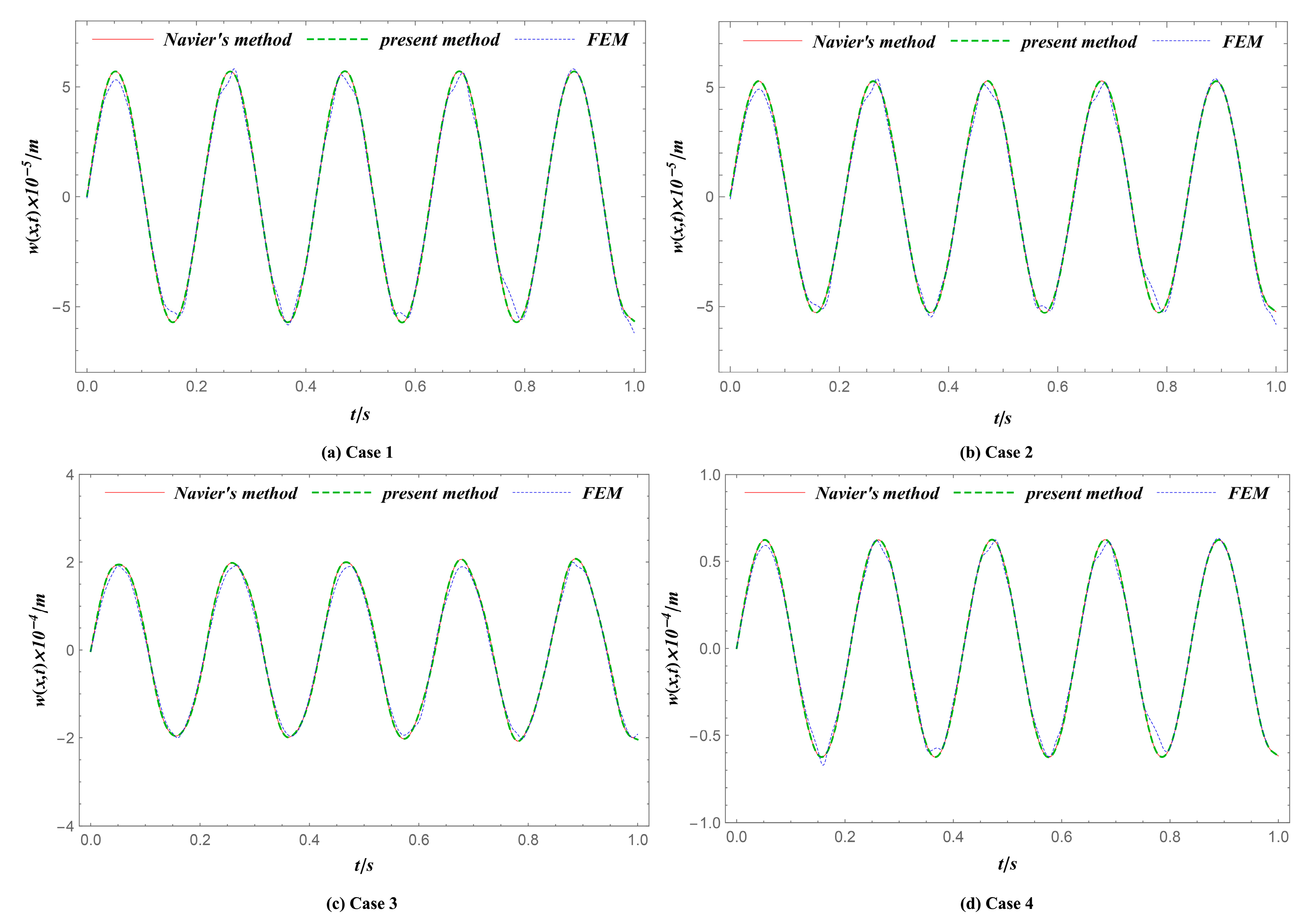
4.2.2. Validation by Comparison with Analytical and FEM Solutions
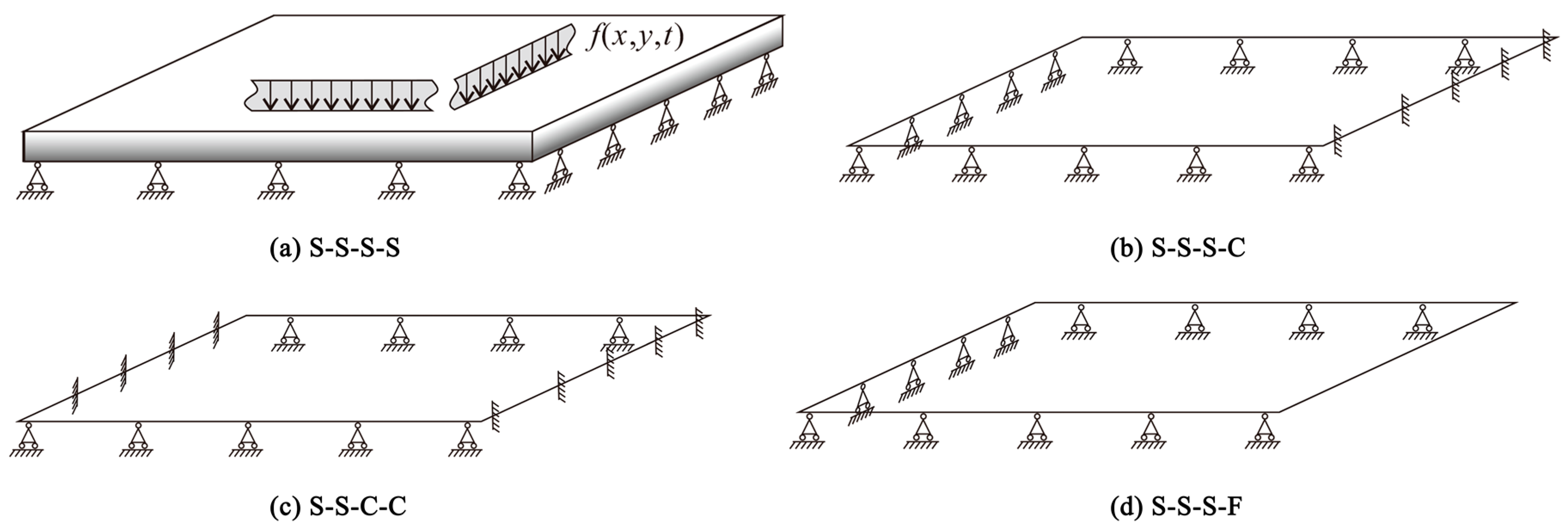
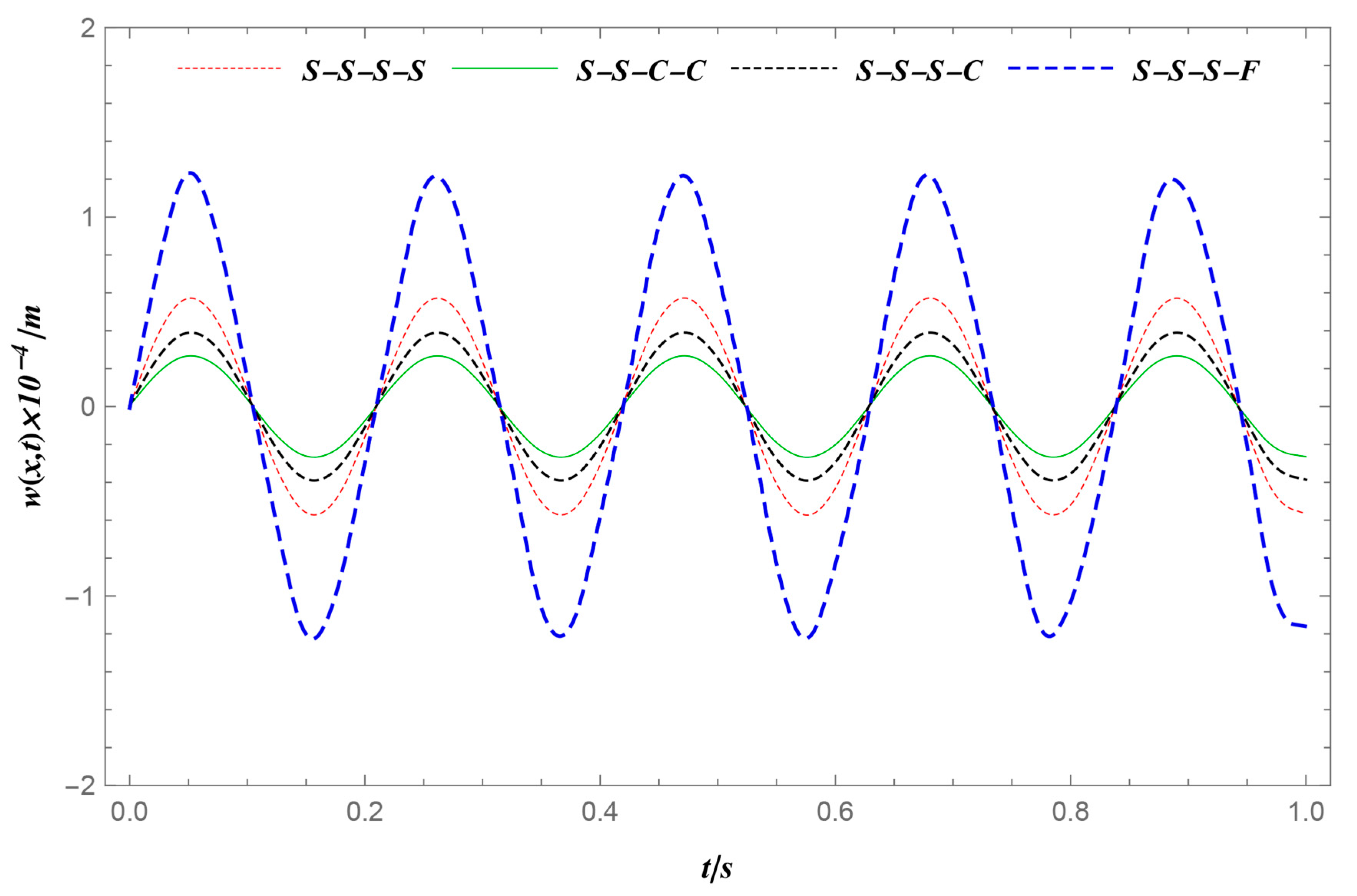
4.3. The Influence of the Boundary Conditions at the Ends
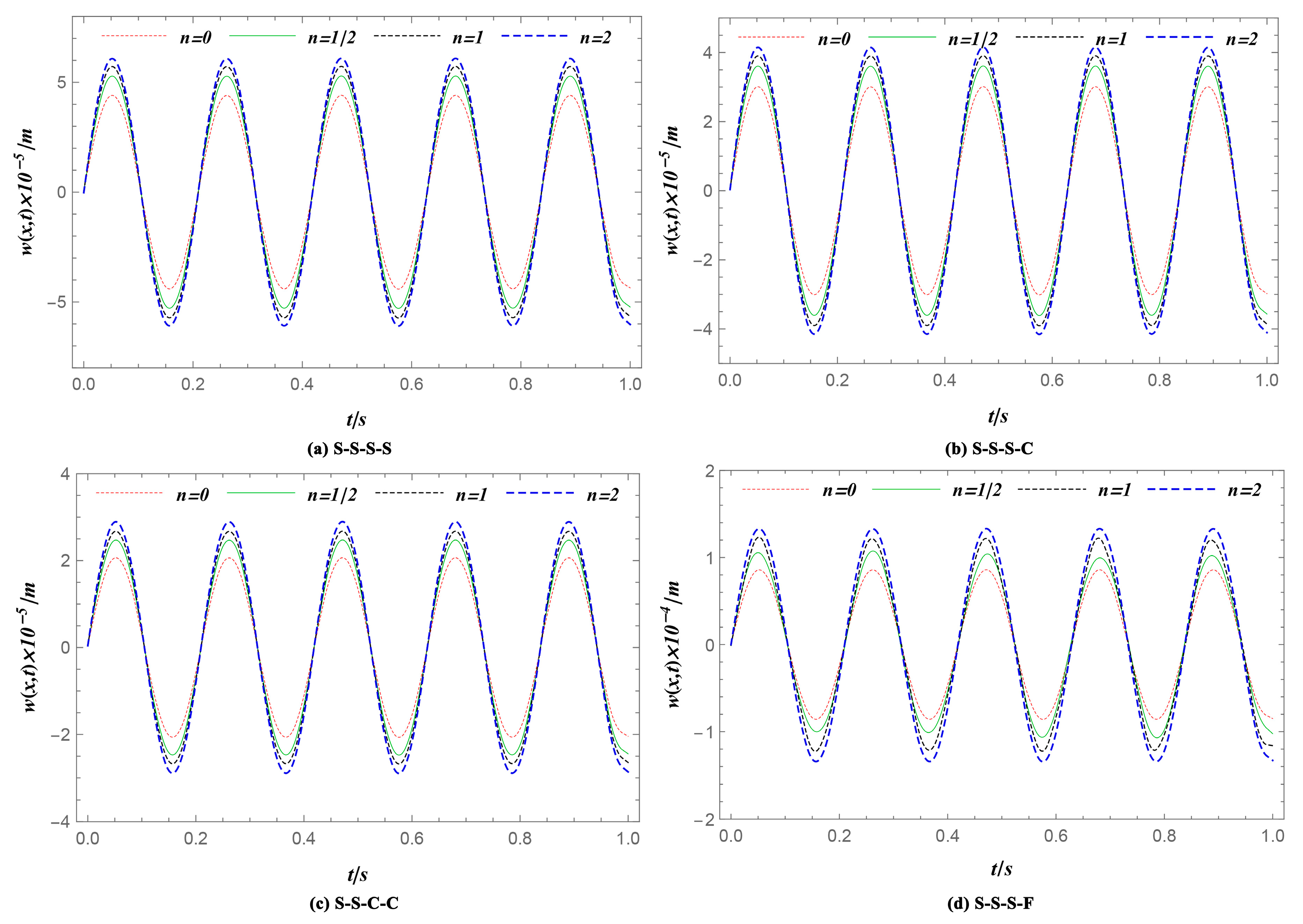
4.4. The Influence of Material Graded Index n
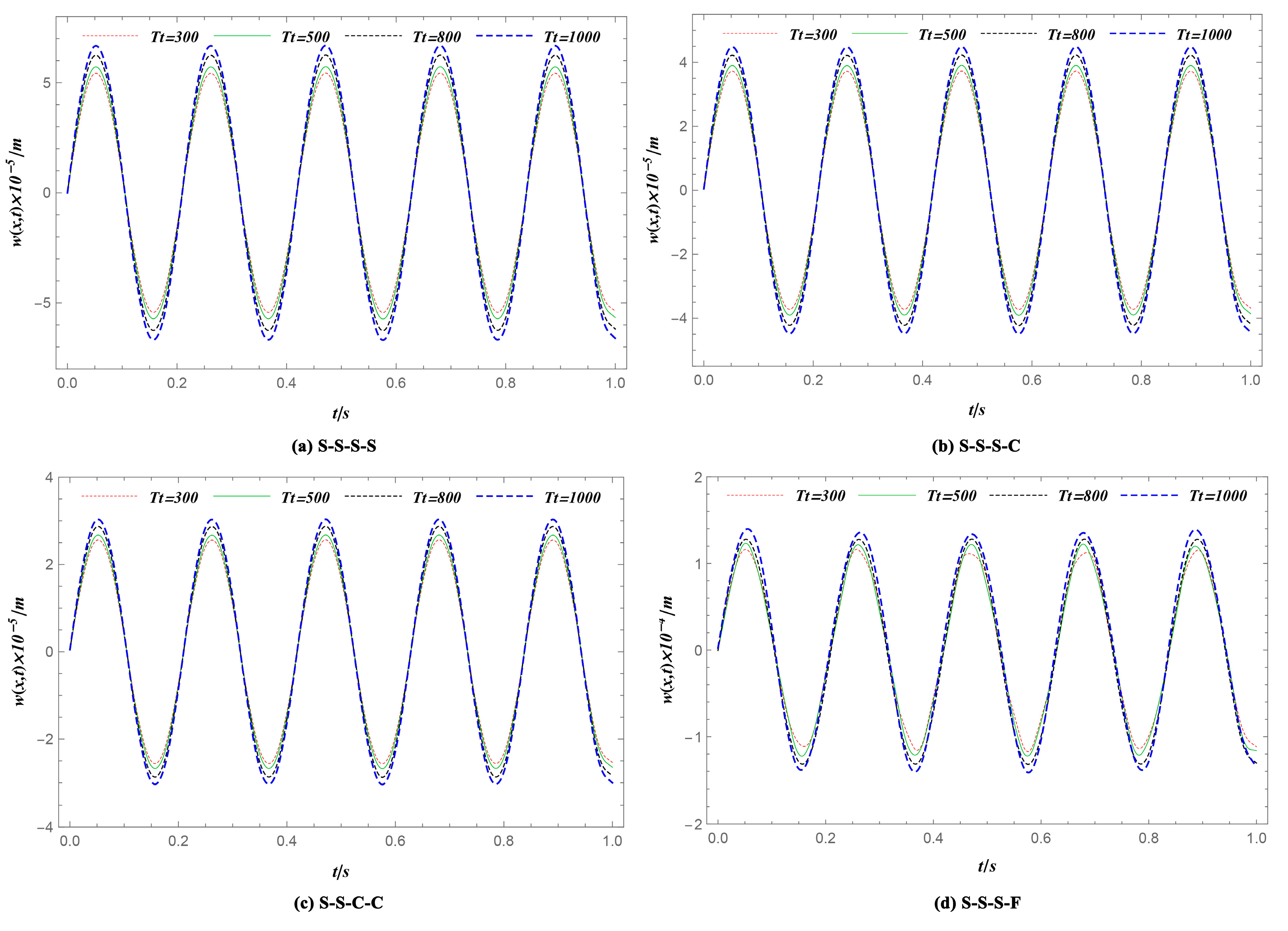
4.5. The Influence of Temperature Changes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jasim, K.M.; Rawlings, R.D.; West, D.R.F. Metal-ceramic functionally gradient material produced by laser processing. J. Mater. Sci. 1993, 28, 2820–2826. [Google Scholar] [CrossRef]
- Jin, Z.H.; Naotake, N. Transient thermal stress intensity factors for a crack in a semi-infinite plate of a functionally gradient material. Int. J. Solids Struct. 1994, 31, 203–218. [Google Scholar]
- Obata, Y.; Noda, N. Steady thermal stresses in a hollow circular cylinder and a hoolow sphere of a functionally gradient material. J. Therm. Stresses 1994, 17, 471–487. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional analysis of transient thermal stresses in functionally graded plates. Int. J. Solids Struct. 2003, 40, 7181–7196. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.S. Dynamic response of initially stressed functionally graded rectangular thin plates. Compos. Struct. 2001, 54, 497–508. [Google Scholar] [CrossRef]
- Lü, C.F.; Lim, C.W.; Chen, W.Q. Semi-analytical analysis for multi-directional functionally graded plates: 3-D elasticity solutions. Int. J. Numer. Methods Eng. 2010, 79, 25–44. [Google Scholar] [CrossRef]
- Behrens, B.; Müller, M. Technologies for thermal protection systems applied on re-usable launcher. Acta Astronaut. 2004, 55, 529–536. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Jomehzadeh, E. Exact analytical solution for free vibration of functionally graded thin annular sector plates resting on elastic foundation. J. Vib. Control 2012, 18, 246–267. [Google Scholar] [CrossRef]
- Yin, S.; Yu, T.; Liu, P. Free Vibration Analyses of FGM Thin Plates by Isogeometric Analysis Based on Classical Plate Theory and Physical Neutral Surface. Adv. Mech. Eng. 2013, 5, 1436–1449. [Google Scholar] [CrossRef]
- Asghari, M.; Taati, E. A size-dependent model for functionally graded micro-plates for mechanical analyses. J. Vib. Control 2013, 19, 1614–1632. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Tai, H.T.; Vo, T.P. A refined higher-order shear deformation theory for bending, vibration and buckling analysis of functionally graded sandwich plates. Steel Compos. Struct. 2015, 18, 91–120. [Google Scholar] [CrossRef]
- Yang, Y.; Kou, K.P.; Iu, V.P.; Lam, C.C.; Zhang, C. Free vibration analysis of two-dimensional functionally graded structures by a meshfree boundary–domain integral equation method. Compos. Struct. 2014, 110, 342–353. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Beni, A.A. Free vibration of functionally graded arbitrary straight-sided quadrilateral plates in thermal environment. Compos. Struct. 2010, 92, 2758–2767. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Shahpari, S.A.; Ziaee, H.R. Three-dimensional free vibration of thick functionally graded annular plates in thermal environment. J. Sound Vib. 2010, 329, 425–442. [Google Scholar] [CrossRef]
- Shenas, A.G.; Malekzadeh, P. Free vibration of functionally graded quadrilateral microplates in thermal environment. Thin-Walled Struct. 2016, 106, 294–315. [Google Scholar] [CrossRef]
- Shi, P.; Dong, C.Y. Vibration analysis of functionally graded annular plates with mixed boundary conditions in thermal environment. J. Sound Vib. 2012, 331, 3649–3662. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. Free vibration of functionally graded sandwich plates in thermal environment using a layerwise theory. Eur. J. Mech. 2015, 51, 55–66. [Google Scholar] [CrossRef]
- Li, Q.; Iu, V.P.; Kou, K.P. Three-dimensional vibration analysis of functionally graded material sandwich plates. J. Sound Vib. 2009, 311, 498–515. [Google Scholar] [CrossRef]
- Wang, Z.X.; Shen, H.S. Nonlinear analysis of sandwich plates with FGM face sheets resting on elastic foundations. Compos. Struct. 2011, 93, 2521–2532. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Non-linear analysis of functionally graded fiber reinforced composite laminated plates, Part II: Numerical results. Int. J. Non-Linear Mech. 2012, 47, 1055–1064. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Mohammadi, Y. Free vibration analysis of sandwich plates with functionally graded face sheets and temperature-dependent material properties: A new approach. Eur. J. Mech. 2012, 35, 61–74. [Google Scholar] [CrossRef]
- George, N.; Jeyaraj, P.; Murigendrappa, S.M. Buckling and Free Vibration of Nonuniformly Heated Functionally Graded Carbon Nanotube Reinforced Polymer Composite Plate. Int. J. Struct. Stab. Dyn. 2017, 17, 17500064. [Google Scholar] [CrossRef]
- Huang, X.L.; Shen, H.S. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments. Int. J. Solids Struct. 2005, 41, 2403–2427. [Google Scholar] [CrossRef]
- Kim, K.S.; Noda, N. A Green’s function approach to the deflection of a FGM plate under transient thermal loading. Arch. Appl. Mech. 2002, 72, 127–137. [Google Scholar] [CrossRef]
- Praveen, G.N.; Reddy, J.N. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. Int. J. Solids Struct. 1998, 35, 4457–4476. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Monajjemzadeh, S.M. Dynamic response of functionally graded plates in thermal environment under moving load. Mech. Compos. Mater. Struct. 2016, 23, 248–258. [Google Scholar] [CrossRef]
- Idesman, A.; Samajder, H.; Aulisa, E.; Seshaiyer, P. Benchmark problems for wave propagation in elastic materials. Comput. Mech. 2009, 43, 797–814. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, X.; Liu, G. An Analytical Method for Evaluating the Dynamic Response of Plates Subjected to Underwater Shock Employing Mindlin Plate Theory and Laplace Transforms. Math. Probl. Eng. 2013, 2013, 927–940. [Google Scholar] [CrossRef]
- Lang, Z.; Li, X. Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells. Appl. Math. Model. 2013, 37, 2279–2292. [Google Scholar] [CrossRef]
- Kim, Y.W. Temperature dependent vibration analysis of functionally graded rectangular plates. J. Sound Vib. 2005, 284, 531–549. [Google Scholar] [CrossRef]
- Jang, S.K.; Bert, C.W.; Striz, A.G. Application of differential quadrature to static analysis of structural components. Int. J. Numer. Methods Eng. 2010, 28, 561–577. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Z.; Wang, L.; Liu, G. Semi-analytical solution for three-dimensional transient response of functionally graded annular plate on a two parameter viscoelastic foundation. J. Sound Vib. 2014, 333, 2649–2663. [Google Scholar] [CrossRef]
- Durbin, F. Numerical Inversion of Laplace Transforms: An Efficient Improvement to Dubner and Abate’s Method. Comput. J. 1972, 17, 371–376. [Google Scholar] [CrossRef]
- Liang, X.; Cao, Z.; Sun, H.; Zha, X.; Leng, J. Analytical and semi-analytical methods for the evaluation of dynamic thermo-elastic behavior of structures resting on a Pasternak foundation. J. Press. Vessel Technol. 2019, 141, 010908. [Google Scholar] [CrossRef]
- Research, I.W. Wolfram Mathematica. Version 11.0.0. 2016. Available online: www.wolfram.com (accessed on 17 November 2019).
- Duc, N.D.; Thang, P.T.; Dao, N.T.; Tac, H.V. Nonlinear buckling of higher deformable S-FGM thick circular cylindrical shells with metal–ceramic–metal layers surrounded on elastic foundations in thermal environment. Compos. Struct. 2015, 121, 134–141. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.S. Vibration characteristics and transient response of shear-deformable functionally graded plates in thermal environments. J. Sound Vib. 2002, 255, 579–602. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Jomehzadeh, E. An Exact solution for free vibration of thin functionally graded rectangular plates. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 526–536. [Google Scholar] [CrossRef]
- Joshi, P.V.; Jain, N.K.; Ramtekkar, G.D. Effect of thermal environment on free vibration of cracked rectangular plate: An analytical approach. Thin-Walled Struct. 2015, 91, 38–49. [Google Scholar] [CrossRef]
| Material | Properties | P0 | P−1 | P1 | P2 | P3 |
|---|---|---|---|---|---|---|
| Si3N4 (Ceramic) | E (Pa) | 3.84 × 1011 | 0 | −3.70 × 10−4 | 2.16 × 10−7 | −8.95 × 10−11 |
| ρ (kg/m3) | 2370 | 0 | 0 | 0 | 0 | |
| α (K−1) | 5.87 × 10−6 | 0 | 9.10 × 10−4 | 0 | 0 | |
| K (W/mK) | 13.723 | 0 | 0 | 0 | 0 | |
| ν | 0.24 | 0 | 0 | 0 | 0 | |
| SUS304 (Metal) | E (Pa) | 2.01 × 1011 | 0 | 3.08 × 10−4 | −13.53 × 10−7 | 0 |
| ρ (kg/m3) | 8166 | 0 | 0 | 0 | 0 | |
| α (K−1) | 1.23 × 10−5 | 0 | 8.09 × 10−4 | 0 | 0 | |
| K (W/mK) | 15.379 | 0 | 0 | 0 | 0 | |
| ν | 0.3177 | 0 | 0 | 0 | 0 |
| Material Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Length a (m) | 2 | 2 | 2 | 2 |
| Width b (m) | 2 | 2 | 2 | 2 |
| thickness h (m) | 0.1 | 0.1 | 0.05 | 0.1 |
| Temperature Tc (K) | 500 | 500 | 500 | 800 |
| Power law index n | 1 | 2 | 1 | 1 |
| The external pressure Q (N/m2) | 2 × 104 | 2 × 104 | 2 × 104 | 2 × 104 |
| Boundary Conditions | n | m | Baferani [39] | Present | Error (%) |
|---|---|---|---|---|---|
| S-S-S-S | 0 | 1 | 115.8695(1,1) | 115.9250 | 0.048 |
| 2 | 289.7770(1,2) | 289.7708 | 0.002 | ||
| 0.5 | 1 | 98.0136(1,1) | 98.1594 | 0.149 | |
| 2 | 245.3251(1,2) | 245.3680 | 0.017 | ||
| 1 | 1 | 88.3093(1,1) | 88.4500 | 0.159 | |
| 2 | 221.0643(1,2) | 221.0950 | 0.014 | ||
| 2 | 1 | 80.3517(1,1) | 80.4195 | 0.084 | |
| 2 | 200.8793(1,2) | 201.0104 | 0.065 | ||
| S-C-S-C | 0 | 1 | 170.0196(1,1) | 170.0270 | 0.004 |
| 2 | 321.4069(1,2) | 321.5180 | 0.035 | ||
| 0.5 | 1 | 143.8179(1,1) | 143.9700 | 0.106 | |
| 2 | 272.1090(1,2) | 272.2440 | 0.050 | ||
| 1 | 1 | 129.6496(1,1) | 129.7290 | 0.061 | |
| 2 | 245.1310(1,2) | 245.3130 | 0.074 | ||
| 2 | 1 | 117.8104(1,1) | 117.9460 | 0.115 | |
| 2 | 222.8111(1,2) | 223.0280 | 0.097 | ||
| S-S-S-C | 0 | 1 | 138.7717(1,1) | 138.8740 | 0.074 |
| 2 | 303.3569(1,2) | 303.4670 | 0.036 | ||
| 0.5 | 1 | 117.4222(1,1) | 117.5913 | 0.144 | |
| 2 | 256.7762(1,2) | 256.9595 | 0.071 | ||
| 1 | 1 | 105.7770(1,1) | 105.9598 | 0.173 | |
| 2 | 231.3509(1,2) | 231.5406 | 0.082 | ||
| 2 | 1 | 96.2668(1,1) | 96.3352 | 0.071 | |
| 2 | 210.3895(1,2) | 210.5070 | 0.056 | ||
| S-S-S-F | 0 | 1 | 68.5125(1,1) | 68.6417 | 0.189 |
| 2 | 162.8384(2,1) | 163.1933 | 0.218 | ||
| 0.5 | 1 | 58.0318(1,1) | 58.1223 | 0.156 | |
| 2 | 137.9954(2,1) | 138.183 | 0.136 | ||
| 1 | 1 | 52.2092(1,1) | 52.3732 | 0.314 | |
| 2 | 124.2452(2,1) | 124.5145 | 0.217 | ||
| 2 | 1 | 47.5511(1,1) | 47.6162 | 0.137 | |
| 2 | 112.9582(2,1) | 113.2039 | 0.218 |
| Cases | CT of the Proposed Method (s) | CT of Navier’s Method (s) | CT of FEM (s) | |
|---|---|---|---|---|
| Case 1 | N = 7 | 174.23 | 281.64 | 445 |
| N = 9 | 287.92 | |||
| Case 2 | N = 7 | 187.45 | 283.23 | 510 |
| N = 9 | 316.52 | |||
| Case 3 | N = 7 | 169.32 | 278.53 | 468 |
| N = 9 | 304.77 | |||
| Case 4 | N = 7 | 177.23 | 287.55 | 498 |
| N = 9 | 314.06 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Liang, X.; Deng, Y.; Zha, X.; Zhu, R.; Leng, J. Novel Semi-Analytical Solutions for the Transient Behaviors of Functionally Graded Material Plates in the Thermal Environment. Materials 2019, 12, 4084. https://doi.org/10.3390/ma12244084
Cao Z, Liang X, Deng Y, Zha X, Zhu R, Leng J. Novel Semi-Analytical Solutions for the Transient Behaviors of Functionally Graded Material Plates in the Thermal Environment. Materials. 2019; 12(24):4084. https://doi.org/10.3390/ma12244084
Chicago/Turabian StyleCao, Zeng, Xu Liang, Yu Deng, Xing Zha, Ronghua Zhu, and Jianxing Leng. 2019. "Novel Semi-Analytical Solutions for the Transient Behaviors of Functionally Graded Material Plates in the Thermal Environment" Materials 12, no. 24: 4084. https://doi.org/10.3390/ma12244084
APA StyleCao, Z., Liang, X., Deng, Y., Zha, X., Zhu, R., & Leng, J. (2019). Novel Semi-Analytical Solutions for the Transient Behaviors of Functionally Graded Material Plates in the Thermal Environment. Materials, 12(24), 4084. https://doi.org/10.3390/ma12244084



_Zhu.png)

