Abstract
The three-dimensional vibration of a functionally graded sandwich rectangular plate on an elastic foundation with normal boundary conditions was analyzed using a semi-analytical method based on three-dimensional elasticity theory. The material properties of the sandwich plate varied with thickness according to the power law distribution. Two types of functionally graded material (FGM) sandwich plates were investigated in this paper: one with a homogeneous core and FGM facesheets, and another with homogeneous panels and an FGM core. Various displacements of the plates were created using an improved Fourier series consisting of a standard Fourier cosine series along with a certain number of closed-form auxiliary functions satisfying the essential boundary conditions. The vibration behavior of the FGM sandwich plate, including the natural frequencies and mode shapes, was obtained using the Ritz method. The effectiveness and accuracy of the suggested technique were fully verified by comparing the natural frequencies of sandwich plates with results from investigations of other functionally graded sandwich rectangular plates in the literature. A parametric study, including elastic parameters, foundation parameters, power law exponents, and layer thickness ratios, was performed, and some new results are presented.
1. Introduction
In previous decades, functionally graded materials (FGMs) have been widely used in aviation, nuclear energy, and other fields because of their special physical characteristics under high temperatures. The development of pure functionally gradient materials and FGM sandwich plates has been aimed at easing large interfacial shear stresses. Compared with pure functionally graded materials, there are relatively few studies on FGM sandwich structures. Thus, further research on these structures will be helpful for scientists.
Mechanical properties of sandwich plates with a homogeneous and functionally graded material core have been investigated in the area of long-span lightweight structures [1,2,3,4]. Theoretical models, such as shear deformation plate theory, energy method, finite element method, and three-dimensional elastic theory, have been used to investigate the mechanical behavior of FGM structures. To account for specific deformations and stresses, many specific plate and shell models for sandwich/laminate/FGM plates have been developed. Four theoretical models are often used to analyze the complex mechanical behavior of sandwich/laminate/FGM plates: (1) equivalent single-layer theory (ESLT), which can be divided into three main categories, namely classical plate theory (CPT) [5,6], first-order shear deformation theory (FSDT) [7,8], and higher-order shear deformation theory (HSDT) [9,10,11]; (2) refined higher-order shear deformation theory (RHSDT) [12,13,14,15,16]; (3) 3D elasticity theory [17,18]; and (4) layer-wise theory (LWT) [19,20,21,22]. In ESLT, the sandwich plate is analyzed in terms of displacement functions related to a single reference surface. Exact 3D elasticity benchmark solutions for the staticity, vibrations, and dynamics of sandwich plates have been presented by researchers [9,12]. The unified formulation proposed by Carrera [23,24] provides a procedure to describe and implement numerous plate/shell theories and finite elements in a unified manner by referring to a few fundamental nuclei. Individual layers in LWT are considered separately as independent displacement fields with compatibility enforced by appropriate interface compatibility constraints. In addition to ESLT and LWT, other theories exist; for example, simplified equivalent single-layer theory (SESLT) [25,26,27], global–local higher-order theory [28,29], and mixed layer-wise theory (MLWT) [30,31]. SESLT divides transverse displacement into bending and shear parts and reduces the displacement field unknowns. By contrast, MLWT is formulated on the basis of the displacement and transverse stress at interfaces.
The study of vibration characteristics of sandwich rectangular plates with an isotropic or FGM core has made some improvement in recent years. Guided by Reddy’s third-order shear deformation theory, Moita et al. [32] researched the vibration characteristics of material sandwich structures with passive damping by utilizing the finite element method. Taking into account high-order shear deformation theory (HSDT), Thai et al. [33] studied various properties of sandwich FGM plates, including free vibration, bending, and buckling, by applying a moving Kriging mesh-free method. Tounsi et al. [34] proposed a refined trigonometric shear deformation theory (RTSDT) produced using functional gradient sandwich plates under classical boundary conditions. In the analysis of free and forced vibrations on an elastic foundation, Trinh and Kim [35] presented analytical closed-form solutions for thin FGM sandwich shells with a resting double curvature. Aiming at a dynamic, as well as static, analysis of FGM sandwich plates, Pandey and Pradyumna [36,37] extended the higher-order hierarchical finite element formula. According to the theory of higher-order shear deformation plates, Daikh and Megueni [38] applied closed-form analytical solutions to analyze the thermal buckling of functionally graded sandwich plates with simple support boundary conditions. Using a meshless technique, Neves et al. [39] investigated the characteristics of free vibration and analyzed the buckling of functionally graded sandwich plates on the condition that the boundary is simply supported under the guidance of a theory called quasi-3D higher-order shear deformation. Furthermore, using four-variable refinement plate theory as a guideline, Bourada et al. [40] determined the thermal buckling characteristics of FGM sandwich plates. In light of the theory of hyperbolic shear deformation, Houari et al. [41] explored buckling, as well as the free vibration, of thick FGM sandwich plates under the conditions of an ordinary supported boundary. Using 3D linear elastic theory, Li et al. [42] adopted the theoretical content of the Ritz method to study the vibration characteristics of rectangular plates. Jalali et al. [43] used a pseudo-spectral method to study the thermal stability features of FGM sandwich plates subject to a uniform temperature. Houari et al. [44] discussed the thermoelastic bending deformation of FGM sandwich plates under simply supported boundary conditions in detail according to the two-variable refined plate theory and analyzed stresses. In order to explore the vibration characteristics of FGM sandwich plates, Thai et al. [45,46], Hadji and Tounsi et al. [47,48] proposed an innovative simple modified plate theory, which proved to be in good agreement with experiments. Neves et al. [49] conducted a static analysis of FGM sandwich plates under the guidance of a meshless method with a radial basis function assignment. For more related research results on sandwich beams and sandwich shells, see References [50,51,52,53,54,55,56,57,58,59].
The above review shows that most existing studies on sandwich rectangular plates are confined to two-dimensional elastic theory, including the first-order shear deformation theory (FSDT) and the high-order shear deformation theory (HSDT). So far, only Li’s [42] work has been in accordance with the theory of three-dimensional elasticity. Besides, most researchers limited their study to classical boundary conditions, e.g., simply supported boundary conditions. Based on existing research results, the main objective of this study was to establish a three-dimensional sandwich rectangular plate vibration analysis model with general boundary conditions and an elastic foundation. The Pasternak model was used to model the elastic foundation. Also, general boundary conditions were realized using three sets of linear springs uniformly distributed at the edges. The theoretical formulation was achieved based on the Ritz and three-dimensional elasticity theories. Throughout this paper, the authors aim to enrich existing research results of sandwich rectangular plates and provide reference data for future follow-up studies.
2. Theoretical Formulations
2.1. Geometrical Configuration
Figure 1 gives a schematic diagram of a three-dimensional sandwich rectangular plate on an elastic foundation under general boundary conditions. Figure 1a utilizes the Cartesian coordinate system (x, y, z), with the origin (0, 0, 0) at the bottom of a rectangular plate. The letter a, b, and h denote the length, width, and thickness of a rectangular plate in the x-, y-, and z-directions, respectively. Figure 1b shows general boundary conditions using three sets of linear springs (ku, kv, kw). Three elastic layers make up the sandwich plate; h1 = 0, and h2, h3, and h4 = h represent vertical coordinates from the bottom to the top, including the two middle interfaces. For the sake of simplicity, a combination of three numbers (1–0–1, 2–1–2, etc.) are used to represent the thickness ratio of each layer from the bottom to the top.

Figure 1.
Geometry of a three-dimensional (3D) functionally graded (FG) sandwich rectangular plate: (a) the geometry and coordinates, and (b) the boundary restraining springs.
In this paper, two common sandwich structures are used to describe the material characteristics of three-dimensional sandwich rectangular plates, as shown in Figure 2. Two kinds of sandwich structures are denoted as type A and type B. Type A contains an FGM face sheet and a homogeneous core; type B contains a homogeneous face sheet and an FGM core. The volume fraction V1 of an FGM sandwich rectangular plate is defined as:
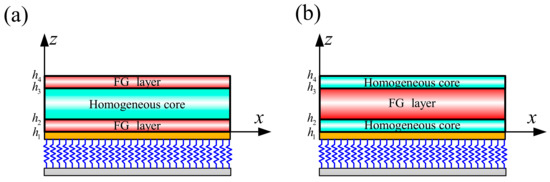
Figure 2.
The material variation along the thickness of the 3D FG sandwich rectangular plate: (a) FGM facesheet and homogeneous core, and (b) homogeneous facesheet and FGM core.
The Voigt criteria can efficiently evaluate the effectiveness of each layer of material, and the Young’s modulus (Ee), Poisson’s ratio (µe), and mass density (ρe) of the eth layer are given using the following equationos:
The subscripts b and t represent the bottom face and the top face of each layer, respectively. In order to highlight the basic principles of Equations (1) and (2), Figure 3 shows the volume fraction of the FGM sandwich rectangular plate along the thickness direction z as a function of the power law index p.
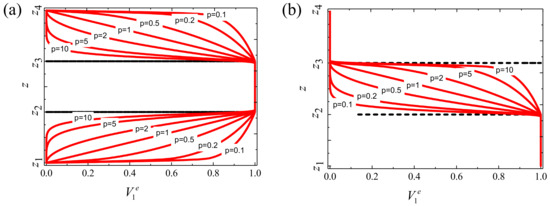
Figure 3.
Variation of the volume fraction
through the thickness for different values of the power law exponent: (a) type A and (b) type B.
2.2. Admissible Displacement Functions
The Ritz method is suitable for studying the vibration performance of three-dimensional FGM sandwich rectangular plates under general boundary conditions. Therefore, selecting appropriate displacement admissible functions is critical [58]. It can be found that the conventional displacement admissible functions are usually defined according to the boundary conditions, such as a conventional Fourier series, Chebyshev polynomial, and so on. The latter would cause a tedious formula deduction and reduce computational efficiency. In previous work, the author’s team proposed a new type of displacement admissible function by adding an auxiliary function for the boundary based on the traditional Fourier series [60,61]. In this way, the admissible displacement function and its derivative at the edges of the structure can be solved mechanically. Therefore, an improved Fourier series is used in this study to represent the allowable displacement function of three-dimensional functionally graded sandwich rectangular plates. The specific expressions are as follows [62]:
where UΩ, VΩ, and WΩ refer to the internal displacement distribution functions of the functionally graded sandwich rectangular plate; UqS, VqS, and WqS are the complementary sequences of boundary displacements of the functionally graded sandwich rectangular plate; and Amnq, Bmnq, and Cmnq are 3D Fourier coefficient vectors. The following formulas represent the specific parameters of each vector symbol [61]:
2.3. Energy Expressions
Based on the theory of 3D elasticity [9], the relationship between linear strain and displacement for a three-dimensional functional gradient sandwich rectangular plate are given as:
The stress of the three-dimensional FGM sandwich rectangular plate using the theory of three-dimensional constraint of a linear elastic can be expressed as follows:
where the stiffness coefficient Cij is obtained as follows:
Then, based on the elasticity theory, the strain energy U for a three-dimensional functionally graded sandwich rectangular plate can be obtained (detailed descriptions of Equation (8) are given in Appendix A).
The corresponding kinetic energy (T) function of the three-dimensional FGM sandwich rectangular plate can be given as follows:
The energy (Usp) kept in reserve by the boundary spring during deformation strain vibrations can be given as follows:
As stated above, the vibration behavior of the 3D functionally graded sandwich rectangular plate placed on an elastic foundation with a Pasternak type Winkler layer (stiffness Kw) was determined, as well as for the shear layer (stiffness Ks), drawn in Figure 1. The following formula shows the total energy stored in the foundation spring:
The Lagrangian energy function for the three-dimensional functionally graded sandwich rectangular plate can be expressed as:
2.4. Solution Methodology
By applying the Ritz method, the Lagrangian function (L) should not be variable, i.e, its variety is equal to zero under time constraint implemented between a fixed primary and final moment of time t0 and t1. A homogeneous quadratic function of Fourier series coefficients is given by the Lagrange function L. Partial derivatives of the Lagrangian function L from Equation (12) with respect to Amnq, Bmnq, and Cmnq is as follows:
The controlling eigenvalues matrix can be obtained using:
where the parameters of K and M represent the overall stiffness matrix and the mass matrix, respectively. H is the sealed Fourier coefficient vector. The natural frequencies and mode shapes of the three-dimensional FGM sandwich rectangular plate can be obtained by solving Equation (14). Due to space limitations, detailed expressions of matrices K, M, and H are not given here.
3. Numerical Results and Discussion
Section 2 established a theoretical model based on the Ritz method. This section highlights numerical discussions based on the above-mentioned Ritz method. The discussion can be divided into three parts: (a) a study of the convergence characteristics of this method, (b) verification of the correctness and efficiency of the current method using a series of numerical examples, and (c) further development of new numerical examples and parametric studies. The material constituents of the functionally graded layers were set as alumina (top surface) and aluminum (bottom surface) in the absence of other provisions. During the course of this research, material properties were defined as follows: aluminum: Em = 70 GPa, μm = 0.3, ρm = 2702 kg/m3; alumina: Em = 380 GPa, μm = 0.3, ρm = 3800 kg/m3. For simplicity, the dimensionless natural frequency Ω, equivalent shear , and Winkler parameters , respectively, are expressed as followings:
In addition, in order to further simplify the study, only one group of foundation coefficients = (10,10) was adopted for this research. From bottom to top, the proportion of the layer thicknesses was taken to be 1–2–1 in the absence of other provisions.
3.1. Convergence Study
In theory, the Ritz method can obtain quite accurate solutions by increasing the number of displacement tolerance function terms. However, due to limited computing hardware resources, too many expansion terms of displacement admissible functions will greatly reduce the computational efficiency of the Ritz method. Convergence properties of the Ritz method under the improved Fourier series were used in this study. Table 1 presents the first six frequency parameters Ω of FGM sandwich plates with diverse truncated numbers of modified Fourier series. The boundary condition of the structure was limited to CCCC (four edges clamped) and SSSS (four edges simply-supported). Furthermore, b/a = 1 and h/a = 0.5 represent geometric parameters, and p = 1 represents a power law index. Two cases of inelastic and elastic foundations are considered in this case. Table 1 highlights the advantages of the proposed methodology, e.g., fast convergence characteristics and good numerical stability. Compared with the 4 × 4 × 4 terms, the 8 × 8 × 8 terms provided a sufficiently accurate solution. Table 2 shows the convergence of type B FGM sandwich plates with different truncated numbers. Both geometric parameters and the power law exponents were the same as for Table 1. The above-mentioned results exhibited the same trend as the Type A FGM plates. Thus, in the example given below, the admissible function truncated number was chosen as follows: M × N × Q = 8 × 8 × 8.

Table 1.
Convergence of frequency parameters Ω of FGM sandwich plates of type A with different numbers of terms and p = 1.

Table 2.
Convergence of frequency parameters Ω of FGM sandwich plates of type B with different numbers of terms and p = 1.
3.2. Validation Studies
The numerical results of the simply supported and clamped FGM sandwich rectangular plates and pure FGM plates are verified in this section. Table 3 presents the first five frequency parameters Ω = ωb2/h(1/109)1/2 for a type A FGM sandwich square plate with four edges simply supported, compared with the clamped boundary conditions. Geometric parameters and material parameters were set as follows: b/a = 1, h/a = 0.1, and p = 1 and 10. The thickness scheme 2–1–2 was adopted in this example. Compared with Table 3, the maximum error of the method given in this paper was less than 1%. Table 4 provides a comparison of frequency parameter Ω for pure FGM plates (type B, 0–1–0) with different power law exponents p. Geometric and material parameters were set as follows: b/a = 1 and h/a = 0.5. Table 4 shows four kinds of boundary conditions (SSSS, SCSC, SFSF, and SSSF). Based on the above study, four elastic boundary conditions and the classical boundary conditions are described as follow (taking the x = 0 edge as an example): clamped (C): ku = kv = kw = 1015; free (F): ku = kv = kw = 0; simply-supported (S): ku = 0, kv = kw = 1015; elastic restraint 1 (E1): ku = 1010, ku = kw = 1015; elastic restraint 2 (E2): kv = 1010, ku = kw = 1015; elastic restraint 3 (E3): kw =1010, ku = kv = 1015; and elastic restraint 4 (E4): ku = kv = kw = 1010. Table 3 and Table 4 shows that the present method was verified as being able to handle the study problems.

Table 3.
Comparison of frequency parameter Ω for type A FGM plates (2–1–2) with a different power law exponent p.

Table 4.
Comparison of frequency parameter Ω for type B FGM plates (0–1–0) with different a power-law exponent p.
3.3. Parametric Studies
Based on the above study, this section highlights the parametric study of three-dimensional functionally graded sandwich rectangular plates. Figure 4 gives variations of the first three frequency parameters Ω of the 3D FGM sandwich rectangular plate with respect to diverse elastic parameters. The elastic boundary conditions were as follows: the boundary of x = constant was defined as a fixed boundary; y = 0 as a free boundary; y = b as an elastic boundary; and only one type of elastic stiffness, which varied from 104 to 1016, and the remaining type of elastic stiffness was 0. The geometric and material parameters were consistent with Table 1 and Table 2. It can be seen from Figure 4 that the Ω of the plate increased gradually under the trend where the boundary stiffness coefficient increased. When the stiffness exceeded 1013, the stiffness coefficient hardly affected the vibration characteristics of the plate. Based on the above, four elastic boundary conditions and the classical boundary conditions were taken to be as follows (taking x = 0 edge as an example): clamped (C): ku = kv = kw = 1015; free (F): ku = kv = kw = 0; simply supported (S): ku = 0, kv = kw = 1015; elastic restraint 1 (E1): ku = 1010, ku = kw = 1015; elastic restraint 2 (E2): kv = 1010, ku = kw = 1015; elastic restraint 3 (E3): kw = 1010, ku = kv = 1015; and elastic restraint 4 (E4): ku = kv = kw = 1010. Figure 5 and Figure 6 present variations of the first two frequency parameters Ω of type A and type B 3D FGM sandwich rectangular plates with respect to different foundation parameters, where the foundation parameters were changed from 10−6 to 106. In Figure 5 and Figure 6, it can be seen that there was an active region for the foundation parameters, which significantly affected the vibration characteristics of the plate, and the influence of the foundation parameters could be neglected outside this region. Figure 7 and Figure 8 show changes in the first two frequency parameters Ω of type A and type B 3D FGM sandwich rectangular plates related to the power law exponent p. Different boundary conditions were considered, including two classical and two elastic boundary conditions. It is clear that there was an influence of p on vibration characteristics of the plate under different boundary conditions. For SSSS and CCCC, vibration characteristics initially decreased rapidly with the increased gradient coefficient, and then decreased slowly. For the elastic boundary conditions, the impact of p on the vibration behavior of the plate became more complex. For example, for the FGM plates with the E1E1E1E1 elastic boundary condition, the increased power law exponent caused an increase of the first-order frequency parameters, while second-order frequency parameters were the opposite. Because the vibration of the 3D FGM sandwich rectangular plate was insufficient, new vibration results are given in Table 5 and Table 6 that can provide reference data for a follow-up study. Table 5 and Table 6 show four classical boundaries (CCCC, SSSS, CFCF, and CSCF) and four elastic boundary conditions (E1E1E1E1, E2E2E2E2, E3E3E3E3, and E4E4E4E4). It is clear that increasing the thickness of the functionally graded layer reduced the Ω of the 3D FGM sandwich rectangular plate. This phenomenon can be directly seen from the modal shapes, as shown in Figure 9 and Figure 10.
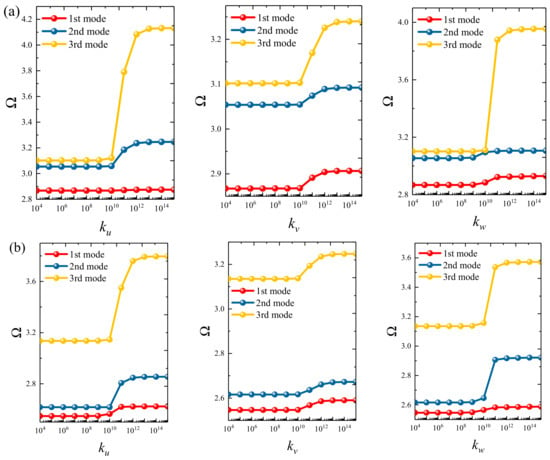
Figure 4.
Variation of the non-dimensional frequency parameter Ω of a 3D FG sandwich rectangular plate with respect to different elastic parameters: (a) type A and (b) type B.

Figure 5.
Variation of the non-dimensional frequency parameter Ω of a 3D FG sandwich rectangular plate of type A with respect to different foundation parameters: (a) CCCC and (b) E4E4E4E4.
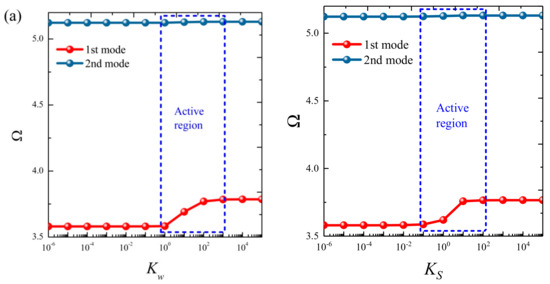

Figure 6.
Variation of the non-dimensional frequency parameter Ω of a 3D FG sandwich rectangular plate of type B with respect to different foundation parameters: (a) CCCC and (b) E4E4E4E4.
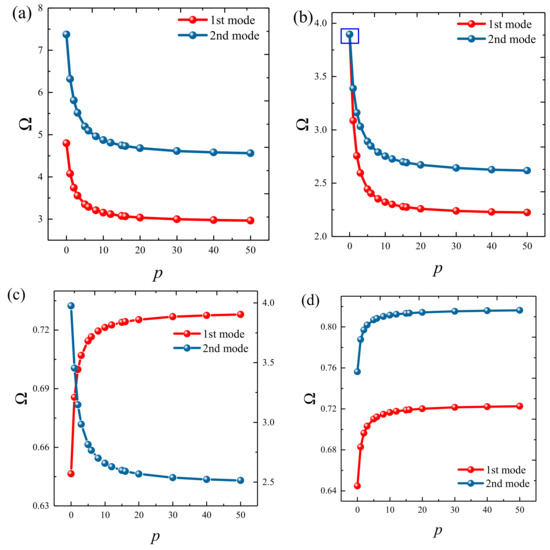
Figure 7.
Variation of the non-dimensional frequency parameter Ω of a 3D FG sandwich rectangular plate of type A with respect to different volume fraction indices: (a) CCCC, (b) SSSS, (c) E1E1E1E1, and (d) E4E4E4E4.
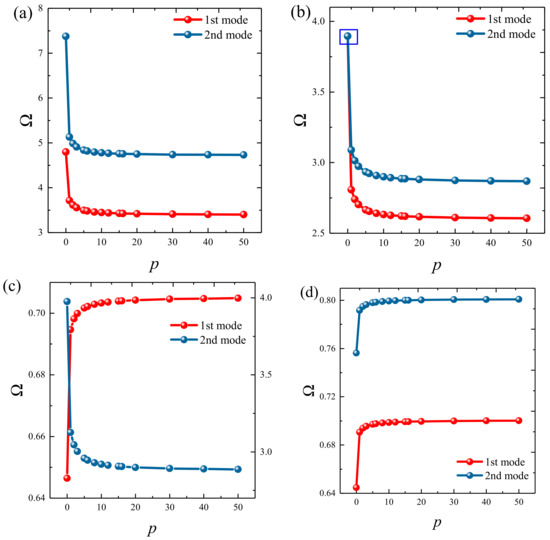
Figure 8.
Variation of the non-dimensional frequency parameter Ω of a 3D FG sandwich rectangular plate of type B with respect to different volume fraction indices: (a) CCCC, (b) SSSS, (c) E1E1E1E1, and (d) E4E4E4E4.

Table 5.
Frequency parameter Ω of the FGM plates of type A with different boundary conditions.

Table 6.
Frequency parameter Ω of the FGM plates of type B with different boundary conditions.
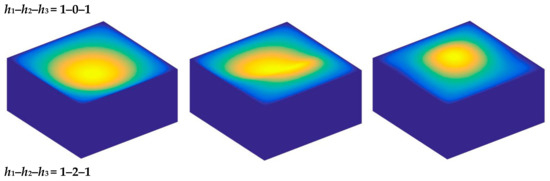

Figure 9.
Mode shapes of CCCC 3D FG sandwich rectangular plates of type A with different laminated distribution parameters.
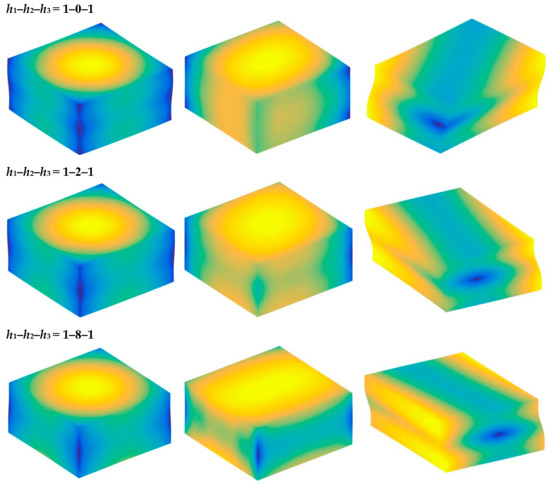
Figure 10.
Mode shapes of E4E4E4E4 3D FG sandwich rectangular plates of type B with different laminated distribution parameters.
4. Conclusions
We studied the vibration characteristics of FGM sandwich rectangular plates on an elastic foundation under general boundary constraints. According to the power-law distribution, it was assumed that the material characteristics vary continuously throughout the thickness range. This paper has studied four common kinds of sandwich FGM plates. The FGM plates’ displacement was represented as the superposition of a Fourier series and an auxiliary polynomial that was used to account for discontinuities of the original displacement function and its related derivatives. In order to overcome the problem of convergence caused by the discontinuity of boundary conditions, the authors have adopted an improved Fourier series based on a traditional Fourier series. The unknown Fourier series expansion coefficients were obtained using the Rayleigh–Ritz method. The technology of an artificial virtual spring could be used to imitate the general boundary constraints of FGM sandwich rectangular plates. It was concluded that the natural characteristics of the FGM sandwich rectangular plate with elastic properties were affected by different boundary conditions, foundation coefficients, material schemes, and elastic restraints. By comparing results existing in the available literature and results obtained by the method used in this paper, the accuracy of the method in predicting the vibration characteristics of FGM sandwich rectangular plate on an elastic foundation was verified. The influence of elastic parameters, foundation parameters, power-law exponents, and layer thickness ratios were studied in detail in this paper, and some important results have been obtained.
Author Contributions
Conceptualization, J.C. and R.Y.; methodology, R.Y.; software, Z.L.; validation, Z.L., T.Z. and R.Y.; formal analysis, J.C.; investigation, R.Y.; resources, J.C.; data curation, S.T.; writing—original draft preparation, R.Y.; writing—review and editing, O.G.; visualization, S.T.; supervision, O.G.; project administration, J.C.; funding acquisition, J.C.
Funding
This study was financially supported by the National Natural Science Foundation of China (grant no. 51109101/51779111/51622902), the Key University Science Research Project of Jiangsu Province (grant no. 17KJA416003), and the Key Laboratory Foundation of Jiangsu Province (grant no. CJ1601).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
References
- Tian, A.; Ye, R.; Chen, Y. A new higher order analysis model for sandwich plates with flexible core. J. Compos. Mater. 2016, 50, 949–961. [Google Scholar] [CrossRef]
- Cui, J.; Ye, R.; Zhao, N.; Wu, J.; Wang, M. Assessment on energy absorption of double layered and sandwich plates under ballistic impact. Thin-Walled Struct. 2018, 130, 520–534. [Google Scholar] [CrossRef]
- Tian, A.; Ye, R.; Ren, P.; Jiang, P.; Chen, Z.; Yin, X.; Zhao, Y. New higher-order models for sandwich plates with a flexible core and their accuracy assessment. Int. J. Struct. Stab. Dyn. 2019, 19, 1950024. [Google Scholar] [CrossRef]
- Zhao, N.; Ye, R.; Tian, A.; Cui, J.; Ren, P.; Wang, M. Experimental and numerical investigation on the anti-penetration performance of metallic sandwich plates for marine applications. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Kirchhoff, V.G. Uber das gleichgewicht und die bewegung einer elastischen scheibe. J. Fur Die Reine Und Angew. Math. 1850, 40, 51–88. [Google Scholar]
- Mohammadi, M.; Saidi, A.R.; Jomehzadeh, E. Levy solution for buckling analysis of functionally graded rectangular plates. Appl. Compos. Mater. 2010, 17, 81–93. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar]
- Ardestani, M.M.; Soltani, B.; Shams, S. Analysis of functionally graded stiffened plates based on FSDT utilizing reproducing kernel particle method. Compos. Struct. 2014, 112, 231–240. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Najafizadeh, M.M.; Heydari, H.R. Thermal buckling of functionally graded circular plates based on higher order shear deformation plate theory. Eur. J. Mech. A/Solids 2004, 23, 1085–1100. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory. Compos. Struct. 2008, 84, 132–146. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Petrolo, M.; Zappino, E. Recent developments on refined theories for beams with applications. Mech. Eng. Rev. 2015, 2, 14-00298. [Google Scholar] [CrossRef]
- Al Khateeb, S.A.; Zenkour, A.M. A refined four-unknown plate theory for advanced plates resting on elastic foundations in hygrothermal environment. Compos. Struct. 2014, 111, 240–248. [Google Scholar] [CrossRef]
- Zidi, M.; Tounsi, A.; Houari, M.S.A.; Bedia, E.A.A.; Bég, O.A. Bending analysis of FGM plates under hygro-thermo-mechanical loading using a four variable refined plate theory. Aerosp. Sci. Technol. 2014, 34, 24–34. [Google Scholar] [CrossRef]
- Bennoun, M.; Houari MS, A.; Tounsi, A. A novel five-variable refined plate theory for vibration analysis of functionally graded sandwich plates. Mech. Adv. Mater. Struct. 2016, 23, 423–431. [Google Scholar] [CrossRef]
- Benachour, A.; Tahar, H.D.; Atmane, H.A.; Tounsi, A.; SidAhmed, M. A four variable refined plate theory for free vibrations of functionally graded plates with arbitrary gradient. Compos. Part B Eng. 2011, 42, 1386–1394. [Google Scholar] [CrossRef]
- Hebali, H.; Tounsi, A.; Houari, M.S.A.; Bessaim, A.; Bedia, E.A. New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J. Eng. Mech. 2014, 140, 374–383. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Menshykova, M. Three-dimensional elasticity solution for sandwich panels with a functionally graded core. Compos. Struct. 2009, 87, 36–43. [Google Scholar] [CrossRef]
- Carrera, E. Evaluation of layerwise mixed theories for laminated plates analysis. AIAA J. 1998, 36, 830–839. [Google Scholar] [CrossRef]
- Yan, Y.; Pagani, A.; Carrera, E. Exact solutions for free vibration analysis of laminated, box and sandwich beams by refined layer-wise theory. Compos. Struct. 2017, 175, 28–45. [Google Scholar] [CrossRef]
- Komarsofla, M.K.; Salami, S.J.; Shakeri, M. Thermo elastic-up to yielding behavior of three dimensional functionally graded cylindrical panel based on a full layer-wise theory. Compos. Struct. 2019, 208, 261–275. [Google Scholar] [CrossRef]
- Kumar, P.; Srinivas, J. Vibration, buckling and bending behavior of functionally graded multi-walled carbon nanotube reinforced polymer composite plates using the layer-wise formulation. Compos. Struct. 2017, 177, 158–170. [Google Scholar] [CrossRef]
- Carrera, E. CZ requirements—Models for the two dimensional analysis of multilayered structures. Compos. Struct. 1997, 37, 373–383. [Google Scholar] [CrossRef]
- Mantari, J.L.; Ramos, I.A.; Carrera, E.; Petrolo, M. Static analysis of functionally graded plates using new non-polynomial displacement fields via Carrera Unified Formulation. Compos. Part B Eng. 2016, 89, 127–142. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 101, 332–340. [Google Scholar] [CrossRef]
- Bourada, M.; Kaci, A.; Houari MS, A.; Tounsi, A. A new simple shear and normal deformations theory for functionally graded beams. Steel Compos. Struct. 2015, 18, 409–423. [Google Scholar] [CrossRef]
- Belabed, Z.; Houari MS, A.; Tounsi, A.; Mahmoud, S.R.; Bég, O.A. An efficient and simple higher order shear and normal deformation theory for functionally graded material (FGM) plates. Compos. Part B Eng. 2014, 60, 274–283. [Google Scholar] [CrossRef]
- Zhen, W.; Wanji, C. Free vibration of laminated composite and sandwich plates using global–local higher-order theory. J. Sound Vib. 2006, 298, 333–349. [Google Scholar] [CrossRef]
- Shariyat, M.; Hosseini, S.H. Accurate eccentric impact analysis of the preloaded SMA composite plates, based on a novel mixed-order hyperbolic global–local theory. Compos. Struct. 2015, 124, 140–151. [Google Scholar] [CrossRef]
- Brischetto, S.; Carrera, E. Advanced mixed theories for bending analysis of functionally graded plates. Comput. Struct. 2010, 88, 1474–1483. [Google Scholar] [CrossRef]
- Cinefra, M.; Soave, M. Accurate vibration analysis of multilayered plates made of functionally graded materials. Mech. Adv. Mater. Struct. 2011, 18, 3–13. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.L.; Soares, C.M.M.; Soares, C.A.M. Vibration analysis of functionally graded material sandwich structures with passive damping. Compos. Struct. 2018, 183, 407–415. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Wahab, M.A.; Nguyen-Xuan, H. A moving Kriging meshfree method with naturally stabilized nodal integration for analysis of functionally graded material sandwich plates. Acta Mech. 2018, 229, 2997–3023. [Google Scholar] [CrossRef]
- Tounsi, A.; Houari, M.S.A.; Benyoucef, S.; Bedia, E. A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerosp. Sci. Technol. 2013, 24, 209–220. [Google Scholar] [CrossRef]
- Trinh, M.-C.; Kim, S.-E. Nonlinear thermomechanical behaviors of thin functionally graded sandwich shells with double curvature. Compos. Struct. 2018, 195, 335–348. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. Analysis of functionally graded sandwich plates using a higher-order layerwise theory. Compos. Part B Eng. 2018, 153, 325–336. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. A finite element formulation for thermally induced vibrations of functionally graded material sandwich plates and shell panels. Compos. Struct. 2017, 160, 877–886. [Google Scholar] [CrossRef]
- Daikh, A.A.; Megueni, A. Thermal buckling analysis of functionally graded sandwich plates. J. Therm. Stresses 2018, 41, 139–159. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Jorge, R.M.N.; Soares, C.M.M. Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Compos. Part B Eng. 2013, 44, 657–674. [Google Scholar] [CrossRef]
- Bourada, M.; Tounsi, A.; Houari, M.S.A.; Bedia, E.A. A new four-variable refined plate theory for thermal buckling analysis of functionally graded sandwich plates. J. Sandw. Struct. Mater. 2012, 14, 5–33. [Google Scholar] [CrossRef]
- Houari, S.A.M.; Tounsi, A.; Bég, O.A. Thermoelastic bending analysis of functionally graded sandwich plates using a new higher order shear and normal deformation theory. Int. J. Mech. Sci. 2013, 76, 102–111. [Google Scholar] [CrossRef]
- Li, Q.; VIu, P.; Kou, K.P. Three-dimensional vibration analysis of functionally graded material sandwich plates. J. Sound Vib. 2008, 311, 498–515. [Google Scholar] [CrossRef]
- Jalali, S.K.; Naei, M.H.; Poorsolhjouy, A. Thermal stability analysis of circular functionally graded sandwich plates of variable thickness using pseudo-spectral method. Mater. Des. 2010, 31, 4755–4763. [Google Scholar] [CrossRef]
- Ahmed Houari, M.S.; Benyoucef, S.; Mechab, I.; Tounsi, A.; Bedia, E.A. Two-Variable Refined Plate Theory for Thermoelastic Bending Analysis of Functionally Graded Sandwich Plates. J. Therm. Stresses 2011, 34, 315–334. [Google Scholar] [CrossRef]
- Thai, H.-T.; Nguyen, T.; Vo, T.P.; Lee, J. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. Eur. J. Mech. A/Solids 2014, 45, 211–225. [Google Scholar] [CrossRef]
- Nguyen, V.-H.; Nguyen, T.; Thai, H.; Vo, T.P. A new inverse trigonometric shear deformation theory for isotropic and functionally graded sandwich plates. Compos. Part B Eng. 2014, 66, 233–246. [Google Scholar] [CrossRef]
- Hadji, L.; Hassen, A.A.; Tounsi, A.; Mechab, I.; Bedia, E.A.A. Free vibration of functionally graded sandwich plates using four-variable refined plate theory. Appl. Math. Mech. 2011, 32, 925–942. [Google Scholar] [CrossRef]
- Merdaci, S.; Tounsi, A.; Houari, M.S.A.; Mechab, I.; Hebali, H.; Benyoucef, S. Two new refined shear displacement models for functionally graded sandwich plates. Arch. Appl. Mech. 2011, 81, 1507–1522. [Google Scholar] [CrossRef]
- Neves, A.M.A.; AFerreira, J.M.; Carrera, E.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M.M. Static analysis of functionally graded sandwich plates according to a hyperbolic theory considering Zig-Zag and warping effects. Adv. Eng. Softw. 2012, 52, 30–43. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N. Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with constrained viscoelastic core. J. Sound Vib. 2006, 295, 294–316. [Google Scholar] [CrossRef]
- Mahi, A.; Bedia, E.A.A.; Tounsi, A. A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl. Math. Model. 2015, 39, 2489–2508. [Google Scholar] [CrossRef]
- Apetre, N.A.; Sankar, B.V.; Ambur, D.R. Low-velocity impact response of sandwich beams with functionally graded core. Int. J. Solids Struct. 2006, 43, 2479–2496. [Google Scholar] [CrossRef]
- Venkataraman, S.; Sankar, B.V. Elasticity Solution for Stresses in a Sandwich Beam with Functionally Graded Core. AIAA J. 2015, 41, 2501–2505. [Google Scholar] [CrossRef]
- Venkataraman, S.; Sankar, B. Analysis of sandwich beams with functionally graded core. AIAA J. 2013, 16–19. [Google Scholar] [CrossRef]
- Vo, T.P.; Thai, H.; Nguyen, T.; Maheri, A.; Lee, J. Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng. Struct. 2014, 64, 12–22. [Google Scholar] [CrossRef]
- Loja, M.A.R.; Soares, C.M.M.; Barbosa, J.I. Analysis of functionally graded sandwich plate structures with piezoelectric skins, using B-spline finite strip method. Compos. Struct. 2013, 96, 606–615. [Google Scholar] [CrossRef]
- Ye, T.; Jin, G.; Chen, Y.; Ma, X.; Su, Z. Free vibration analysis of laminated composite shallow shells with general elastic boundaries. Compos. Struct. 2013, 106, 470–490. [Google Scholar] [CrossRef]
- Wang, Q.; Xiaohui, C.; Bin, Q.; Qian, L.; Jinyuan, T. A semi-analytical method for vibration analysis of functionally graded (FG) sandwich doubly-curved panels and shells of revolution. Int. J. Mech. Sci. 2017, 134 (Suppl. C), 479–499. [Google Scholar] [CrossRef]
- El Meiche, N.; Tounsi, A.; Ziane, N.; lMechab, I.; Bedi, E. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate. Int. J. Mech. Sci. 2011, 53, 237–247. [Google Scholar] [CrossRef]
- Cui, J.; Li, Z.; Ye, R.; Jiang, W.; Tao, S. A Semianalytical Three-Dimensional Elasticity Solution for Vibrations of Orthotropic Plates with Arbitrary Boundary Conditions. Shock Vib. 2019, 2019, 1237674. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Ehteshami, H. Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, F.; Wang, A.; Shuai, C.; Tang, J.; Wang, Q. Vibration behavior of the functionally graded porous (FGP) doubly-curved panels and shells of revolution by using a semi-analytical method. Compos. Part B Eng. 2019, 157, 219–238. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).