Current-Induced Changes of Surface Morphology in Printed Ag Thin Wires
Abstract
1. Introduction
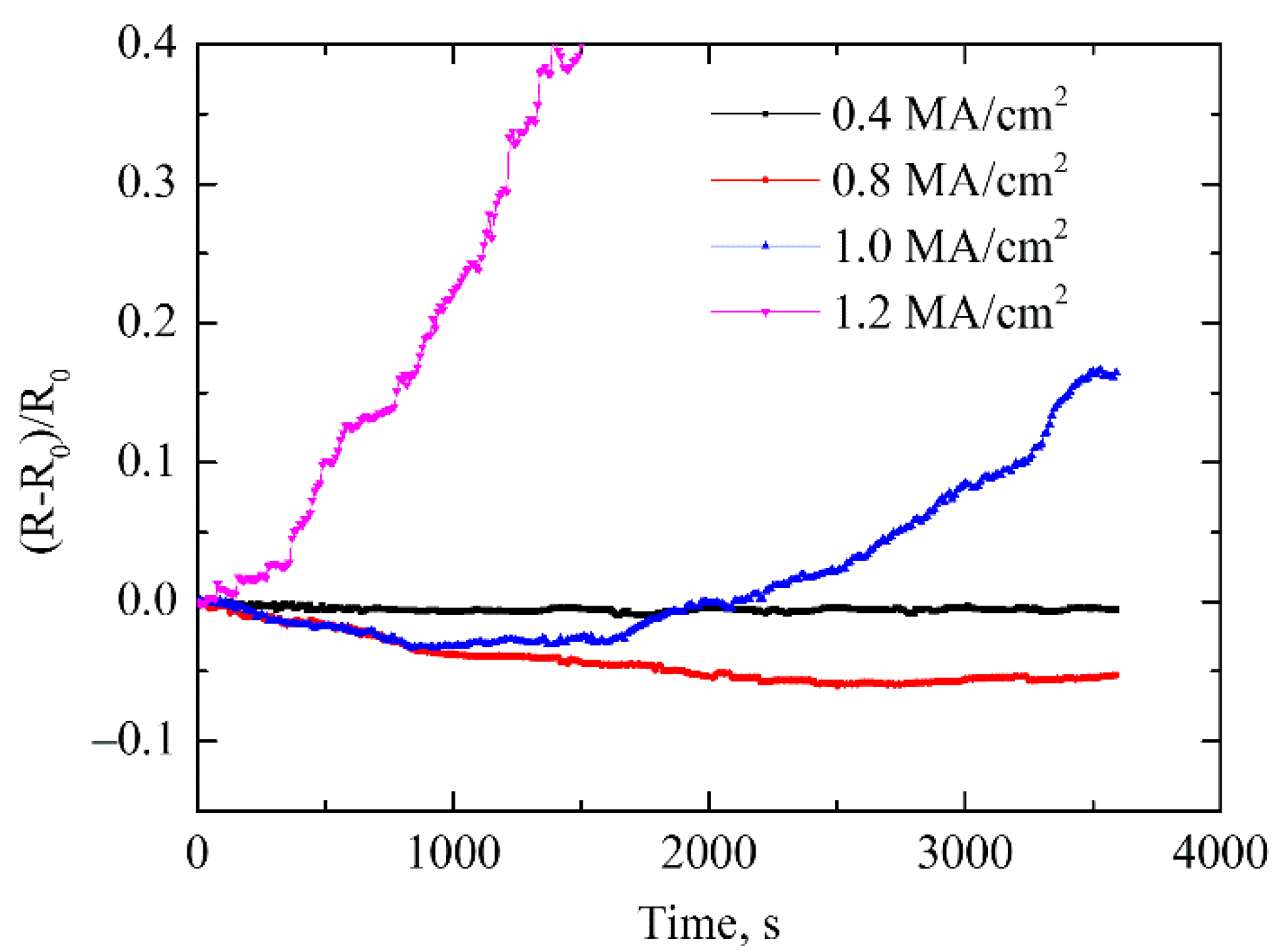
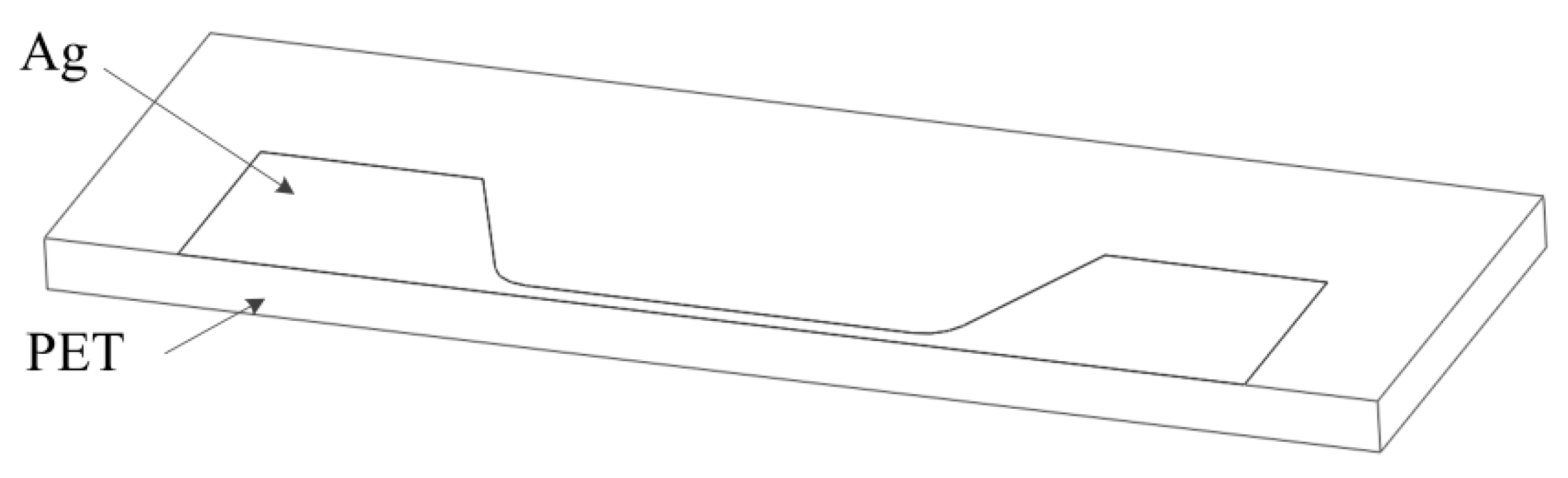
2. Experimental Procedures and Results
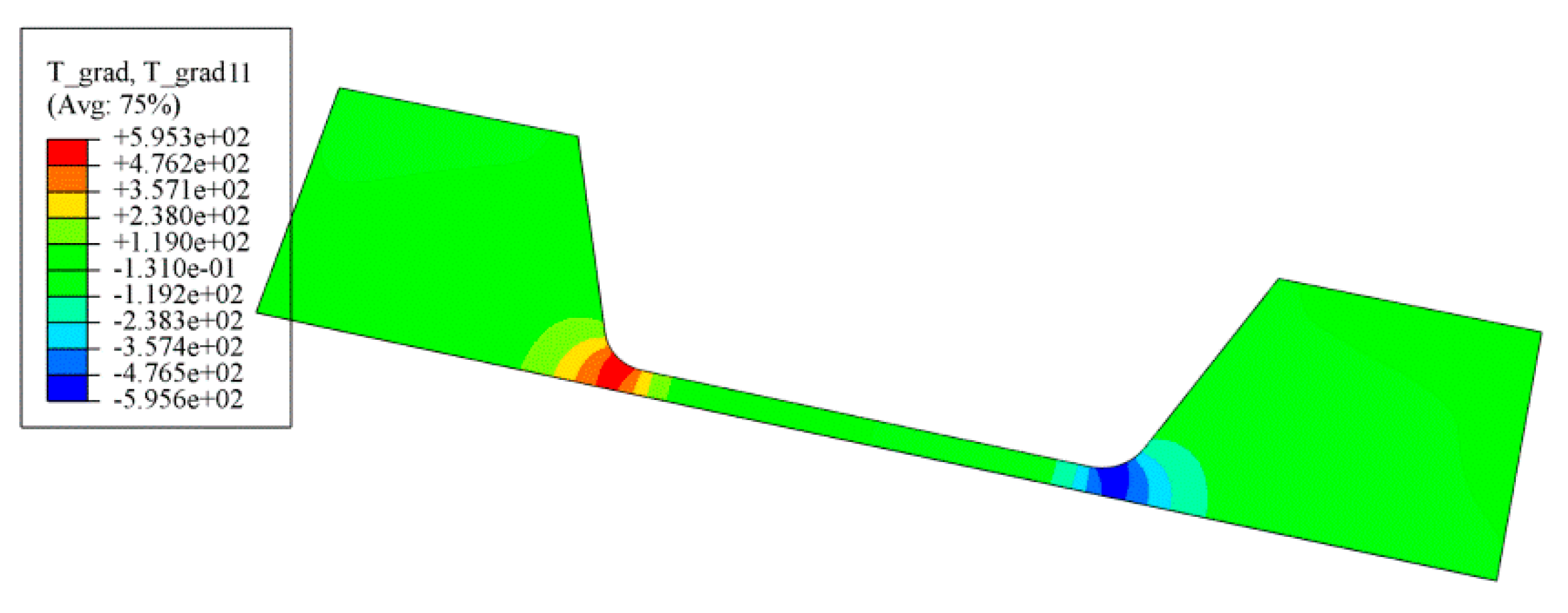
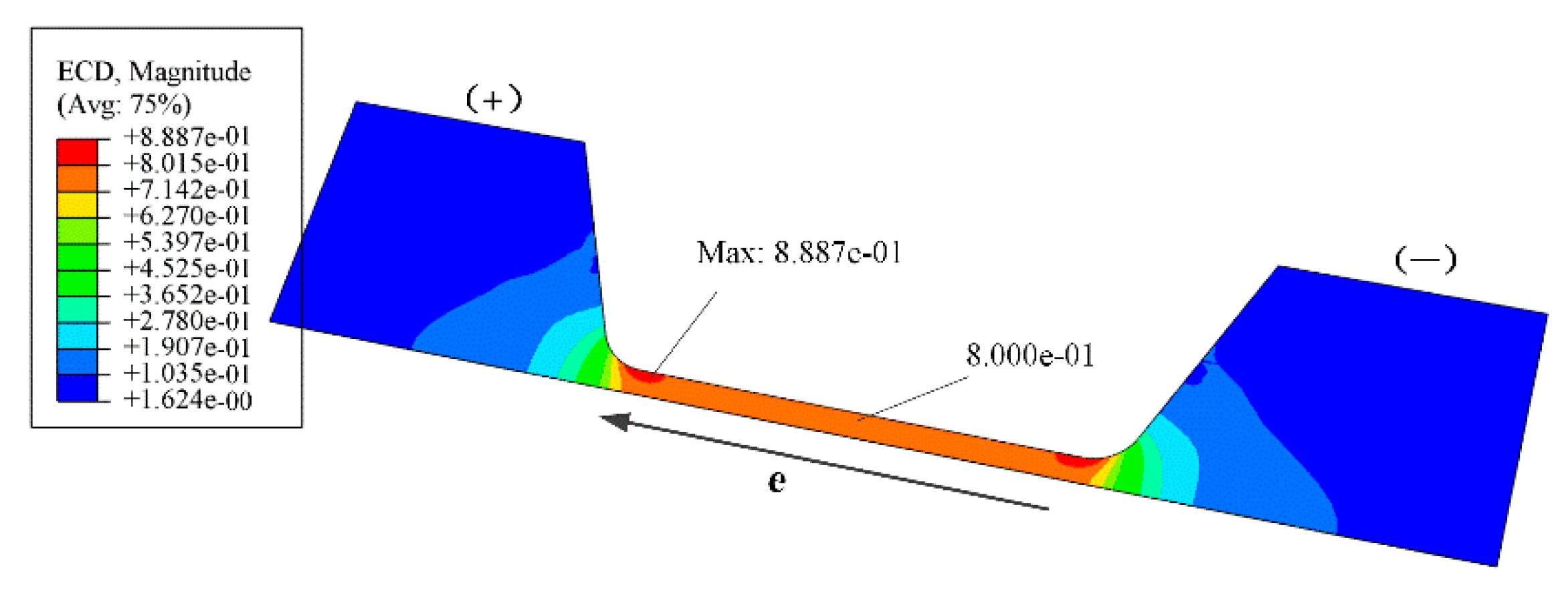
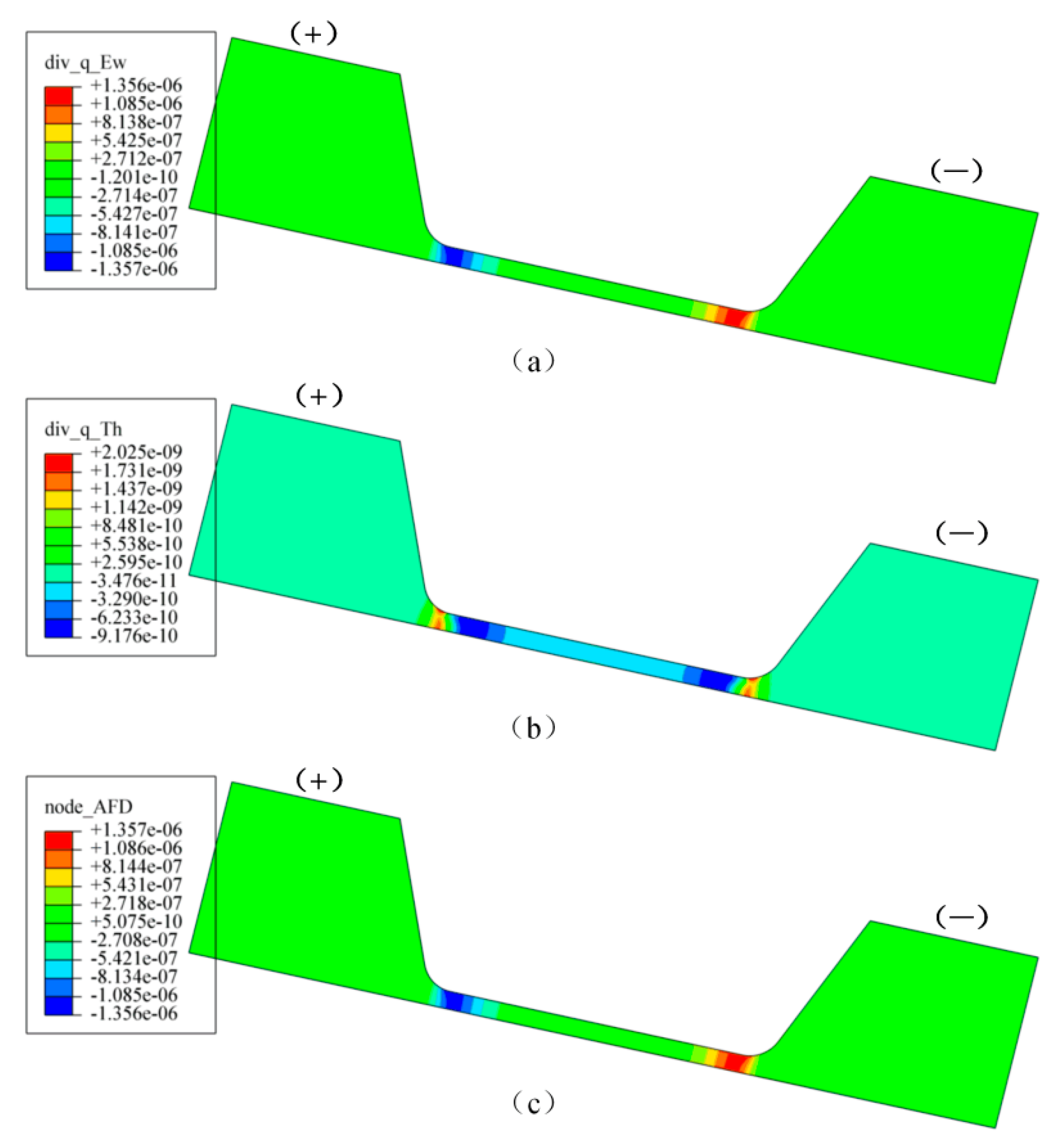
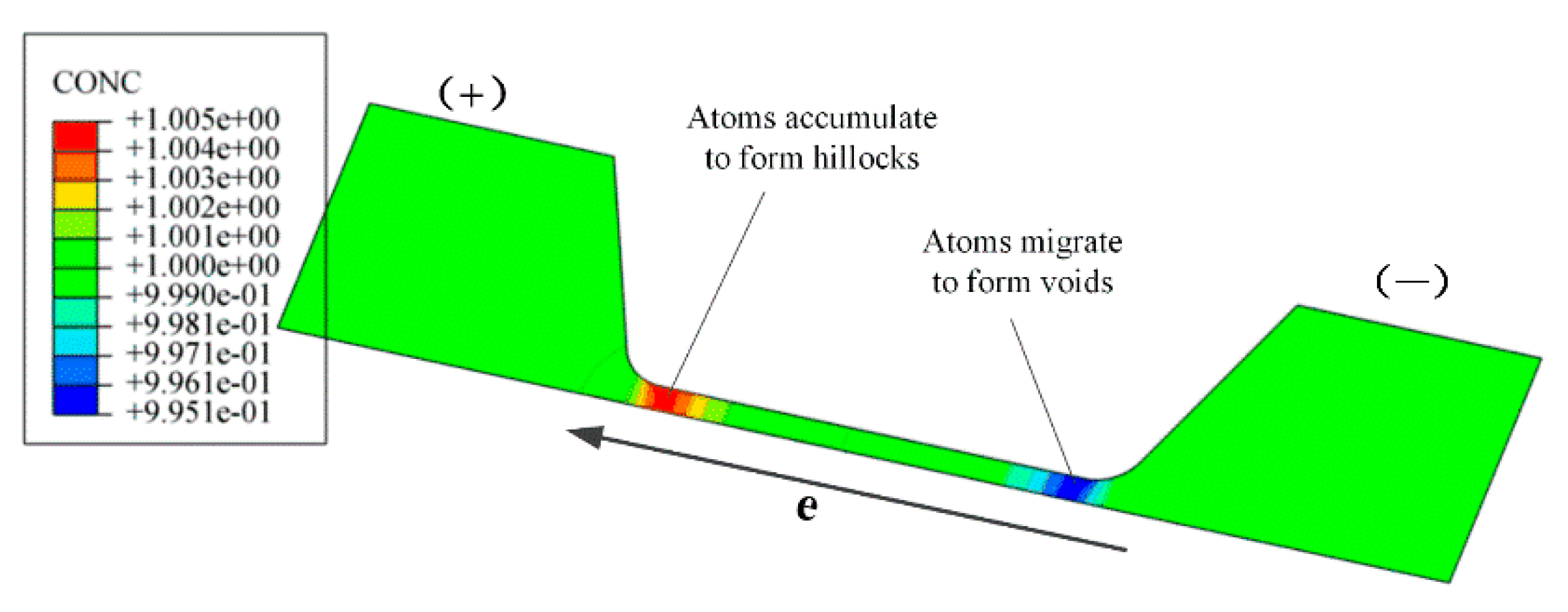
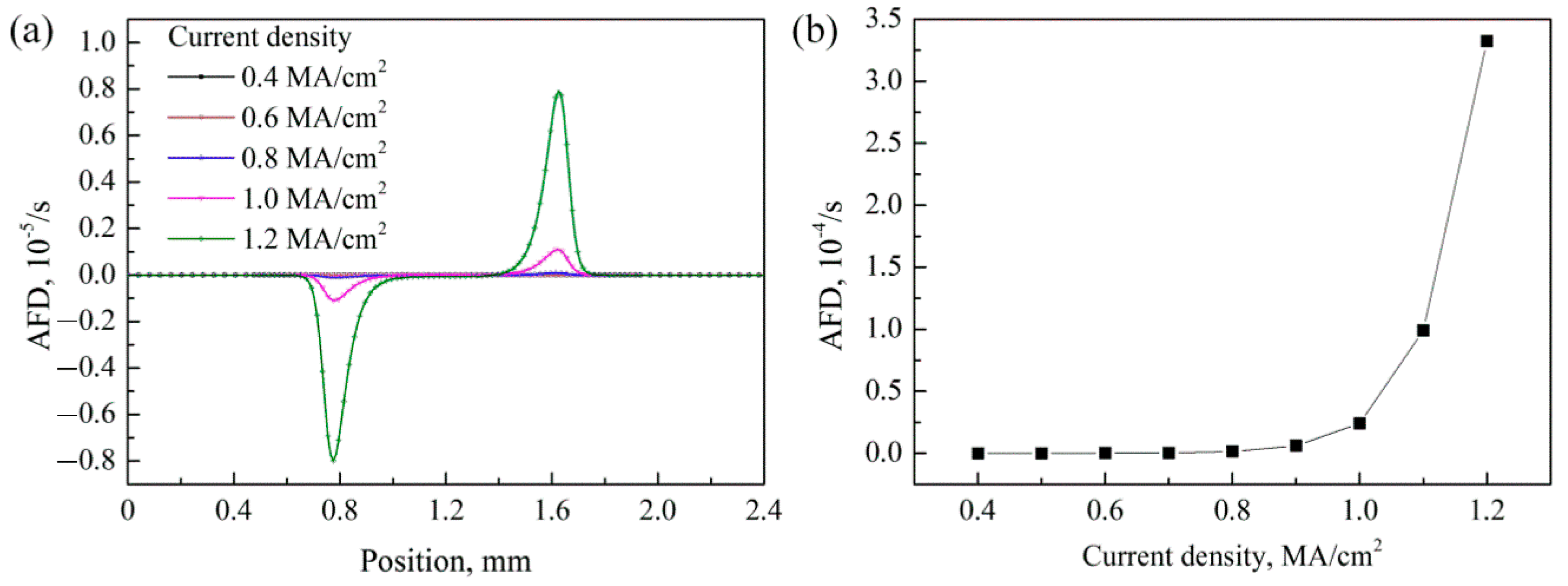
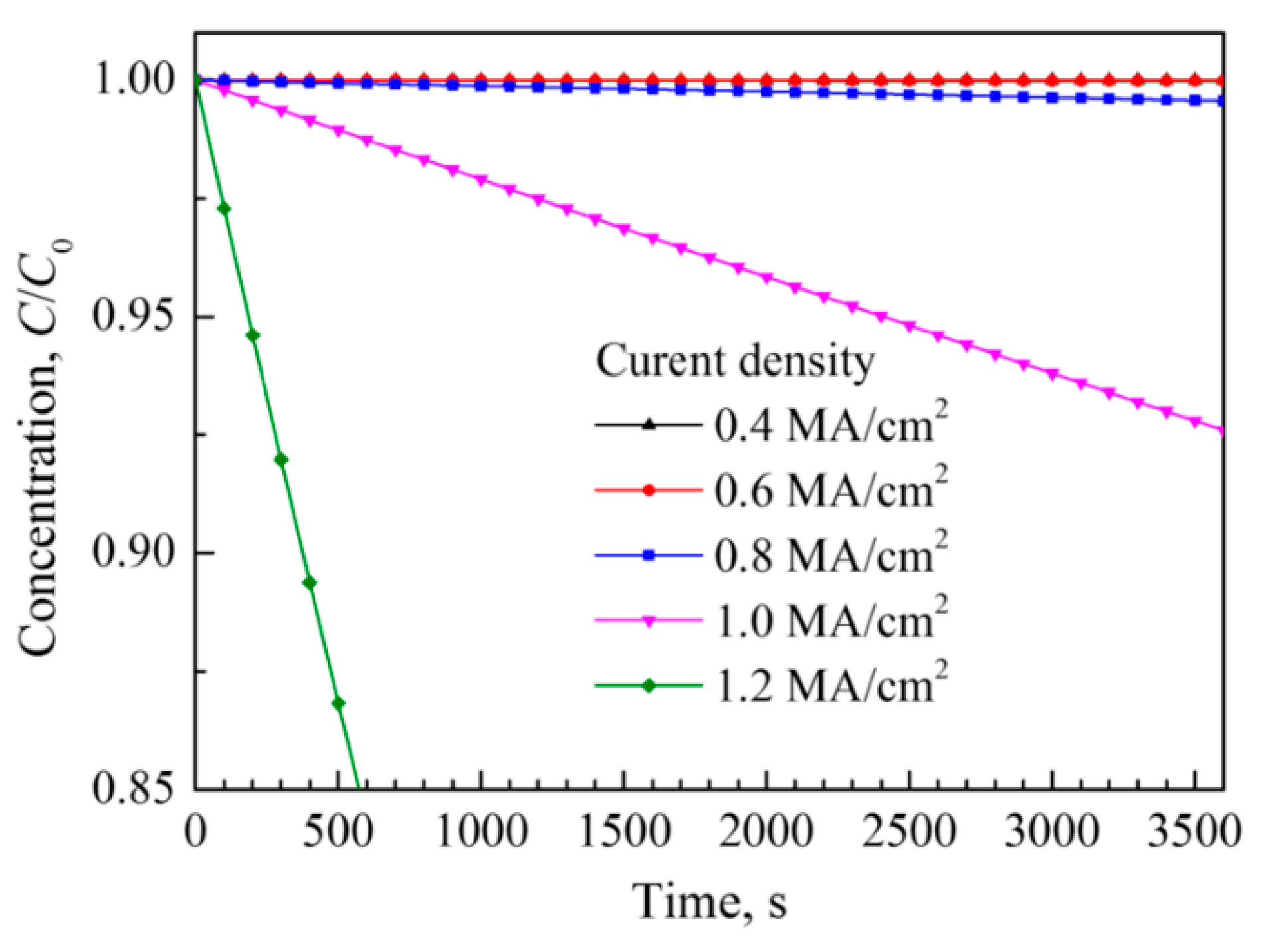
3. Atomic Migration and Simulation
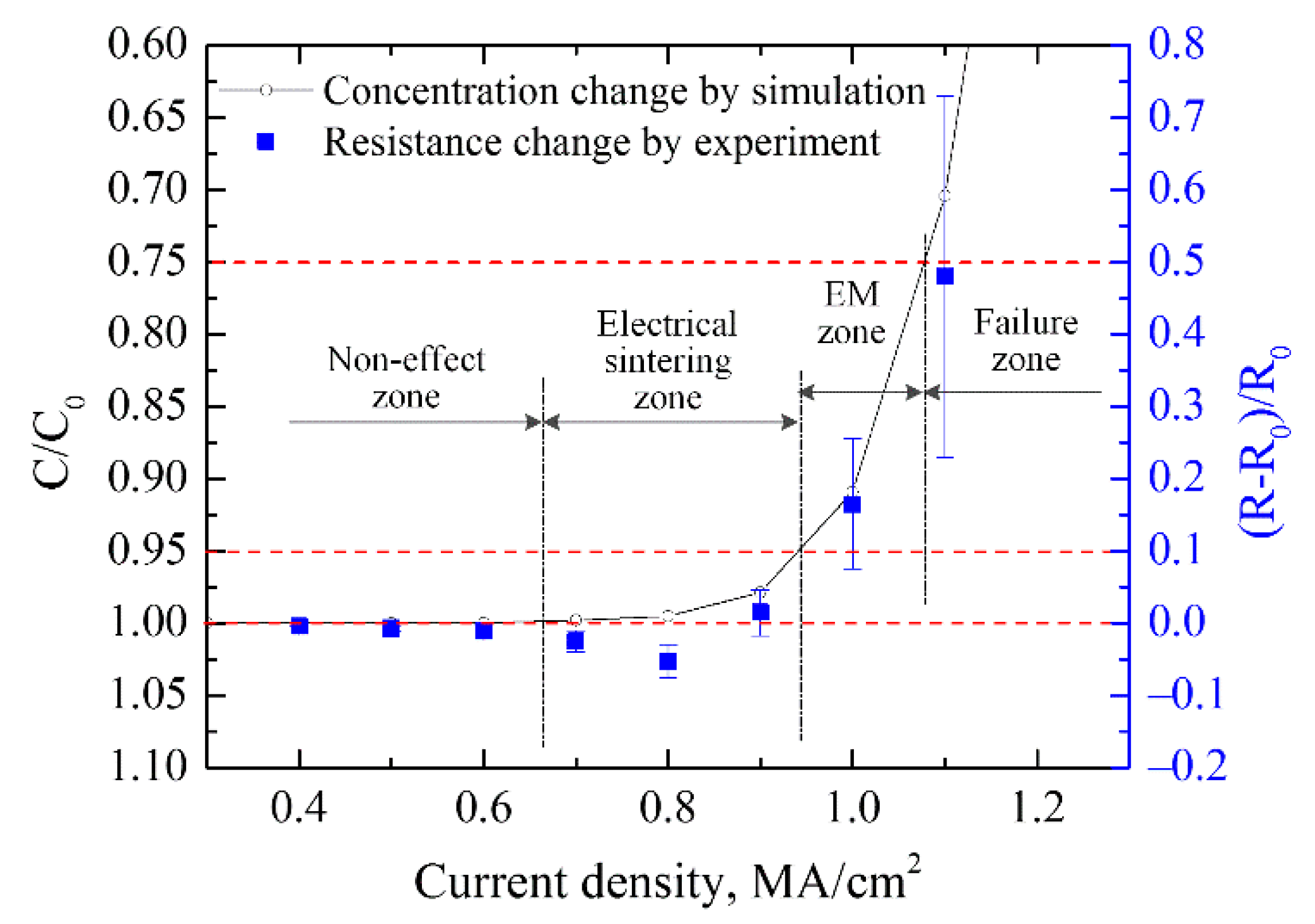
4. Discussion
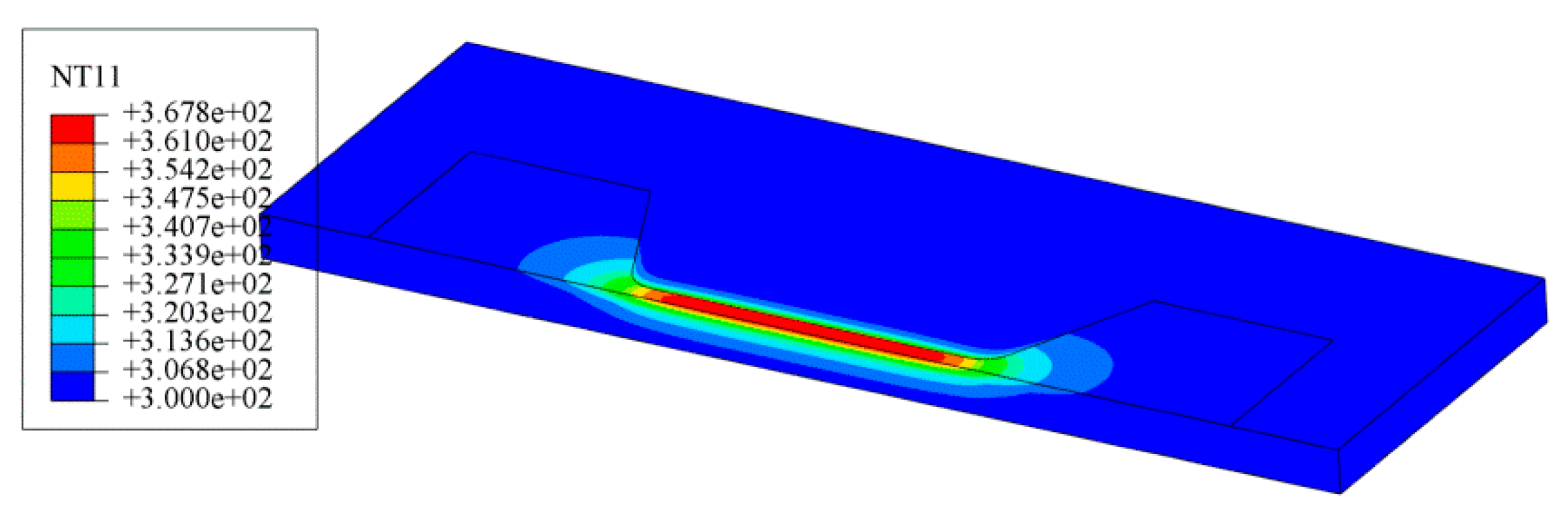
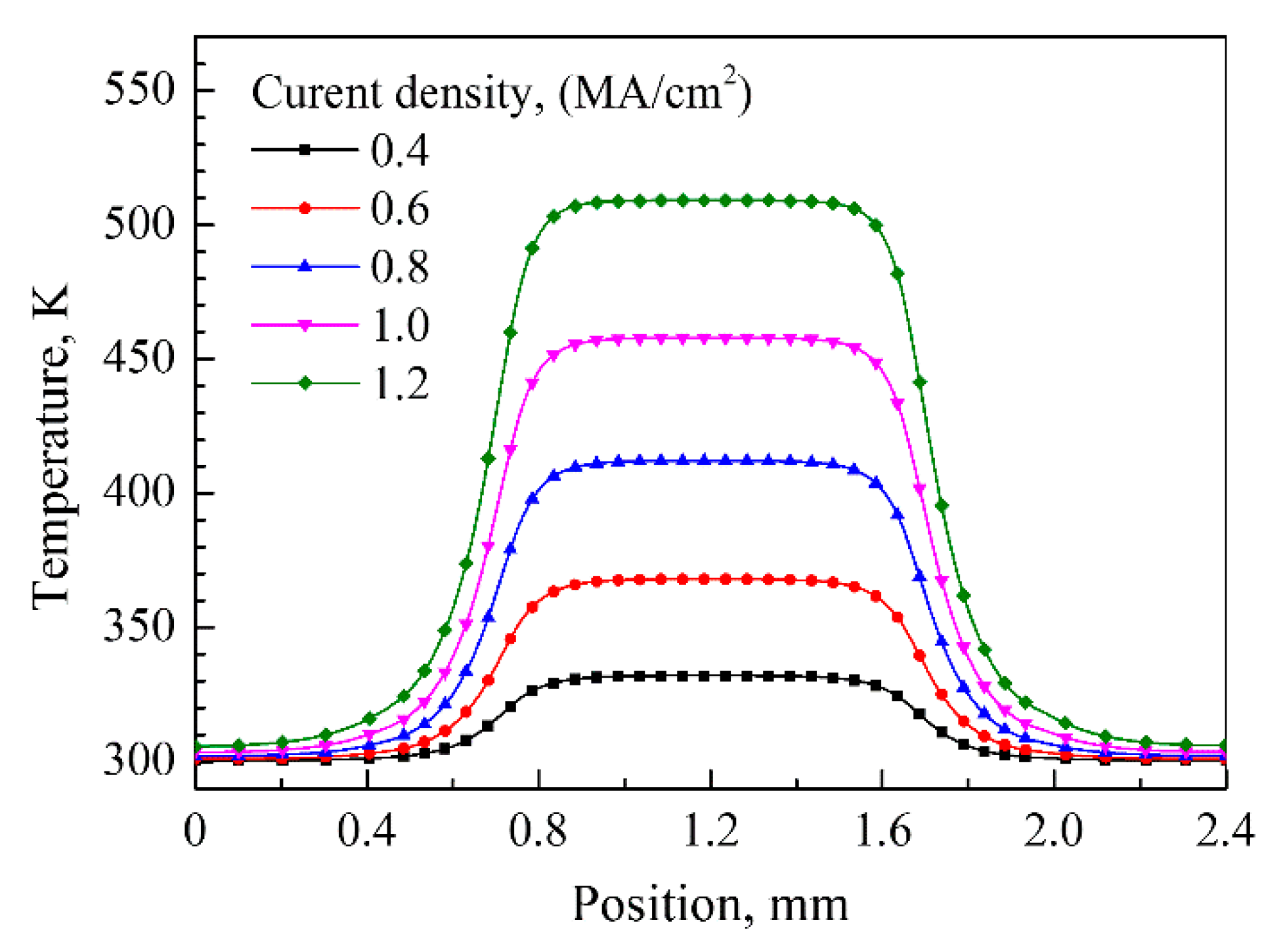
4.1. Joule Heating of Silver Wire under Current Supply
4.2. Atomic Migration of Silver Wire by EM and TM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arafat, Y.; Dutta, I.; Panat, R. On the deformation mechanisms and electrical behavior of highly stretchable metallic interconnects on elastomer substrates. Appl. Phys. 2016, 120, 62–810. [Google Scholar] [CrossRef]
- Sim, G.D.; Won, S.; Jin, C.; Park, I.; Lee, S.B.; Vlassak, J. Improving the stretchability of as-deposited Ag coatings on poly-ethylene-terephthalate substrates through use of an acrylic primer. Appl. Phys. 2011, 109, 1984–1989. [Google Scholar] [CrossRef]
- Shen, W.F.; Zhang, X.P.; Huang, Q.J.; Xu, Q.S.; Song, W.J. Preparation of solid silver nanoparticles for inkjet printed flexible electronics with high conductivity. Nanoscale 2014, 6, 1622–1628. [Google Scholar] [PubMed]
- Kim, B.J.; Haas, T.; Friederich, A.; Lee, J.H.; Nam, D.H.; Binder, J.R.; Bauer, W.; Choi, I.S.; Joo, Y.C.; Gruber, P.A. Improving mechanical fatigue resistance by optimizing the nanoporous structure of inkjet-printed Ag electrodes for flexible devices. Nanotechnology 2014, 25, 125706. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Yao, W.; Zeng, P.; Li, X.; Wang, H.J.; Liu, L.; Feng, Y.; Luo, C.S.; Wu, W. All-printed, low-cost, tunable sensing range strain sensors based on Ag nanodendrite conductive inks for wearable electronics. J. Mater. Chem. C 2019, 7, 809–818. [Google Scholar] [CrossRef]
- Chen, S.Y.; Guan, Y.W.; Li, Y.; Yan, X.W.; Ni, H.T.; Li, L. A water based silver nanowire ink for large-scale flexible transparent conductive films and touch screens. J. Mater. Chem. C 2017, 5, 2404–2414. [Google Scholar] [CrossRef]
- Cui, Z.; Han, Y.; Huang, Q.; Dong, J.; Zhu, Y. Electrohydrodynamic printing of silver nanowires for flexible and stretchable electronics. Nanoscale 2018, 10, 6806–6811. [Google Scholar] [CrossRef] [PubMed]
- Rosati, G.; Ravarotto, M.; Scaramuzza, M.; Toni, A.D.; Paccagnella, A. Silver nanoparticles inkjet-printed flexible biosensor for rapid label-free antibiotic detection in milk. Sens. Actuators B 2019, 280, 280–289. [Google Scholar] [CrossRef]
- Lin, W.H.; Ouyang, F.Y. Electromigration behavior of screen-printing silver nanoparticles interconnects. JOM 2019, 71, 3084–3093. [Google Scholar] [CrossRef]
- Batra, N.M.; Syed, A.; Costa, P.M.F.J. Current-induced restructuring in bentsilvernanowires. Nanoscale 2019, 11, 3606–3618. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Fan, X.; Zhang, G. General coupling model for electromigration and one-dimensional numerical solutions. J. Appl. Phys. 2019, 125, 105101. [Google Scholar] [CrossRef]
- Xu, X.; Lu, Y.; Tang, C.; Sun, Q.; Huang, F. A simple technique to prevent electromigration damage in printed Ag thin wires. Mater. Lett. 2018, 225, 21–23. [Google Scholar] [CrossRef]
- Tan, C.M.; Hou, Y.; Li, W. Revisit to the finite element modeling of electromigration for narrow interconnects. J. Appl. Phys. 2007, 102, 150–161. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Electromigration analysis of solder joints under ac load: A mean time to failure model. J. Appl. Phys. 2012, 111, 1587–1594. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Computational damage mechanics of electromigration and thermomigration. J. Appl. Phys. 2013, 114, 143–151. [Google Scholar] [CrossRef]
- Hauder, M.; Gstöttner, J.; Hansch, W.; Schmitt-Landsiedel, D. Scaling properties and electromigration resistance of sputtered Ag metallization lines. Appl. Phys. Lett. 2001, 78, 838–840. [Google Scholar] [CrossRef]
- Chatterjee, A.; Bai, T.; Edler, F.; Tegenkamp, C.; Weide-Zaage, K.; Herbert, P. Electromigration and morphological changes in Ag nanostructures. J. Phys. Condens. Mat. 2018, 30, 084002. [Google Scholar] [CrossRef] [PubMed]
- Jang, K.T.; Hwang, J.S.; Park, Y.J.; Lee, J.C.; Kim, N.R.; Joo, Y.C. Current-induced morphological evolution and reliability of Ag interconnects fabricated by a printing method based on nanoparticles. RSC Adv. 2017, 7, 9719–9723. [Google Scholar] [CrossRef]
- Weide-Zaage, K.; Kashanchi, F.; Aubel, O. Simulation of migration effects in nanoscaled copper metallizations. Microelectron. Reliab. 2008, 48, 1398–1402. [Google Scholar] [CrossRef]


| Samples | Current Density (MA/cm2) | Current Supply Time (h) | Resistance Change | Surface Morphology |
|---|---|---|---|---|
| I | 0.4 | 1 | −0.4% | Unchanged |
| II | 0.8 | 1 | −5.3% | Densification |
| III | 1.0 | 1 | 16.5% | Voids and hillocks |
| IV | 1.2 | less than 1 | +∞ | Open circuit |
| Parameters | Unit | Ag | PET |
|---|---|---|---|
| Density | g/cm3 | 10.49 | 1.33 |
| Young’s Modulus | GPa | 73.2 | 4 |
| Poisson’s Ratio | - | 0.38 | 0.3 |
| Thermal Conductivity | W/(m·K) | 429 | 0.2 |
| Electrical Conductivity | S/m | 6.3 × 107 | 0 |
| Specific Heat | J/(g·K) | 240 | 1200 |
| Emissivity | - | 0.04 | 0.8 |
| Parameters | Value |
|---|---|
| Ea | 0.9 eV |
| D0 | 1.71 × 10−5 m2/s |
| Z* | −21 |
| Q* | −0.0867 eV |
| Ω | 1.71 ×10−29 m3/atom |
| ρ0 | 1.6 × 10−7 Ω·m |
| α | 3.8 × 10−3 1/K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Lu, Y.; Tang, C.; Song, H.; Li, C.; Zuo, C. Current-Induced Changes of Surface Morphology in Printed Ag Thin Wires. Materials 2019, 12, 3288. https://doi.org/10.3390/ma12203288
Sun Q, Lu Y, Tang C, Song H, Li C, Zuo C. Current-Induced Changes of Surface Morphology in Printed Ag Thin Wires. Materials. 2019; 12(20):3288. https://doi.org/10.3390/ma12203288
Chicago/Turabian StyleSun, Quan, Yebo Lu, Chengli Tang, Haijun Song, Chao Li, and Chuncheng Zuo. 2019. "Current-Induced Changes of Surface Morphology in Printed Ag Thin Wires" Materials 12, no. 20: 3288. https://doi.org/10.3390/ma12203288
APA StyleSun, Q., Lu, Y., Tang, C., Song, H., Li, C., & Zuo, C. (2019). Current-Induced Changes of Surface Morphology in Printed Ag Thin Wires. Materials, 12(20), 3288. https://doi.org/10.3390/ma12203288





