Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls
Abstract
1. Introduction
2. Research Programme
- to use the most common materials in Poland to erect masonry structures,
- to use the minimum amount of reinforcement,
- to use squat walls with an h/l ratio close to real structures,
- to build a unique test stand to perform tests on shearing and compression at the same time in a partially fixed static scheme.
- ceramic solid brick (CB), calcium-silicate masonry units (Ca-Si) from group I, and AAC masonry units from 600 density class,
- cement-lime mortar with a cement:lime:sand ratio of 1:1:6 to make CB walls and the system mortar for thin joints for Ca-Si and AAC walls,
- two types of reinforcement for bed joints in walls made of solid brick: smooth rebars with a diameter of 6 mm and made of stainless steel and structural reinforcement in the form of steel, galvanized trusses, in which the strips were made of steel rebars with a diameter of 5 mm and the struts were made of rebars with a diameter of 3.75 mm as in Figure 1a,
- plastic meshes and steel trusses for thin joints as in Figure 1b.
2.1. Masonry Walls Made of Clay Brick
2.2. Masonry Walls Made of Calcium-Silicate (Ca-Si) Masonry Units
2.3. Masonry Walls Made of Autoclaved Aerated Concrete (AAC) Masonry Units
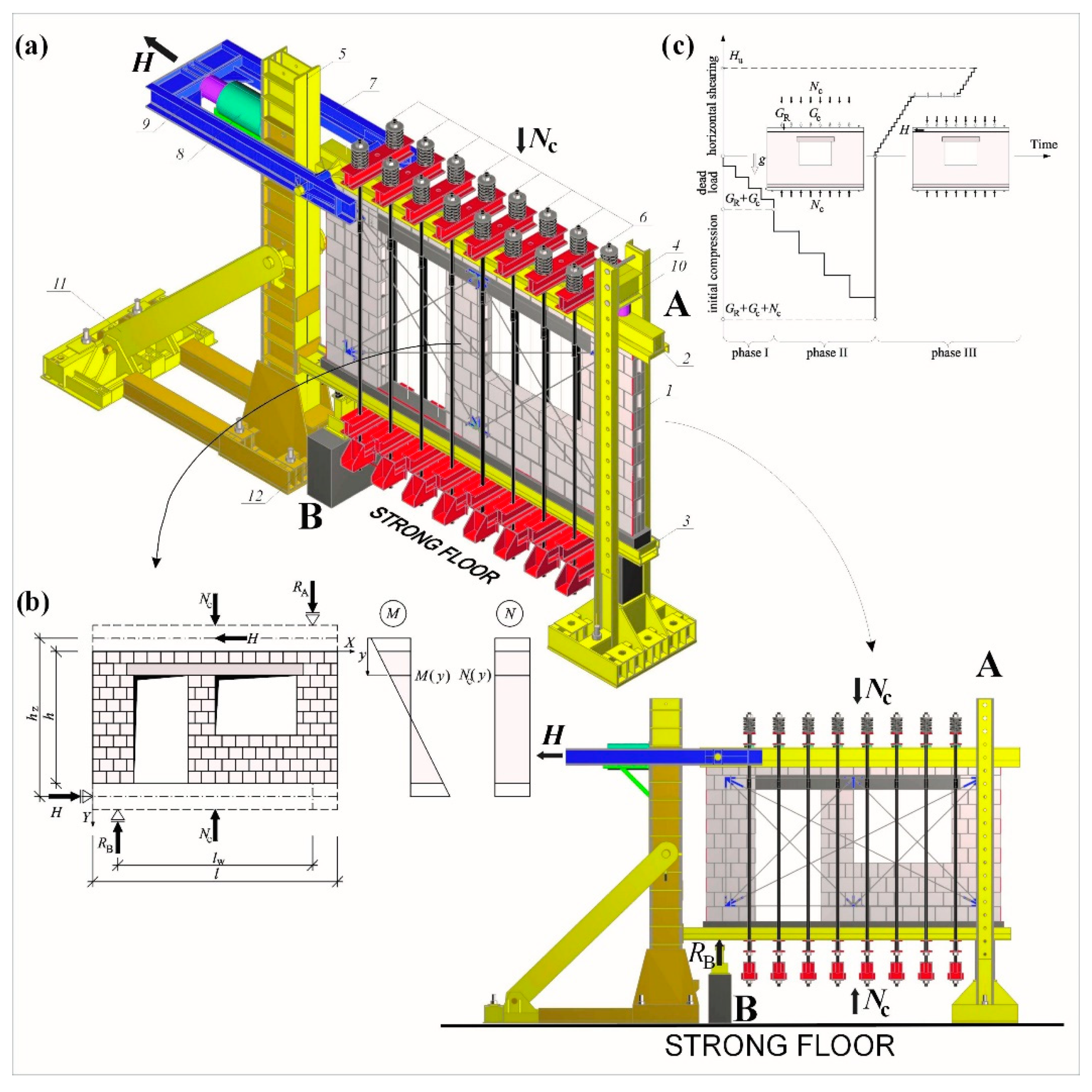
3. Test Stand and Testing Technique
ljc = lj0 + Δj, lgc = lg0 + Δg,
lcc = lc0 + Δc, lhc = lh0 + Δh.
4. Test Results
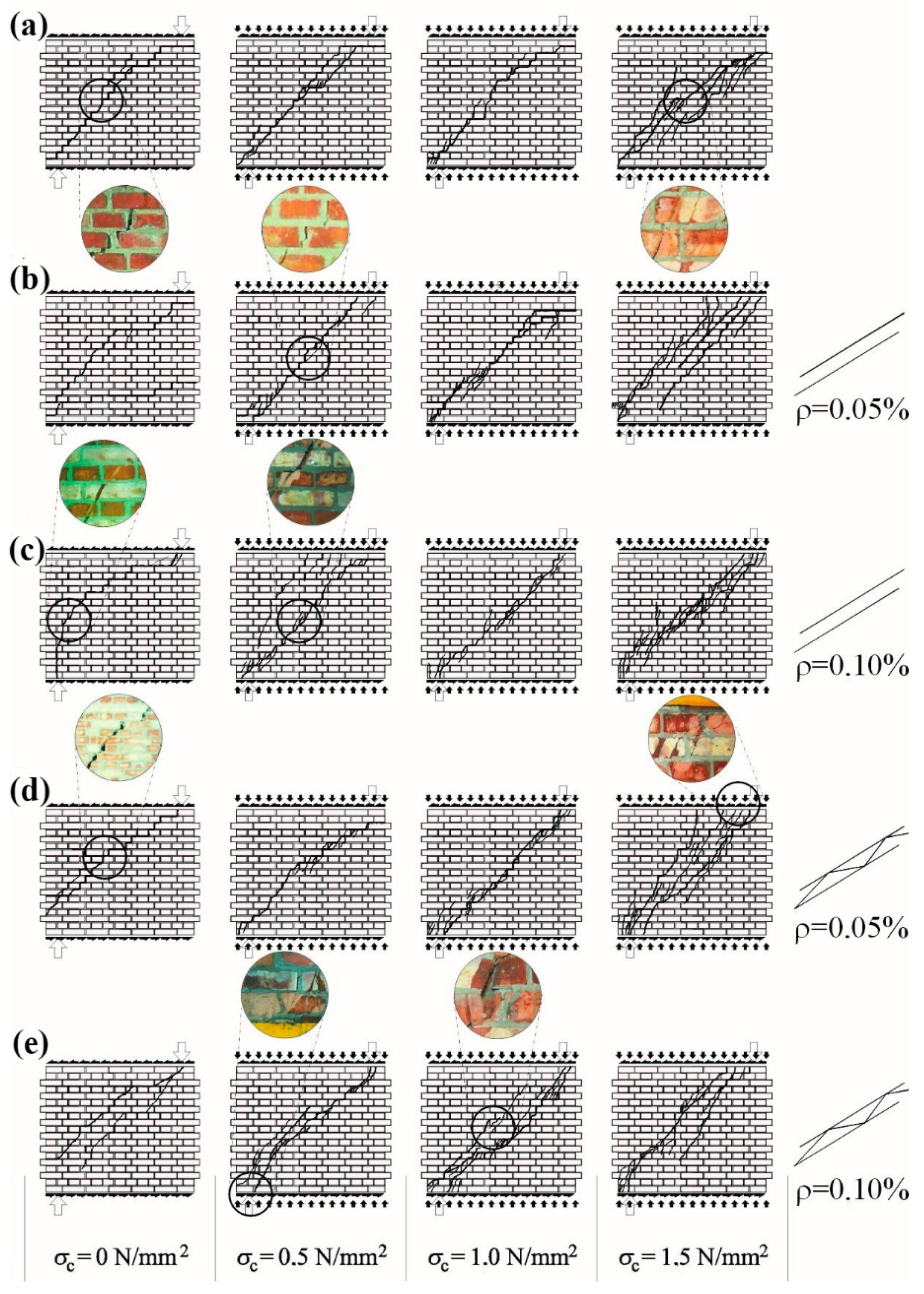
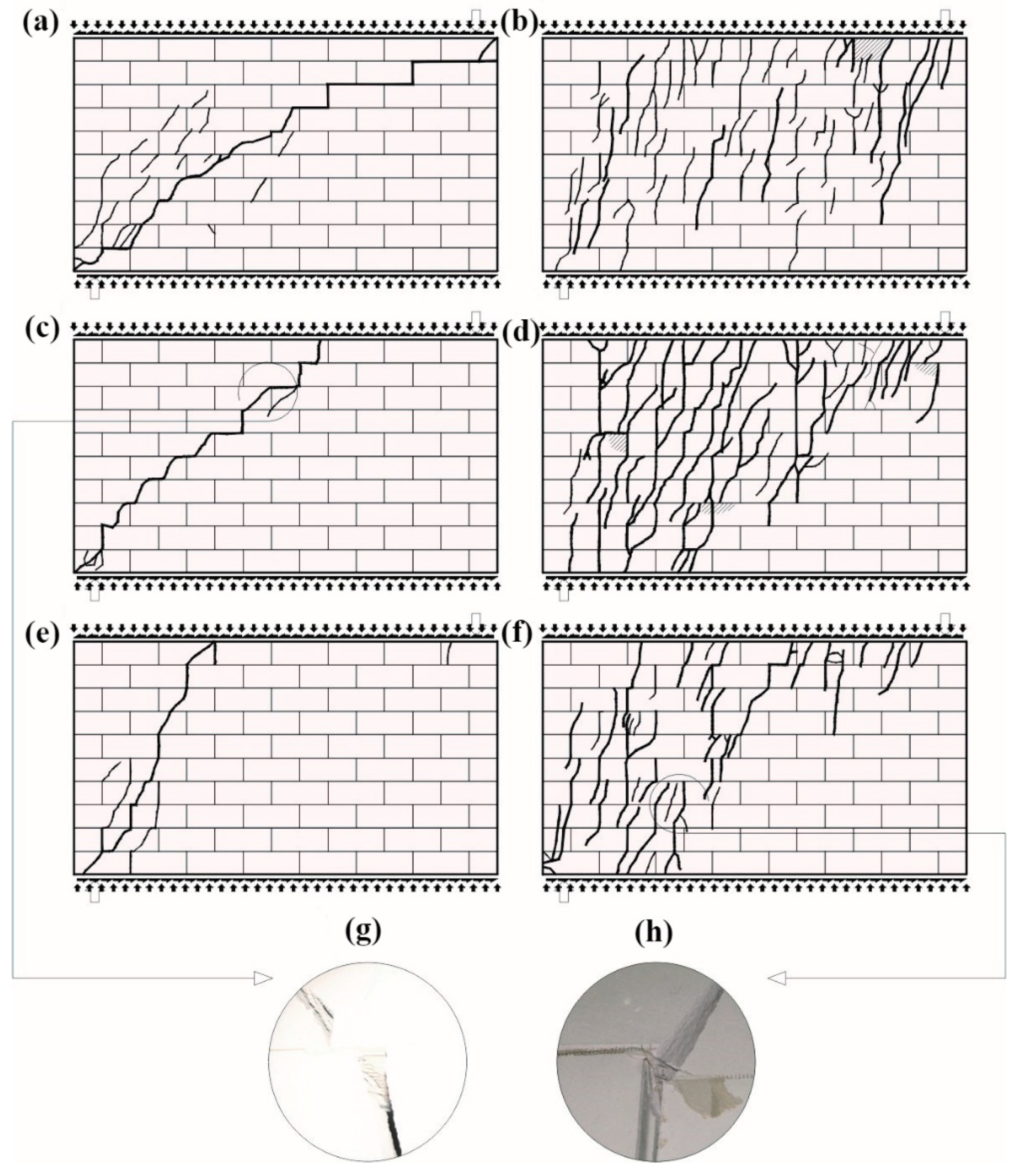
4.1. Morphology of Cracks in Walls
4.1.1. Solid Brick Walls
4.1.2. Walls Made of Silicate Masonry Units
4.1.3. Walls Made of AAC Masonry Units
4.2. Effect of Reinforcement
4.2.1. Solid Brick Walls
4.2.2. Walls Made of Calcium-Silicate Masonry Units
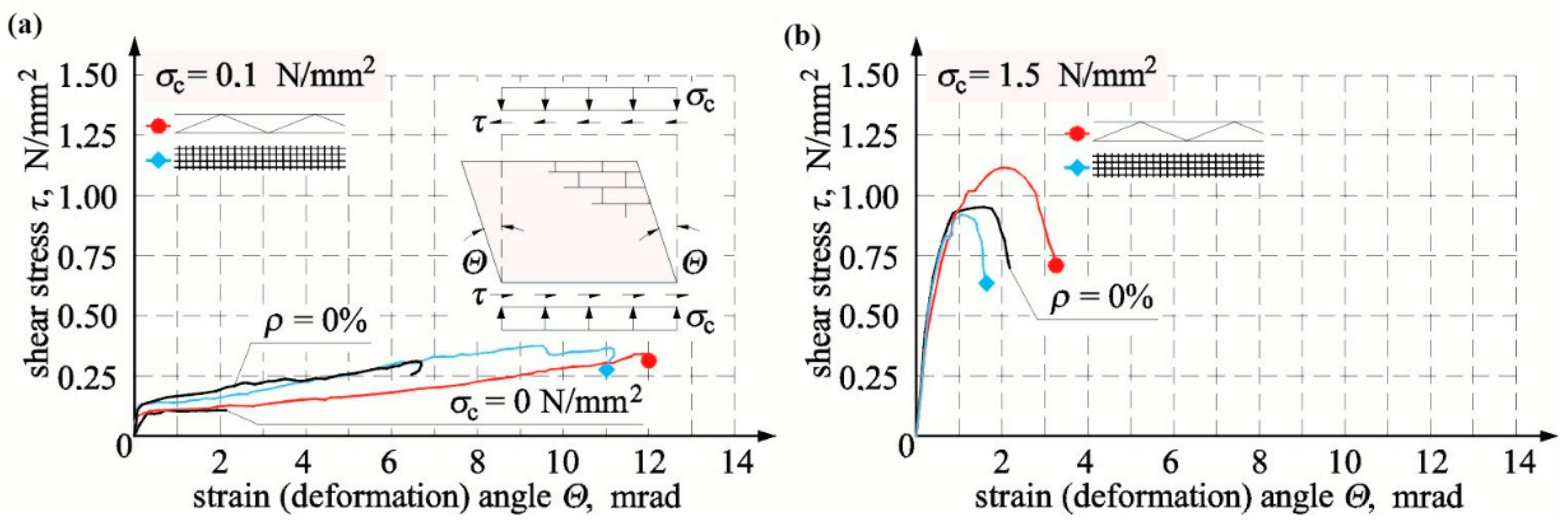
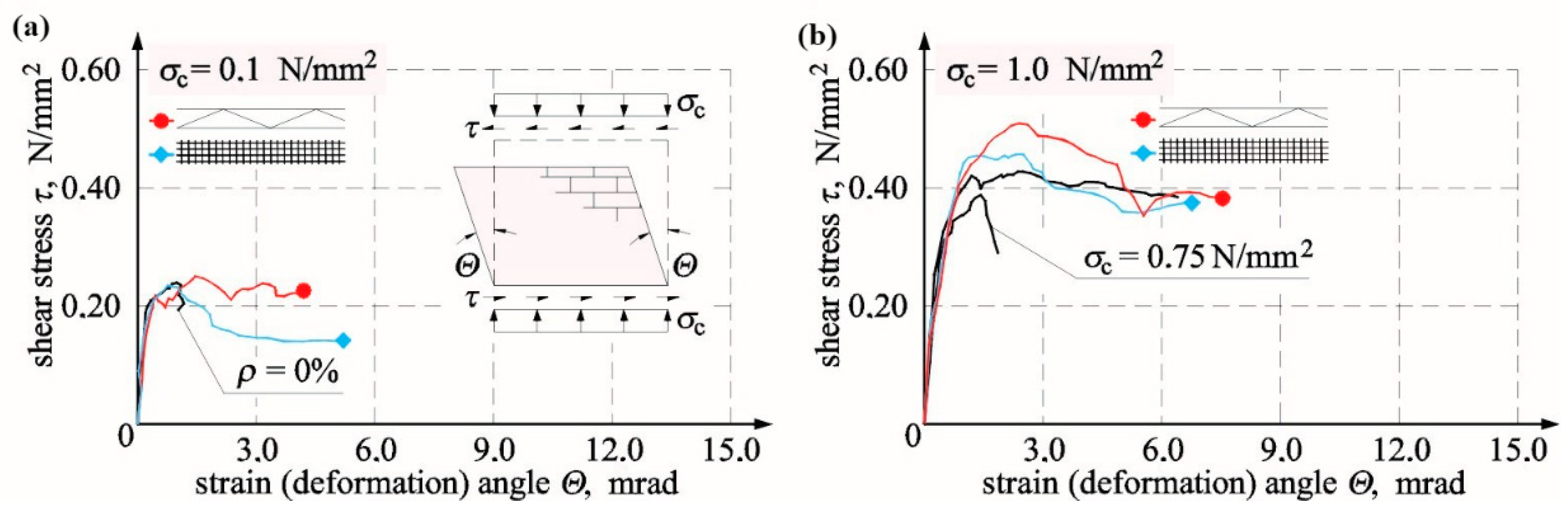
4.2.3. Walls Made of AAC Masonry Units
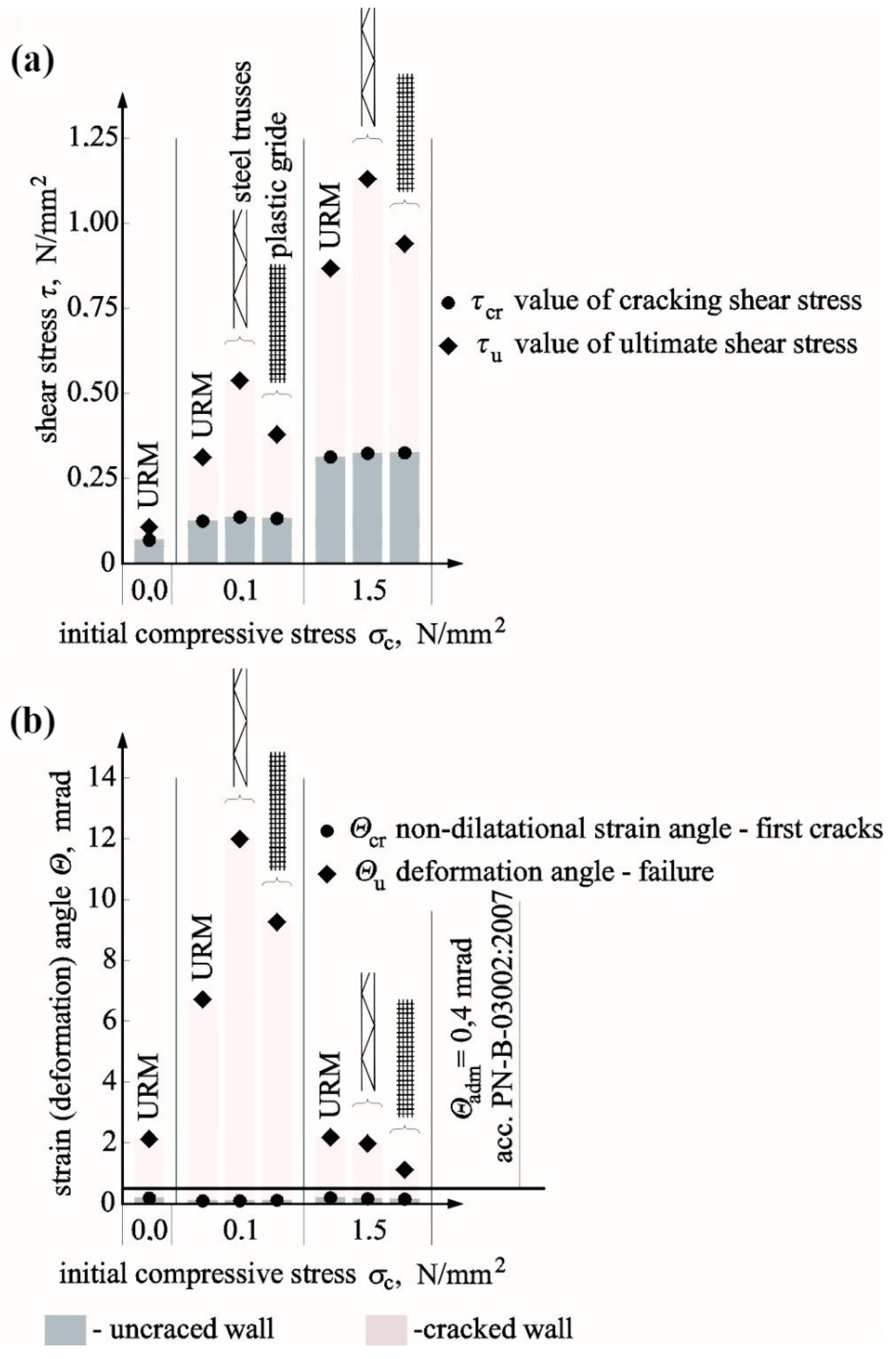
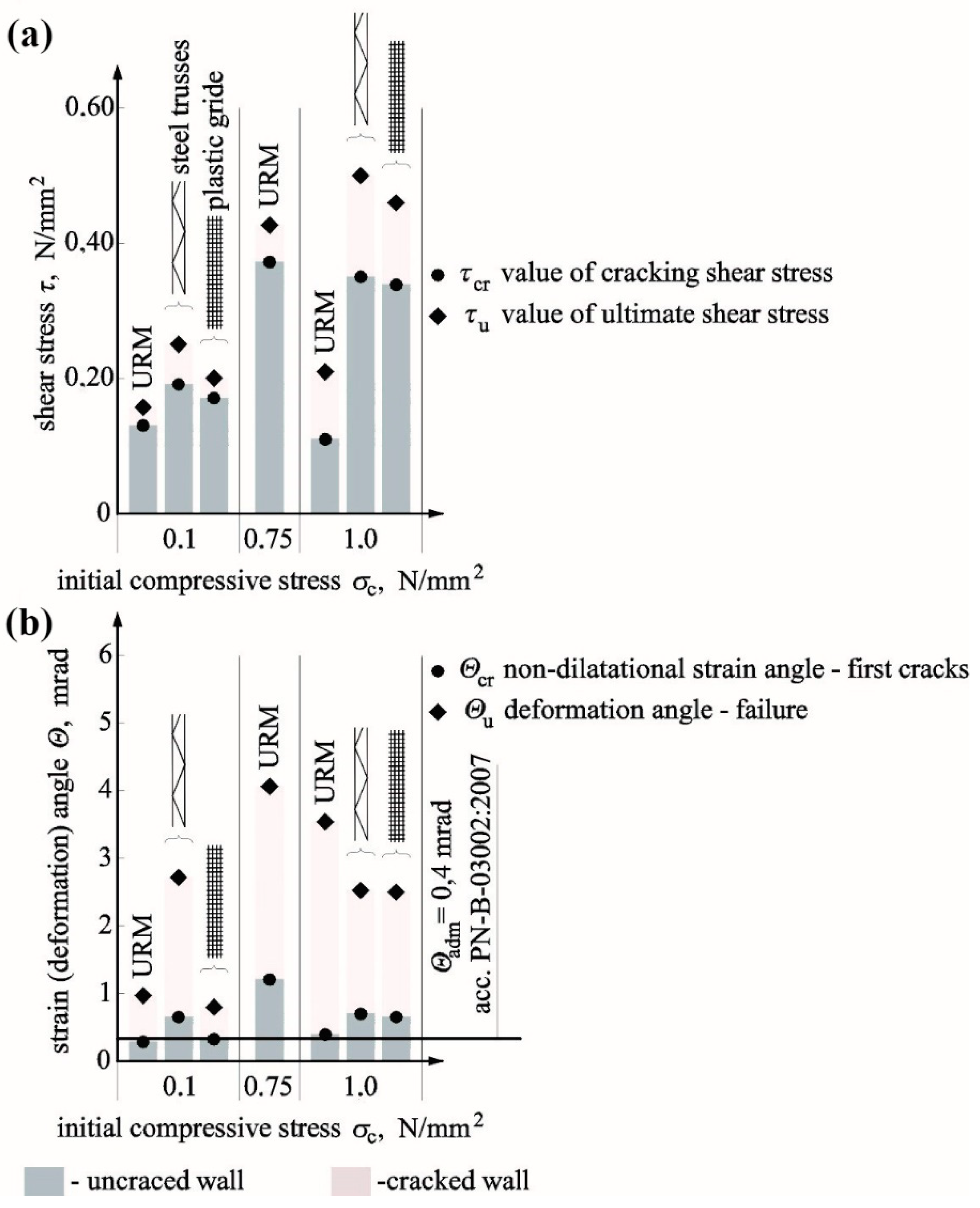
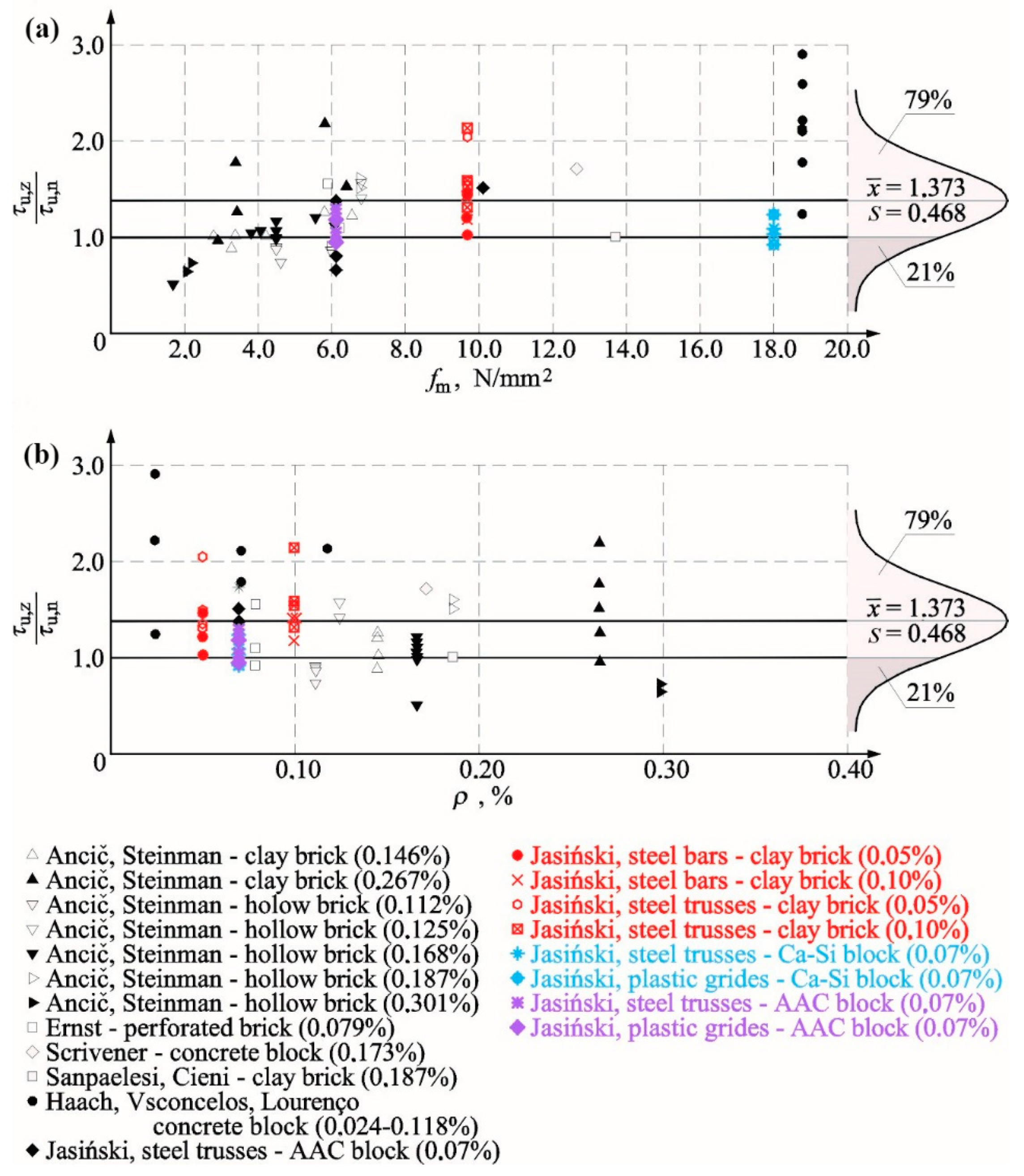
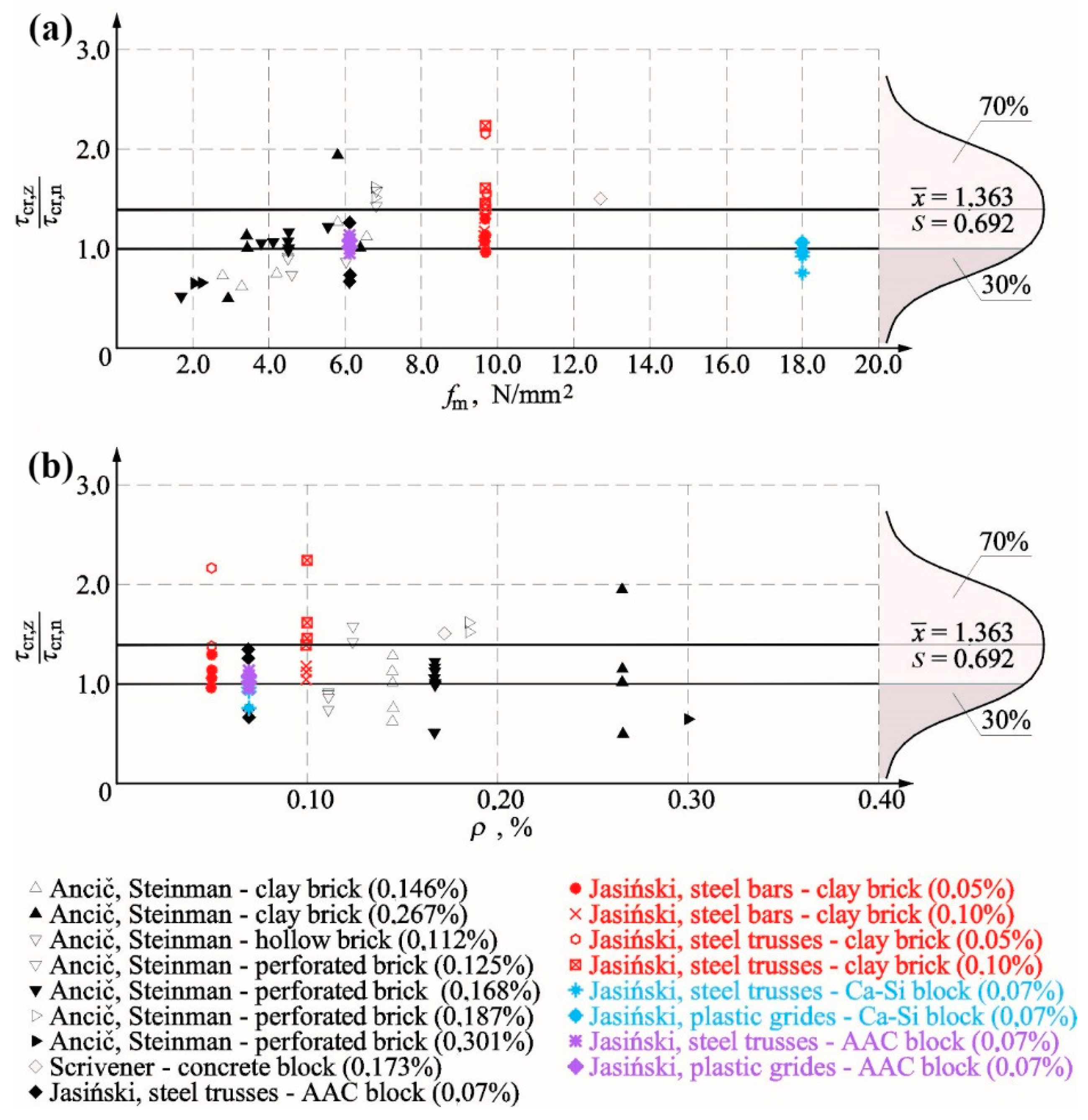
5. Analysis on Effects of Reinforcement in Bed Joints
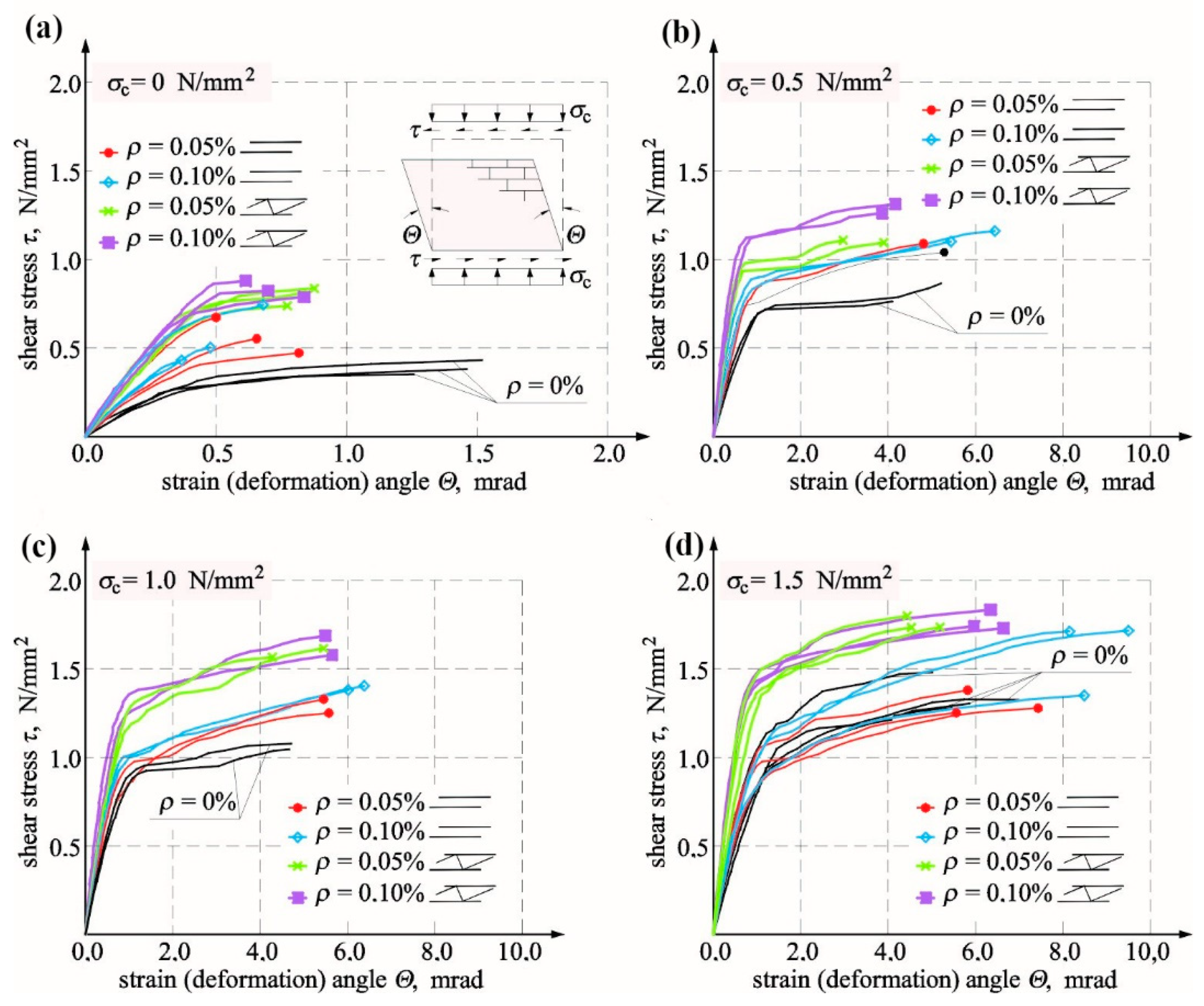
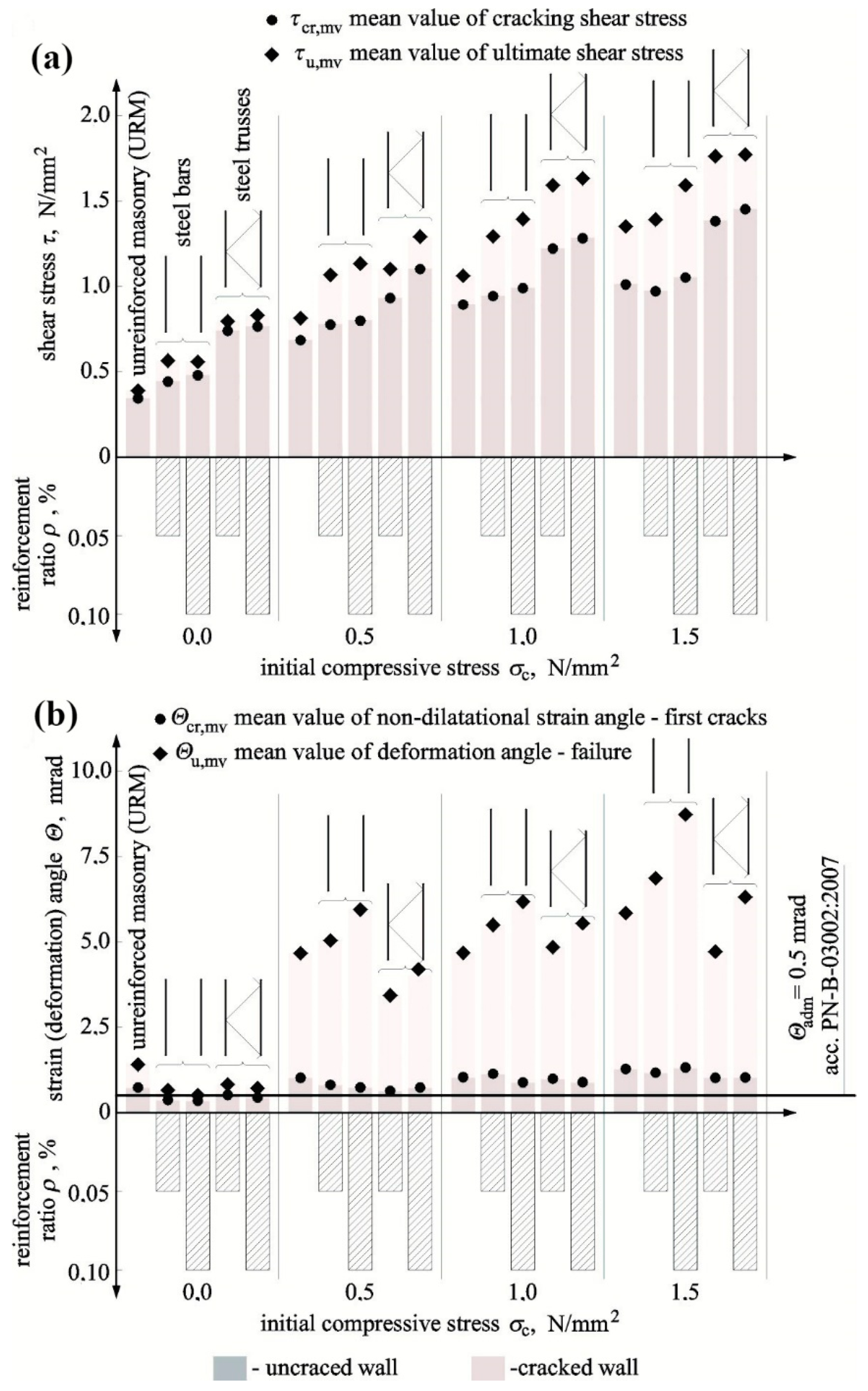
5.1. Cracking and Ultimate Shear Stresses
5.2. Shear Strain and Stiffness
6. Conclusions
- Initial compressive stress was the factor affecting crack morphology. In walls subjected to minimum compressive stress, there was a predominant single crack running through head and bed joints, whereas in walls subjected to maximum compressive stress, including masonry units, there were many diagonal and even vertical cracks;
- horizontal reinforcement in bed joints constrained the number of cracks;
- differences in masonry behaviour were observed at the phase close to failure as unreinforced units or the ones with plastic mesh type reinforcement were gently wearing out, and masonry with truss type reinforcement were destroyed immediately by crushing with simultaneous reinforcement breaking.
- the noticeable effect of compressive stress on values of shear stress at the time of cracking and failure was confirmed;
- steel reinforcement in the form of unbonded steel bars and trusses used in the minimum quantity in solid brick walls (acc. to PN-EN 1996-1-1 [32]) ρmin = 0.1%, and lower than minimum quantity did not result in an undesirable reduction of shear stress at the time of cracking and failure;
- the average increases in cracking and failure stress were 25% and 34%, respectively;
- the conducted statistical analysis of our own tests and those by other authors indicated that the reinforcement placed in bed joints increases average values of cracking and failure stress by 22% and 28%, respectively.
- a significant impact of initial compressive stress was found in all tested series of units, and the tendency was that an increase in initial compressive stress resulted in increased angles of shear strain;
- generally, at the time of cracking, reinforcement reduced angles of shear strain by 11% on average and increased angles of shear deformation by 7% on average;
- including statistical analyses, shear–strain angles decreased by 8%, and an increase of shear deformation was equal to 18%,
- limitations of shear–strain angle, accepted in Polish design rules PN-B-03002:2007 [38], which meet SLS conditions, were found to be dangerous for unreinforced and reinforced walls made of solid brick and AAC and evidently overestimated for Ca-Si walls.
- the highest increase in the initial stiffness and stiffness at the time of cracking was observed in walls under maximum compression;
- in reinforced walls, there was a noticeable increase in the initial stiffness Ko and stiffness at the time of cracking Kcr by 70% and 58% on average;
- after taking into account statistical analyses, reinforcement in bed joints caused an increase in average values of Ko and Kcr by 52% and 36%.
Funding
Conflicts of Interest
References
- Dialer, C.H. Some Remarks on the Strength and Deformation Behavior of Shear Stressed Masonry Panels under Static Monotonic Loading. In Proceedings of the 9th International Brick/Block Masonry Conference, Berlin, Germany, 13–16 October 1991; pp. 276–282. [Google Scholar]
- Timperman, P.; Rice, J.A. Bed Joint Reinforcement Masonry. In Proceedings of the 4th International Masonry Conference, London, UK, 1995; pp. 451–453. Available online: https://www.masonry.org.uk/downloads/proceedings-of-the-4th-international-masonry-conference/ (accessed on 1 August 2010).
- Shing, P.B.; Lofti, P.B.; Barzegarmehrabi, A.; Brunner, J. Finite Element Analysis of Shear Resistance of Masonry Wall Panels with and Without Confining Frames. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Shing, P.B.; Noland, J.L.; Klamerus, E.; Spaeh, H. Inelastic Behavior of Concrete Masonry Shear Walls. J. Struct. Eng. 1989, 115, 2204–2225. [Google Scholar] [CrossRef]
- Shing, P.B.; Schuller, M.; Hoskere, V.S.; Carter, E. Flexural and Shear Response of Reinforced Masonry Walls. ACI Struct. J. 1990, 87, 646–656. [Google Scholar]
- Shing, P.B.; Schuller, M.; Hoskere, V.S. In-Plane Resistance of Reinforced Masonry Shear Walls. J. Struct. Eng. 1990, 116, 619–640. [Google Scholar] [CrossRef]
- Tripathy, D.; Singhal, V. Estimation of in-plane shear capacity of confined masonry walls with and without openings using strut-and-tie analysis. Eng. Struct. 2019, 188, 290–304. [Google Scholar] [CrossRef]
- Bernat-Masó, E.; Gil, L. Assessing the performance of CFRP strengthening on masonry walls using experimental modal analysis. Eng. Struct. 2019, 193, 184–193. [Google Scholar] [CrossRef]
- Aykaç, B.; Özbek, E.; Babayani, R.; Baran, M.; Aykaç, S. Seismic strengthening of infill walls with perforated steel plates. Eng. Struct. 2017, 152, 168–179. [Google Scholar]
- Tomaževič, M.; Lutman, M. Influence of Reinforcement and Block Strength on Seismic Behavior of Reinforcement Masonry Walls. In Proceedings of the 11th International Brick/Block Masonry Conference, Shanghai, China, 14–16 October 1997; pp. 217–226. [Google Scholar]
- Sucuoglu, H.; McNiven, H.D. Seismic Shear Capacity of Reinforced Masonry Piers. J. Struct. Eng. 1991, 117, 2166–2186. [Google Scholar] [CrossRef]
- Shedid, M.T.; Hamid, A.A.; Drysdale, R.G. Ductility of Reinforced Masonry Shear Walls and Impact of Incomplete Grouting. In Proceedings of the 10th Canadian Masonry Symposium, Banff, Alberta, 8–12 June 2005. [Google Scholar]
- Calderón, S.; Sandoval, C.; Arnau, O. Shear response of partially-grouted reinforced masonry walls with a central opening: Testing and detailed micro-modelling. Mater. Des. 2017, 118, 122–137. [Google Scholar] [CrossRef]
- Mahmoud, A.; Abdu Elmagd, S. Masonry reinforced with FRP—Walls with openings. In Proceedings of the IABSE Symposium, Rio de Janeiro, Brazil, 25–27 June 1999; pp. 175–182. [Google Scholar]
- Valluzzi, M.R.; Tinazzi, D.; Modena, C. Shear behavior of masonry panels strengthened by FRP laminates. Constr. Build. Mater. 2002, 16, 409–416. [Google Scholar] [CrossRef]
- Konthesingha, K.M.C.; Masia, M.J.; Petersen, R.B.; Mojsilović, N.; Simundić, G.; Page, A.W. Static cyclic in-plane shear response of damaged masonry walls retrofitted with NSM FRP strips—An experimental evaluation. Eng. Struct. 2013, 50, 126–136. [Google Scholar] [CrossRef]
- Scrivener, J.C. Static Racking Tests on Concrete Masonry Walls, Designing Engineering and Construction with Masonry Product. In Proceedings of the International Conference on Masonry Structural System, Austin, TX, USA, November 30–December 2 1969; pp. 185–191. [Google Scholar]
- Ernst, M. Tests of Reinforced Masonry Walls Subjected to in In-Plane Loading. Darmstad Concr. 1995, 10, 131–143. [Google Scholar]
- König, G.; Ötes, A.; Ernst, M. Test on Masonry Walls with Openings Subjected to In-Plane Loads. In Proceedings of the 4th International Masonry Conference, London, UK, 1995; pp. 101–104. Available online: https://www.masonry.org.uk/downloads/proceedings-of-the-4th-international-masonry-conference/ (accessed on 1 August 2010).
- Brunner, J.D.; Shing, B. Shear Strength of Reinforced Masonry. Mason. Soc. J. 1996, 14, 65–77. [Google Scholar]
- Jäger, W.; Khorramabadi, S.M.T. The Effects of Bed Joint and Vertical Reinforcement on Adobe Masonry (Mud Brick) Walls Under Compressive and In-Plane Shear Loading. In Proceedings of the 7th International Masonry Conference, London, UK, 1–30 October 2006. [Google Scholar]
- Borri, A.; Castori, G.; Corradi, M. Shear behavior of masonry panels strengthened by high strength steel cords. Constr. Build. Mater. 2011, 25, 494–503. [Google Scholar] [CrossRef]
- Haach, V.G.; Vasconcelos, G.; Lourenço, P.B. Study of The Behaviour of Reinforced Masonry Wallets Subjected to Diagonal Compression through Numerical Modeling. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Binici, B.; Canbay, E.; Aldemir, A.; Demirel, I.O.; Yakut, A. Seismic behavior and improvement of autoclaved aerated concrete infill walls. Eng. Struct. 2019, 193, 68–81. [Google Scholar] [CrossRef]
- D’Ambra, C.; Lignola, G.P.; Prota, A.; Sacco, E.; Fabbrocino, F. Experimental performance of FRCM retrofit on out-of-plane behaviour of clay brick walls. Compos. Part B Eng. 2018, 148, 198–206. [Google Scholar] [CrossRef]
- D’Ambra, C.; Lignola, G.P.; Prota, A.; Fabbrocino, F.; Sacco, E. FRCM strengthening of clay brick walls for out of plane loads. Compos. Part B Eng. 2019, 174, 107050. [Google Scholar] [CrossRef]
- Xingzahi, C.; Jinguo, L.; Jiang, X. Shear Strength of Brick Masonry with Reinforced Networks in Bed Joints Subject to Combined Actions. In Proceedings of the 9th International Brick/Block Masonry Conference, Berlin, Germany, 13–16 October 1991; pp. 458–464. [Google Scholar]
- Sanpaelesi, L.; Cieni, P. Experimental Analysis of a Reinforced Masonry Tipology Under Static and Cyclic Loadings to be Used in Seismic Areas. In Proceedings of the 3rd International CIB Symposium—Wall Structures, Warsaw, Poland, June 1984; Volume II, pp. 323–330. [Google Scholar]
- Ančić, D.; Steinman, V. Tensile Strength of Masonry Walls as a Factor of Earthquake Resistance of Masonry Buildings. In Proceedings of the 3rd International CIB Symposium—Wall Structures, Warszawa, Poland, June 1984; Volume II, pp. 253–260. [Google Scholar]
- Jasiński, R. Study of Reinforced Clay Brick Masonry Walls Horizontally Sheared. In Proceedings of the 8th International Masonry Conference, Dresden, Germany, 4–7 July 2010; pp. 1231–1242. [Google Scholar]
- Piekarczyk, A. Shear Modulus and Non-dilatational Strains of Unreinforced and Reinforced Clay Brick Masonry. In Proceedings of the 8th International Masonry Conference, Dresden, Germany, 4–7 July 2010; pp. 315–324. [Google Scholar]
- Eurocode 6: Design of Masonry Structures. Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures; PN-EN 1996-1-1; The European Union: Brussels, Belgium, 2005. (In Polish)
- Specification for Ancillary Components for Masonry. Part 3: Bed Joint Reinforcement of Steel Meshwork; EN 845-3:2013+A1:2016; NSAI Standards: Dublin, Germany, 2016.
- Methods of Test for Masonry Units. Determination of Compressive Strength; EN 772-1; The British Standards Institution: London, UK, 2011.
- Methods of Test for Mortar for Masonry. Part 11: Determination of Flexural and Compressive Strength of Hardened Mortar; EN 1015-11; The British Standards Institution: London, UK, 2007.
- Methods of Test for Masonry. Part 1: Determination of Compressive Strength; EN 1052-1; The British Standards Institution: London, UK, 2000.
- Methods of Test for Masonry. Part 3: Determination of Initial Shear Strength; EN 1052-3; The British Standards Institution: London, UK, 2004.
- Masonry Structures. Design and Calculation; PN-B-03002; The European Union: Brussels, Belgium, 2007.
- Jasiński, R.; Drobiec, Ł. Comparison Research of Bed Joints Construction and Bed Joints Reinforcement on Shear Parameters of AAC Masonry Walls. J. Civ. Eng. Archit. 2016, 12, 1329–1343. [Google Scholar] [CrossRef]
- Jasiński, R.; Drobiec, Ł. Study of Autoclaved Aerated Concrete Masonry Walls with Horizontal Reinforcement under Compression and Shear. Procedia Eng. 2016, 161, 918–924. [Google Scholar] [CrossRef]
- Volk, W. Applied Statistics for Engineers; Literary Licensing LLC: Whitefish, MT, USA, 2013. [Google Scholar]

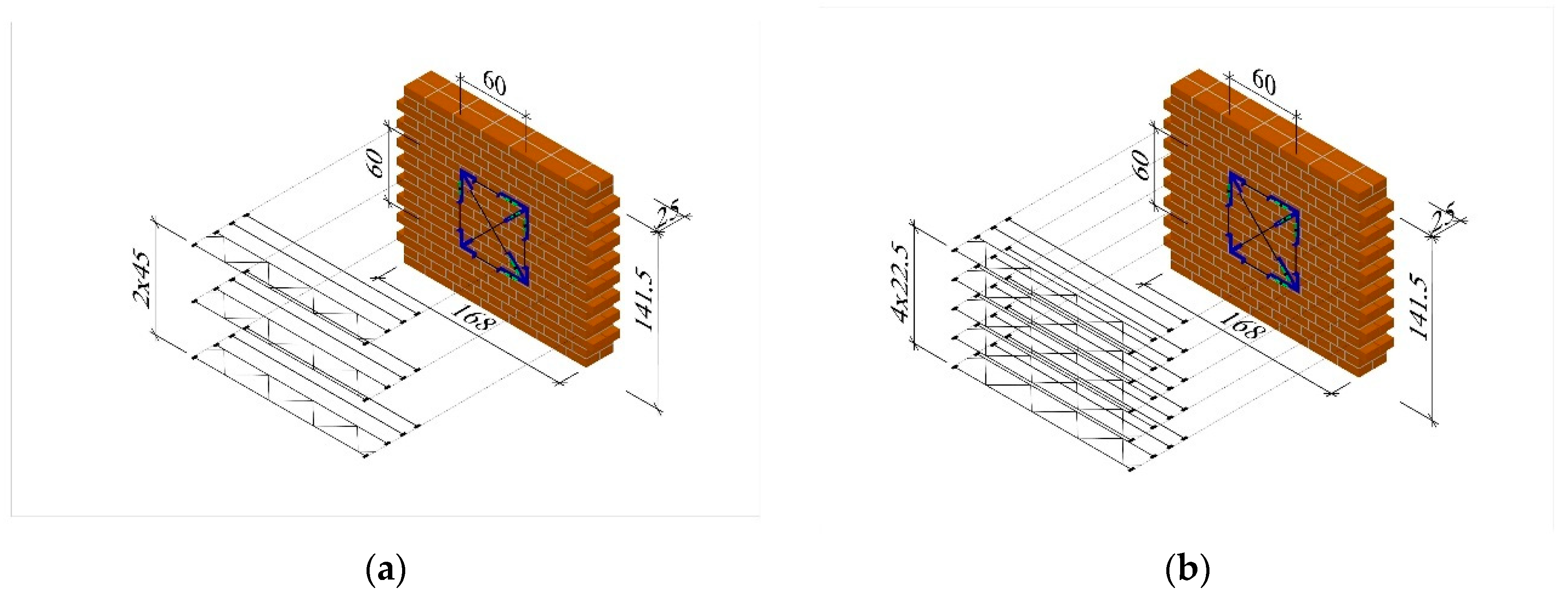
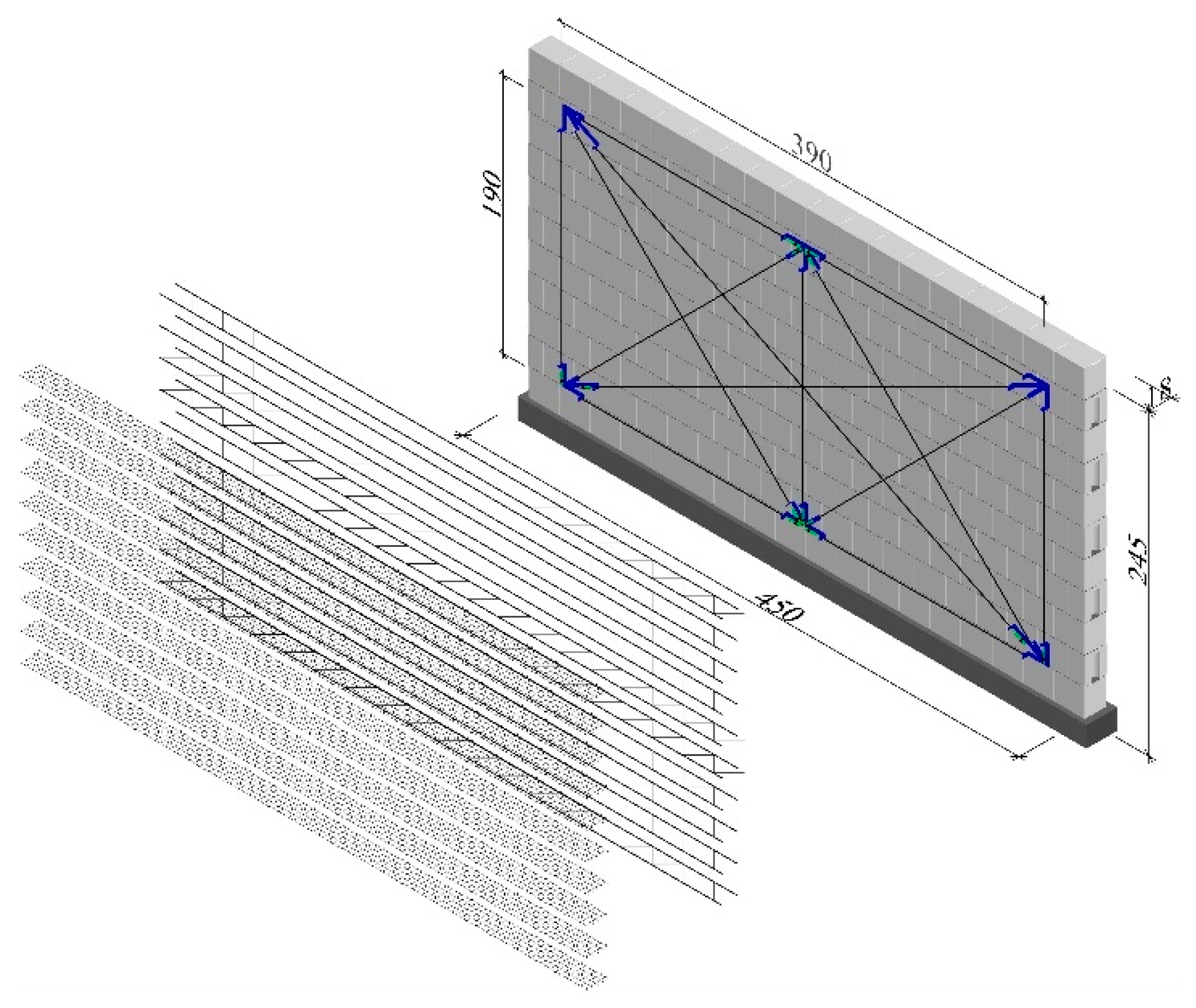
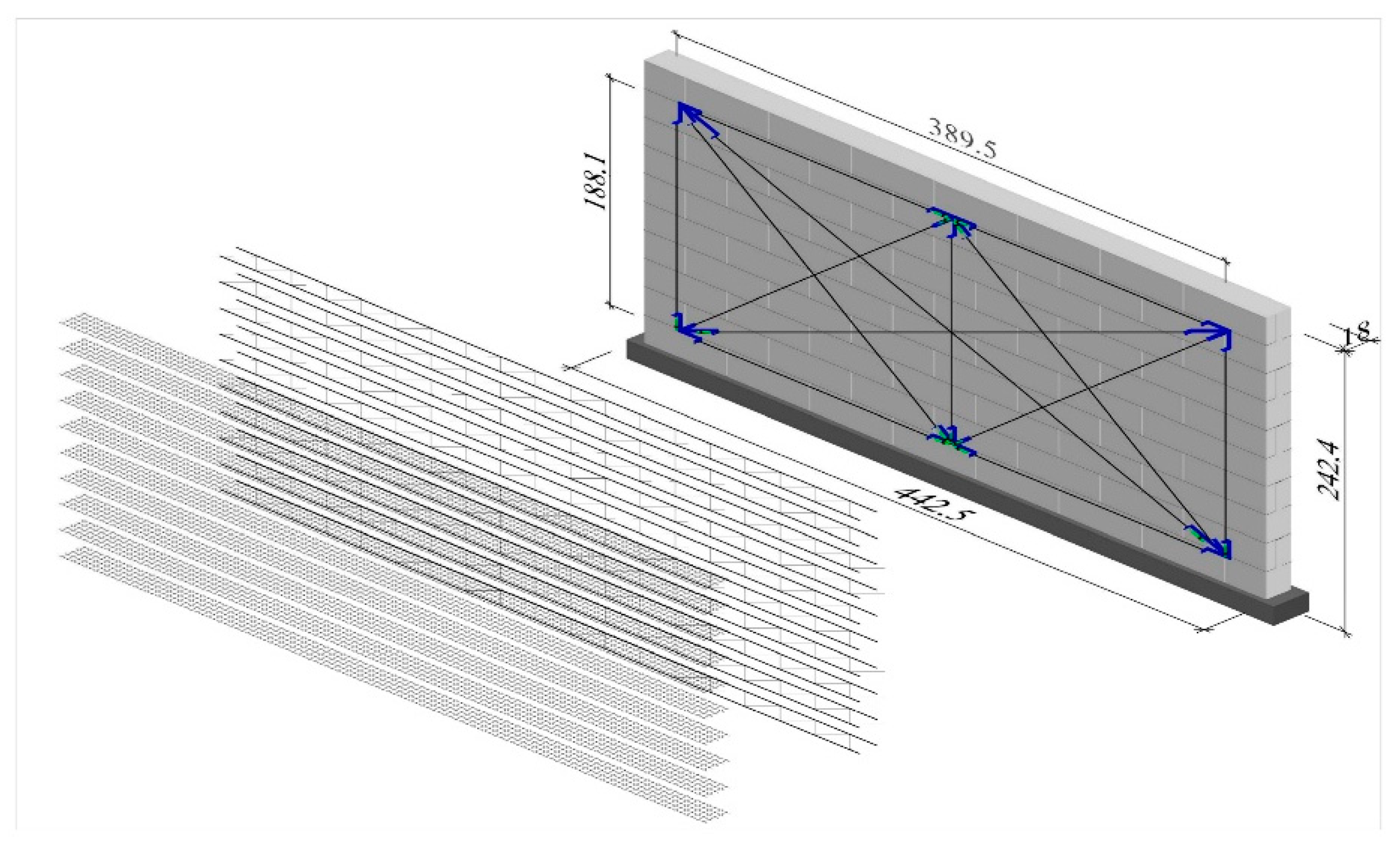


| Series Marking | Wall Dimensions h/l, m | Type of Reinforcement | Reinforcement % ρ, % | σc N/mm2 | Number of Test Units | |
|---|---|---|---|---|---|---|
| at σc | Total | |||||
| HC | 1.42/1.68 | Without reinforcement | - | 0 | 3 | 11 |
| 0.5 | 2 | |||||
| 1.0 | 2 | |||||
| 1.5 | 4 | |||||
| HC-ZPI | Smooth bars ϕ 6 mm (Figure 1a) | 0.05 | 0 | 3 | 10 | |
| 0.5 | 2 | |||||
| 1.0 | 2 | |||||
| 1.5 | 3 | |||||
| HC-ZPII | Smooth bars ϕ 6 mm (Figure 1a) | 0.10 | 0 | 3 | 10 | |
| 0.5 | 2 | |||||
| 1.0 | 2 | |||||
| 1.5 | 3 | |||||
| HC-ZKI | Trusses (Figure 1b) | 0.05 | 0 | 3 | 10 | |
| 0.5 | 2 | |||||
| 1.0 | 2 | |||||
| 1.5 | 3 | |||||
| HC-ZKII | Trusses (Figure 1b) | 0.10 | 0 | 3 | 10 | |
| 0.5 | 2 | |||||
| 1.0 | 2 | |||||
| 1.5 | 3 | |||||
| Series Marking | Wall External Dimensions h/l, m | Type of Reinforcement | Reinforcement % ρ, % | σc (N/mm2) | Number of Test Units | |
|---|---|---|---|---|---|---|
| at σc | Total | |||||
| HOS | 2.45/4.50 | Without reinforcement | 0 | 0 | 1 | 3 |
| 0.1 | 1 | |||||
| 1.5 | 1 | |||||
| HOS-Z1-S | Trusses (Figure 1c) | 0.07 | 0.1 | 1 | 2 | |
| 1.5 | 1 | |||||
| HOS-Z2-S | Plastic meshes (Figure 1d) | 0.07 | 0.1 | 1 | 2 | |
| 1.5 | 1 | |||||
| Series Marking | Wall External Dimensions h/l, m | Type of Reinforcement | Reinforcement % ρ, % | σc (N/mm2) | Number of Test Units | |
|---|---|---|---|---|---|---|
| at σc | Total | |||||
| HOS-AAC | 2.43/4.43 | Without reinforcement | 0 | 0.1 | 1 | 4 |
| 0.75 | 1 | |||||
| 1.0 | 2 | |||||
| HOS-AAC-Z1 | Trusses (Figure 1c) | 0.07 | 0.1 | 1 | 2 | |
| 1.0 | 1 | |||||
| HOS-AAC-Z2 | Plastic meshes (Figure 1d) | 0.07 | 0.1 | 1 | 2 | |
| 1.0 | 1 | |||||
| Type of Reinforcement | ρ,% | σc N/mm2 | Stresses | Angles of Shear Strain (Deformation) | Total Stiffness | |||
|---|---|---|---|---|---|---|---|---|
| Cracking | Failure | Cracking | Failure | Initial | At the Time of Cracking | |||
| τcr,mv N/mm2 | τu,mv N/mm2 | Θcr,mv mrad | Θu,mv mrad | Ko, mv MN/m | Kcr,mv MN/m | |||
| no reinforcement | 0 | 0 | 0.343 | 0.388 | 0.735 | 1.413 | 301 | 118 |
| 0.5 | 0.684 | 0.812 | 1.02 | 4.665 | 282 | 168 | ||
| 1.0 | 0.892 | 1.06 | 1.04 | 4.671 | 374 | 214 | ||
| 1.5 | 1.01 | 1.35 | 1.28 | 5.84 | 370 | 197 | ||
| smooth rebars | 0.05 | 0 | 0.442 | 0.564 | 0.373 | 0.658 | 577 | 305 |
| 0.5 | 0.775 | 1.066 | 0.816 | 5.04 | 668 | 239 | ||
| 1.0 | 0.942 | 1.291 | 1.14 | 5.49 | 605 | 206 | ||
| 1.5 | 0.970 | 1.39 | 1.17 | 6.86 | 484 | 209 | ||
| 0.1 | 0 | 0.479 | 0.557 | 0.347 | 0.510 | 493 | 346 | |
| 0.5 | 0.798 | 1.132 | 0.739 | 5.94 | 539 | 273 | ||
| 1.0 | 0.988 | 1.392 | 0.888 | 6.17 | 624 | 264 | ||
| 1.5 | 1.05 | 1.59 | 1.32 | 8.72 | 453 | 199 | ||
| truss | 0.05 | 0.0 | 0.739 | 0.794 | 0.523 | 0.827 | 732 | 353 |
| 0.5 | 0.930 | 1.10 | 0.638 | 3.43 | 700 | 364 | ||
| 1.0 | 1.22 | 1.59 | 0.994 | 4.84 | 593 | 308 | ||
| 1.5 | 1.38 | 1.76 | 1.02 | 4.71 | 751 | 340 | ||
| 0.1 | 0.0 | 0.764 | 0.829 | 0.445 | 0.717 | 740 | 430 | |
| 0.5 | 1.10 | 1.29 | 0.735 | 4.01 | 816 | 375 | ||
| 1.0 | 1.28 | 1.63 | 0.892 | 5.54 | 717 | 357 | ||
| 1.5 | 1.45 | 1.77 | 1.03 | 6.31 | 1095 | 353 | ||
| Type of Reinforcement | ρ,% | σc N/mm2 | Stresses | Angles of Shear Strain (Deformation) | Total Stiffness | |||
|---|---|---|---|---|---|---|---|---|
| Cracking | Failure | Cracking | Failure | Initial | At the Time of Cracking | |||
| τcr N/mm2 | τu N/mm2 | Θcr mrad | Θu mrad | Ko MN/m | Kcr MN/m | |||
| no reinforcement | 0 | 0 | 0.069 | 0.107 | 0.175 | 2.126 | 137 | 131 |
| 0.1 | 0.124 | 0.313 | 0.086 | 6.714 | 1378 | 477 | ||
| 1.5 | 0.346 | 0.954 | 0.197 | 2.182 | 1674 | 580 | ||
| truss | 0.07 | 0.1 | 0.088 | 0.35 | 0.087 | 11.99 | 1039 | 333 |
| 1.5 | 0.324 | 1.13 | 0.169 | 1.968 | 1525 | 635 | ||
| plastic mesh | 0.07 | 0.1 | 0.133 | 0.379 | 0.109 | 9.262 | 1478 | 403 |
| 1.5 | 0.326 | 0.939 | 0.143 | 1.125 | 1496 | 753 | ||
| Type of Reinforcement | ρ,% | σc N/mm2 | Stresses | Angles of Shear Strain (Deformation) | Total Stiffness | |||
|---|---|---|---|---|---|---|---|---|
| Cracking | Failure | Cracking | Failure | Initial | At the Time of Cracking | |||
| τcr N/mm2 | τu N/mm2 | Θcr mrad | Θu mrad | Ko MN/m | Kcr MN/m | |||
| no reinforcement | 0 | 0.1 | 0.196 | 0.235 | 0.281 | 0.97 | 932 | 229 |
| 0.75 | 0.372 | 0.426 | 0.724 | 2.44 | 1168 | 169 | ||
| 1.0 | 0.298 | 0.385 | 0.524 | 1.45 | 1541 | 187 | ||
| 1.0 * | 0.11 | 0.25 | 0.651 | 2.72 | 379 | 75 | ||
| truss | 0.07 | 0.1 | 0.191 | 0.250 | 0.358 | 1.49 | 1262 | 175 |
| 1.0 | 0.350 | 0.50 | 0.695 | 2.52 | 1782 | 165 | ||
| plastic mesh | 0.07 | 0.1 | 0.205 | 0.23 | 0.322 | 0.80 | 1193 | 208 |
| 1.0 | 0.338 | 0.46 | 0.649 | 2.50 | 1374 | 171 | ||
| Wall Type | Type of Reinforcement | ρ,% | σc N/mm2 | Stresses | Angles of Shear Strain (Deformation) | Total Stiffness | |||
|---|---|---|---|---|---|---|---|---|---|
| Cracking | Failure | Cracking | Failure | Initial | At the Time of Cracking | ||||
| solid brick | smooth bars | 0.05 | 0 | 1.29 | 1.45 | 0.51 | 0.47 | 1.92 | 2.58 |
| 0.5 | 1.13 | 1.31 | 0.80 | 1.08 | 2.37 | 1.42 | |||
| 1.0 | 1.06 | 1.22 | 1.10 | 1.18 | 1.62 | 0.96 | |||
| 1.5 | 0.96 | 1.03 | 0.91 | 1.17 | 1.31 | 1.06 | |||
| 0.1 | 0 | 1.40 | 1.44 | 0.47 | 0.36 | 1.64 | 2.93 | ||
| 0.5 | 1.17 | 1.39 | 0.72 | 1.27 | 1.91 | 1.63 | |||
| 1.0 | 1.11 | 1.31 | 0.85 | 1.32 | 1.67 | 1.23 | |||
| 1.5 | 1.04 | 1.18 | 1.03 | 1.49 | 1.22 | 1.01 | |||
| truss | 0.05 | 0.0 | 2.15 | 2.05 | 0.71 | 0.59 | 2.43 | 2.99 | |
| 0.5 | 1.36 | 1.35 | 0.63 | 0.74 | 2.48 | 2.17 | |||
| 1.0 | 1.37 | 1.50 | 0.96 | 1.04 | 1.59 | 1.44 | |||
| 1.5 | 1.37 | 1.30 | 0.80 | 0.81 | 2.03 | 1.73 | |||
| 0.1 | 0.0 | 2.23 | 2.14 | 0.61 | 0.51 | 2.46 | 3.64 | ||
| 0.5 | 1.61 | 1.59 | 0.72 | 0.86 | 2.89 | 2.23 | |||
| 1.0 | 1.43 | 1.54 | 0.86 | 1.19 | 1.92 | 1.67 | |||
| 1.5 | 1.44 | 1.31 | 0.80 | 1.08 | 2.96 | 1.79 | |||
| wall made of silicate masonry units | truss | 0.07 | 0.1 | 0.71 | 1.12 | 1.01 | 1.79 | 0.75 | 0.70 |
| 1.5 | 0.94 | 1.18 | 0.86 | 0.90 | 0.91 | 1.09 | |||
| plastic mesh | 0.07 | 0.1 | 1.07 | 1.21 | 1.27 | 1.38 | 1.07 | 0.84 | |
| 1.5 | 0.94 | 0.98 | 0.73 | 0.52 | 0.89 | 1.30 | |||
| wall made of AAC masonry units | truss | 0.07 | 0.1 | 0.97 | 1.06 | 1.27 | 1.54 | 1.35 | 0.76 |
| 1.0 | 1.17 | 1.30 | 1.33 | 1.74 | 1.16 | 0.88 | |||
| plastic mesh | 0.07 | 0.1 | 1.05 | 0.98 | 1.15 | 0.82 | 1.28 | 0.91 | |
| 1.0 | 1.13 | 1.19 | 1.24 | 1.72 | 0.89 | 0.91 | |||
| Average value : | 1.25 | 1.34 | 0.89 | 1.07 | 1.70 | 1.58 | |||
| Standard deviation S: | 0.355 | 0.287 | 0.244 | 0.419 | 0.648 | 0.801 | |||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, R. Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls. Materials 2019, 12, 2543. https://doi.org/10.3390/ma12162543
Jasiński R. Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls. Materials. 2019; 12(16):2543. https://doi.org/10.3390/ma12162543
Chicago/Turabian StyleJasiński, Radosław. 2019. "Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls" Materials 12, no. 16: 2543. https://doi.org/10.3390/ma12162543
APA StyleJasiński, R. (2019). Research on the Influence of Bed Joint Reinforcement on Strength and Deformability of Masonry Shear Walls. Materials, 12(16), 2543. https://doi.org/10.3390/ma12162543





