Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities
Abstract
1. Introduction
2. Materials and Methods
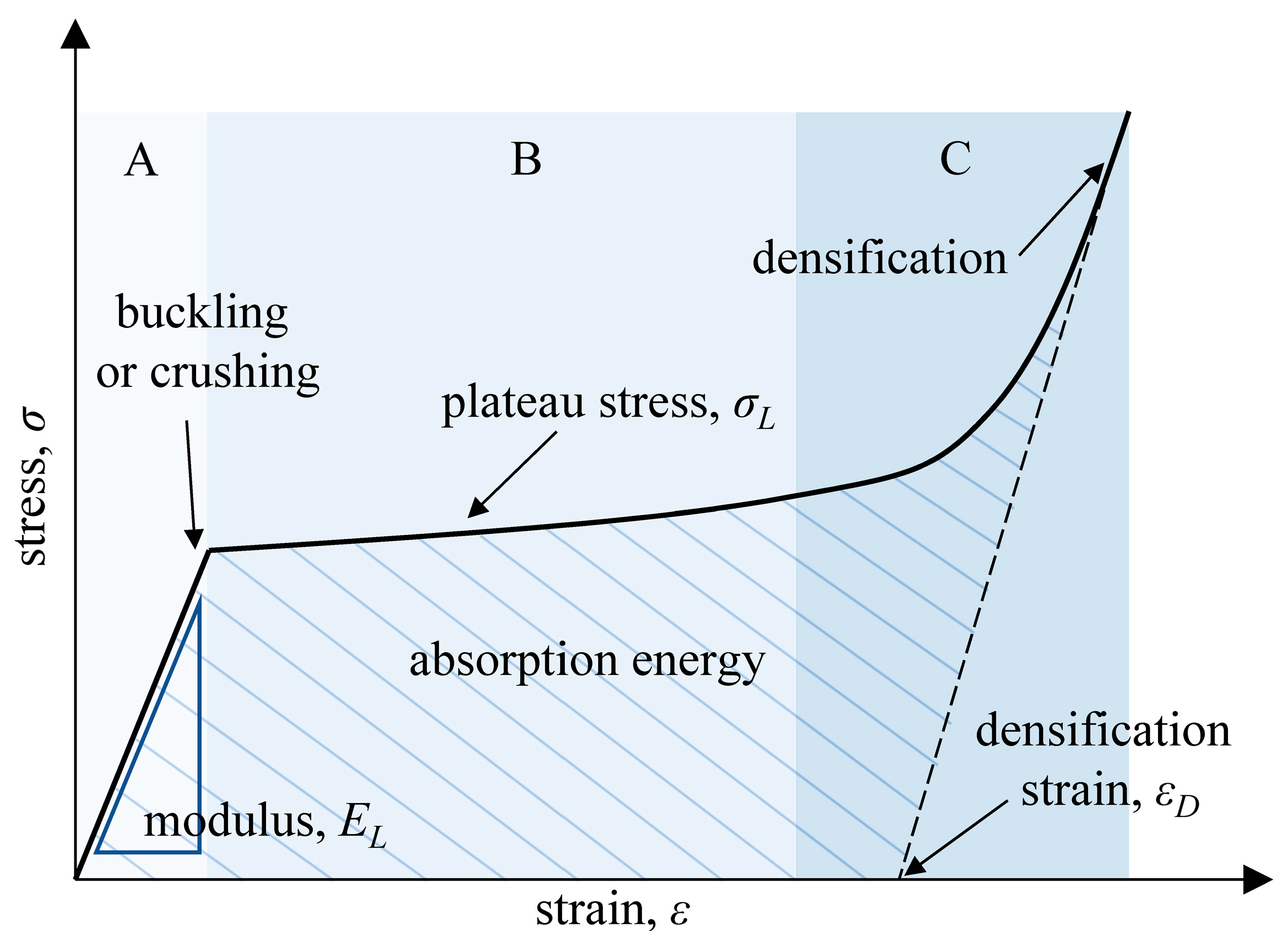
2.1. The Gibson-Ashby Model of Cellular Structures
2.2. Design of Gyroid-Based Cellular Structures
2.3. Manufacturing the Cellular Specimens
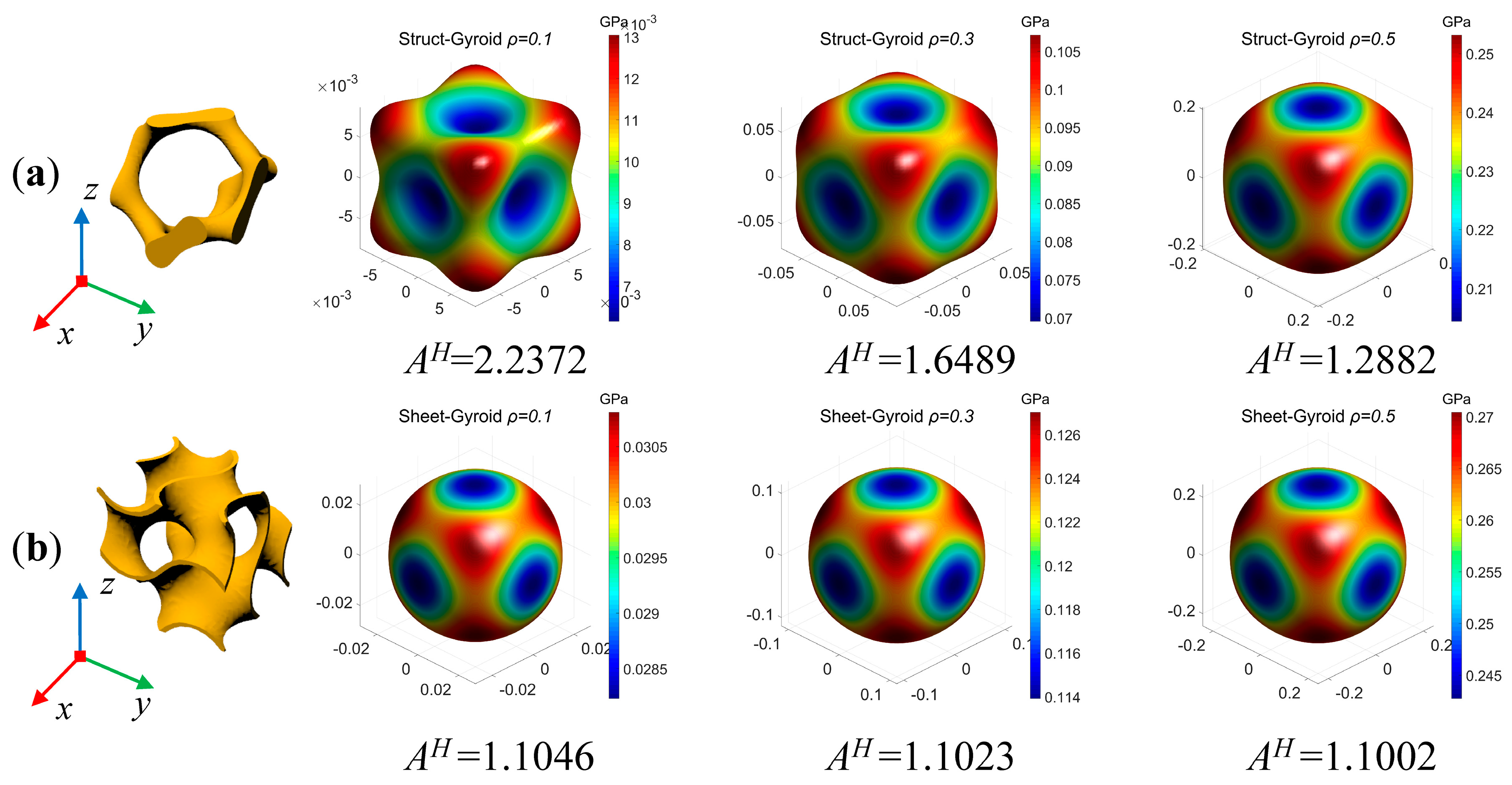
2.4. Numerical Homogenization
2.5. Mechanical Testing
3. Results and Discussion
3.1. Formatting of Mathematical Components
3.2. Deformation of Uniform Gyroid-Based Cellular Structure
3.3. Deformation of Graded Gyroid-Based Cellular Structures
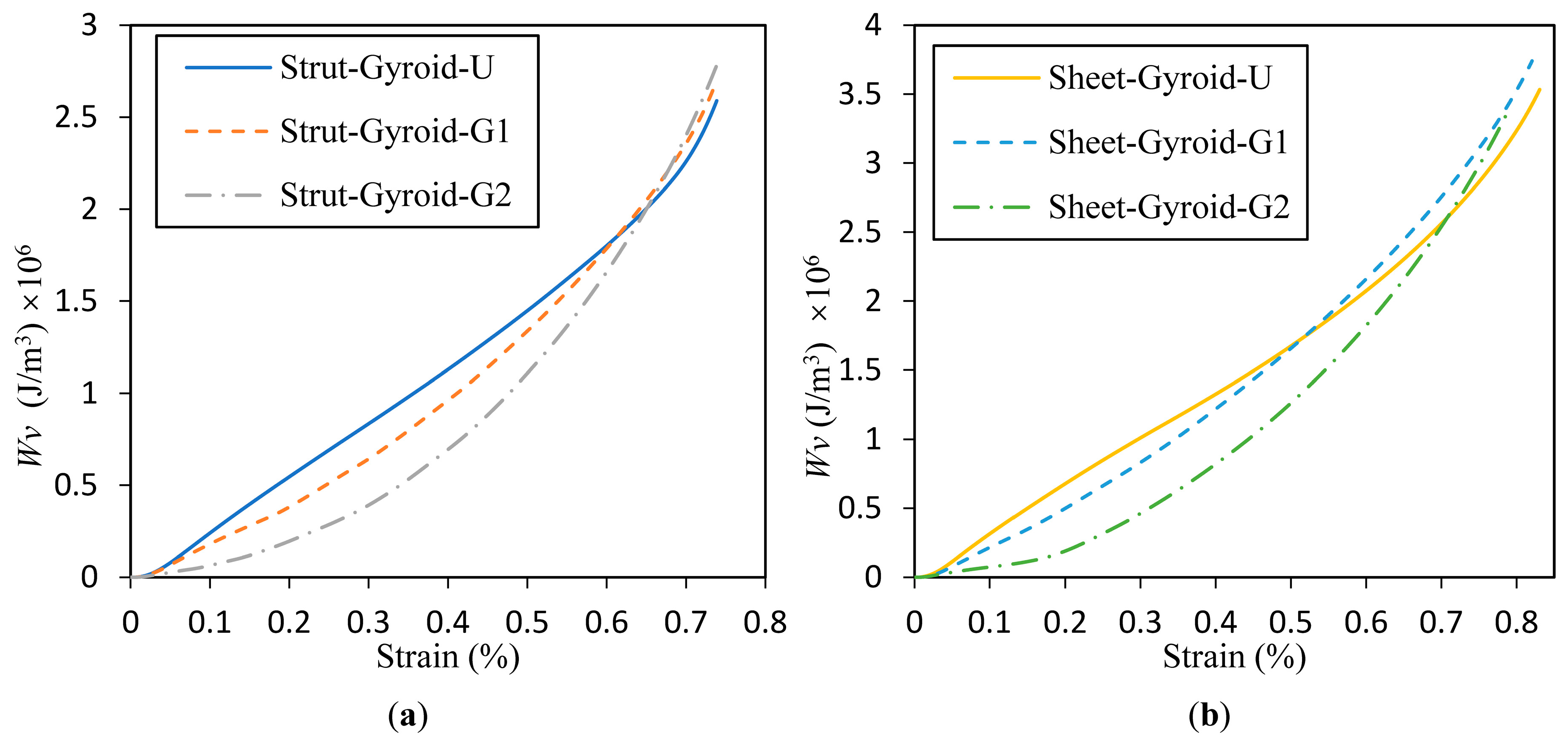
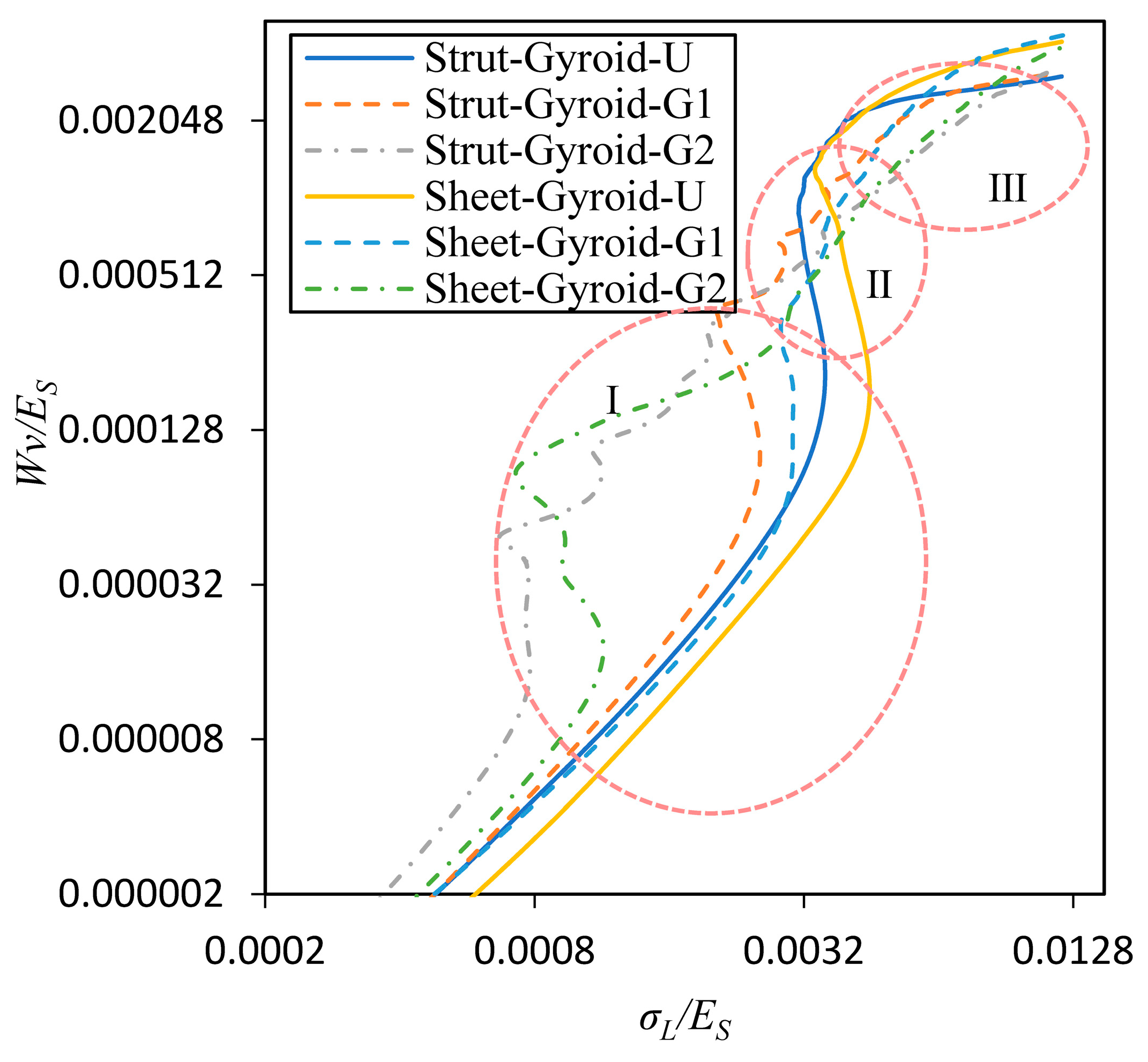
3.4. Energy Absorption Capability of the Cellular Structures
4. Conclusions
- (1)
- Anisotropic analysis of strut-based gyroid cellular structure and sheet-based gyroid cellular structure was performed by numerical homogenization method. It is found that the sheet-based gyroid cellular structure tends to be isotropic over the entire density interval and theoretically more suited for energy absorption. In addition, the strut-based gyroid structure exhibits anisotropy, and its Young’s modulus is also smaller than the sheet-based gyroid structure at the same density.
- (2)
- It is found from the video recorded in the experiment that the uniform structure exhibits a global collapse deformation mode during the compression process, and the graded structure exhibits a layer-by-layer collapse deformation mode from a low-density. Besides, the modulus and yield strength of the two structures are calculated according to the values of the linear elastic phase. It can be seen from the results that the modulus and the yield strength of the sheet-based gyroid structure are higher than the corresponding strut-based gyroid structure.
- (3)
- The energy absorption per unit volume of each sample was calculated separately based on the data recorded in the experiment. It can be seen from the results that the energy absorption capacity of the graded structure is better than that of the uniform structure, and the graded structure exhibits a smoother energy absorption process until the fully dense strain. However, the uniform structure will suddenly increase sharply when it is fully dense. Additionally, the sheet-based gyroid structure has better energy absorption than the strut-based gyroid structure. Besides, the gradient levels also have an effect on energy absorption and deformation. From the results of this work, it is known that cellular structures with large gradient exhibit better energy absorption capacity than those with a small gradient.
Author Contributions
Funding
Conflicts of Interest
References
- Schaedler, T.A.; Carter, W.B. Architected cellular materials. Ann. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Bitzer, T.N. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing; Springer Science Business Media: New York, NY, USA, 1997. [Google Scholar]
- Xu, F.; Zhang, X.; Zhang, H. A review on functionally graded structures and materials for energy absorption. Eng. Struct. 2018, 171, 309–325. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Lin, Z.; Shang, C.; Li, B. A review of the design methods of complex topology structures for 3D printing. Vis. Comput. Ind. Biomed. Art. 2018, 1, 5. [Google Scholar] [CrossRef]
- Correa, D.M.; Klatt, T.; Cortes, S.; Haberman, M.; Kovar, D.; Seepersad, C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyp. J. 2015, 21, 193–200. [Google Scholar] [CrossRef]
- Bates, S.R.; Farrow, I.R.; Trask, R.S. 3D printed polyurethane honeycombs for repeated tailored energy absorption. Mater. Des. 2016, 112, 172–183. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. In-plane energy absorption evaluation of 3D printed polymeric honeycombs. Virtual Phys. Prototyp. 2017, 12, 117–131. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight Metamaterials for energy absorption. Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Bates, S.R.; Farrow, I.R.; Trask, R.S. 3D printed elastic honeycombs with graded density for tailorable energy absorption. Active and Passive Smart Structures and Integrated Systems 2016. In Proceedings of the 2016 International Society for Optics and Photonics, San Diego, CA, USA, 28 August–1 September 2016. [Google Scholar]
- Bates, S.R.; Farrow, I.R.; Trask, R.S. Compressive behavior of 3D printed thermoplastic polyurethane honeycombs with graded densities. Mater. Des. 2019, 162, 130–142. [Google Scholar] [CrossRef]
- Maskery, I.; Hussey, A.; Panesar, A.; Aremu, A.; Tuck, C.; Ashcroft, I.; Hague, R. An investigation into reinforced and functionally graded lattice structures. J. Cell. Plast. 2017, 53, 151–165. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.N.; Leong, K.F.; Wei, J. Compressive properties of functionally graded lattice structures manufactured by selective laser melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and failure behavior of Ti-6Al-4V lattice structures manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar]
- Smith, M.; Guan, Z.; Cantwell, W.J. Finite element modelling of the compressive response of lattice structures manufactured using the selective laser melting technique. Int. J. Mech. Sci. 2013, 67, 28–41. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, D.; Zhang, P.; Zhao, M.; Jafar, S. Mechanical properties of optimized diamond lattice structure for bone scaffolds fabricated via selective laser melting. Materials 2018, 11, 374. [Google Scholar] [CrossRef]
- Li, D.; Dai, N.; Jiang, X.; Chen, X. Interior structural optimization based on the density-variable shape modeling of 3D printed objects. Int. J. Adv. Manuf. Technol. 2016, 83, 1627–1635. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. Comput.-Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.A.; Pang, S.; Al-Rub, R.K.A.; Jasiuk, I.M. Mechanical properties of 3D printed polymeric Gyroid cellular structures, Experimental and finite element study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous graded Gyroid cellular structures fabricated by selective laser melting, Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- Ashby, M.F.; Medalist, R.M. The mechanical properties of cellular solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams, A Design Guide; Elsevier, Butterworth Heinemann: Stoneham, MA, USA, 2000. [Google Scholar]
- Schoen, A.H. Infinite Periodic Minimal Surfaces without Self-Intersections; National Aeronautics and Space Administration (NASA) Tech: Washington, DC, USA, 1970.
- Michielsen, K.; Stavenga, D.G. Gyroid cuticular structures in butterfly wing scales: Biological photonic crystals. J. R. Soc. Interface 2007, 5, 85–94. [Google Scholar] [CrossRef]
- Qin, Z.; Jung, G.S.; Kang, M.J.; Buehler, M.J. The mechanics and design of a lightweight three-dimensional graphene assembly. Sci. Adv. 2017, 3, e1601536. [Google Scholar] [CrossRef]
- Steven, G.P. Homogenization of multicomponent composite orthotropic materials using FEA. Commun. Numer. Methods Eng. 1997, 13, 517–531. [Google Scholar] [CrossRef]
- Tan, P.; Tong, L.; Steven, G.P. Behavior of 3D orthogonal woven CFRP composites. Part II. FEA and analytical modeling approaches. Compos. Part A Appl. Sci. Manuf. 2000, 31, 273–281. [Google Scholar] [CrossRef]
- Xu, S.; Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Design of lattice structures with controlled anisotropy. Mater. Des. 2016, 93, 443–447. [Google Scholar] [CrossRef]
- Zener, C.M.; Siegel, S. Elasticity and Anelasticity of Metals. J. Phys. Chem. 1949, 53, 1468. [Google Scholar] [CrossRef]
- ASTM D695-15. Standard Test Method for Compressive Properties of Rigid Plastics; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]







| Properties | Strut- Gyroid-U | Sheet- Gyroid-U | Strut- Gyroid-G1 | Sheet- Gyroid-G1 | Strut- Gyroid-G2 | Sheet- Gyroid-G2 |
|---|---|---|---|---|---|---|
| EH (MPa) | 40.56 | 63.67 | — | — | — | — |
| EL (MPa) | 39.21 ± 0.23 | 62.51 ± 0.44 | 28.25 ± 0.31 | 36.67 ± 0.18 | 23.96 ± 0.16 | 32.21 ± 0.31 |
| E* (10−3) | 46.12 ± 0.02 | 73.54 ± 0.02 | 33.23 ± 0.05 | 43.14 ± 0.03 | 28.18 ± 0.01 | 37.89 ± 0.03 |
| σL (MPa) | 2.92 ± 0.08 | 3.89 ± 0.12 | 1.98 ± 0.04 | 2.46 ± 0.16 | 0.69 ± 0.02 | 0.87 ± 0.05 |
| σ* (10−3) | 22.12 ± 0.02 | 29.46 ± 0.11 | 15.00 ± 0.12 | 18.63 ± 0.09 | 5.23 ± 0.10 | 6.59 ± 0.06 |
| εD (%) | 62.3 ± 0.12 | 66.4 ± 0.01 | 68.5 ± 0.06 | 69.8 ± 0.13 | 70.1 ± 0.02 | 72.2 ± 0.03 |
| Wv (KJ/m3) | 1734 ± 4 | 2276 ± 2 | 2116 ± 6 | 2623 ± 1 | 2341 ± 5 | 2781 ± 4 |
| Coefficients | C1 | C2 | α |
|---|---|---|---|
| Strut-Gyroid-U | 0.512 | 0.135 | 1.257 |
| Sheet-Gyroid-U | 0.817 | 0.179 | 1.120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities. Materials 2019, 12, 2183. https://doi.org/10.3390/ma12132183
Li D, Liao W, Dai N, Xie YM. Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities. Materials. 2019; 12(13):2183. https://doi.org/10.3390/ma12132183
Chicago/Turabian StyleLi, Dawei, Wenhe Liao, Ning Dai, and Yi Min Xie. 2019. "Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities" Materials 12, no. 13: 2183. https://doi.org/10.3390/ma12132183
APA StyleLi, D., Liao, W., Dai, N., & Xie, Y. M. (2019). Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities. Materials, 12(13), 2183. https://doi.org/10.3390/ma12132183




