Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements
Abstract
:1. Introduction
2. Experimental Work
2.1. Preparation of SFRELC
2.2. Fabrication of Test Beams
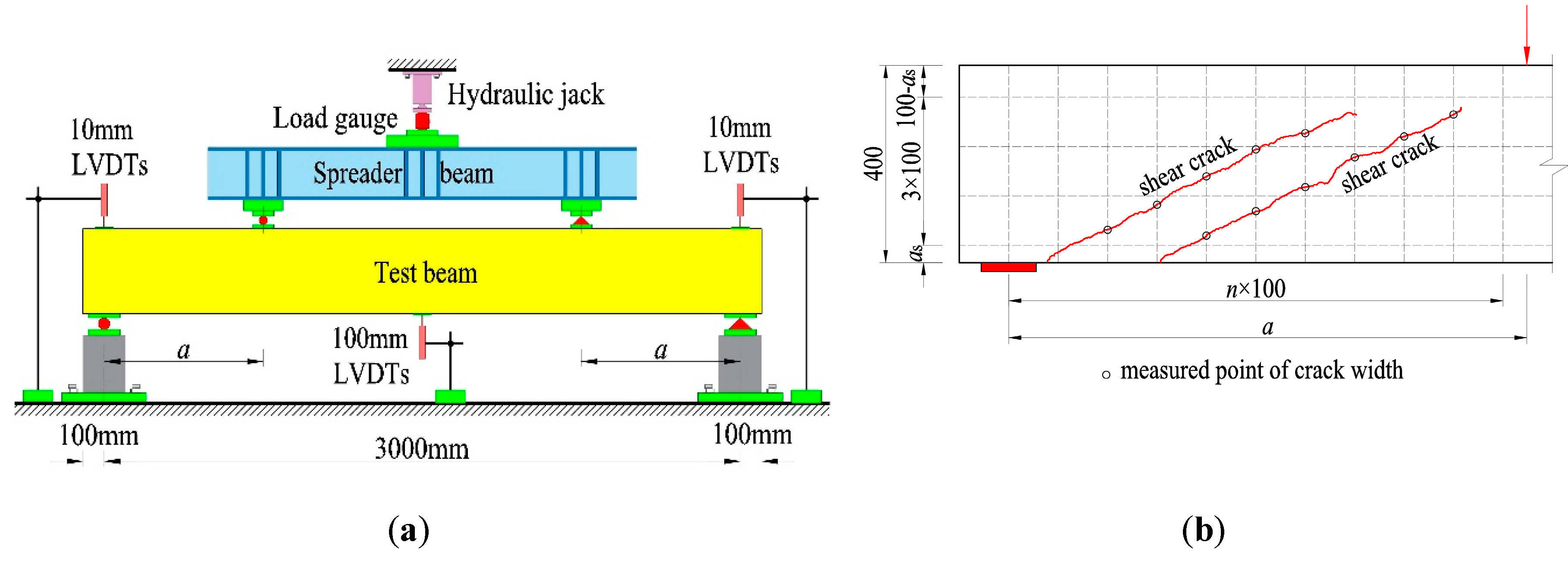
2.3. Test Method
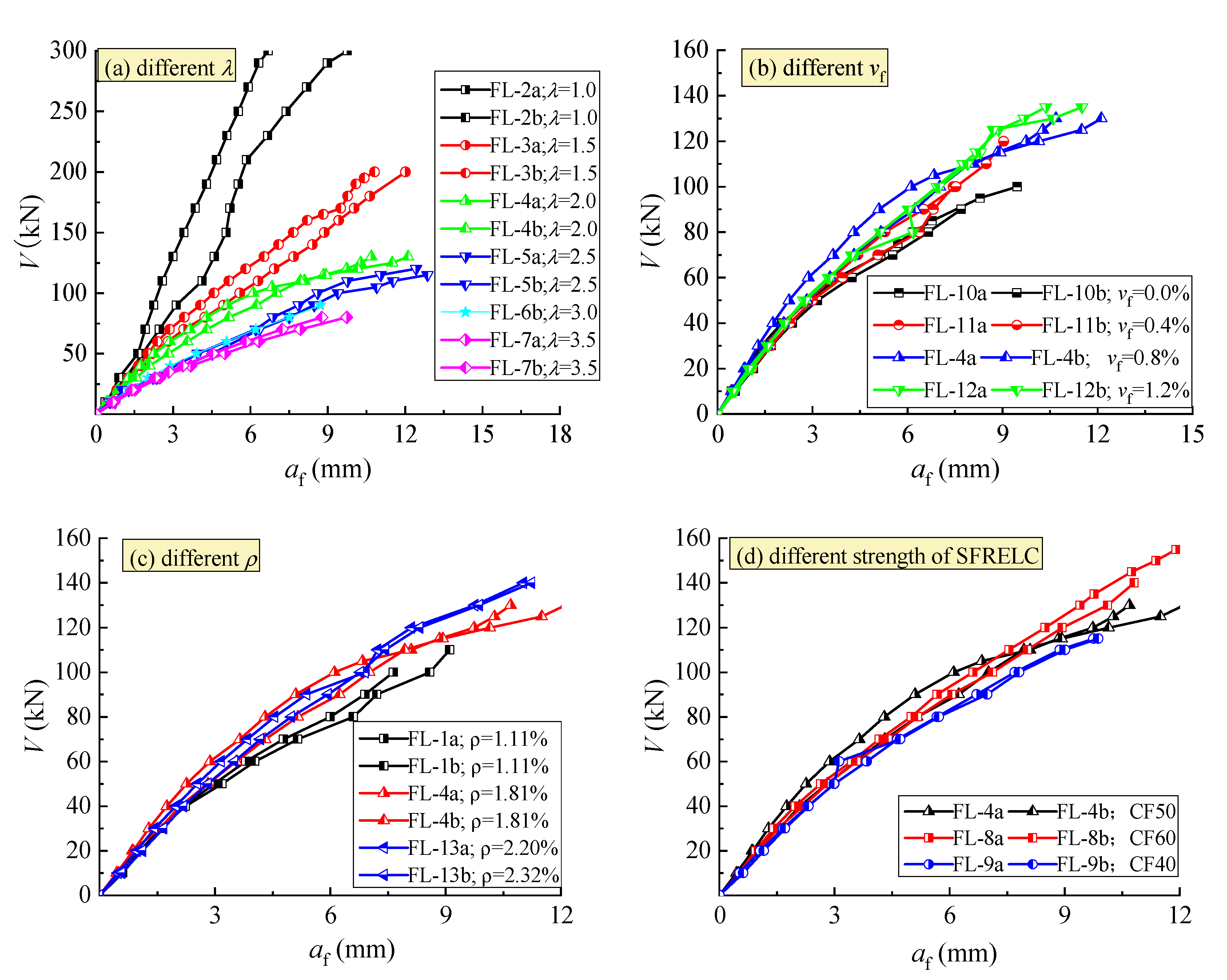
3. Discussion of Test Results
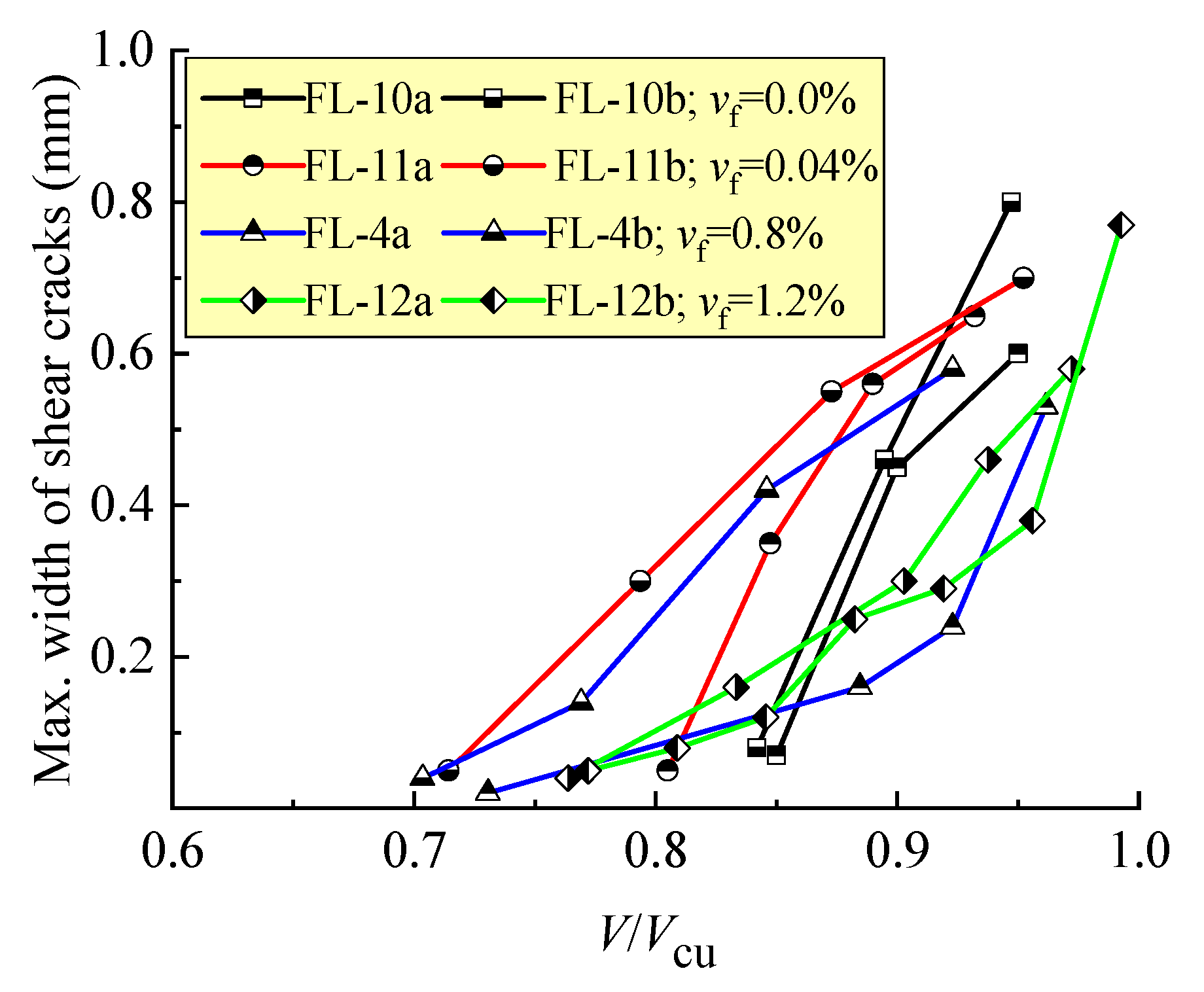
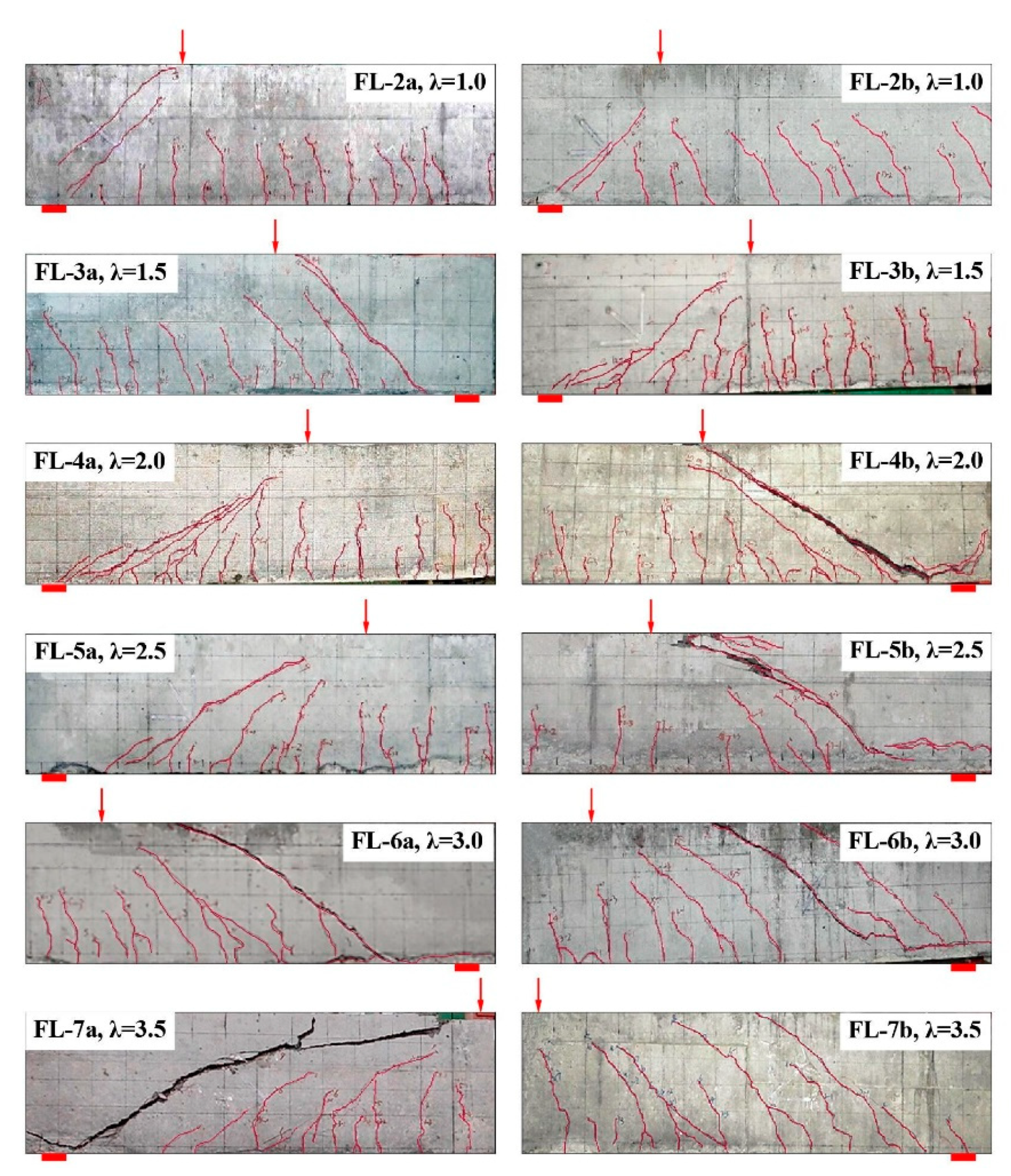
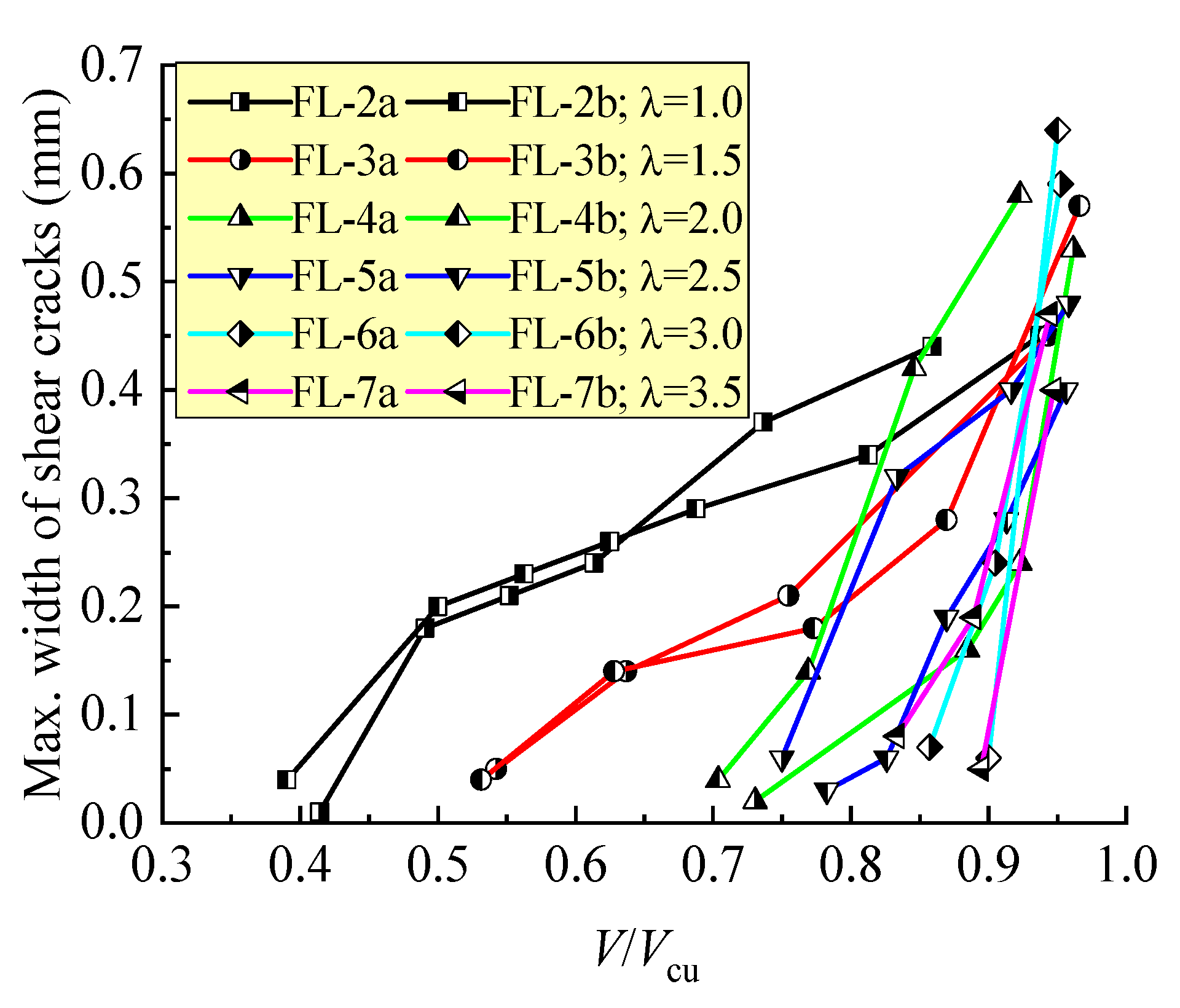
3.1. Crack Distribution in Shear-Span and Failure Modes
3.2. Mid-Span Deflection
4. Prediction of Shear Performances
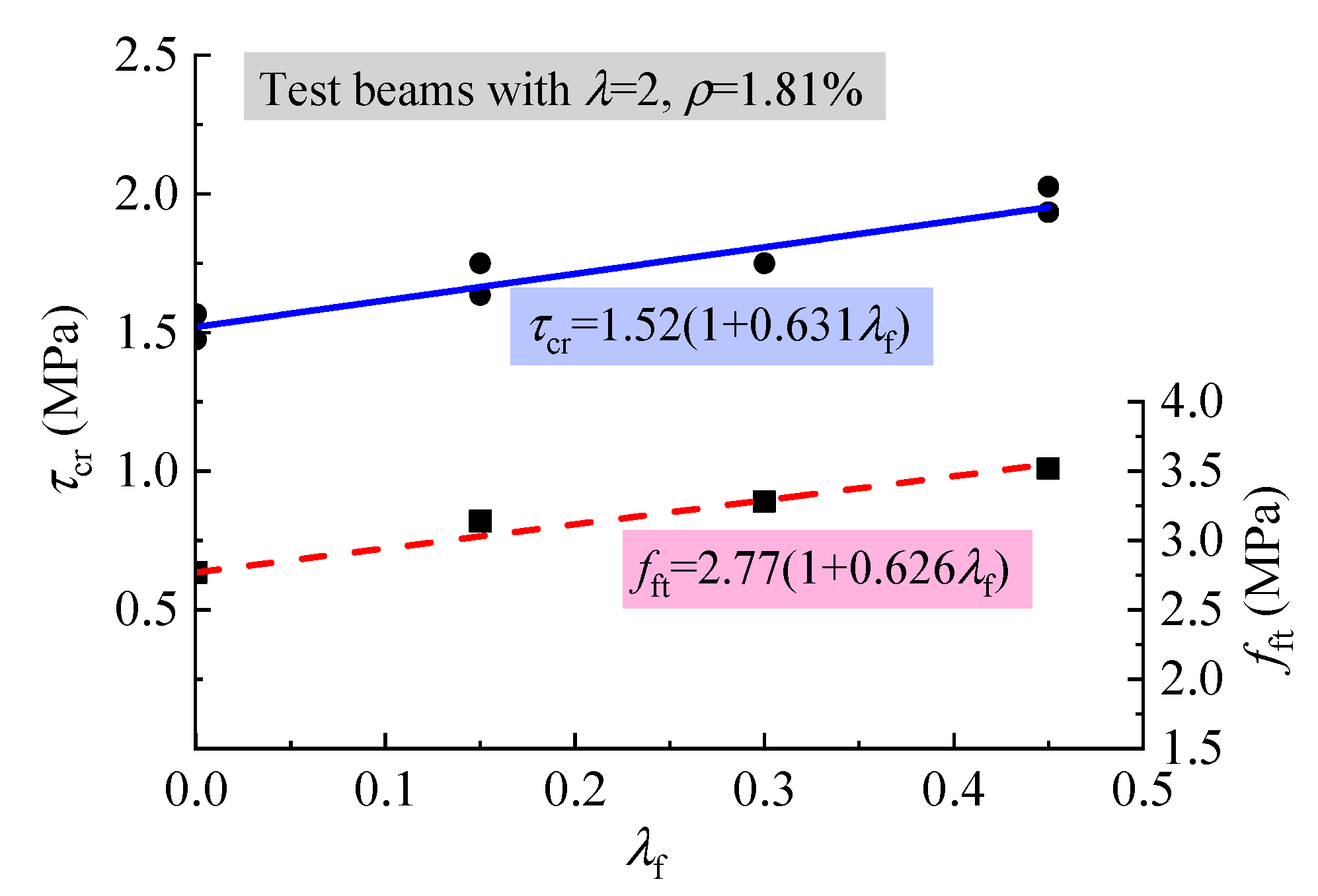
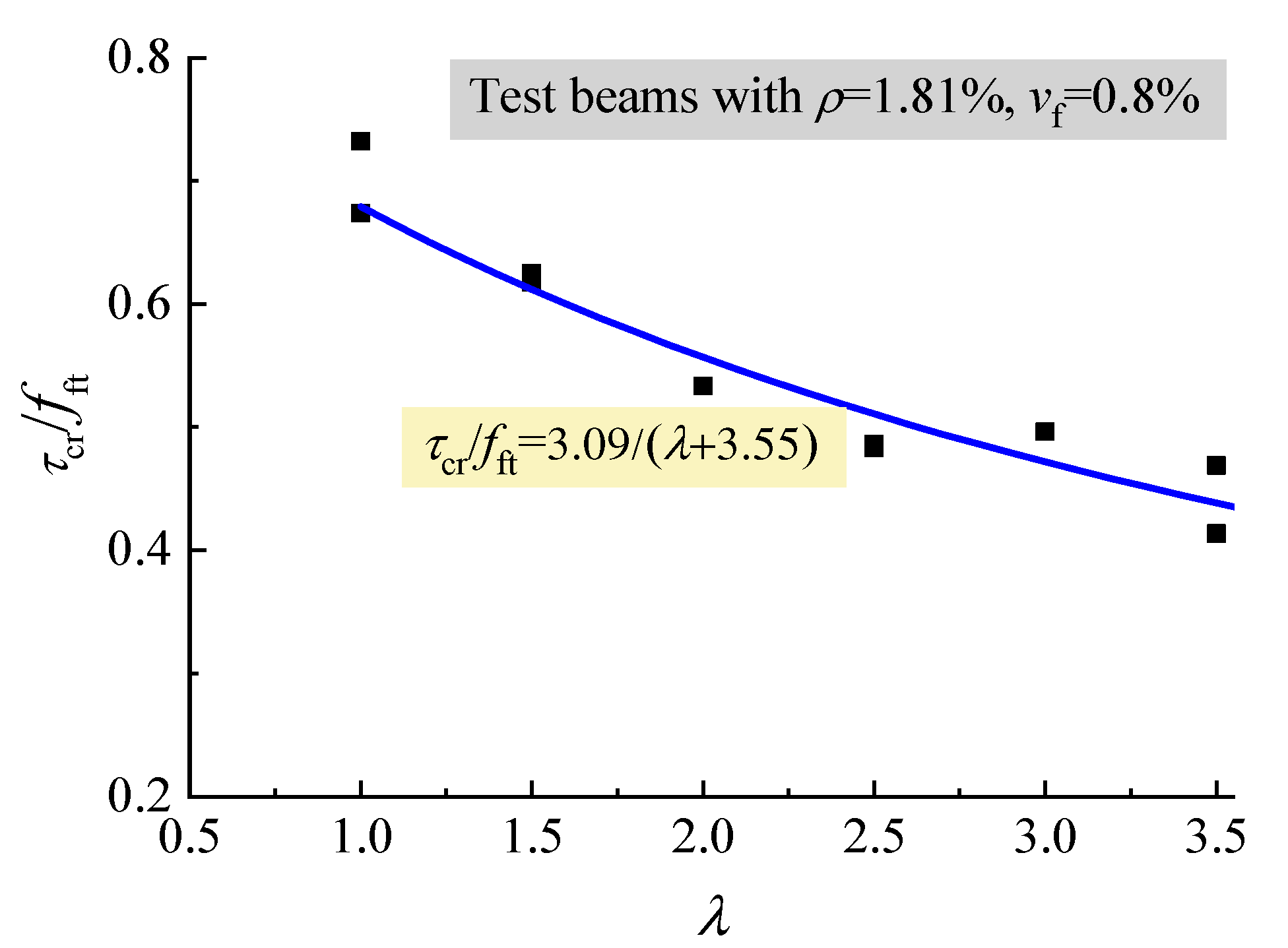
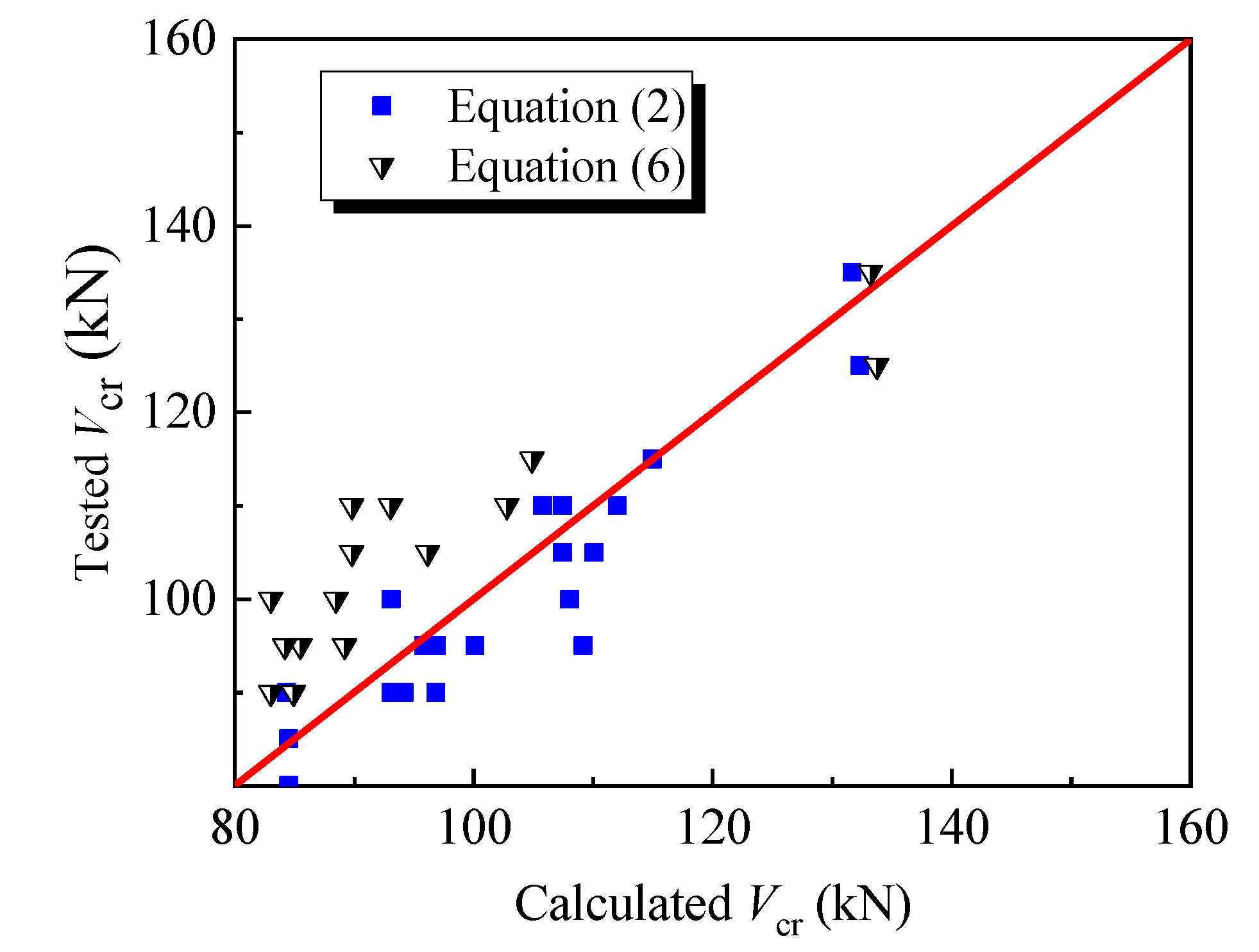
4.1. Shear-Cracking Performance
4.2. Shear Capacity
5. Suggestion for Design of Shear Capacity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hassanpour, M.; Shafigh, P.; Mahmud, H.B. Lightweight aggregate concrete fiber reinforcement—A review. Constr. Build. Mater. 2012, 37, 452–461. [Google Scholar] [CrossRef]
- Hulimka, J.; Krzywoń, R.; Jędrzejewska, A. Laboratory tests of foam concrete slabs reinforced with composite grid. Procedia Eng. 2017, 193, 337–344. [Google Scholar] [CrossRef]
- Falliano, D.; De Domenico, D.; Ricciardi, G.; Gugliandolo, E. Improving the flexural capacity of extrudable foamed concrete with glass-fiber bi-directional grid reinforcement: An experimental study. Compos. Struct. 2019, 209, 45–59. [Google Scholar] [CrossRef]
- Falliano, D.; De Domenico, D.; Ricciardi, G.; Gugliandolo, E. Compressive and flexural strength of fiber-reinforced foamed concrete: Effect of fiber content, curing conditions and dry density. Constr. Build. Mater. 2019, 198, 479–493. [Google Scholar] [CrossRef]
- Zhao, S.B.; Li, C.Y.; Qian, X.J. Experimental study on mechanical properties of steel fiber reinforced full lightweight concrete. Geotech. Spec. Publ. 2011, 212, 233–239. [Google Scholar]
- Pan, L.Y.; Yuan, H.; Zhao, S.B. Experimental study on mechanical properties of hybrid fiber reinforced full lightweight aggregate concrete. Adv. Mater. Res. 2011, 197–198, 911–914. [Google Scholar] [CrossRef]
- Zhao, M.L.; Zhao, M.S.; Chen, M.H.; Li, J.; Law, D. An experimental study on strength and toughness of steel fiber reinforced expanded-shale lightweight concrete. Constr. Build. Mater. 2018, 183, 493–501. [Google Scholar] [CrossRef]
- Li, X.K.; Zhang, X.Y.; Li, M.Q.; Zhao, M.S.; Li, C.Y. Experiments on development of strength and carbonization of steel fiber reinforced full-lightweight concrete. J. Civ. Eng. Manag. 2017, 2, 46–50. [Google Scholar]
- Zhao, S.B.; Zhao, M.S.; Zhang, X.Y.; Peng, Z.J.; Huang, T.H. Experimental study on complete stress-strain curves of steel fiber reinforced lightweight-aggregate concrete under uniaxial compression. J. Build. Struct. 2019, 5, 181–190. [Google Scholar]
- Zhao, S.B.; Li, C.Y.; Zhao, M.S.; Zhang, X.Y. Experimental study on autogenous and drying shrinkage of steel fiber reinforced lightweight-aggregate concrete. Adv. Mater. Sci. Eng. 2016, 2016, 2589383. [Google Scholar] [CrossRef]
- Zhao, M.S.; Zhang, X.Y.; Song, W.H.; Li, C.Y.; Zhao, S.B. Development of steel fiber reinforced expanded-shale lightweight concrete with high freeze-thaw resistance. Adv. Mater. Sci. Eng. 2018, 2018, 9573849. [Google Scholar] [CrossRef]
- Zhao, M.S.; Zhang, X.Y.; Yan, K.; Fei, T.; Zhao, S.B. Bond performance of deformed rebar in steel fiber reinforced lightweight-aggregate concrete affected by multi-factors. Civ. Eng. J. 2018, 3, 276–290. [Google Scholar] [CrossRef]
- Li, C.Y.; Zhao, S.B.; Chen, H.; Gao, D.Y. Experimental study on flexural capacity of reinforced SFRFLC superposed beams. J. Build. Struct. 2015, 2, 257–264. [Google Scholar]
- Li, C.Y.; Zhao, Z.F.; Ding, X.X.; Zhao, S.B. Experimental study on crack width of reinforced HSC-on-SFRFLC superposed beams. Adv. Eng. Res. 2016, 44, 16–22. [Google Scholar]
- Li, C.Y.; Ding, X.X.; Zhao, S.B.; Zhang, X.Y.; Li, X.K. Cracking resistance of reinforced SFRFLC superposed beams with partial ordinary concrete in compression zone. Open Civ. Eng. J. 2016, 10, 727–737. [Google Scholar] [CrossRef]
- Pei, S.W.; Du, Z.H.; Li, C.Y.; Shi, F.J. Research of punching performance of reinforced SFRLAC superposed two-way slabs. Appl. Mechan. Mater. 2013, 438–439, 667–672. [Google Scholar] [CrossRef]
- Zhao, M.S.; Su, J.Z.; Shang, P.R.; Zhao, S.B. Experimental study and theoretical prediction of flexural behaviors of reinforced SFRELC beams. Constr. Build. Mater. 2019, 208, 454–463. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Specification for Lightweight Aggregate Concrete Structures; JGJ12-2006; China Building Industry Press: Beijing, China, 2006.
- Canadian Standards Association. Design of Concrete Structures: Structures Design; CSA A23.3-04; Canadian Standards Association: Mississauga, ON, Canada, 2004. [Google Scholar]
- Eurocode 2. Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete; ACI 318-14; American Concrete Institute: Farmington Hill, MI, USA, 2014. [Google Scholar]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Code for Design of Concrete Structures; GB50010-2010; China Building Industry Press: Beijing, China, 2010. [Google Scholar]
- China Association for Engineering Construction Standardization. Technical Specification for Steel Fiber Reinforced Concrete Structures; CECS38:2004; China Plan Press: Beijing, China, 2004. [Google Scholar]
- ACI Committee 544. Design Considerations for Steel Fiber Reinforced Concrete; ACI 544.4R-2009; American Concrete Institute: Farmington Hill, MI, USA, 2009. [Google Scholar]
- Kotsovos, M.D. Compressive force path concept: Basis for reinforced concrete ultimate limit stat design. ACI Struct. J. 1988, 1, 68–75. [Google Scholar]
- Arslan, G. Shear strength of steel fiber reinforced concrete (SFRC) slender beams. KSCE J. Civ. Eng. 2014, 2, 587–594. [Google Scholar] [CrossRef]
- Li, S.K.; Yu, Y.Y. Shear strength calculation of simple-supported reinforced concrete beams considering shear-span to depth ratio. J. Tongji Univ. 1978, 1, 81–93. [Google Scholar]
- Li, F.L.; Zhao, S.B.; Huang, C.K. Design method of shear-resistance of steel fiber reinforced concrete beams. Ind. Constr. 2003, 10, 66–68. [Google Scholar]
- Rebeiz, K.S. Shear strength prediction for concrete members. J. Struct. Eng. 1999, 3, 301–308. [Google Scholar] [CrossRef]
- Kim, J.K.; Park, Y.D. Prediction of shear strength of reinforced concrete beams without web reinforcement. ACI Mater. J. 1996, 3, 213–222. [Google Scholar]
- Tang, C.-W.; Yen, T.; Chen, H.-J. Shear behavior of reinforced concrete beams made with sedimentary lightweight aggregate without shear reinforcement. J. Mater. Civ. Eng. 2009, 12, 730–739. [Google Scholar] [CrossRef]
- Walraven, J.; Belletti, B.; Esposito, R. Shear capacity of normal, lightweight, and high-strength concrete beams according to Model Code 2010. I: Experimental results versus analytical model results. J. Struct. Eng. 2013, 9, 1593–1599. [Google Scholar] [CrossRef]
- Lu, Y.; Ye, L.P.; Sun, H.L.; Ding, J.T. Experimental study on shear strength of lightweight high strength concrete beams. Build. Struct. 2008, 5, 16–21. [Google Scholar]
- Yi, W.J.; Ding, Y.B.; Chen, H. Experimental study on shear behavior of lightweight aggregate concrete beams without stirrups. J. Build. Struct. 2017, 6, 123–132. [Google Scholar]
- Yang, K.-H.; Ashour, A.F. Modification factor for shear capacity of lightweight concrete beams. ACI Struct. J. 2015, 4, 485–492. [Google Scholar] [CrossRef]
- Swamy, R.N.; Jones, R.; Chiam, A.T.P. Influence of steel-fibers on the shear resistance of lightweight concrete I-beams. ACI Struct. J. 1993, 1, 103–114. [Google Scholar]
- Kang, T.H.K.; Kim, K.W.; Kwak, Y.K.; Hong, S.G. Shear testing of steel fiber-reinforced lightweight concrete beams without web reinforcement. ACI Struct. J. 2011, 5, 554–561. [Google Scholar]
- Campione, G. Flexural and shear resistance of steel fiber-reinforced lightweight concrete beams. J. Struct. Eng. 2014, 4, 04013103. [Google Scholar] [CrossRef]
- Zhao, S.B.; Zhao, G.F.; Huang, C.K. Experimental research on shear cracking strength of steel fiber reinforced concrete beams. J. Hydroelectr. Eng. 1997, 4, 18–29. [Google Scholar]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Lightweight Aggregate and Its Test Methods; GB/T 17431-2010; China Standard Press: Beijing, China, 2010.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Specification for Lightweight Aggregate Concrete; JGJ51-2002; China Building Industry Press: Beijing, China, 2002.
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Steel Fiber Reinforced Concrete; JG/T472-2015; China Standard Press: Beijing, China, 2015.
- Del Vecchio, C.; Di Ludovico, M.; Balsamo, A.; Prota, A. Seismic retrofit of real beam-column joints using fiber-reinforced cement composites. J. Struct. Eng. ASCE 2018, 5, 04018026. [Google Scholar] [CrossRef]
- Arslan, G. Cracking shear strength of RC slender beams without stirrups. J. Civ. Eng. Manag. 2008, 3, 177–182. [Google Scholar] [CrossRef]

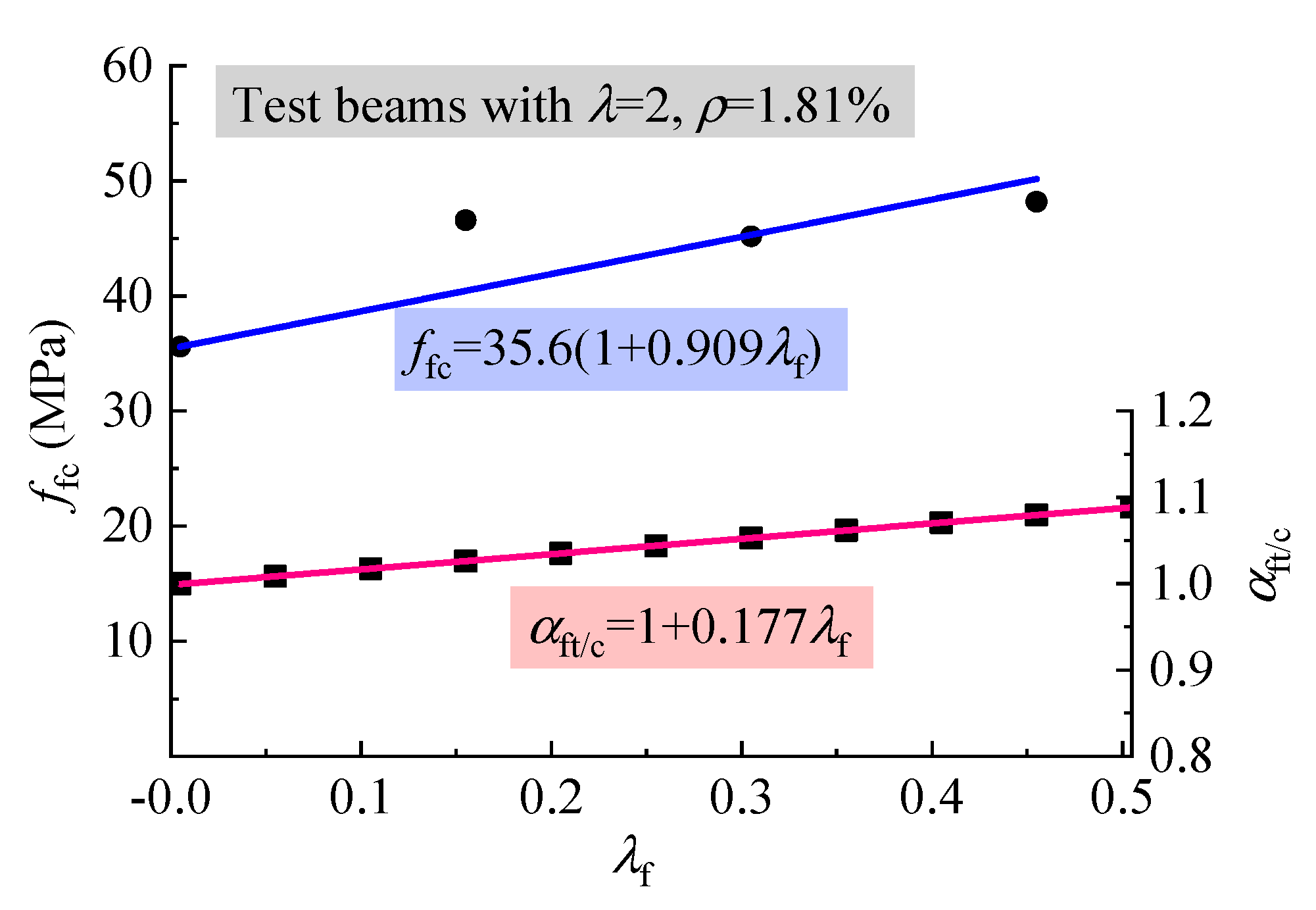
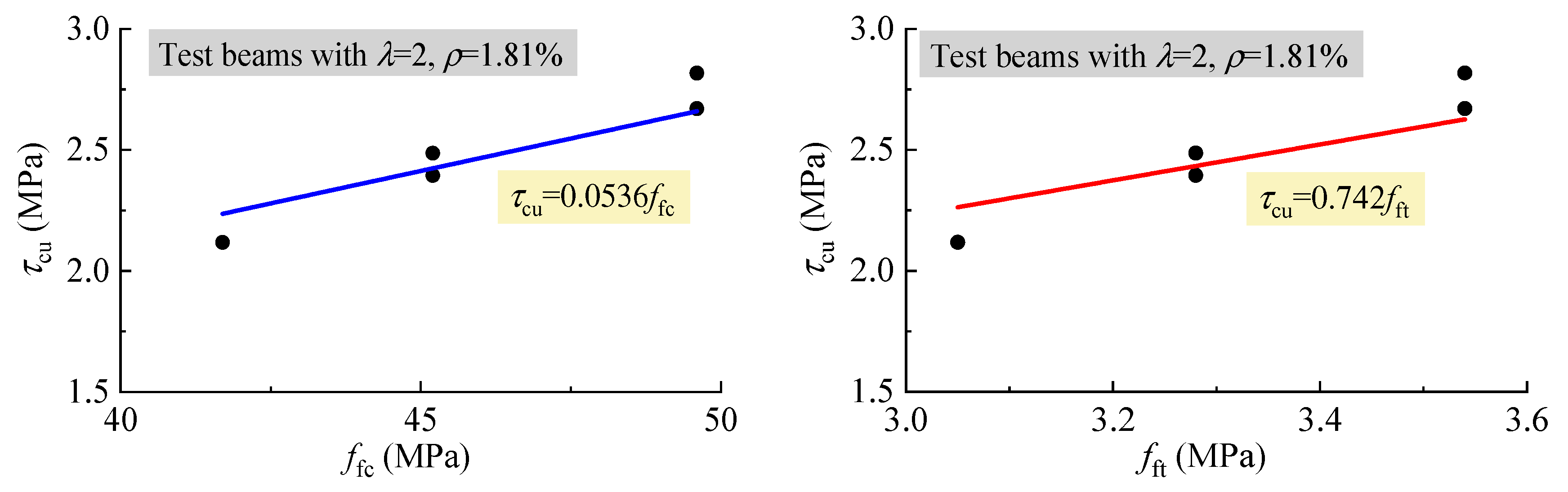
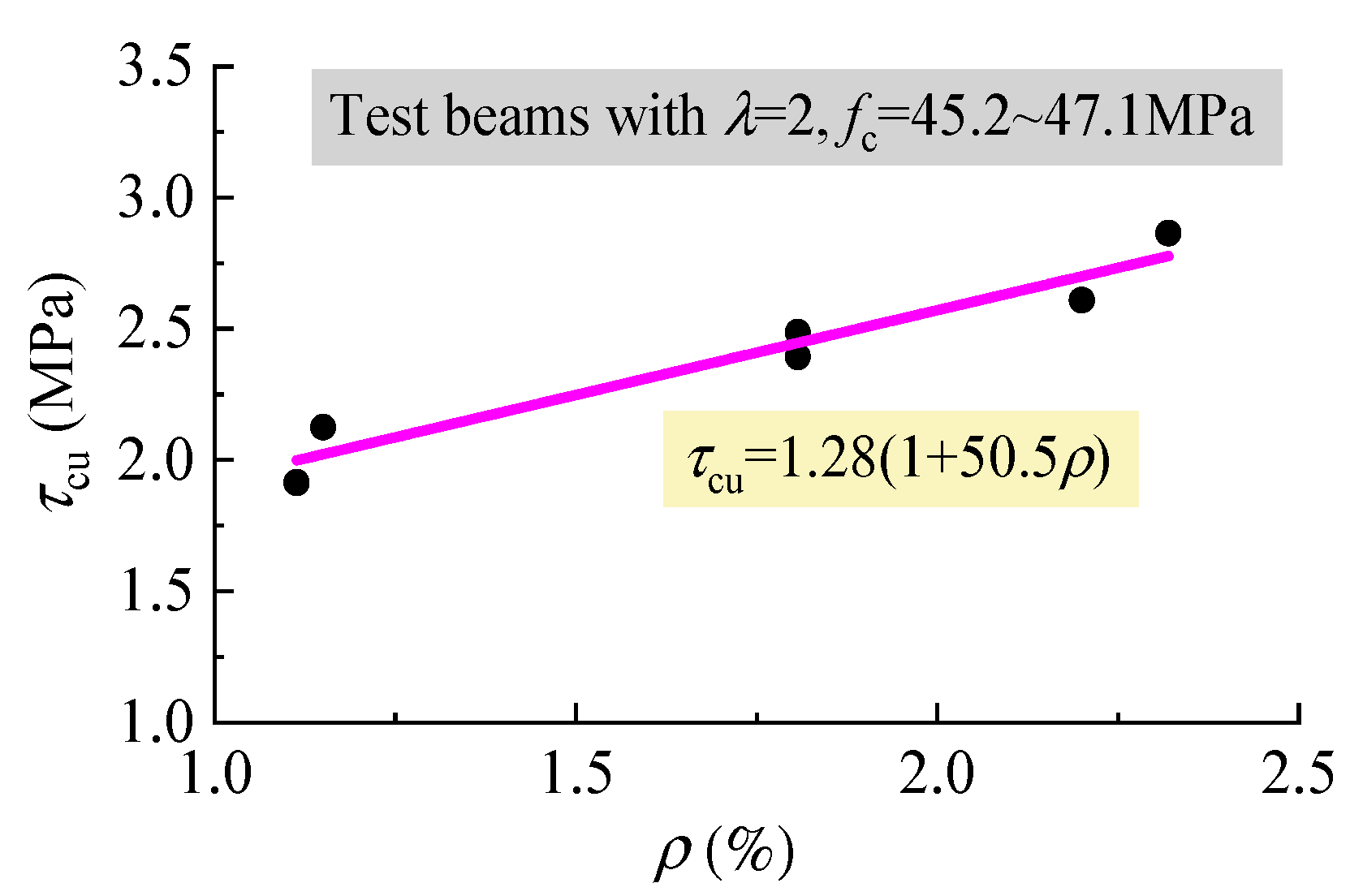
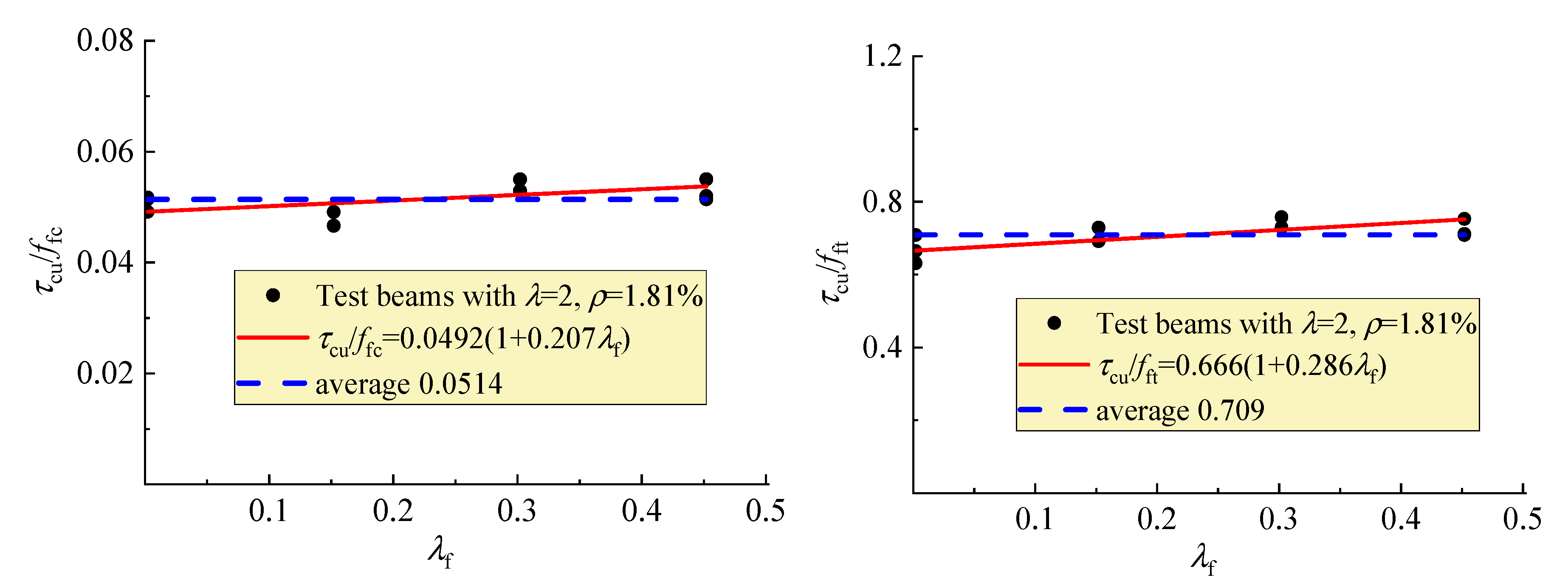
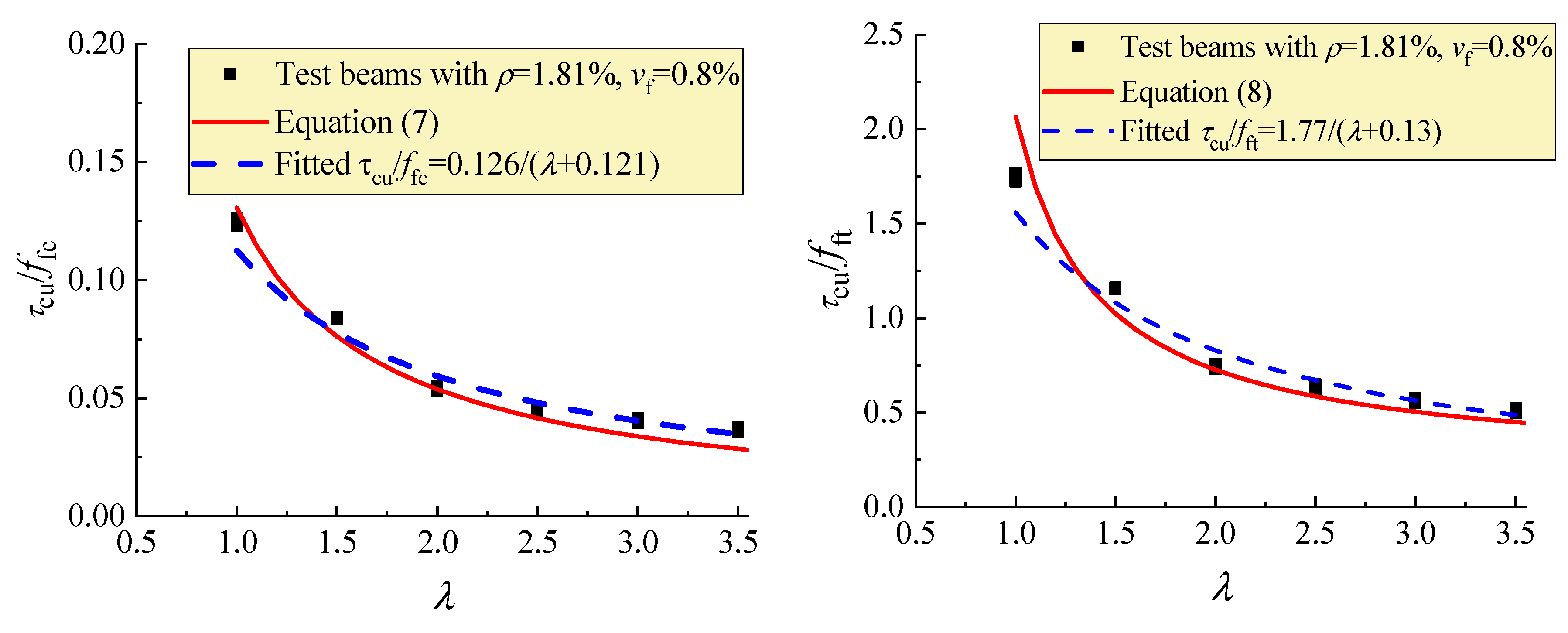
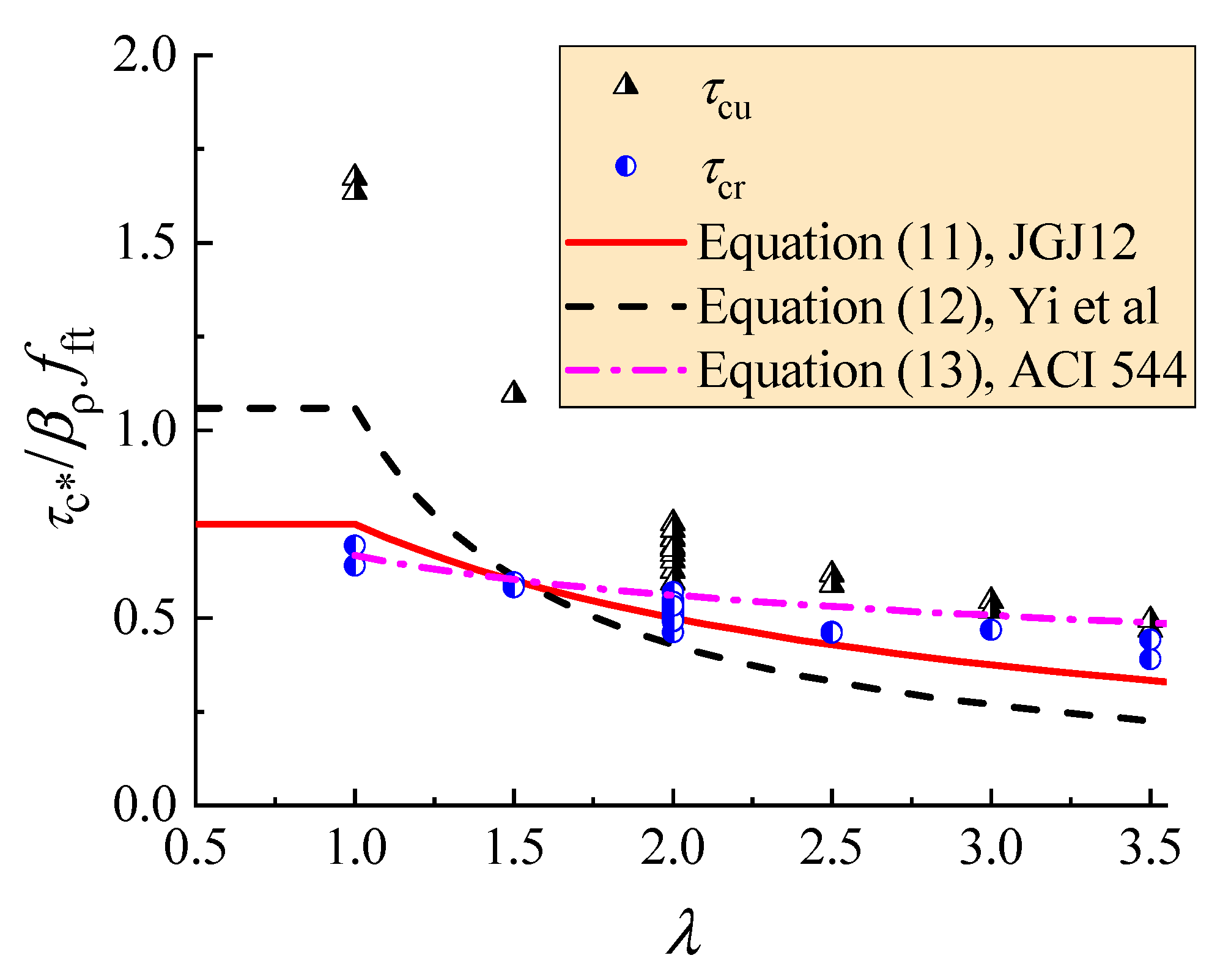
| Identifier | b (mm) | h0 (mm) | a (mm) | ρ (%) | λ | vf (%) | Tested Strength of SFRELC (MPa) | Tested Vcr (kN) | Tested Vcu (kN) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grade | fcu | ffc | fft | |||||||||
| FL-1a | 155 | 364 | 728 | 1.11 | 2.0 | 0.8 | CF50 | 58.2 | 47.1 | 3.32 | 95 | 108 |
| FL-1b | 150 | 364 | 728 | 1.15 | 2.0 | 0.8 | CF50 | 58.2 | 47.1 | 3.32 | 90 | 116 |
| FL-2a | 152 | 362 | 362 | 1.78 | 1.0 | 0.8 | CF50 | 58.6 | 47.0 | 3.35 | 135 | 326 |
| FL-2b | 153 | 362 | 362 | 1.77 | 1.0 | 0.8 | CF50 | 58.6 | 47.0 | 3.35 | 125 | 320 |
| FL-3a | 155 | 362 | 543 | 1.75 | 1.5 | 0.8 | CF50 | 54.8 | 45.2 | 3.28 | 115 | 212 |
| FL-3b | 150 | 362 | 543 | 1.81 | 1.5 | 0.8 | CF50 | 54.8 | 45.2 | 3.28 | 110 | 207 |
| FL-4a | 150 | 362 | 724 | 1.81 | 2.0 | 0.8 | CF50 | 54.8 | 45.2 | 3.28 | 95 | 130 |
| FL-4b | 150 | 362 | 724 | 1.81 | 2.0 | 0.8 | CF50 | 54.8 | 45.2 | 3.28 | 95 | 135 |
| FL-5a | 154 | 362 | 905 | 1.76 | 2.5 | 0.8 | CF50 | 58.2 | 47.1 | 3.32 | 90 | 120 |
| FL-5b | 155 | 362 | 905 | 1.75 | 2.5 | 0.8 | CF50 | 58.2 | 47.1 | 3.32 | 90 | 115 |
| FL-6a | 150 | 362 | 1086 | 1.81 | 3.0 | 0.8 | CF50 | 56.2 | 46.6 | 3.34 | 90 | 105 |
| FL-6b | 150 | 362 | 1086 | 1.81 | 3.0 | 0.8 | CF50 | 56.2 | 46.6 | 3.34 | 90 | 100 |
| FL-7a | 150 | 362 | 1267 | 1.81 | 3.5 | 0.8 | CF50 | 56.2 | 46.6 | 3.34 | 75 | 90 |
| FL-7b | 150 | 362 | 1267 | 1.81 | 3.5 | 0.8 | CF50 | 56.2 | 46.6 | 3.34 | 85 | 95 |
| FL-8a | 152 | 362 | 724 | 1.78 | 2.0 | 0.8 | CF60 | 60.0 | 49.6 | 3.54 | 95 | 155 |
| FL-8b | 150 | 362 | 724 | 1.81 | 2.0 | 0.8 | CF60 | 60.0 | 49.6 | 3.54 | 100 | 145 |
| FL-9a | 150 | 362 | 724 | 1.81 | 2.0 | 0.8 | CF40 | 48.0 | 41.7 | 3.05 | 90 | 115 |
| FL-9b | 150 | 362 | 724 | 1.81 | 2.0 | 0.8 | CF40 | 48.0 | 41.7 | 3.05 | 100 | 115 |
| FL-10a | 150 | 362 | 724 | 1.81 | 2.0 | 0 | CF50 | 42.0 | 35.6 | 2.77 | 85 | 100 |
| FL-10b | 150 | 362 | 724 | 1.81 | 2.0 | 0 | CF50 | 42.0 | 35.6 | 2.77 | 80 | 95 |
| FL-11a | 150 | 362 | 724 | 1.81 | 2.0 | 0.4 | CF50 | 56.3 | 46.6 | 3.14 | 95 | 118 |
| FL-11b | 152 | 362 | 724 | 1.78 | 2.0 | 0.4 | CF50 | 56.3 | 46.6 | 3.14 | 90 | 126 |
| FL-12a | 150 | 362 | 724 | 1.81 | 2.0 | 1.2 | CF50 | 59.2 | 48.2 | 3.52 | 110 | 144 |
| FL-12b | 150 | 362 | 724 | 1.81 | 2.0 | 1.2 | CF50 | 59.2 | 48.2 | 3.52 | 105 | 136 |
| FL-13a | 155 | 361 | 722 | 2.20 | 2.0 | 0.8 | CF50 | 58.6 | 47.0 | 3.35 | 105 | 146 |
| FL-13b | 147 | 361 | 722 | 2.32 | 2.0 | 0.8 | CF50 | 58.6 | 47.0 | 3.35 | 110 | 152 |
| Identifier | λ | vf (%) | Equation (7) | Equation (8) | Equation (9) | Equation (10) |
|---|---|---|---|---|---|---|
| FL-1a | 2.0 | 0.8 | 0.925 | 0.986 | 0.853 | 0.949 |
| FL-1b | 2.0 | 0.8 | 1.014 | 1.080 | 0.934 | 1.040 |
| FL-2a | 1.0 | 0.8 | 0.972 | 0.864 | 0.961 | 1.055 |
| FL-2b | 1.0 | 0.8 | 0.951 | 0.846 | 0.940 | 1.032 |
| FL-3a | 1.5 | 0.8 | 1.115 | 1.146 | 0.946 | 1.111 |
| FL-3b | 1.5 | 0.8 | 1.107 | 1.135 | 0.941 | 1.107 |
| FL-4a | 2.0 | 0.8 | 0.985 | 1.004 | 0.887 | 1.006 |
| FL-4b | 2.0 | 0.8 | 1.023 | 1.043 | 0.921 | 1.045 |
| FL-5a | 2.5 | 0.8 | 1.1143 | 1.120 | 1.269 | 1.236 |
| FL-5b | 2.5 | 0.8 | 1.064 | 1.069 | 1.212 | 1.180 |
| FL-6a | 3.0 | 0.8 | 1.2264 | 1.148 | 1.215 | 1.473 |
| FL-6b | 3.0 | 0.8 | 1.168 | 1.094 | 1.157 | 1.403 |
| FL-7a | 3.5 | 0.8 | 1.246 | 1.102 | 1.102 | 1.351 |
| FL-7b | 3.5 | 0.8 | 1.315 | 1.163 | 1.163 | 1.426 |
| FL-8a | 2.0 | 0.8 | 1.063 | 1.102 | 1.008 | 1.142 |
| FL-8b | 2.0 | 0.8 | 1.002 | 1.038 | 0.950 | 1.077 |
| FL-9a | 2.0 | 0.8 | 0.945 | 0.955 | 0.812 | 0.923 |
| FL-9b | 2.0 | 0.8 | 0.945 | 0.955 | 0.812 | 0.923 |
| FL-10a | 2.0 | 0 | 0.962 | 0.915 | 0.754 | 0.861 |
| FL-10b | 2.0 | 0 | 0.914 | 0.869 | 0.717 | 0.818 |
| FL-11a | 2.0 | 0.4 | 0.867 | 0.952 | 0.794 | 0.901 |
| FL-11b | 2.0 | 0.4 | 0.920 | 1.010 | 0.842 | 0.954 |
| FL-12a | 2.0 | 1.2 | 1.024 | 1.036 | 0.955 | 1.083 |
| FL-12b | 2.0 | 1.2 | 0.967 | 0.979 | 0.902 | 1.023 |
| FL-13a | 2.0 | 0.8 | 0.936 | 0.965 | 0.873 | 1.001 |
| FL-13b | 2.0 | 0.8 | 0.999 | 1.028 | 0.937 | 1.077 |
| Mean ratio | - | - | 1.029 | 1.023 | 0.956 | 1.084 |
| Variation coefficient | - | - | 0.109 | 0.089 | 0.154 | 0.159 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, C.; Zhao, M.; Yang, H.; Zhou, S. Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements. Materials 2019, 12, 1594. https://doi.org/10.3390/ma12101594
Li X, Li C, Zhao M, Yang H, Zhou S. Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements. Materials. 2019; 12(10):1594. https://doi.org/10.3390/ma12101594
Chicago/Turabian StyleLi, Xiaoke, Changyong Li, Minglei Zhao, Hui Yang, and Siyi Zhou. 2019. "Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements" Materials 12, no. 10: 1594. https://doi.org/10.3390/ma12101594
APA StyleLi, X., Li, C., Zhao, M., Yang, H., & Zhou, S. (2019). Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements. Materials, 12(10), 1594. https://doi.org/10.3390/ma12101594





