Optimum Selection of Variable Pitch for Chatter Suppression in Face Milling Operations
Abstract
1. Introduction
2. Stability Lobes for Variable Pitch Cutters
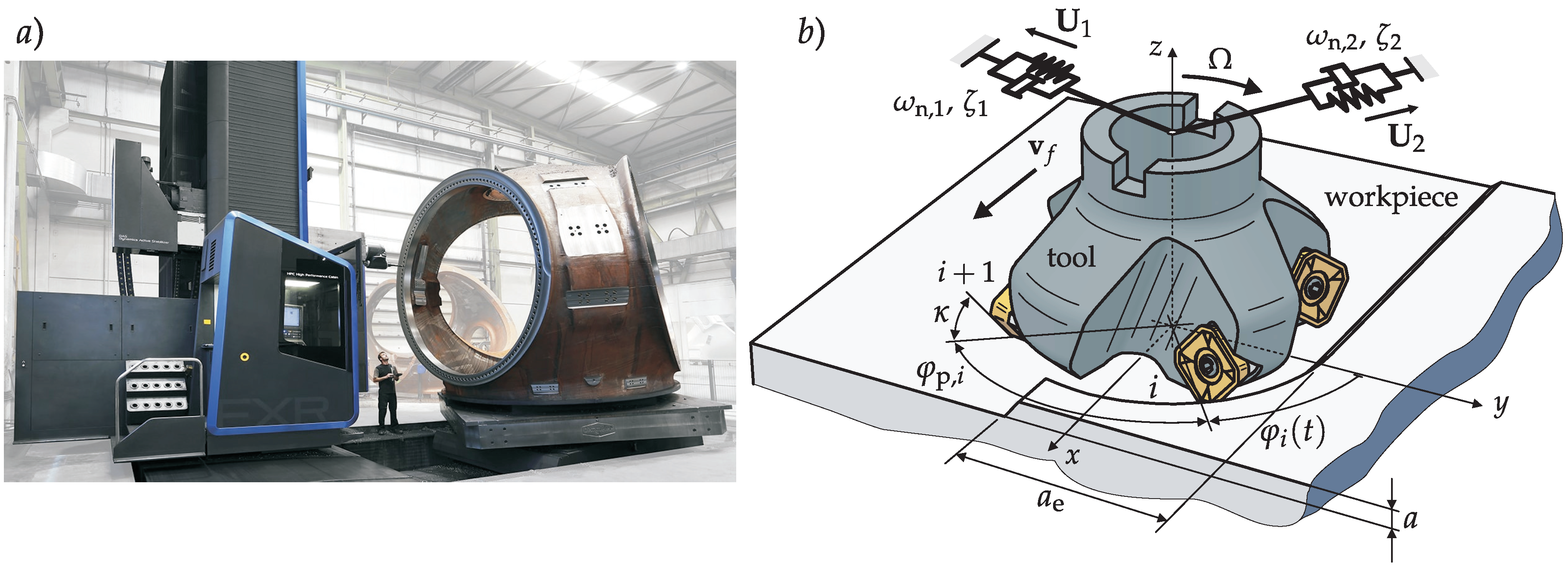
2.1. Stability Model for Variable Pitch Cutters
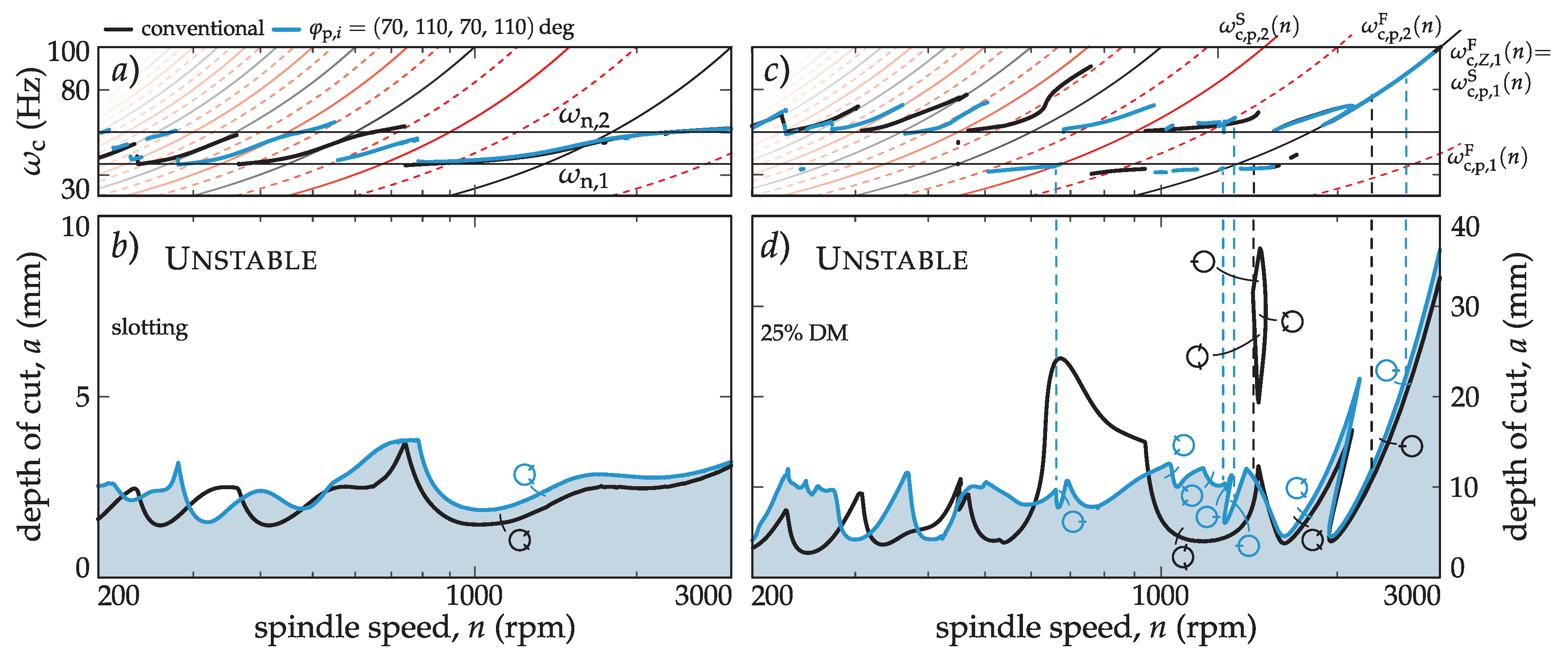
2.2. Stability Property of Variable Pitch Tools
3. Variable Pitch Tool Design Process
3.1. Slavicek´s Methodology
3.2. Budak´s Method
3.3. BF Methodology
- Selection of technological parameters in the stability chart;
- perform pre-calculation for the vibration frequency using [37];
- bisection algorithm is used to iterate the best possible angle; and
- perform feasibility analysis to check whether the tool can be manufactured at all considering the in modulo recurrences.
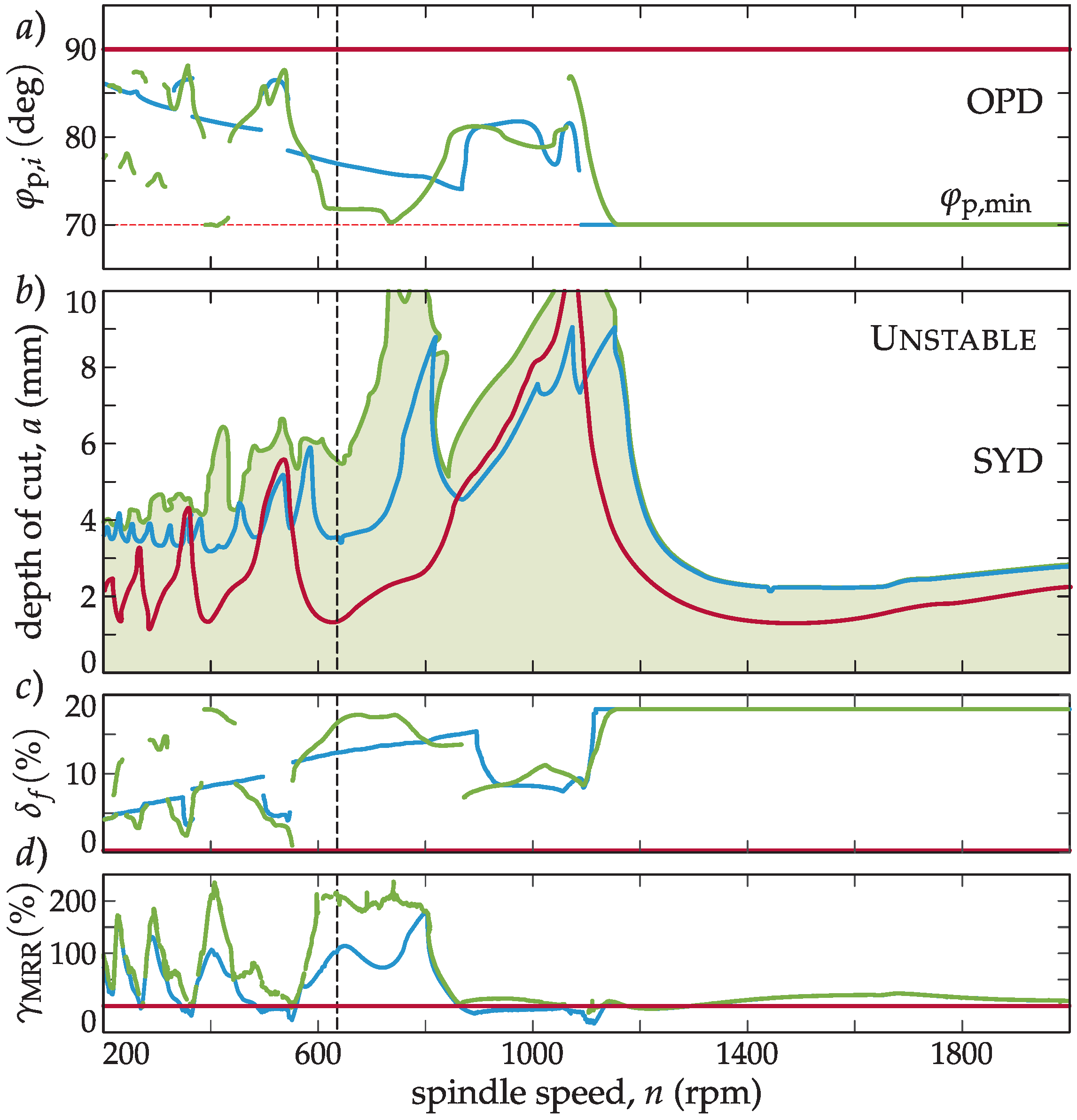
3.4. Stabilizability (SYD) and Optimal Pitch Angle Diagrams
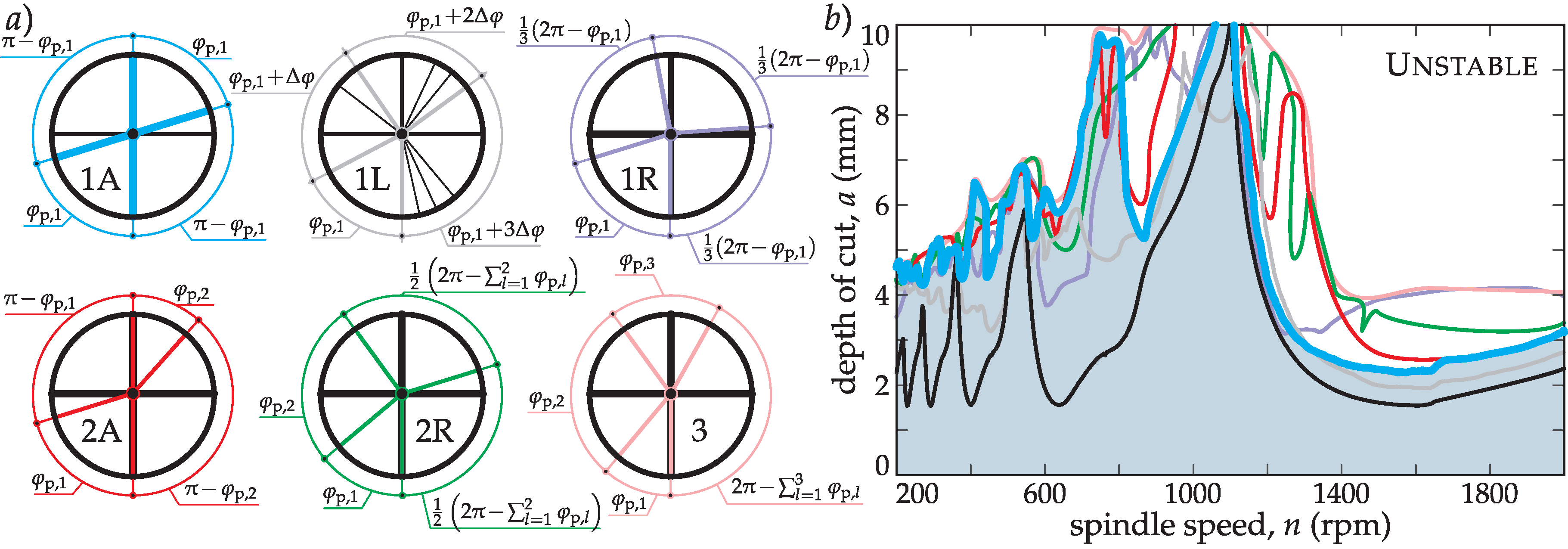
3.5. The Effect of Different Cutting Tool Topologies
3.6. Selecting the Optimal Pitch Angle
3.7. Productivity of Variable Pitch Tools
4. Experimental Validation
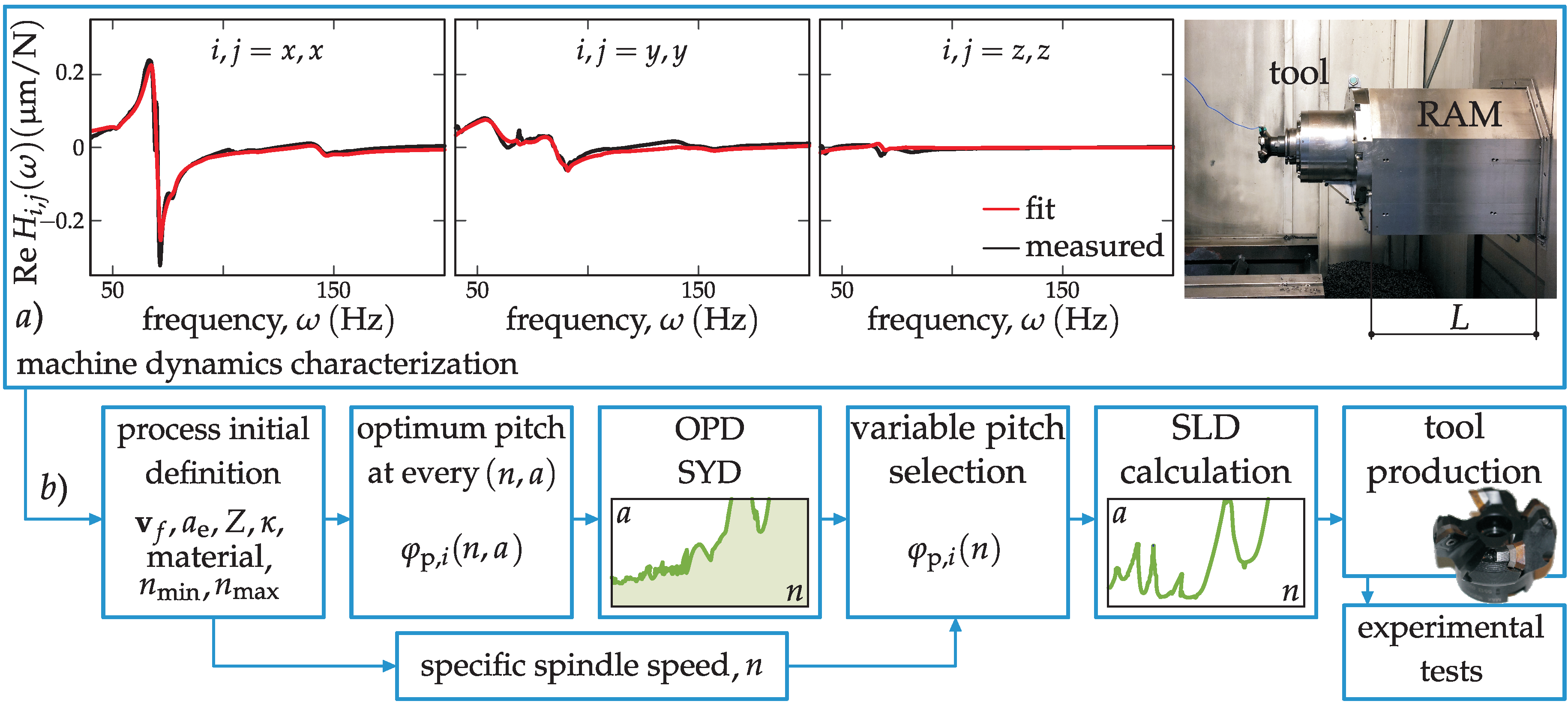
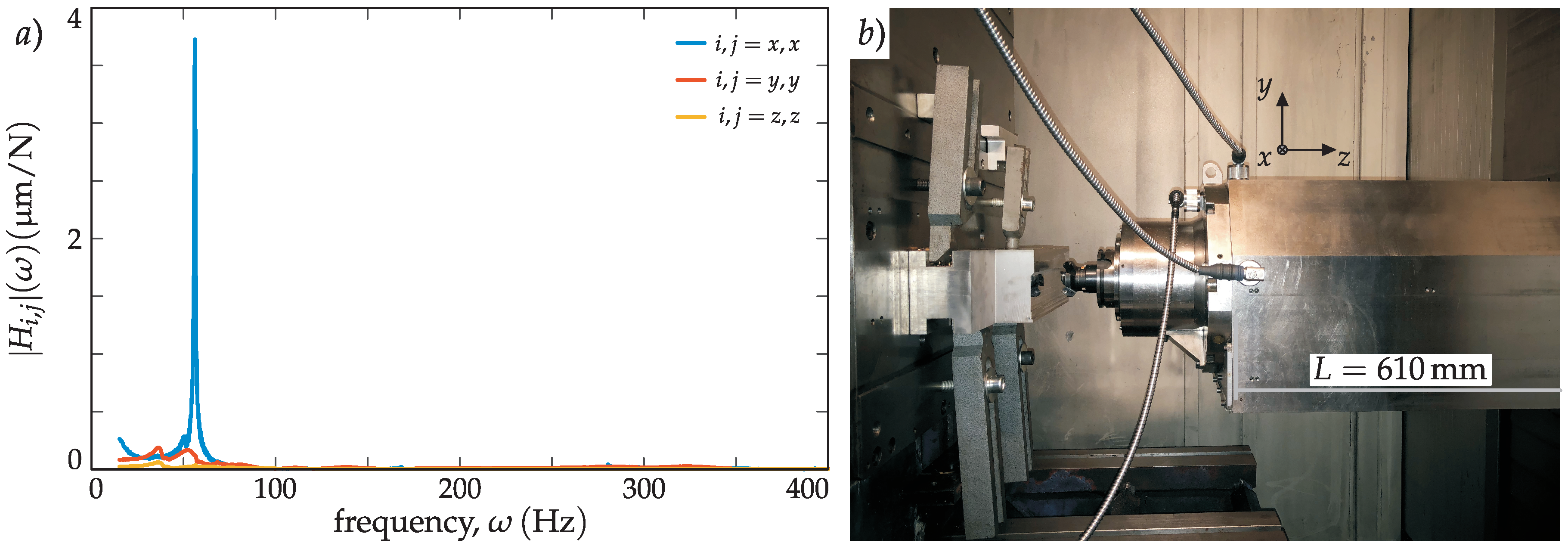
4.1. Machine Dynamics Characterization and Process Definition
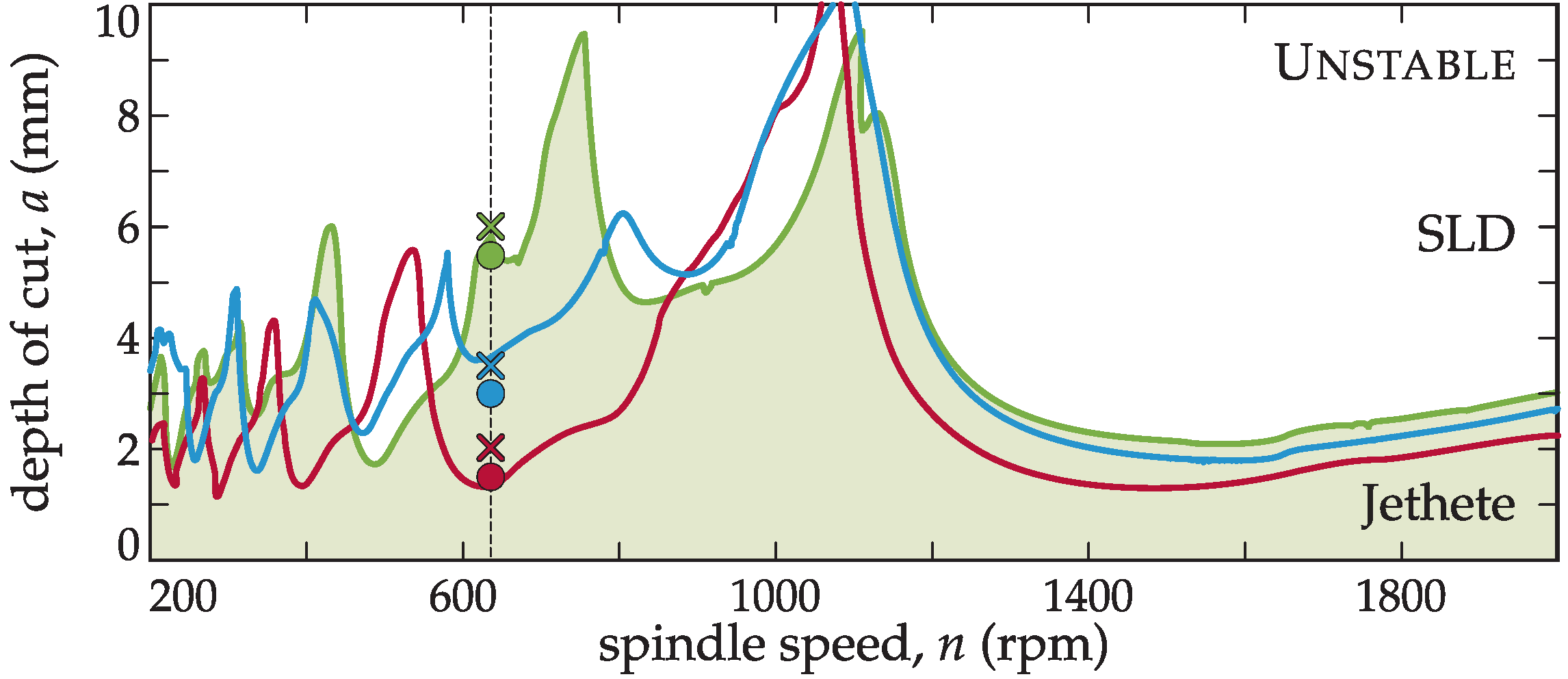
4.2. Objective 1: Optimum Pitch Design Through the BF Method
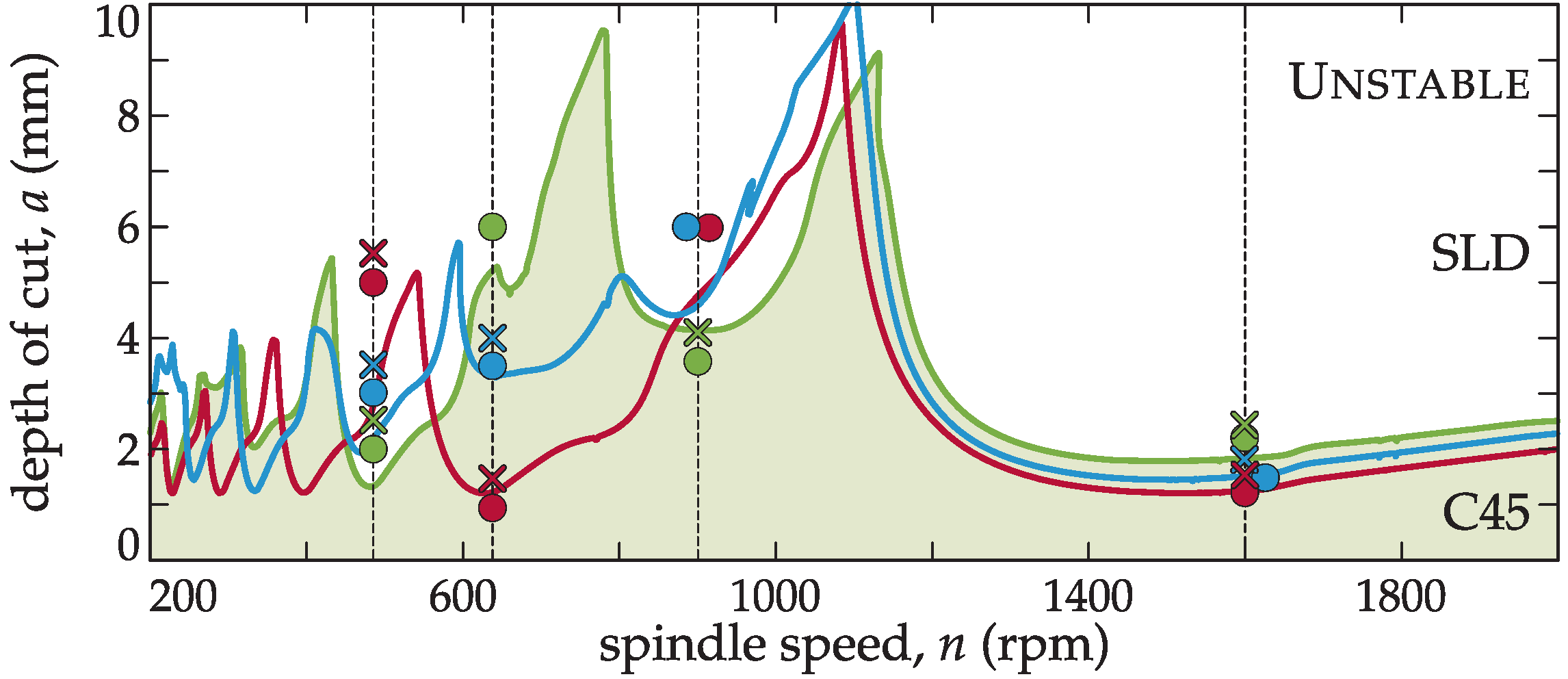
4.3. Objective 2: Optimum pitch variation with spindle speed
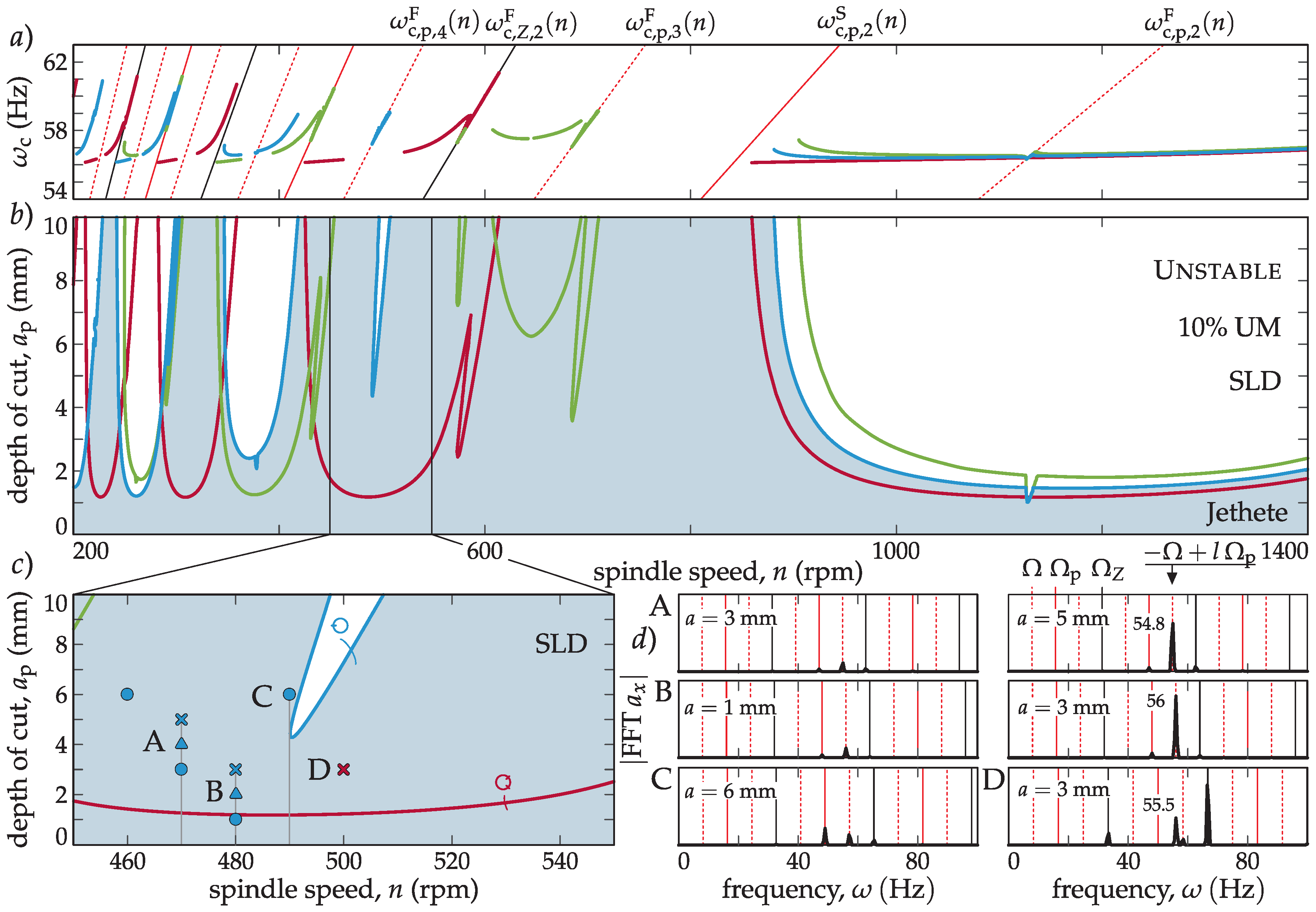
4.4. Objective 3: Experimental Evidence of New Flip Family
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a (m) | axial depth of cut, |
| ae (m) | radial engagement, |
| Ai (1) | ith periodic directional coefficient matrices in (x, y, z) system, |
| g (1) | screen function of radial immersion, |
| G (N) | only time dependent periodic part of the cutting force, |
| hi (m) | local momentary chip thickness on the ith edge, |
| H (m/N) | frequency response function (FRF), |
| f (m/rev) | complete feed per revolution, |
| fi (m) | feed motion during ith delay τi, |
| fi (m) | feed vector describing fi motion in x direction, |
| fZ (m/tooth) | feed per tooth, |
| fZ,max (m) | maximum allowed feed per tooth allowed on an insert, |
| F (N) | momentary resultant cutting force, |
| Kc,t (N/m2) | tangential cutting coefficient, |
| Ke (N/m) | edge coefficient vector in (t,r,a) system, |
| kk (N/m) | approximated modal stiffness in proportionally damped sense, |
| L (m) | overhang of the RAM of the machine, |
| n (rpm) | spindle speed, |
| n (1) | normal vector to the local edge, |
| q (m (kg/s)1/2) | modal displacement vector, |
| Qk (m/N/s) | modal scaling factor, |
| qp (m (kg/s)1/2) | time periodic stationary solution in modal space, |
| r (m/N) | magnitude of the FRF, |
| t (s) | process time, |
| (t,r,a) | local edge system, |
| T (1) | transformation matrix from (t,r,a) to (x, y, z) system, |
| u (m (kg/s)1/2) | perturbation in modal space for asymptotic analysis, |
| U ((s/kg)1/2) | mass normalized modal transformation matrix, |
| Uk ((s/kg)1/2) | kth mass normalized mode shape vector, |
| (x, y, z) | spatial system, |
| x (m) | spatial displacement vector in spatial directions (x, y, z), |
| xp (m) | spatial time periodic stationary solution, |
| y (m) | spatial perturbation for asymptotic analysis, |
| vc (m/s) | cutting speed, |
| vf (m/s) | feed (secondary motion) speed, |
| MRR (m3/s) | material removal rate, |
| N (1) | integer divisor of tool period T to the principle period Tp, |
| Nτ (1) | number of delays, |
| T (s) | tool period, |
| Tp (s) | principle period, |
| Z (1) | number of inserts (teeth), |
| z (m (kg/s)1/2) | discrete state vector for semidiscretization, |
| γMRR (1) | relative gain on MRR, |
| δf (1) | relative drop on the complete feed f, |
| ε (rad) | regenerative phase, |
| ζk (1) | kth damping ratio, |
| κ (rad) | lead angle, |
| κc (1) | nominal cutting coefficient vector in (t,r,a) system, |
| λ (rad/s) | characteristic exponent, |
| λk (rad/s) | kth pole, |
| μ (1) | Floquet multiplier, |
| τi (s) | ith delay corresponding to the ith pitch angle φp,i, |
| τmax (s) | maximum delay, |
| φi (rad) | position angle of the ith edge, |
| φp,i (rad) | pitch angle between the ith and (i + 1)th edges, |
| ψ (rad) | phase of the FRF |
| ω (rad/s, Hz) | vibration frequency, |
| ωc,b (rad/s) | base critical (chatter) frequency, |
| (rad/s, Hz) | lth critical frequency of flip stability loss corresponding to the principal period, |
| (rad/s, Hz) | lth critical frequency of the saddle-node stability loss on principal period, |
| (rad/s, Hz) | lth critical frequency of flip stability loss corresponding to tooth passing period, |
| ωn,k (rad/s) | kth natural angular frequency, |
| Δ (rad) | regenerative phase difference, |
| Δt (s) | time in semidiscretization, |
| Λ (N/m) | eigenvalue in zeroth order solution, |
| Φ (1) | Floquet transition matrix compiled by semidiscretization, |
| Ω (rad/s) | angular velocity of the tool, |
| Ωp (rad/s) | principle angular frequency. |
References
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Burtscher, J.; Fleischer, J. Adaptive tuned mass damper with variable mass for chatter avoidance. CIRP Ann. 2017, 66, 397–401. [Google Scholar] [CrossRef]
- Munoa, J.; Iglesias, A.; Olarra, A.; Dombovari, Z.; Zatarain, M.; Stepan, G. Design of self-tuneable mass damper for modular fixturing systems. CIRP Ann. 2016, 65, 389–392. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Kleinwort, R.; Fagerer, P.; Altintas, Y. Automatic tuning of active vibration control systems using inertial actuators. CIRP Ann. 2017, 66, 365–369. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Erkorkmaz, K.; Iglesias, A.; Barrios, A.; Zatarain, M. Active suppression of structural chatter vibrations using machine drives and accelerometers. CIRP Ann. 2015, 64, 385–388. [Google Scholar] [CrossRef]
- Seguy, S.; Insperger, T.; Arnaud, L.; Dessein, G.; Peigné, G. On the stability of high-speed milling with spindle speed variation. Int. J. Adv. Manuf. Technol. 2010, 48, 883–895. [Google Scholar] [CrossRef]
- Bediaga, I.; Egaña, I.; Munoa, J.; Zatarain, M.; De Lacalle, L.L. Chatter avoidance method for milling process based on sinusoidal spindle speed variation method: Simulation and experimental results. In Proceedings of the 10th CIRP International Workshop on Modeling of Machining Operations, Reggio Calabria, Italy, 27–28 August 2007. [Google Scholar]
- Bediaga, I.; Munoa, J.; Hernández, J.; De Lacalle, L.L. An automatic spindle speed selection strategy to obtain stability in high-speed milling. Int. J. Mach. Tools Manuf. 2009, 49, 384–394. [Google Scholar] [CrossRef]
- Ezugwu, E.O. High speed machining of aero-engine alloys. J. Braz. Soc. Mech. Sci. Eng. 2004, 26, 1–11. [Google Scholar] [CrossRef]
- Iglesias, A.; Munoa, J.; Ciurana, J. Optimisation of face milling operations with structural chatter using a stability model based process planning methodology. Int. J. Adv. Manuf. Technol. 2014, 70, 559–571. [Google Scholar] [CrossRef]
- Budak, E.; Kops, L. Improving productivity and part quality in milling of titanium based impellers by chatter suppression and force control. CIRP Ann. -Manuf. Technol. 2000, 49, 31–36. [Google Scholar] [CrossRef]
- Hahn, R.S. Metal-Cutting Chatter & Its Elimination. Trans. ASME 1952, 74, 1073–1080. [Google Scholar]
- Altıntas, Y.; Engin, S.; Budak, E. Analytical stability prediction and design of variable pitch cutters. J. Manuf. Sci. Eng. 1999, 121, 173–178. [Google Scholar] [CrossRef]
- Slavicek, J. The effect of irregular tooth pitch on stability of milling. In Proceedings of the 6th MTDR Conference, Manchester, UK, 13–15 September 1965. [Google Scholar]
- Vanherck, P. Increasing milling machine productivity by use of cutters with non-constant cutting edge pitch. In Proceedings of the 8th MTDR Conference; University of Manchester: Manchester, UK, 1967; pp. 947–960. [Google Scholar]
- Varterasian, J.H. White noise: A deterrent to milling cutter chatter. Manuf. Eng. Manag. 1971, 67, 26. [Google Scholar]
- Tlusty, J.; Ismail, F.; Zaton, W. Use of special milling cutters against chatter. In NAMRC; University of Wisconsin: Madison, WI, USA, 1983; Volume 11, pp. 408–415. [Google Scholar]
- Olgac, N.; Sipah, R. Dynamics & stability of variable-pitch milling. J. Vib. Control 2007, 13, 1031–1043. [Google Scholar]
- Munoa, J.; Dombovari, Z.; Mancisidor, I.; Yang, Y.; Zatarain, M. Interaction between multiple modes in milling processes. Mach. Sci. Technol. 2013, 17, 165–180. [Google Scholar] [CrossRef]
- Dombovari, Z.; Altintas, Y.; Stepan, G. The effect of serration on mechanics and stability of milling cutters. Int. J. Mach. Tools Manuf. 2010, 50, 511–520. [Google Scholar] [CrossRef]
- Stepan, G.; Hajdu, D.; Iglesias, A.; Takacs, D.; Dombovari, Z. Ultimate capability of variable pitch milling cutters. CIRP Ann. 2018, 67, 373–376. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Maruda, R.W.; Barrans, S.; Nieslony, P.; Krolczyk, G.M. Optimisation of machining parameters during ball end milling of hardened steel with various surface inclinations. Measurement 2017, 111, 18–28. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Maruda, R.W.; Krolczyk, G.M.; Nieslony, P. Application of signal to noise ratio and grey relational analysis to minimize forces and vibrations during precise ball end milling. Precis. Eng. 2018, 51, 582–596. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Iglesias, A.; Munoa, J.; Ciurana, J.; Dombovari, Z.; Stepan, G. Analytical expressions for chatter analysis in milling operations with one dominant mode. J. Sound Vib. 2016, 375, 403–421. [Google Scholar] [CrossRef]
- Dombovari, Z.; Munoa, J.; Stepan, G. General Milling Stability Model for Cylindrical Tools. Procedia CIRP 2012, 4, 90–97. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Semidiscretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Compean, F.I.; Olvera, D.; Campa, F.J.; López De Lacalle, L.N.; Elias-Zuniga, A.; Rodriguez, C.A. Characterization and stability analysis of a multivariable milling tool by the enhanced multistage homotopy perturbation method. Int. J. Mach. Tools Manuf. 2012, 57, 27–33. [Google Scholar] [CrossRef]
- Bachrathy, D.; Stepan, G. Improved Prediction of Stability Lobes with Extended Multi Frequency Solution. CIRP Ann. 2013, 62, 411–414. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical Prediction of Chatter Stability in Milling—Part I: General Formulation. J. Dyn. Syst. Meas. Control. 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Ewins, D. Modal Testing: Theory, Practice, and Applications; Research Studies Press: Letchworth, UK, 2000. [Google Scholar]
- Budak, E. An analytical design method for milling cutters with nonconstant pitch to increase stability-Part I: Theory. ASME J. Manuf. Sci. Eng. 2003, 125, 29–34. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. -Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Szalai, R.; Stepan, G.; Hogan, J. Global dynamics of low immersion high-speed milling. Chaos 2004, 14, 1069–1077. [Google Scholar] [CrossRef]
- Farkas, M. Periodic Motions; Springer: Berlin, Germany; New York, NY, USA, 1994. [Google Scholar]
- Dombovari, Z.; Iglesias, A.; Stepan, G. Study of the tuning of variable pitch milling cutters. In Proceedings of the 39th MATADOR Conference on Advanced Manufacturing, Manchester, UK, 5–7 July 2017. [Google Scholar]
- Dombovari, Z.; Iglesias, A.; Zatarain, M.; Insperger, T. Prediction of multiple dominant chatter frequencies in milling processes. Int. J. Mach. Tools Manuf. 2011, 51, 457–464. [Google Scholar] [CrossRef]
- Bachrathy, D.; Stepan, G. Bisection method in higher dimensions and the efficiency number. Period. Polytech. Mech. Eng. 2012, 56, 81–87. [Google Scholar] [CrossRef]
- Comak, A.; Budak, E. Modeling dynamics and stability of variable pitch and helix milling tools for development of a design method to maximize chatter stability. Precis. Eng. 2017, 47, 459–468. [Google Scholar] [CrossRef]
- Dombovari, Z. Dominant modal decomposition method. J. Sound Vib. 2017, 392, 56–69. [Google Scholar] [CrossRef]
| ωn,k (Hz) | ζk (%) | Qk (μm/N/s) | ~kk (N/μm) | Uk/|Uk| (1) | |
|---|---|---|---|---|---|
| 1 | 37.8 | 4.86 | 0.09–1.17j | 101.36 | [0.07 0.75 0.66]T |
| 2 | 58.0 | 13.27 | 2.07–3.08j | 59.05 | [0.22 0.97 0.08]T |
| 3 | 69.6 | 3.10 | 1.34–5.30j | 41.28 | [0.98 0.13 0.11]T |
| 4 | 86.6 | 5.85 | −0.90–2.68j | 101.32 | [0.09 0.97 0.22]T |
| 5 | 144.8 | 3.02 | −0.48–1.08j | 422.24 | [0.83 0.55 0.10]T |
| fZ (mm/tooth) | vc (m/min) | n (rpm) | ae (%) | Cutting Direction | L (mm) | Workpiece | Cutting Coefficient (N/mm2) |
|---|---|---|---|---|---|---|---|
| 0.20 | 100 | 636 | 80 | X- up milling | 400 | Jethete M152 | Kc, t = 1843 Kc, r = 625 Kc, a = 467 |
| Tuning Methodology | Pitch Angles, φp,i (deg) | Picture |
|---|---|---|
| none | (90, 90, 90, 90) |  |
| BS | (77, 103, 77, 103) |  |
| BF | (72, 108, 72, 108) |  |
| fZ (mm/tooth) | N (rpm) | ae (%) | Cutting Direction | L (mm) | Workpiece | Cutting Coefficient (N/mm2) |
|---|---|---|---|---|---|---|
| 0.20 | 486 636 950 1600 | 80 | -X Up milling | 400 | Steel C45 | Kc, t = 1836 Kc, r = 734 Kc, a = 387 |
| fZ (mm/tooth) | N (rpm) | ae (%) | Cutting Direction | L (mm) | Workpiece | Cutting Coefficient (N/mm2) |
|---|---|---|---|---|---|---|
| 0.20 | 460 470 480 490 500 | 10 | -X up milling | 610 | Jethete M152 | Kc, t = 1843 Kc, r = 625 Kc, a = 467 |
| k | ωn,k (Hz) | ζk (%) | Qk (μm/N/s) | kk (N/μm) | Uk/|Uk| (1) |
|---|---|---|---|---|---|
| 1 | 49.8 | 2.73 | 0.27–0.59j | 264.78 | [1 0 0]T |
| 2 | 56.1 | 0.58 | 0.66–6.26j | 28.19 | [1 0 0]T |
| 3 | 53.0 | 9.90 | −0.47–5.24j | 31.94 | [0 0 1]T |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglesias, A.; Dombovari, Z.; Gonzalez, G.; Munoa, J.; Stepan, G. Optimum Selection of Variable Pitch for Chatter Suppression in Face Milling Operations. Materials 2019, 12, 112. https://doi.org/10.3390/ma12010112
Iglesias A, Dombovari Z, Gonzalez G, Munoa J, Stepan G. Optimum Selection of Variable Pitch for Chatter Suppression in Face Milling Operations. Materials. 2019; 12(1):112. https://doi.org/10.3390/ma12010112
Chicago/Turabian StyleIglesias, Alex, Zoltan Dombovari, German Gonzalez, Jokin Munoa, and Gabor Stepan. 2019. "Optimum Selection of Variable Pitch for Chatter Suppression in Face Milling Operations" Materials 12, no. 1: 112. https://doi.org/10.3390/ma12010112
APA StyleIglesias, A., Dombovari, Z., Gonzalez, G., Munoa, J., & Stepan, G. (2019). Optimum Selection of Variable Pitch for Chatter Suppression in Face Milling Operations. Materials, 12(1), 112. https://doi.org/10.3390/ma12010112





