Evolution of Grain Interfaces in Annealed Duplex Stainless Steel after Parallel Cross Rolling and Direct Rolling
Abstract
:1. Introduction
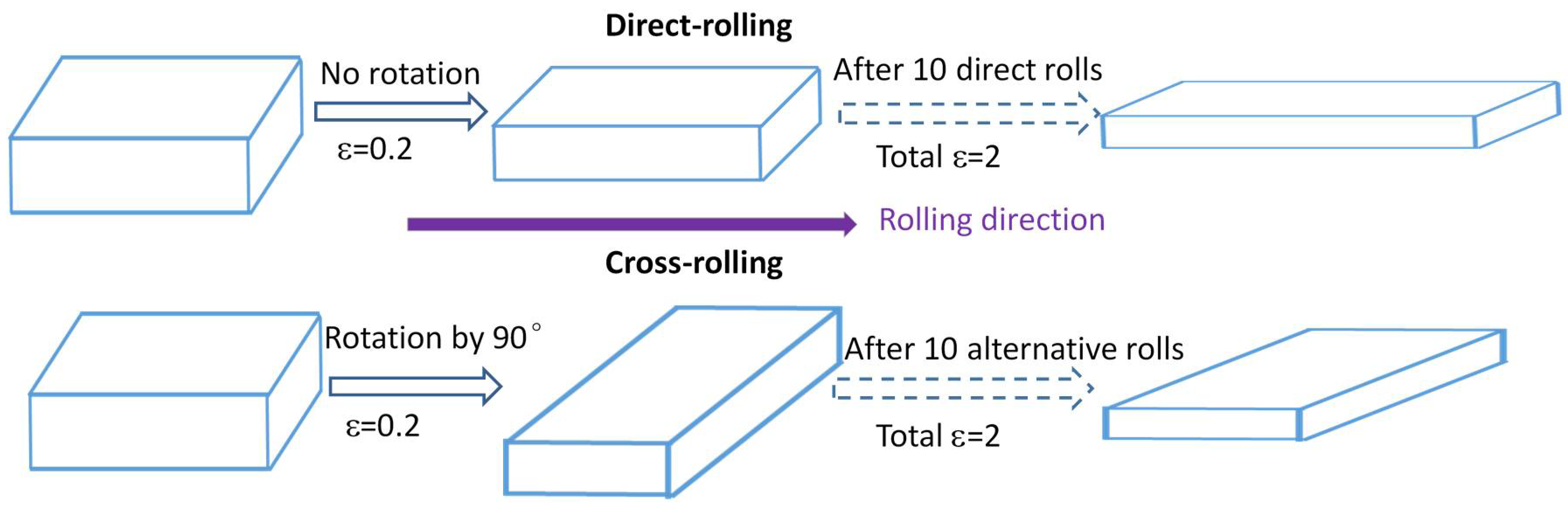
2. Materials and Methods
3. Results and Discussion
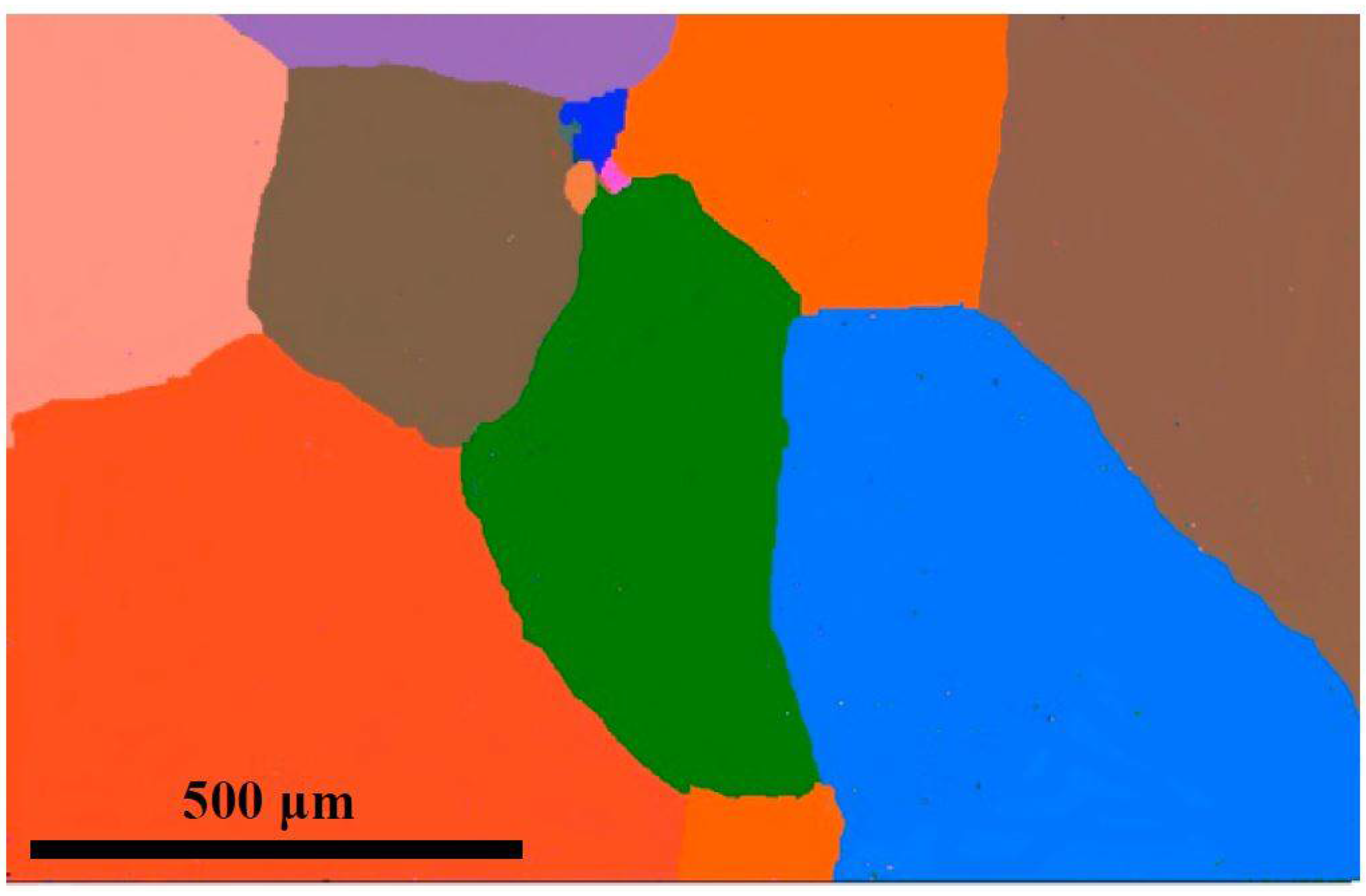
3.1. Microstructure after TMP
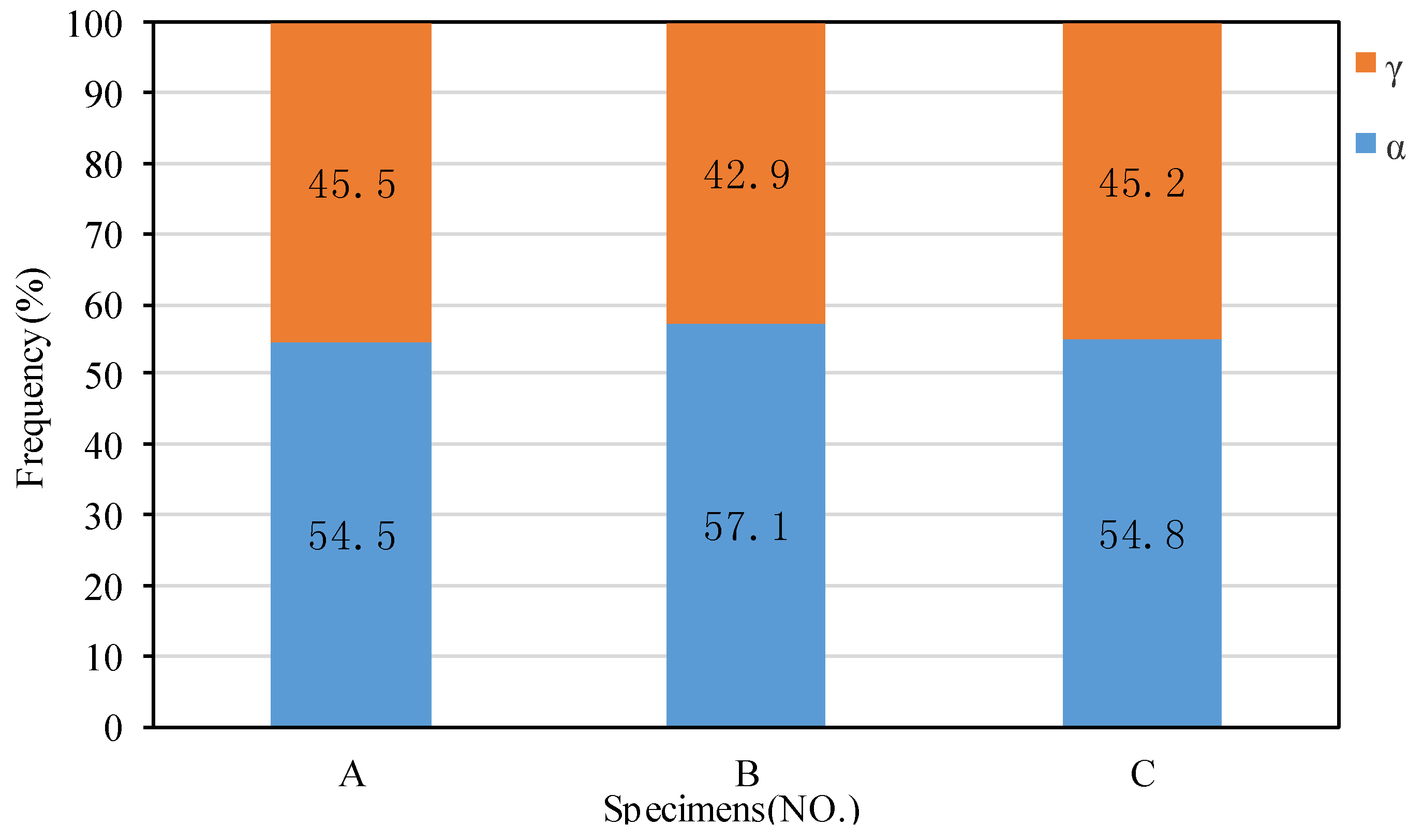
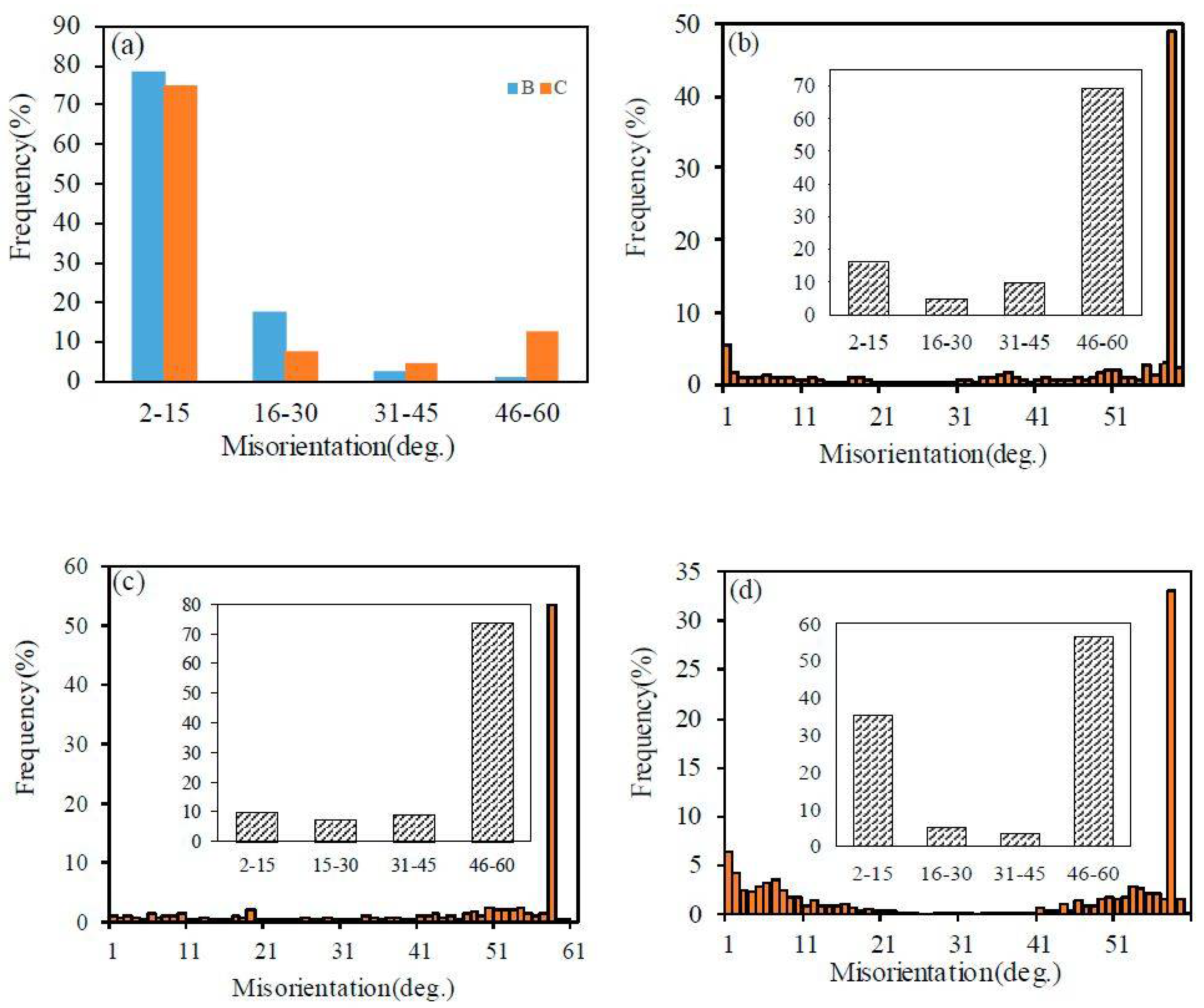
3.2. Grain Boundary Character Distribution (GBCD)
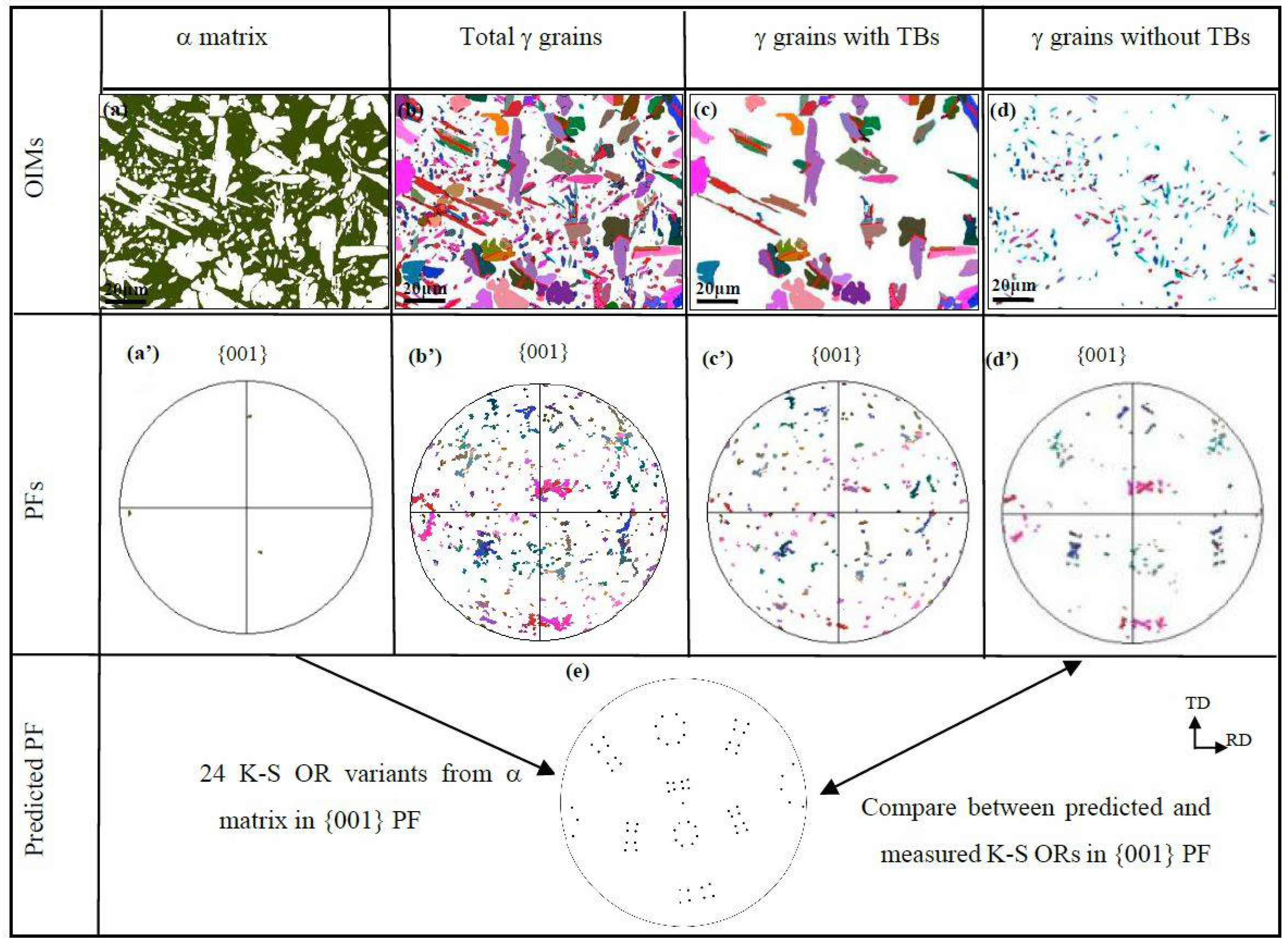
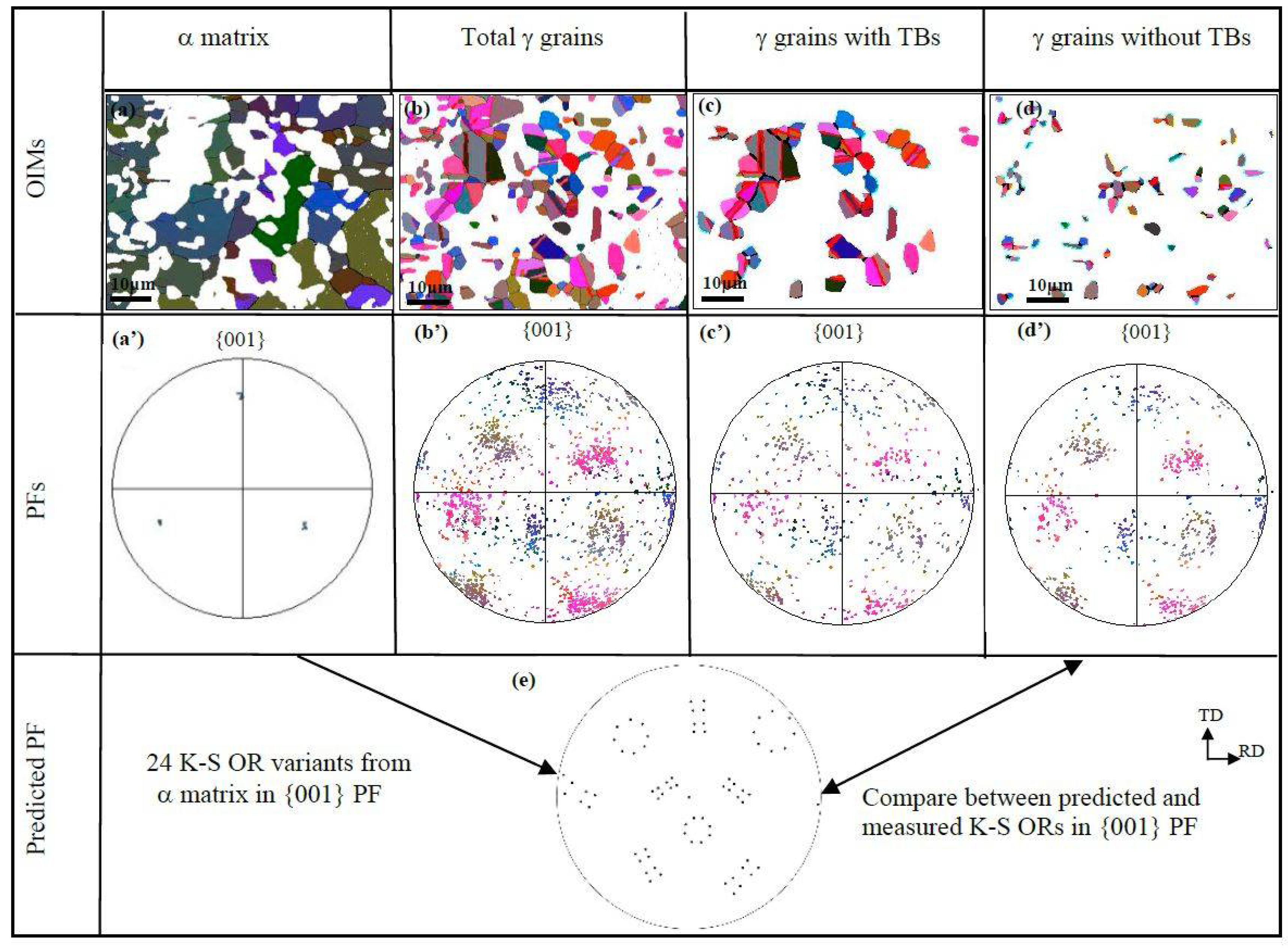
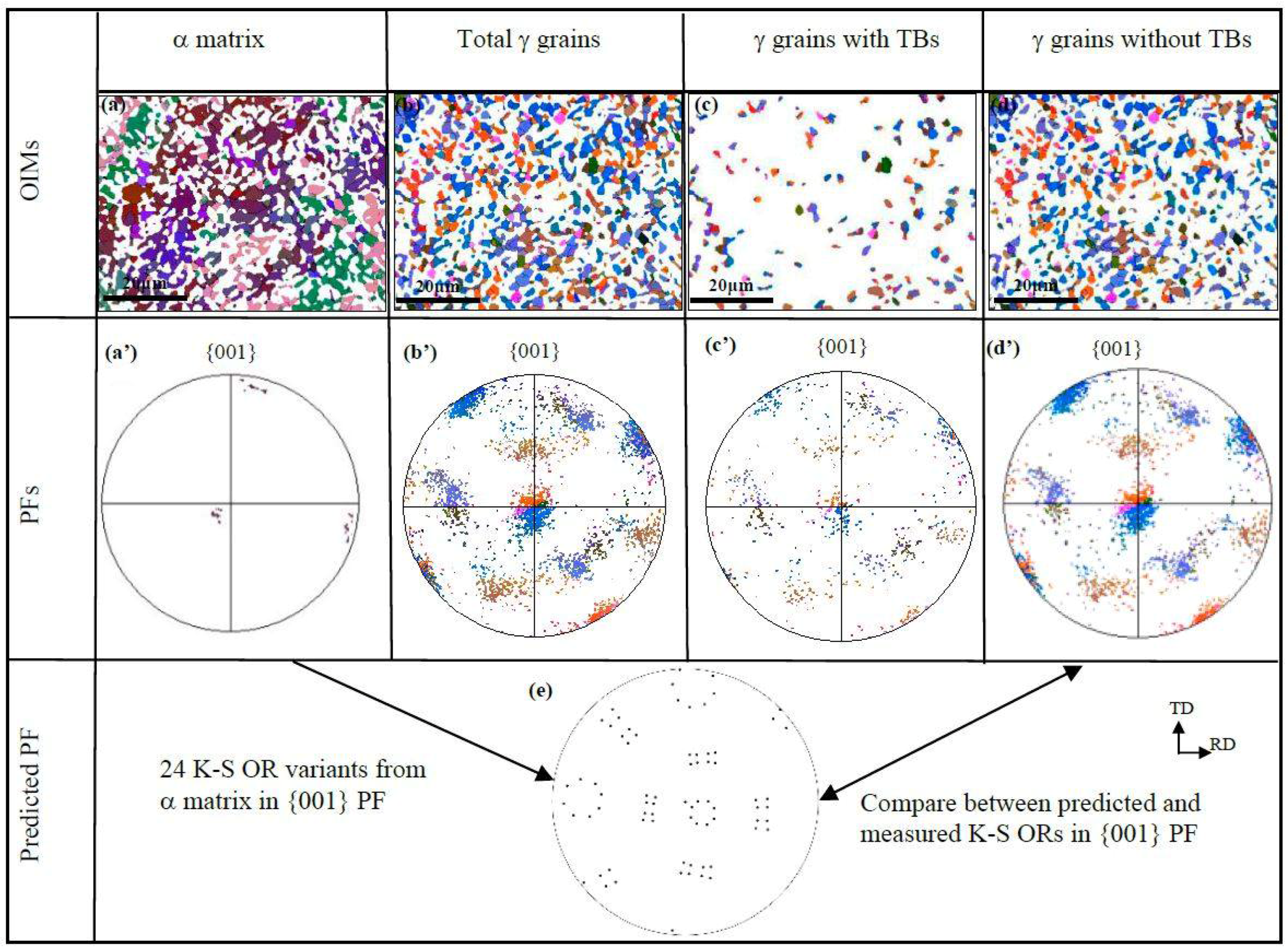
3.3. Grain Orientation and Interfaces after TMP
4. Summary
- A more homogeneous and refined microstructure was obtained in the cross-rolled and annealed sample than in the direct rolled and annealed sample, in which γ grains were prone to clustering.
- TBs were frequently found within γ grains precipitated from the direct-rolled supersaturated α due to the absence of phase boundary in the γ grain-clustered region during annealing. LAGBs and TBs coexist within γ precipitation from the cross-rolled supersaturated α due to the sympathetic nucleation during annealing.
- The formation of TBs leads the γ grain orientation to be random and deviate from K-S OR, whereas the presence of LAGBs intensifies the γ grain orientation, maintaining the K-S OR with the α matrix.
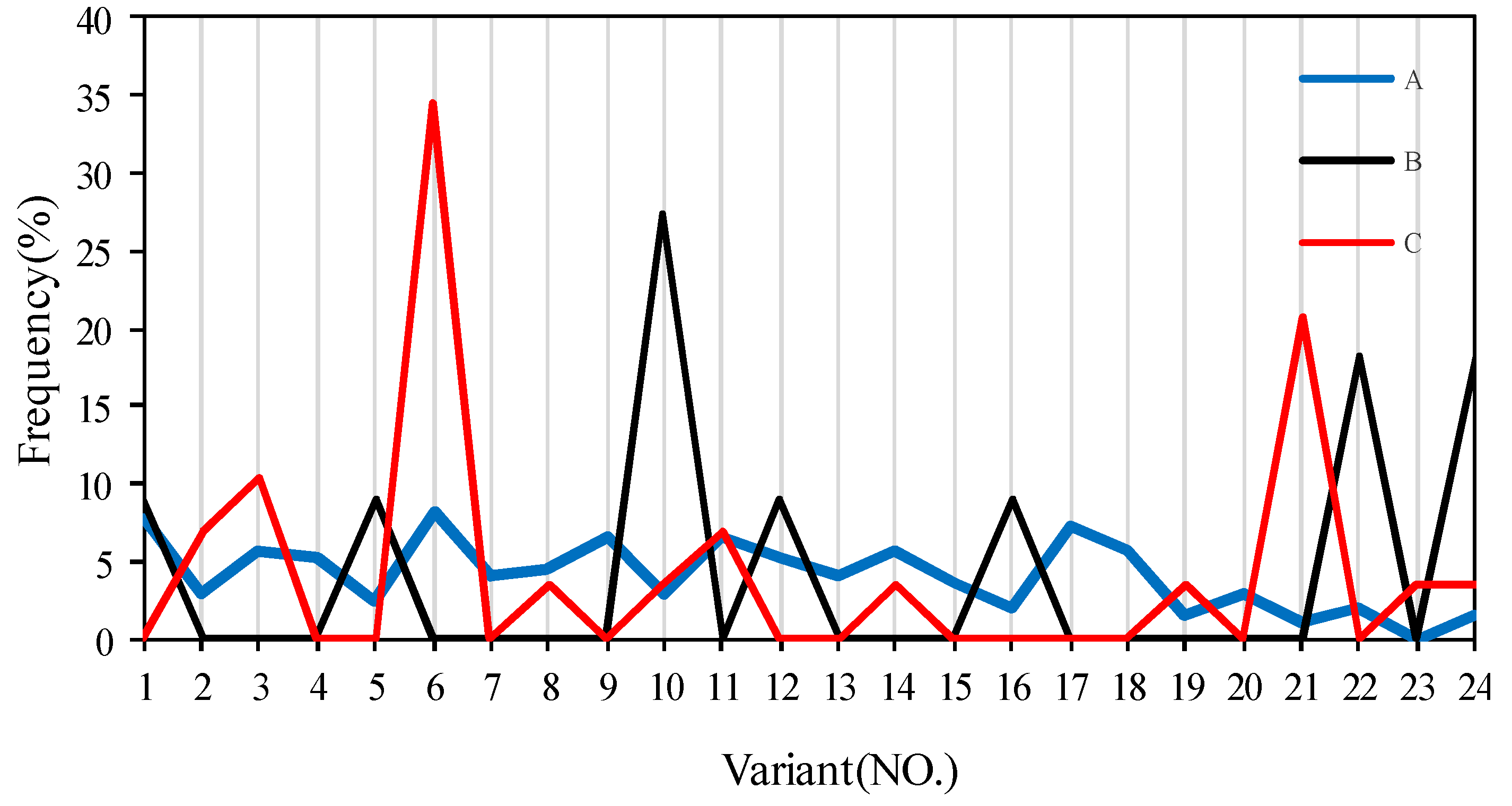
- Variant selection tends to occur more often in the rolled and annealed samples as compared to the directly annealed sample without pre-deformation. Variants 6 and 19 are frequently produced and are related by LAGBs in the cross-rolled and annealed samples.
Author Contributions
Funding
Conflicts of Interest
References
- Chen, L.; Yuan, F.P.; Liang, P.; Wu, X.L. Mechanical properties and nanostructures in a duplex stainless steel subjected to equal channel angular pressing. Mater. Sci. Eng. A 2012, 551, 154–159. [Google Scholar] [CrossRef]
- Frechard, S.; Martin, F.; Clement, C.; Cousty, J. AFM and EBSD combined studies of plastic deformation in a duplex stainless steel. Mater. Sci. Eng. A 2006, 418, 312–319. [Google Scholar] [CrossRef]
- Soylu, B.; Honeycombe, R.W.K. Microstructural refinement of duplex stainless steels. Mater. Sci. Technol. 1991, 7, 137–146. [Google Scholar] [CrossRef]
- Fargas, G.; Akdut, N.; Anglada, M.; Mateo, A. Microstructural Evolution during Industrial Rolling of a Duplex Stainless Steel. ISIJ Int. 2008, 48, 1596–1602. [Google Scholar] [CrossRef]
- Tan, H.; Jiang, Y.; Deng, B.; Sun, T.; Xu, J.L.; Li, J. Effect of annealing temperature on the pitting corrosion resistance of super duplex stainless steel UNS S32750. Mater. Charact. 2009, 60, 1049–1054. [Google Scholar] [CrossRef]
- Gironès, A.; Villechaise, P.; Mateo, A.; Anglada, M.; Mendez, J. EBSD studies on the influence of texture on the surface damage mechanisms developed in cyclically loaded aged duplex stainless steels. Mater. Sci. Eng. A 2004, S387–S389, 516–521. [Google Scholar] [CrossRef]
- Pan, Y.; Adams, B.L.; Olson, T. Grain boundary structure effects on intergranular stress corrosion cracking of alloy X-750. Acta Mater. 1996, 44, 4685–4695. [Google Scholar] [CrossRef]
- Lin, P.; Palumbo, G.; Erb, U.; Aust, K.T. Influence of grain boundary character distribution on sensitization and intergranular corrosion of alloy 600. Scr. Metall. Mater. 1995, 33, 1387–1392. [Google Scholar] [CrossRef]
- Shimada, M.; Kokawa, H.; Wang, Z.J. Optimization of grain boundary character distribution forintergranular corrosion resistant 304 stainless steel by twin-nducedgrain boundary engineering. Acta Mater. 2002, 50, 2331–2341. [Google Scholar] [CrossRef]
- Michiuchi, M.; Kokawa, H.; Wang, Z.J.; Sato, Y.S.; SaKai, K. Twin-induced grain boundary engineering for 316 austenitic stainless steel. Acta Mater. 2006, 54, 5179–5184. [Google Scholar] [CrossRef]
- Huang, Y.D.; Froyen, L. Important factors to obtain homogeneous and ultrafine ferrite–pearlite microstructure in low carbon steel. J. Mater. Proc. Technol. 2002, 124, 216–226. [Google Scholar] [CrossRef]
- Adachi, Y.; Tomida, T.; Hinotani, S. Ferrite grain size refinement by heavy deformation during accelerated cooling in low-carbon steel. Tetsu Hagane 1999, 85, 620. [Google Scholar] [CrossRef]
- Fang, X.Y.; Yin, W.H.; Qin, C.X.; Wang, W.G.; Lo, K.H.; Shek, C.H. The interface character distribution of cold-rolled and annealed duplex stainless steel. Mater. Charact. 2016, 118, 397–404. [Google Scholar] [CrossRef]
- Huang, X.X.; Tsuzaki, K.; Maki, T. Subgrain growth and misorientation of the α matrix in an (α + γ) microduplex stainless steel. Acta Metall. Mater. 1995, 43, 3375–3384. [Google Scholar] [CrossRef]
- Wronski, S.; Wrobel, M.; Baczmanski, A.; Wierzbanowski, K. Effects of cross-rolling on residual stress, texture and plastic anisotropy in f.c.c. and b.c.c. metals. Mater. Charact. 2013, 77, 116–126. [Google Scholar] [CrossRef]
- Gu, X.F. TCLab-Home. Available online: https://itclab.weebly.com/ (accessed on 28 January 2014).
- Huang, X.X.; Tsuzaki, K.; Maki, T. Effect of initial structure on recrystallization of the α matrix in an (α + γ) microduplex stainless steel. Scr. Metall. Mater. 1995, 33, 341–346. [Google Scholar] [CrossRef]
- Fang, X.Y.; Liu, Z.Y.; Tikhonova, M.; Belyakov, A.; Kaibyshev, R.; Rohrer, G.S.; Wang, W.G. Grain boundary plane distributions in 304 steel annealed at high temperature after a parallel processing of multiple forging and direct rolling. Acta Metall. Sin. 2012, 48, 895. [Google Scholar] [CrossRef]
- Tikhonova, M.; Kuzminova, Y.; Fang, X.Y.; Wang, W.G.; Kaibyshev, R.; Belyyakov, A. Σ3 CSL boundary distributions in an austenitic stainless steel subjected to multidirectional forging followed by annealing. Philos. Mag. 2014, 94, 4181–4196. [Google Scholar] [CrossRef]
- Chen, C.Y.; Yen, H.W.; Yang, J.R. Sympathetic nucleation of austenite in a Fe–22Cr–5Ni duplex stainless steel. Scr. Mater. 2007, 56, 673–676. [Google Scholar] [CrossRef]
- Aaronson, H.I.; Plichta, M.R.; Franti, G.W.; Russel, K.C. Precipitation at interphase boundaries. Metall. Trans. A 1978, 9, 363–371. [Google Scholar] [CrossRef]
- Chowdhury, S.G.; Datta, S.; Kumar, B.R.; De, P.K.; Ghosh, R.N. Randomization of texture during recrystallization of austenite in a cold rolled metastable austenitic stainless steel. Mater. Sci. Eng. A 2007, 443, 114–119. [Google Scholar] [CrossRef]
- Lischewski, I.; Gottstein, G. Nucleation and variant selection during the α-γ-α phase transformation in microalloyed steel. Acta Mater. 2011, 59, 1530–1541. [Google Scholar] [CrossRef]
- Butrón-Guillén, M.P.; Da Costa Viana, C.S.; Jonas, J.J. A Variant Selection Model for Predicting the Transformation Texture of Deformed Austensite. Metall. Mater. Trans. A 1997, 28, 1755–1768. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Li, H.; Tian, Y.; Guo, H.; Fang, X.; Guo, Y. Evolution of Grain Interfaces in Annealed Duplex Stainless Steel after Parallel Cross Rolling and Direct Rolling. Materials 2018, 11, 816. https://doi.org/10.3390/ma11050816
Wang M, Li H, Tian Y, Guo H, Fang X, Guo Y. Evolution of Grain Interfaces in Annealed Duplex Stainless Steel after Parallel Cross Rolling and Direct Rolling. Materials. 2018; 11(5):816. https://doi.org/10.3390/ma11050816
Chicago/Turabian StyleWang, Ming, Haoqing Li, Yujing Tian, Hong Guo, Xiaoying Fang, and Yuebin Guo. 2018. "Evolution of Grain Interfaces in Annealed Duplex Stainless Steel after Parallel Cross Rolling and Direct Rolling" Materials 11, no. 5: 816. https://doi.org/10.3390/ma11050816
APA StyleWang, M., Li, H., Tian, Y., Guo, H., Fang, X., & Guo, Y. (2018). Evolution of Grain Interfaces in Annealed Duplex Stainless Steel after Parallel Cross Rolling and Direct Rolling. Materials, 11(5), 816. https://doi.org/10.3390/ma11050816



