Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods
Abstract
1. Introduction
2. Experimental Techniques and Configurations
2.1. Fabrication of Binary and Ternary Alloy Samples
2.2. Preparation of the Surfaces and Size of the Alloy Disc Samples
3. Experimental Methods for Vibration Spectrum Data Acquisition
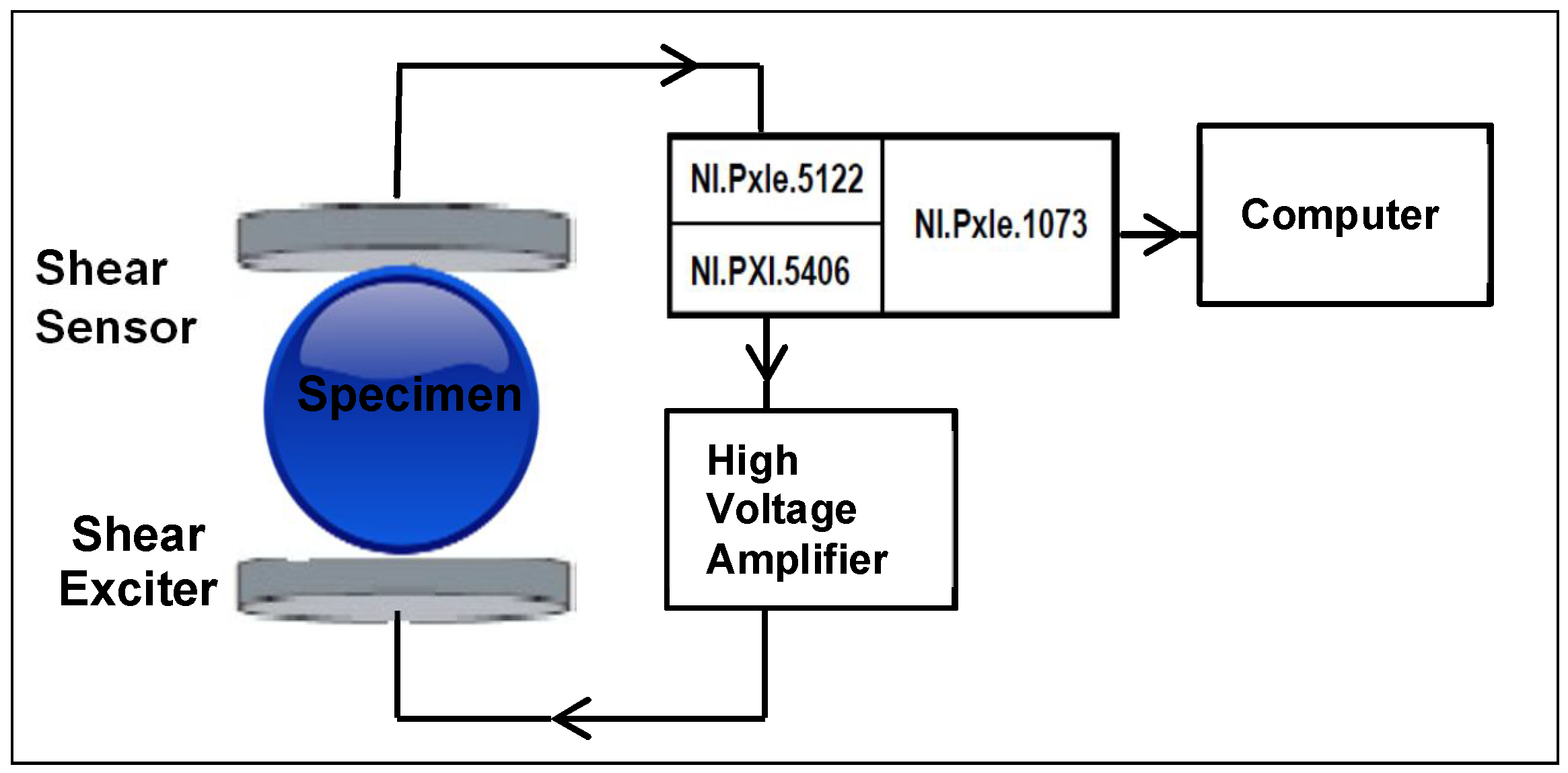
3.1. Configuration Using Shear Wave Transducers
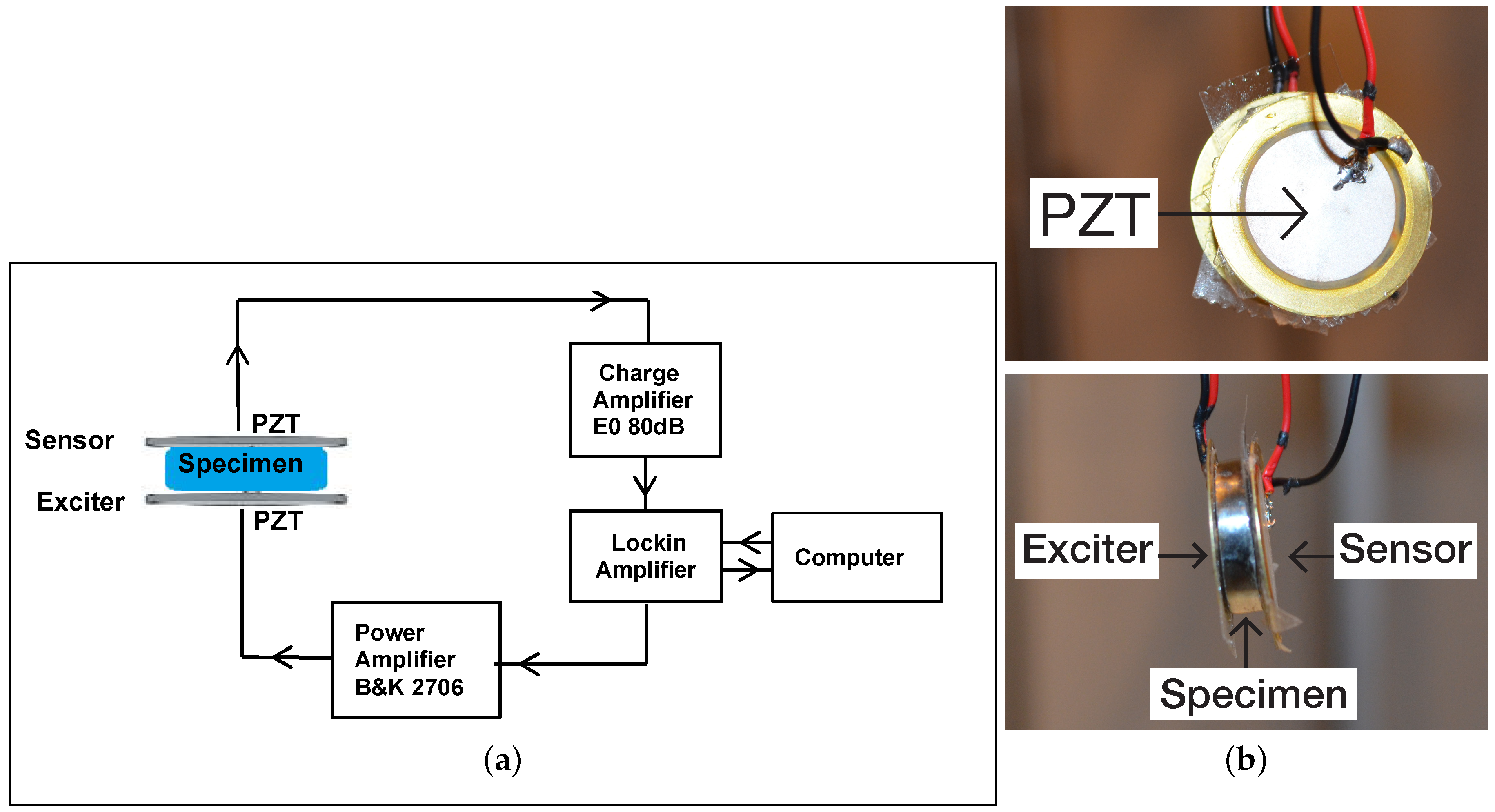
4. Configuration with Piezoelectric Discs
5. The Ingredients for Estimating Alloy Disc Sample Elastic Moduli
5.1. First Model for Solving the Direct Problem
5.2. Second Model for Solving the Direct Problem
5.3. Solving the Inverse Problem of Vibrational Spectroscopy
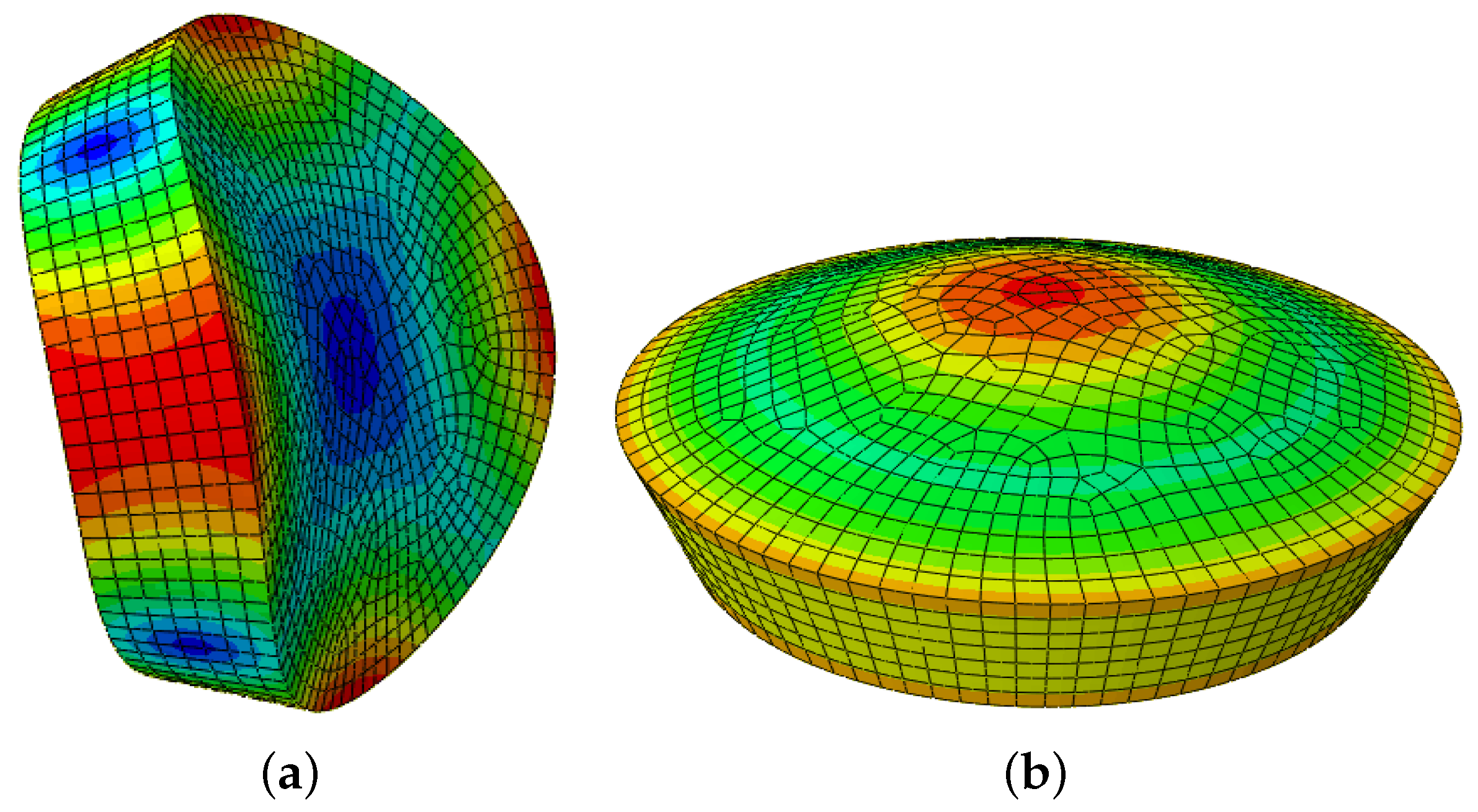
5.4. How to Identify and Classify the Modes of Vibration in the Response Spectrum of the Specimen
6. Results
6.1. Identification and Classification of Vibration Modes in the Spectrum and Validation of the Interaction Model Used for Inversion
6.2. Validation of the Interaction Model for the Inverse Problem Using Synthetic Data
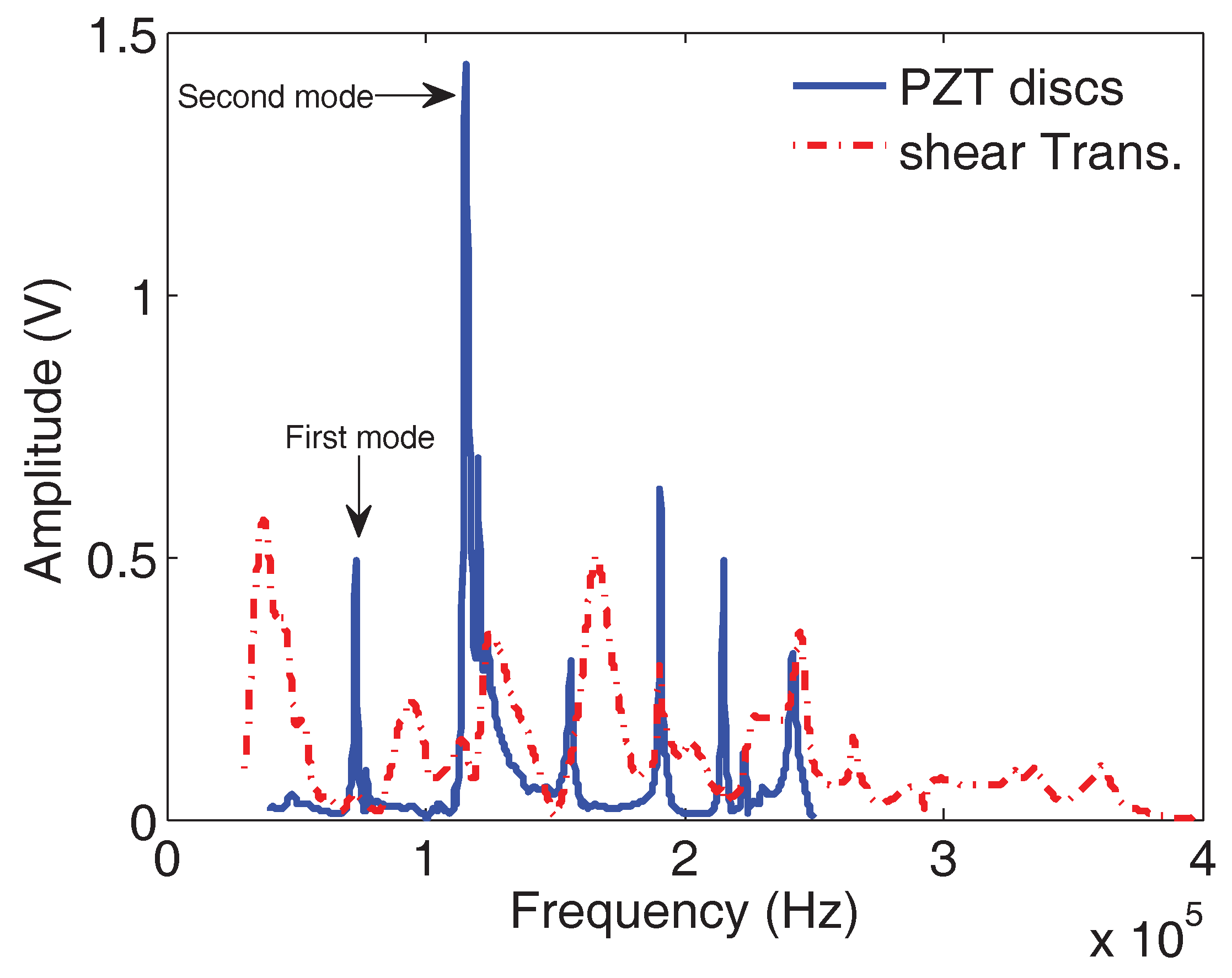
6.3. Comparison between the Two Experimental Resonance Ultrasound Vibrational Methods
7. Discussion
7.1. Comparison with Some Published Results in the Literature
7.2. The Influence of the Formed Phases and Their Crystallographic Structures on the Mechanical Properties
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stoloff, N. Iron aluminides: Present status and future prospects. Mater. Sci. Eng. A 1998, 258, 1–14. [Google Scholar] [CrossRef]
- Hartig, C.; Yoo, M.H.; Koeppe, M.; Mecking, H. Effect of temperature on elastic constants and deformation behavior in shear tests of Fe-30%Al single crystals. Mater. Sci. Eng. A 1998, 258, 59–64. [Google Scholar] [CrossRef]
- Barbier, D.; Huang, M.; Bouaziz, O. A novel eutectic Fe-15 wt.% Ti alloy with an ultrafine lamellar structure for high temperature applications. Intermetallics 2013, 35, 41–44. [Google Scholar] [CrossRef]
- Zamanzade, M.; Barnoush, A.; Motz, C. A Review on the Properties of Iron Aluminide Intermetallics. Crystals 2016, 6, 10. [Google Scholar] [CrossRef]
- Matysik, P.; Jóźwiak, S.; Czujko, T. Characterization of Low-Symmetry Structures from Phase Equilibrium of Fe-Al System–Microstructures and Mechanical Properties. Materials 2015, 8, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Moret, F.; Baccino, R.; Martel, P.; Guetaz, L. Propriétés et applications des alliages intermétalliques B2-FeAl. J. Phys. IV Fr. 1996, 6, 281–289. [Google Scholar] [CrossRef]
- Engelier, C.; Béchet, J. Transformations structurales dans l’alliage de titane , β-CEZ études des mécanismes de précipitation après traitement de mise en solution. J. Phys. IV Fr. 1994, 4, 111–116. [Google Scholar] [CrossRef]
- He, W.W.; Tang, H.P.; Liu, H.Y.; Jia, W.P.; Yong, L.I.U.; Xin, Y.A.N.G. Microstructure and tensile properties of containerless near-isothermally forged TiAl alloys. Trans. Nonferrous Met. Soc. China 2011, 21, 2605–2609. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation Behaviour and Oxidation Resistance of Single-Phase and Two-Phase L21 Fe-Al-Ti Alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Barrett, C.; Massalski, T. Structure of Metals: Crystallographic Methods, Principles And Data; International Series on Materials Science and Technology: Pergamon, Turkey, 1980. [Google Scholar]
- Lamirand, M. Influence de L’oxygène, De L’azote Et Du Carbone Sur La Microstructure Et La Ductilité Des Alliages TiAl. Ph.D. Thesis, Université Paris-Est Créteil Val de Marne, Paris, France, 2004. [Google Scholar]
- Rigaud, V. Contribution à L’étude de La solidification et à la description thermodynamique des équilibres de phases du système quaternaire Fe-Al-Ti-Zr. Ph.D. Thesis, Université de Lorraine, Vandoeuvre-les-Nancy, France, 2009. [Google Scholar]
- Kwiatkowska, M.; Zasada, D.; Bystrzycki, J.; Polański, M. Synthesis of Fe-Al-Ti Based Intermetallics with the Use of Laser Engineered Net Shaping (LENS). Materials 2015, 8, 2311–2331. [Google Scholar] [CrossRef]
- Agote, I.; Coleto, J.; Gutiérrez, M.; Sargsyan, A.; de Cortazar, M.G.; Lagos, M.; Borovinskaya, I.; Sytschev, A.; Kvanin, V.; Balikhina, N.; et al. Microstructure and mechanical properties of gamma TiAl based alloys produced by combustion synthesis+compaction route. Intermetallics 2008, 16, 1310–1316. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting: A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Gui, L.J.; Jin, S. Ab initio investigation of the mechanical properties of copper. Chin. Phys. B 2012, 21, 096102. [Google Scholar] [CrossRef]
- Begum, A.N.; Rajendran, V.; Jayakumar, T.; Palanichamy, P.; Priyadharsini, N.; Aravindan, S.; Raj, B. On-line ultrasonic velocity measurements for characterisation of microstructural evaluation during thermal aging of β-quenched zircaloy-2. Mater. Charact. 2007, 58, 563–570. [Google Scholar] [CrossRef]
- Svilainis, L. Review of Ultrasonic Signal Acquisition and Processing Techniques for Mechatronics and Material Engineering. In Solid State Phenomena; Mechatronic Systems and Materials VII; Trans Tech Publications: Zurich, Switzerland, 2016; Volume 251, pp. 68–74. [Google Scholar]
- Angrisani, L.; Daponte, P.; D’Apuzzo, M. A method for the automatic detection and measurement of transients. Part I: The measurement method. Measurement 1999, 25, 19–30. [Google Scholar] [CrossRef]
- Angrisani, L.; Daponte, P.; D’Apuzzo, M. A method for the automatic detection and measurement of transients. Part II: Applications. Measurement 1999, 25, 31–40. [Google Scholar] [CrossRef]
- Dunn, H.L.M.; Couper, M. Calculated elastic constants of alumina-mullite ceramic particles. J. Mater. Sci. 1995, 30, 639–642. [Google Scholar] [CrossRef]
- Maynard, J. Resonant Ultrasound Spectroscopy. Phys. Today 1996, 49, 26–31. [Google Scholar] [CrossRef]
- Migliori, A.; Maynard, J.D. Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev. Sci. Instrum. 2005, 76, 121301. [Google Scholar] [CrossRef]
- Leisure, R.G. Ultrasonic Spectroscopy: Applications in Condensed Matter Physics and Materials Science; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Bernard, S.; Schneider, J.; Varga, P.; Laugier, P.; Raum, K.; Grimal, Q. Elasticity–density and viscoelasticity–density relationships at the tibia mid-diaphysis assessed from resonant ultrasound spectroscopy measurements. Biomech. Model. Mechanobiol. 2016, 15, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Migliori, A.; Sarrao, J.L.; Visscher, W.M.; Bell, T.; Lei, M.; Fisk, Z.; Leisure, R.G. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Phys. B Condens. Matter 1993, 183, 1–24. [Google Scholar] [CrossRef]
- Demarest, H.H. Cube-Resonance Method to Determine the Elastic Constants of Solids. J. Acoust. Soc. Am. 1971, 49, 768–775. [Google Scholar] [CrossRef]
- Ohno, I. Free vibration of a rectangular parallelepiped crystal and its application to determination of elastic constants of orthorhombic crystals. J. Phys. Earth 1976, 24, 355–379. [Google Scholar] [CrossRef]
- Chiroiu, V.; Delsanto, P.P.; Munteanu, L.; Rugina, C.; Scalerandi, M. Determination of the second- and third-order elastic constants in Al from the natural frequencies. J. Acoust. Soc. Am. 1997, 102, 193–198. [Google Scholar] [CrossRef]
- Goodlet, B.; Torbet, C.; Biedermann, E.; Jauriqui, L.; Aldrin, J.; Pollock, T. Forward models for extending the mechanical damage evaluation capability of resonant ultrasound spectroscopy. Ultrasonics 2017, 77, 183–196. [Google Scholar] [CrossRef] [PubMed]
- Ichitsubo, T.; Matsubara, E.; Kai, S.; Hirao, M. Ultrasound-induced crystallization around the glass transition temperature for Pd40Ni40P20 metallic glass. Acta Mater. 2004, 52, 423–429. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. (Eds.) Principles of Emar for Spectral Response. In EMATs for Science and Industry; Springer: Boston, MA, USA, 2003; Chapter 4; pp. 83–92. [Google Scholar]
- APCI. Piezoelectric Ceramics: Principles and Applications; American Piezo Ceramics, Inc.: Mackeyville, PA, USA, 2004. [Google Scholar]
- Hughes, T.J.R. Finite Element Method—Linear Static and Dynamic Finite Element Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Ogam, E.; Fellah, Z.; Ogam, G. Identification of the mechanical moduli of closed-cell porous foams using transmitted acoustic waves in air and the transfer matrix method. Compos. Struct. 2016, 135, 205–216. [Google Scholar] [CrossRef]
- Sorensen, H.K. Abaqus 6.14 Online Documentation: Theory Manual, v6.14 ed.; Dassault Systèmes: Vélizy-Villacoublay, France, 2014; Chapter 2. [Google Scholar]
- Martinček, G. The determination of poisson’s ratio and the dynamic modulus of elasticity from the frequencies of natural vibration in thick circular plates. J. Sound Vib. 1965, 2, 116–127. [Google Scholar] [CrossRef]
- ASTM E1876-01(2006). Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Ogam, E.; Wirgin, A.; Schneider, S.; Fellah, Z.; Xu, Y. Recovery of elastic parameters of cellular materials by inversion of vibrational data. J. Sound Vibr. 2008, 313, 525–543. [Google Scholar] [CrossRef]
- Sorensen, H.K. Abaqus Online Documentation: Abaqus Standard User’s Manual, v6.14 ed.; Dassault Systèmes: Vélizy-Villacoublay, France, 2014; Volume I. [Google Scholar]
- Zope, R.R.; Mishin, Y. Interatomic potentials for atomistic simulations of the Ti-Al system. Phys. Rev. B 2003, 68, 024102. [Google Scholar] [CrossRef]
- Connétable, D.; Maugis, P. First principle calculations of the k-Fe3AlC perovskite and iron aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
- Friàk, M.; Hickel, T.; Körmann, F.; Udyansky, A.; Dick, A.; von Pezold, J.; Ma, D.; Kim, O.; Counts, W.; Šob, M.; et al. Determining the Elasticity of Materials Employing Quantum-mechanical Approaches: From the Electronic Ground State to the Limits of Materials Stability. Steel Res. Int. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Zhu, L.F.; Friák, M.; Udyansky, A.; Ma, D.; Schlieter, A.; Kühn, U.; Eckert, J.; Neugebauer, J. Ab initio based study of finite-temperature structural, elastic and thermodynamic properties of FeTi. Intermetallics 2014, 45, 11–17. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef]
- Sai, V.S.; Satyanarayana, M.R.S.; Murthy, V.B.K.; Rao, G.S.; Prasad, A.S. An Experimental Simulation to Validate FEM to Predict Transverse Young’s Modulus of FRP Composites. Adv. Mater. Sci. Eng. 2013, 2013, 648527. [Google Scholar] [CrossRef]
- Acharyan, N.; Fatima, B.; Chouhan, S.S.; Sanyal, S.P. First Principles Study on Structural, Electronic, Elastic and Thermal Properties of Equiatomic MTi (M = Fe, Co, Ni). Chem. Mater. Res. 2013, 3, 22–30. [Google Scholar]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k, An Augmented Plane Wave Local Orbitals Program For Calculating Crystal Properties; K. Schwartz Technical Universitat: Vienna, Austria, 2001. [Google Scholar]
- Wen, Y.; Wang, L.; Liu, H.; Song, L. Ab Initio Study of the Elastic and Mechanical Properties of B19 TiAl. Crystals 2017, 7, 39. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kim, Y.W. Intermetallic alloys based on gamma titanium aluminide. JOM 1989, 41, 24–30. [Google Scholar] [CrossRef]
- Mouturat, P.; Sainfort, G.; Cabane, G. Module d’elasticite des alliages fer-aluminium en fonction de la temperature et de la teneur en aluminium. J. Nucl. Mater. 1967, 21, 149–157. [Google Scholar] [CrossRef]
- Guo, F. Influence of Microstructure on the Mechanical Properties And Internal Stresses of a Two-Phase TiAl-Based Alloy. Ph.D. Thesis, Arts et Métiers ParisTech, Paris, France, 2001. [Google Scholar]
- Friák, M.; Deges, J.; Krein, R.; Frommeyer, G.; Neugebauer, J. Combined ab initio and experimental study of structural and elastic properties of Fe3Al-based ternaries. Intermetallics 2010, 18, 1310–1315. [Google Scholar] [CrossRef]
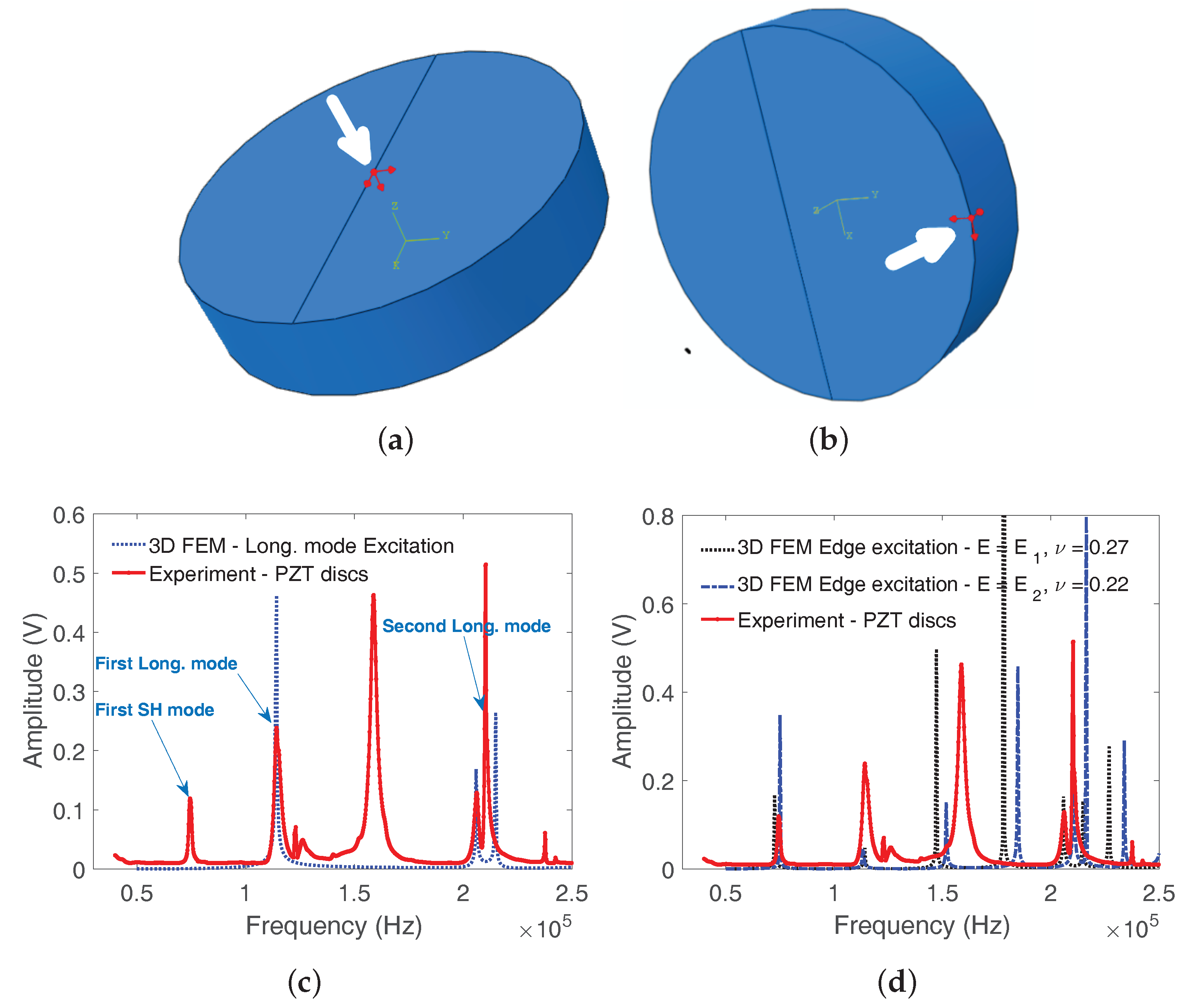
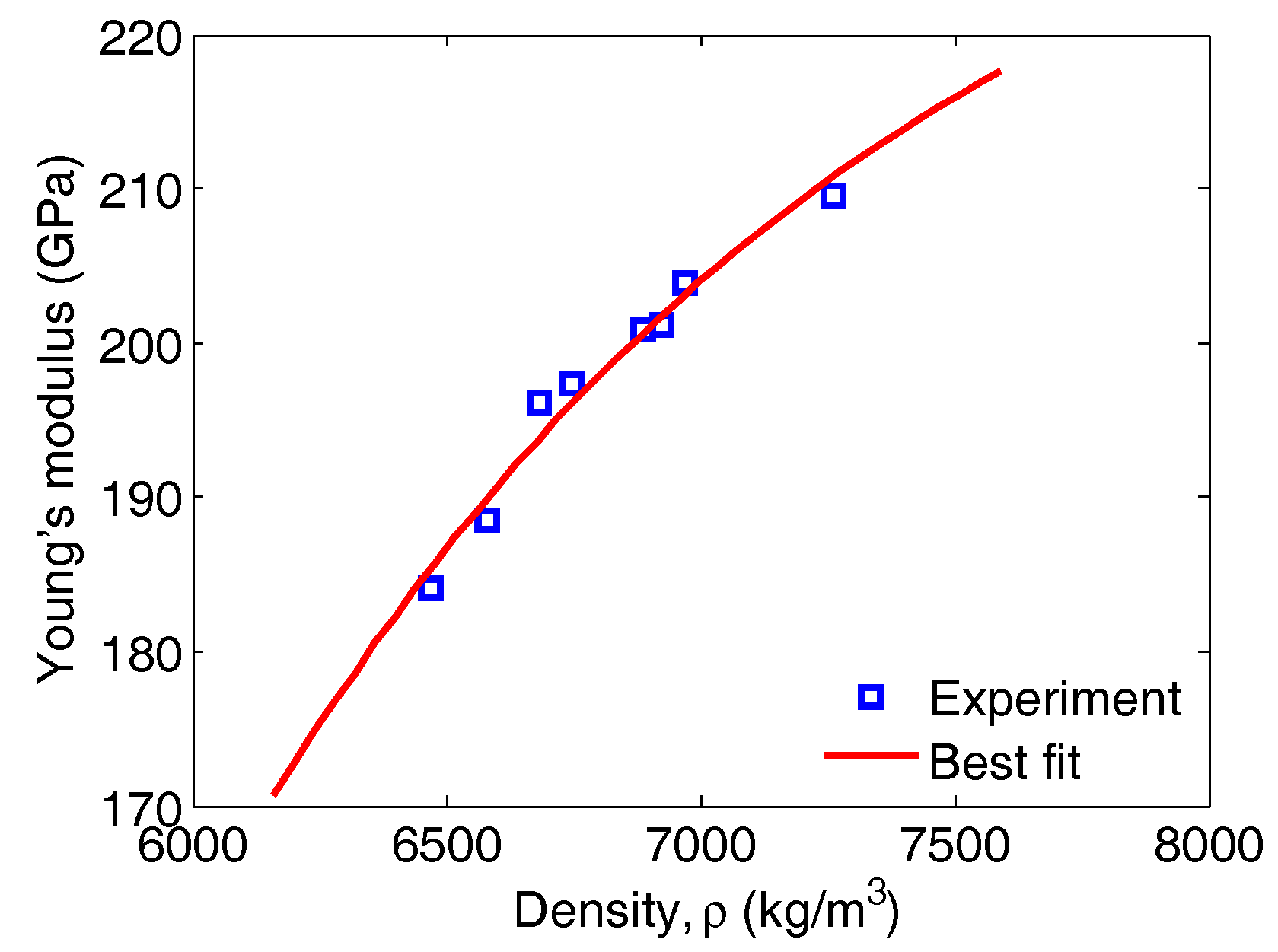
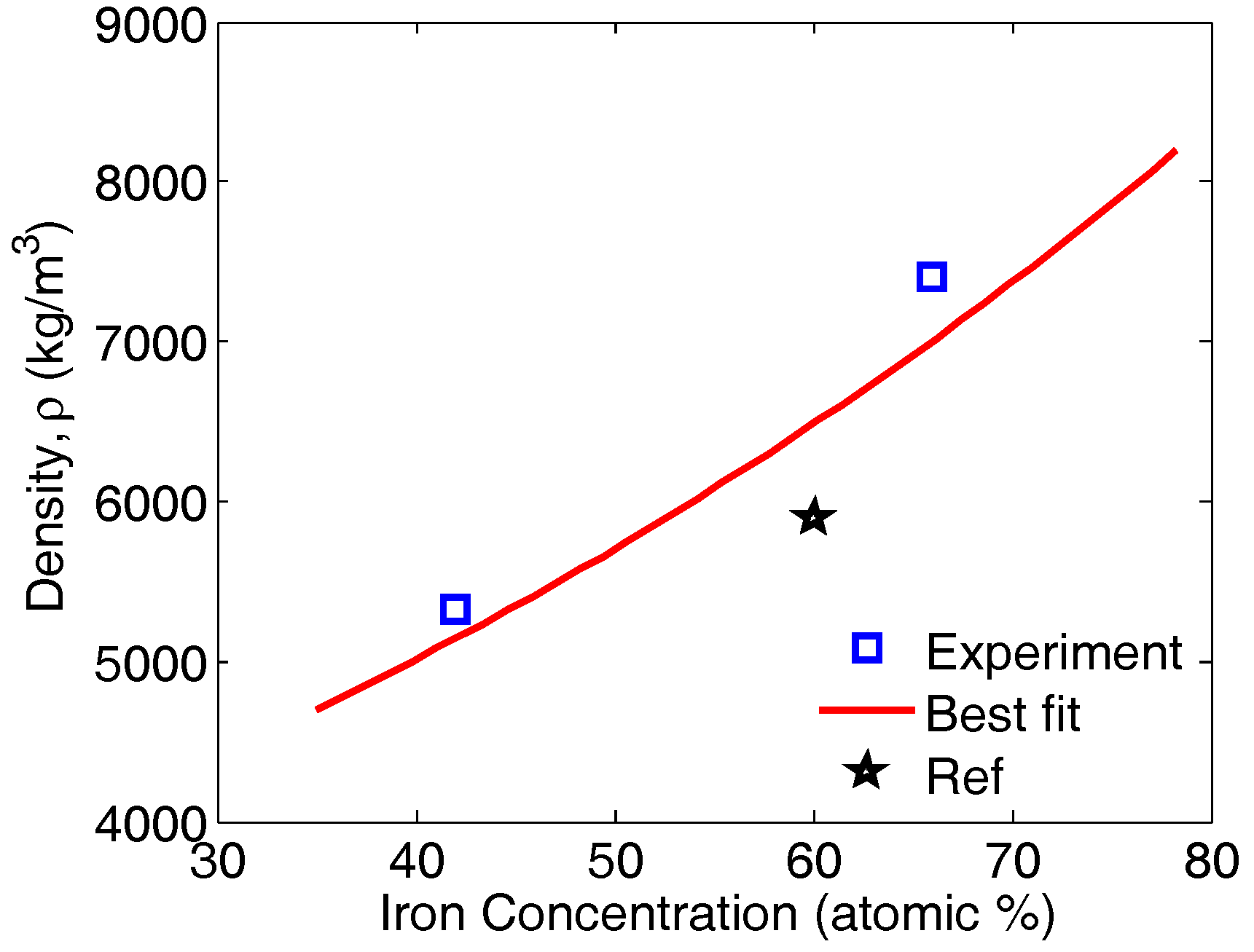
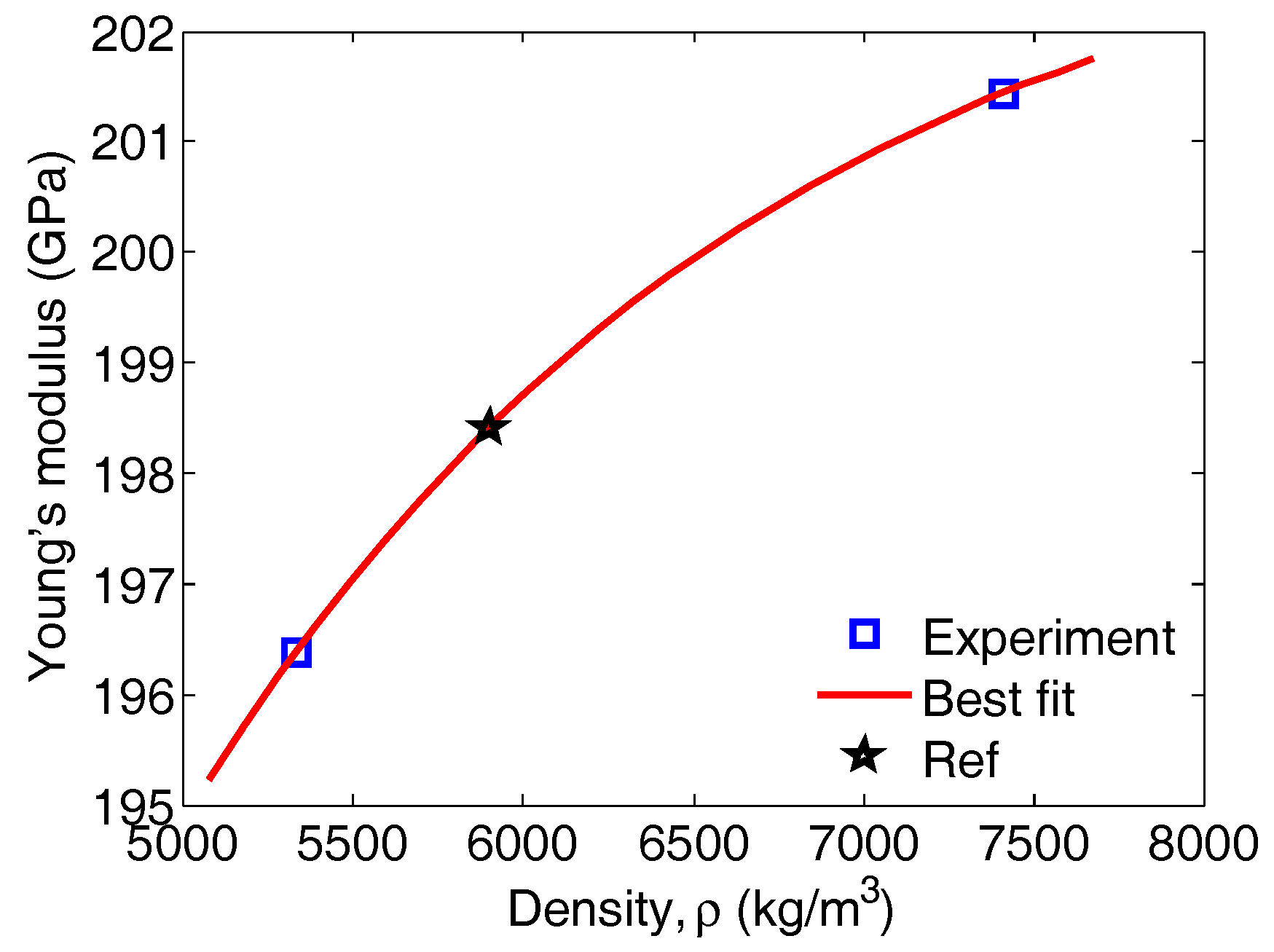
| Base Alloy Studied | Phases | Prototype | Space Group | Crystal Structure [12] | References |
|---|---|---|---|---|---|
| FeTi | FeTi | CsCl | Pm-3m | B2 | [10,13,14] |
| Fe2Ti | MgZn2 | P636/mmc | C14 | ||
| TiAl | TiAl | AuCu | P4/mmm | L10 | [13,14,15] |
| TiAl2 | HfGa2 | I41/amd | - | ||
| FeAl | FeAl | CsCl | Pm-3m | B2 | [10,13,14] |
| FeAl2 | FeAl2 | P1 | - | ||
| FeTiAl | Fe2AlTi | - | Pm-3m | L21 | [10,13,14] |
| Element | Density (Kg/m3) | Young’s Modulus | Poisson Ratio (ν) | F1 (Hz) | F2 (Hz) | ||
|---|---|---|---|---|---|---|---|
| Fe | 7874 Ref. [45] | 212 Ref. [46] | 0.27 | 70480 | 110577 | 213.27 | 210.05 |
| Ti | 4500 Ref. [47] | 114.6 Ref. [44,48] | 0.3 | 67932 | 109053 | 111.14 | 114.60 |
| Al | 2707 Ref. [45] | 69.3 Ref. [45,49] | 0.3 | 68230 | 109530 | 67.27 | 69.36 |
| Composition | Composition | Density | E (Gpa) | (Hz) | (Hz) | Difference Percentage | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (wt. %) | (at. %) | (Hz) | (Hz) | (Kg/m3) | (GPa) | (GPa) | 3D FEM | 3D FEM | 3D FEM | − E (%) | E (GPa), |
| 72,600 | 114,200 | 6469 | 185.92 | 184.04 | 184.04 | 72,682 | 114000 | 1.02 | |||
| 73,000 | 114,600 | 6580 | 191.20 | 188.54 | 188.54 | 72,942 | 114,440 | 1.41 | |||
| 73,800 | 116,000 | 6682 | 198.44 | 196.16 | 196.16 | 73,883 | 115,836 | 1.16 | |||
| 73,800 | 115,800 | 6748 | 199.31 | 197.42 | 197.42 | 73,665 | 115,637 | 0.96 | |||
| 73,000 | 115,600 | 6888 | 200.14 | 200.82 | 200.82 | 73,665 | 115,575 | 0.34 | |||
| 73,000 | 115,400 | 6925 | 201.22 | 201.20 | 201.20 | 73,450 | 115,238 | 0.01 | |||
| 73,000 | 115,800 | 6972 | 202.59 | 203.97 | 203.97 | 73,704 | 115,638 | 0.68 | |||
| 72,800 | 115,200 | 7263 | 209.89 | 209.56 | 209.56 | 73,196 | 114,038 | 0.16 | |||
| 70,600 | 111,200 | 7412 | 201.44 | 199.56 | 199.56 | 70,706 | 110,933 | 0.94 | 200 Ref. [6] | ||
| 82,200 | 130,400 | 5330 | 196.37 | 197.73 | 197.73 | 82,997 | 130,216 | 0.69 | “ | ||
| 70,800 | 111,600 | 7050 | 192.69 | 191.57 | 191.57 | 71,033 | 111,445 | 0.58 | 191.66, = 0.287 Ref. [47] † | ||
| 70,000 | 110,000 | 6950 | 185.69 | 183.47 | 183.47 | 70,013 | 109,845 | 1.21 | 182.38, = 0.28 Ref. [50] † | ||
| 88,200 | 140,000 | 3880 | 164.58 | 165.92 | 165.92 | 89,109 | 139,805 | 0.81 | 160–176 Ref. [54] | ||
| 91,200 | 144,200 | 3609 | 163.37 | 163.70 | 163.70 | 91,774 | 143,986 | 0.02 | 161.99, = 0.265 Ref. [52] † |
| Composition | Composition | Density | E (Gpa) | (Hz) | (Hz) | Difference Percentage | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (wt. %) | (at. %) | (Hz) | (Hz) | (Kg/m3) | (GPa) | (Gpa) | 3D FEM | 3D FEM | 3D FEM | − E (%) | E (GPa), |
| 72,400 | 113,900 | 6469 | 184.80 | 183.10 | 184.80 | 72,512 | 137,700 | 0.92 | |||
| 73,600 | 114,800 | 6580 | 192.20 | 189.10 | 192.20 | 73,000 | 114,770 | 1.61 | |||
| 72,200 | 116,000 | 6682 | 189.90 | 196.10 | 189.90 | 73,900 | 115,936 | 3.26 | |||
| 73,200 | 115700 | 6748 | 197.10 | 197.08 | 197.10 | 73,600 | 115,500 | 0.01 | |||
| 72,700 | 114,800 | 6888 | 198.50 | 198.05 | 198.50 | 73,150 | 114,700 | 0.23 | |||
| 72,600 | 115,000 | 6925 | 199.02 | 199.80 | 199.02 | 73,050 | 114,600 | 0.39 | |||
| 72,800 | 116,800 | 6972 | 201.40 | 207.50 | 201.40 | 72,931 | 115,300 | 3.03 | |||
| 72,600 | 114,700 | 7263 | 208.73 | 208.47 | 208.73 | 72,900 | 114,400 | 0.12 | |||
| 70400 | 110,200 | 7412 | 200.03 | 196.30 | 200.03 | 70,650 | 110,800 | 1.86 | 200 Ref. [6] | ||
| 82,400 | 130,200 | 5330 | 197.30 | 197.10 | 197.30 | 82,840 | 130,000 | 0.10 | “ | ||
| 70,400 | 111400 | 7050 | 190.50 | 190.80 | 190.50 | 70740 | 111,000 | 0.16 | 191.66, = 0.287 Ref. [47] † | ||
| 69,200 | 108,700 | 6950 | 181.47 | 179.16 | 181.47 | 69,174 | 108,700 | 1.27 | 182.38, = 0.28 Ref. [50] † | ||
| 88,700 | 139,800 | 3880 | 166.45 | 165.40 | 166.45 | 88,521 | 139,270 | 0.63 | 160–176 Ref. [54] | ||
| 90,800 | 145,700 | 3609 | 162.60 | 166.90 | 162.60 | 91,460 | 143,000 | 2.64 | 161.99, = 0.265 Ref. [52] † |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanbi, D.; Ogam, E.; Amara, S.E.; Fellah, Z.E.A. Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials 2018, 11, 746. https://doi.org/10.3390/ma11050746
Chanbi D, Ogam E, Amara SE, Fellah ZEA. Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials. 2018; 11(5):746. https://doi.org/10.3390/ma11050746
Chicago/Turabian StyleChanbi, Daoud, Erick Ogam, Sif Eddine Amara, and Z. E. A. Fellah. 2018. "Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods" Materials 11, no. 5: 746. https://doi.org/10.3390/ma11050746
APA StyleChanbi, D., Ogam, E., Amara, S. E., & Fellah, Z. E. A. (2018). Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials, 11(5), 746. https://doi.org/10.3390/ma11050746







