Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles
Abstract
:1. Introduction
2. Experimental Programme
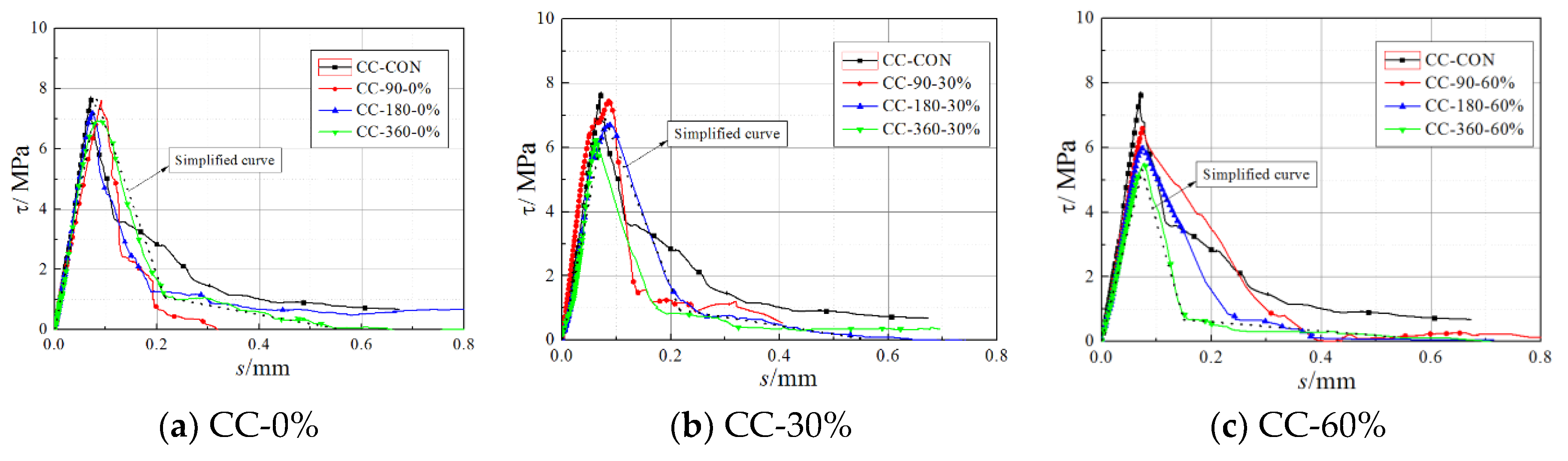
3. Interfacial Fracture Energy, Gf
4. Discussion of Fracture Energy, Gf
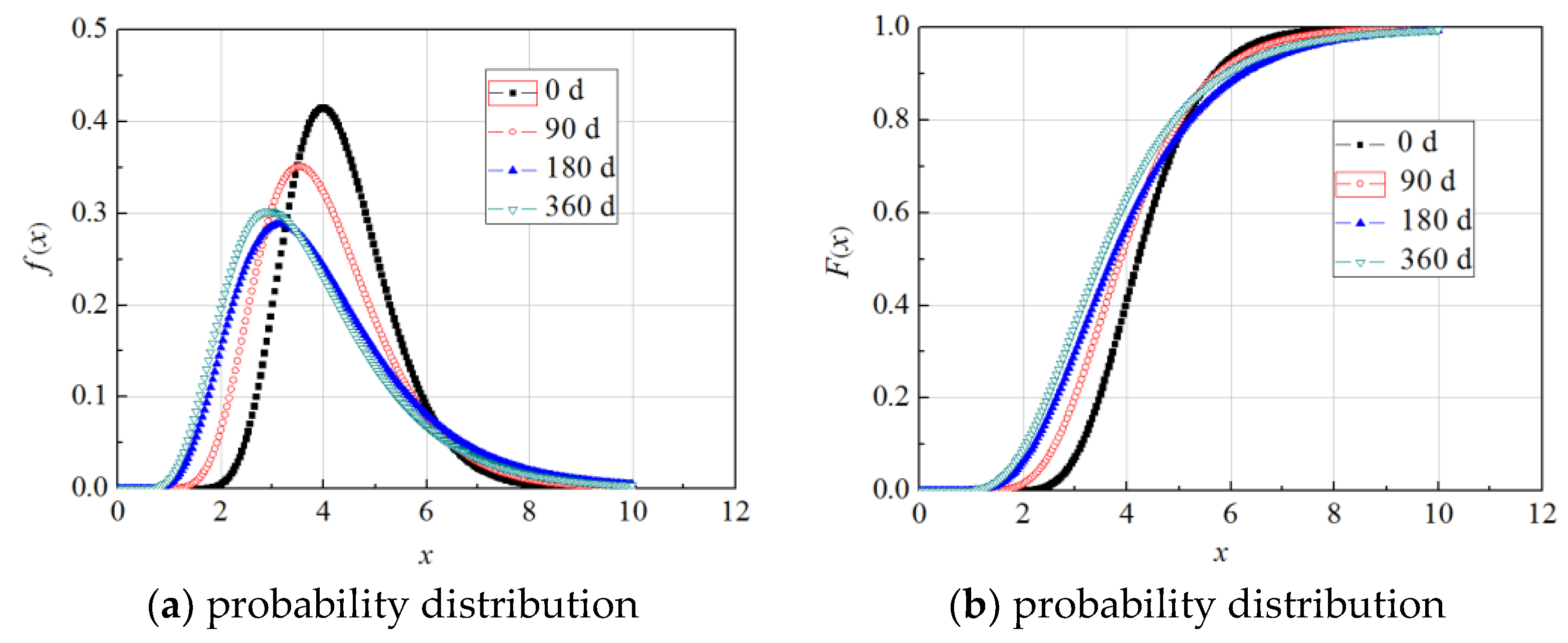
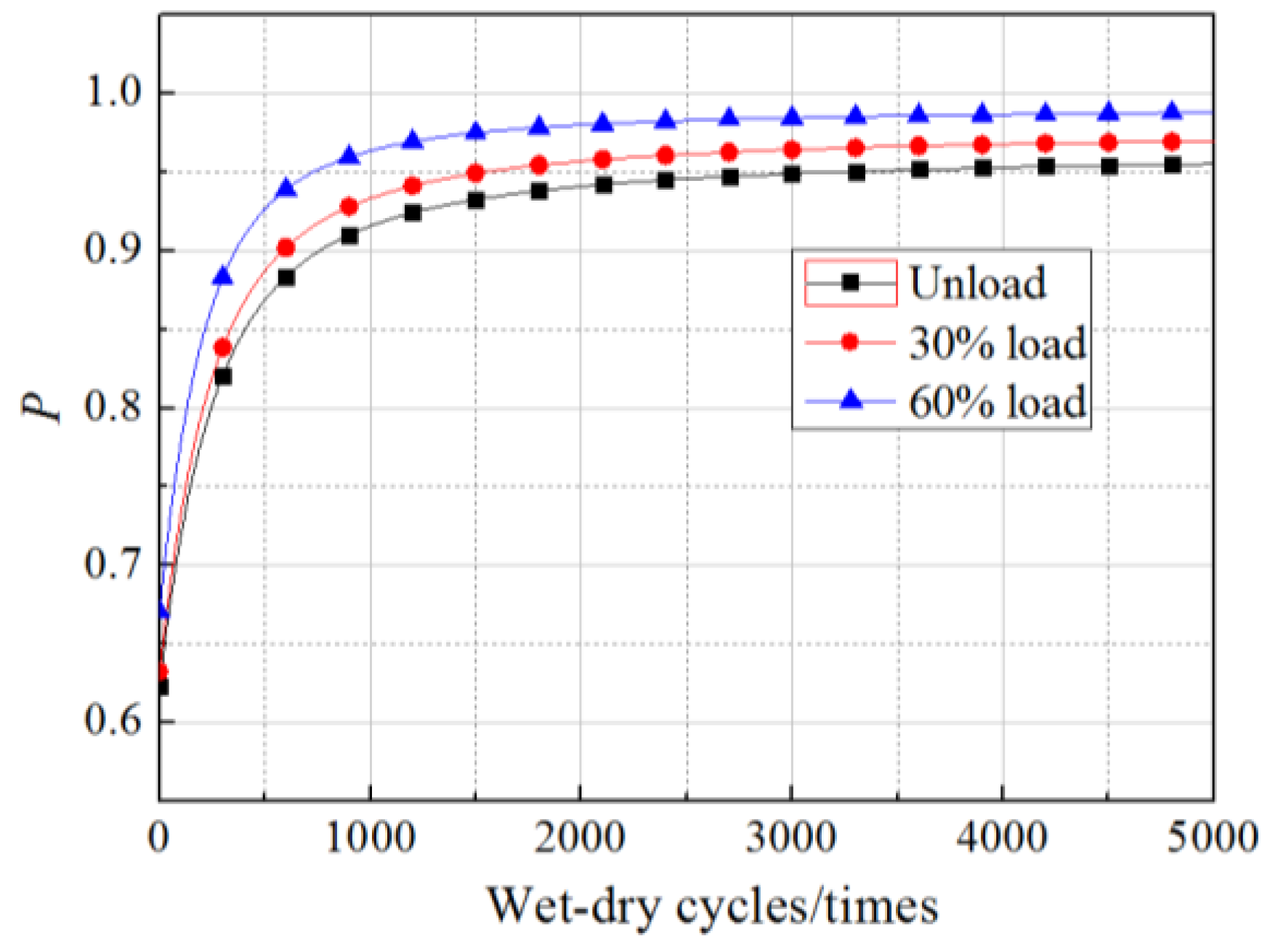
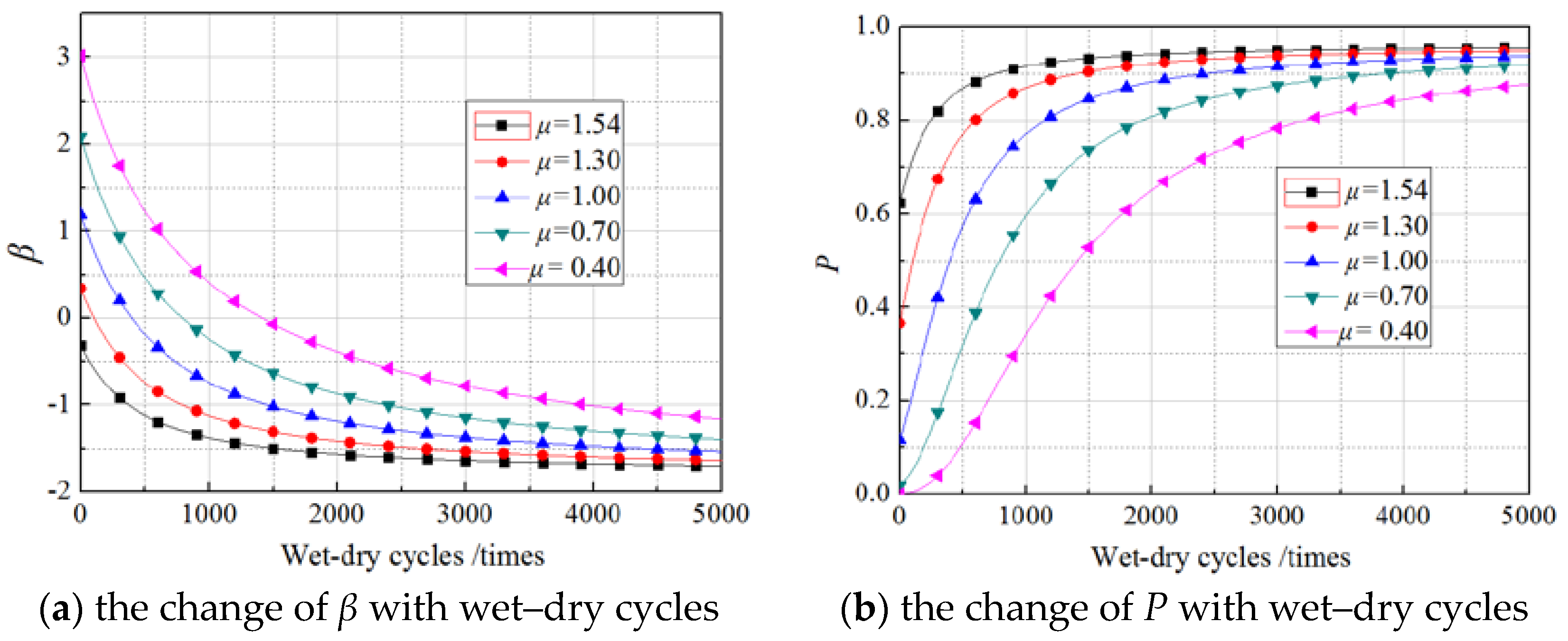
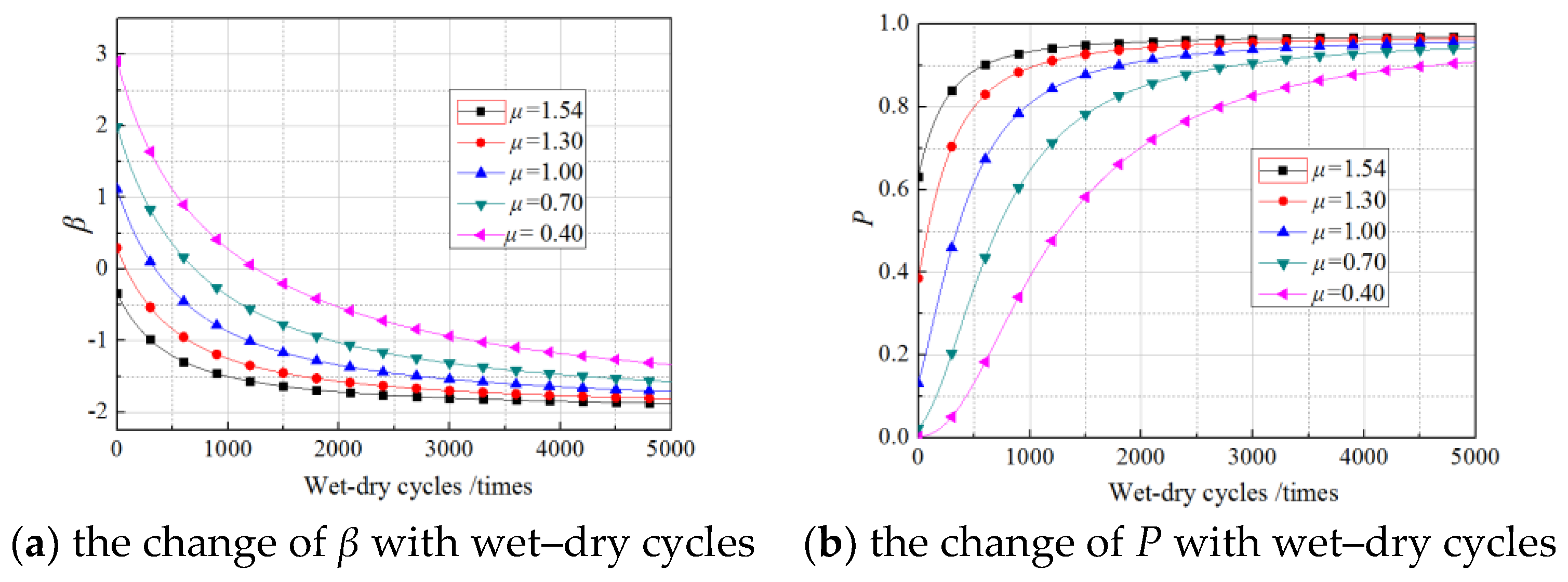
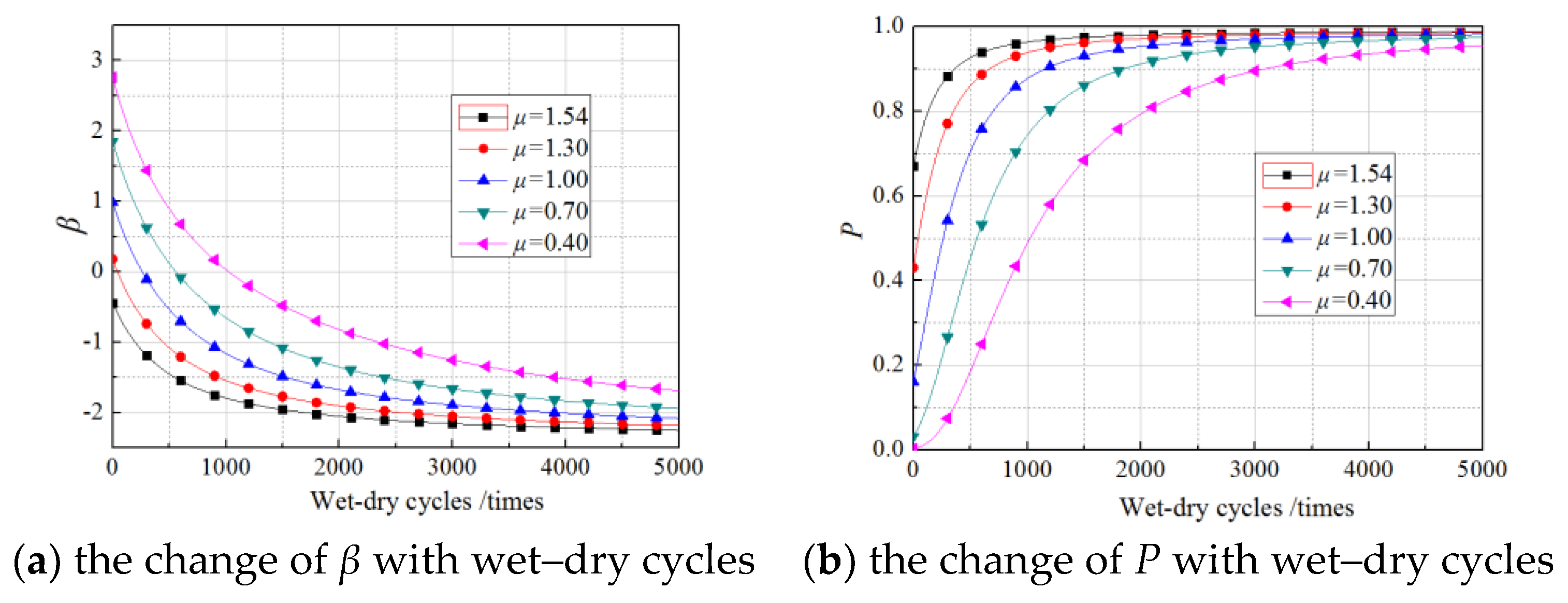
5. Reliability Index of Gf
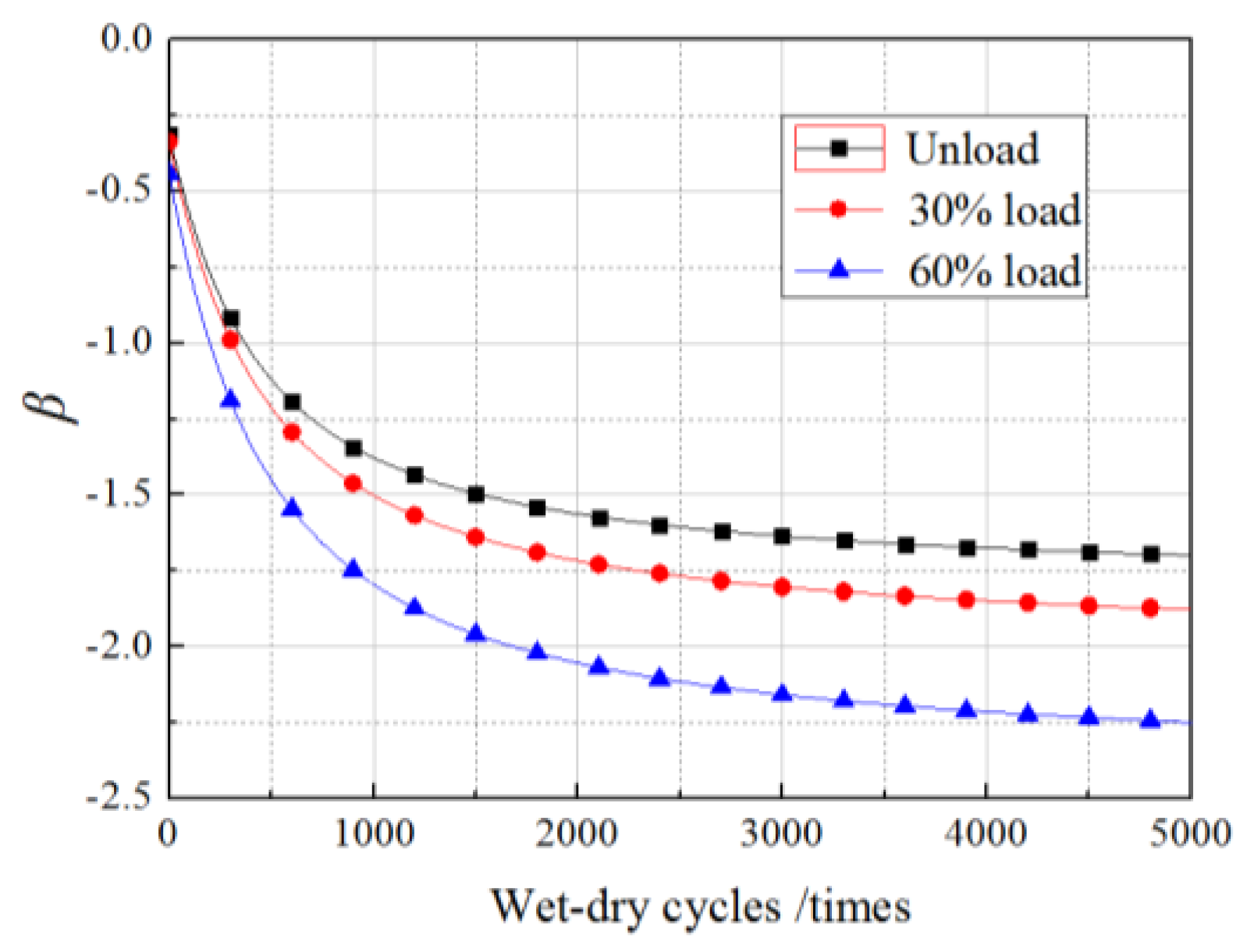
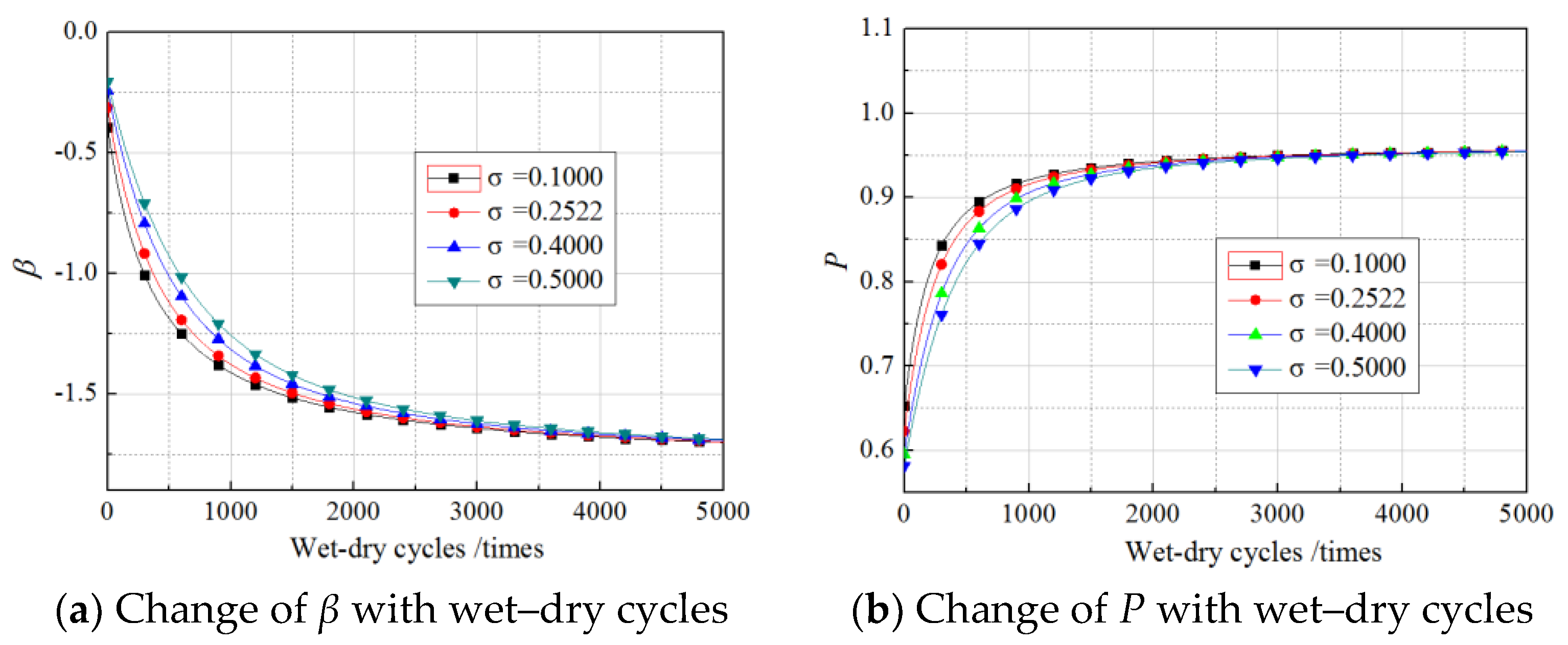
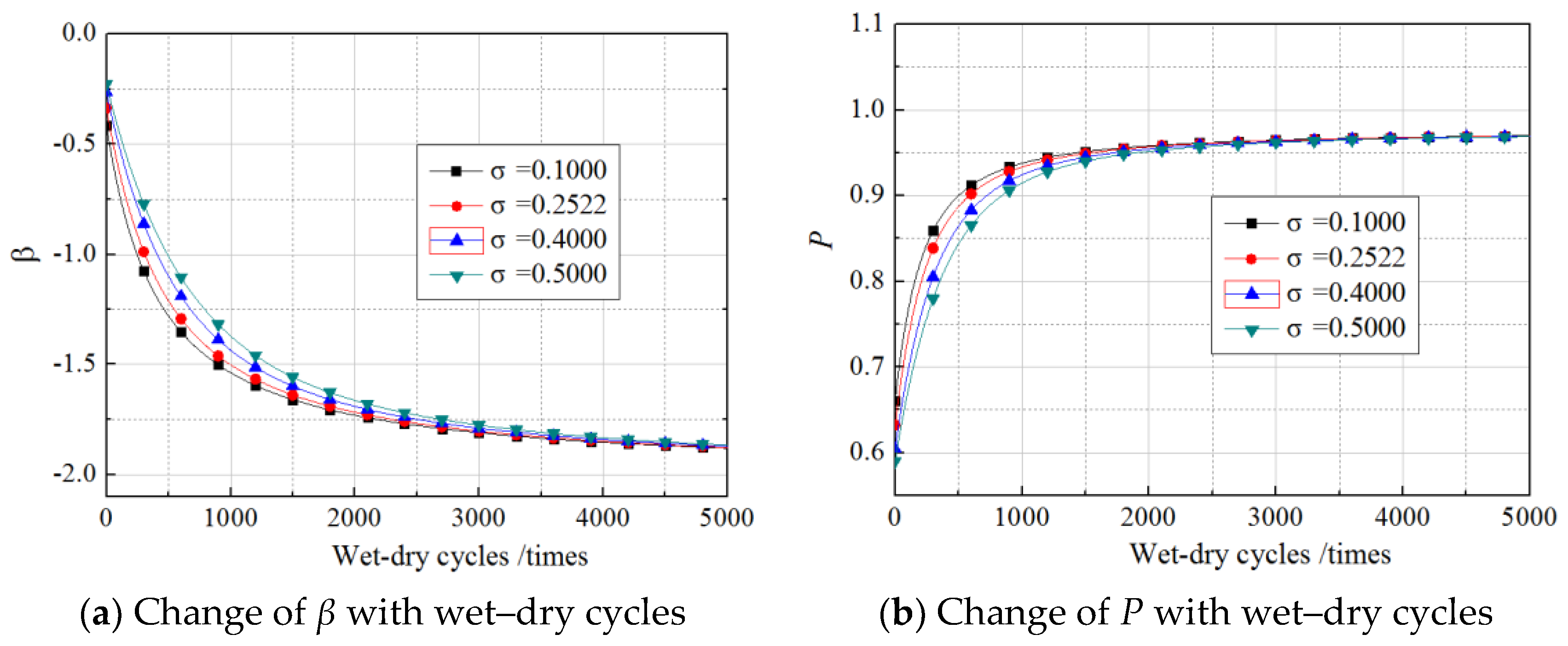
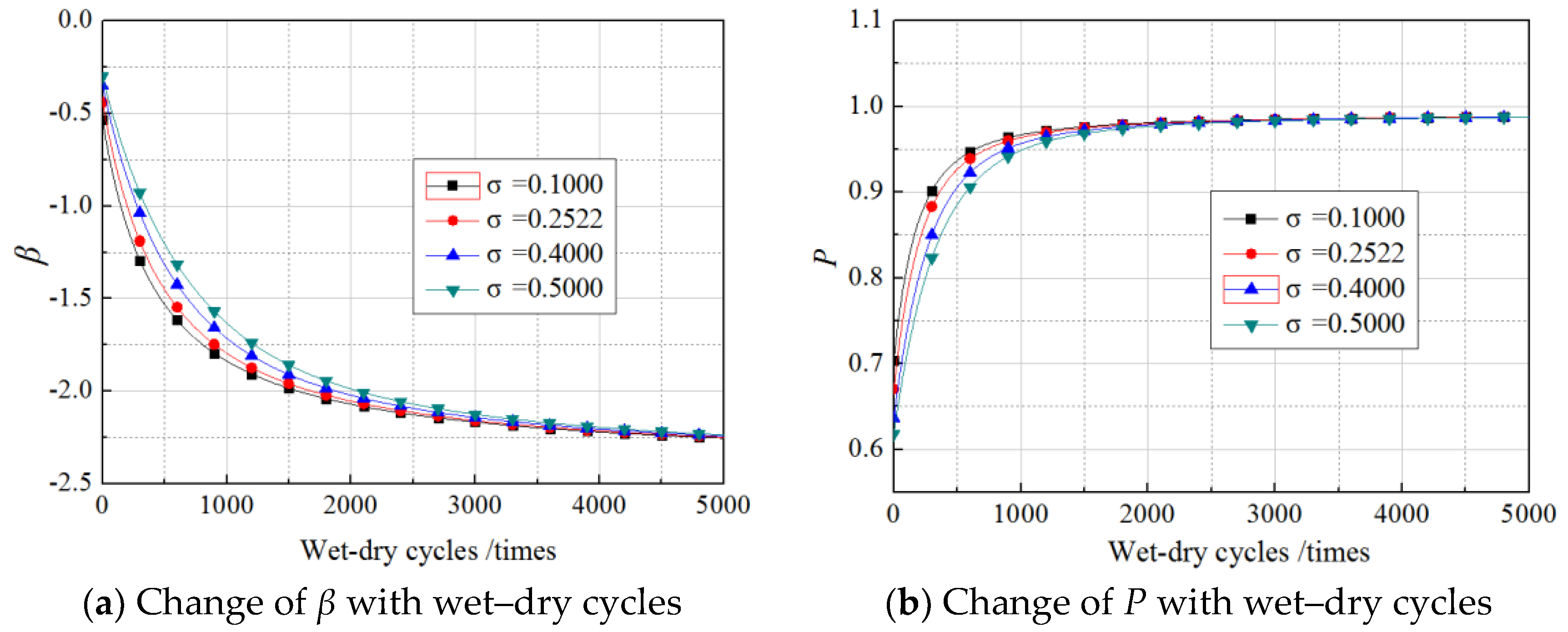
6. Effects of Load Distribution on Reliability of Gf
6.1. Effects of Mean Values of Load
6.2. Effects of Standard Deviation of the Load
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Shi, H.; Zhu, J.H.; Su, M.N.; Jin, W.L. Cover separation of CFRP strengthened beam-type cantilevers with steel bolt anchorage. Eng. Struct. 2018, 156, 224–234. [Google Scholar] [CrossRef]
- Lee, L.S.; Estrada, H.; Baumert, M. Time-Dependent Reliability Analysis of FRP Rehabilitated Pipes. J. Compos. Construct. ASCE 2010, 14, 272–279. [Google Scholar] [CrossRef]
- Liang, H.J.; Li, S.; Lu, Y.; Yang, T. The combined effects of wet–dry cycles and sustained load on the bond behaviour of FRP–concrete interface. Polym. Compos. 2018. [Google Scholar] [CrossRef]
- Ali-Ahmad, M.; Subramaniam, K.; Ghosn, M. Experimental investigation and fracture analysis of debonding between concrete and FRP sheets. J. Eng. Mech. 2006, 132, 914–923. [Google Scholar] [CrossRef]
- Mazzotti, C.; Savoia, M.; Ferracuti, B. An experimental study on delamination of FRP plates bonded to concrete. Constr. Build. Mater. 2008, 22, 1409–1421. [Google Scholar] [CrossRef]
- Hong, S.; Sun-Kyu, P. Effect of bonded lengths and wrappings on energy capacity and debonding strain of reinforced concrete beams strengthened with carbon-fiber-reinforced polymer. Polym. Compos. 2015, 38, 1418–1426. [Google Scholar] [CrossRef]
- Wan, B.; Petrou, M.F.; Harries, K.A. Effect of the Presence of Water on the Durability of Bond between CFRP and Concrete. J. Reinf. Plast. Compos. 2006, 25, 875–890. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Wu, Y.F.; Yun, Y.C. Analytical modeling of the bond-slip relationship at FRP—Concrete interfaces for adhesively-bonded joints. Compos. Part B 2010, 41, 423–433. [Google Scholar] [CrossRef]
- Li, K.; Cao, S.; Yang, Y.; Zhu, J.T. Bond-Slip Relationship for CFRP Sheets Externally Bonded to Concrete under Cyclic Loading. Materials 2018, 11, 336. [Google Scholar] [CrossRef] [PubMed]
- Selman, E.; Alver, N. A modified fiber-reinforced plastics concrete interface bond-slip law for shear-strengthened RC elements under cyclic loading. Polym. Compos. 2016, 37, 3373–3383. [Google Scholar] [CrossRef]
- Wu, Y.F.; Zhou, Y.W. Unified strength model based on Hoek-Brown failure criterion for circular and square concrete columns confined by FRP. J. Compos. Constr. ASCE 2010, 14, 175–184. [Google Scholar] [CrossRef]
- Lu, X.Z.; Jiang, J.J.; Teng, J.G.; Ye, L.P. Finite element simulation of debonding in FRP to concrete bonded joints. Constr. Build. Mater. 2006, 20, 412–424. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wang, Z.Y.; Liu, K.; He, W. Numerical analyses of hybrid-bonded FRP strengthened concrete beams. Comput. Aided Civ. Infrastruct. Eng. 2009, 24, 371–384. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Development of the Nonlinear Bond Stress—Slip Model of Fiber Reinforced Plastics Sheet—Concrete Interfaces with a Simple Method. J. Compos. Constr. ASCE 2005, 9, 52–62. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, W.W.; Harries, K.A. Bonding Behaviour of Wet-Bonded GFRP-Concrete Interface. J. Compos. Constr. ASCE 2015, 19, 04015001. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P. Bond—Slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. Evaluation of Parameters of Bond Action between FRP and Concrete. J. Compos. Constr. 2013, 17, 626–635. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers. Recommendations for Upgrading of Concrete Structures with the Use of Continuous Fiber Sheets; Japan Society of Civil Engineers: Tokyo, Japan, 2001. [Google Scholar]
- Neubauer, U.; Rostasy, F.S. Design Aspect of Concrete Structures Strengthened with Externally Bonded CFRP Plates. In Proceedings of the 7th International Conference on Structural Faults and Repairs, Edinburgh, UK, 8 July 1997; pp. 109–118. [Google Scholar]
- Ulaga, T.; Vogel, T.; Meier, U. Bilinear stress-slip bond model: Theoretical background and significance. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete, Singapore, 8–10 July 2003; pp. 153–162. [Google Scholar]
- Kaiser, H.; Karbhari, V.M. Identification of potential defects in the rehabilitation of concrete structures with FRP composites. Int. J. Mater. Prod. Technol. 2003, 19, 498–520. [Google Scholar] [CrossRef]
- Atadero, R.A.; Karbhari, V.M. Sources of uncertainty and design values for field-manufactured FRP. Compos. Struct. 2009, 89, 83–93. [Google Scholar] [CrossRef]
- Tatar, J.; Hamilton, H.R. Bond Durability Factor for Externally Bonded CFRP Systems in Concrete Structures. J. Compos. Constr. ASCE 2015, 20, 04015027. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Abanilla, M.A. Design factors, reliability, and durability prediction of wet layup carbon/epoxy used in external strengthening. Compos. Part B Eng. 2007, 38, 10–23. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI 440.2R-08; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Farmer, N.; Gee, T. Design Guidance for Strengthening Concrete Structures Using Fibre Composite Materials; The Concrete Society: Camberley, UK, 2000. [Google Scholar]
- Ellingwood, B.R. Toward Load and Resistance Factor Design for Fiber-Reinforced Polymer Composite Structures. J. Struct. Eng. ASCE 2003, 129, 449–458. [Google Scholar] [CrossRef]
- Monti, G.; Santini, S. Reliability-based Calibration of Partial Safety Coefficients for Fiber-Reinforced Plastic. J. Compos. Constr. ASCE 2002, 6, 162–167. [Google Scholar] [CrossRef]
- Okeil, A.M.; El-Tawil, S.; Shahawy, M. Flexural Reliability of Reinforced Concrete Bridge Girders Strengthened with Carbon Fiber-Reinforced Polymer Laminates. J. Bridge Eng. 2002, 7, 290–299. [Google Scholar] [CrossRef]
- Atadero, R.; Lee, L.; Karbhari, V.M. Consideration of material variability in reliability analysis of FRP strengthened bridge decks. Compos. Struct. 2005, 70, 430–443. [Google Scholar] [CrossRef]
- Sadiq, R.; Rajani, B.; Kleiner, Y. Probabilistic risk analysis of corrosion associated failures in cast iron water mains. Reliab. Eng. Syst. Saf. 2004, 86, 1–10. [Google Scholar] [CrossRef]
- Val, D.V. Reliability of Fiber-Reinforced Polymer-Confined Reinforced Concrete Columns. J. Struct. Eng. ASCE 2003, 129, 1122–1130. [Google Scholar] [CrossRef]
- American Association of State and Highway Transportation Officials. AASHTO LRFD Bridge Design Specifications; Customary US Units Second Edition; American Association of State and Highway Transportation Officials: Washington, DC, USA, 1998. [Google Scholar]
- Wieghaus, K.T.; Atadero, R.A. Effect of Existing Structure and FRP Uncertainties on the Reliability of FRP-Based Repair. J. Compos. Constr. ASCE 2011, 15, 635–643. [Google Scholar] [CrossRef]
- Wang, N.; Ellingwood, B.R.; Zureick, A.H. Reliability-Based Evaluation of Flexural Members Strengthened with Externally Bonded Fiber-Reinforced Polymer Composites. J. Struct. Eng. ASCE 2010, 136, 1151–1160. [Google Scholar] [CrossRef]
- Gomes, S.; Dias-Da-Costa, D.; Neves, L.A.C.; Hadigheh, S.A.; Fernandes, P.; Julio, E. Probabilistic-based characterisation of the mechanical properties of CFRP laminates. Constr. Build. Mater. 2018, 169, 132–141. [Google Scholar] [CrossRef]
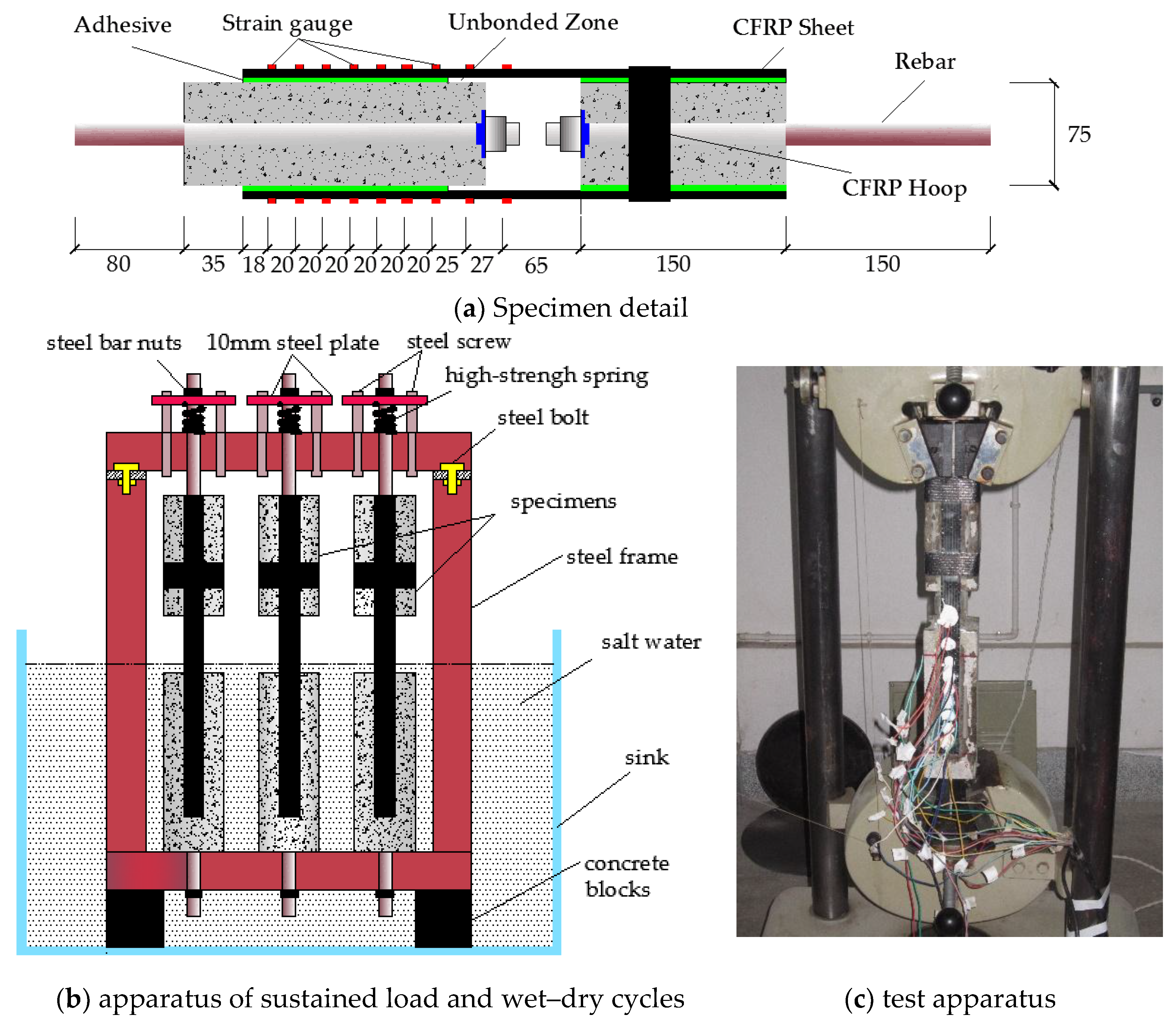
| Specimens | Number of Pieces | Wet–Dry Cycle N (d) | Sustained Loading β (%) | Concrete Strength fcu (MPa) | Young’s Modulus Ef (GPa) | Ultimate Strength fu (MPa) | (N/mm) | |
|---|---|---|---|---|---|---|---|---|
| Mean | COV | |||||||
| CC-CON | 3 | 0 | 0 | 24.8 | 236 | 3947 | 1.436 | 0.1635 |
| CC-90-0% | 3 | 90 | 0 | 32.1 | 240 | 3765 | 1.354 | 0.2270 |
| CC-180-0% | 3 | 180 | 0 | 37.3 | 240 | 3614 | 1.311 | 0.3083 |
| CC-360-0% | 3 | 360 | 0 | 43.5 | 234 | 3579 | 1.248 | 0.3304 |
| CC-90-30% | 3 | 90 | 30 | 32.1 | 240 | 3765 | 1.300 | 0.2782 |
| CC-180-30% | 3 | 180 | 30 | 37.3 | 240 | 3614 | 1.243 | 0.3167 |
| CC-360-30% | 3 | 360 | 30 | 43.5 | 234 | 3579 | 1.183 | 0.3310 |
| CC-90-60% | 3 | 90 | 60 | 32.1 | 240 | 3765 | 1.228 | 0.2799 |
| CC-180-60% | 3 | 180 | 60 | 37.3 | 240 | 3614 | 1.182 | 0.3165 |
| CC-360-60% | 3 | 360 | 60 | 43.5 | 234 | 3579 | 1.025 | 0.3936 |
| Test Methods | Normal | Lognormal | Weibull | Gamma |
|---|---|---|---|---|
| (a) Gf for cases not exposed to environment | ||||
| S–W test | 0.230 | 0.173 | - | - |
| K–S test | >0.150 | >0.150 | - | - |
| C–M test | >0.250 | >0.250 | >0.250 | - |
| A–D test | >0.250 | >0.250 | 0.230 | - |
| χ2 test | 0.123 | 0.092 | 0.079 | 0.073 |
| (b) Gf for cases not subjected to sustained loading | ||||
| S–W test | 0.358 | 0.383 | - | - |
| K–S test | >0.150 | >0.150 | - | >0.500 |
| C–M test | >0.250 | 0.378 | >0.250 | >0.250 |
| A–D test | >0.250 | 0.445 | >0.250 | >0.500 |
| χ2 test | 0.110 | 0.228 | 0.113 | 0.204 |
| (c) Gf for 30% sustained loading cases | ||||
| S–W test | 0.644 | 0.655 | - | - |
| K–S test | >0.150 | >0.150 | - | >0.500 |
| C–M test | >0.250 | >0.500 | >0.250 | >0.500 |
| A–D test | >0.250 | >0.500 | >0.250 | >0.500 |
| χ2 test | 0.423 | 0.623 | 0.454 | 0.617 |
| (d) Gf for 60% sustained loading cases | ||||
| S–W test | 0.557 | 0.639 | - | - |
| K–S test | >0.150 | >0.150 | - | >0.500 |
| C–M test | >0.250 | >0.500 | >0.250 | >0.500 |
| A–D test | >0.250 | >0.500 | >0.250 | >0.500 |
| χ2 test | 0.472 | 0.456 | 0.558 | 0.512 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Li, S.; Lu, Y.; Yang, T. Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles. Materials 2018, 11, 741. https://doi.org/10.3390/ma11050741
Liang H, Li S, Lu Y, Yang T. Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles. Materials. 2018; 11(5):741. https://doi.org/10.3390/ma11050741
Chicago/Turabian StyleLiang, Hongjun, Shan Li, Yiyan Lu, and Ting Yang. 2018. "Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles" Materials 11, no. 5: 741. https://doi.org/10.3390/ma11050741
APA StyleLiang, H., Li, S., Lu, Y., & Yang, T. (2018). Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles. Materials, 11(5), 741. https://doi.org/10.3390/ma11050741






