Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
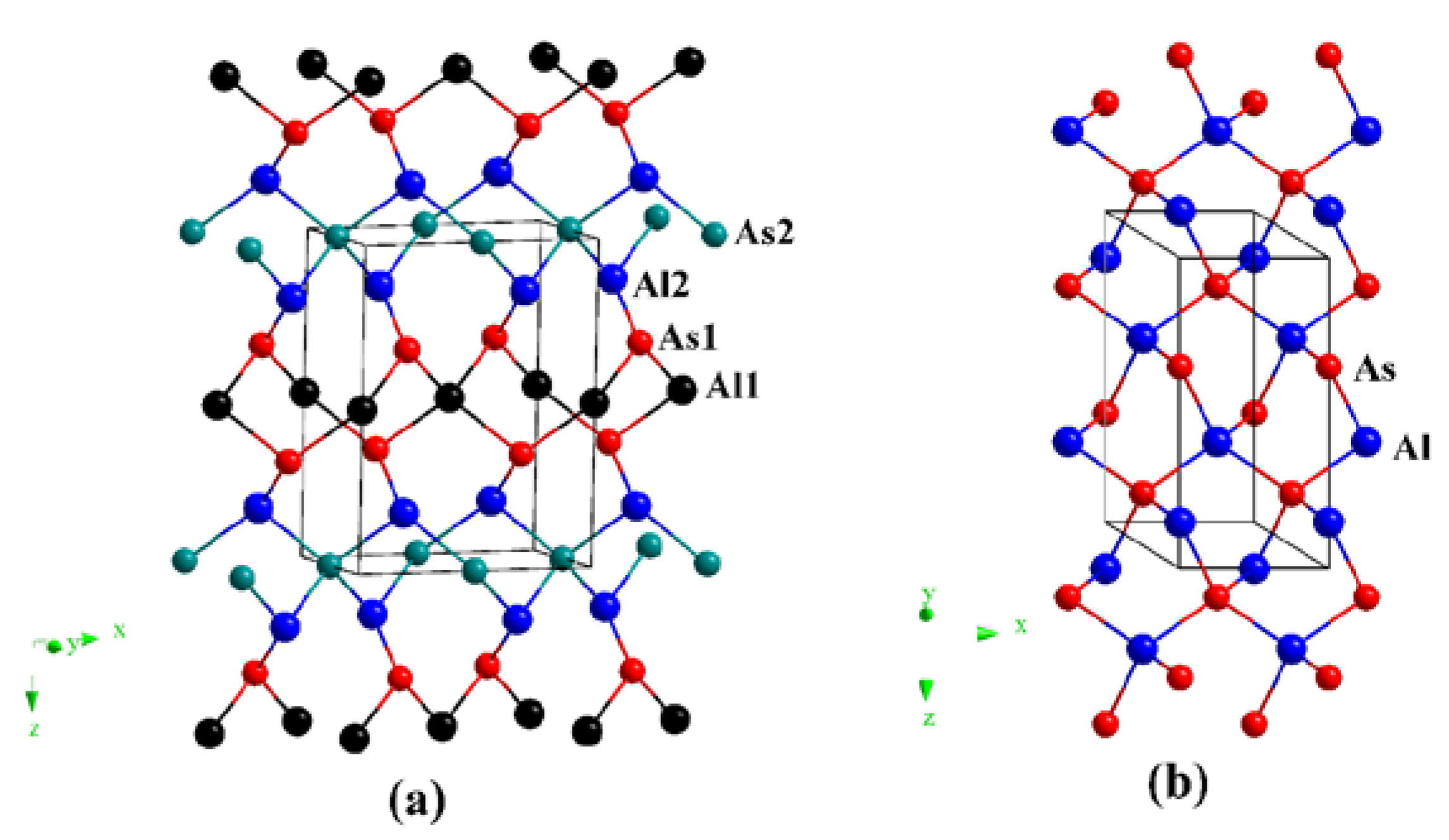
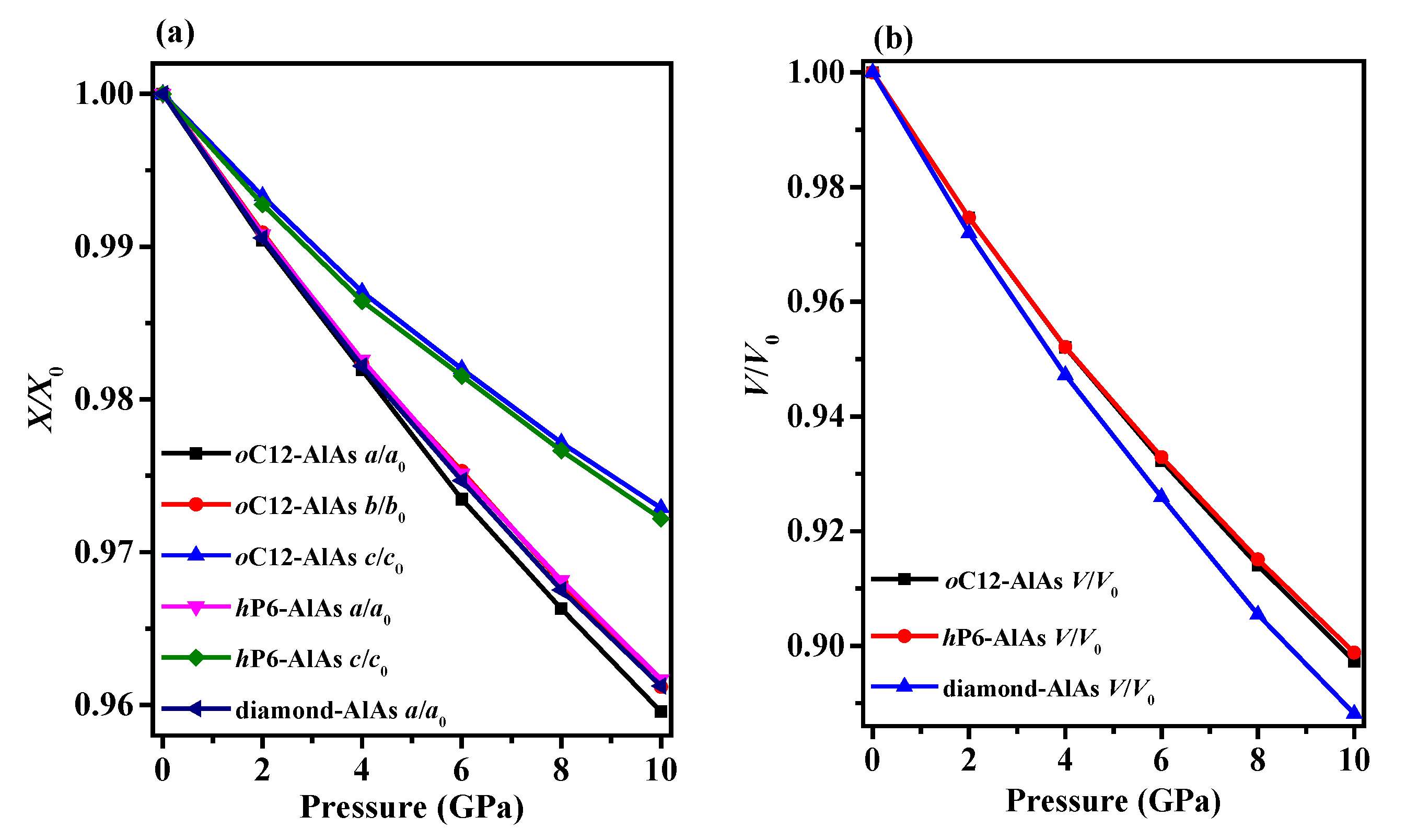
3.1. Structural Properties
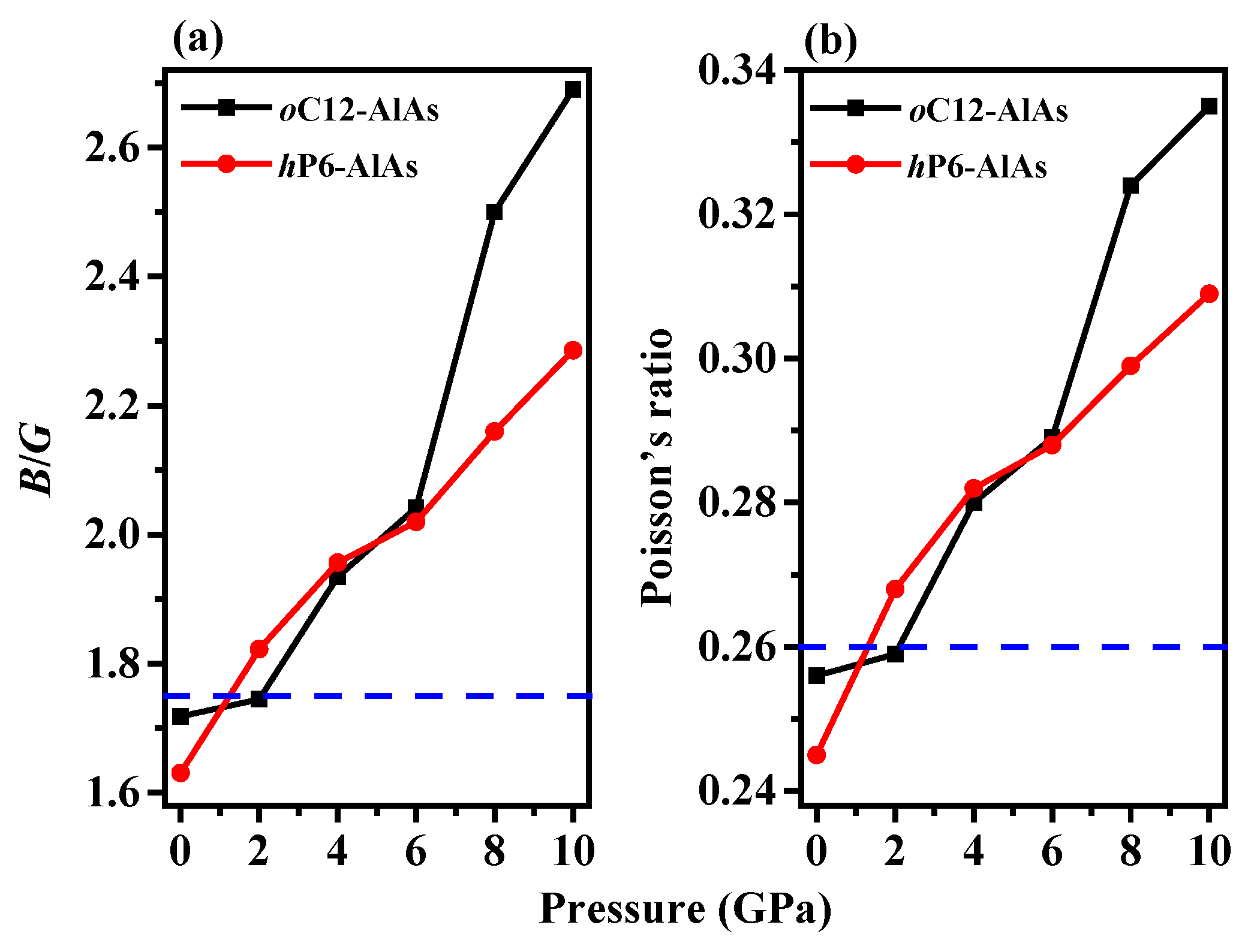
3.2. Mechanical Properties
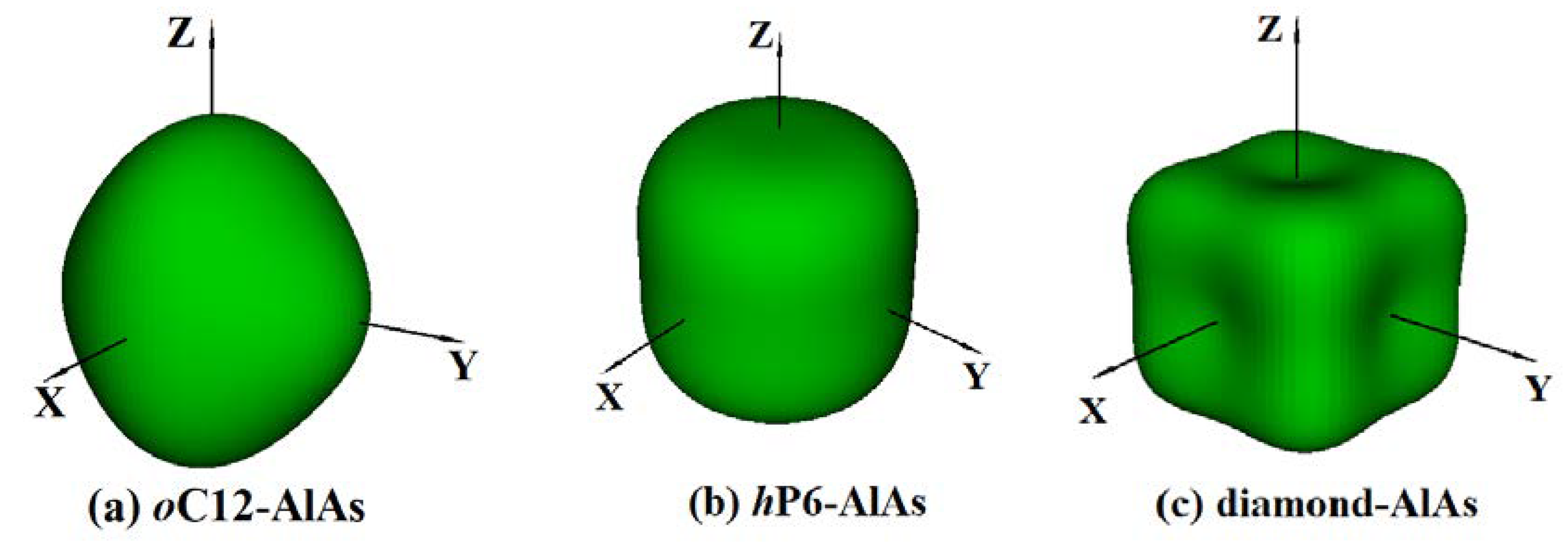
3.3. Anisotropic Properties
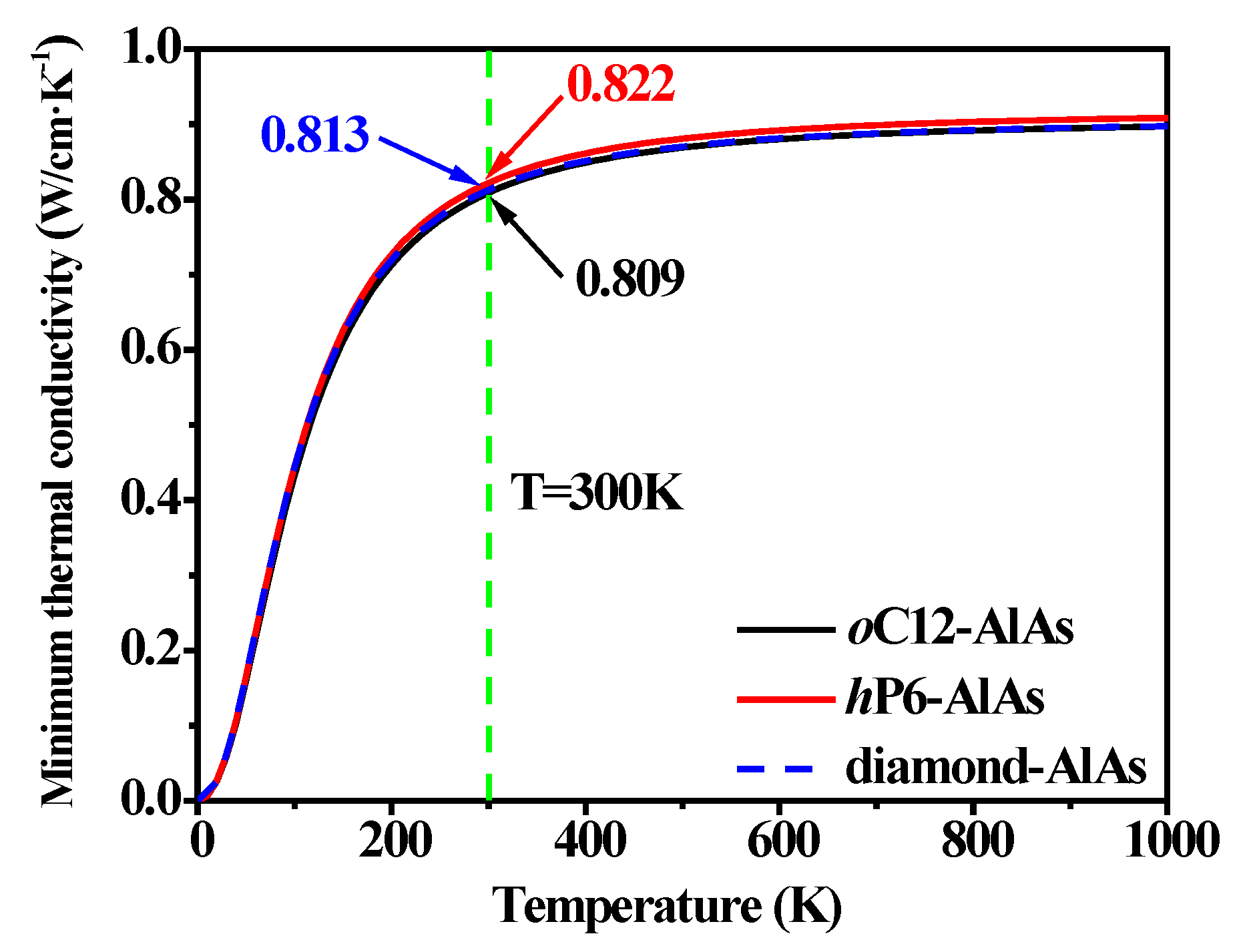
3.4. Thermal Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schroten, E.; Goossens, A.; Schoonman, J. Photo and electroreflectance of cubic boron phosphide. J. Appl. Phys. 1998, 83, 1660–1663. [Google Scholar] [CrossRef]
- Durandurdu, M. Pressure-induced phase transition of zinc-blende AlN: An ab initio molecular dynamics study. J. Phys. Chem. Solids 2008, 69, 2894–2897. [Google Scholar] [CrossRef]
- Gomez, H.; Taylor, T.R.; Neumark, D.M. Anion photoelectron spectroscopy of aluminum phosphide clusters. J. Phys. Chem. A 2001, 105, 6886–6893. [Google Scholar] [CrossRef]
- Bowen, P.; Highfield, J.G.; Mocellin, A.; Ring, T.A. Degradation of aluminum nitride powder in an aqueous environmet. J. Am. Ceram. Soc. 1990, 73, 724–728. [Google Scholar] [CrossRef]
- Takahashi, N.; Matsumoto, Y.; Nakamura, T. Investigations of structure and morphology of the AlN nano-pillar crystal films prepared by halide chemical vapor deposition under atmospheric pressure. J. Phys. Chem. Solids 2006, 67, 665–668. [Google Scholar] [CrossRef]
- Golikova, O.A. Boron and Boron-based semiconductors. Phys. Status Solidi A 1979, 51, 31–40. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T. Thermodynamic, elastic, elastic anisotropy and minimum thermal conductivity of β-GaN under high temperature. Chin. J. Phys. 2017, 55, 400–411. [Google Scholar] [CrossRef]
- Adachi, S. GaAs, AlAs, and AlxGa1−x As: Material parameters for use in research and device applications. J. Appl. Phys. 1985, 58, R1–R29. [Google Scholar] [CrossRef]
- Guo, L. Structural, energetic, and electronic properties of hydrogenated aluminum arsenide clusters. J. Nanopart. Res. 2011, 13, 2029–2039. [Google Scholar] [CrossRef]
- Shen, L.Y.; Xu, X.S.; Lu, W.; Shi, B. Aluminum nitride shaping by non-aqueous gelcasting of low-viscosity and high solid-loading slurry. Ceram. Int. 2016, 42, 5569–5574. [Google Scholar] [CrossRef]
- Chen, B.C.; Ho, C.Y.; Wen, M.Y.; Chen, C.S.; Ma, C.; Tsai, Y.H. Ultrashort-laser-pulse machining characteristics of aluminum nitride and aluminum oxide. Ceram. Int. 2015, 41, S191–S196. [Google Scholar] [CrossRef]
- McNeil, L.E.; Grimsditch, M.; French, R.H. Vibrational spectroscopy of aluminum nitride. J. Am. Ceram. Soc. 1993, 76, 1132–1136. [Google Scholar] [CrossRef]
- Mujica, A.; Rubio, A.; Munoz, A.; Needs, R.J. High-pressure phases of group-IV, III-V, and II-VI compounds. Rev. Mod. Phys. 2003, 75, 863. [Google Scholar] [CrossRef]
- Lei, T.; Fanciulli, M.; Molnar, R.J.; Moustakas, T.D.; Graham, R.J.; Scanlon, J. Epitaxial growth of zinc blende and wurtzitic gallium nitride thin films on (001) silicon. Appl. Phys. Lett. 1991, 59, 944–946. [Google Scholar] [CrossRef]
- Serrano, J.; Rubio, A.; Hernández, E.; Muñoz, A.; Mujica, A. Theoretical study of the relative stability of structural phases in group-III nitrides at high pressures. Phys. Rev. B 2000, 62, 16612. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, J.H.; Zhou, P.K.; Zhang, D.Y.; Yang, Y.T. A New Phase of GaN. J. Chem. 2016, 2016, 8612892. [Google Scholar] [CrossRef]
- Liu, C.; Hu, M.; Luo, K.; Cui, L.; Yu, D.L.; Zhao, Z.S.; He, J.L. Novel high-pressure phases of AlN: A first-principles study. Comput. Mater. Sci. 2016, 117, 496–501. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Du, Z.A. First-principles study of the properties of four predicted novel phases of AlN. J. Phys. Chem. Solids 2017, 104, 68–78. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Du, Z. Phase stability, mechanical and optoelectronic properties of two novel phases of AlN. Mod. Phys. Lett. B 2017, 31, 1750201. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Zhang, D.Y. First-principles study on phases of AlP. Solid State Commun. 2017, 267, 23–28. [Google Scholar] [CrossRef]
- Froyen, S.; Cohen, M.L. Structural properties of III-V zinc-blende semiconductors under pressure. Phys. Rev. B 1983, 28, 3258. [Google Scholar] [CrossRef]
- Greene, R.G.; Luo, H.; Li, T.; Ruoff, A.L. Phase transformation of AlAs to NiAs structure at high pressure. Phys. Rev. Lett. 1994, 72, 2045. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.C.; Lu, Z.W.; Klein, B.M. Pressure-induced phase transformations in AlAs: Comparison between ab initio theory and experiment. Phys. Rev. B 1995, 51, 5678. [Google Scholar] [CrossRef]
- Mujica, A.; Needs, R.J.; Munoz, A. First-principles pseudopotential study of the phase stability of the III-V semiconductors GaAs and AlAs. Phys. Rev. B 1995, 2, 8881. [Google Scholar] [CrossRef]
- Mujica, A.; Rodríguez-Hernández, P.; Radescu, S.; Needs, R.J.; Munoz, A. AlX (X = As, P, Sb) compounds under pressure. Phys. Status Solidi B 1999, 211, 39–43. [Google Scholar] [CrossRef]
- Srivastava, A.; Tyagi, N. High pressure behavior of AlAs nanocrystals: The first-principle study. High Press. Res. 2012, 32, 43–47. [Google Scholar] [CrossRef]
- Liu, C.; Ma, M.D.; Yuan, X.H.; Sun, H.; Ying, P.; Xu, B.; Zhao, Z.S.; He, J.L. Metastable phases, phase transformation and properties of AlAs based on first-principle study. Comput. Mater. Sci. 2017, 128, 337–342. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T. Two novel silicon phases with direct band gaps. Phys. Chem. Chem. Phys. 2016, 18, 12905–12913. [Google Scholar] [CrossRef] [PubMed]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Chem. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Wasilewski, Z.R.; Dion, M.M.; Lockwood, D.J.; Poole, P.; Streater, R.W.; SpringThorpe, A.J. Determination of AlxGa(1-x) As composition: The MBE perspective. J. Cryst. Growth 1997, 175, 238–243. [Google Scholar] [CrossRef]
- Gehrsitz, S.; Sigg, H.; Herres, N.; Bachem, K.; Köhler, K.; Reinhart, F.K. Compositional dependence of the elastic constants and the lattice parameter of AlxGa1−xAs. Phys. Rev. B 1999, 60, 11601. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T.; Yang, Q.; Chen, P.Y.; Xing, M.J.; Zhang, J.Q.; Yao, R. Prediction of novel phase of silicon and Si-Ge alloys. J. Solid State Chem. 2016, 233, 471–483. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Zhou, P.K.; Zhang, J.Q.; Yang, Y.T. Si96: A new silicon allotrope with interesting physical properties. Materials 2016, 9, 284. [Google Scholar] [CrossRef] [PubMed]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. First-principles study of structural and electronic properties of C14-type Laves phase Al2Zr and Al2Hf. Comput. Mater. Sci. 2014, 83, 27–34. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768–773. [Google Scholar] [CrossRef]
- Sun, L.; Gao, Y.M.; Xiao, B.; Li, Y.F.; Wang, G.L. Anisotropic elastic and thermal properties of titanium borides by first-principles calculations. J. Alloys Compd. 2013, 579, 457–467. [Google Scholar] [CrossRef]
- Duan, Y.H.; Sun, Y.; Peng, M.J.; Zhou, S.G. Anisotropic elastic properties of the Ca-Pb compounds. J. Alloys Compd. 2014, 595, 14–21. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Zhang, M.G.; Yan, H.Y.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Imm2- and I4-m2-BCN. Comput. Mater. Sci. 2015, 97, 6–13. [Google Scholar] [CrossRef]
- Grimmeiss, H.G.; Monema, B. Temperature dependence of the refractive index of AlAs and AlP. Phys. Status Solidi A 1971, 5, 109–114. [Google Scholar] [CrossRef]
- Sichel, E.K.; Pankove, J.I. Thermal conductivity of GaN, 25–360 K. J. Phys. Chem. Solids 1977, 38, 330. [Google Scholar] [CrossRef]
| Materials | PBE | Exp. | ||
|---|---|---|---|---|
| a | b | c | a | |
| diamond-AlAs | 5.675 | 5.661 1 | ||
| oC12-AlAs | 6.972 | 3.968 | 9.108 | |
| 6.975 2 | 3.977 2 | 9.094 2 | ||
| hP6-AlAs | 4.019 | 8.990 | ||
| 4.026 2 | 8.973 2 | |||
| Materials | P | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 | B | G | E | v |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| oC12-AlAs | 0 | 120 | 41 | 50 | 130 | 45 | 145 | 40 | 52 | 42 | 76 | 44 | 111 | 0.257 |
| 0 1 | 127 | 39 | 45 | 121 | 52 | 153 | 47 | 38 | 43 | 74 | 43 | 108 | 0.257 | |
| 2 | 133 | 48 | 59 | 138 | 51 | 155 | 47 | 58 | 44 | 82 | 47 | 118 | 0.259 | |
| 4 | 137 | 56 | 65 | 145 | 59 | 163 | 44 | 55 | 41 | 89 | 46 | 118 | 0.280 | |
| 6 | 146 | 63 | 74 | 154 | 67 | 177 | 47 | 59 | 45 | 98 | 48 | 124 | 0.289 | |
| 8 | 156 | 68 | 82 | 161 | 73 | 186 | 33 | 41 | 45 | 105 | 42 | 111 | 0.324 | |
| 10 | 162 | 77 | 91 | 169 | 80 | 195 | 41 | 33 | 44 | 113 | 42 | 112 | 0.335 | |
| hP6-AlAs | 0 | 127 | 42 | 49 | 140 | 53 | 43 | 75 | 46 | 115 | 0.245 | |||
| 0 1 | 126 | 38 | 51 | 147 | 44 | 75 | 44 | 110 | 0.256 | |||||
| 2 | 133 | 50 | 56 | 147 | 50 | 42 | 82 | 45 | 114 | 0.268 | ||||
| 4 | 140 | 57 | 64 | 158 | 52 | 41 | 90 | 46 | 118 | 0.282 | ||||
| 6 | 165 | 62 | 75 | 171 | 53 | 51 | 103 | 51 | 131 | 0.288 | ||||
| 8 | 165 | 67 | 82 | 182 | 53 | 49 | 108 | 50 | 130 | 0.299 | ||||
| 10 | 171 | 75 | 86 | 174 | 53 | 48 | 112 | 49 | 128 | 0.309 | ||||
| diamond-AlAs | 0 | 116 | 53 | 55 | 74 | 44 | 110 | 0.252 | ||||||
| 0 2 | 120 | 57 | 57 | 78 | 45 |
| Materials | Directions | Pressure | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | |||
| oC12-AlAs | [100] | [100]vl | 5464 | 5675 | 5691 | 5813 | 5948 | 6007 |
| [010]vt1 | 3232 | 3264 | 3113 | 3227 | 3194 | 3130 | ||
| [001]vt2 | 3597 | 3747 | 3606 | 3696 | 3049 | 2711 | ||
| [010] | [010]vl | 5687 | 5780 | 5855 | 5971 | 6042 | 6135 | |
| [100]vt1 | 3232 | 3264 | 3113 | 3227 | 3194 | 3130 | ||
| [001]vt2 | 3154 | 3373 | 3225 | 3298 | 2736 | 3022 | ||
| [001] | [001]vl | 6006 | 6126 | 6208 | 6401 | 6494 | 6590 | |
| [100]vt1 | 3597 | 3747 | 3606 | 3696 | 3049 | 2711 | ||
| [010]vt2 | 3154 | 3373 | 3225 | 3298 | 2736 | 3022 | ||
| hP6-AlAs | [100] | [100]vl | 3243 | 3166 | 3129 | 3450 | 3333 | 3269 |
| [010]vt1 | 5607 | 5667 | 5747 | 6176 | 6116 | 6171 | ||
| [001]vt2 | 3622 | 3475 | 3502 | 3500 | 3466 | 3436 | ||
| [001] | [001]vl | 5887 | 5958 | 6105 | 6287 | 6424 | 6225 | |
| [100]vt1 | 3622 | 3475 | 3502 | 3500 | 3466 | 3436 | ||
| [010]vt2 | 3622 | 3475 | 3502 | 3500 | 3466 | 3436 | ||
| diamond-AlAs | [100] | [100]vl | 5676 | |||||
| [010]vt1 | 3909 | |||||||
| [001]vt2 | 3909 | |||||||
| [110] | [110]vl | 6225 | ||||||
| [10]vt1 | 4183 | |||||||
| [001]vt2 | 3837 | |||||||
| [111] | [111]vl | 6397 | ||||||
| [11]vt1 | 3305 | |||||||
| [11]vt2 | 3305 | |||||||
| Materials | Pressure | ρ (g/cm3) | vl | vt | vm | ΘD |
|---|---|---|---|---|---|---|
| oC12-AlAs | 0 | 4.02 | 5781 | 3305 | 3672 | 463 |
| 2 | 4.13 | 5916 | 3372 | 3748 | 476 | |
| 4 | 4.23 | 5960 | 3297 | 3673 | 473 | |
| 6 | 4.32 | 6123 | 3333 | 3718 | 484 | |
| 8 | 4.41 | 6044 | 3087 | 3458 | 457 | |
| 10 | 4.49 | 6135 | 3058 | 3432 | 458 | |
| hP6-AlAs | 0 | 4.04 | 5812 | 3376 | 3746 | 471 |
| 2 | 4.14 | 5856 | 3297 | 3668 | 468 | |
| 4 | 4.24 | 5975 | 3294 | 3671 | 474 | |
| 6 | 4.33 | 6287 | 3433 | 3829 | 498 | |
| 8 | 4.41 | 6293 | 3367 | 3761 | 494 | |
| 10 | 4.49 | 6284 | 3303 | 3694 | 490 | |
| diamond-AlAs | 0 | 3.60 | 6068 | 3495 | 3880 | 433 |
| 0 1 | 3.73 | 450 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chai, C.; Song, Y.; Fan, Q.; Yang, Y. Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials 2018, 11, 740. https://doi.org/10.3390/ma11050740
Zhang W, Chai C, Song Y, Fan Q, Yang Y. Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials. 2018; 11(5):740. https://doi.org/10.3390/ma11050740
Chicago/Turabian StyleZhang, Wei, Changchun Chai, Yanxing Song, Qingyang Fan, and Yintang Yang. 2018. "Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure" Materials 11, no. 5: 740. https://doi.org/10.3390/ma11050740
APA StyleZhang, W., Chai, C., Song, Y., Fan, Q., & Yang, Y. (2018). Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials, 11(5), 740. https://doi.org/10.3390/ma11050740





