Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review
Abstract
1. Introduction
2. Phase Change Materials in Concrete Technology
2.1. Classification of Phase Change Materials
2.2. Incorporation of PCMs in Concrete
- Using pipes filled with PCM incorporated in concrete.
- Using porous carriers such as lightweight aggregates (LWAs) impregnated with PCMs.
- Using microencapsulated PCMs.
- Impregnating PCMs in the concrete pores from the surface.
2.2.1. Embedded Pipes
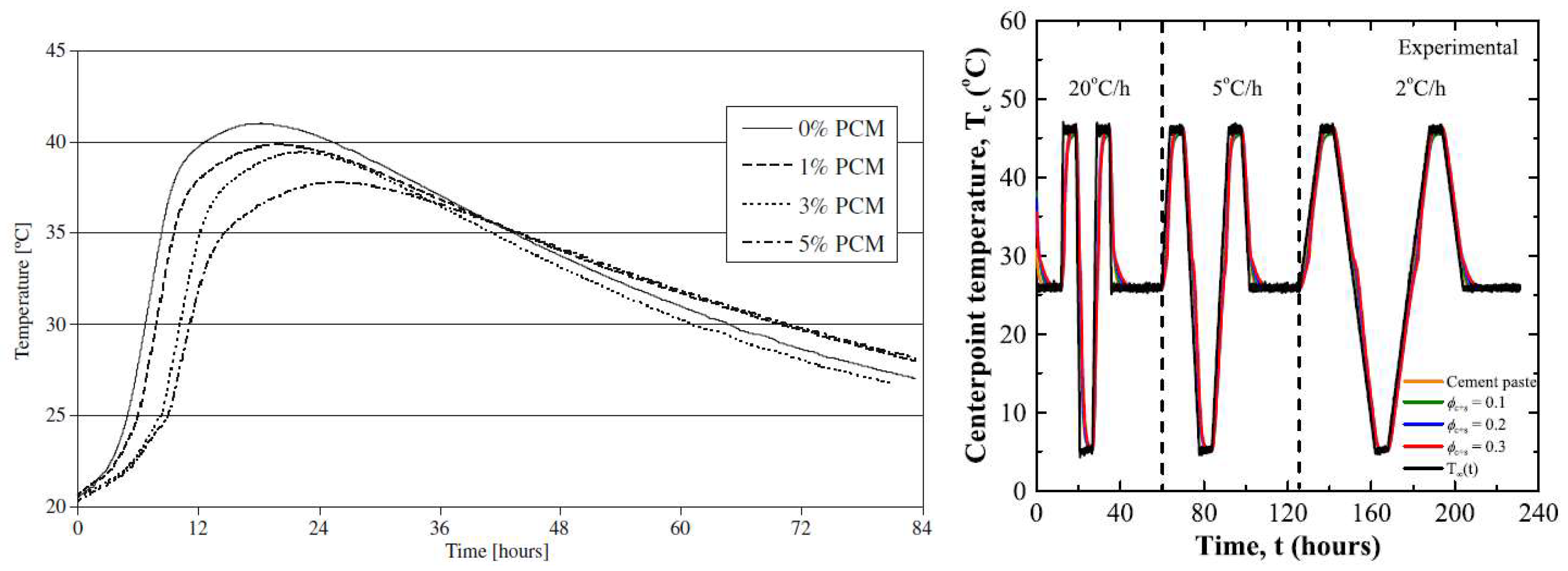
2.2.2. Lightweight Aggregates
2.2.3. Microencapsulation
2.2.4. Surface Impregnation
3. Use of PCM to Reduce Concrete Cracking
3.1. Cracking of Concrete at Early Age Due to Hydration Heat Development
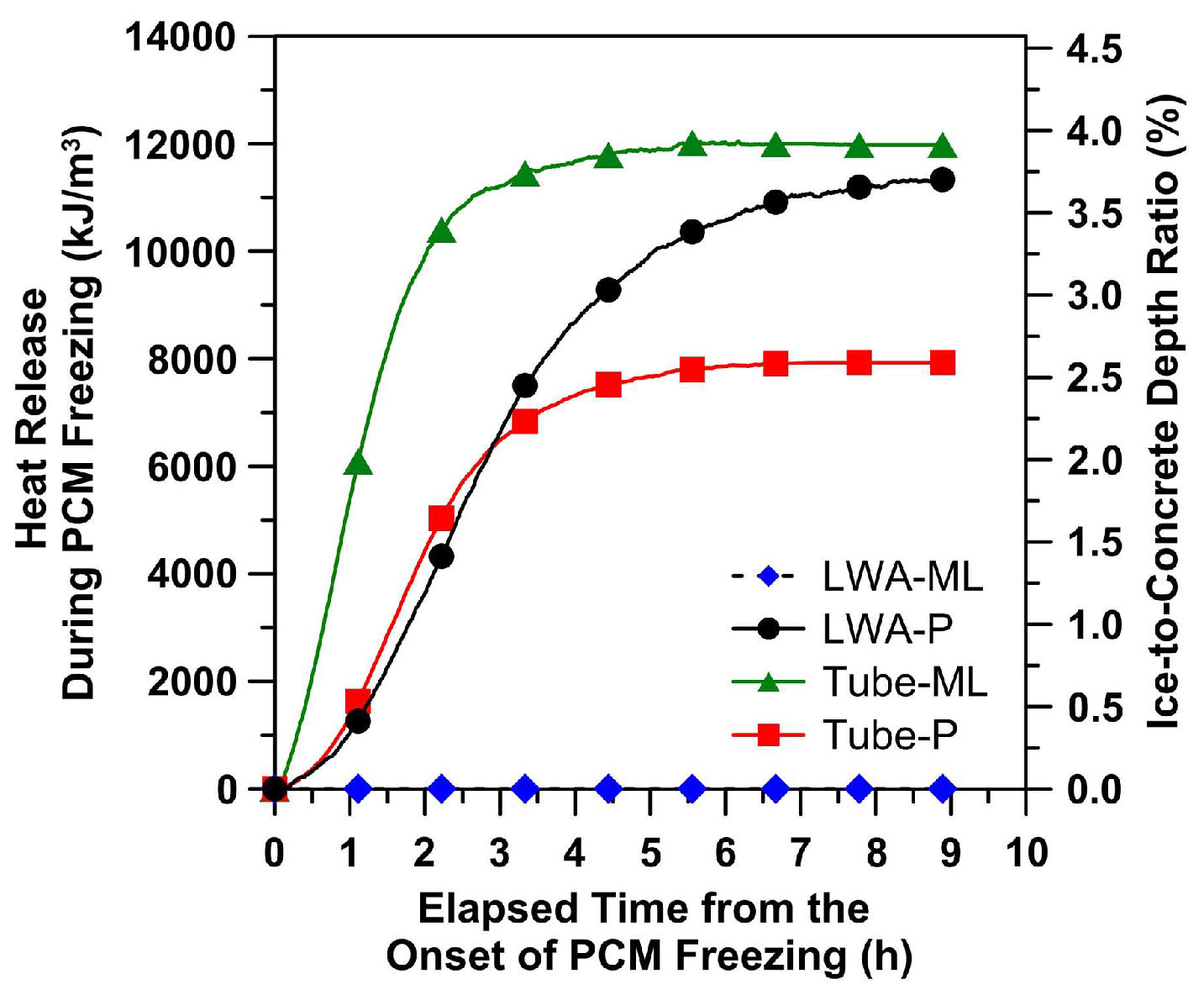
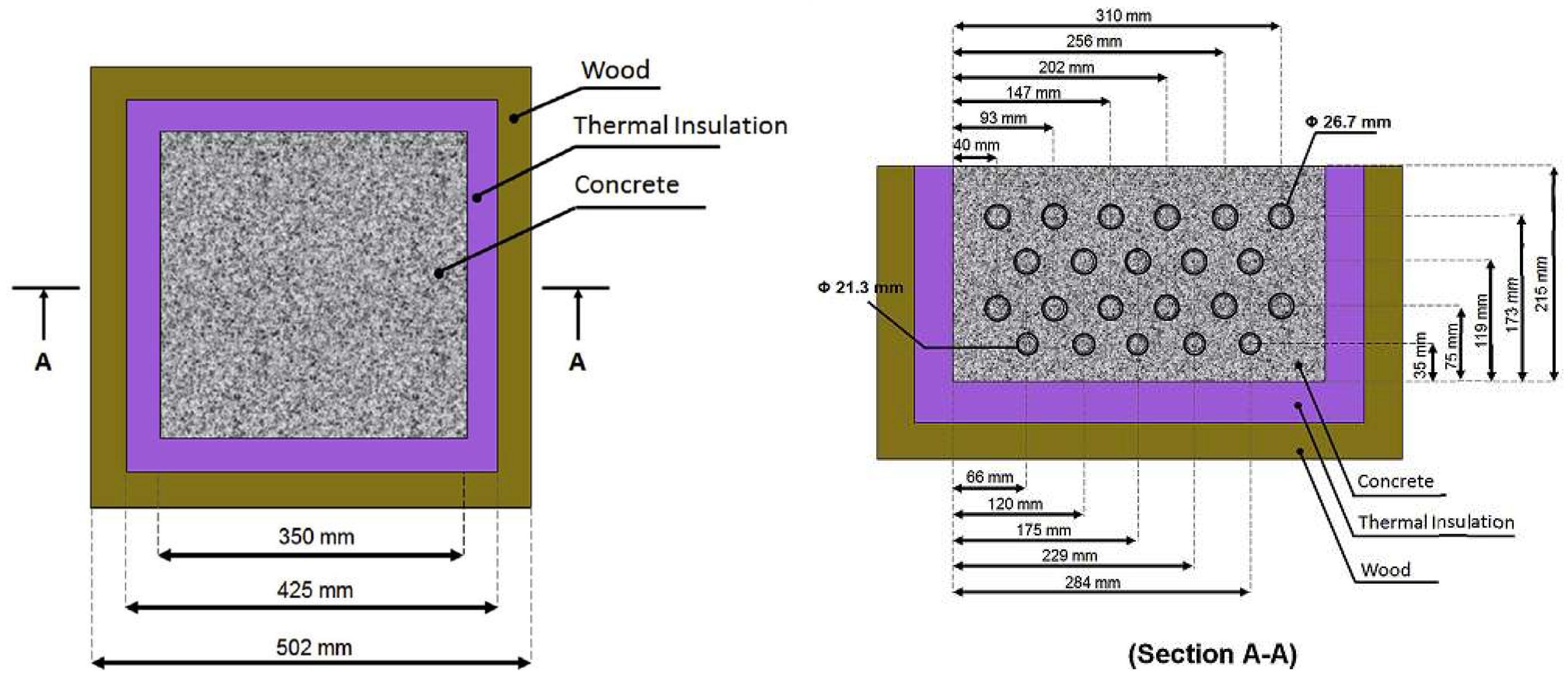
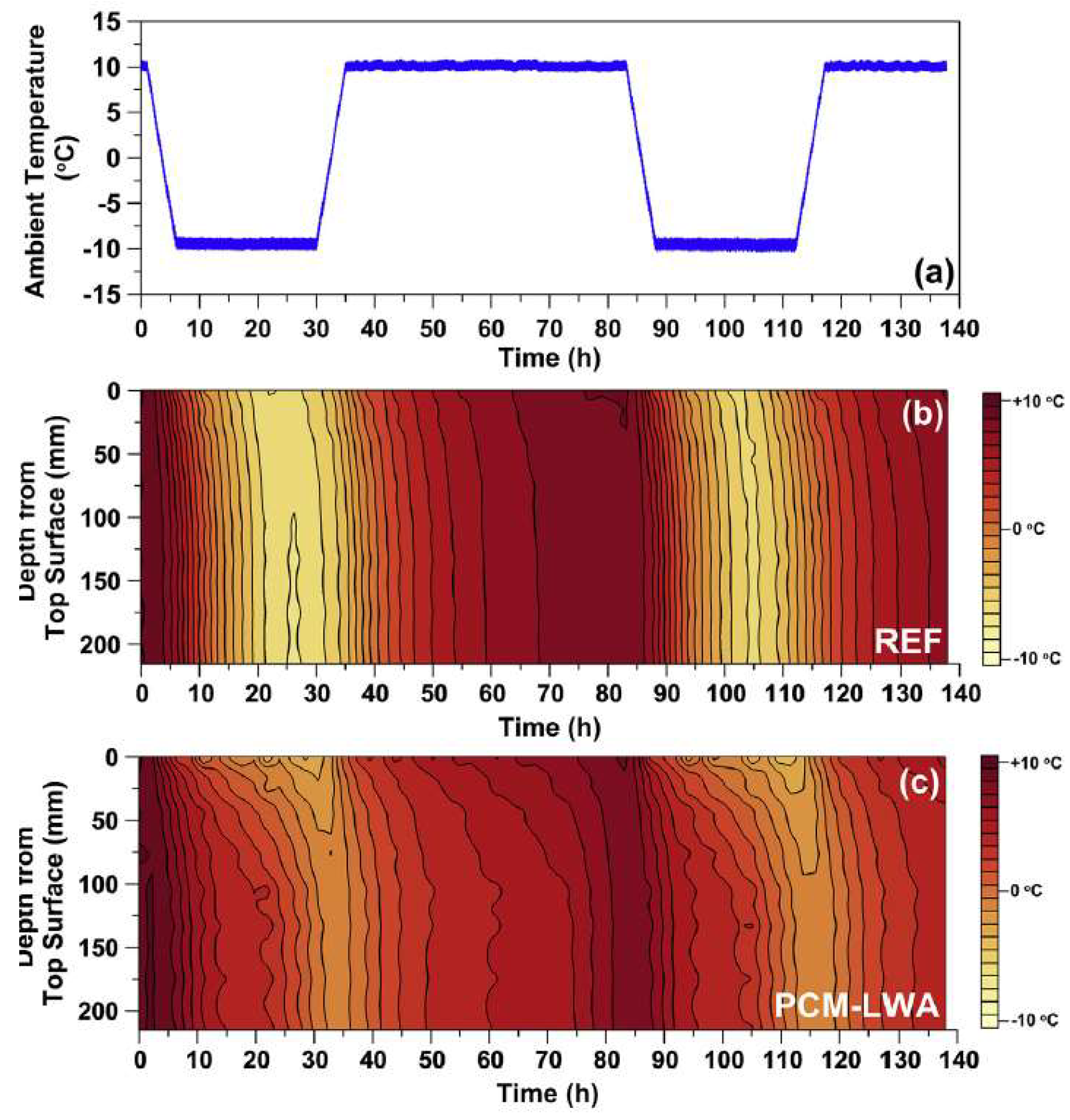
3.2. Cracking of Concrete Due to Freeze/Thaw Cycles
4. Effects of PCM on Concrete Properties
4.1. Fresh Concrete Properties
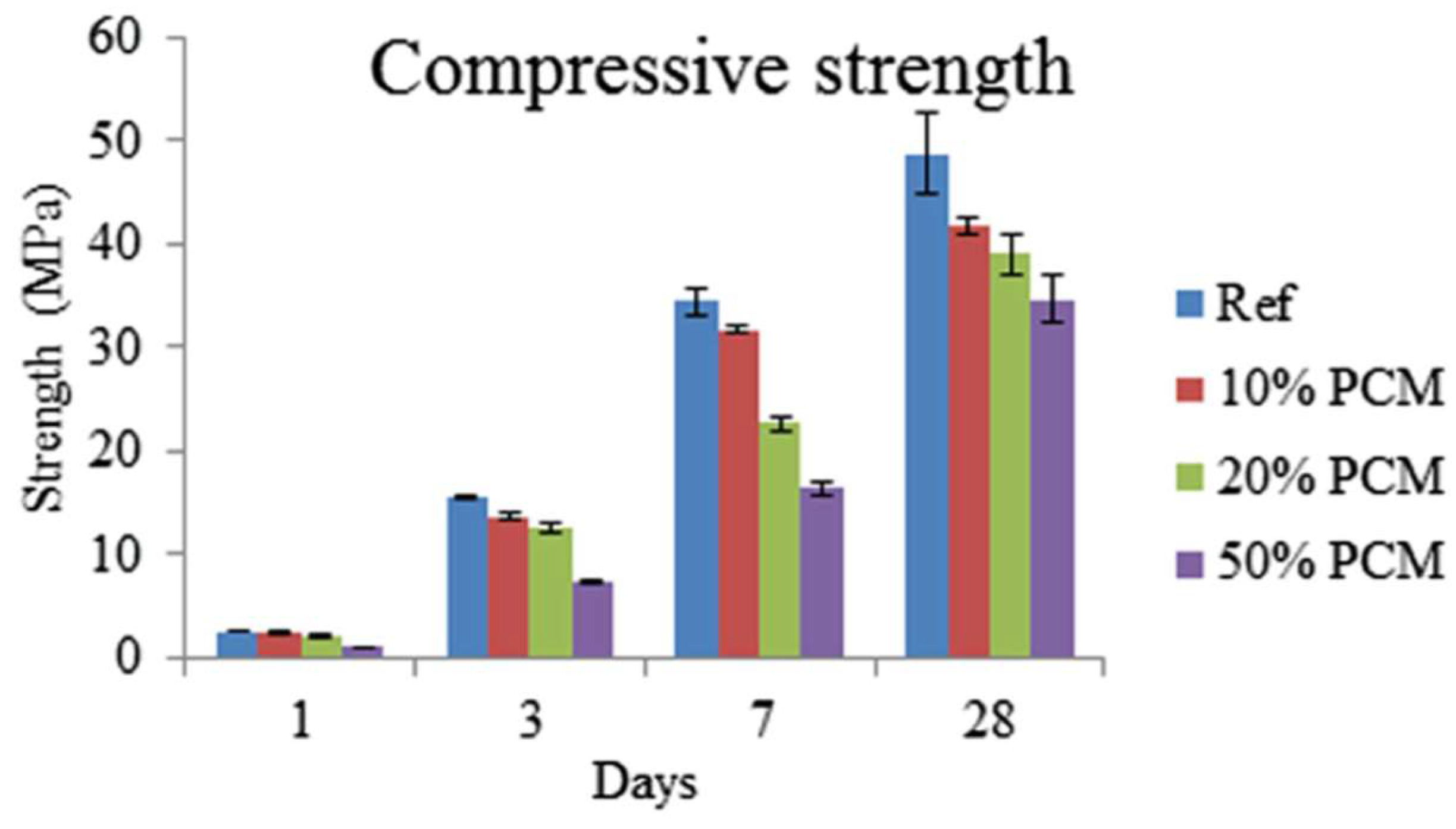
4.2. Mechanical Properties
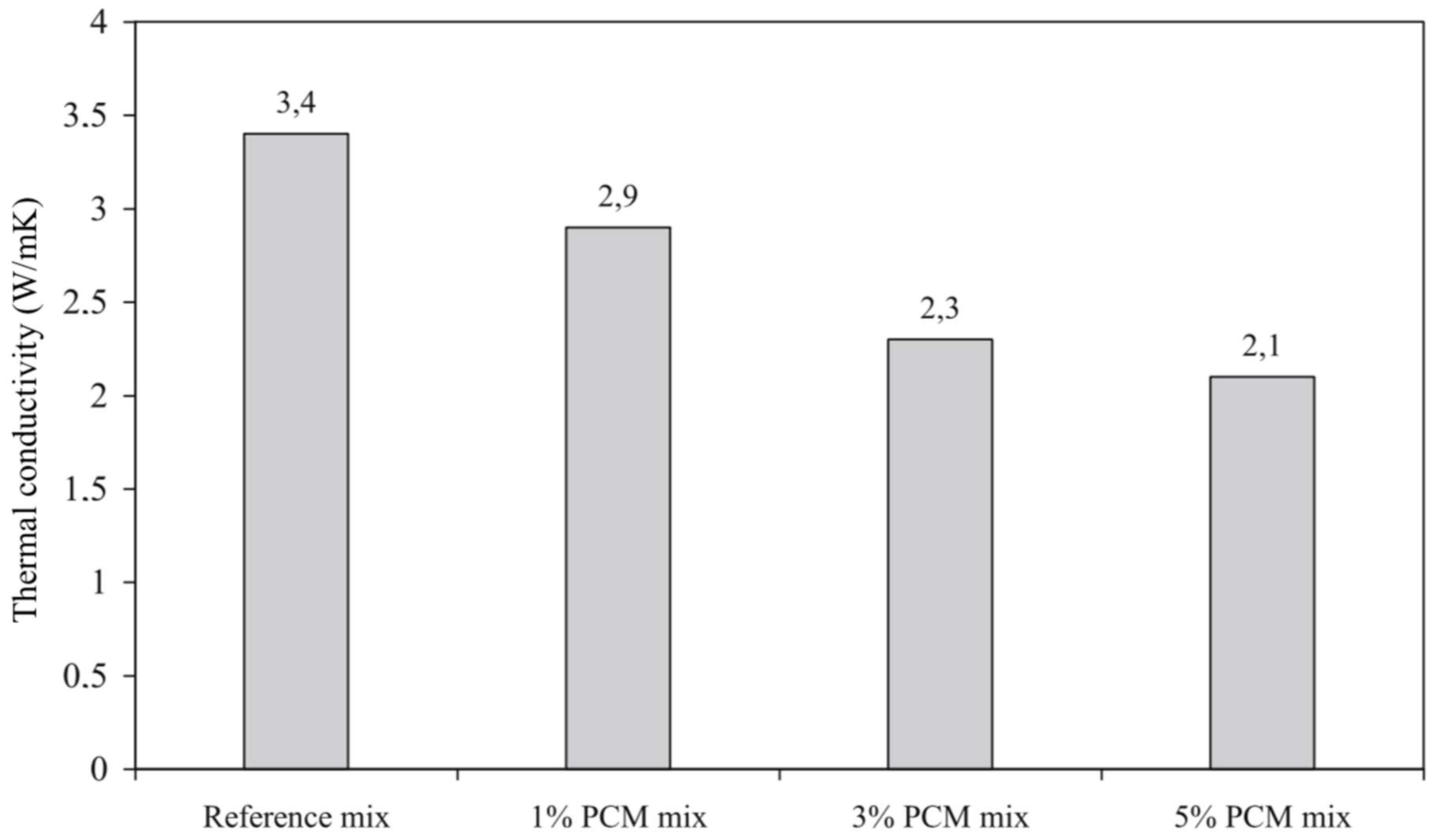
4.3. Thermal Properties
4.4. Durability
5. Modeling of PCM Composites
5.1. Effective Properties
5.1.1. Mechanical Properties
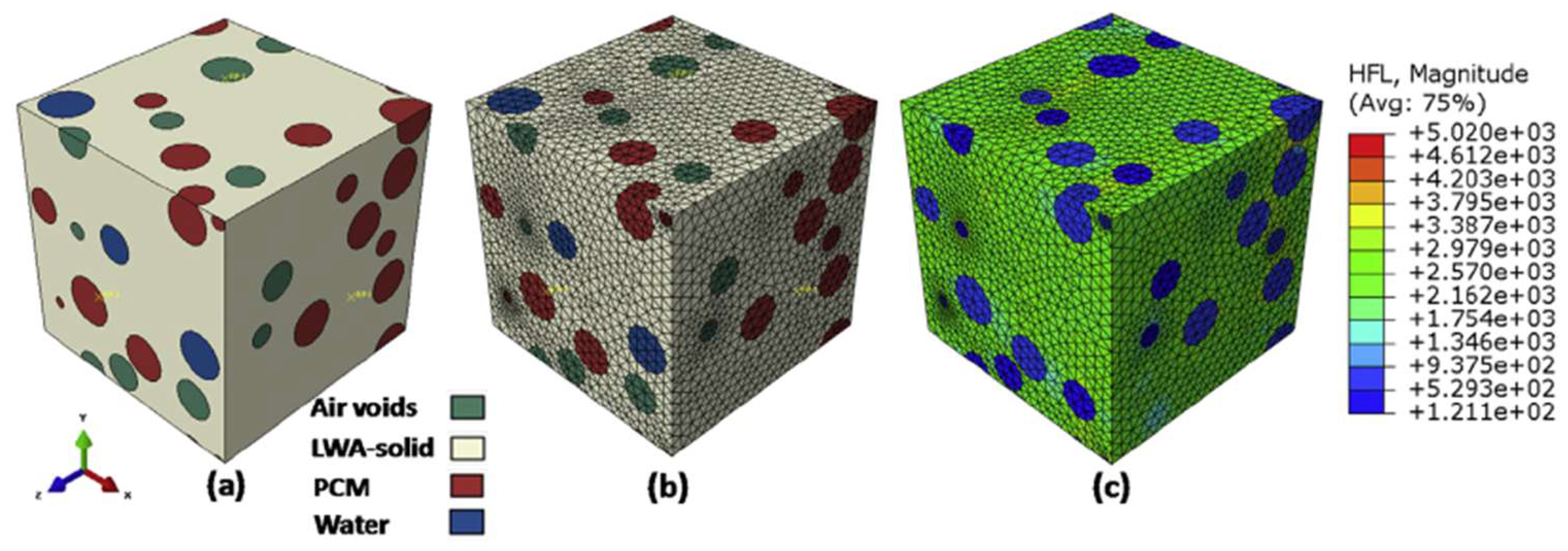
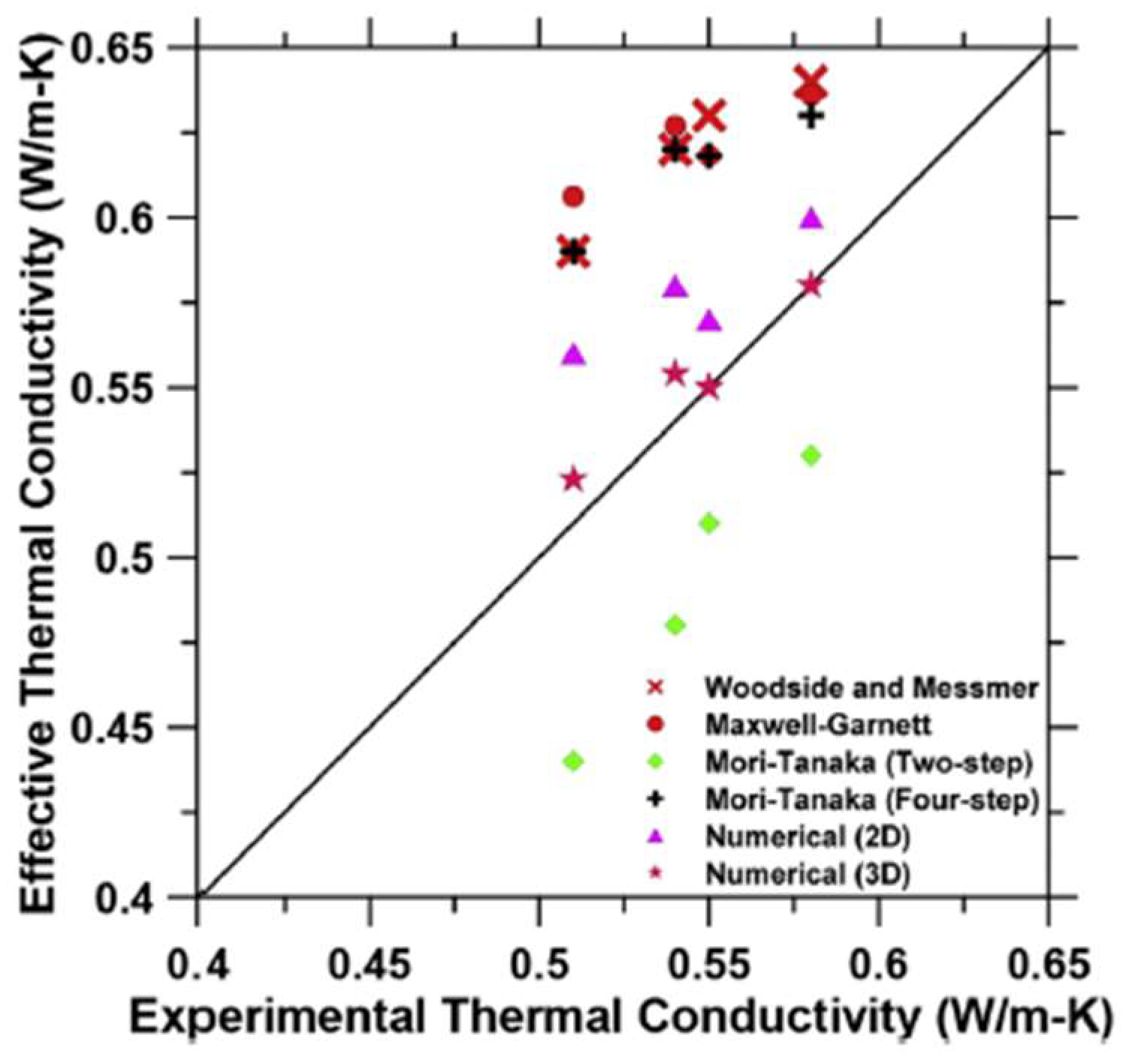
5.1.2. Thermal Conductivity
5.2. Material and Structural Performance
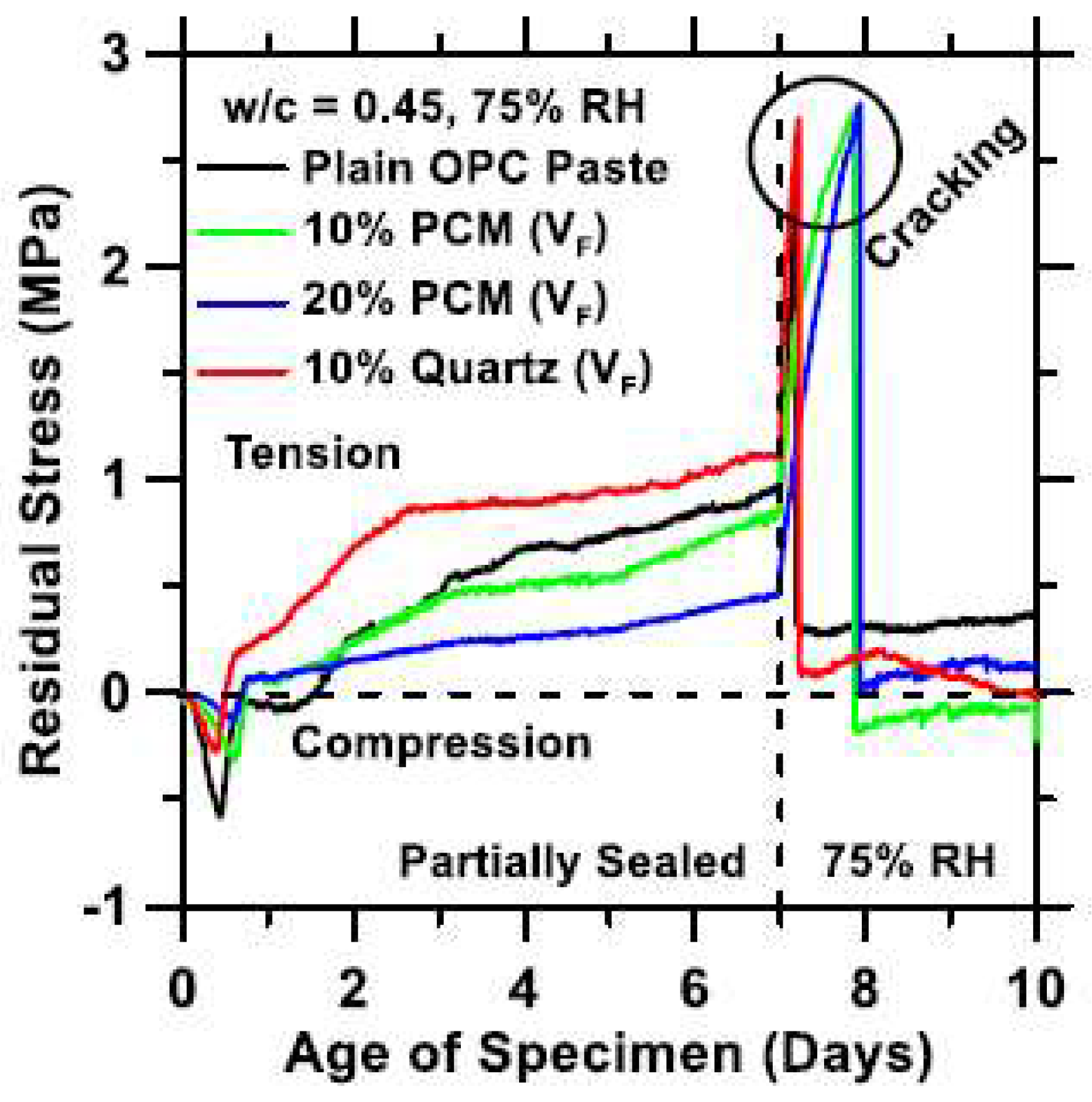
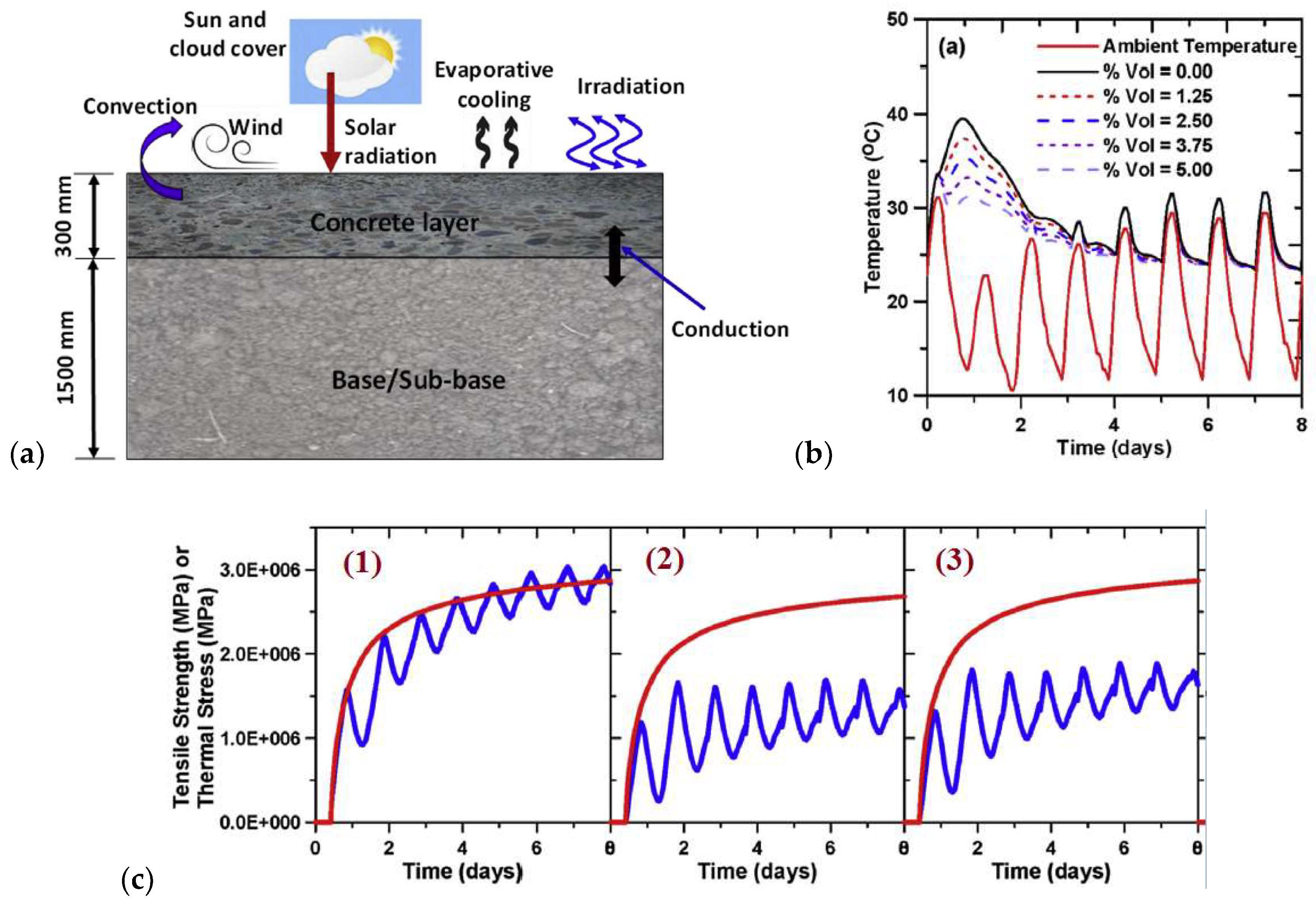
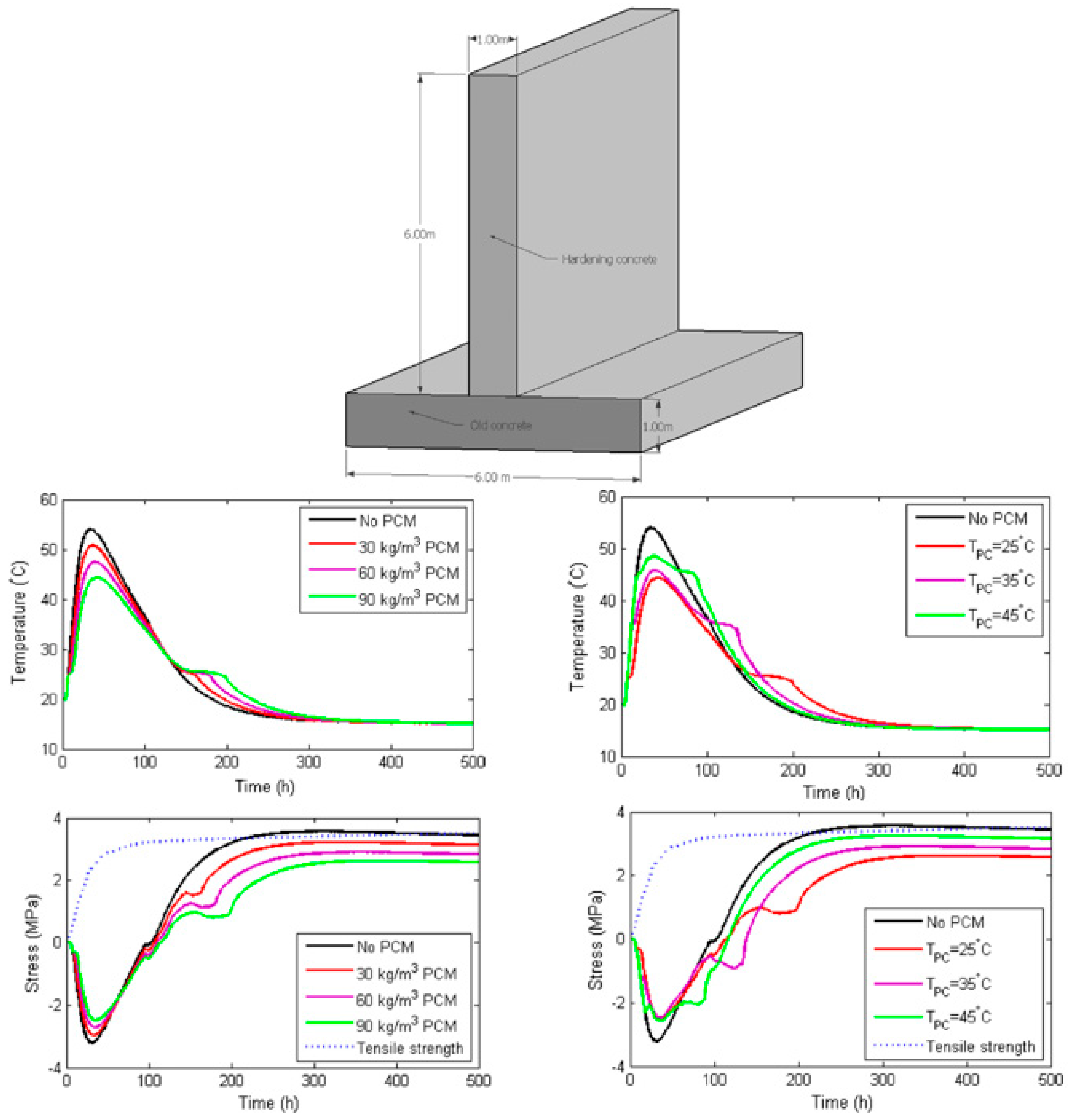
- In semi-adiabatic (i.e., field) conditions, the addition of PCM in hardening concrete has potential to delay the temperature rise, reduce the maximum tensile stress, and delay its occurrence. The maximum tensile stress is inversely proportional to the amount of PCM added to the mix (see Figure 30).
- In semi-adiabatic conditions, the phase change temperature does influence the maximum temperature developing in the structure (Figure 30).
- An increase in the latent heat of fusion serves the same purpose as an increase in PCM addition: it lowers the maximum temperature and maximum stress and delays their occurrence. Especially the cooling phase is prolonged. Therefore, a trade-off between the heat of fusion and quantity of PCM microcapsules is possible, where a smaller amount of PCMs with a higher heat of fusion can be used with the same (thermal) efficiency. This would be beneficial also in terms of mechanical properties of the concrete.
6. Summary and Future Research Needs
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Radaelli, E.; Polder, R.B. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Revert, A.B.; De Weerdt, K.; Hornbostel, K.; Geiker, M.R. Carbonation-induced corrosion: Investigation of the corrosion onset. Constr. Build. Mater. 2018, 162, 847–856. [Google Scholar] [CrossRef]
- Montemor, M.F.; Simoes, A.M.P.; Ferreira, M.G.S. Chloride-induced corrosion of reinforcing steel: From fundamentals to the monitoring techniques. Cem. Concr. Compos. 2003, 25, 491–502. [Google Scholar] [CrossRef]
- Šavija, B.; Luković, M.; Hosseini, S.A.S.; Pacheco, J.; Schlangen, E. Corrosion induced cover cracking studied by X-ray computed tomography, nanoindentation, and energy dispersive X-ray spectrometry (EDS). Mater. Struct. 2015, 48, 2043–2062. [Google Scholar] [CrossRef]
- Šavija, B.; Luković, M.; Pacheco, J.; Schlangen, E. Cracking of the concrete cover due to reinforcement corrosion: A two-dimensional lattice model study. Constr. Build. Mater. 2013, 44, 626–638. [Google Scholar] [CrossRef]
- Helland, S. Design for service life: Implementation of fib Model Code 2010 rules in the operational code ISO 16204. Struct. Concr. 2013, 14, 10–18. [Google Scholar] [CrossRef]
- Maage, M.; Helland, S.; Poulsen, E.; Vennesland, O.; Carl, J.E. Service life prediction of existing concrete structures exposed to marine environment. ACI Mater. J. 1996, 6, 602–608. [Google Scholar]
- Van Mier, J.G.M. Fracture Processes of Concrete; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Weiss, W.J.; Yang, W.; Shah, S.P. Shrinkage cracking of restrained concrete slabs. J. Eng. Mech. 1998, 124, 602–608. [Google Scholar] [CrossRef]
- Yuan, Y.; Wan, Z.L. Prediction of cracking within early-age concrete due to thermal, drying and creep behavior. Cem. Concr. Res. 2002, 32, 1053–1059. [Google Scholar] [CrossRef]
- Copuroglu, O.; Schlangen, E. Modeling of frost salt scaling. Cem. Concr. Res. 2008, 38, 27–39. [Google Scholar] [CrossRef]
- Šavija, B. Experimental and Numerical Investigation of Chloride Ingress in Cracked Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- De Schutter, G. Quantification of the influence of cracks in concrete structures on carbonation and chloride penetration. Mag. Concr. Res. 1999, 51, 427–435. [Google Scholar] [CrossRef]
- Blagojevic, A. The Influence of Cracks on the Durability and Service Life of Reinforced Concrete Structures in Relation to Reinforcement Corrosion. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Barros, J.A.; Cunha, V.M.; Ribeiro, A.F.; Antunes, J.A.B. Post-cracking behaviour of steel fibre reinforced concrete. Mater. Struct. 2005, 38, 47–56. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). ACI Mater. J. 2001, 98, 483–492. [Google Scholar]
- Merta, I.; Tschegg, E.K. Fracture energy of natural fibre reinforced concrete. Constr. Build. Mater. 2013, 40, 991–997. [Google Scholar] [CrossRef]
- Huang, H.; Ye, G.; Qian, C.; Schlangen, E. Self-healing in cementitious materials: Materials, methods and service conditions. Mater. Des. 2016, 92, 499–511. [Google Scholar] [CrossRef]
- Van Tittelboom, K.; De Belie, N. Self-healing in cementitious materials—A review. Materials 2013, 6, 2182–2217. [Google Scholar] [CrossRef] [PubMed]
- Šavija, B.; Feiteira, J.; Araujo, M.; Chatrabhuti, S.; Raquez, J.M.; Van Tittelboom, K.; Gruyaert, E.; De Belie, N.; Schlangen, E. Simulation-aided design of tubular polymeric capsules for self-healing concrete. Materials 2017, 10, 10. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Fernandes, F.; Manari, S.; Aguayo, M.; Santos, K.; Oey, T.; Wei, Z.; Falzone, G.; Neithalath, N.; Sant, G. On the feasibility of using phase change materials (PCMs) to mitigate thermal cracking in cementitious materials. Cem. Concr. Compos. 2014, 51, 14–26. [Google Scholar] [CrossRef]
- Bentz, D.P.; Turpin, R. Potential applications of phase change materials in concrete technology. Cem. Concr. Compos. 2007, 29, 527–532. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Phase change materials for building applications: A state-of-the-art-review. Energy Build. 2010, 42, 1361–1368. [Google Scholar] [CrossRef]
- Ling, T.C.; Poon, C.S. Use of phase change materials for thermal energy storage in concrete: An overview. Constr. Build. Mater. 2013, 45, 55–62. [Google Scholar] [CrossRef]
- Kalnæs, S.E.; Jelle, B.P. Phase change materials and products for building applications: A state-of-the-art review and future research opportunities. Energy Build. 2015, 94, 150–176. [Google Scholar] [CrossRef]
- Choi, W.C.; Khil, B.S.; Chae, Y.S.; Liang, Q.B.; Yun, H.D. Feasibility of using phase change materials to control the heat of hydration in massive concrete structures. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.R.; Khil, B.S.; Jang, S.J.; Choi, W.C.; Yun, H.D. Effect of barium based phase change material (PCM) on the mechanical properties of mass concrete. Thermochimica Acta 2015, 613, 100–107. [Google Scholar] [CrossRef]
- Farnam, Y.; Krafcik, M.; Liston, L.; Washington, T.; Erk, K.; Tao, B.; Weiss, W.J. Evaluating the use of phase change materials in concrete pavement to melt ice and snow. J. Mater. Civ. Eng. 2015, 28. [Google Scholar] [CrossRef]
- Kim, J.K.; Kim, K.H.; Yang, J.K. Thermal analysis of hydration heat in concrete structures with pipe-cooling system. Comput. Struct. 2001, 79, 163–171. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, L.; Zhang, H. Study on anti-freezing functional design of phase change and temperature control composite bridge decks. Constr. Build Mater. 2016, 122, 714–720. [Google Scholar] [CrossRef]
- Farnam, Y.; Esmaeeli, H.S.; Zavattieri, P.D.; Haddock, J.; Weiss, W.J. Incorporating phase change materials in concrete pavement to melt snow and ice. Cem. Concr. Compos. 2017, 84, 134–145. [Google Scholar] [CrossRef]
- Qian, C.; Gao, G.; Zhu, C.; Guo, Z. Influence of phase change materials on temperature rise caused by hydration heat evolution of cement-based materials. Mag. Concr. Res. 2010, 62, 789–794. [Google Scholar] [CrossRef]
- Qian, C.; Gao, G. Reduction of interior temperature of mass concrete using suspension of phase change materials as cooling fluid. Constr. Build. Mater. 2012, 26, 527–531. [Google Scholar] [CrossRef]
- Bentur, A.; Igarashi, S.I.; Kovler, K. Prevention of autogeneous shrinkage in high-strength concrete by internal curing using wet lightweight aggregates. Cem. Concr. Res. 2001, 29, 1863–1867. [Google Scholar] [CrossRef]
- Bentz, D.P.; Snyder, K.A. Protected paste volume in concrete: Extension to internal curing using saturated lightweight fine aggregate. Cem. Concr. Res. 1999, 29, 1863–1867. [Google Scholar] [CrossRef]
- Suzuki, M.; Meddah, M.S.; Sato, R. Use of porous ceramic waste aggregates for internal curing of high-performance concrete. Cem. Concr. Res. 2009, 39, 373–381. [Google Scholar] [CrossRef]
- Wiktor, V.; Jonkers, H.M. Quantification of crack-healing in novel bacteria-based self-healing concrete. Cem. Concr. Compos. 2011, 33, 763–770. [Google Scholar] [CrossRef]
- Tziviloglou, E.; Wiktor, V.; Jonkers, H.M.; Schlangen, E. Bacteria-based self-healing concrete to increase liquid tightness of cracks. Constr. Build. Mater. 2016, 122, 118–125. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Z.; Zhou, J.; Wu, K. Development of thermal energy storage concrete. Cem. Concr. Res. 2004, 34, 927–934. [Google Scholar] [CrossRef]
- Sharifi, N.P.; Sakulich, A. Application of phase change materials to improve the thermal performance of cementitious material. Energy Build. 2015, 103, 83–95. [Google Scholar] [CrossRef]
- Aguayo, M.; Das, S.; Castro, C.; Kabay, N.; Sant, G.; Neithalath, N. Porous inclusions as hosts for phase change materials in cementitious composites: Characterization, thermal performance, and analytical models. Constr. Build. Mater. 2017, 134, 574–584. [Google Scholar] [CrossRef]
- Sakulich, A.R.; Bentz, D.P. Increasing the service life of bridge decks by incorporating phase-change materials to reduce freeze-thaw cycles. J. Mater. Civ. Eng. 2011, 24, 1034–1042. [Google Scholar] [CrossRef]
- Sakulich, A.R.; Bentz, D.P. Incorporation of phase change materials in cementitious systems via fine lightweight aggregate. Constr. Build. Mater. 2012, 35, 483–490. [Google Scholar] [CrossRef]
- Nepomuceno, M.C.; Silva, P.D. Experimental evaluation of cement mortars with phase change material incorporated via lightweight expanded clay aggregate. Constr. Build. Mater. 2014, 63, 89–96. [Google Scholar] [CrossRef]
- Memon, S.A.; Cui, H.Z.; Zhang, H.; Xing, F. Utilization of macro encapsulated phase change materials for the development of thermal energy storage and structural lightweight aggregate concrete. Appl. Energy 2015, 139, 43–55. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Sanjayan, J.; Wang, X.; Alam, M.; Wilson, J. A novel paraffin/expanded perlite composite phase change material for prevention of PCM leakage in cementitious composites. Appl. Energy 2015, 157, 85–94. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, J.; Sun, G.; Xu, B.; Li, Z.; Gong, C. Effects of form-stable expanded perlite/paraffin composite on cement manufactured by extrusion technique. Energy 2015, 82, 43–53. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z. Paraffin/diatomite composite phase change material incorporated cement-based composite for thermal energy storage. Appl. Energy 2013, 105, 229–237. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z. Paraffin/diatomite/multi-wall carbon nanotubes composite phase change material tailor-made for thermal energy storage cement-based composites. Energy 2014, 72, 371–380. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z. Performance of novel thermal energy storage engineered cementitious composites incorporating a paraffin/diatomite composite phase change material. Appl. Energy 2014, 121, 114–122. [Google Scholar] [CrossRef]
- Xu, B.; Ma, H.; Lu, Z.; Li, Z. Paraffin/expanded vermiculite composite phase change material as aggregate for developing lightweight thermal energy storage cement-based composites. Appl. Energy 2015, 160, 358–367. [Google Scholar] [CrossRef]
- Huang, J.; Lu, S.; Kong, X.; Liu, S. Form-stable phase change materials based on eutectic mixture of tetradecanol and fatty acids for building energy storage: Preparation and performance analysis. Materials 2013, 6, 4758–4775. [Google Scholar] [CrossRef] [PubMed]
- Lv, L.Y.; Zhang, H.; Schlangen, E.; Yang, Z.; Xing, F. Experimental and numerical study of crack behaviour for capsule-based self-healing cementitious materials. Constr. Build. Mater. 2017, 156, 219–229. [Google Scholar] [CrossRef]
- Lv, L.Y.; Yang, Z.; Chen, G.; Zhu, G.; Han, N.; Schlangen, E.; Xing, F. Synthesis and characterization of a new polymeric microcapsule and feasibility investigation in self-healing cementitious materials. Constr. Build. Mater. 2016, 105, 487–495. [Google Scholar] [CrossRef]
- Beglarigale, A.; Seki, Y.; Demir, N.Y. Sodium silicate/polyurethane microcapsules used for self-healing in cementitious materials: Monomer optimization, characterization, and fracture behavior. Constr. Build. Mater. 2018, 162, 57–64. [Google Scholar] [CrossRef]
- Xiong, W.; Tang, J.; Zhu, G.; Han, N.; Schlangen, E.; Dong, B.; Wang, X.; Xing, F. A novel capsule-based self-recovery system with a chloride ion trigger. Sci. Rep. UK 2015, 5, 10866. [Google Scholar] [CrossRef] [PubMed]
- Norvell, C.; Sailor, D.J.; Dusicka, P. The effect of microencapsulated phase-change material on the compressive strength of structural concrete. J. Green Build. 2013, 8, 116–124. [Google Scholar] [CrossRef]
- Eddhahak, A.; Drissi, S.; Colin, J.; Care, S.; Neji, J. Effect of phase change materials on the hydration reaction and kinetic of PCM-mortars. J. Therm. Anal. Calorim. 2014, 117, 537–545. [Google Scholar] [CrossRef]
- Eddhahak-Ouni, A.; Drissi, S.; Colin, J.; Neji, J.; Care, S. Experimental and multi-scale analysis of the thermal properties of Portland cement concretes embedded with microencapsulated Phase Change Materials (PCMs). Appl. Therm. Eng. 2014, 64, 32–39. [Google Scholar] [CrossRef]
- Drissi, S.; Eddhahak, A.; Care, J.; Neji, J. Thermal analysis by DSC of Phase Change Materials, study of the damage effect. J. Build. Eng. 2015, 1, 13–19. [Google Scholar] [CrossRef]
- Figueiredo, A.; Lapa, J.; Vincente, R.; Cardoso, C. Mechanical and thermal characterization of concrete with incorporation of microencapsulated PCM for applications in thermally activated slabs. Constr. Build. Mater. 2016, 112, 639–647. [Google Scholar] [CrossRef]
- Snoeck, D.; Priem, B.; Dubruel, P.; De Belie, N. Encaplsulated phase-change materials as additives in cementitious materials to promote thermal comfort in concrete constructions. Mater. Struct. 2016, 49, 225–239. [Google Scholar] [CrossRef]
- Fenollera, M.; Miguez, J.L.; Goicoechea, I.; Lorenzo, J.; Angel-Alvarez, M. The influence of phase change materials on the properties of self-compacting concrete. Materials 2013, 6, 3530–3546. [Google Scholar] [CrossRef] [PubMed]
- Aguayo, M.; Das, S.; Maroli, A.; Kabay, N.; Mertens, J.C.E.; Rajan, S.D.; Sant, G.; Chawla, N.; Neithalath, N. The influence of microencapsulated phase change material (PCM) characteristics on the microstructure and strength of cementitious composites: Experiments and finite element simulations. Cem. Concr. Compos. 2016, 73, 29–41. [Google Scholar] [CrossRef]
- Lecompte, T.; Le Bideau, P.; Glouannec, P.; Nortershauser, D.; Le Masson, S. Mechanical and thermo-physical behaviour of concretes and mortars containing phase change material. Energy Build. 2015, 94, 52–60. [Google Scholar] [CrossRef]
- Ricklefs, A.; Thiele, A.M.; Falzone, G.; Sant, G.; Pilon, L. Thermal conductivity of cementitious materials containing microencapsulated phase change materials. Int. J. Heat Mass Transf. 2017, 104, 71–82. [Google Scholar] [CrossRef]
- Wei, Z.; Falzone, G.; Das, S.; Saklani, N.; Le Pape, Y.; Pilon, L.; Neithalath, N.; Sant, G. Restrained shrinkage cracking of cementitious composites containing soft PCM inclusions: A paste (matrix) controlled response. Mater. Des. 2017, 132, 367–374. [Google Scholar] [CrossRef]
- Wei, Z.; Falzone, G.; Wang, B.; Thiele, A.; Puerta-Falla, G.; Pilon, L.; Neithelath, N.; Sant, G. The durability of cementitious composites containing microencapsulated phase change materials. Cem. Concr. Compos. 2017, 81, 66–76. [Google Scholar] [CrossRef]
- Wei, Z. Phase Change Materials and Clinkering-Free Cementation for Sustainable Building Materials. Ph.D. Thesis, UCLA (University of California at Los Angeles), Los Angeles, CA, USA, 2017. [Google Scholar]
- Cui, H.; Liao, W.; Memon, S.A.; Dong, B.; Tang, W. Thermophysical and mechanical properties of hardened cement paste with microencapsulated phase change materials for energy storage. Materials 2014, 7, 8070–8087. [Google Scholar] [CrossRef] [PubMed]
- Hunger, M.; Entrop, A.G.; Mandilaras, I.; Brouwers, H.J.H.; Founti, M. The behavior of self-compacting concrete containing micro-encapsulated phase change materials. Cem. Concr. Compos. 2009, 31, 731–743. [Google Scholar] [CrossRef]
- Šavija, B.; Lukovic, M.; Kotteman, G.M.; Figuieredo, S.C.; de Mendica Filho, F.F.; Schlangen, E. Development of ductile cementitious composites incorporating microencapsulated phase change materials. Int. J. Adv. Eng. Sci. Appl. Math. 2017, 9, 169–180. [Google Scholar] [CrossRef]
- Jayalath, A.; San Nicolas, R.; Sofi, M.; Shanks, R.; Ngo, T.; Aye, L.; Mendis, P. Properties of cementitious mortar and concrete containing micro-encapsulated phase change materials. Constr. Build. Mater. 2016, 120, 408–417. [Google Scholar] [CrossRef]
- Dehdezi, P.K.; Hall, M.R.; Dawson, A.R.; Casey, S.P. Thermal, mechanical and microstructural analysis of concrete containing microencapsulated phase change materials. Int. J. Pavement Eng. 2013, 14, 449–462. [Google Scholar] [CrossRef]
- Liu, D.; Šavija, B.; Smith, G.E.; Flewitt, P.E.J.; Lowe, T.; Schlangen, E. Towards understanding the influence of porosity on mechanical and fracture behaviour of quasi-brittle materials: Experiments and modelling. Int. J. Fract. 2017, 205, 57–72. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew Sust. Energ. Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Neeper, D.A. Thermal dynamics of wallboard with latent heat storage. Sol. Energy 2000, 68, 393–403. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Emborg, M.; Bernander, S. Assessment of risk of thermal cracking in hardening concrete. J. Struct. Eng. 1994, 120, 2893–2912. [Google Scholar] [CrossRef]
- Bofang, Z. Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Benboudjema, F.; Torrenti, J.M. Early-age behaviour of concrete nuclear containments. Nucl. Eng. Des. 2008, 238, 2495–2506. [Google Scholar] [CrossRef]
- De Schutter, G. Finite element simulation of thermal cracking in massive hardening concrete elements using degree of hydration based material laws. Comput. Struct. 2002, 80, 2035–2042. [Google Scholar] [CrossRef]
- Pan, Y.; Prado, A.; Porras, R.; Hafez, O.M.; Bolander, J.E. Lattice modeling of early-age behavior of structural concrete. Materials 2017, 10, 231. [Google Scholar] [CrossRef] [PubMed]
- Waller, V.; d’Aloia, L.; Cussigh, F.; Lecrux, S. Using the maturity method in concrete cracking control at early ages. Cem. Concr. Compos. 2004, 26, 287–296. [Google Scholar] [CrossRef]
- Nobuhiro, M.; Kazuo, U. Nonlinear thermal stress analysis of a massive concrete structure. Comput Struct. 1987, 26, 287–296. [Google Scholar] [CrossRef]
- Mihashi, H.; Nishiyama, N.; Kobayashi, T.; Hanada, M. Development of a smart material to mitigate thermal stress in early age concrete. In Control of Cracking in Early Age Concrete; Taylor & Francis: Abingdon, UK, 2004; pp. 385–392. [Google Scholar]
- Thiele, A.M.; Wei, Z.; Falzone, G.; Young, B.A.; Neithalath, N.; Sant, G.; Pilon, L. Figure of merit for the thermal performance of cementitious composites containing phase change materials. Cem. Concr. Compos. 2016, 65, 214–226. [Google Scholar] [CrossRef]
- Young, B.A.; Falzone, G.; She, Z.; Thiele, A.M.; Wei, Z.; Neithalath, N.; Sant, G.; Pilon, L. Early-age temperature evolutions in concrete pavements containing microencapsulated phase change materials. Constr. Build. Mater. 2017, 147, 466–477. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.M.; Yan, H.D.; Mu, R. Damage and damage resistance of high strength concrete under the action of load and freeze-thaw cycles. Cem. Concr. Res. 1999, 29, 1519–1523. [Google Scholar] [CrossRef]
- Li, W.; Pour-Ghaz, M.; Castro, J.; Weiss, W.J. Water absorption and critical degree of saturation relating to freeze-thaw damage in concrete pavement joints. J. Mater. Civ. Eng. 2011, 24, 299–307. [Google Scholar] [CrossRef]
- Liu, L.; Ye, G.; Schlangen, E.; Chen, H.; Qian, Z.; Sun, W.; van Breugel, K. Modeling of the internal damage of saturated cement paste due to ice crystallization pressure during freezing. Cem. Concr. Compos. 2011, 33, 562–571. [Google Scholar] [CrossRef]
- Liu, L.; Wu, S.; Chen, H.; Haitao, Z. Numerical investigation of the effects of freezing on micro-internal damage and macro-mechanical properties of cement pastes. Cold Reg. Sci. Technol. 2014, 106, 141–152. [Google Scholar] [CrossRef]
- Cai, H.; Liu, X. Freeze-thaw durability of concrete: Ice formation process in pores. Cem. Concr. Res. 1998, 28, 1281–1287. [Google Scholar] [CrossRef]
- Jacobsen, S.; Marchand, J.; Hornain, H. SEM observations of the microstructure of frost deteriorated and self-healed concretes. Cem. Concr. Res. 1995, 25, 1781–1790. [Google Scholar] [CrossRef]
- Du, L.; Folliard, K.J. Mechanisms of air entrainment in concrete. Cem. Concr. Res. 2005, 35, 1463–1471. [Google Scholar] [CrossRef]
- Attiogbe, E.K. Mean spacing of air voids in hardened concrete. ACI Mater. J. 1993, 90, 174–181. [Google Scholar]
- Bentz, D.P. A Computer Model to Predict the Surface Temperature and Time-of-Wetness of Concrete Pavements and Bridge decks. Available online: https://www.nist.gov/publications/computer-model-predict-surface-temperature-and-time-wetness-concrete-pavements-and (accessed on 1 March 2018).
- Lukovic, M.; Ye, G. Effect of moisture exchange on interface formation in the repair system studied by X-ray absorption. Materials 2015, 9, 2. [Google Scholar] [CrossRef] [PubMed]
- Cunha, S.; Lima, M.; Aguiar, J.B. Influence of adding phase change materials on the physical and mechanical properties of cement mortars. Constr. Build. Mater. 2016, 127, 1–10. [Google Scholar] [CrossRef]
- Šavija, B.; Zhang, H.; Schlangen, E. Influence of microencapsulated phase change material (PCM) addition on (micro) mechanical properties of cement paste. Materials 2017, 10, 863. [Google Scholar] [CrossRef] [PubMed]
- Golewski, G.L. Generalized Fracture Toughness and Compressive Strength of Sustainable Concrete Including Low Calcium Fly Ash. Materials 2017, 10, 1393. [Google Scholar] [CrossRef] [PubMed]
- Golewski, G.L. Improvement of fracture toughness of green concrete as a result of addition of coal fly ash. Characterization of fly ash microstructure. Mater. Charact. 2017, 134, 335–346. [Google Scholar] [CrossRef]
- Golewski, G.L. Green concrete composite incorporating fly ash with high strength and fracture toughness. J. Clean. Prod. 2018, 172, 218–226. [Google Scholar] [CrossRef]
- Pilehvar, S.; Cao, V.D.; Szczotok, A.M.; Valentini, L.; Salvioni, D.; Magistri, M.; Pamies, R.; Kjoniksen, A.-L. Mechanical properties and microscale changes of geopolymer concrete and Portland cement concrete containing micro-encapsulated phase change materials. Cem. Concr. Res. 2017, 100, 341–349. [Google Scholar] [CrossRef]
- Lukovic, M.; Šavija, B.; Schlangen, E.; Ye, G.; van Breugel, K. A 3D lattice modelling study of drying shrinkage damage in concrete repair systems. Materials 2016, 9, 575. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Ueda, T. Mesoscale modeling of water penetration into concrete by capillary absorption. Ocean Eng. 2011, 38, 519–528. [Google Scholar] [CrossRef]
- Bolander, J.E.; Berton, S. Simulation of shrinkage induced cracking in cement composite overlays. Cem. Concr. Compos. 2004, 26, 861–871. [Google Scholar] [CrossRef]
- Šavija, B.; Pacheco, J.; Schlangen, E. Lattice modeling of chloride diffusion in sound and cracked concrete. Cem. Concr. Compos. 2013, 42, 30–40. [Google Scholar] [CrossRef]
- Wang, L.; Ueda, T. Mesoscale modelling of chloride diffusion in cracks and cracked concrete. J. Adv. Concr. Technol. 2011, 9, 241–249. [Google Scholar] [CrossRef]
- Cellat, K.; Tezcan, F.; Beyhan, B.; Kardas, G.; Paksov, H. A comparative study on corrosion behavior of rebar in concrete with fatty acid additive as phase change material. Constr. Build. Mater. 2017, 143, 490–500. [Google Scholar] [CrossRef]
- Shin, K.J.; Bucher, B.; Weiss, W.J. Role of lightweight synthetic particles on the restrained shrinkage cracking behavior of mortar. J. Mater. Civ. Eng. 2010, 23, 597–605. [Google Scholar] [CrossRef]
- Hobbs, D.W. The dependence of the bulk modulus, Young’s modulus, creep, shrinkage and thermal expansion of concrete upon aggregate volume concentration. Materiaux et Constr. 1971, 4, 107–114. [Google Scholar] [CrossRef]
- Xu, W.; Jia, M.; Zhu, Z.; Liu, M.; Lei, D.; Gou, X. n-Phase micromechanical framework for the conductivity and elastic modulus of particulate composites: Design to microencapsulated phase change materials (MPCMs)-cementitious composites. Mater. Des. 2018, 145, 108–115. [Google Scholar] [CrossRef]
- Felske, J.D. Effective thermal conductivity of composite spheres in a continuous medium with contact resistance. Int. J. Heat Mass Transf. 2004, 47, 3453–3461. [Google Scholar] [CrossRef]
- Das, S.; Aguayo, M.; Rajan, S.D.; Sant, G.; Neithalath, N. Microstructure-guided numerical simulations to predict the thermal performance of a hierarchical cement-based composite material. Cem. Concr. Compos. 2018, 87, 20–28. [Google Scholar] [CrossRef]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lamberg, P.; Lehtiniemi, R.; Henell, A.M. Numerical and experimental investigation of melting and freezing processes in phase change material storage. Int. J. Therm. Sci. 2004, 43, 277–287. [Google Scholar] [CrossRef]
- Šavija, B.; Schlangen, E. Use of phase change materials (PCMs) to mitigate early age thermal cracking in concrete: Theoretical considerations. Constr. Build. Mater. 2016, 126, 332–344. [Google Scholar] [CrossRef]
- Thiele, A.M.; Sant, G.; Pilon, L. Diurnal thermal analysis of microencapsulated PCM-concrete composite walls. Energy Convers. Manag. 2015, 93, 215–227. [Google Scholar] [CrossRef]
- Sharifi, N.P.; Freeman, G.E.; Sakulich, A.R. Using COMSOL modeling to investigate the efficiency of PCMs at modifying temperature changes in cementitious materials—Case study. Constr. Build. Mater. 2015, 101, 965–974. [Google Scholar] [CrossRef]
- Esmaeeli, H.S.; Farnam, Y.; Haddock, J.E.; Zavattieri, P.D.; Weiss, W.J. Numerical analysis of the freeze-thaw performance of cementitious composites that contain phase change material (PCM). Mater. Des. 2018, 145, 74–87. [Google Scholar] [CrossRef]
- Arora, A.; Sant, G.; Neithalath, N. Numerical simulations to quantify the influence of phase change materials (PCMs) on the early-and later-age thermal response of concrete pavements. Cem. Concr. Compos. 2017, 81, 11–24. [Google Scholar] [CrossRef]
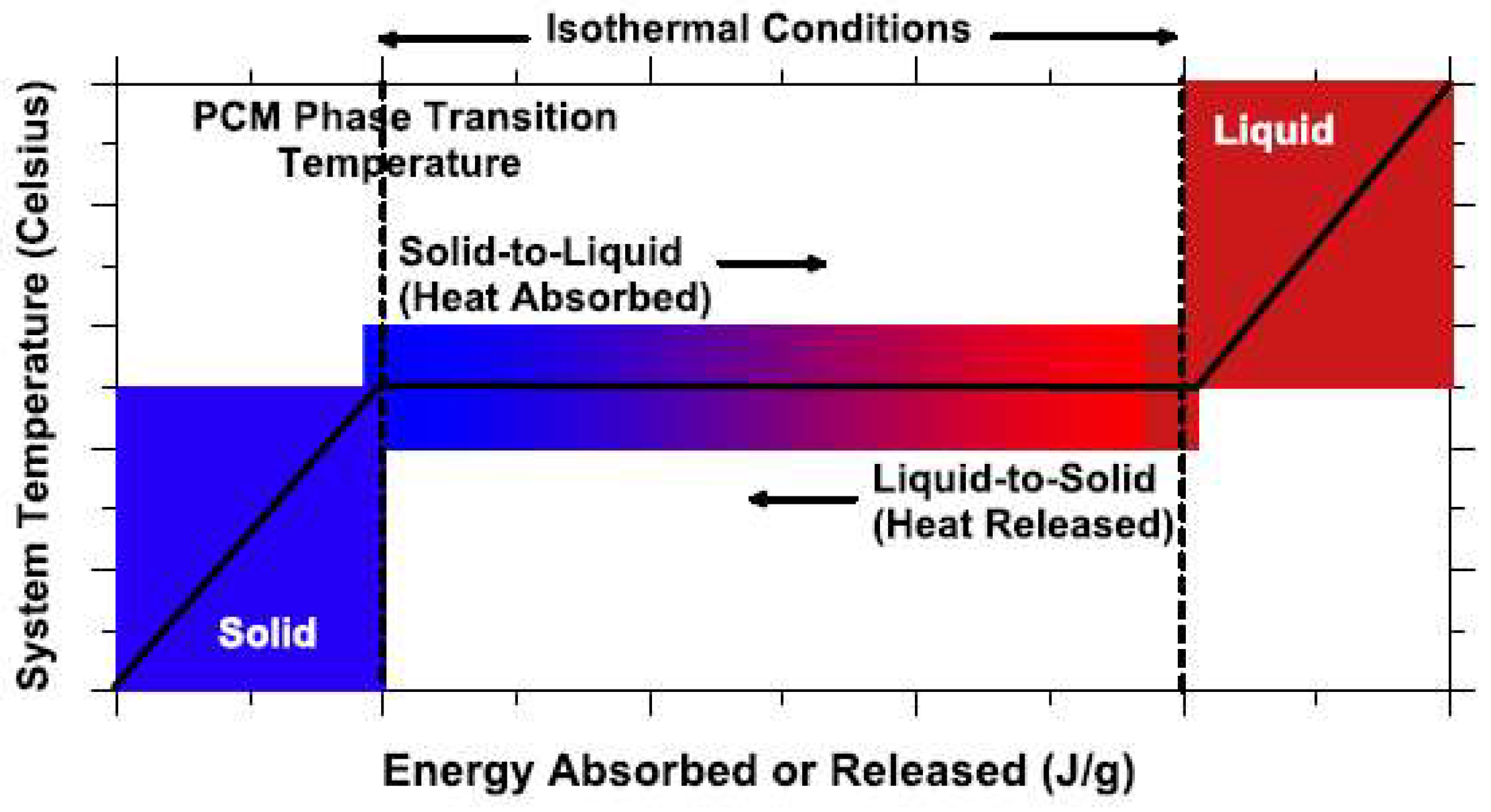
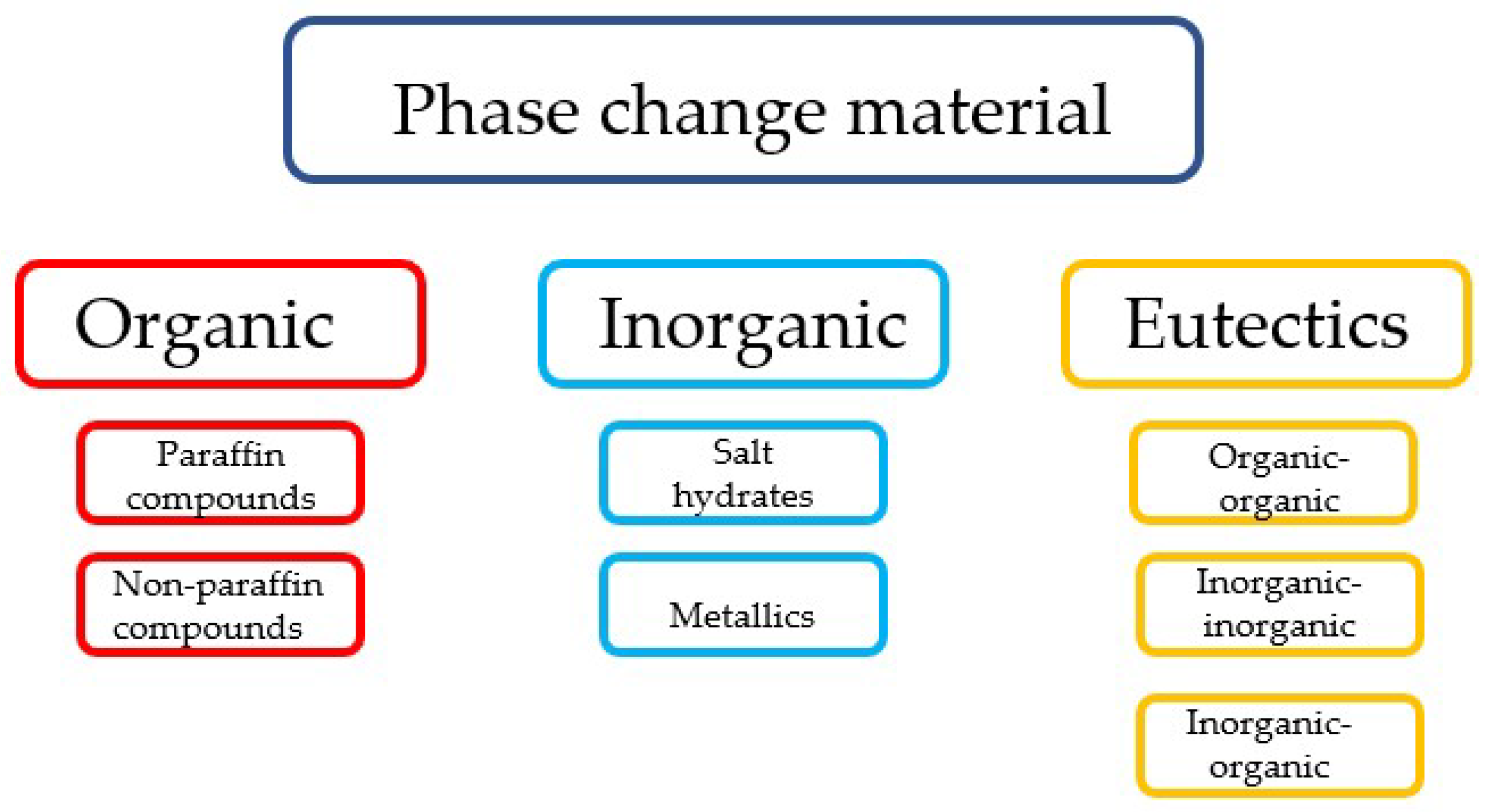
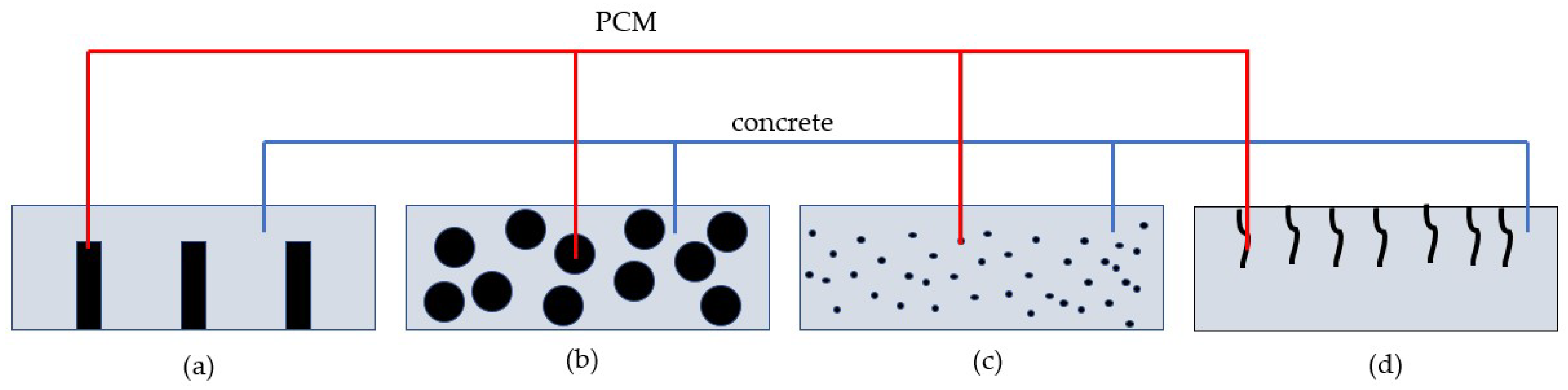
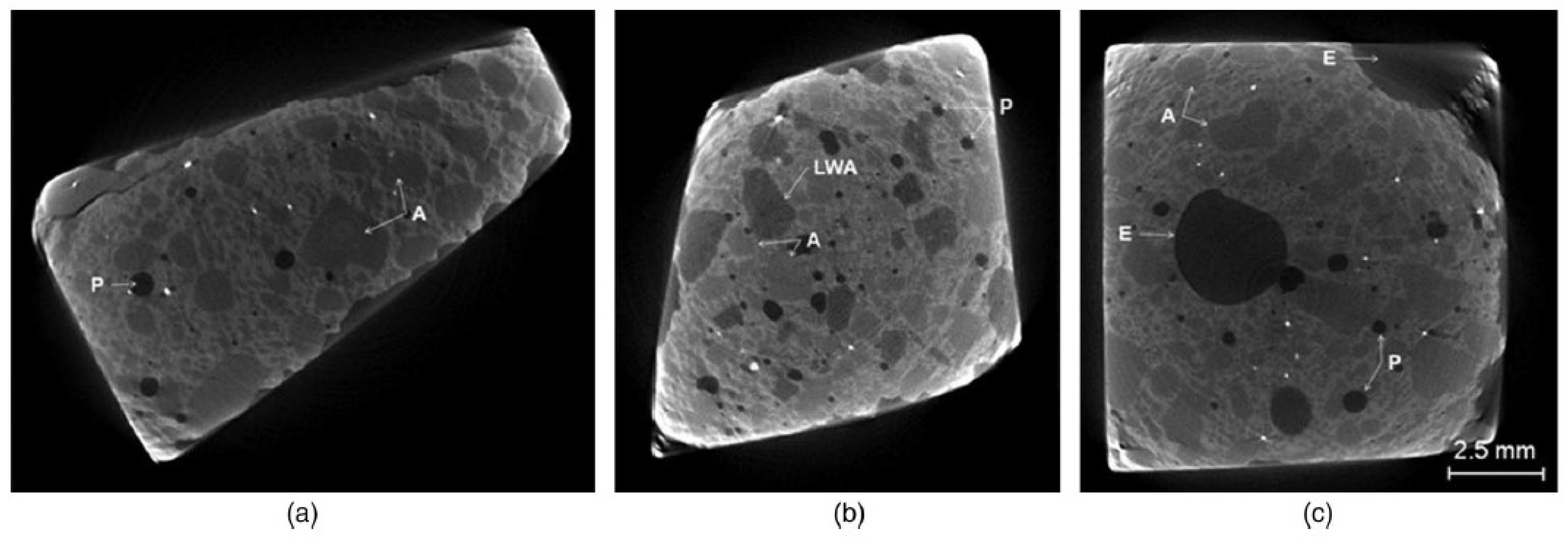


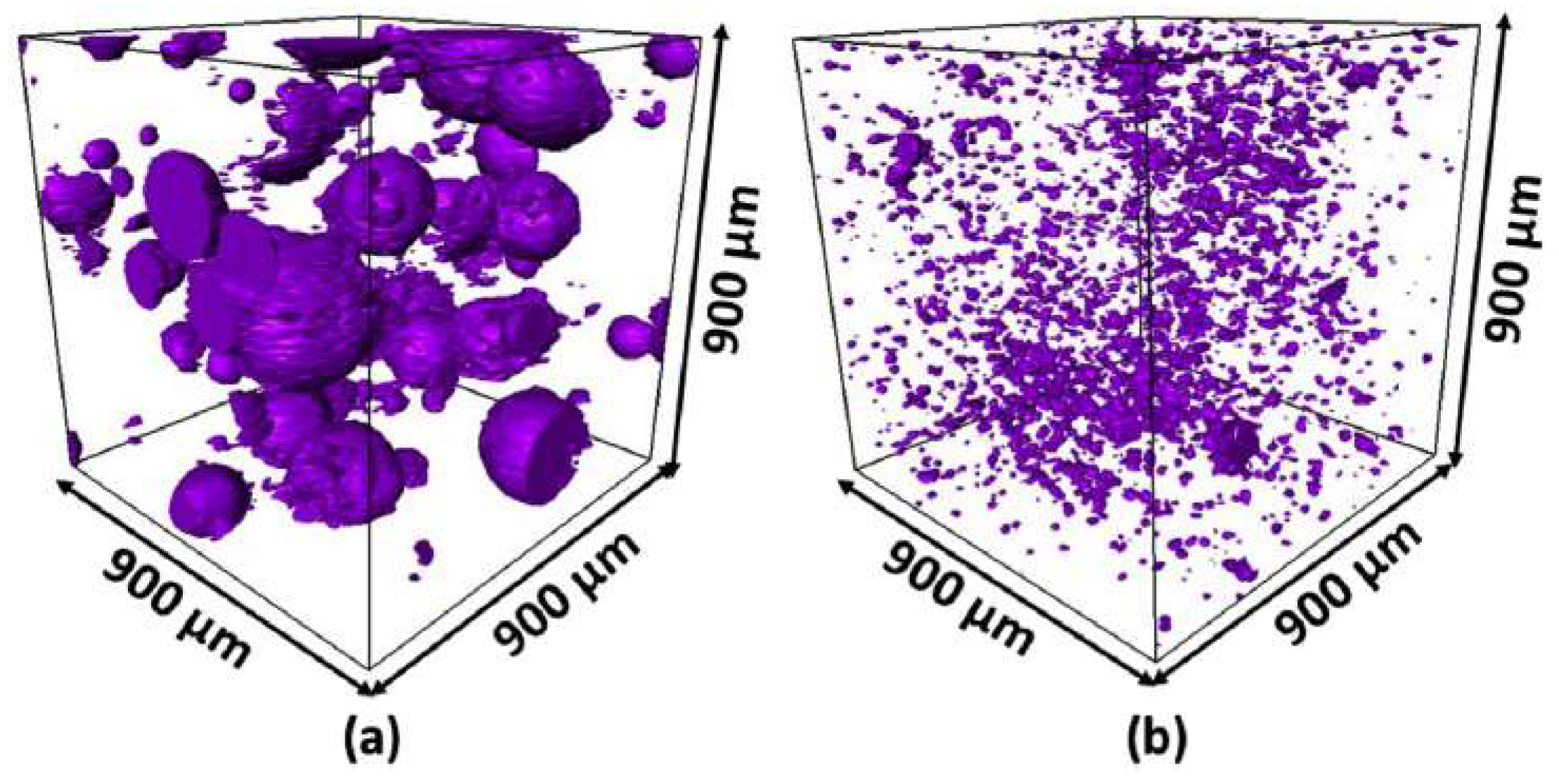
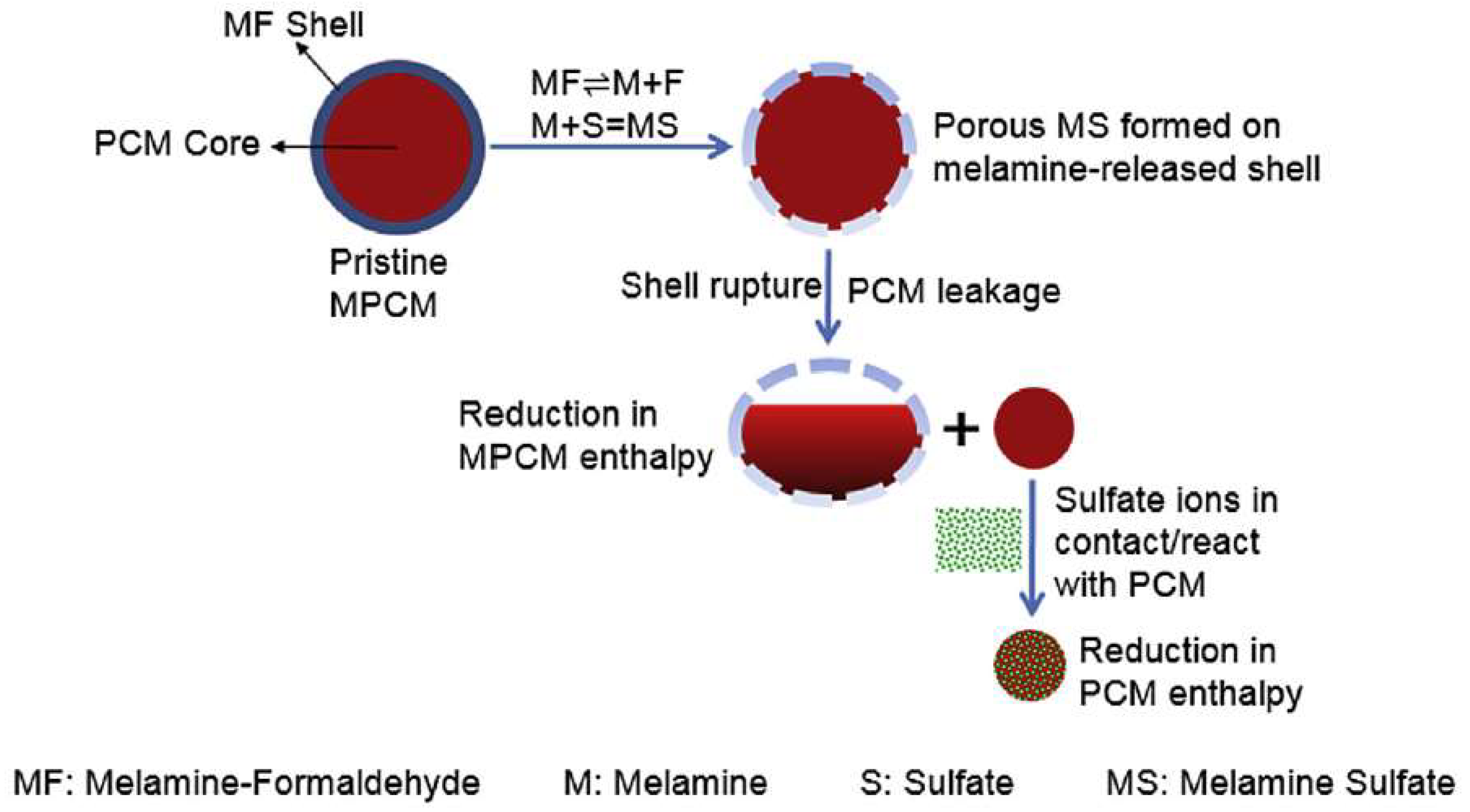

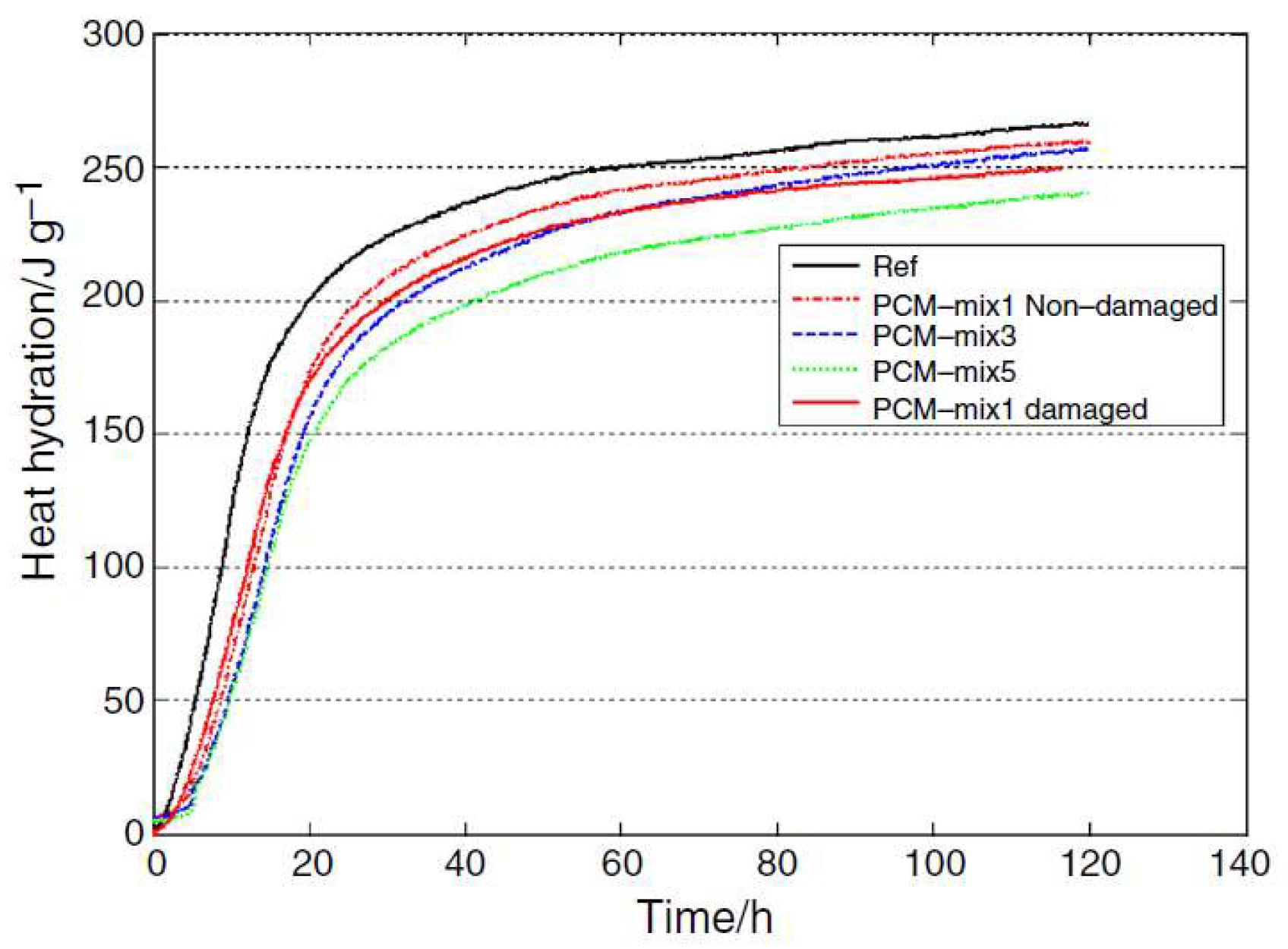
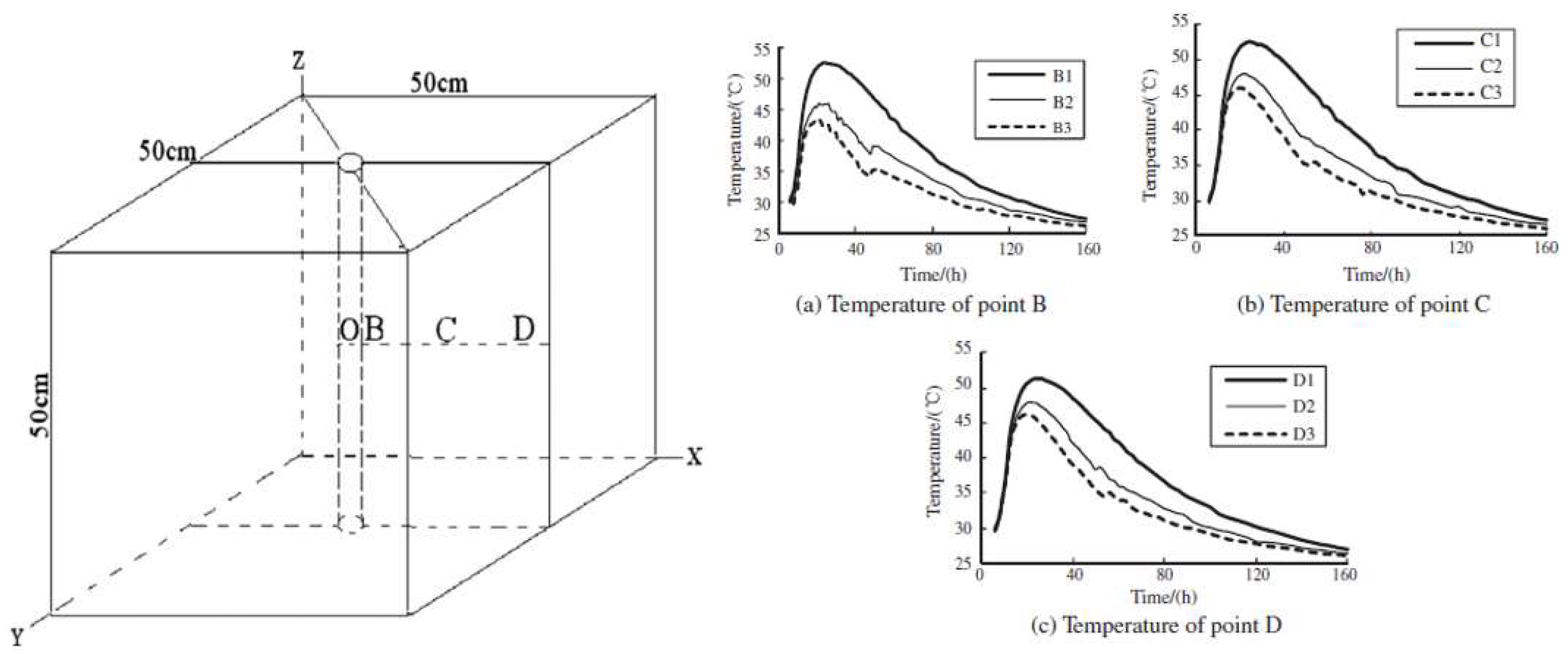



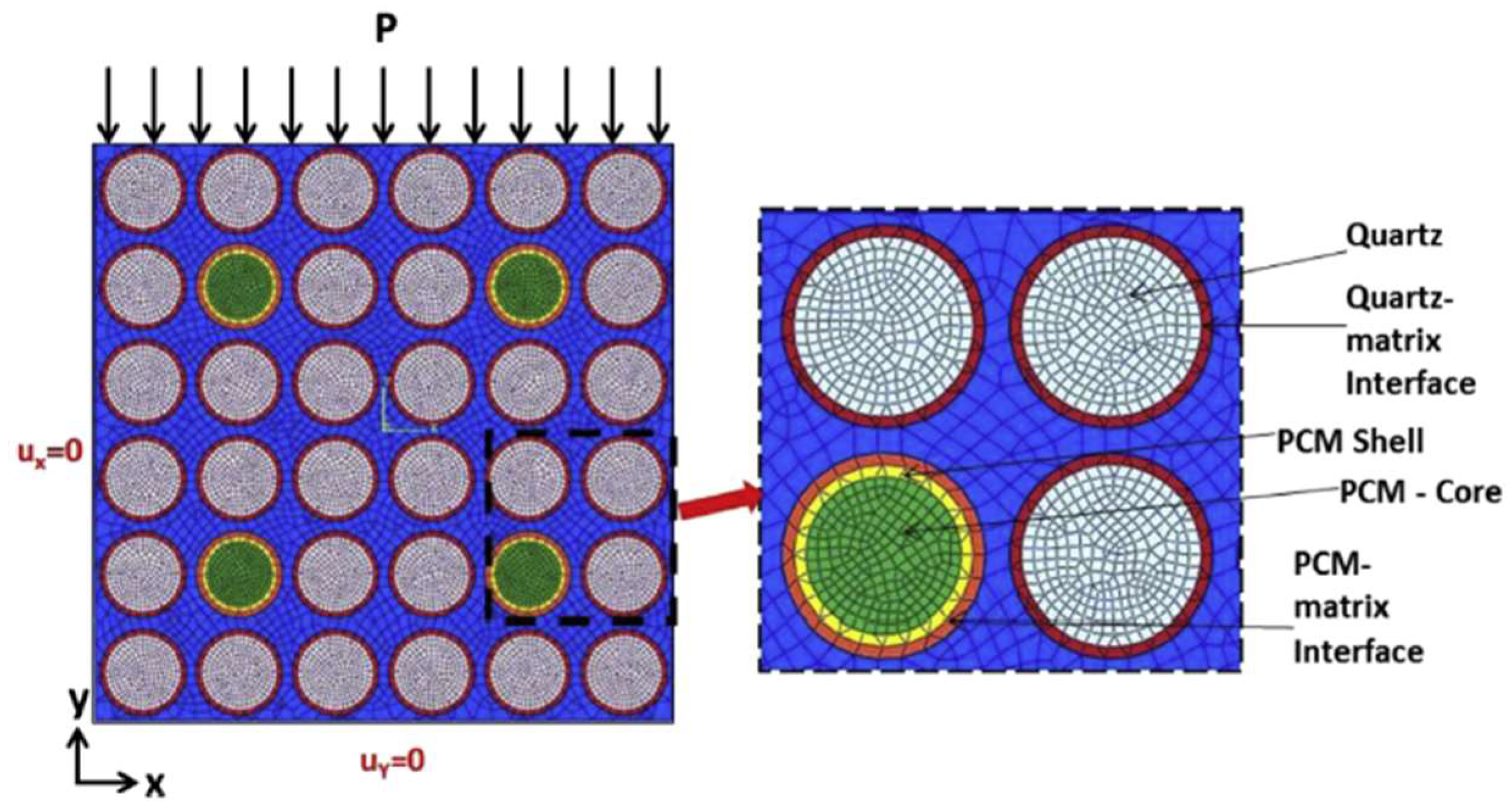
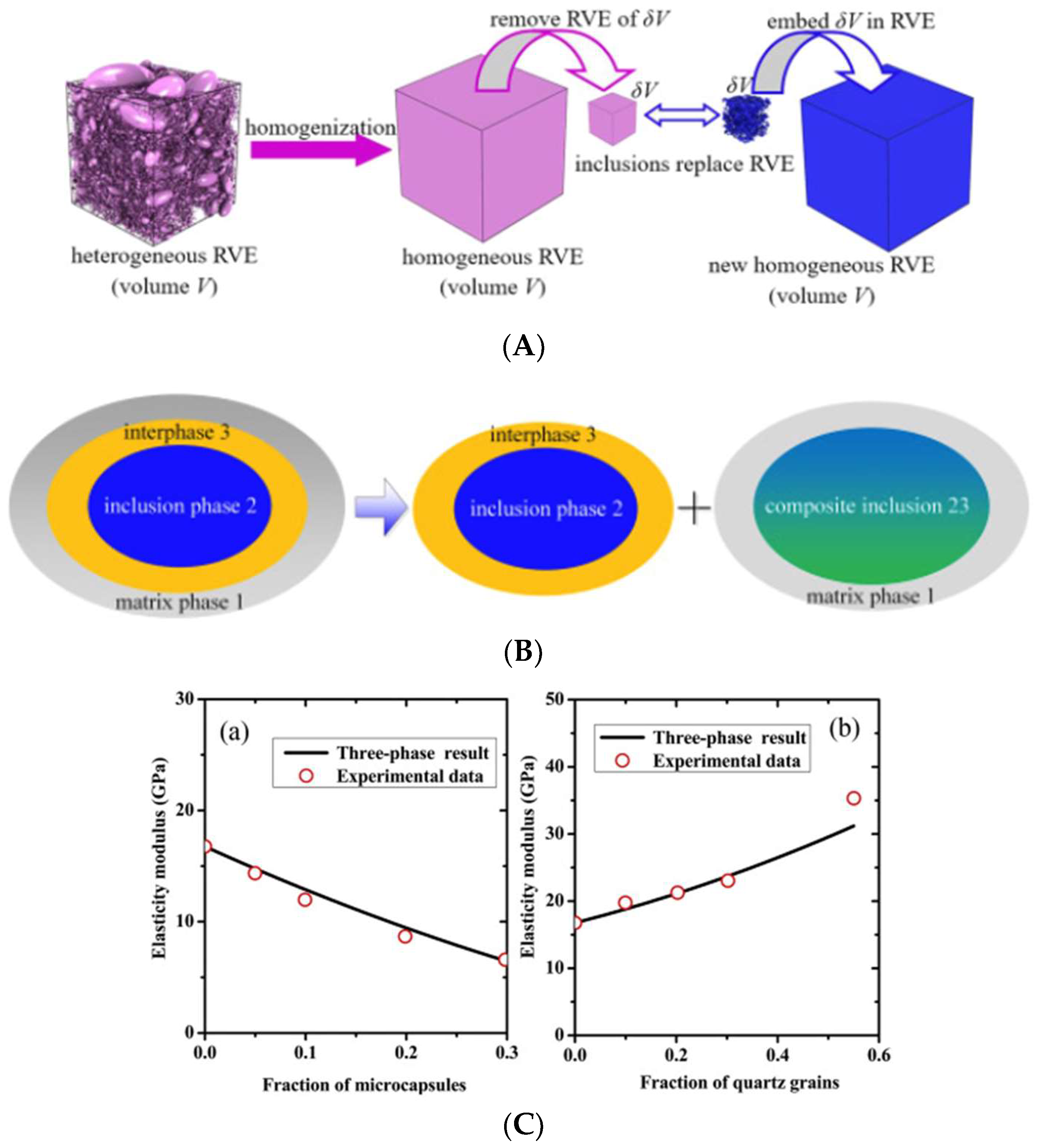
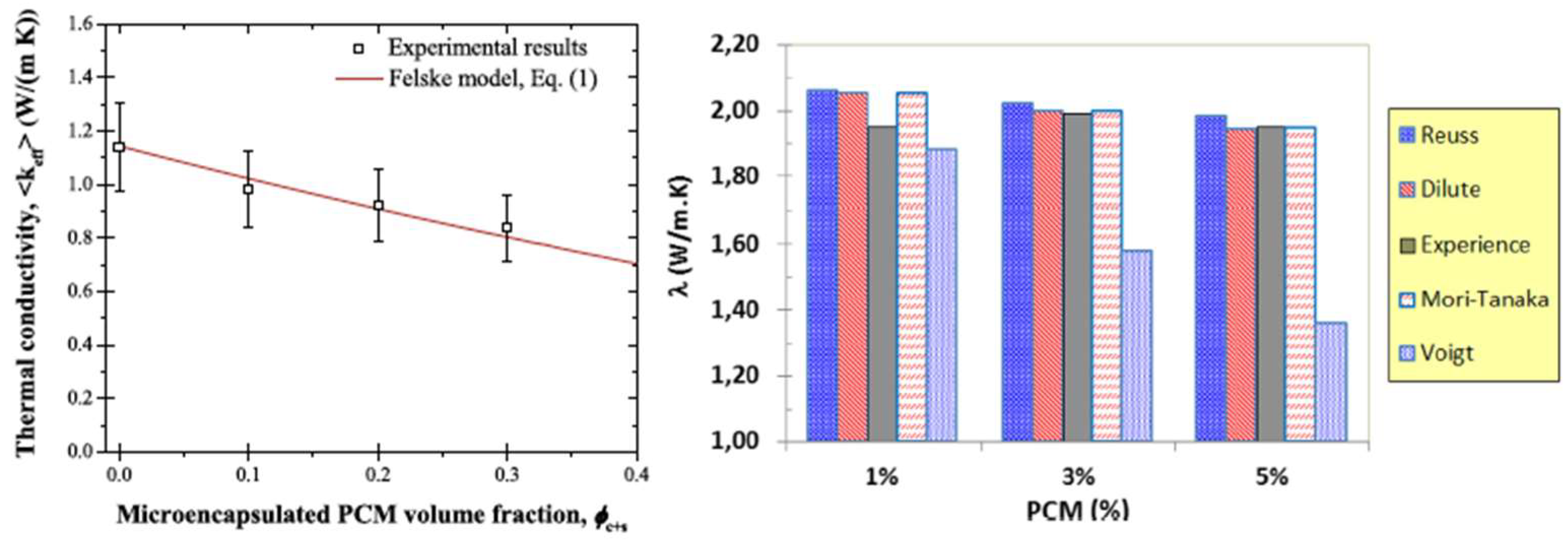
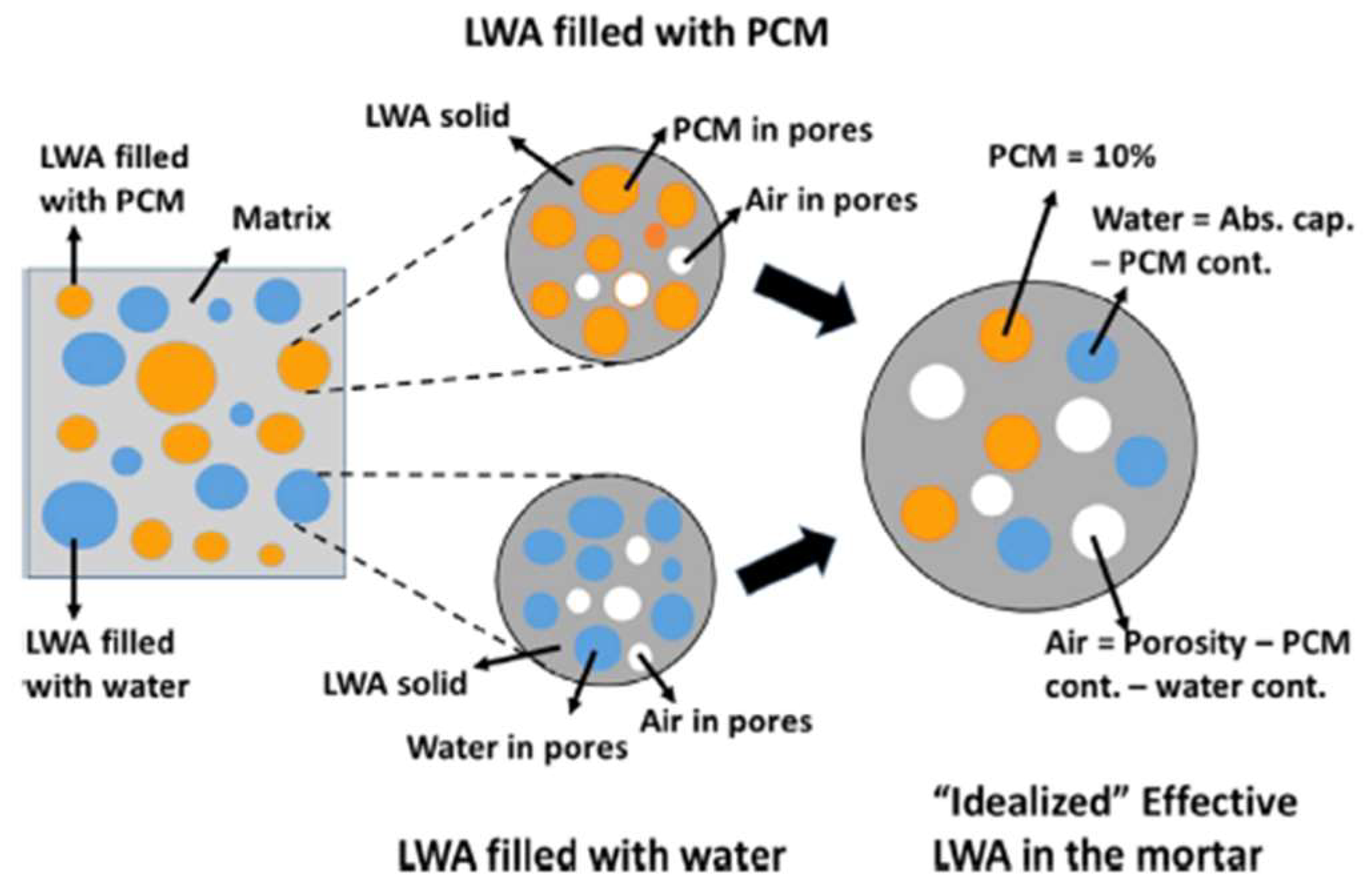
| Classification | Advantages | Drawbacks |
|---|---|---|
| Organic PCMs | 1. Availability in a large temperature range 2. High heat of fusion 3. No supercooling 4. Chemically stable and recyclable 5. Good compatibility with conventional construction materials | 1. Low thermal conductivity 2. Relatively large volume change 3. Flammable |
| Inorganic PCMs | 1. High heat of fusion 2. High thermal conductivity 3. Low volume change 4. Low cost 5. Sharp phase change 6. Non-flammable | 1. Corrosive to metals 2. Supercooling |
| Eutectics | 1. Sharp melting point 2. Properties can be tailored to match specific requirements 3. High volumetric thermal storage density | 1. Limited data on thermo-physical properties for many combinations 2. High cost |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šavija, B. Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review. Materials 2018, 11, 654. https://doi.org/10.3390/ma11050654
Šavija B. Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review. Materials. 2018; 11(5):654. https://doi.org/10.3390/ma11050654
Chicago/Turabian StyleŠavija, Branko. 2018. "Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review" Materials 11, no. 5: 654. https://doi.org/10.3390/ma11050654
APA StyleŠavija, B. (2018). Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review. Materials, 11(5), 654. https://doi.org/10.3390/ma11050654





