Abstract
The structural, mechanical, anisotropic, electronic, and thermal properties of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 in the tetragonal phase are systematically investigated in the present work. The mechanical stability is proved by the elastic constants of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4. Moreover, they all demonstrate brittleness, because B/G < 1.75, and v < 0.26. The elastic anisotropy of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 is characterized by Poisson’s ratio, Young’s modulus, the percentage of elastic anisotropy for bulk modulus AB, the percentage of elastic anisotropy for shear modulus AG, and the universal anisotropic index AU. The electronic structures of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are all wide band gap semiconductor materials, with band gaps of 4.26 eV, 3.94 eV, 3.83 eV, and 3.25 eV, respectively, when using the Heyd-Scuseria-Ernzerhof (HSE06) hybrid functional. Moreover, t-Ge3N4 is a quasi-direct gap semiconductor material. The thermodynamic properties of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are investigated utilizing the quasi-harmonic Debye model. The effects of temperature and pressure on the thermal expansion coefficient, heat capacity, Debye temperature, and Grüneisen parameters are discussed in detail.
1. Introduction
IV A Group nitrides have attracted considerable interest as high-performance ceramics due to their outstanding physical properties [1]. Silicon nitride has many advantages, such as high strength, wear resistance, a high decomposition temperature, oxidation resistance, outstanding thermal shock resistance, a low friction coefficient, and low corrosion resistance, thus making it the ideal material for use in engineering ceramics [2]. Germanium nitride also has advantages, such as corrosion resistance and an adjustable band gap [3,4].
Si3N4 under normal temperature and pressure has two polymorphs: α-Si3N4 and β-Si3N4. It is generally accepted that α-Si3N4 is a metastable state, and β-Si3N4 is the low-temperature phase of Si3N4 crystal [5]. In 1999, Zerr et al. synthesized the third polymorph, γ-Si3N4 (cubic spinel structure, also named c-Si3N4 [6]) [7]. Since then, more researchers have studied the transitions among the three phases of Si3N4. Togo et al. [8] found that the phase transition pressure of β → γ was 12.5 GPa at 300 K. Through X-ray diffraction experiments, Kruger et al. [9] found that the α-Si3N4 could remain stable at room temperature and in the pressure range of 0–48 GPa. The phase transition pressure of α → γ was 15.22 GPa at 300 K, as reported by Yu and Chen [6]; they also found that the stability order of the three types of polymorphs was β-Si3N4 > α-Si3N4 > γ-Si3N4. Kroll predicted two new phases of Si3N4: post-spinel and wII- [10,11]. Yu et al. [12] investigated the structural and elastic properties of post-spinel and wII- of Si3N4. They found that post-spinel and wII-Si3N4 were stable at 160 GPa and 0 GPa, respectively. The post-spinel Si3N4 could be obtained when γ-Si3N4 was at 152.5 GPa and 0 K, while β → wII occurred at 20 GPa and 300 K.
Ge3N4 was first identified in 1930, when β-Ge3N4 was first synthesized [13]. Ruddlesden and Popper [14] found that the α phase was closely related to β-Ge3N4; however, it is generally believed to be a metastable phase under ambient conditions. Ge3N4 is considered to be a better candidate for obtaining the wII phase than Si3N4, because the transition to higher coordination states could be easier; it also may occur at lower pressures in germanium nitride than in silicon nitride because of the larger ionic size of Ge [15]. McMillan et al. [16] observed the first-order phase transition between the β and σ (space group: P3) phases at 23 GPa and 298 K. They also predicted the β → P → σ phase transitions at 20 GPa and 28 GPa, respectively. Wang et al. [17] found that γ-Ge3N4 could retain its stability up to 69.2 GPa at room temperature. The critical pressure of the β → wII phase transition was 10.7 GPa (at 300 K), and the β → wII transformation occurred at 13.5 GPa and 1100 K; further compression led to the wII → γ transition at 35.7 GPa, as reported by Luo et al. [18] In addition to silicon nitride and germanium nitride, IV A Group and V A Group elements compounds have been investigated, such as Si3P4 and Ge3P4 [19,20,21], W3N4 [22,23,24], BN [25,26,27,28,29,30] and C3N4 [31,32,33,34,35].
Recently, Cui et al. discovered three new phases of Si3N4: the tetragonal phase t-Si3N4, the monoclinic phase m-Si3N4, and the orthorhombic phase o-Si3N4 [36]. They found that ΔH for m-Si3N4 and t-Si3N4 were smaller than γ-Si3N4 below 2.9 GPa and 2.5 GPa, respectively. o-Si3N4 is a high pressure phase, with Pt = 198 GPa from γ-Si3N4. Subsequently, other researchers studied the physical properties of t-Si3N4, m-Si3N4, and o-Si3N4 [37,38,39]. Yao and Chen reported on the structural properties, mechanical properties, Vickers hardnesses, and electronic properties of t-Ge3N4, m-Ge3N4, and o-Ge3N4 [37]. When the pressure was below 20 GPa, the formation enthalpies of t-Ge3N4, m-Ge3N4, and o-Ge3N4 were, negative indicating they are stable. Fan et al. [38] investigated the elastic anisotropic and electronic properties of m-Si3N4, o-Si3N4, and t-Si3N4 under high pressure. They found that the m-Si3N4 transition from the direct band gap to the indirect band gap state occurred at ~32 GPa. Most of the Si3N4 and Ge3N4 semiconductors are wide band gap semiconductors; however, most of them are also indirect band gap semiconductors, such as α-Si3N4, β-Si3N4, o-Si3N4, t-Si3N4, post-spinel Si3N4, and α-Ge3N4 [7,36,40,41]. It is reported that the band gaps of (Si1−xGex)3N4 could be adjusted by the ratio of Si:Ge [42]. The cubic spinel c-Si3N4, c-SiGe2N4, and c-Ge3N4 were theoretically predicted to have wide and direct band gaps of 3.45 eV, 1.85 eV, and 2.22 eV, respectively, and c-GeSi2N4 had an indirect band gap of 2.56 eV and a direct band gap of 2.64 eV [43]. The cubic spinel SiGe2N4 has been shown to be of particular interest, because it is a stable compound with a direct band gap [44]. Ma et al. [45] studied the structural, mechanical, elastic, anisotropic, and electronic properties of the monoclinic phase of m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys. Their results indicated that the m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are all direct and wide band gap semiconductor materials, and that the band gaps could be adjusted from 3.34–5.08 eV. From Ref. [43,44,45], it could be envisioned that the proper mixing of (Si, Ge)3N4 in the cubic spinel and monoclinic phases may lead to compounds with appropriate properties, which we needed. For example, the band gaps of (Si, Ge)3N4 could be tuned by changing the Si:Ge ratio. These tunable band gap materials are particularly useful in applications such as light-emitting diodes (LEDs), hybrid solar cells, sensors, and photocatalysts.
Since there are no studies regarding the mixing of (Si, Ge)3N4 in the tetragonal phase, we propose two new double nitrides, t-Si2GeN4 and t-SiGe2N4, in the I-42m space group. In the present work, we investigate and discuss the structural, elastic, electronic, and thermodynamic properties for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, which would be helpful for future experiments and theoretical explorations.
2. Calculation Methods
This work was performed based on the density functional theory (DFT) [46,47] using the Cambridge Serial Total Energy Package (CASTEP) plane-wave code [48]. The calculations were performed with the generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PBE) functional, [49], the Perdew–Burke–Ernzerhof functional for solids (PBEsol) [50], and the local density approximation (LDA) in the form of Ceperley and Alder data, as parameterized by the Perdew and Zunger (CA–PZ) [46] exchange correlation potential. The valence electron configurations of Si, Ge, and N atoms were Si-3s23p2, Ge-4s24p2, and N-2s22p3, respectively. The cut-off energy was set as 500 eV. The Brillouin zone of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 could be described by the k-points of 10 × 10 × 5, 10 × 10 × 5, 9 × 9 × 5, and 9 × 9 × 5 using the Monkhorst–Pack mesh, [51] respectively. The crystal structures were optimized by the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [52]. The self-consistent convergence of the total energy was 5 × 10−6 eV/atom; the maximum force on the atom was 0.01 eV/Å, the maximum ionic displacement was within 5 × 10−4 Å, and the maximum stress was within 0.02 GPa. The thermodynamic properties of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys were investigated utilizing the quasi-harmonic Debye model [53,54].
3. Results and Discussion
3.1. Structural Properties
The crystal structures of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are displayed in Figure 1. The t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are obtained when germanium atoms replace the Si atom of t-Si3N4 with the smallest energy. The equilibrium lattice parameters of t-SixGe3−xN4 and c-SixGe3−xN4 (x = 0, 1, 2, 3) alloys with the related reference data are listed in Table 1. As seen, our calculated lattice parameters for t-Si3N4 and c-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are in excellent agreement with the existing results. The lattice parameters of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys as a function with the Ge component are shown in Figure 2a. From Figure 2a, the lattice parameter a increases with an increase in the percentage of the germanium composition, except for t-Ge3N4. The lattice parameter a of t-Ge3N4 is slightly smaller than t-SiGe2N4; the possible cause of this phenomenon is that the angle of ∠Si-N-Ge (113.95°) and ∠Ge-N-Ge (112.16°) in t-SiGe2N4 decreases in t-Ge3N4 (∠Si-N-Ge: 112.86°; ∠Ge-N-Ge: 111.75°) parallel to the ac plane. Moreover, the lattice parameter c of t-Si3N4, t-Si2GeN4, and t-SiGe2N4 is almost the same; however, the lattice parameter c of t-Ge3N4 is far greater than that of the others. The bond length of the silicon nitrogen bond is certainly smaller than that of the germanium nitrogen bond in the same structure. From t-Si3N4 and t-Ge3N4, as the substitution of germanium atoms for silicon atoms increases and the substitution occurs primarily along the c axis, the growth of germanium nitrogen bonds is mainly manifested in the c axis direction. In Figure 1c, the silicon or germanium atoms occupy five of the nine layers of atoms along the c axis. From t-Si3N4 to t-Si2GeN4, the germanium atoms only replace two of the silicon atoms; thus, at this time, the increase along the c axis is very small. In addition, from t-Si2GeN4 to t-SiGe2N4, the germanium atoms are replaced on the same layers, so the increase along the c axis is very small. From t-SiGe2N4 to t-Ge3N4, all of the germanium atoms replace the silicon atoms, so the lattice parameter c suddenly increases.
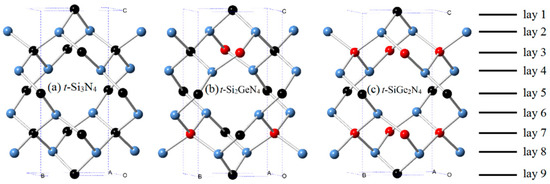
Figure 1.
Crystal structures of t-Si3N4 (a); t-Si2GeN4 (b); and t-SiGe2N4 (c) at ambient pressure. The silicon, germanium, and nitrogen atoms are represented as black, red, and blue spheres, respectively.

Table 1.
The lattice parameters a and c (in Å) and band gaps Eg (in eV) of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 and c-Si3N4, c-Si2GeN4, c-SiGe2N4, and c-Ge3N4. PBE: Perdew–Burke–Ernzerhof functional; PBEsol: Perdew–Burke–Ernzerhof functional for solids; CA–PZ: Perdew and Zunger.
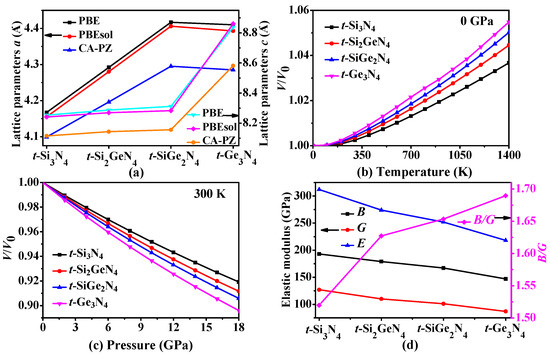
Figure 2.
Calculated lattice parameters a and c (a) of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 by PBE, PBEsol, and CA–PZ methods; the volume V/V0 compression as functions of temperature (b) and pressure (c); the elastic moduli for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 (d).
In addition, we further investigate the influence of pressure and temperature for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4. The ratio of volume V/V0 affected by temperature and pressure is shown in Figure 2b,c. As shown in Figure 2b,c, the volume of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 increases as the temperature increases. When T < 300 K, the growth rate is very small; however, when T > 300 K, the volume is found to increase linearly. Furthermore, the ratio of V/V0 clearly decreases as the pressure increases, approaching a linear decrease. Moreover, Figure 2b,c indicates that the effect of the pressure on the V/V0 is more significant than that of the temperature in the pressure and temperature ranges that are considered in our study. In addition, the volume of t-Ge3N4 changes more than do those of t-Si3N4, t-Si2GeN4, and t-SiGe2N4.
3.2. Mechanical and Anisotropic Properties
The elastic constants, elastic moduli, and Poisson’s ratio for t-SixGe3−xN4, c-SixGe3−xN4, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are all listed in Table 2. The elastic constant is an index that reflects the ability of materials to resist elastic deformation. From Table 2, the elastic constants of the t-Si2GeN4 and t-SiGe2N4 satisfy Born’s mechanical stability criteria of tetragonal symmetry [57]; as a result, t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are mechanically stable. In order to confirm the stability of t-Si2GeN4 and t-SiGe2N4, the phonon spectra are calculated at ambient pressure, which are shown in Figure 3. There is no imaginary frequency, proving that the alloys are stable.

Table 2.
Calculated elastic constants Cij (in GPa), bulk modulus BH, shear modulus GH, and Young’s modulus E (in GPa), the ratio of BH/GH and Poisson’s ratio v of t-SixGe3−xN4, c-SixGe3−xN4, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys compared with other calculated results.
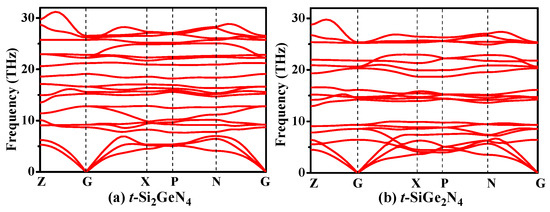
Figure 3.
Phonon spectra for t-Si2GeN4 (a) and t-SiGe2N4 (b).
The Voigt–Reuss–Hill approximation [60] is typically used to calculate bulk modulus BH and shear modulus GH. The Young’s modulus E and Poisson’s ratio v could be obtained as: E = 9BHGH/(3BH + GH) and v = (3BH − 2GH)/[2(3BH + GH)], respectively. The bulk modulus BH represents the resistance to compressibility, and the shear modulus GH represents the resistance to plastic deformation. The calculated bulk modulus BH and shear modulus GH are listed in Table 2. For t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, the bulk modulus are larger than the shear modulus, which indicates that it is more difficult for volume deformation to occur in alloys than shape deformation. The bulk modulus BH, shear modulus GH, and Young’s modulus E all decrease with an increase in the Ge component. Comparing t-SixGe3−xN4, c-SixGe3−xN4, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, the elastic modulus for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys is slightly larger than that for m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, whereas it is much smaller than that for c-SixGe3−xN4 (x = 0, 1, 2, 3) alloys.
Pugh [61] proposed that the ratio of BH/GH could accurately distinguish the brittleness or ductility of a material. If BH/GH > 1.75, then the material exhibits a ductile property; otherwise, it exhibits a brittle property. The ratio BH/GH of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys as a function with a Ge component are shown in Figure 2d. From Figure 2d, although the value of BH/GH increases with the increasing percentage of the Ge composition, they are all less than 1.75. This suggests that t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys all exhibit brittleness. Poisson’s ratio v can also be used to distinguish the brittleness or ductility of a material [62]. If v >0.26, then the material will behave in a ductile manner; otherwise, the material demonstrates brittleness. The calculated Poisson’s ratios v of t-SixGe3−xN4, c-SixGe3−xN4 and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are all listed in Table 2. From Table 2, all of the v are less than 0.26. Thus, t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys all demonstrate brittleness; this is consistent with the conclusion based on BH/GH. Moreover, c-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are quite brittle because of the small ratio of BH/GH; m-SiGe2N4 is ductile; and m-Si3N4, m-Si2GeN4, and m-Ge3N4 are brittle in nature.
It is well known that elastic anisotropy has important implications in engineering science and crystal physics. The directional dependence of the anisotropy is calculated by the elastic anisotropy measures (ELAM) [63,64] code. The two-dimensional (2D) representation of Poisson’s ratio v in (001), (010), (100), (101), (110), and (111) planes for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are shown in Figure 4. Clearly, the 2D figures of Poisson’s ratio all have a great deviation degree from a circular shape, indicating that the t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys exhibit anisotropy in Poisson’s ratio. Moreover, the four alloys present the different degree of anisotropy on Poisson’s ratio in different planes. The maximum Poisson’s ratio for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are 0.59, 0.60, 0.62, and 0.70, respectively, following the sequence t-Si3N4 > t-Si2GeN4 > t-SiGe2N4 > t-Ge3N4. The following directional dependence of anisotropy is usually described by vector direction (θ, φ), where θ (φ) represents the angle between the vector and the x-axis (z-axis) positive direction, and they are expressed in radians [63,64]. The positions of the maximum Poisson’s ratio for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 appear at θ = 0.79, φ = 0.00; θ = 2.36, φ = 0.00; θ = 1.57, φ = 3.93; and θ = 2.33, φ = 0.00, respectively.
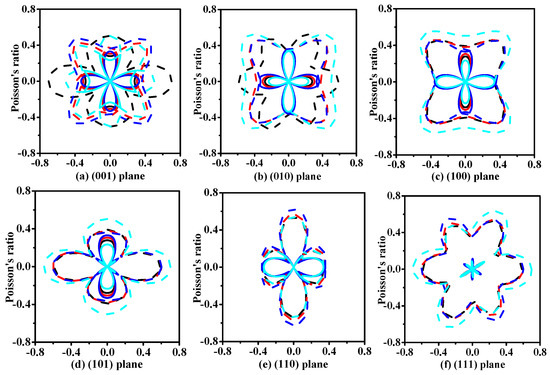
Figure 4.
Two-dimensional (2D) representations of Poisson’s ratio for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys in the (001) plane (a); (010) plane (b); (100) plane (c); (101) plane (d); (110) plane (e); and (111) plane (f). The dash dot and solid lines represent the maximum and minimum values, respectively. The black, red, blue, and cyan lines represent the Poisson’s ratios of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4, respectively.
The 2D figures of Young’s modulus for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are shown in Figure 5. Clearly, t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys exhibit large anisotropy in Young’s modulus in all of the planes except the (111) plane. The Young’s modulus of the materials in the (111) plane are approximately circular in shape, indicating that the materials exhibited the smallest anisotropy in the (111) plane. In addition, the shapes of the four lines are similar; thus, the anisotropy of Young’s modulus should change little with an increasing percentage of Ge composition. The maximum (minimum) values of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are 421 GPa (179 GPa), 373 GPa (159 GPa), 347 GPa (149 GPa), and 306 GPa (111 GPa), respectively. The positions of the maximum values of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are θ = 2.19, φ = 3.93; θ = 0.95, φ = 3.93; θ = 2.19, φ = 3.93; and θ = 2.17, φ = 3.93, respectively. The minimum value of t-Si3N4, t-Si2GeN4, and t-Ge3N4 appears at θ = 1.57, φ = 0.00, and the minimum value of t-SiGe2N4 appears at θ = 0.00, φ = 0.00. The values of Emax/Emin for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are 2.352, 2.346, 2.329, and 2.757, respectively. From these results, t-Ge3N4 has the largest anisotropy, and those of t-Si3N4, t-Si2GeN4, and t-SiGe2N4 are similar.
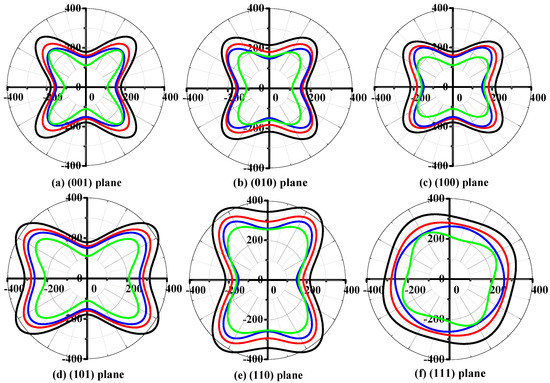
Figure 5.
2D representation of Young’s modulus for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys in the (001) plane (a); (010) plane (b); (100) plane (c); (101) plane (d); (110) plane (e); and (111) plane (f). The black, red, blue, and green lines represent the Poisson’s ratios of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4, respectively. All units are in GPa.
Moreover, the elastic anisotropic of the material could be shown by the percentage of elastic anisotropy for the bulk modulus AB, the percentage of elastic anisotropy for the shear modulus AG, and the universal anisotropic index AU: AU = 5GV/GR + BV/BR − 6, AB = (BV − BR)/(BV + BR), and AG = (GV − GR)/(GV + GR) [65]. The calculated values of AB, AG and AU of t-SixGe3−xN4, c-SixGe3−xN4, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are all listed in Table 3. From Table 3, t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys show a slight degree in anisotropy in the bulk modulus, because AB is very close to zero. For t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, the percentage of elastic anisotropy for shear modulus AG is the smallest for t-Si2GeN4, and is slightly smaller than that of t-Si3N4; meanwhile, t-Ge3N4 has the largest AG. For t-Si3N4, c-Si3N4, and m-Si3N4, the AG of c-Si3N4 is approximately half that of t-Si3N4. The t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys exhibit the largest anisotropy compared with c-SixGe3−xN4 and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, except for m-SiGe2N4. At the same time, m-SiGe2N4 exhibits the largest AG among the t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, c-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys. The greater the value of AU, the greater the anisotropy. The values of the universal anisotropic index AU of the t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are 1.231, 1.261, 1.283, and 1.637, respectively. It was also found that t-Ge3N4 has the greatest AU, indicating that t-Ge3N4 has the largest anisotropy among t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, which is consistent with the results of AB and AG.

Table 3.
Calculated bulk modulus BV, BR and shear modulus GV, GR by the Voigt and Reuss method respectively; percent compressibility of bulk modulus and shear modulus factors (AB, AG) % and universal anisotropic indexes AU for t-SixGe3−xN4, c-SixGe3−xN4, and m-SixGe3−xN4 (x = 0, 1, 2, 3) alloys.
3.3. Electronic Properties
As is known, the electronic structure determines the physical and chemical properties of materials. The electronic band structures of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are shown in Figure 6, according to calculations with the HSE06 hybrid functional [66,67]. From Figure 6, the t-SixGe3−xN4 (x = 1, 2, 3) alloys are all indirect band gap semiconductor materials, and t-Ge3N4 is a quasi-direct band gap semiconductor material. In addition, the band gaps of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 are 4.26 eV, 3.94 eV, 3.83 eV, and 3.25 eV, respectively; the conduction band minima are all located at the M point, and the valence band maxima are all located at the G point. With the increasing percentage of the Ge composition, the band gap decreases. For t-Ge3N4, the direct gap at G point is 3.34 eV, which is slightly larger than the indirect gap of 3.25 eV; as a result, t-Ge3N4 is a quasi-direct gap semiconductor. The calculated band gaps that utilize other functions, such as PBE, PBEsol, and CA–PZ, are listed in Table 1. It is known that the calculated band gaps are usually underestimated with DFT; i.e., the true band gap is larger than the calculated results. The band gaps of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 with the HSE06 hybrid functional are found to be much larger than those calculated by other functions.
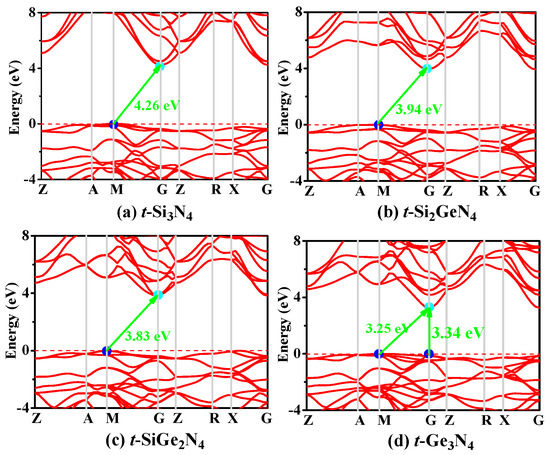
Figure 6.
Electronic band structures of t-Si3N4 (a); t-Si2GeN4 (b); t-SiGe2N4 (c); and t-Ge3N4 (d) with the HSE06 hybrid functional.
To further investigate the nature of the electronic band structure for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4, we also investigated the partial density of states (PDOS) for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys displayed in Figure 7. Since the t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys are all tetragonal crystal and Si and Ge belong to the IV A Group, their PDOS are similar and consist of three regions. The first region is from approximately −20 eV to −15 eV; the second and third regions are from −10 eV to the Fermi energy (EF) and from 5 eV to 12 eV, respectively. For t-Si3N4 and t-Ge3N4, the first region originates from the N-s, Si-s/p or Ge-s/p states. The second region is from the N-p states, with a mixture of Si-s/p or Ge-s/p states. The last region is primarily from Si/Ge-p states and a mixture of Si/Ge-s states and N-p states. For t-Si2GeN4 and t-SiGe2N4, the first region is primarily from N-s states, with an admixture from Si-s/p and Ge-s/p states. The second region primarily originates from N-p states, with significant contributions from the Si-s and Ge-s states between −9 and −7 eV, and the Si-p and Ge-p states between −7 eV and EF. The Ge-s/p and Si-p states dominate the last region, ranging from 5 eV to approximately 10 eV.
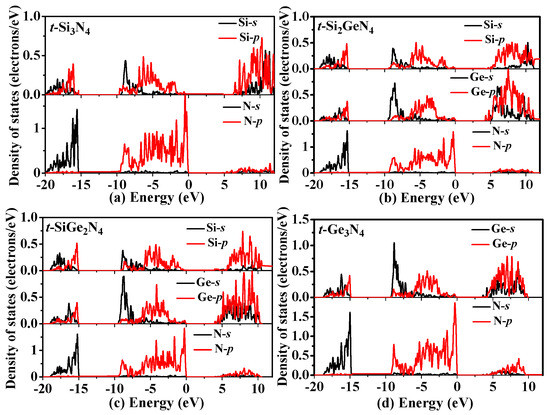
Figure 7.
Comparison of total density of states and partial density of states for t-Si3N4 (a); t-Si2GeN4 (b); t-SiGe2N4 (c); and t-Ge3N4 (d). The black and red curves represent the s states and p states, respectively, of silicon, germanium, and nitrogen atoms.
3.4. Thermodynamic Properties
The thermodynamic properties of semiconductors are very important at higher temperatures and pressures. In this work, the highest temperature is 1400 K, and the highest pressure is 18 GPa. In the above conditions, the thermal expansion coefficient α, the heat capacities CV and CP, and the Debye temperature ΘD are all investigated here. The thermal expansion coefficient describes how the size of a material changes with a change in temperature. Specifically, the thermal expansion coefficient measures the fractional change in size per degree change in temperature at a constant pressure; it is one of the important parameters to measure for determining the thermodynamic properties of materials. The values of the thermal expansion coefficient α of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys as functions of temperature and pressure are shown in Figure 8. Figure 8a shows that α increases exponentially with an increase in temperature until 300 K at 0 GPa. When T > 300 K, the growth rate of α decreases, and α increases linearly after T > 800 K. The growth rate of thermal expansion α at a high temperature is far less than that at a low temperature; i.e., the temperature dependence of α is very small at a high temperature. In addition, at a given temperature, α decreases with an increase in pressure, and the decline rate decreases with the increase in pressure. The effect of the temperature on the thermal expansion coefficient α is found to be more significant than that of pressure. Note that the thermal expansion coefficient α is the smallest for t-Si3N4, whereas t-Ge3N4 has the largest thermal expansion coefficient α in t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys.
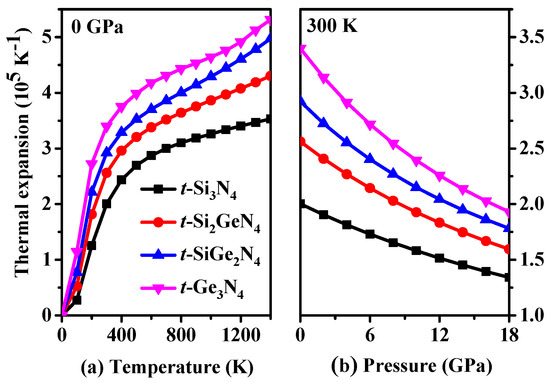
Figure 8.
Temperature (a) and pressure (b) dependence of the thermal expansion coefficients for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4.
The variation of the heat capacity (CV) at constant volume and the heat capacity (Cp) of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 at a constant pressure versus temperature and pressure variations are shown in Figure 9. The curves of heat capacity for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 have similar tendencies, as do the variations of the temperature and pressure that are shown in Figure 9. From Figure 9a, the heat capacity curves are proportional to T3 when T < 300 K, and the growth rate of the heat capacity decreases above 300 K. For T > 800 K, the heat capacity gradually approaches the fixed value of the Dulong–Petit limit (174.54 J mol−1 K−1) [68]. As shown in Figure 9c, the change regulation of CP is similar to that of CV below 800 K. CP increases linearly as the temperature increases above 800 K. From Figure 9b,d, the effect of pressure and temperature on heat capacity is the opposite; i.e., the heat capacities for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys decrease with an increase in pressure at a given temperature. Moreover, the sensitivity of heat capacity to temperature is far greater than that to pressure. Figure 9 also shows that the heat capacity for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys follows the sequence: t-Ge3N4 > t-SiGe2N4 > t-Si2GeN4 > t-Si3N4.
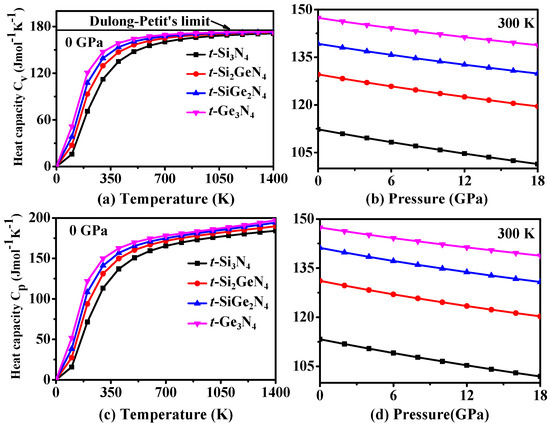
Figure 9.
Calculated specific volume CV as a function of temperature (a) and as a function of pressure (b); the pressure heat capacity CP as a function of temperature (c) and as a function of temperature pressure (d) for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4.
Figure 10a–d shows the variations of Debye temperature ΘD of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys with the temperature and pressure. From Figure 10a–d, the change regulation of ΘD for t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys has the same trend under variable temperature and variable pressure. In addition, the effect of the pressure on ΘD is found to be more significant than that of temperature. To better illustrate the effect of temperature and pressure variation on the ΘD of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys, the ΘD values as functions of temperature or pressure are shown in Figure 10e–f. From Figure 10e, the ΘD remains nearly constant from 0 K to 200 K, and when T > 200 K, the ΘD decreases linearly. Moreover, at a given temperature, the value of ΘD almost increases monotonously with an increase in pressure, as shown in Figure 10f. From 0 K to 1400 K, ΘD decreases by 5.2%, 6.7%, 7.8%, and 8.8% for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4, respectively, and from 0 GPa to 18 GPa, ΘD decreases by 12.2%, 13.7%, 15.3%, and 17.1%. In addition, the larger the Ge composition is, the larger the influence to ΘD is. The values of ΘD for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 calculated by the quasi-harmonic Debye model (938 K, 761 K, 658 K, and 567 K) are in agreement with those calculated by the elastic modulus [65] (ΘD = (h/kB)[(3n/4π)(NAρ/M)]1/3vm, vm = [(2/ + 1/)/3]−1/3, vp = [(B + 4G/3)/ρ]1/2, vs = (G/ρ)1/2; 937 K, 767 K, 666 K, and 571 K) at 0 K and 0 GPa.
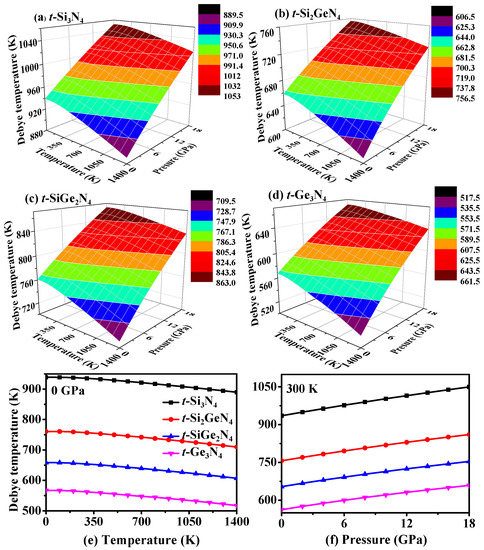
Figure 10.
(a–d) Three-dimensional contour plots of the Debye temperature versus pressure and temperature for t-Si3N4 (a); t-Si2GeN4 (b); t-SiGe2N4 (c); and t-Ge3N4 (d). The Debye temperature as functions of temperature (e) and pressure (f) for t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4.
4. Conclusions
In the present work, the structural, mechanical, elastic anisotropic, electronic, and thermal properties of t-Si3N4, t-Si2GeN4, t-SiGe2N4, and t-Ge3N4 in the tetragonal phase were investigated using density functional theory. The mechanically stable forms of t-Si2GeN4 and t-SiGe2N4 were proved by elastic constants. The t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys were all found to be brittle according to Poisson’s ratio v and B/G. The elastic modulus was found to decrease with an increase in the proportion of Ge. Also, t-Ge3N4 was found to exhibit the largest anisotropy among the t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys. It was found that t-Si3N4, t-Si2GeN4, and t-SiGe2N4 were indirect band gap semiconductors, but t-Ge3N4 was a quasi-direct gap semiconductor material. The band gaps of t-SixGe3−xN4 (x = 0, 1, 2, 3) alloys decreased with germanium content, which was suitable for visible light applications such as LEDs and photocatalysts. Moreover, all of the alloys considered were found to be wide band gap semiconductor materials, which indicated that transistors made from them could withstand higher temperatures and voltages, and the switching speed would be faster. In addition, their thermodynamic properties were investigated in detail utilizing the quasi-harmonic Debye model. The thermal expansion coefficient α and heat capacity were found to be more susceptible to temperature than pressure, whereas the Debye temperature was found to be more susceptible to pressure than temperature. These results would provide reference data for the experiments and make current theoretical research on these alloys more plenitude. It also could be envisioned that, by adjusting the Si:Ge ratio, the double nitrides in the tetragonal phases would lead to alloys with tailored electronic and thermodynamic properties for specific applications.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 61474089).
Author Contributions
Qingyang Fan designed the project; Qingyang Fan, Changchun Chai, Jionghao Yang and Chenxi Han performed the calculations; Chenxi Han, Qingyang Fan, Jionghao Yang, Yintang Yang and Changchun Chai analyzed the results, Chenxi Han and Changchun Chai wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reshak, A.H.; Khan, S.A.; Auluck, S. Linear and nonlinear optical properties for AA and AB stacking of carbon nitride polymorph (C3N4). RSC Adv. 2014, 4, 11967–11974. [Google Scholar] [CrossRef]
- Jack, K.H. Sialons and related nitrogen ceramics. J. Mater. Sci. 1976, 11, 1135–1158. [Google Scholar] [CrossRef]
- Salamat, A.; Hector, A.L.; Kroll, P.; McMillan, P.F. Nitrogen-rich transition metal nitrides. Coord. Chem. Rev. 2013, 257, 2063–2072. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, M.; Wu, W. Theoretical calculations of stability, mechanical and thermodynamic properties of IVA group Willemite-II nitrides. J. Theor. Comput. Chem. 2015, 14, 1550024. [Google Scholar] [CrossRef]
- Xu, B.; Dong, J.; McMillan, P.F.; Shebanova, O.; Salamatet, A. Equilibrium and metastable phase transitions in silicon nitride at high pressure: A first-principles and experimental study. Phys. Rev. B 2011, 84, 014113. [Google Scholar] [CrossRef]
- Yu, B.-H.; Chen, D. First-principles study on the electronic structure and phase transition of α-, β- and γ-Si3N4. Acta Phys. Sin. 2012, 61, 197102. [Google Scholar] [CrossRef]
- Zerr, A.; Miehe, G.; Serghiou, G.; Schwarz, M.; Kroke, E.; Riedel, R.; Fueß, H.; Kroll, P.; Boehler, R. Synthesis of cubic silicon nitride. Nature 1999, 400, 340–342. [Google Scholar] [CrossRef]
- Togo, A.; Kroll, P. First-principles lattice dynamics calculations of the phase boundary between β-Si3N4 and γ-Si3N4 at elevated temperatures and pressures. J. Comput. 2008, 29, 2255–2259. [Google Scholar] [CrossRef]
- Kruger, M.B.; Nguyen, J.H.; Li, Y.M.; Caldwell, W.A.; Manghnani, M.H.; Jeanloz, R. Equation of state of α-Si3N4s. Phys. Rev. B 1997, 55, 3456. [Google Scholar] [CrossRef]
- Kroll, P.; von Appen, J. Post-Spinel Phases of Silicon Nitride. Phys. Status Solidi B 2001, 226. [Google Scholar] [CrossRef]
- Kroll, P. Pathways to metastable nitride structures. J. Solid State Chem. 2003, 176, 530–537. [Google Scholar] [CrossRef]
- Yu, B.-H.; Chen, D. Investigations of meta-stable and post-spinel silicon nitrides. Phys. B Condens. Matter 2012, 407, 4660–4664. [Google Scholar] [CrossRef]
- Johnson, W.C. Nitrogen compounds of germanium. I. The preparation and properties of Germanic nitride. J. Am. Chem. Soc. 1930, 52, 5160–5165. [Google Scholar] [CrossRef]
- Ruddlesden, S.N.; Popper, P. On the crystal structure of the nitrides of silicon and germanium. Acta Cryst. 1958, 11, 465–468. [Google Scholar] [CrossRef]
- He, H.; Sekine, T.; Kobayashi, T.; Kimoto, K. Phase transformation of germanium nitride (Ge3N4) under shock wave compression. J. Appl. Phys. 2001, 90, 4403–4406. [Google Scholar] [CrossRef]
- McMillan, P.F.; Deb, S.K.; Dong, J.-J. High-pressure metastable phase transitions in β-Ge3N4 studied by Raman spectroscopy. J. Raman Spectrosc. 2003, 34, 567–577. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Schiferl, D.; Qian, J. Threshold pressure for disappearance of size-induced effect in spinel-structure Ge3N4 nanocrystals. J. Phys. Chem. B 2003, 107. [Google Scholar] [CrossRef]
- Luo, Y.; Cang, Y.; Chen, D. Determination of the finite-temperature anisotropic elastic and thermal properties of Ge3N4: A first-principles study. Comput. Condens. Matter 2014, 1, 1–7. [Google Scholar] [CrossRef]
- Molina, B.; Sansores, L.E. Electronic structure of Ge3N4 possible structures. Int. J. Quantum Chem. 2000, 80, 249–257. [Google Scholar] [CrossRef]
- Huang, M.; Feng, Y.; Lim, A.T.L.; Zheng, J. Structural and electronic properties of Si3P4. Phys. Rev. B 2004, 69, 054112. [Google Scholar] [CrossRef]
- Gopal, K.G.; Clark, S.J.; Bandyopadhyay, N.R. Electronic, mechanical and optical properties of Si3P4 and Ge3P4: AN AB initio study. Int. J. Mod. Phys. B 2010, 24, 5487–5494. [Google Scholar] [CrossRef]
- Brazhkin, V.V.; Lyapin, A.G.; Hemley, R.J. Harder than diamond: Dreams and reality. Philos. Mag. A 2002, 82, 231–253. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Lin, Z.; Zhang, R.; He, D.; Qin, J.; Zhu, J.; Han, J.; Wang, L.; Mao, H.; et al. Synthesis, crystal structure, and elastic properties of novel tungsten nitrides. Chem. Mater. 2012, 24, 3023–3028. [Google Scholar] [CrossRef]
- Liu, K.; Wang, S.; Zhou, X.; Chang, J. Theoretical calculations for structural, elastic, and thermodynamic properties of c-W3N4 under high pressure. J. Appl. Phys. 2013, 114, 063512. [Google Scholar] [CrossRef]
- He, D.; Zhao, Y.; Daemen, L.; Qian, J.; Shen, T. Boron suboxide: As hard as cubic boron nitride. Appl. Phys. Lett. 2002, 81, 643–645. [Google Scholar] [CrossRef]
- Zhang, R.; Veprek, S.; Argon, A.S. Anisotropic ideal strengths and chemical bonding of wurtzite BN in comparison to zincblende BN. Phys. Rev. B 2008, 77, 172103. [Google Scholar] [CrossRef]
- Zhang, R.; Lin, Z.; Mao, H.; Zhao, Y. Thermodynamic stability and unusual strength of ultra-incompressible rhenium nitrides. Phys. Rev. B 2011, 83, 060101. [Google Scholar] [CrossRef]
- Fan, Q.; Wei, Q.; Yan, H.; Zhang, M.; Zhang, Z.; Zhang, J.; Zhang, D. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- Ma, Z.; Han, Z.; Liu, X.; Yu, X.; Wang, D.; Tian, Y. Pnma-BN: Another boron nitride polymorph with interesting physical properties. Nanomaterials 2017, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Pournamdari1, E.; Akbarzadeh, E. AB initio and DFT study of energetic, stability, and nuclear magnetic resonance of BN nanotube. Med. Chem. (Los Angel.) 2017, 7, 8. [Google Scholar] [CrossRef]
- Teter, D.M.; Hemley, R.J. Low-compressibility carbon nitrides. Science 1996, 271, 53. [Google Scholar] [CrossRef]
- Fang, C.; Wijs, G.A. Lattice vibrations and thermal properties of carbon nitride with defect ZnS structure from first-principles calculations. J. Phys. Condens. Matter 2004, 16, 3027–3034. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, C. First-principles study on hardness of five polymorphs of C3N4. Phys. B Condens. Matter 2008, 403, 1956–1959. [Google Scholar] [CrossRef]
- Li, Q.; Liu, H.; Zhou, D.; Zheng, W.; Wu, Z.; Ma, Y. A novel low compressible and superhard carbon nitride: Body-centered tetragonal CN2. Phys. Chem. Chem. Phys. 2012, 14, 13081–13087. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Chai, C.; Wei, Q.; Yang, Y. Two novel C3N4 phases: Structural, mechanical and electronic properties. Materials 2016, 9, 427. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Hu, M.; Wang, Q.; Yang, Y. Prediction of novel hard phases of Si3N4: First-principles calculations. J. Solid State Chem. 2015, 228, 20–26. [Google Scholar] [CrossRef]
- Yao, X.; Dong, C. Structural, electronic and thermodynamic properties of tetragonal, monoclinic and orthorhombic Ge3N4. Chin. J. Comput. Phys. 2017, 34, 89–98. [Google Scholar]
- Fan, Q.; Chai, C.; Wei, Q.; Zhou, P.; Yang, Y. Elastic anisotropy and electronic properties of Si3N4 under pressures. AIP Adv. 2016, 6, 085207. [Google Scholar] [CrossRef]
- Cang, Y.; Lian, S.; Yang, H.; Chen, D. Predicting physical properties of tetragonal, monoclinic and orthorhombic M3N4 (M = C, Si, Sn) polymorphs via first-principles calculations. Chin. Phys. Lett. 2016, 33, 066301. [Google Scholar] [CrossRef]
- Tatsumi, K.; Tanaka, I.; Adachi, H. Theoretical prediction of post-spinel phases of silicon nitride. J. Am. Ceram. Soc. 2002, 85, 7–10. [Google Scholar] [CrossRef]
- Yang, M.; Wang, S.; Feng, Y.; Peng, G.; Sun, Y. Electronic structure of germanium nitride considered for gate dielectrics. J. Appl. Phys. 2007, 102, 013507. [Google Scholar] [CrossRef]
- Hart, J.N.; Allan, N.L.; Claeyssens, F. Ternary silicon germanium nitrides: A class of tunable band gap materials. Phys. Rev. B 2011, 84, 245209. [Google Scholar] [CrossRef]
- Ching, W.Y.; Mo, S.D.; Ouyang, L. Electronic and optical properties of the cubic spinel phase of c-Si3N4, c-Ge3N4, c-SiGe2N4, and c-GeSi2N4. Phys. Rev. B 2001, 63, 245110. [Google Scholar] [CrossRef]
- Moakafi, M.; Khenata, R.; Bouhemadou, A.; Benkhettou, N.; Rachen, D.; Reshak, A.H. Elastic, electronic and optical properties of SiGe2N4 under pressure: An ab initio study. Phys. Lett. A 2009, 373, 2393–2398. [Google Scholar] [CrossRef]
- Ma, Z.; Yan, F.; Wang, S.; Jia, Q.; Yu, X.; Shi, C. Mechanical, elastic anisotropy and electronic properties of the monoclinic phase of m-SixGe3−xN4. Chin. Phys. B 2017, 26, 126105. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Shanno, D.F.; Kettler, P.C. Optimal conditioning of quasi-newton methods. Math. Comput. 1970, 24, 657–664. [Google Scholar] [CrossRef]
- Blanco, M.A.; Francisco, E.; Luana, V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
- Fan, Q.; Wei, Q.; Chai, C.; Yang, Y.; Yu, X.; Liu, Y.; Zheng, J.; Zhou, P.; Zhang, D. The elastic anisotropic and thermodynamic properties of I4mm-B3C. Acta Phys. Pol. A 2016, 129, 103–108. [Google Scholar] [CrossRef]
- Zerr, A.; Kempf, M.; Schwarz, M.; Kroke, E.; Göken, M.; Riedel, R. Elastic moduli and hardness of cubic silicon nitride. J. Am. Ceram. Soc. 2002, 85, 86–90. [Google Scholar] [CrossRef]
- Serghiou, G.; Miehe, G.; Tschauner, O.; Zerr, A.; Boehler, R. Synthesis of a cubic Ge3N4 phase at high pressures and temperatures. J. Chem. Phys. 1999, 111, 4659–4662. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Bouhemadou, A.; Al-Douri, Y.; Khenata, R.; Haddadi, K. Structural, elastic, electronic, optical and thermal properties of c-SiGe2N4. Eur. Phys. J. B 2009, 71, 185–194. [Google Scholar] [CrossRef]
- Soignard, E.; Somayazulu, M.; Dong, J.; Sankey, O.F.; McMillan, P.F. High pressure-high temperature synthesis and elasticity of the cubic nitride spinel γ-Si3N4. J. Phys. Condens. Matter 2001, 13, 557–563. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Duan, Y.; Sun, Y.; Peng, M.; Zhou, S. Anisotropic elastic properties of the Ca–Pb compounds. J. Alloys Compd. 2014, 595, 14–21. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Xing, M.; Li, B.; Yu, Z.; Chen, Q. C2/m-carbon: Structural, mechanical, and electronic properties. J. Mater. Sci. 2015, 50, 7104–7114. [Google Scholar] [CrossRef]
- Fan, Q.; Chai, C.; Wei, Q.; Yan, H.; Zhao, Y.; Yang, Y.; Yu, X.; Liu, Y.; Xing, M.; Zhang, J.; et al. Novel silicon allotropes: Stability, mechanical, and electronic properties. J. Appl. Phys. 2015, 118, 185704. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Chai, C.; Wei, Q.; Yang, Y. Two novel silicon phases with direct band gaps. Phys. Chem. Chem. Phys. 2016, 18, 12905–12913. [Google Scholar] [CrossRef] [PubMed]
- Debye, P. Zur theorie der spezifischen wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).