A Self-Adaptive Umbrella Model for Vibration Analysis of Graphene
Abstract
1. Introduction
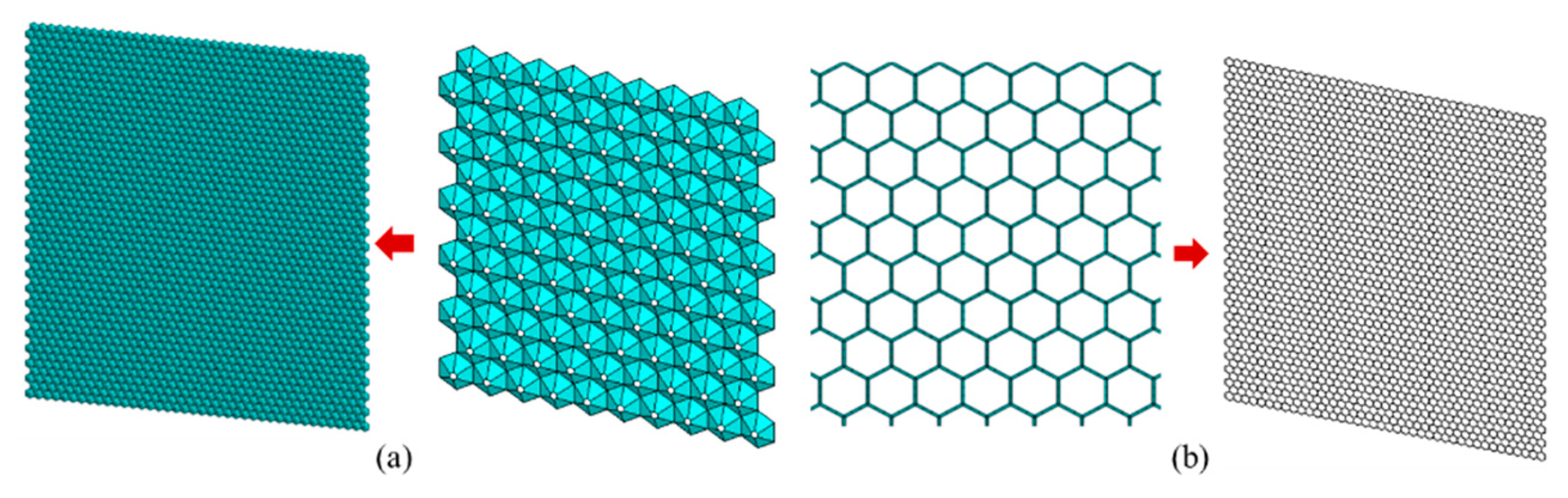
2. Model Formation
2.1. Model Configuration
2.2. Model Parameters
2.3. Mathematical Description
3. Results and Discussion
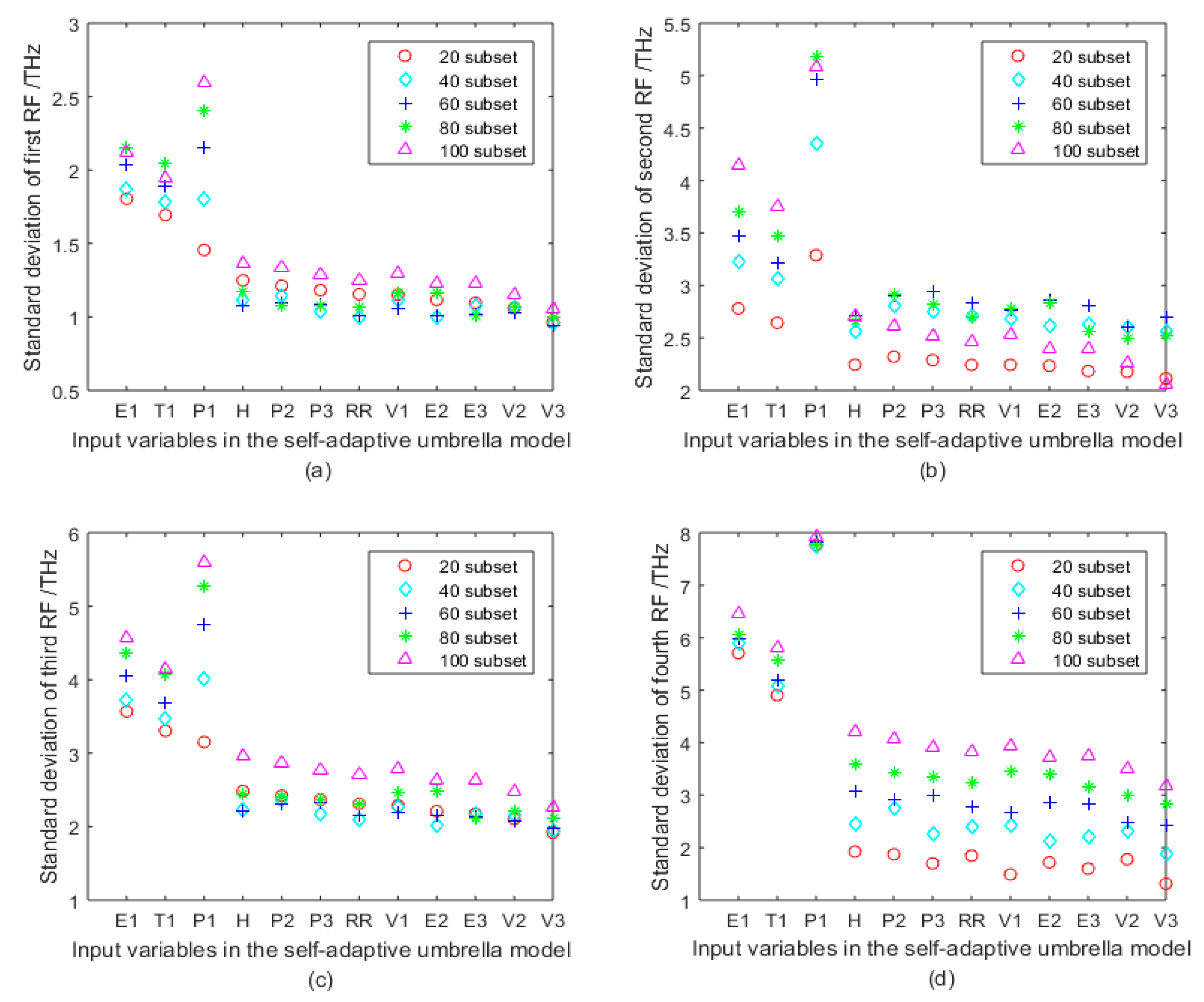
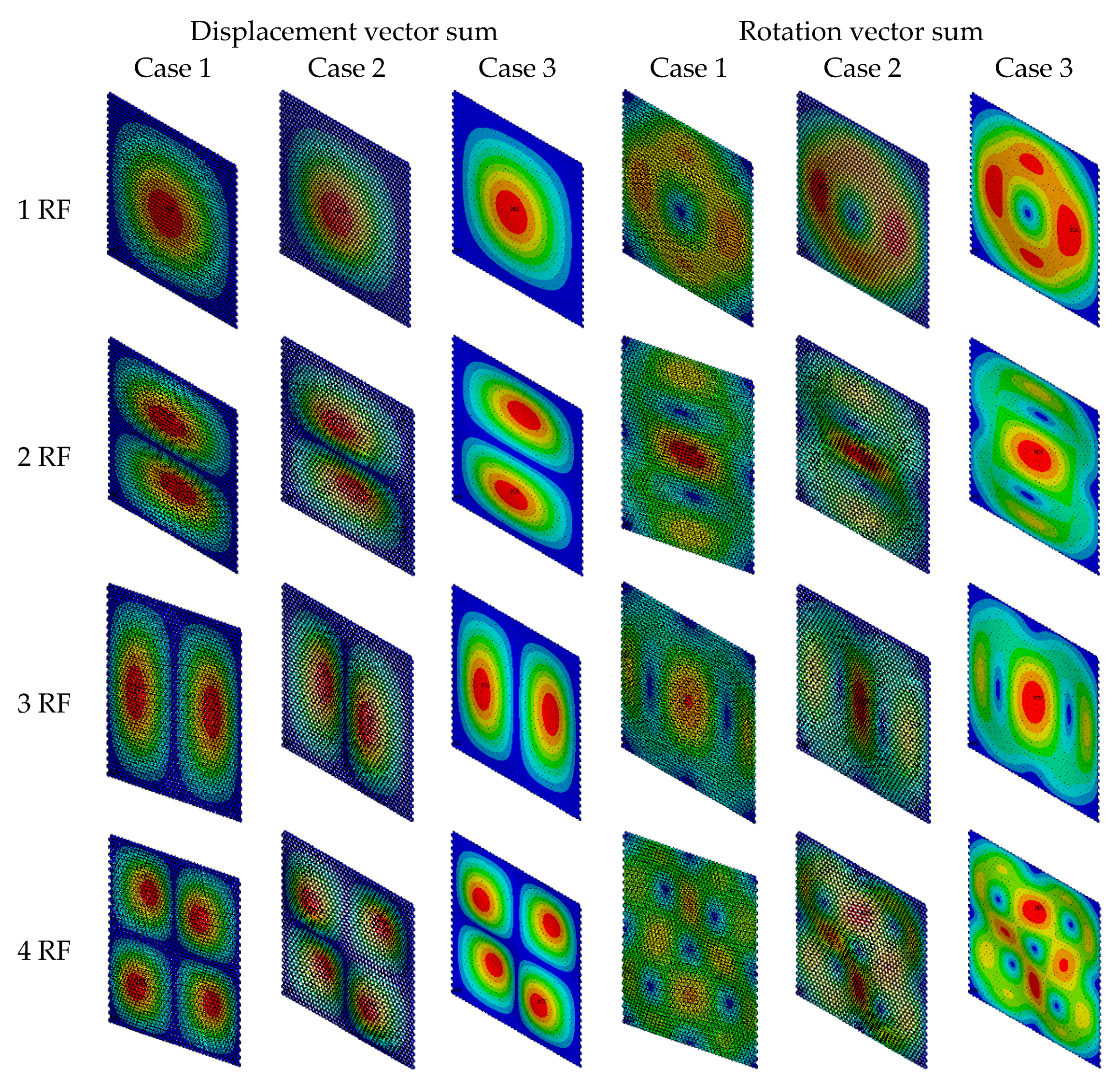
3.1. Sensitivity Analysis
3.2. Result Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.; Jiang, D.; Katsnelson, M.; Grigorieva, I.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef]
- Sheehy, D.E.; Schmalian, J. Optical transparency of graphene as determined by the fine-structure constant. Phys. Rev. B 2009, 80, 193411. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60. [Google Scholar] [CrossRef]
- Duplock, E.J.; Scheffler, M.; Lindan, P.J. Hallmark of perfect graphene. Phys. Rev. Lett. 2004, 92, 225502. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Yanovsky, Y.G.; Nikitina, E.A.; Karnet, Y.N. Quantum mechanics study of the mechanism of deformation and fracture of graphene. Phys. Mesomech. 2009, 12, 254–262. [Google Scholar] [CrossRef]
- Gao, Y.; Hao, P. Mechanical properties of monolayer graphene under tensile and compressive loading. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 41, 1561–1566. [Google Scholar] [CrossRef]
- Hernandez, E.; Goze, C.; Bernier, P. Elastic properties of C and BxCyNz composite nanotubes. Phys. Rev. Lett. 1998, 80, 4502. [Google Scholar] [CrossRef]
- Ni, Z.; Bu, H.; Zou, M. Anisotropic mechanical properties of graphene sheets from molecular dynamics. Phys. B Condens. Matter 2010, 405, 1301–1306. [Google Scholar] [CrossRef]
- Tsai, J.L.; Tu, J.F. Characterizing mechanical properties of graphite using molecular dynamics simulation. Mater. Des. 2010, 31, 194–199. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Motevalli, B. Mechanical properties of defective single-layered graphene sheets via molecular dynamics simulation. Superlattices Microstruct. 2012, 51, 274–289. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, C.M.; Cheng, Y. Mechanical properties of bilayer graphene sheets coupled by sp3 bonding. Carbon 2011, 49, 4511–4517. [Google Scholar] [CrossRef]
- Javvaji, B.; Budarapu, P.R.; Sutrakar, V.K. Mechanical properties of Graphene: Molecular dynamics simulations correlated to continuum based scaling laws. Comput. Mater. Sci. 2016, 125, 319–327. [Google Scholar] [CrossRef]
- Reddy, C.D.; Rajendran, S.; Liew, K.M. Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechnology 2006, 17, 864. [Google Scholar] [CrossRef]
- Natsuki, T.; Tantrakarn, K.; Endo, M. Prediction of elastic properties for single-walled carbon nanotubes. Carbon 2004, 42, 39–45. [Google Scholar] [CrossRef]
- Arroyo, M.; Belytschko, T. Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule. Phys. Rev. B 2004, 69, 115415. [Google Scholar] [CrossRef]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Hemmasizadeh, A.; Mahzoon, M.; Hadi, E. A method for developing the equivalent continuum model of a single layer graphene sheet. Thin Solid Films 2008, 516, 7636–7640. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Giannopoulos, G.I.; Anifantis, N.K. Numerical investigation of elastic mechanical properties of graphene structures. Mater. Des. 2010, 31, 4646–4654. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Katsareas, D.E.; Anifantis, N.K. Graphene characterization: A fully non-linear spring-based finite element prediction. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 43, 1833–1839. [Google Scholar] [CrossRef]
- Scarpa, F.; Adhikari, S.; Phani, A.S. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology 2009, 20, 065709. [Google Scholar] [CrossRef]
- Michele, M.; Marco, R. Prediction of Young’s modulus of single wall carbon nanotubes by molecular-mechanics based finite element modelling. Compos. Sci. Technol. 2006, 66, 1597–1605. [Google Scholar]
- Shokrieh, M.M.; Rafiee, R. Prediction of Young’s modulus of graphene sheets and carbon nanotubes using nanoscale continuum mechanics approach. Mater. Des. 2010, 31, 790–795. [Google Scholar] [CrossRef]
- Pettifor, D.G.; Oleinik, I.I. Bounded analytic bond-order potentials for σ and π bonds. Phys. Rev. Lett. 2000, 84, 4124. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 13104. [Google Scholar] [CrossRef]
- Memarian, F.; Fereidoon, A.; Ganji, M.D. Graphene Young’s modulus: Molecular mechanics and DFT treatments. Superlattices Microstruct. 2015, 85, 348–356. [Google Scholar] [CrossRef]
- Deng, S.; Berry, V. Wrinkled, rippled and crumpled graphene: An overview of formation mechanism, electronic properties, and applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Rajakumar, C. Lanczos algorithm for the quadratic eigenvalue problem in engineering applications. Comput. Methods Appl. Mech. Eng. 1993, 105, 1–22. [Google Scholar] [CrossRef]
- Warner, J.H.; Lee, G.D.; He, K.; Robertson, A.W.; Yoon, E.; Kirkland, A.I. Bond length and charge density variations within extended arm chair defects in graphene. ACS Nano 2013, 7, 9860–9866. [Google Scholar] [CrossRef] [PubMed]
- Fasolino, A.; Los, J.H.; Katsnelson, M.I. Intrinsic ripples in graphene. Nat. Mater. 2007, 6, 858. [Google Scholar] [CrossRef]
- Wei, X.; Fragneaud, B.; Marianetti, C.A.; Kysar, J.W. Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description. Phys. Rev. B Condens. Matter 2009, 80, 205407. [Google Scholar] [CrossRef]
- Gupta, S.; Dharamvir, K.; Jindal, V.K. Elastic moduli of single-walled carbon nanotubes and their ropes. Phys. Rev. B 2005, 72, 16. [Google Scholar] [CrossRef]
- Sadeghzadeh, S.; Khatibi, M.M. Modal identification of single layer graphene nano sheets from ambient responses using frequency domain decomposition. Eur. J. Mech. A/Solids 2017, 65, 70–78. [Google Scholar] [CrossRef]
- Liu, F.; Ming, P.; Li, J. Ab initio, calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B Condens. Matter 2007, 76, 471–478. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E.; Yakobson, B.I. C2F, BN, and C nanoshell elasticity from ab initio, computations. Phys. Rev. B Condens. Matter 2001, 64, 235406. [Google Scholar] [CrossRef]
- Cadelano, E.; Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Nonlinear elasticity of monolayer graphene. Phys. Rev. Lett. 2009, 102, 235502. [Google Scholar] [CrossRef] [PubMed]
- Chu, L.; Shi, J.; Souza de Cursi, E. Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method. Nanomaterials 2018, 87, 489. [Google Scholar] [CrossRef] [PubMed]
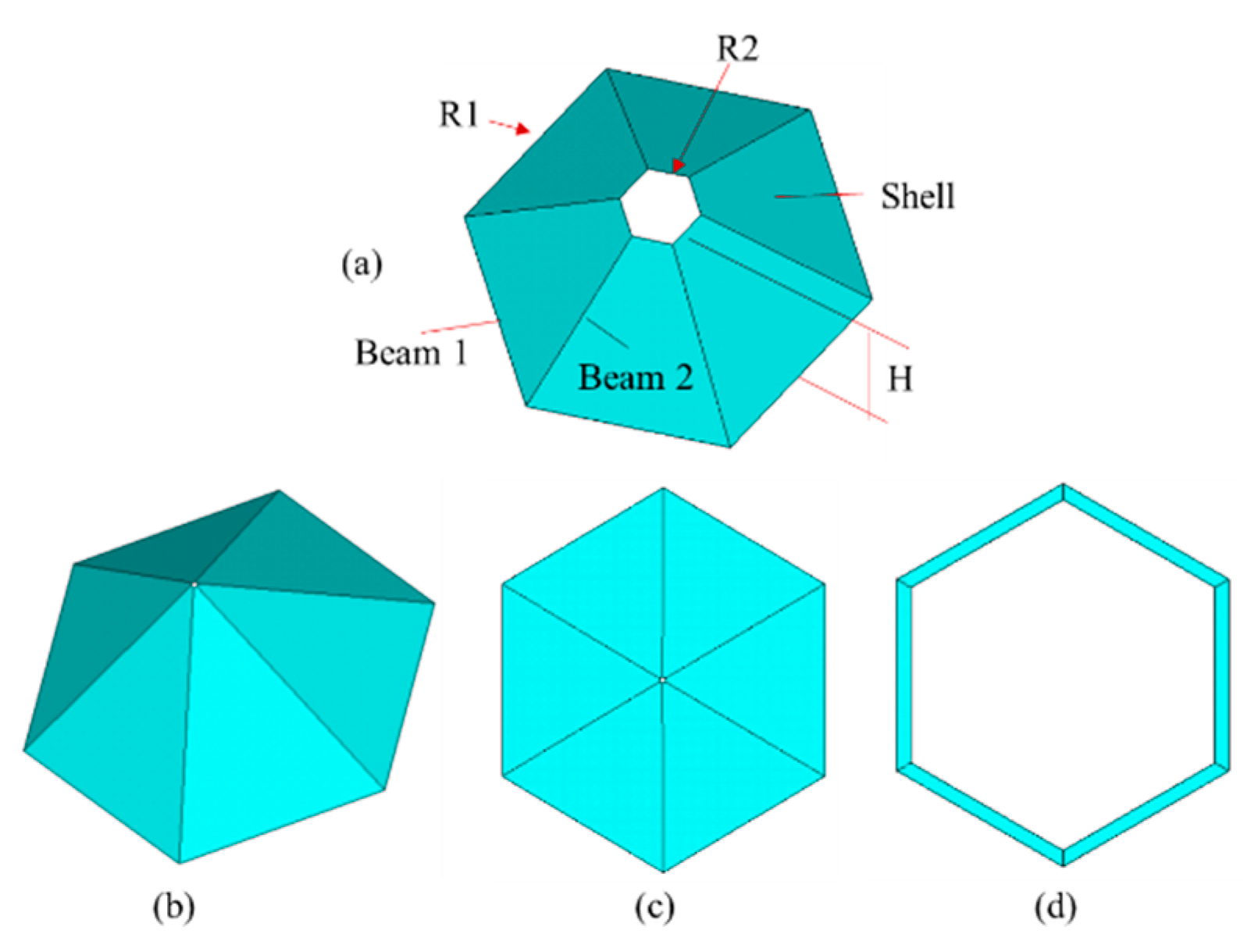

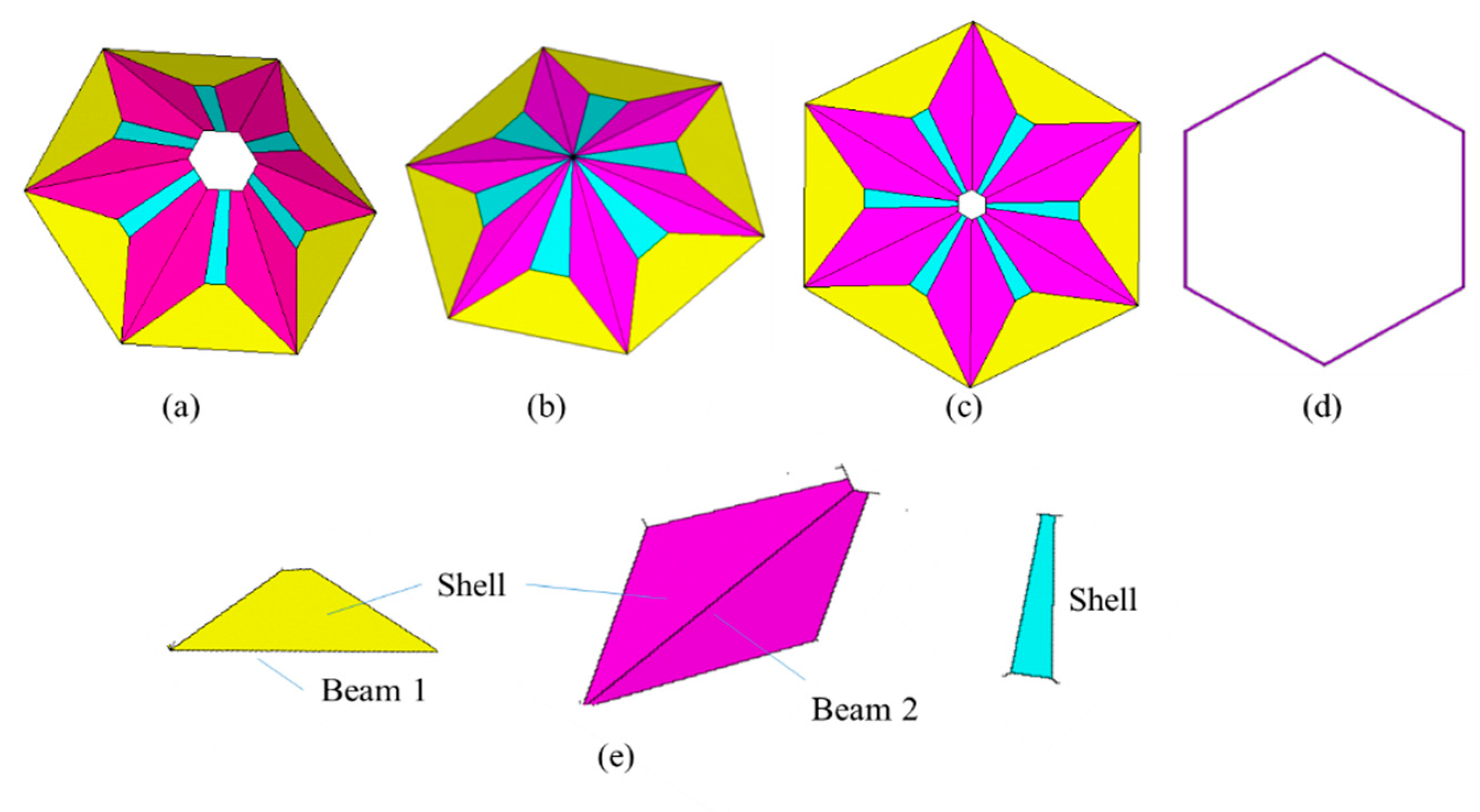
| Definition | Expression | Interval Range | Units |
|---|---|---|---|
| Section diameter of Beam 1 | T1 | 0.001~0.04 | nm |
| Section diameter of Beam 2 | T2 | 0.001~0.04 | nm |
| Thickness of Shell | T3 | 0.001~0.04 | nm |
| Vertical height of model | H | 0.001~1.5R1 | nm |
| Radius of top hexagon | R2 | 0.05R1~0.8R1 | nm |
| Young’s modulus of Beam 1, Beam 2 and Shell | E1, E2, E3 | 1000~1.5 × 1012 | Pa |
| Poisson ratio of Beam 1, Beam 2 and Shell | V1, V2, V3 | 0.1–0.4 | / |
| Physical density of Beam 1, Beam 2 and Shell | P1, P2, P3 | 100–4000 | Kg/m3 |
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| E1* × 1012/TPa | 3.962 | 7.787 | 8.559 | 12.12 |
| E2* × 1012/TPa | −0.164 | −0.3191 | −0.3406 | −0.4842 |
| E3* × 1012/TPa | 0.2622 | 0.5229 | 0.5705 | 0.8151 |
| V1 | 0.1994 | 0.4361 | 0.4946 | 0.7278 |
| V2 | 3.331 | 6.463 | 7.185 | 10.11 |
| V3 | 0.7192 | 1.409 | 1.534 | 2.136 |
| P1* × 103/TPa | −1.778 | −3.484 | −3.837 | −5.427 |
| P2* × 103/TPa | −0.2167 | −0.4286 | −0.4631 | −0.6604 |
| P3* × 103/TPa | −0.2171 | −0.4253 | −0.4681 | −0.6613 |
| H/nm | 3.831 | 8.372 | 8.914 | 13.31 |
| RR | −0.5665 | −1.483 | −1.340 | −2.325 |
| T1* × 10−2/nm | 1.379 | 2.630 | 2.893 | 4.035 |
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| Z0 | 2.6054 | 5.2502 | 5.6752 | 8.2169 |
| E1* × 1012/TPa | 3.8416 | 7.5431 | 8.2937 | 11.7405 |
| E2* × 1012/TPa | −0.0686 | −0.1364 | −0.1367 | −0.1990 |
| E3* × 1012/TPa | −0.1235 | −0.2410 | −0.2655 | −0.3740 |
| V1 | 0.2517 | 0.4019 | 0.5325 | 0.6465 |
| V2 | 1.2982 | 2.4937 | 2.8220 | 3.9513 |
| V3 | −0.9521 | −1.7533 | −2.0136 | −2.7627 |
| P1* × 103/TPa | −1.8113 | −3.5541 | −3.9105 | −5.5364 |
| P2* × 103/TPa | −0.0761 | −0.1515 | −0.1603 | −0.2299 |
| P3* × 103/TPa | −0.0949 | −0.1785 | −0.2010 | −0.2764 |
| H/nm | 4.5777 | 9.8330 | 10.5190 | 15.5773 |
| RR | −1.1605 | −2.6376 | −2.6055 | −4.1091 |
| T1* × 10−2/nm | 1.4620 | 2.7964 | 3.0736 | 4.2942 |
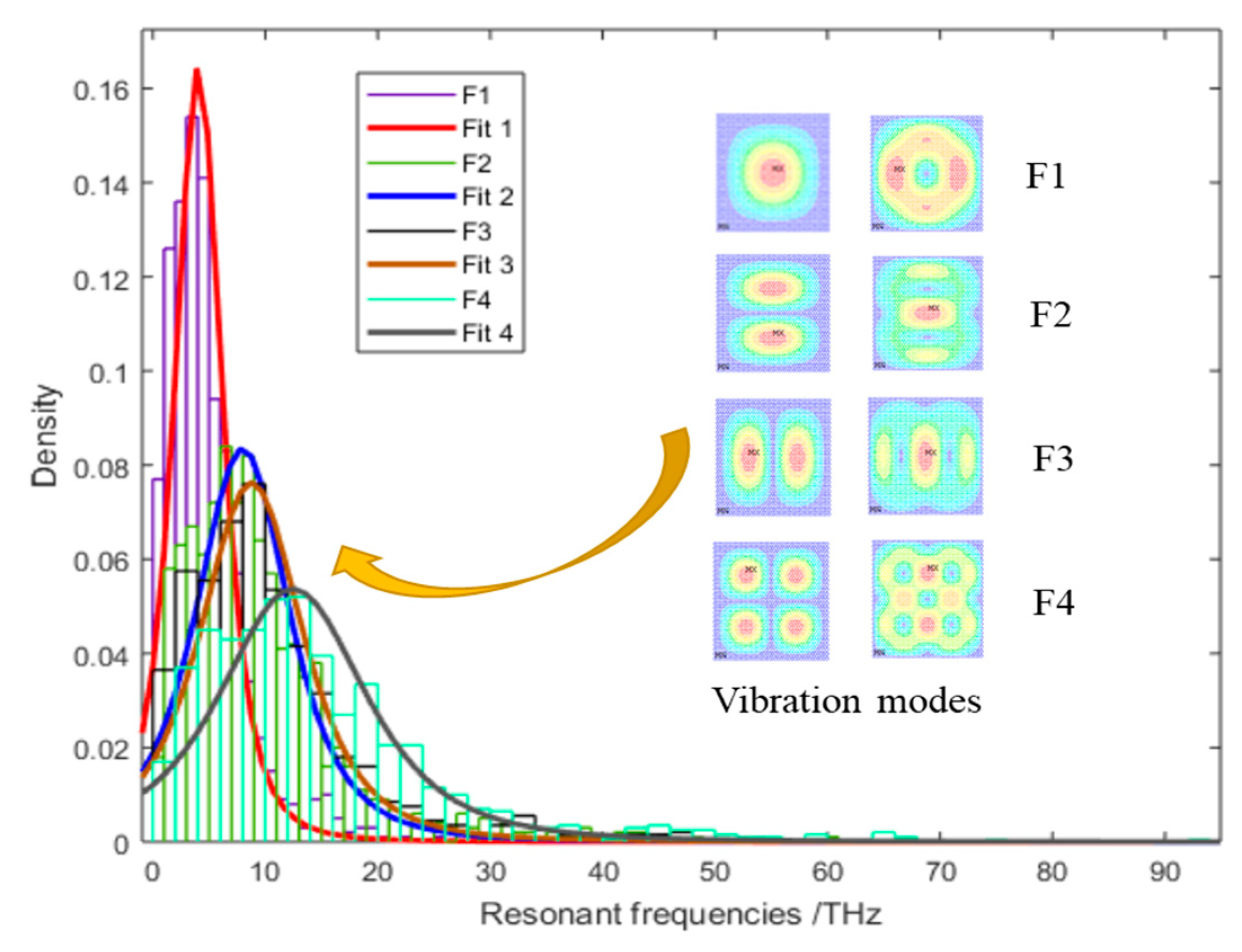
| F1/THz | F2/THz | F3/THz | F4/THz | |
|---|---|---|---|---|
| Mean | 4.8615 | 9.5554 | 10.5010 | 14.8827 |
| Minimum | 0.1034 | 0.2004 | 0.2233 | 0.3137 |
| Maximum | 31.0352 | 60.3568 | 66.4297 | 93.6672 |
| Variance | 3.7665 | 7.3630 | 8.0991 | 11.4460 |
| Gupta [38] | 1.7581 | 4.0706 | 4.7201 | 7.0325 |
| Khatibi [39] | 1.6030 | 2.4970 | 2.5980 | 3.5770 |
| Liu [40] | 1.6081 | 3.7232 | 4.3172 | 6.4323 |
| Kudin [41] | 1.5818 | 3.6623 | 4.2466 | 6.3271 |
| Wei [37] | 1.5946 | 3.6921 | 4.2811 | 6.3786 |
| Cadelano [42] | 1.5649 | 3.6232 | 4.2012 | 6.2595 |
| Reddy [18] | 1.3869 | 3.2111 | 3.7234 | 5.5475 |
| Chu [43] | 1.7282 | 3.2925 | 3.7442 | 5.1892 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Shi, J.; Yu, H.; Souza de Cursi, E. A Self-Adaptive Umbrella Model for Vibration Analysis of Graphene. Materials 2018, 11, 2497. https://doi.org/10.3390/ma11122497
Chu L, Shi J, Yu H, Souza de Cursi E. A Self-Adaptive Umbrella Model for Vibration Analysis of Graphene. Materials. 2018; 11(12):2497. https://doi.org/10.3390/ma11122497
Chicago/Turabian StyleChu, Liu, Jiajia Shi, Hang Yu, and Eduardo Souza de Cursi. 2018. "A Self-Adaptive Umbrella Model for Vibration Analysis of Graphene" Materials 11, no. 12: 2497. https://doi.org/10.3390/ma11122497
APA StyleChu, L., Shi, J., Yu, H., & Souza de Cursi, E. (2018). A Self-Adaptive Umbrella Model for Vibration Analysis of Graphene. Materials, 11(12), 2497. https://doi.org/10.3390/ma11122497





