Dual-Band Unidirectional Reflectionless Propagation in Metamaterial Based on Two Circular-Hole Resonators
Abstract
1. Introduction
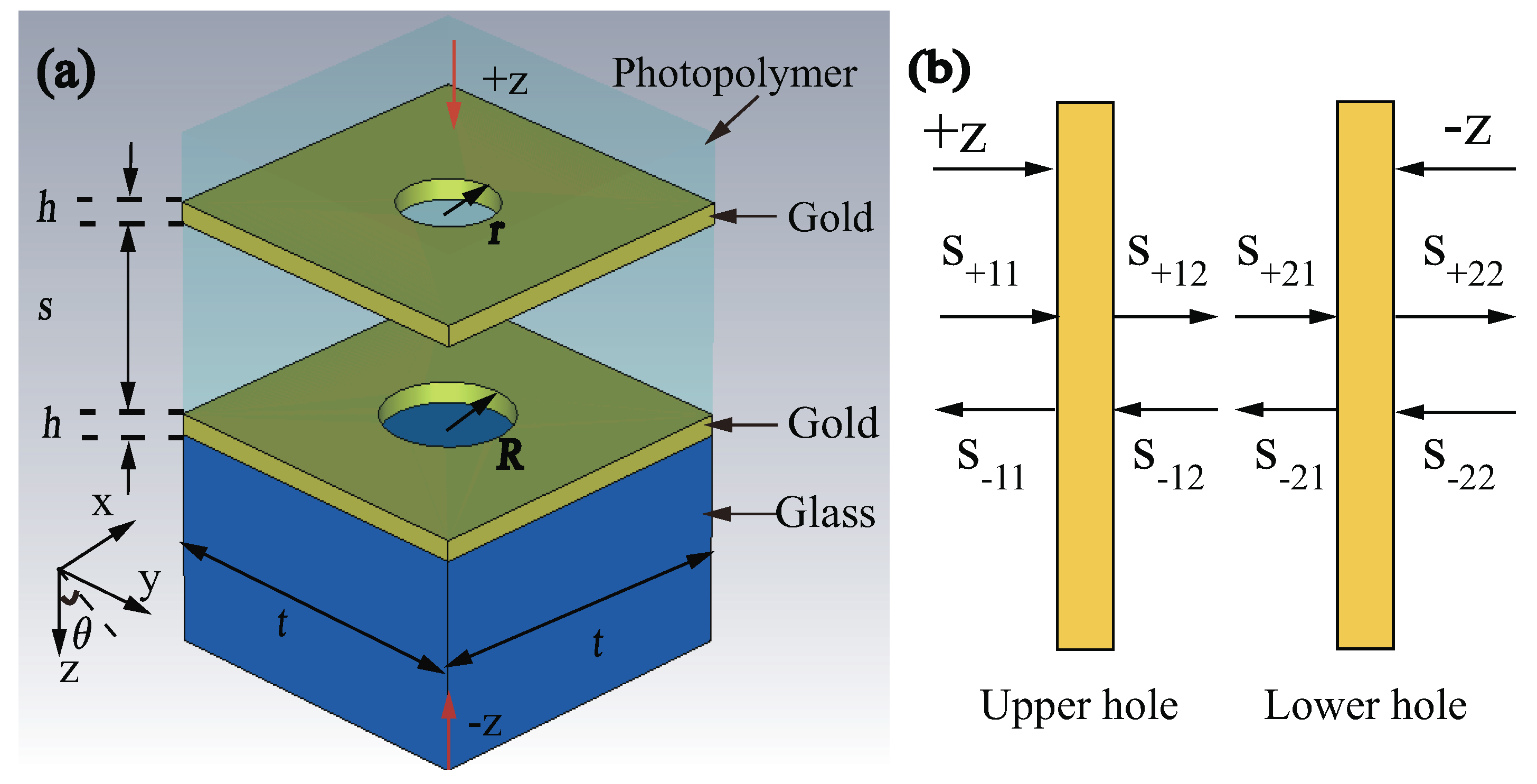
2. Structure
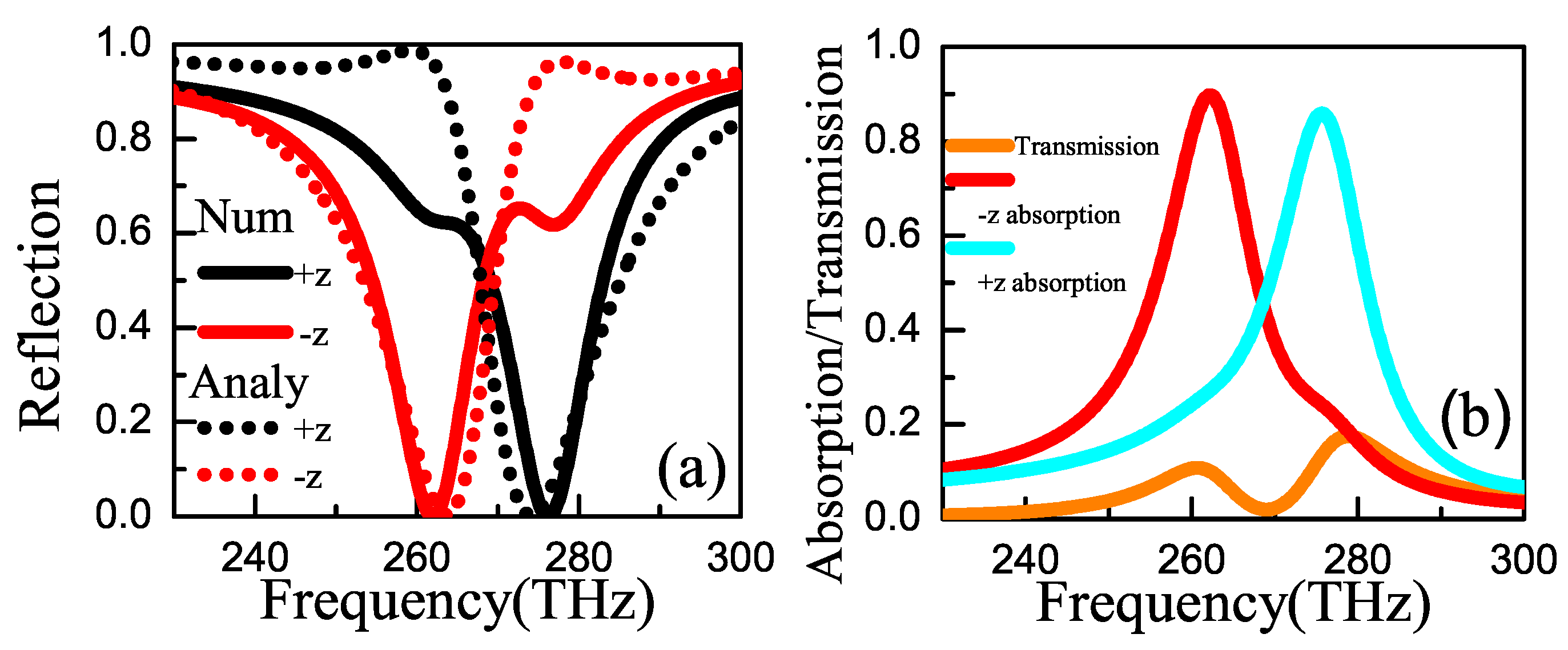
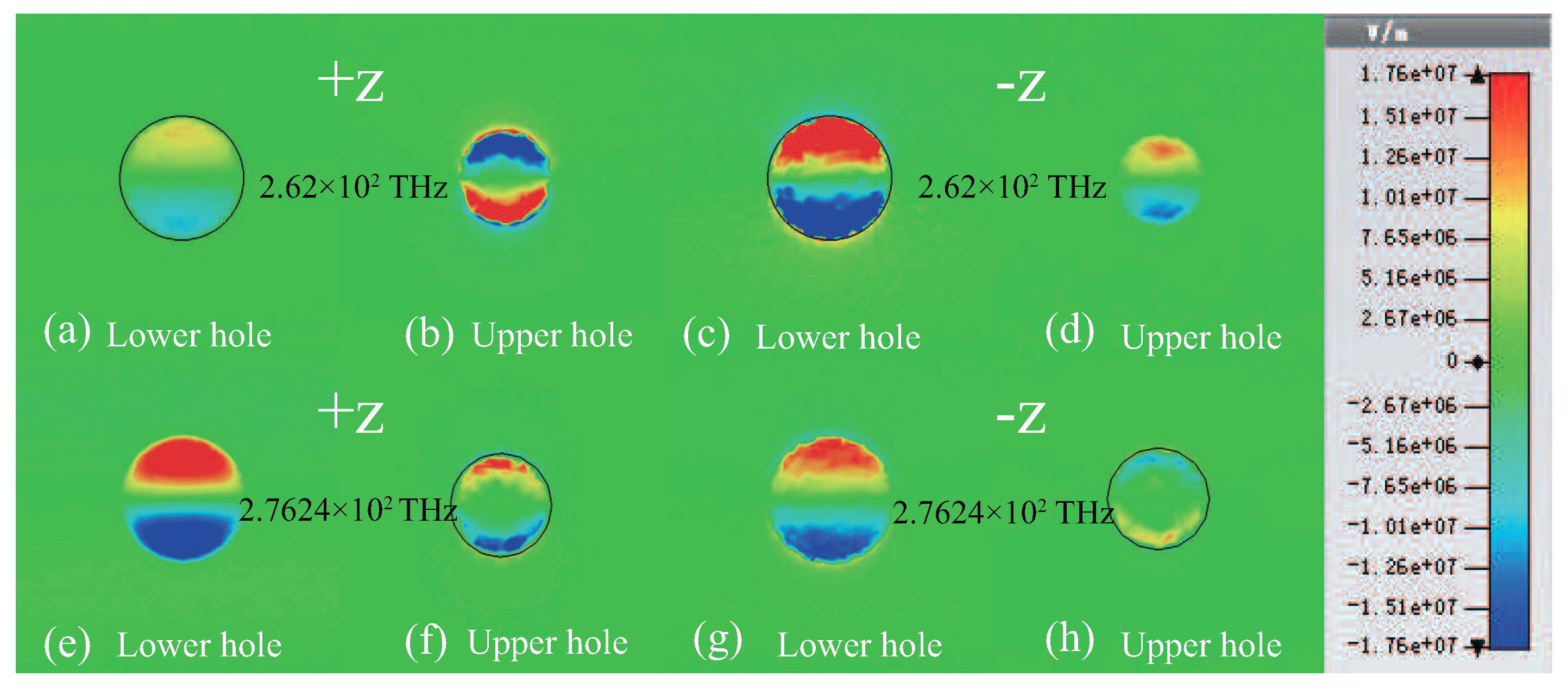
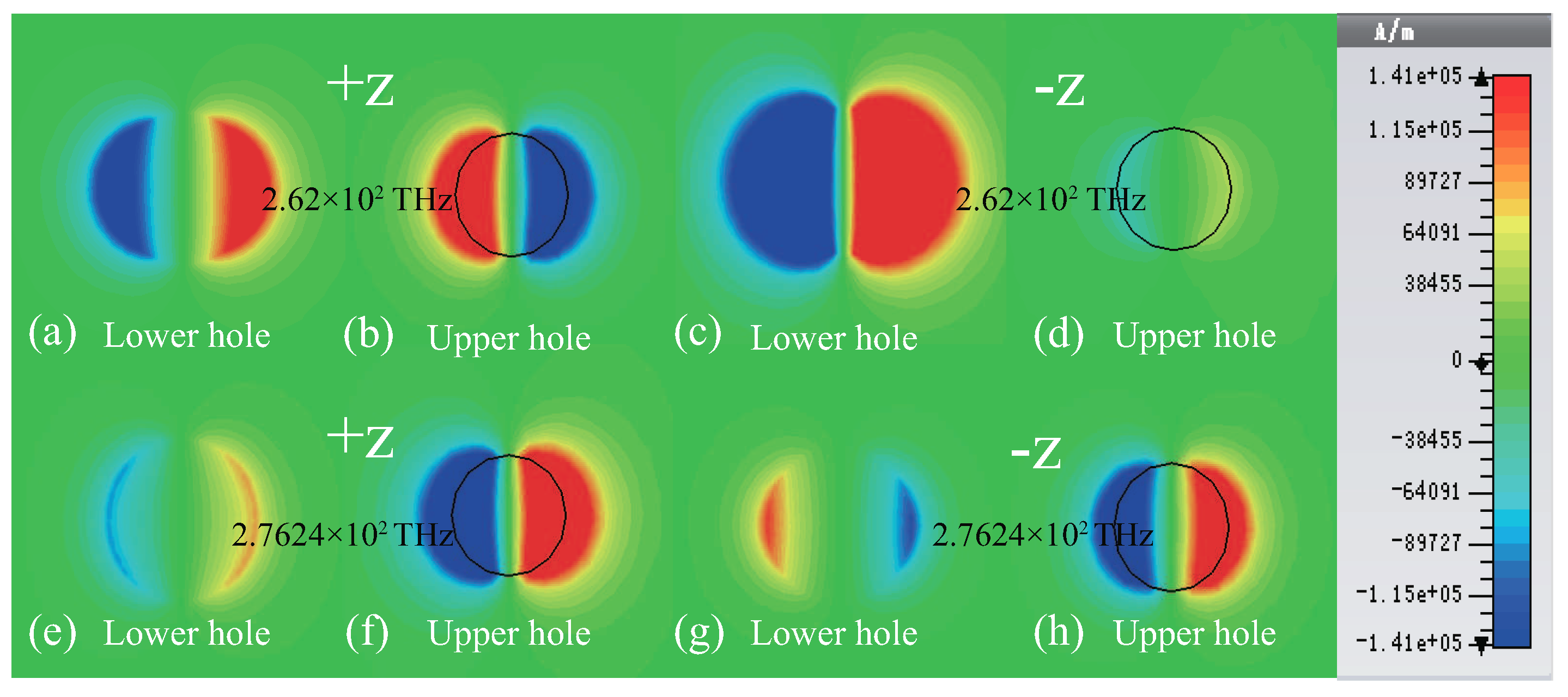
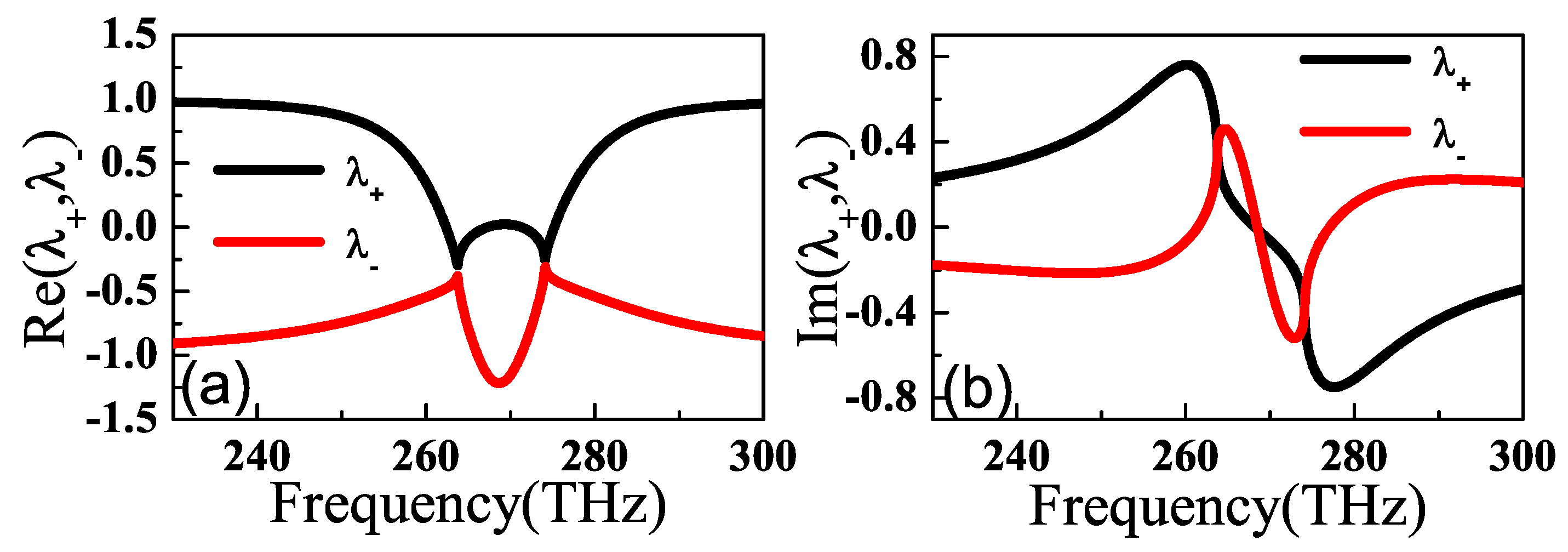
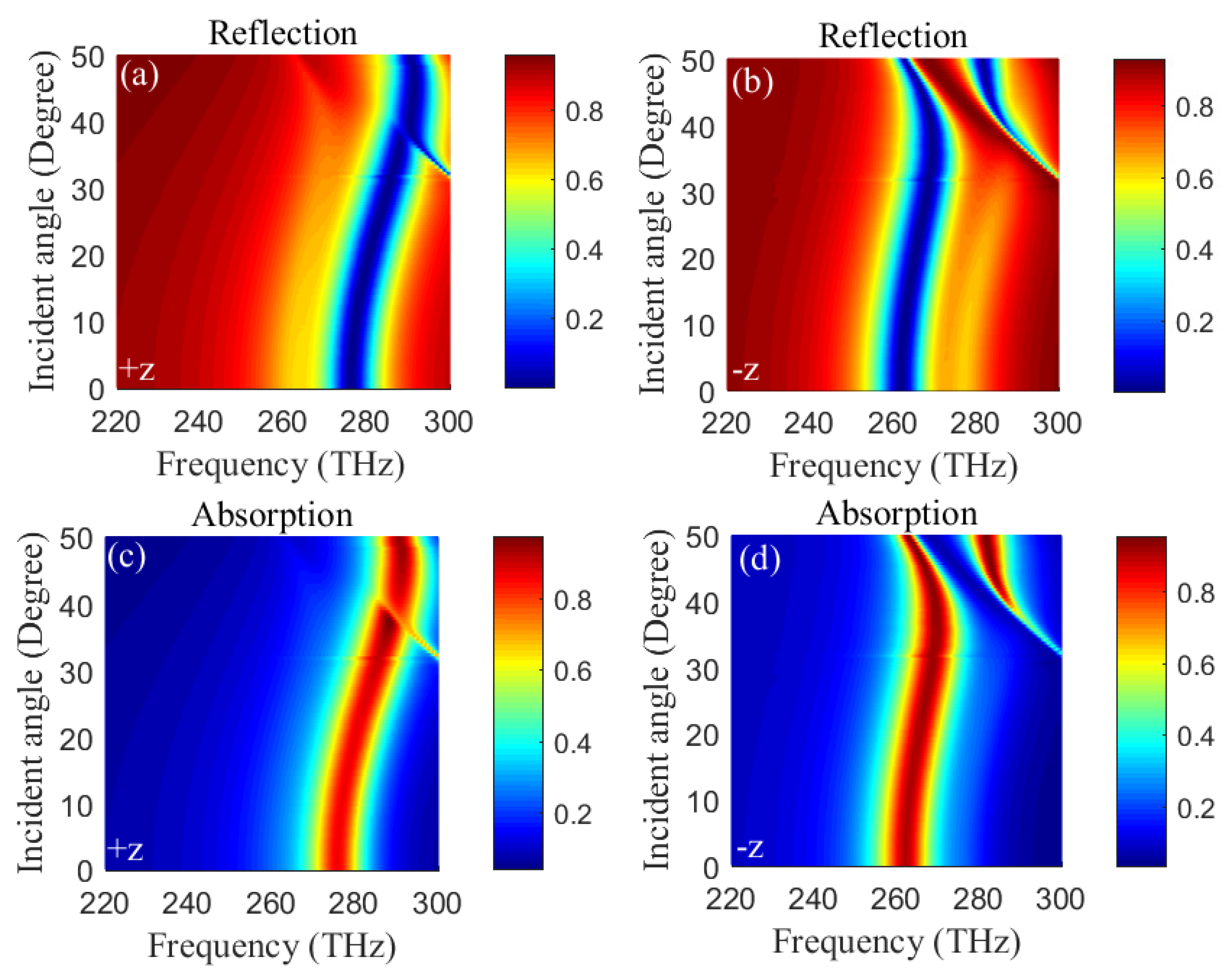
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Jing, H.; Özdemir, Ş.K.; Lü, H.; Nori, F. High-oreder exceptional points in optomechanics. Sci. Rep. 2017, 7, 3386. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, Ş.K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-induced suppression and revial of lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, Ş.K.; Liertzer, M.; Chen, W.J.; Kramer, J.; Yilmaz, H.; Wiersig, J.; Rotter, S.; Yang, L. Chiral modes and directional lasing at exceptioanal points. Proc. Natl. Acad. Sci. USA 2016, 113, 6845. [Google Scholar] [CrossRef] [PubMed]
- Doppler, J.; Mailybaev, A.A.; Böhm, J.; Kuhl, U.; Girschik, A.; Libisch, F.; Milburn, T.J.; Rabl, P.; Moiseyev, N.; Rotter, S. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 2016, 537, 76. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, Ş.K.; Lei, F.C.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.H.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nature 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.S.; Hua, S.Y.; Yang, C.; Wen, J.M.; Jiang, L.; Li, G.Y.; Wang, G.Z.; Xiao, M. Parity-time-symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photonic 2014, 8, 524. [Google Scholar] [CrossRef]
- Baum, B.; Alaeian, H.; Dionne, J. A parity-time symmetric coherent plasmonic absorber-amplifier. Appl. Phys. 2015, 117, 063106. [Google Scholar] [CrossRef]
- Miri, M.A.; Likamwa, P.; Christodoulides, D.N. Large area single-mode parity-timesymmetric laser amplifiers. Opt. Lett. 2012, 37, 764–766. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.Y.; Zhang, N.; Lyu, Q.; Li, M.; Xiao, S.M.; Song, Q.H. Experimental demonstration of PT-symmetric stripe lasers. Laser Photonics Rev. 2015, 10, 588–594. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.A.; Hassan, A.U.; Hayenga, W.E.; Heinrich, M.; Christodouldes, D.N.; Khajavikhan, M. Parity-time-symmetric coupled microring lasers operating around an exceptional point. Opt. Lett. 2015, 40, 4955–4958. [Google Scholar] [CrossRef] [PubMed]
- Jing, H.; Özdemir, Ş.K.; Geng, Z.; Zhang, J.; Lü, X.Y.; Peng, B.; Yang, L.; Nori, F. Optomechanically-induced transparency in parity-time-symmetric microresonators. Sci. Rep. 2015, 5, 09663. [Google Scholar] [CrossRef] [PubMed]
- Sounas, D.L.; Fleury, R.; Alù, A. Unidirectional cloaking based on metasurfaces with balanced loss and gain. Phys. Rev. Appl. 2015, 4, 014005. [Google Scholar] [CrossRef]
- Alaeian, H.; Dionne, J.A. Parity-time-symmetric plasmonic metamaterials. Phys. Rev. A 2014, 89, 033829. [Google Scholar] [CrossRef]
- Gear, J.; Liu, F.; Chu, S.T.; Rotter, S.; Li, J.S. Parity-time symmetry from stacking purely dielectric and magnetic slabs. Phys. Rev. A 2015, 91, 033825. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Xu, Y.D.; Chen, H.Y. Zero index metamaterials with PT symmetry in a waveguide system. Opt. Express 2016, 24, 1648–1657. [Google Scholar] [CrossRef] [PubMed]
- Spada, L.L.; Vegni, L. Near-zero-index wires. Opt. Express 2017, 25, 23699–23708. [Google Scholar] [CrossRef] [PubMed]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed]
- Iovine, R.; Spada, L.L.; Vegni, L. Nanoplasmonic sensor for chemical measurements. Opt. Sens. 2013, 8774, 877411. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveria, J.E.B.; Almeida, V.R.; Chen, Y.F.; Scherer, A. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Zhu, X.F.; Yang, S.; Zhu, H.Y.; Zhang, P.; Yin, X.B.; Wang, Y.; Zhang, X. Demonstration of a large-scale optical exceptional point structure. Opt. Express 2014, 22, 1760–1767. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Deng, X.H.; Chen, L. Unidirectional invisibility in a two-layer non-PT-symmetric slab. Opt. Express 2014, 22, 19440–19447. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Veronis, G.; Min, C.J. Unidirectional reflectionless propagation in plasmonic waveguide-cavity systems at exceptional points. Opt. Express 2015, 23, 29882–29895. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Bai, R.; Gu, X.; Jin, X.R.; Zhang, Y.Q.; Lee, Y.P. Unidirectional reflectionless propagation in plasmonic waveguide system based on phase coupling between two stub resonators. IEEE Photonics J. 2017, 9, 4801409. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, R.; Gu, X.; Jin, Y.J.; Zhang, Y.Q.; Jin, X.R.; Zhang, S.; Lee, Y.P. Unidirectional reflectionless phenomenon in ultracompact non-Hermitian plasmonic waveguide system based on phase coupling. J. Opt. 2017, 19, 125005. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, R.; Gu, X.; Jin, X.R.; Zhang, Y.Q.; Lee, Y.P. Dualband unidirectional reflectionless phenomena in an ultracompact non-Hermitian plasmonic waveguide system based on near-field coupling. Opt. Express 2017, 25, 24281–24289. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.J.; Wang, B.; Ke, S.L.; Long, H.; Wang, K.; Lu, P.X. Exceptional points in Fano-resonant graphene metamaterials. Opt. Express 2017, 25, 7203–7212. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Cui, H.X.; Li, T.F.; Chen, J.; Zhu, W.R.; Premaratne, M. Unidirectional phase singularity in ultrathin metamaterials at exceptional points. Phys. Rev. A 2014, 89, 065801. [Google Scholar] [CrossRef]
- Bai, R.; Zhang, C.; Gu, X.; Jin, X.R.; Zhang, Y.Q.; Lee, Y.P. Unidirectional reflectionlessness and perfect nonreciprocal absorption in stacked asymmetric metamaterial based on near-field coupling. Appl. Phys. Express 2017, 10, 112001. [Google Scholar] [CrossRef]
- Gu, X.; Bai, R.; Zhang, C.; Jin, X.R.; Zhang, Y.Q.; Zhang, S.; Lee, Y.P. Unidirectional reflectionless propagation in a non-ideal parity-time metasurface based on far field coupling. Opt. Express 2017, 25, 11778–11787. [Google Scholar] [CrossRef] [PubMed]
- Bai, R.; Zhang, C.; Gu, X.; Jin, X.R.; Zhang, Y.Q.; Lee, Y.P. Switching the unidirectional refectionlessness by polarization in non-ideal PT metamaterial based on the phase coupling. Sci. Rep. 2017, 7, 10742. [Google Scholar] [CrossRef] [PubMed]
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Bell, R.R.; Alexander, R.W., Jr.; Ward, C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983, 22, 1099–1120. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.R.; Zhang, Y.Q.; Zhang, S.; Lee, Y.P.; Rhee, J.Y. Polarization-independent electromagnetically induced transparency-like effects in stacked metamaterials based on Fabry-Perot resonance. J. Opt. 2013, 15, 125104. [Google Scholar] [CrossRef]
- Cao, G.T.; Li, H.J.; Zhan, S.P.; He, Z.H.; Guo, Z.B.; Xu, X.K.; Yang, H. Uniform theoretical description of plasmon-induced transparency in plasmonic stub waveguide. Opt. Lett. 2014, 39, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, X.M.; Mao, D.; Gong, Y.K.; Wang, G.X. Induced transparency in nanoscale plasmonic resonator systems. Opt. Lett. 2011, 36, 3233–3235. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, X.M.; Wang, G.X.; Mao, D. Tunable high-channel-count bandpass plasmonic filters based on an analogue of electromagnetically induced transparency. Nanotechnology 2012, 23, 444003. [Google Scholar] [CrossRef] [PubMed]
- Spada, L.L.; Vegni, L. Metamaterial-based wideband electromagnetic wave absorber. Opt. Express 2016, 24, 5763–5772. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Langguth, L.; Weiss, T.; Kastel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nano. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Bai, R.; Jin, X.; Zhang, Y.; An, C.; Lee, Y. Dual-Band Unidirectional Reflectionless Propagation in Metamaterial Based on Two Circular-Hole Resonators. Materials 2018, 11, 2353. https://doi.org/10.3390/ma11122353
Han G, Bai R, Jin X, Zhang Y, An C, Lee Y. Dual-Band Unidirectional Reflectionless Propagation in Metamaterial Based on Two Circular-Hole Resonators. Materials. 2018; 11(12):2353. https://doi.org/10.3390/ma11122353
Chicago/Turabian StyleHan, Guofeng, Ruiping Bai, Xingri Jin, Yingqiao Zhang, Chengshou An, and Youngpak Lee. 2018. "Dual-Band Unidirectional Reflectionless Propagation in Metamaterial Based on Two Circular-Hole Resonators" Materials 11, no. 12: 2353. https://doi.org/10.3390/ma11122353
APA StyleHan, G., Bai, R., Jin, X., Zhang, Y., An, C., & Lee, Y. (2018). Dual-Band Unidirectional Reflectionless Propagation in Metamaterial Based on Two Circular-Hole Resonators. Materials, 11(12), 2353. https://doi.org/10.3390/ma11122353





