Multislot Simultaneous Spectrum Sensing and Energy Harvesting in Cognitive Radio
Abstract
:1. Introduction
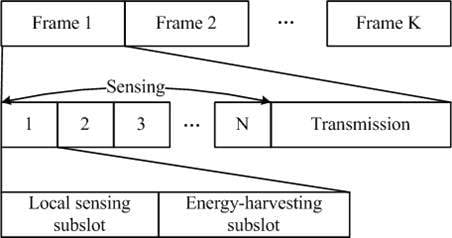
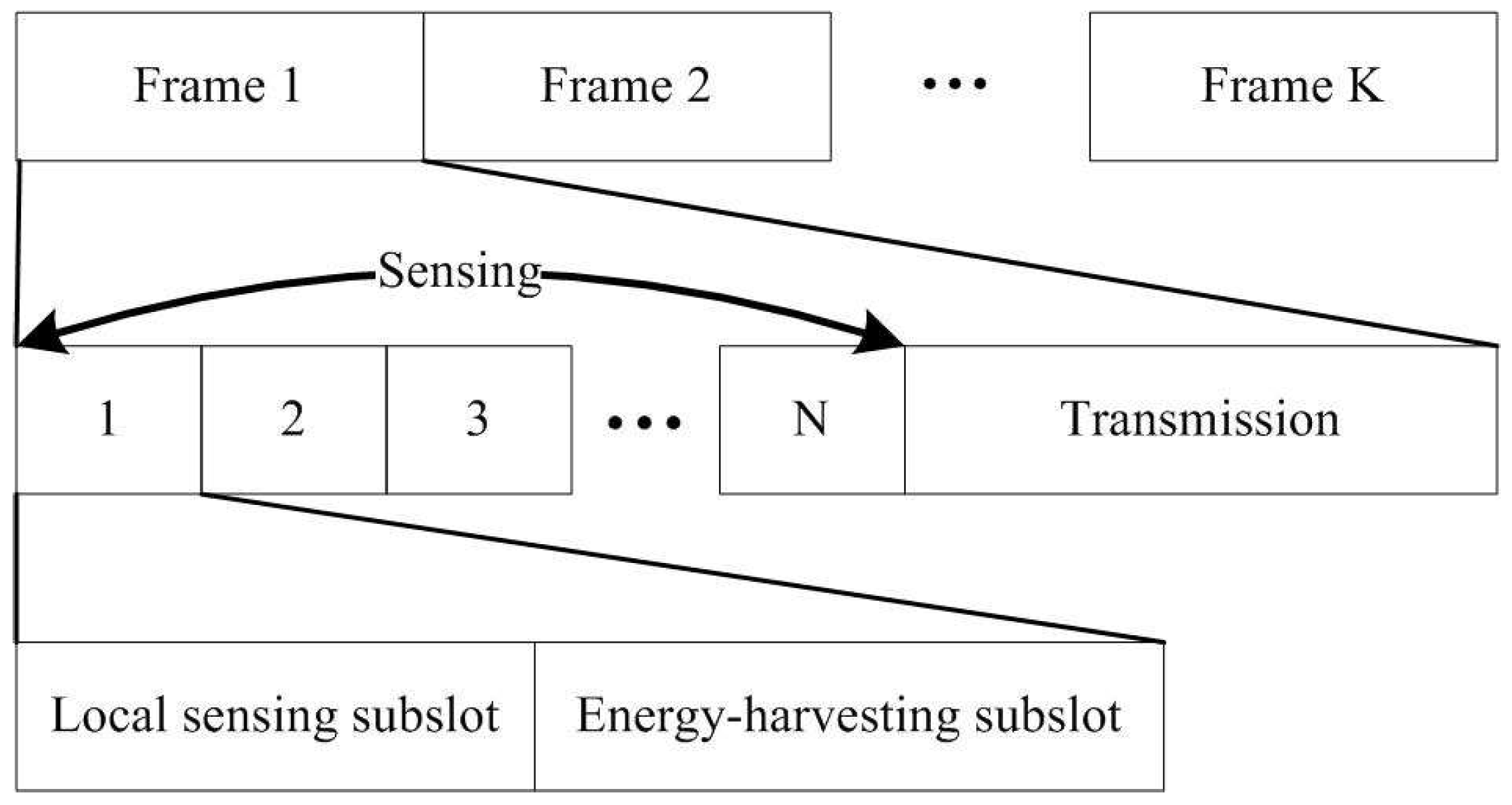
- The paper firstly combines spectrum sensing and energy harvesting, the sensing duration is divided into multiple sensing slots consisted of one local-sensing subslot for energy sensing of the PU and one energy-harvesting subslot for harvesting the RF energy of the PU signal. If the presence of the PU is detected in the local-sensing subslot, the SU will harvest energy in the energy-harvesting subslot. Then the harvested energy is used to supply the spectrum sensing in the following sensing slot.
- The paper has proposed a jointly optimal allocation of sensing time and harvesting time to maximize the achievable throughput of the SU under the constraints that the target probabilities of detection and false alarm are both guaranteed and the harvested energy may supply the spectrum sensing. A joint optimization algorithm based on binary searching and alternating direction optimization (ADO) has been proposed to achieve the optimal solutions to the proposed optimization problem.
2. Energy Sensing and Harvesting
2.1. Energy Sensing
2.2. Energy Harvesting
3. System Model
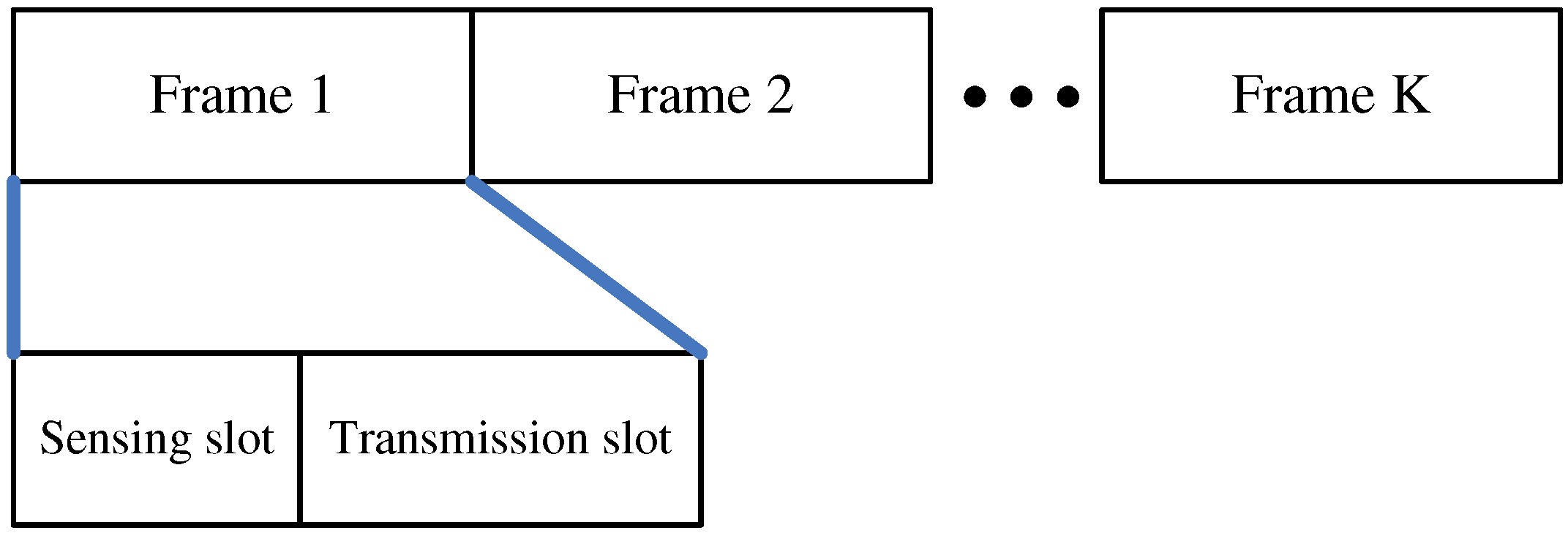
3.1. Traditional Model
- When the PU is really absent in probability of and no false alarm is generated by the SU in probability of , the SU may access the spectrum effectively in probability of ;
- When the PU is really present in probability of but not detected by the SU in probability of , the SU may also access the spectrum but cause harmful interference to the PU in probability of .
3.2. Proposed Model
4. Model Optimization
| Algorithm 1: Searching algorithm of for maximizing |
| (1) Initialize , and estimation error ; |
| (2) While () do: |
| (3) Set ; |
| (4) If (): set ; |
| (5) Else if (): set ; |
| (6) End if; |
| (7) End while; |
| (8) Output . |
| Algorithm 2: Joint optimization algorithm |
| (1) initialize , , where and estimation error ; |
| (2) with given , calculate according to Algorithm 1 and Equation (19); |
| (3) set ; |
| (4) with given , calculate ; |
| (5) set and ; |
| (6) repeat (2)-(5) until both and are satisfied. |
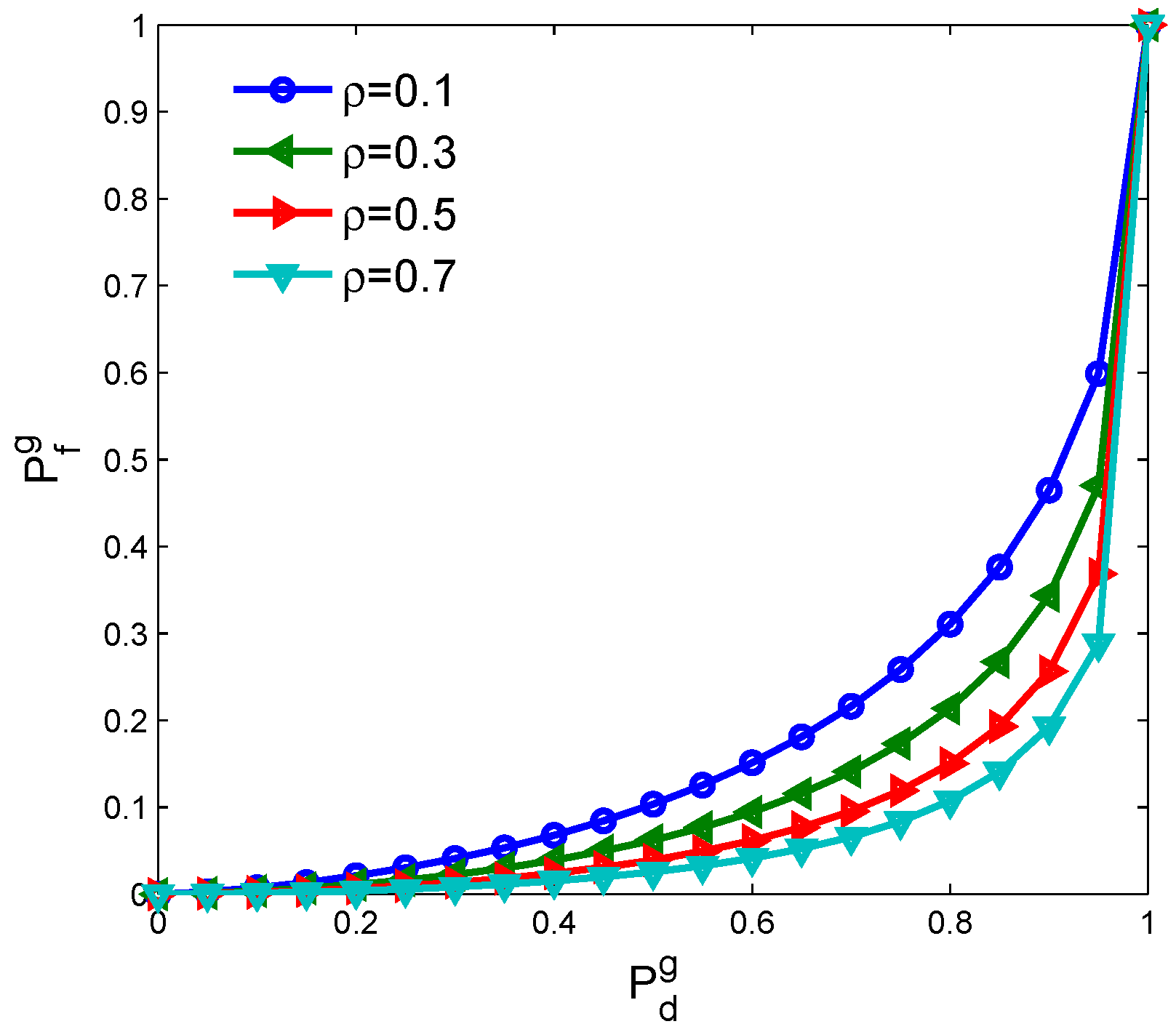
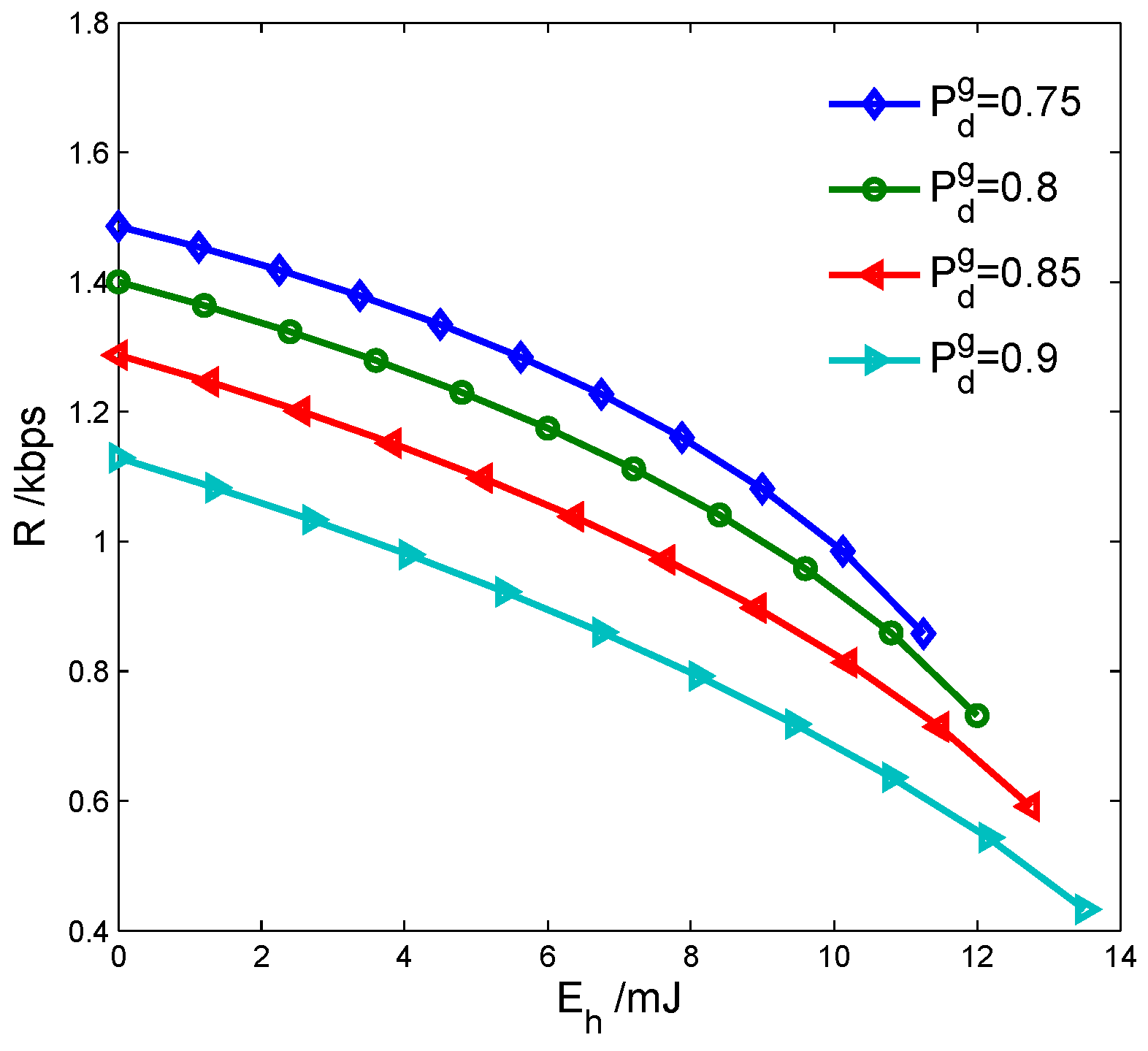
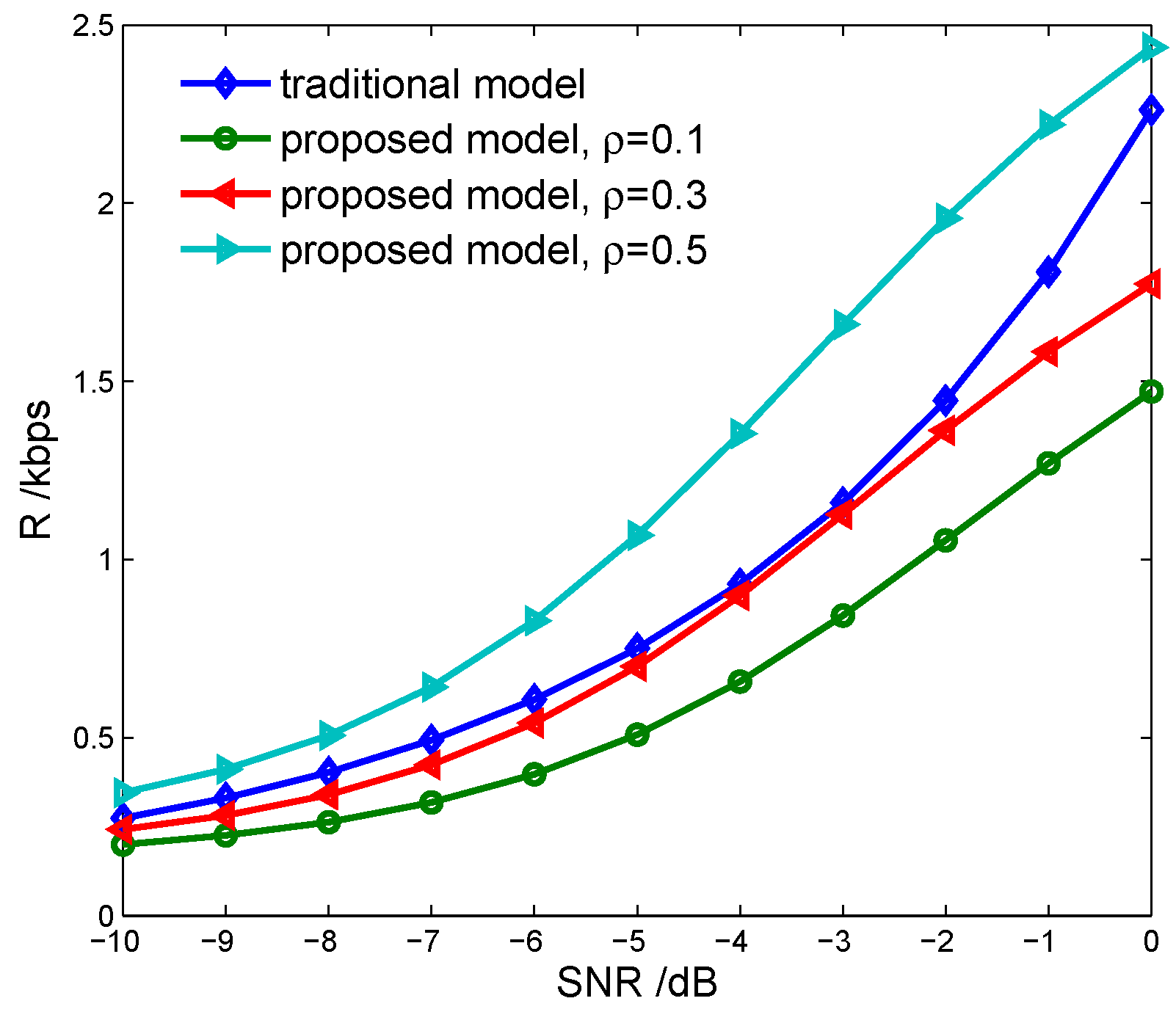
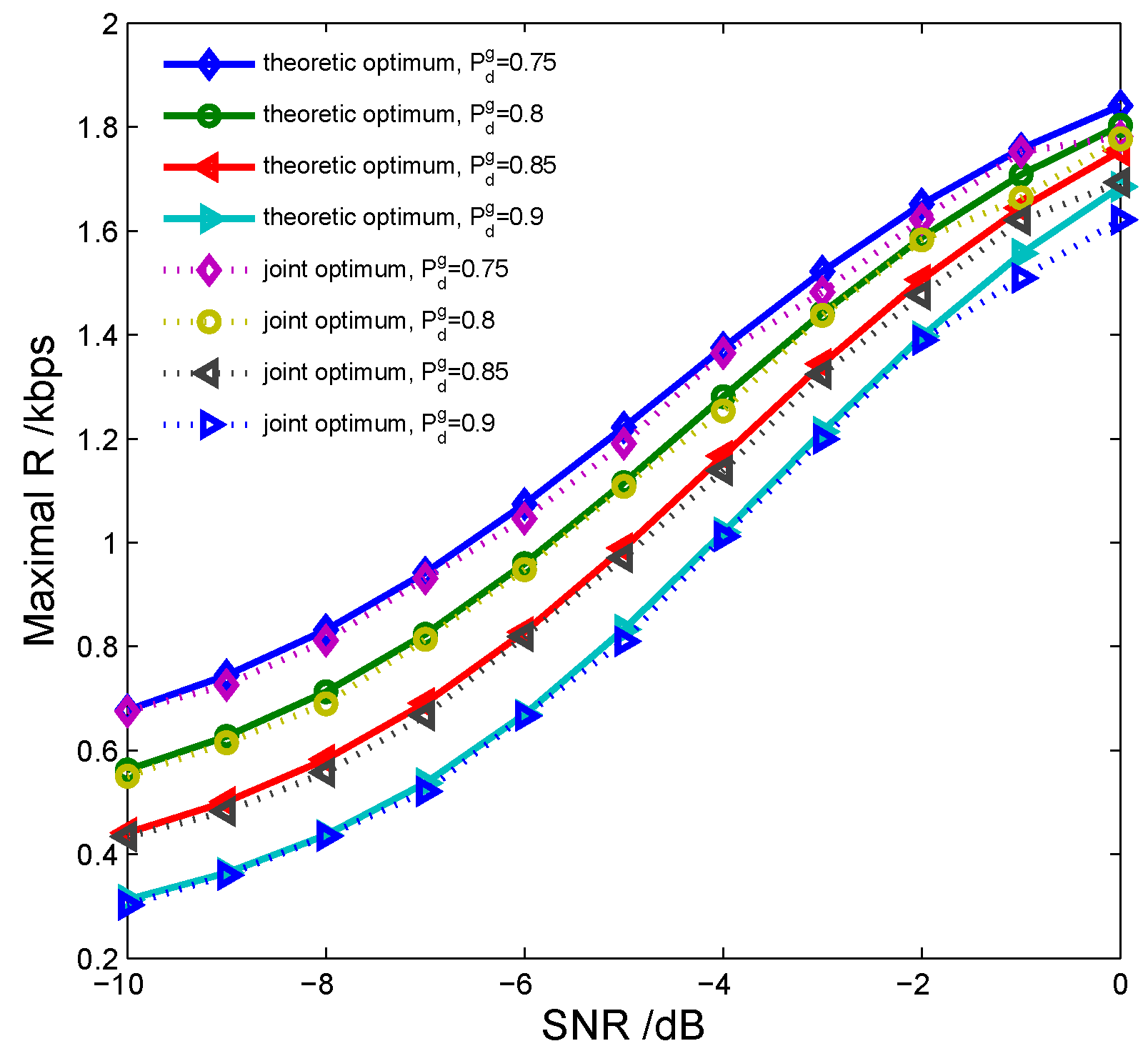
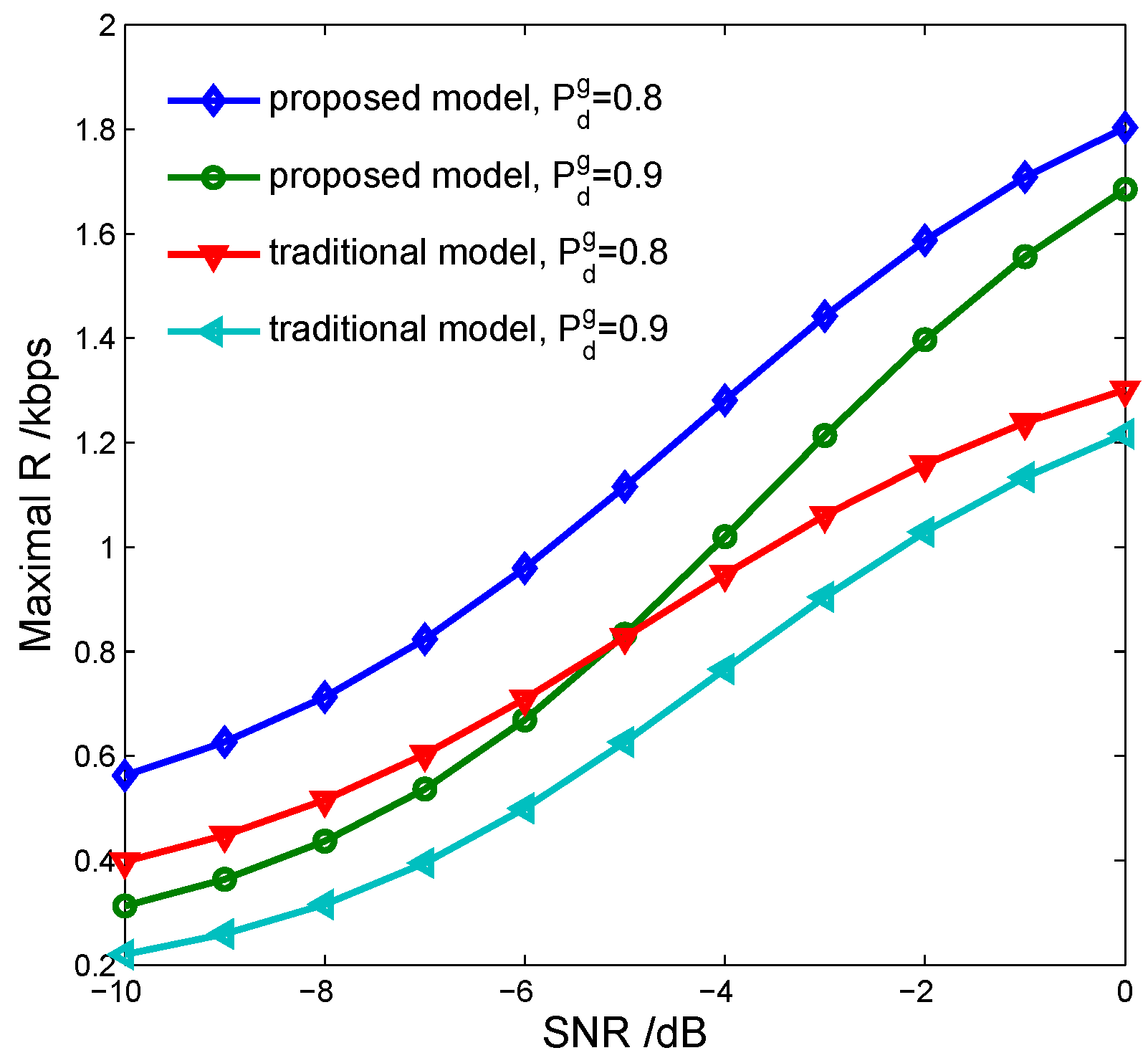
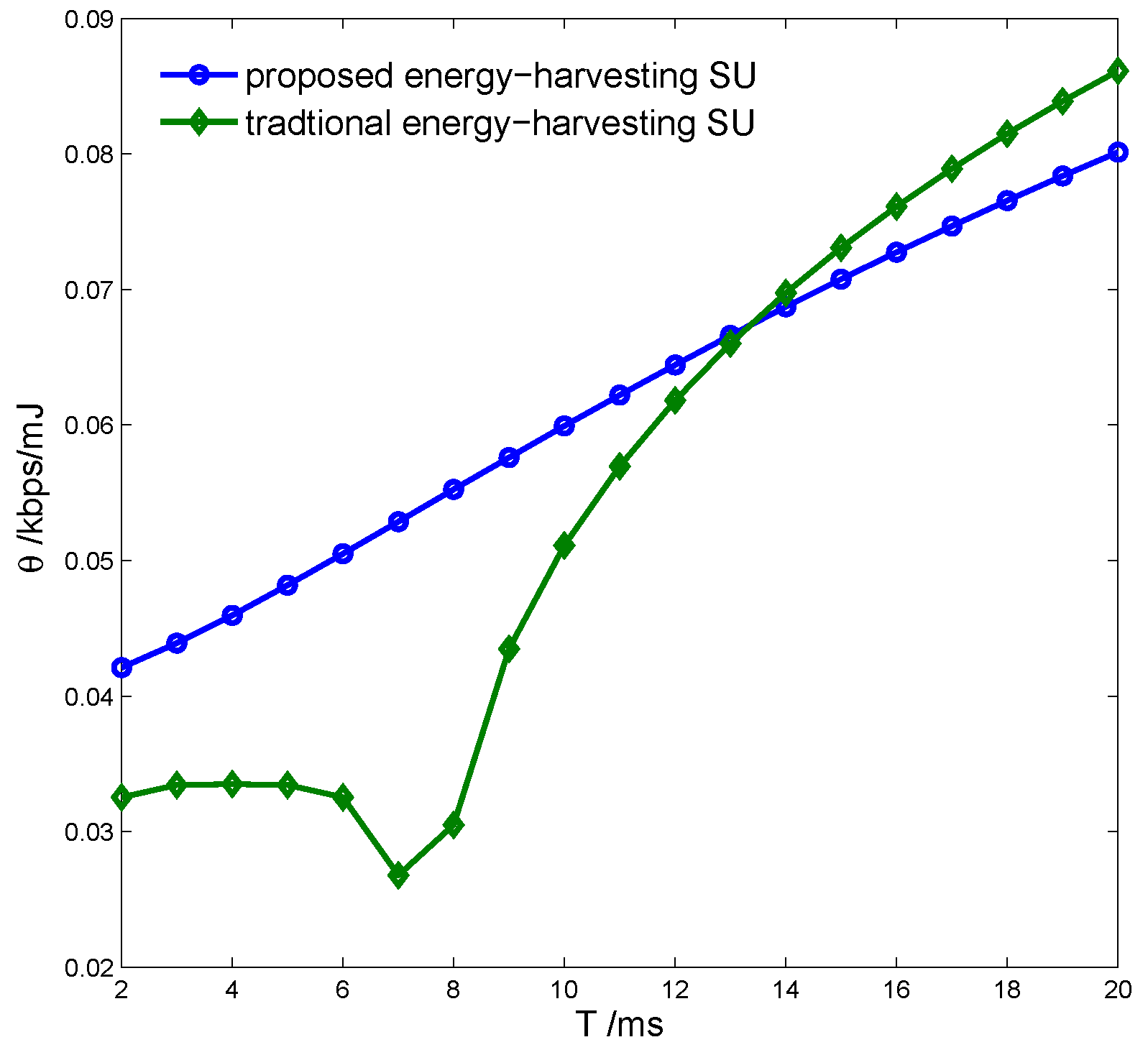
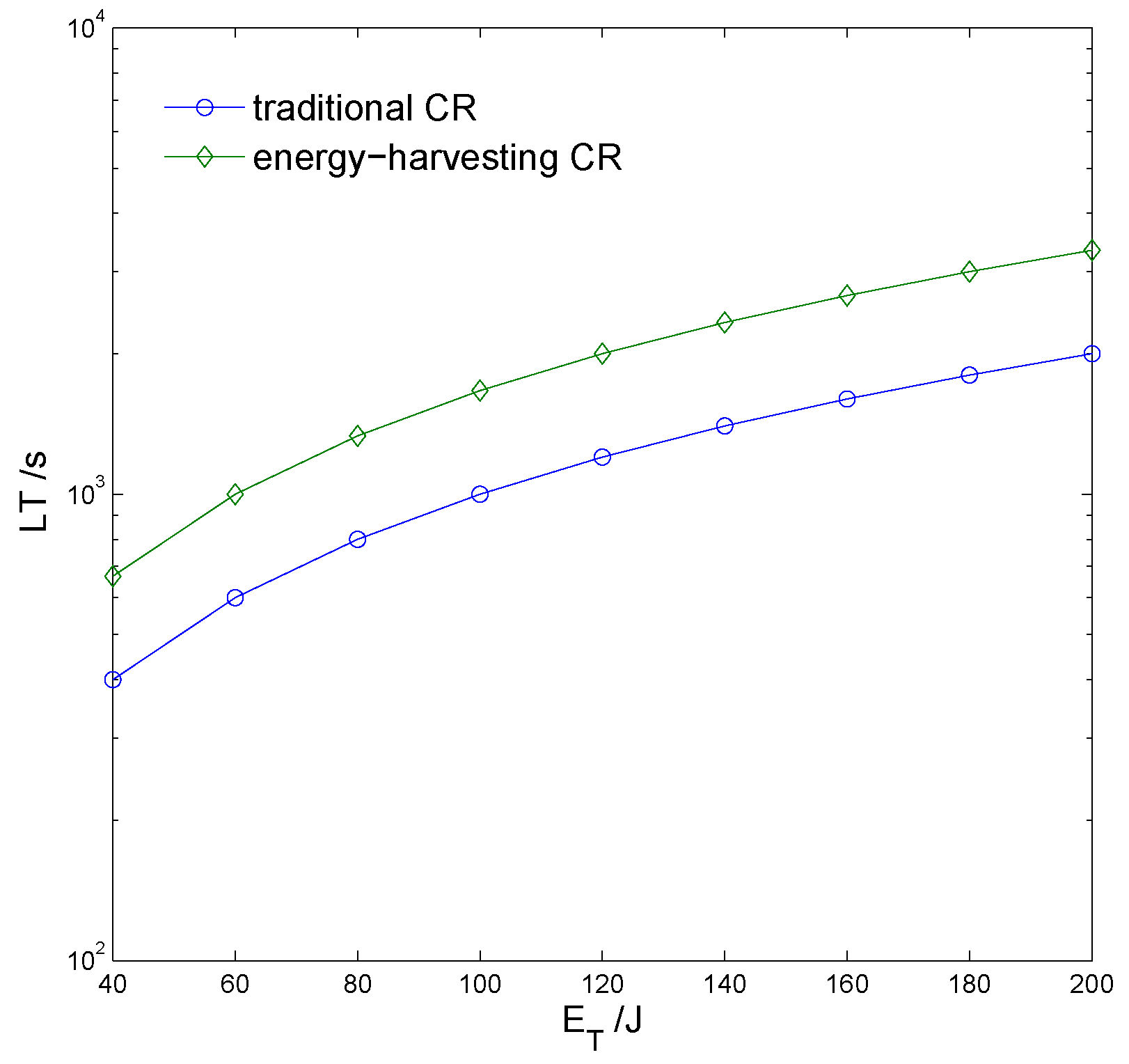
5. Simulations and Discussion
6. Conclusions
- there exists an optimal sensing time that maximizes the average achievable throughput of the SU while the sensing performance is guaranteed;
- the maximal throughput of the SU can be obtained only if the detection probability acquires its lower limit and the harvested energy appropriately supplies spectrum sensing;
- the proposed model can improve the maximal throughput of the SU obviously through using the harvested energy to compensate the energy consumption of spectrum sensing.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hamdaoui, B. Adaptive spectrum assessment for opportunistic access in cognitive radio networks. IEEE Trans. Wirel. Commun. 2009, 8, 922–930. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Liu, X.; Tan, X. Optimization algorithm of periodical cooperative spectrum sensing in cognitive radio. Int. J. Commun. Syst. 2014, 27, 705–720. [Google Scholar] [CrossRef]
- Sun, H.; Nallanathan, A.; Wang, C.; Chen, Y. Wideband spectrum sensing for cognitive radio networks: A survey. IEEE Wirel. Commun. 2013, 20, 74–81. [Google Scholar]
- Liu, X.; Bi, G.; Jia, M.; Guan, Y.L.; Zhong, W.; Lin, R. Joint optimization of sensing threshold and transmission power in wideband cognitive radio. Radio Sci. 2013, 48, 359–370. [Google Scholar]
- Shen, J.; Liu, S.; Wang, Y.; Xie, G.; Rashvand, H.F.; Liu, Y. Robust energy detection in cognitive radio. IET Commun. 2009, 3, 1016–1023. [Google Scholar] [CrossRef]
- Tang, L.; Chen, Y.; Hines, E.L.; Alouini, M.S. Effect of primary user traffic on sensing-throughput tradeoff for cognitive radios. IEEE Trans. Wirel. Commun. 2011, 10, 1063–1068. [Google Scholar] [CrossRef]
- Liang, Y.; Zeng, Y.; Peh, E.C.Y.; Hoang, A.T. Sensing-throughput tradeoff for cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 7, 1326–1337. [Google Scholar] [CrossRef]
- Liu, X. A new sensing-throughput tradeoff scheme in cooperative multiband cognitive radio network. Int. J. Netw. Manag. 2014, 24, 200–217. [Google Scholar] [CrossRef]
- Subhankar, C.; Santi, P.M.; Tamaghna, A. Energy efficient cognitive radio system for joint spectrum sensing and data transmission. IEEE J. Emerg. Sel. Top. Circuits Syst. 2014, 4, 292–300. [Google Scholar]
- Valenta, C.R.; Durgin, G.D. Harvesting wireless power: survey of energy-harvester conversion efficiency in farfield, wireless power transfer systems. IEEE Microw. Mag. 2014, 15, 108–120. [Google Scholar]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless information transfer with opportunistic energy harvesting. IEEE Trans. Wirel. Commun. 2013, 3, 345–362. [Google Scholar]
- Ren, Y.; Li, M.; Chang, K. 35 GHz rectifying antenna for wireless power transmission. Electron. Lett. 2007, 43, 602–603. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, R.; Huang, K. Opportunistic wireless energy harvesting in cognitive radio networks. IEEE Trans. Wirel. Commun. 2013, 12, 4788–4799. [Google Scholar] [CrossRef]
- Ding, T.H.; Niyato, D.; Wang, P.; Kim, D.I. Opportunistic channel access and RF energy harvesting in cognitive radio networks. IEEE J. Sel. Areas Commun. 2014, 32, 2039–2052. [Google Scholar]
- Liu, X.; Chen, K.; Yan, J.; Na, Z.Y. Optimal energy harvesting-based weighed cooperative spectrum sensing in cognitive radio network. Mobile Netw. Appl. 2016, 3, 1–12. [Google Scholar] [CrossRef]
- Liu, X.; Jia, M.; Gu, X.; Tan, X. Optimal periodic cooperative spectrum sensing based on weight fusion in cognitive radio networks. Sensors 2013, 13, 5251–5272. [Google Scholar] [CrossRef] [PubMed]
- Gou, K.; Sun, L.; LI, Y.; Jia, S. Channel-aware and queue-aware joint-layer resource optimization for cognitive radio networks. Sci. China Inf. Sci. 2010, 53, 2576–2583. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Na, Z.; Jia, M.; Gu, X.; Li, X. Multislot Simultaneous Spectrum Sensing and Energy Harvesting in Cognitive Radio. Energies 2016, 9, 568. https://doi.org/10.3390/en9070568
Liu X, Na Z, Jia M, Gu X, Li X. Multislot Simultaneous Spectrum Sensing and Energy Harvesting in Cognitive Radio. Energies. 2016; 9(7):568. https://doi.org/10.3390/en9070568
Chicago/Turabian StyleLiu, Xin, Zhenyu Na, Min Jia, Xuemai Gu, and Xiaotong Li. 2016. "Multislot Simultaneous Spectrum Sensing and Energy Harvesting in Cognitive Radio" Energies 9, no. 7: 568. https://doi.org/10.3390/en9070568
APA StyleLiu, X., Na, Z., Jia, M., Gu, X., & Li, X. (2016). Multislot Simultaneous Spectrum Sensing and Energy Harvesting in Cognitive Radio. Energies, 9(7), 568. https://doi.org/10.3390/en9070568