A New Fault Diagnosis Algorithm for PMSG Wind Turbine Power Converters under Variable Wind Speed Conditions
Abstract
:1. Introduction
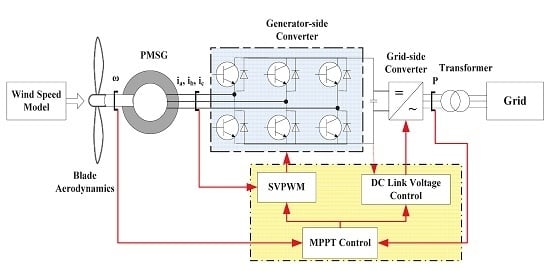
2. PMSG Wind Turbine System Simulation
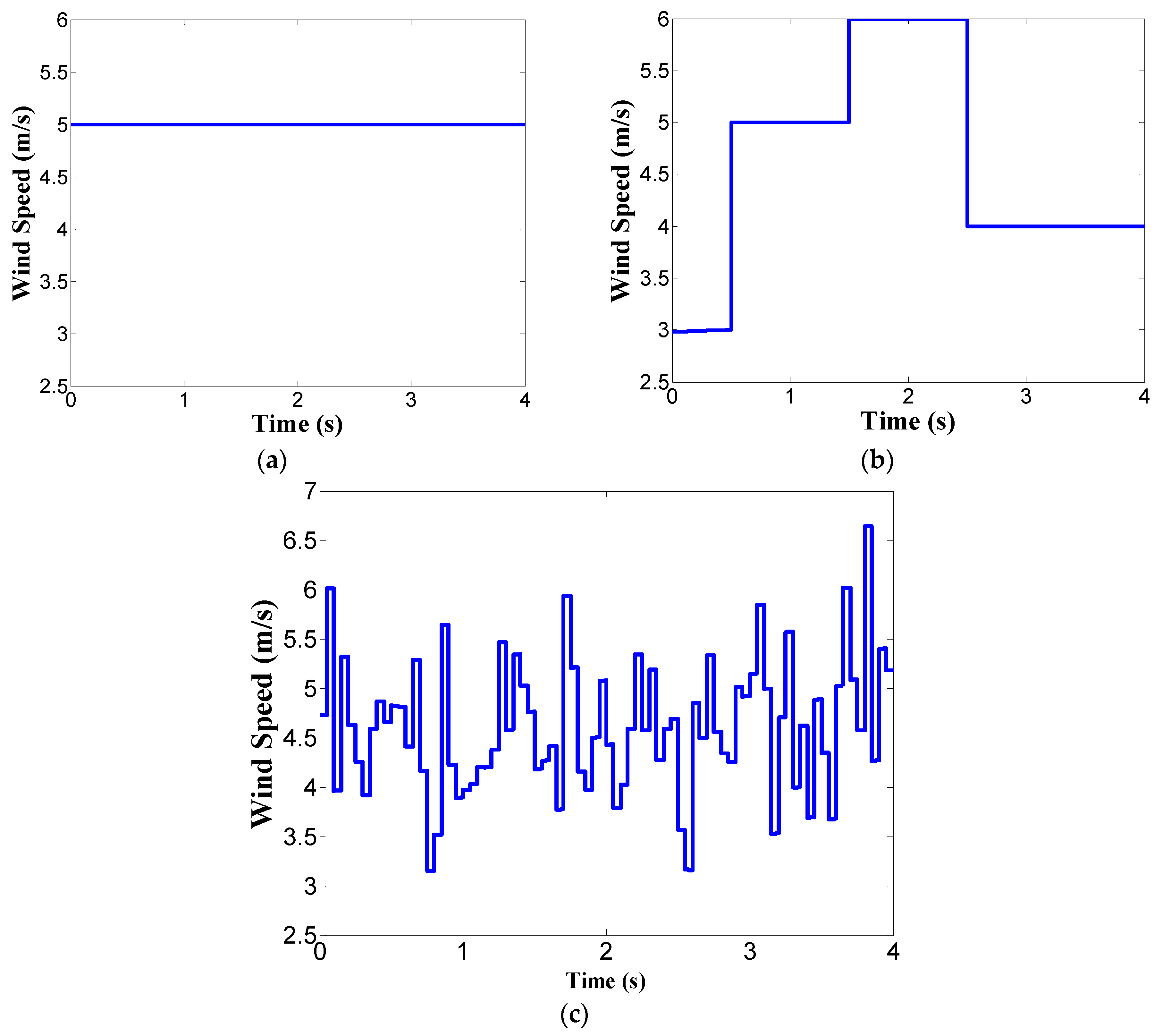
2.1. Wind Speed Simulation
2.2. PMSG Wind Turbine Simulation
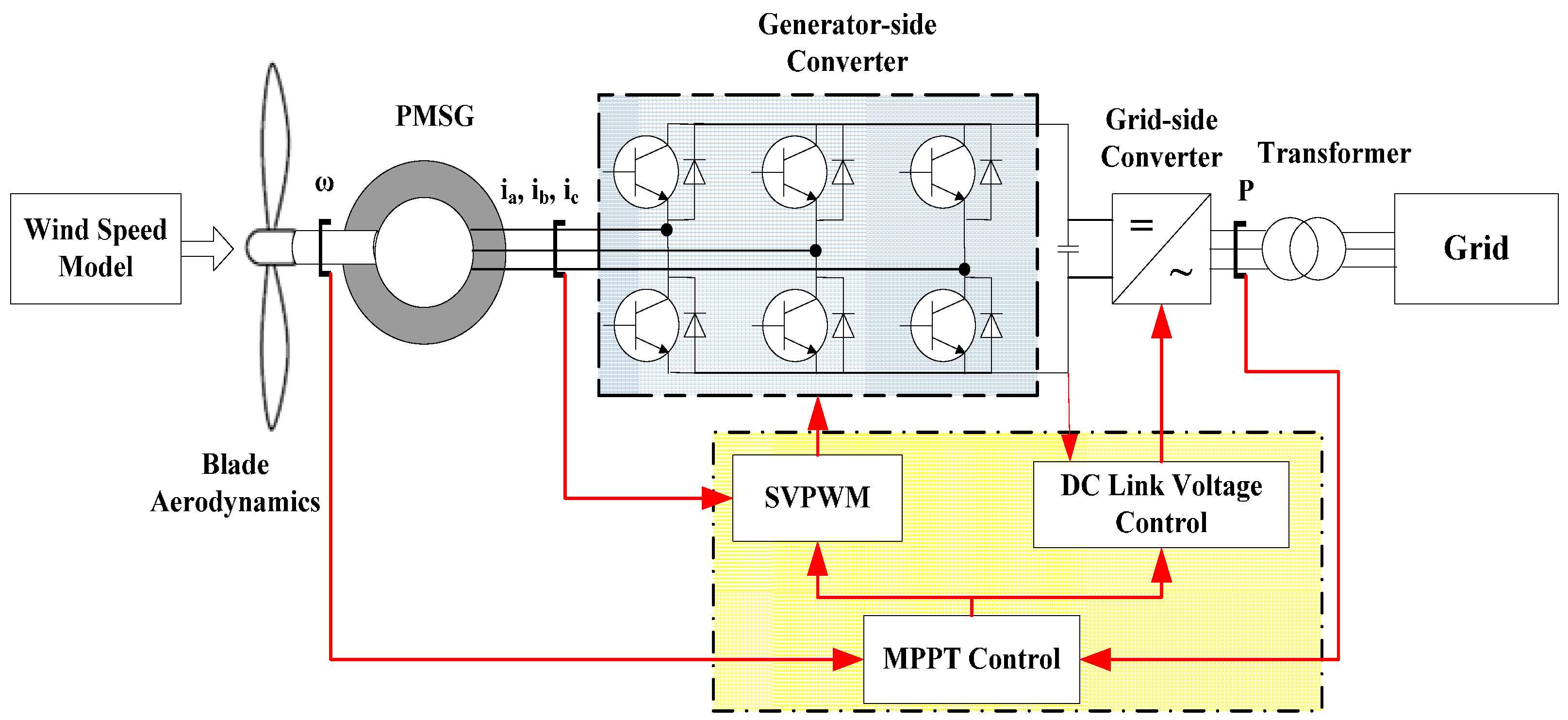
2.3. PMSG Control Logic
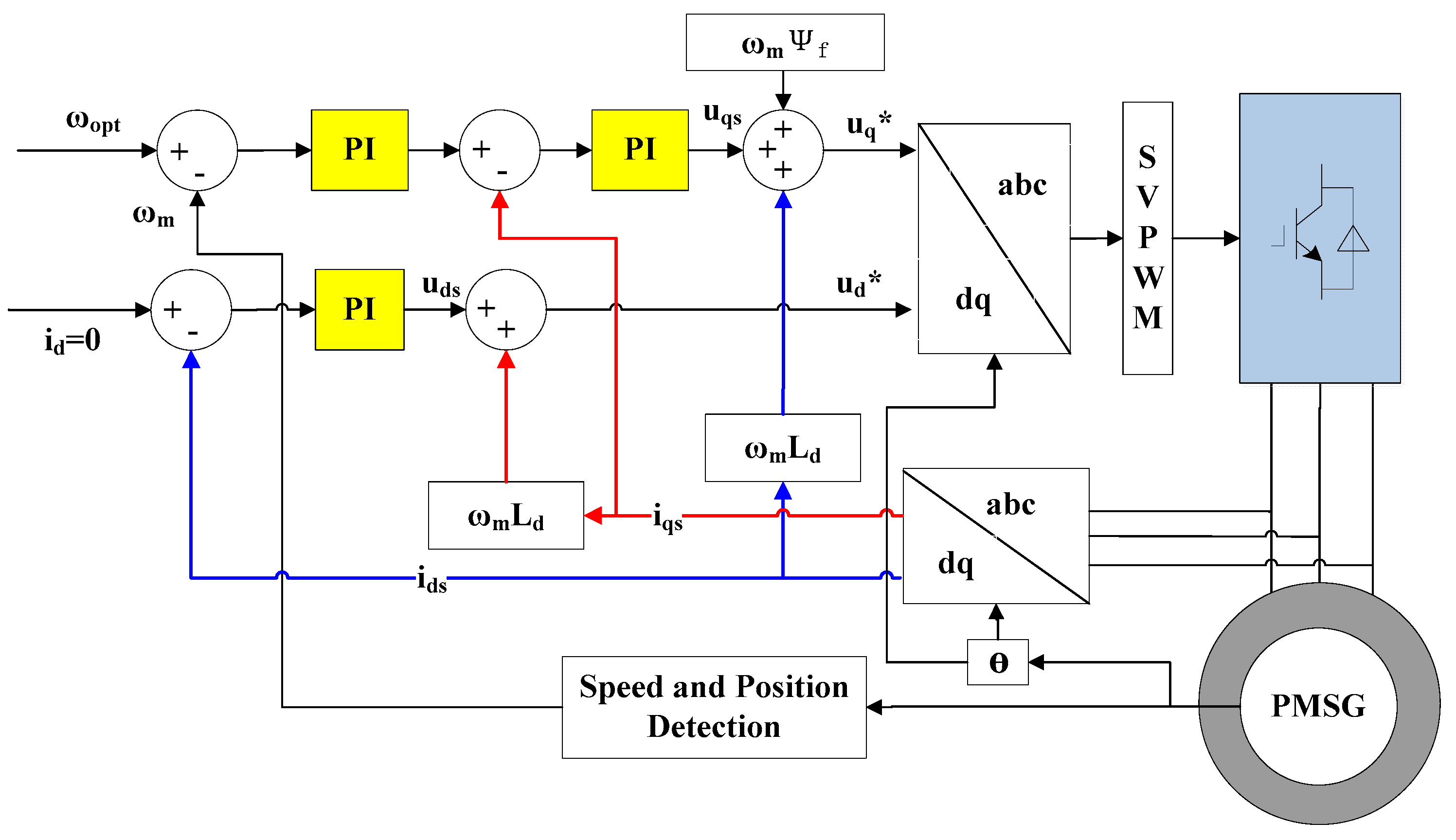
2.4. Generator-Side Converter SVPWM Control Strategy
3. Fault Diagnostic Method
3.1. Direct Current Detection Method
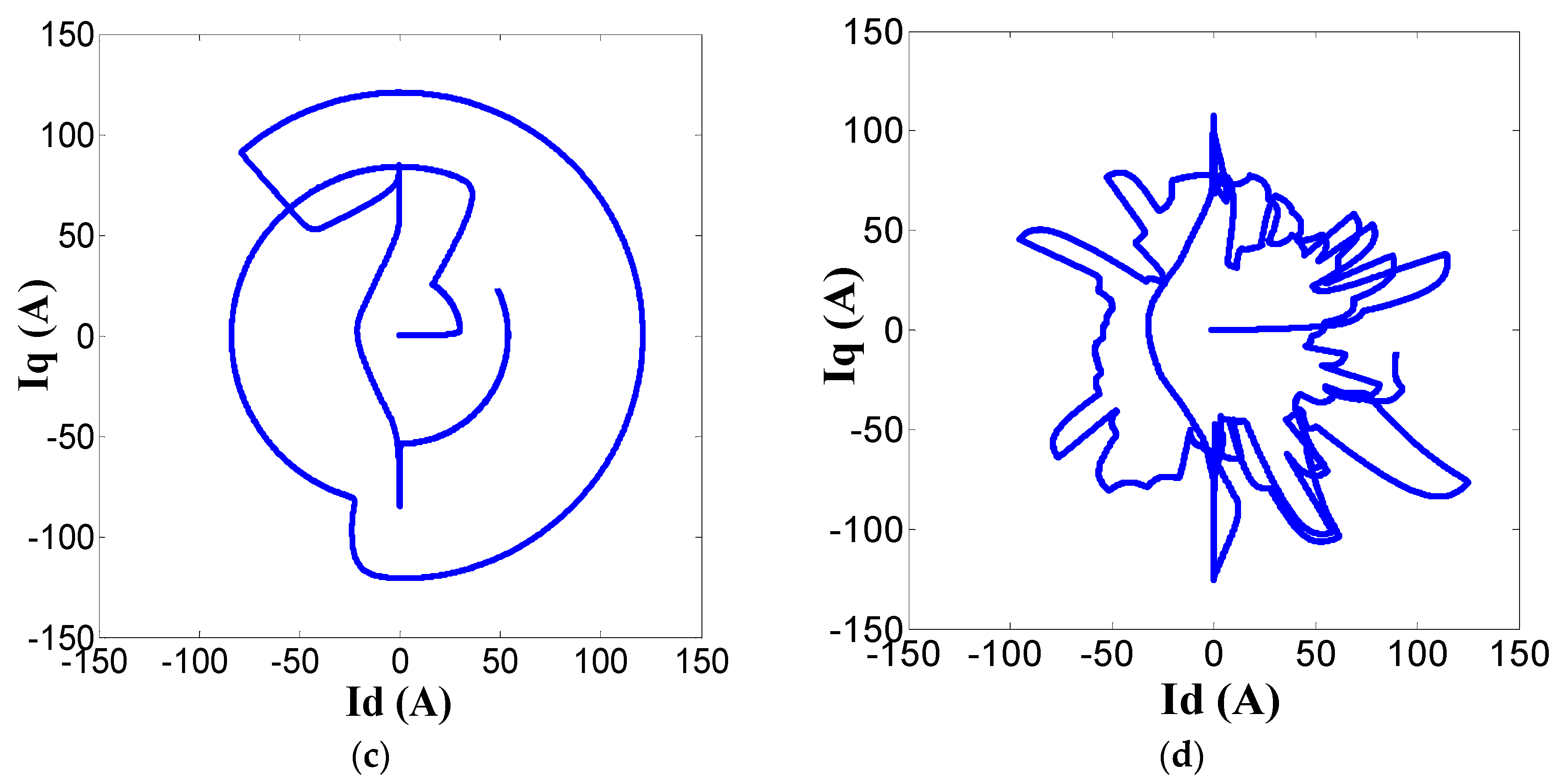
3.2. Current Vector/Trajectory Pattern Recognition
3.3. Comparison of the Two Diagnostic Methods
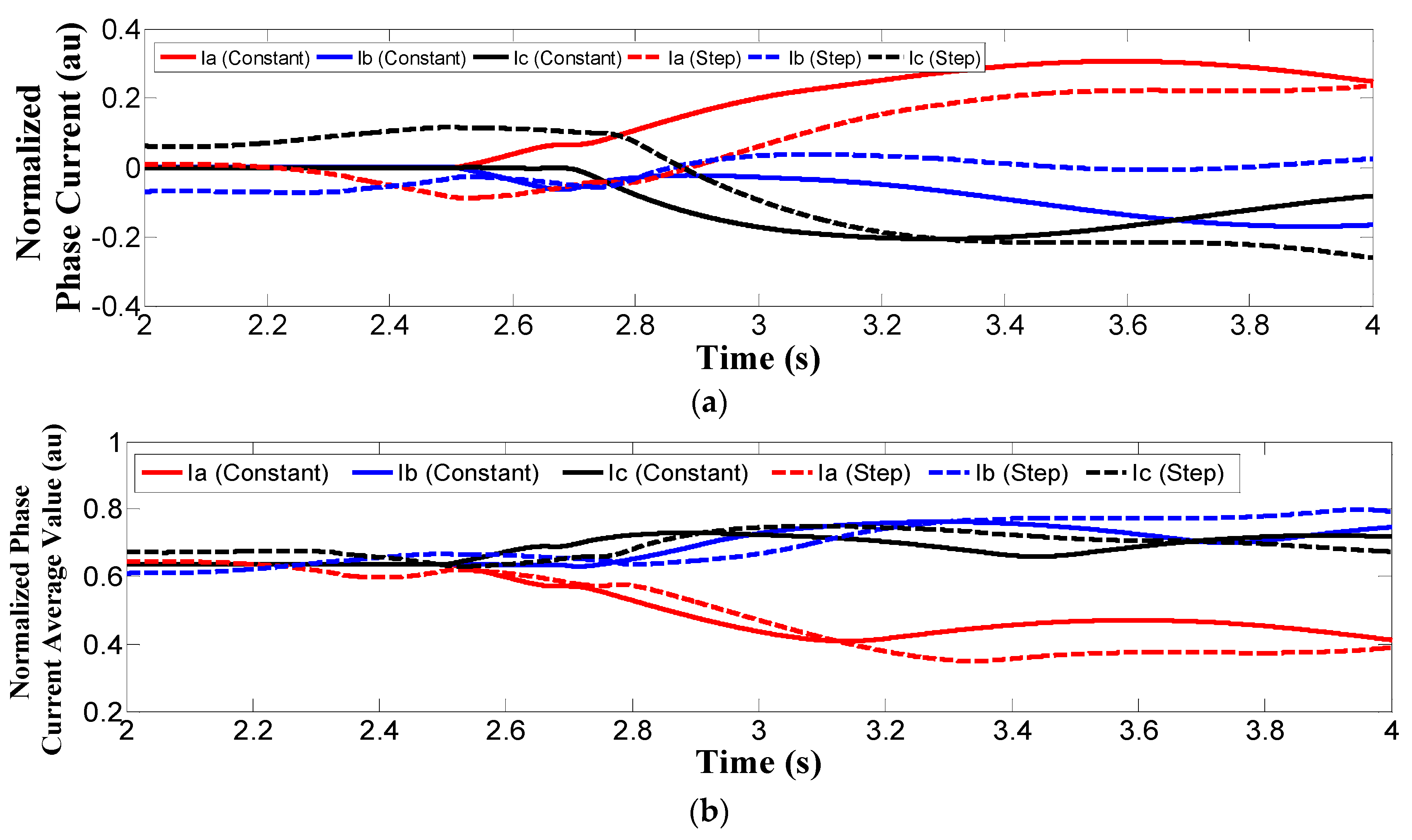
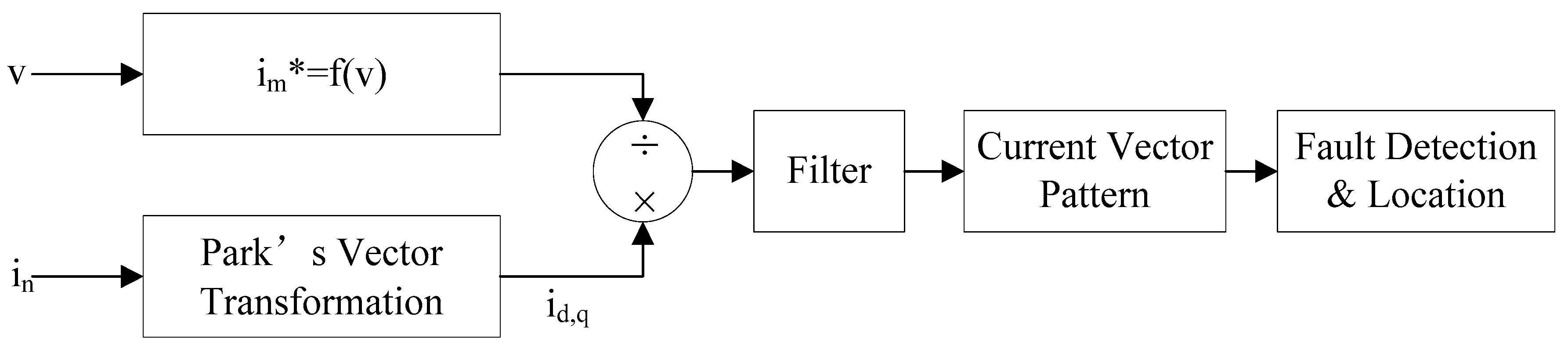
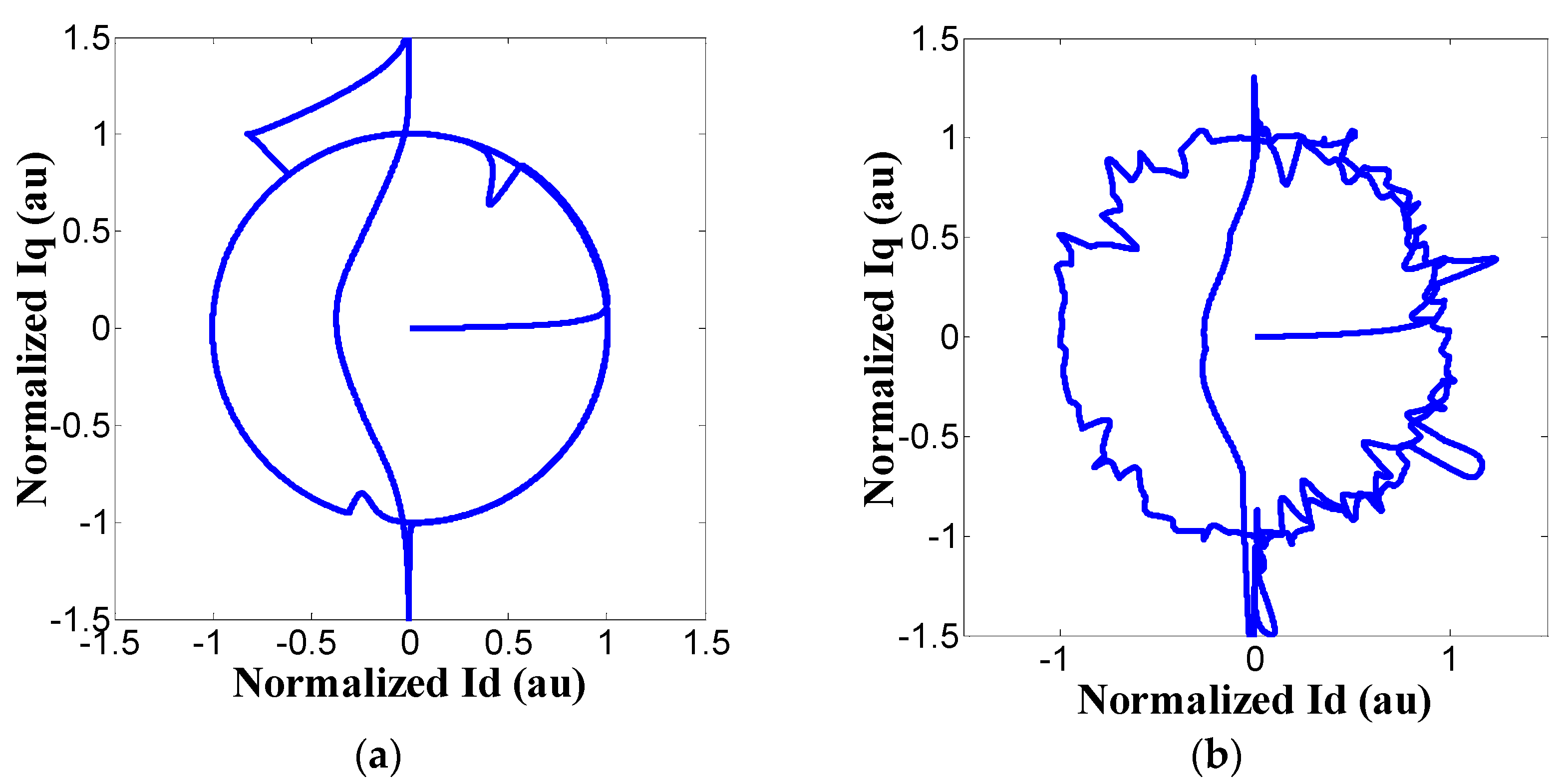
3.4. Wind Speed Based Normalized Current Trajectory Detection
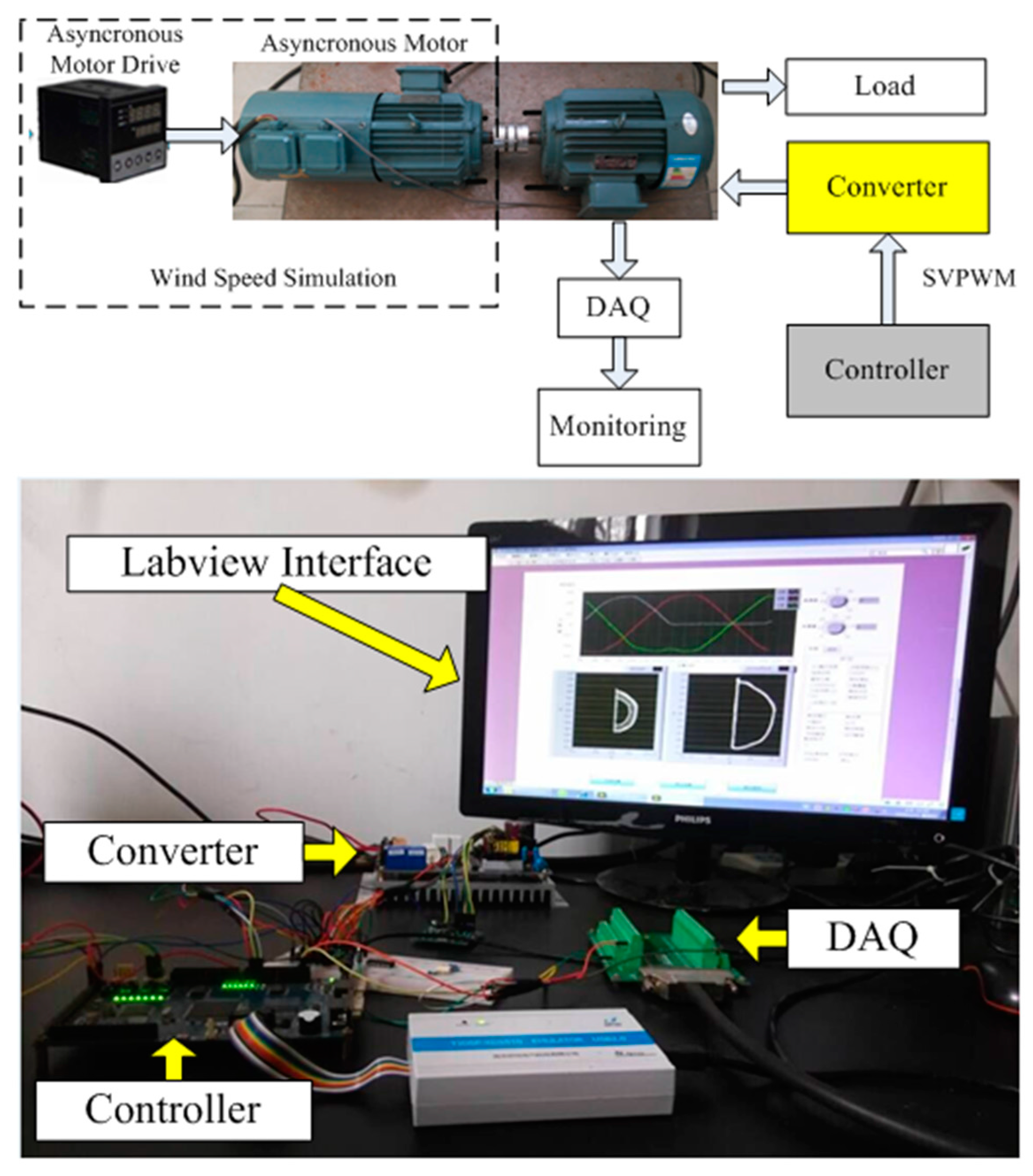
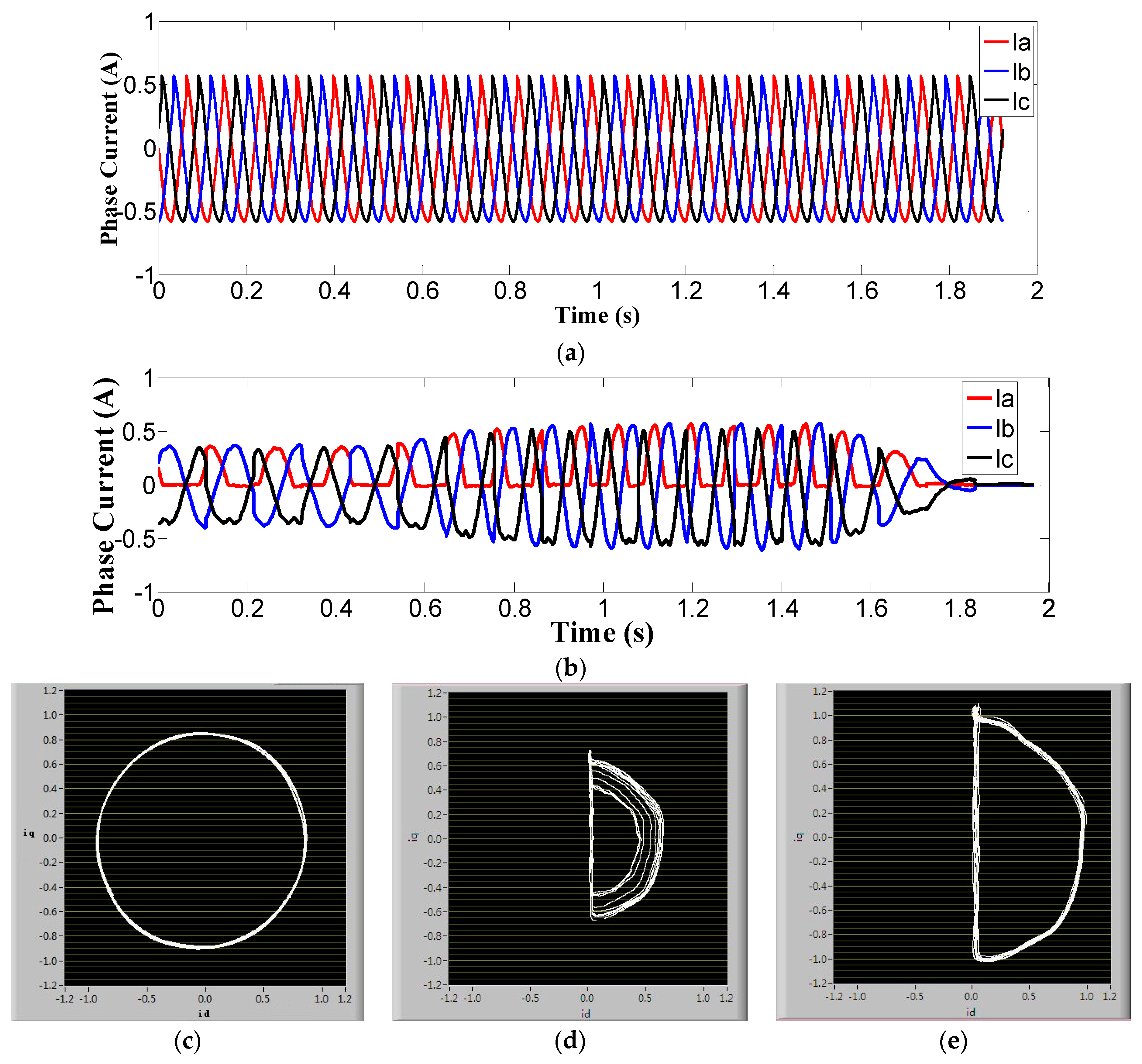
4. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, Z.; Dou, X.; Chu, J.; Hu, M. Operation and control of a direct-driven PMSG-based wind turbine system with an auxiliary parallel grid-side converter. Energies 2013, 6, 3405–3421. [Google Scholar] [CrossRef]
- Spinato, F.; Tavner, P.J.; Van Bussel, G.J.; Koutoulakos, E. Reliability of wind turbine subassemblies. IET Renew. Power Gener. 2009, 3, 387–401. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A survey on wind turbine condition monitoring and fault diagnosis—Part I: Components and subsystems. IEEE Trans. Ind. Electron. 2015, 62, 6536–6545. [Google Scholar] [CrossRef]
- Song, Y.; Wang, B. Survey on reliability of power electronic systems. IEEE Trans. Power Electron. 2013, 28, 591–604. [Google Scholar] [CrossRef]
- Choi, U.M.; Blaabjerg, F.; Lee, K.B. Study and handling methods of power IGBT module failures in power electronic converter systems. IEEE Trans. Power Electron. 2015, 30, 2517–2533. [Google Scholar] [CrossRef]
- Estima, J.O.; Freire, N.M.A.; Cardoso, A.J.M. Recent advances in fault diagnosis by Park’s vector approach. In Proceedings of the IEEE WEMDCD, Paris, France, 11–12 March 2013; pp. 279–288.
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Capolino, G.A. Advances in electrical machine power electronic, and drive condition monitoring and fault detection: State of the art. IEEE Trans. Ind. Electron. 2015, 62, 1746–1759. [Google Scholar] [CrossRef]
- Mendes, A.M.S.; Cardoso, A.J.M.; Saraiva, E.S. Voltage source inverter fault diagnosis in variable speed AC drives, by Park’s vector approach. In Proceedings of the Seventh International Conference on Power Electronics and Variable Speed Drives, London, UK, 21–23 September 1998; Volume 456, pp. 538–543.
- Im, W.S.; Kim, J.M.; Lee, D.C.; Lee, K.B. Diagnosis and fault-tolerant control of three-phase AC–DC PWM converter systems. IEEE Trans. Ind. Appl. 2013, 49, 1539–1547. [Google Scholar] [CrossRef]
- Toubakh, H.; Sayed-Mouchaweh, M. Hybrid dynamic classifier for drift-like fault diagnosis in a class of hybrid dynamic systems: Application to wind turbine converters. Neurocomputing 2016, 171, 1496–1516. [Google Scholar] [CrossRef]
- Shahbazi, M.; Saadate, S.; Poure, P.; Zolghadri, M. Open-circuit switch fault tolerant wind energy conversion system based on six/five-leg reconfigurable converter. Electr. Power Syst. Res. 2016, 137, 104–112. [Google Scholar] [CrossRef] [Green Version]
- Das, P.S.; Kim, K.H. Voltage based online fault detection and faulty switch identification under multiple open switches in grid connected wind power converters. Int. J. Control Autom. 2014, 7, 419–434. [Google Scholar] [CrossRef]
- Freire, N.M.A.; Estima, J.O.; Cardoso, A.J.M. Open-circuit fault diagnosis in PMSG drives for wind turbine applications. IEEE Trans. Ind. Electron. 2013, 60, 3957–3967. [Google Scholar] [CrossRef]
- Ko, Y.J. Fault diagnosis of a three-parallel voltage-source converter for a high-power wind turbine. IET Power Electron. 2012, 3, 1058–1067. [Google Scholar] [CrossRef]
- Slootweg, J.G.; de Haan, S.W.H.; Polinder, H.; Klingl, W.L. General model for representing variable speed wind turbines in power system dynamics simulation. IEEE Trans. Power Syst. 2003, 18, 144–151. [Google Scholar] [CrossRef]
- Qiu, Y.; Sun, J.; Feng, Y. Wind turbine fault simulation. In Proceedings of the 2nd IET Renewable Power Generation Conference, Beijing, China, 9–11 September 2013.
- Sun, T.; Chen, Z.; Blaabjerg, F. Transient stability of DFIG wind turbines at an external short-circuit fault. Wind Energy 2005, 8, 345–360. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Liserre, M.; Ma, K. Power electronics converters for wind turbine systems. IEEE Trans. Ind. Appl. 2012, 48, 708–719. [Google Scholar] [CrossRef]
- Jain, B.; Jain, S.; Nema, R.K. Control strategies of grid interfaced wind energy conversion system: An overview. Renew. Sustain. Energy Rev. 2015, 47, 983–996. [Google Scholar] [CrossRef]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Rated Power | 30 kW |
| Cut in/out Wind Speed | 3 m/s & 25 m/s |
| Rated Wind Speed | 7.2 m/s |
| Power Control Mode | Pitch control |
| Stator Resistance (ohm) | 0.362 |
| Inductance L (H) | 0.0015 |
| Flux ψ (Wb) | 2.34 |
| Pole Pairs P | 10 |
| Damping F (N·M·S) | 0.000139 |
| Inertia J (kg·m2) | 1.2 |
| Asynchronous Motor | |
| Rated Power (kW) | 4 |
| Rated Frequency (Hz) | 50 |
| Rated Voltage and Current | 380 V & 7.9 A |
| Rotational Speed (rpm) | 0–1460 |
| Control Mode | V/F |
| PMSG | |
| Rated Power (kW) | 3 |
| Rated Frequency (Hz) | 50 |
| Rated Voltage and Current | 380 V & 5 A |
| Rotational Speed (rpm) | 0–1500 |
| Converter (Mitsubishi IPM) | |
| Rated Voltage and Current | 600 V & 50 A |
| Rated Power | 3.7 kW/220 VAC |
| Load | |
| Power (kW) | 3kW |
| Resistance (ohm) | 100 |
| Methods | Constant Wind | Step Wind | Turbulent Wind |
|---|---|---|---|
| ENCAAV | √ | × | × |
| CVTPR | √ | × | × |
| WSBNCT | √ | √ | √ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Jiang, H.; Feng, Y.; Cao, M.; Zhao, Y.; Li, D. A New Fault Diagnosis Algorithm for PMSG Wind Turbine Power Converters under Variable Wind Speed Conditions. Energies 2016, 9, 548. https://doi.org/10.3390/en9070548
Qiu Y, Jiang H, Feng Y, Cao M, Zhao Y, Li D. A New Fault Diagnosis Algorithm for PMSG Wind Turbine Power Converters under Variable Wind Speed Conditions. Energies. 2016; 9(7):548. https://doi.org/10.3390/en9070548
Chicago/Turabian StyleQiu, Yingning, Hongxin Jiang, Yanhui Feng, Mengnan Cao, Yong Zhao, and Dan Li. 2016. "A New Fault Diagnosis Algorithm for PMSG Wind Turbine Power Converters under Variable Wind Speed Conditions" Energies 9, no. 7: 548. https://doi.org/10.3390/en9070548
APA StyleQiu, Y., Jiang, H., Feng, Y., Cao, M., Zhao, Y., & Li, D. (2016). A New Fault Diagnosis Algorithm for PMSG Wind Turbine Power Converters under Variable Wind Speed Conditions. Energies, 9(7), 548. https://doi.org/10.3390/en9070548