Quantification and Mitigation of Unfairness in Active Power Curtailment of Rooftop Photovoltaic Systems Using Sensitivity Based Coordinated Control
Abstract
:1. Introduction
2. Problem Formulation
Voltage Sensitivity Estimation
3. Formulation of Key Performance Indices
3.1. Total Curtailed Energy
3.2. Unfairness in Active Power Curtailment
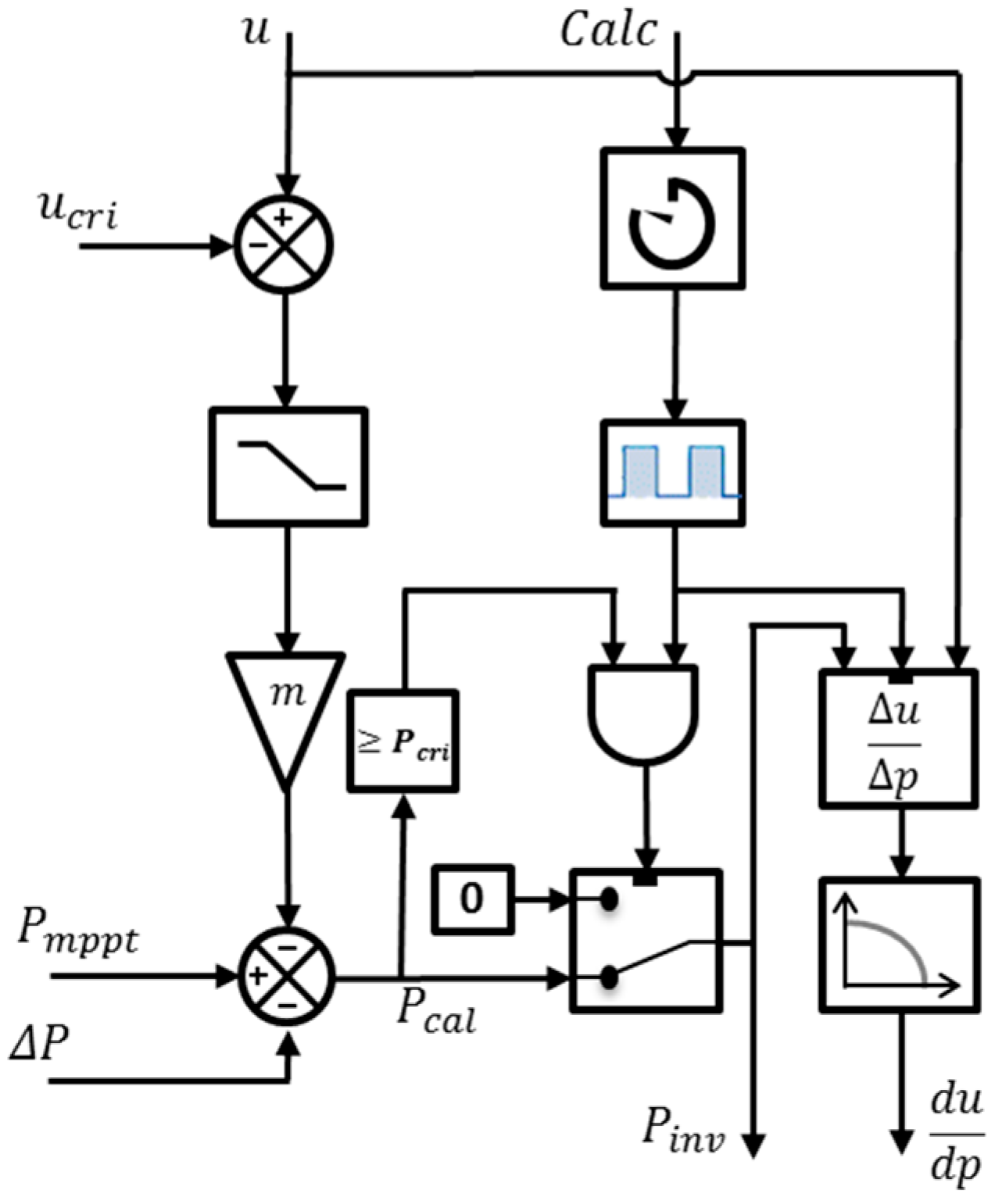
4. Proposed Algorithm
4.1. Calculation of Sensitivity Matrix
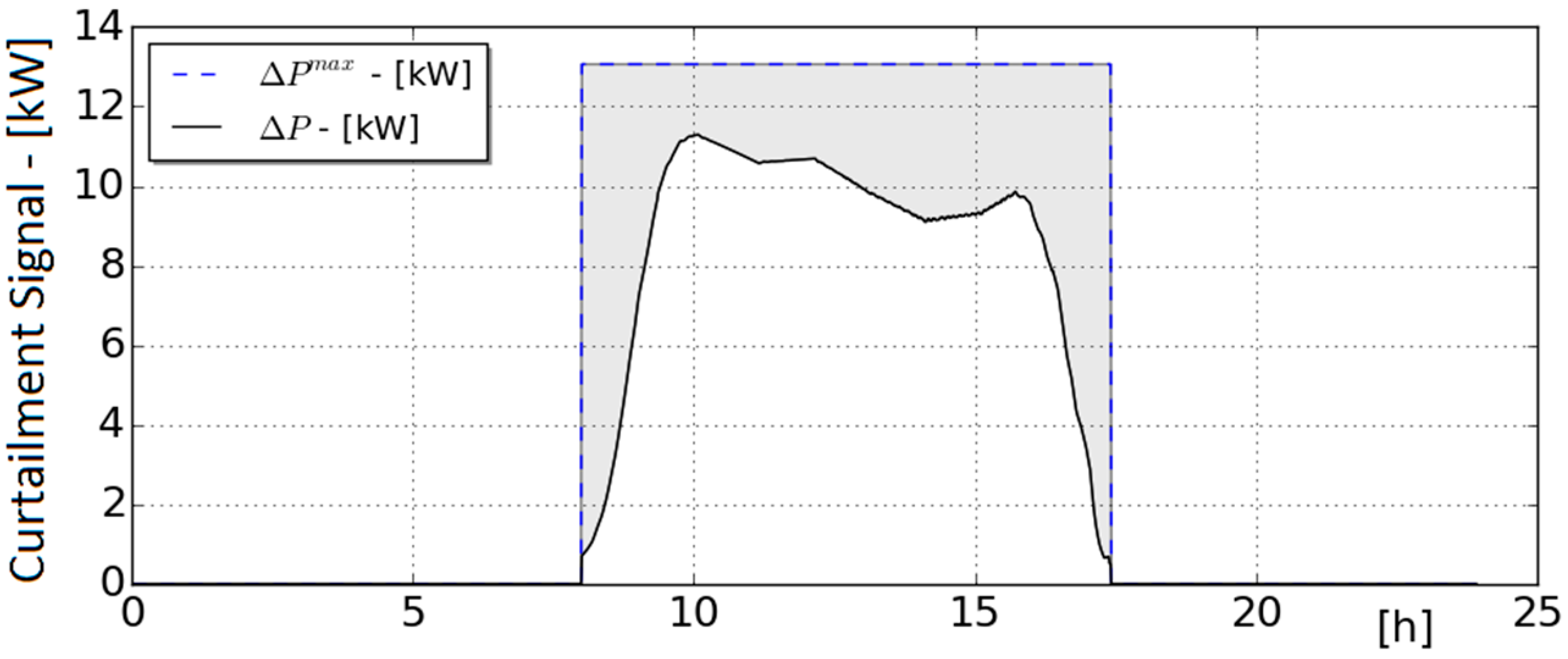
4.2. Active Power Reduction Calculation
4.2.1. Equal Loss of Revenue for Each Photovoltaic Owner
4.2.2. Equal Percentage Reduction in Revenue
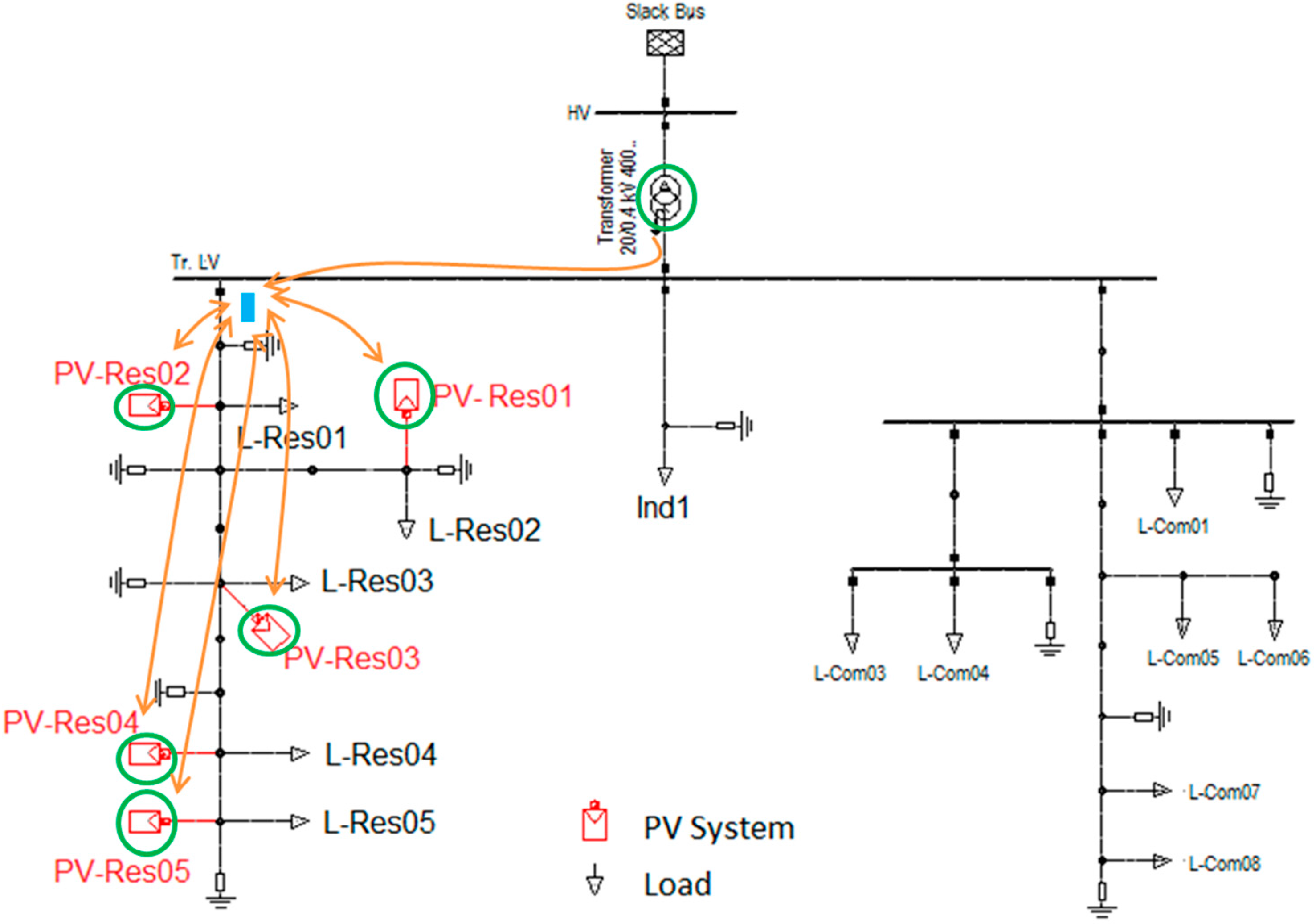
5. Test Case and Simulation Setup
5.1. Network Model
5.2. PowerFactory Python Interfacing
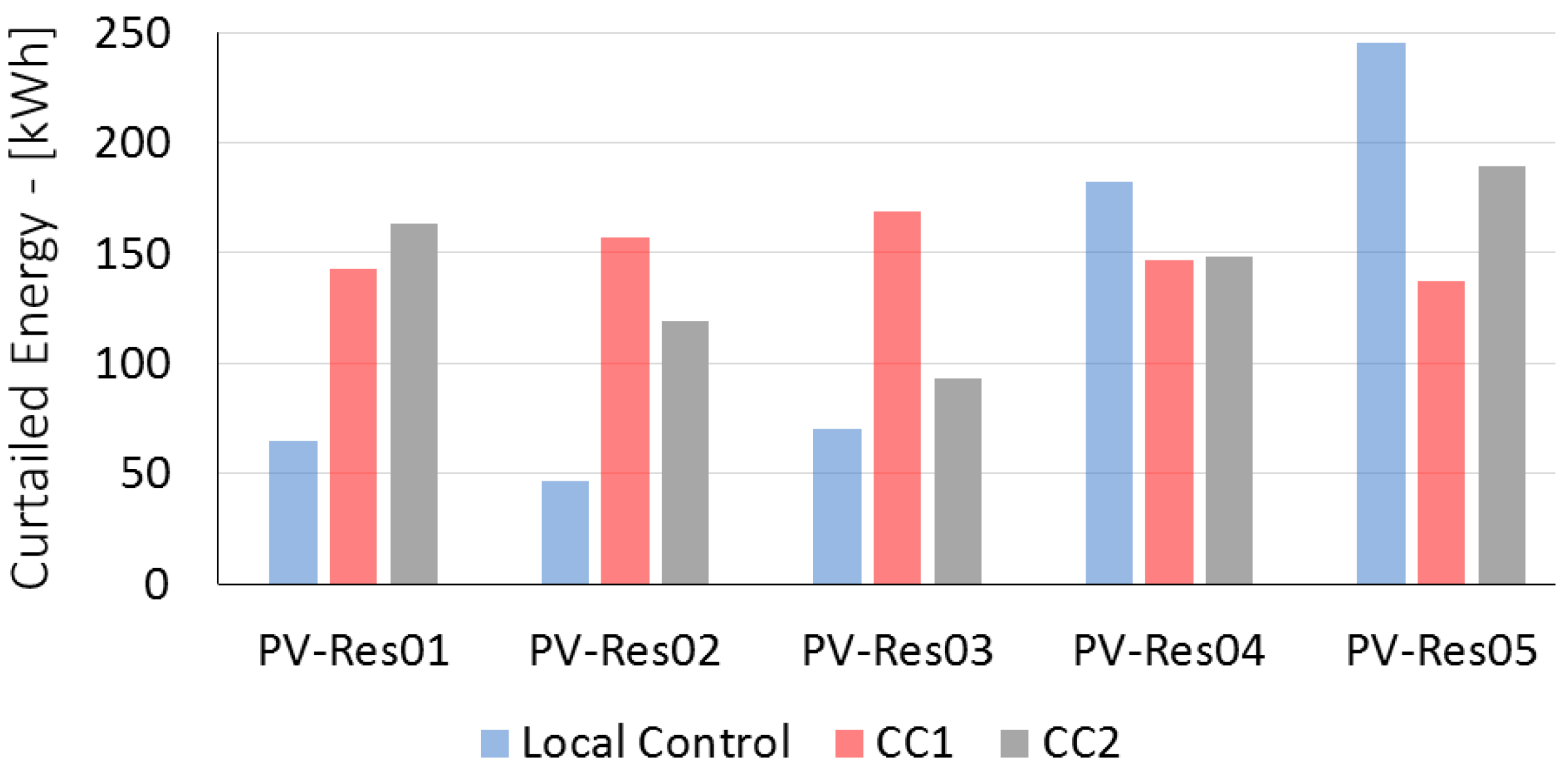
6. Results and Discussion
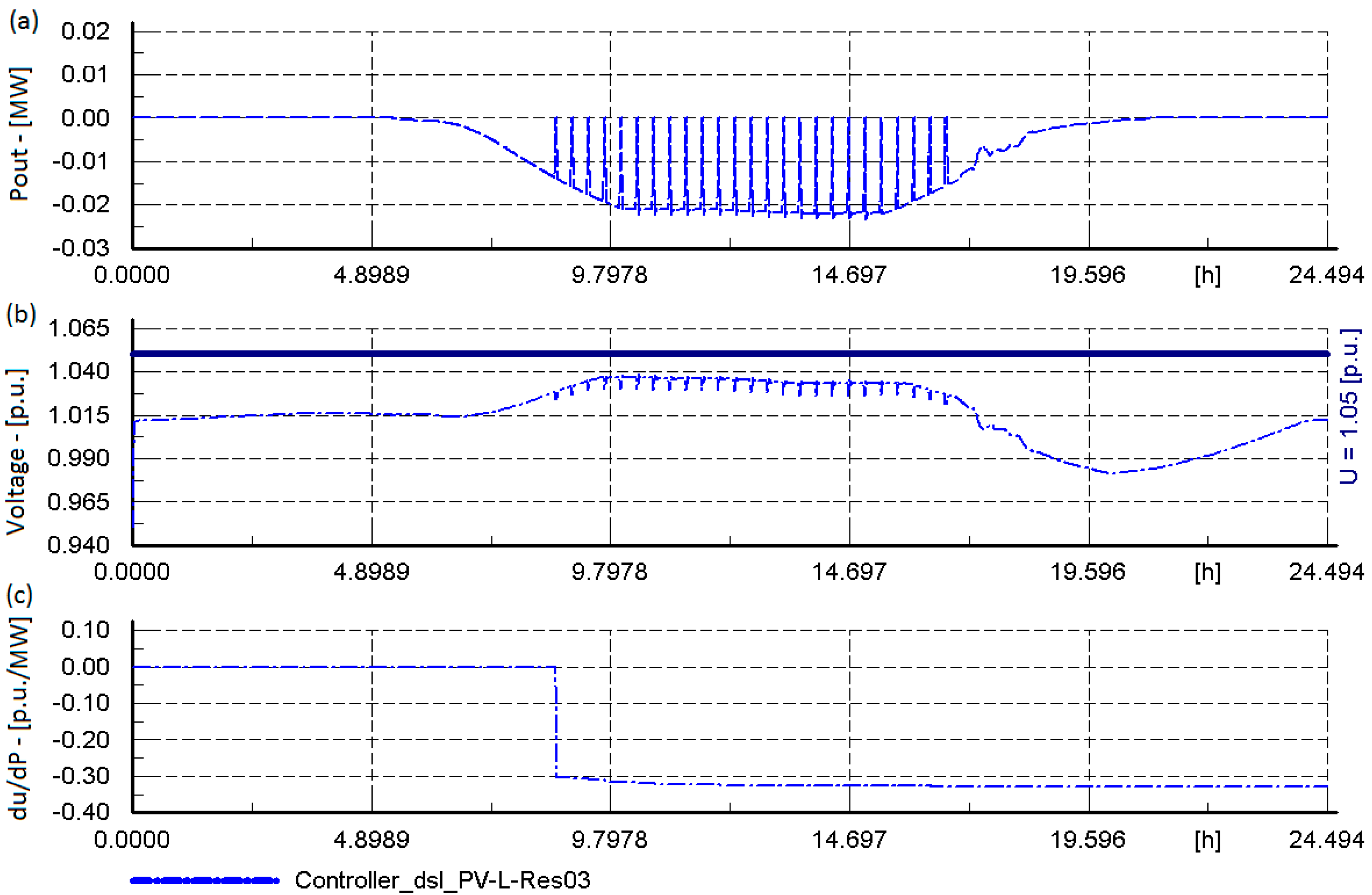
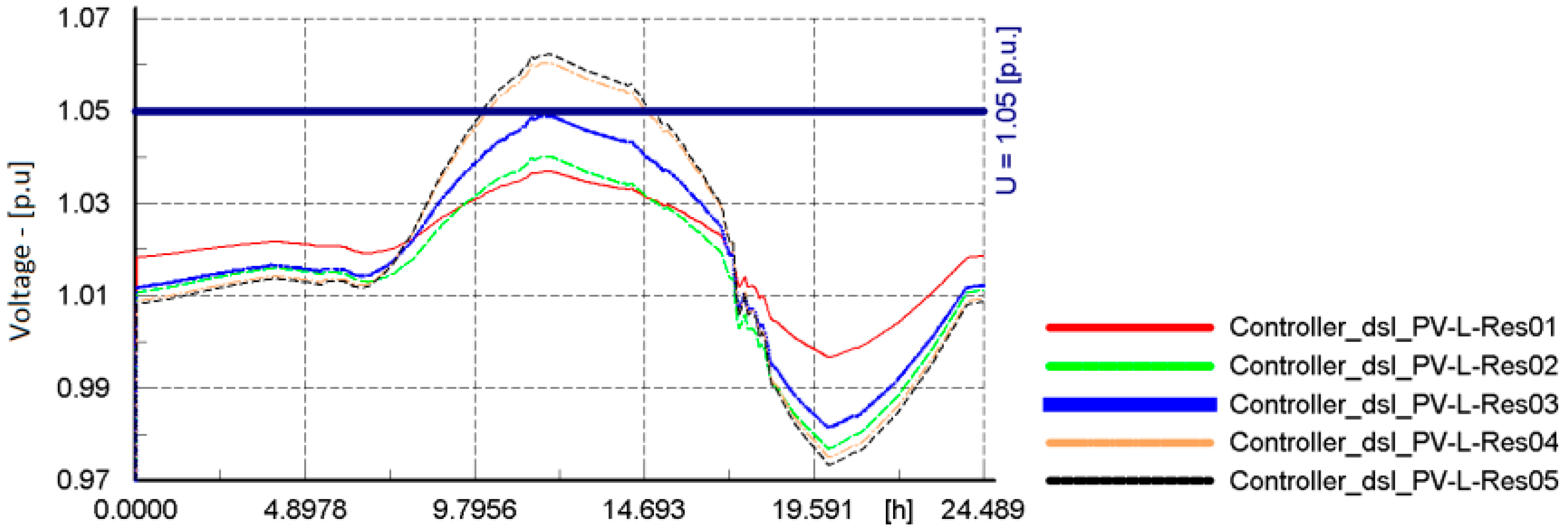
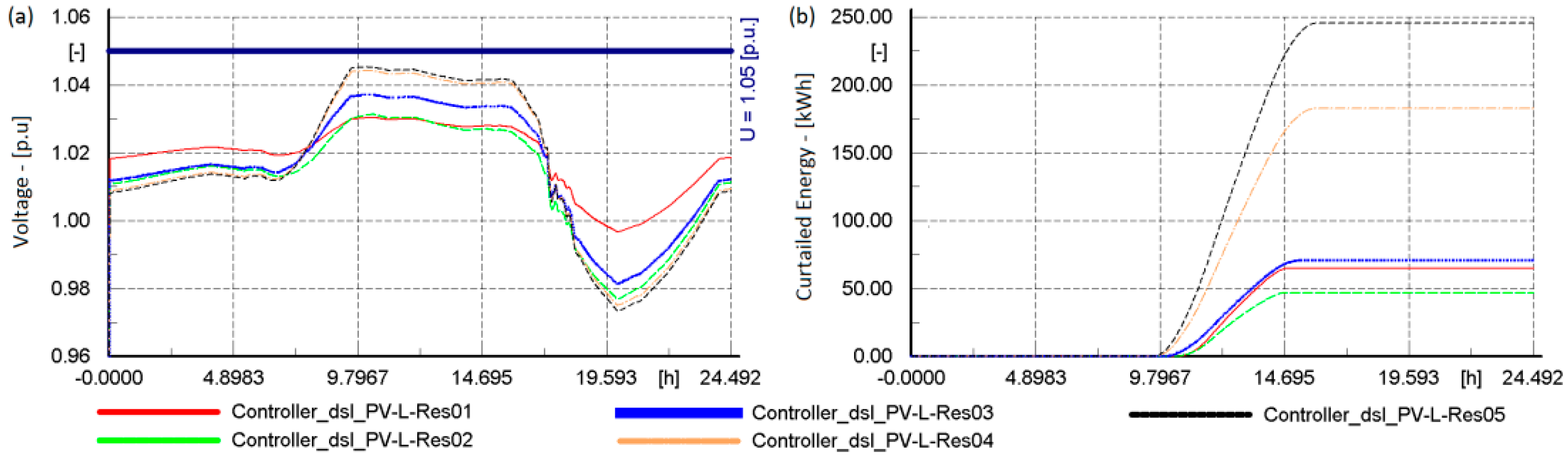
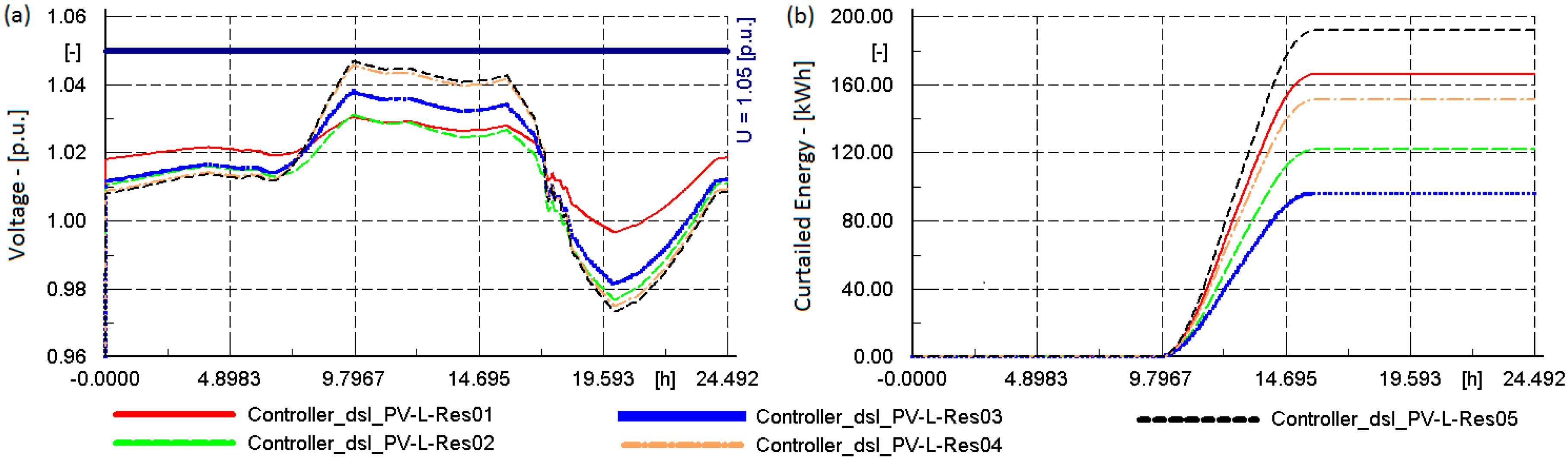
6.1. Local Voltage Regulation
6.2. Coordinated Voltage Regulation
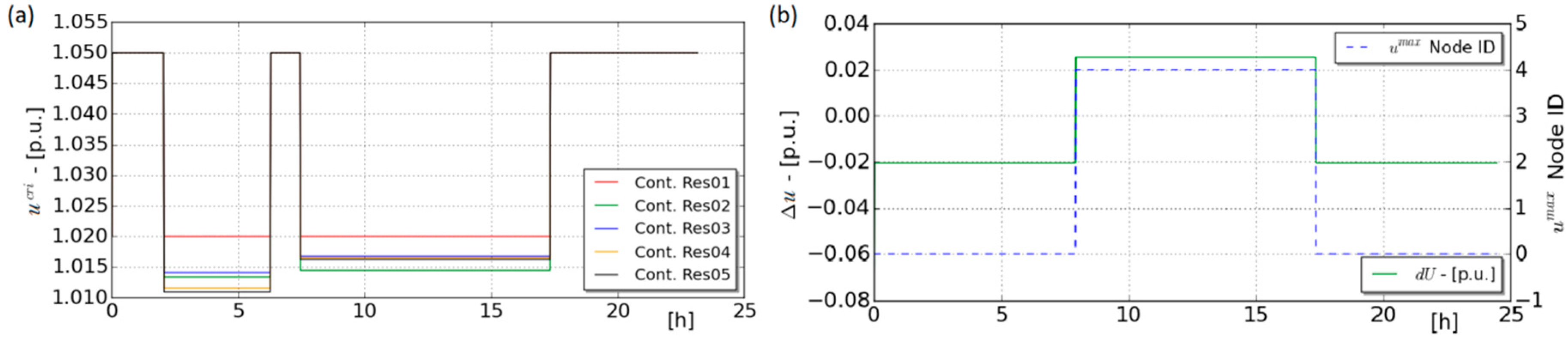
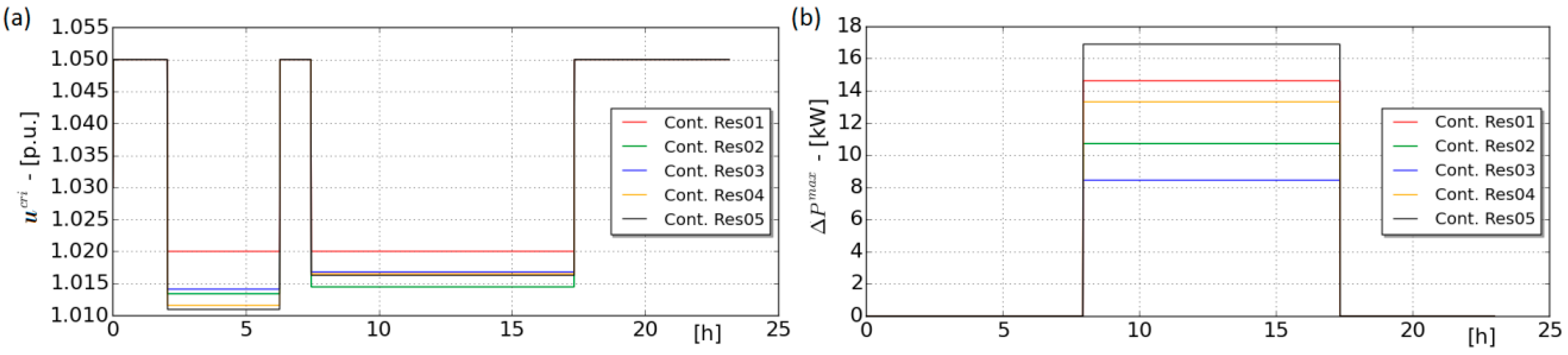
6.2.1. Equal Loss of Revenue for Each Photovoltaic Owner
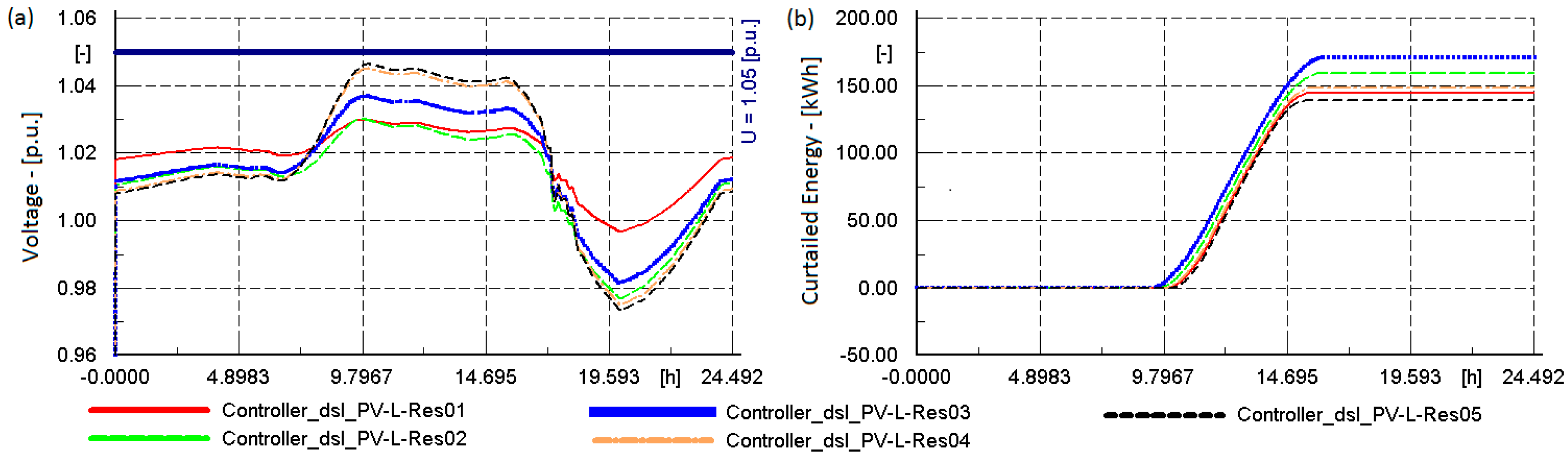
6.2.2. Equal Percentage Reduction in Revenue
7. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| MV/HV/LV | Medium voltage/high voltage/low voltage |
| PV | Photovoltaic |
| DG | Distributed generator |
| PCC | Point of common coupling |
| OLTC | On-load tap changer |
| D-STATCOM | Distribution static synchronous compensator |
| RPC | Reactive power compensation |
| APC | Active power curtailment |
| LVN | Low voltage network |
| DSO | Distribution system operator |
| KPI | Key performance indices |
| DSL | DigSILENT simulation language |
| CCx | Coordinating controller x |
References
- Akinyele, D.O.; Rayudu, R.K.; Nair, N.K.C. Global progress in photo voltaic technologies and the scenario of development of solar panel plant and module performance estimation—Application in Nigeria. Renew. Sustain. Energy Rev. 2015, 48, 112–139. [Google Scholar] [CrossRef]
- Masson, G.; Latour, M.; Rekinger, M.; Theologitis, I.T.; Papoutsi, M. Global market Outlook for Photovoltaics 2013–2017; European Photovoltaic Industry Association: Brussels, Belgium, 2013; pp. 12–32. [Google Scholar]
- Ali, S.; Pearsall, N.; Putrus, G. Impact of High Penetration Level of Grid-Connected Photovoltaic Systems on the UK Low Voltage Distribution Network. In Proceedings of the International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, 28–30 March 2012.
- Isle, D.; Vaziri, M.; Zarghami, M.; Vadhva, S. Review of Concepts to Increase Distributed Generation into the Distribution Network. In Proceedings of the 2014 Sixth Annual IEEE Green Technologies Conference (GreenTech), Corpus Christi, TX, USA, 3–4 April 2014.
- Guisado, J.; Carvalho, P.; Ferreira, L.; Santana, J.J.; Marques, G. Voltage Control Challenges and Potential Solutions for Large-Scale Integration of PV Resources in LV Networks. In Proceedings of the CIRED 2012 Workshop, Integration of Renewables into the Distribution Grid, Lisbon, Portugal, 29–30 May 2012.
- Gonen, T. Electric Power Distribution Engineering; CRC Press: Bota Rancon, FL, USA, 2014. [Google Scholar]
- Stetz, T. Autonomous Voltage Control Strategies in Distribution Grids with Photovoltaic Systems: Technical and Economic Assessment; Kassel University Press GmbH: Kassel, Germany, 2014; Volume 1. [Google Scholar]
- Tonkoski, R.; Lopes, L.A.; El-Fouly, T.H. Coordinated active power curtailment of grid connected PV inverters for overvoltage prevention. IEEE Trans. Sustain. Energy 2011, 2, 139–147. [Google Scholar] [CrossRef]
- Standard, E. Voltage Characteristics of Public Distribution Systems; EN 50160; European Committee for Electrotechnical Standardization: Brussels, Belgium, 2010. [Google Scholar]
- Standerd, A. For Electric Power Systems and Equipment-Voltage Ratings (60 Hz); ANSI C84. 1-2006; National Electrical Manufacturers Association: Rosslyn, VA, USA, 2006. [Google Scholar]
- Descheemaeker, J.; Van Lumig, M.; Desmet, J. Influence of the Supply Voltage on the Performance of Household Appliances. In Proceedings of the 23rd International Conference on Electricity Distribution, Lyon, France, 15–18 June 2015.
- Hashim, T.T.; Mohamed, A.; Shareef, H. A review on voltage control methods for active distribution networks. Prz. Elektrotech. 2012, 88, 304–312. [Google Scholar]
- Kennedy, J.; Ciufo, P.; Agalgaonkar, A. Over-Voltage Mitigation within Distribution Networks with a High Renewable Distributed Generation Penetration. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014.
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Olivier, F.; Aristidou, P.; Ernst, D.; van Cutsem, T. Active management of low-voltage networks for mitigating overvoltages due to photovoltaic units. IEEE Trans. Smart Grid 2015, 7, 926–936. [Google Scholar]
- Mojumdar, M.R.R.; Bhuiyan, A.M.W.; Kadir, H.; Shakil, M.N.H. Design & analysis of an optimized Grid-Tied PV system: Perspective Bangladesh. Int. J. Eng. Technol. 2011, 3, 435. [Google Scholar]
- Deshmukh, R. Grid Integration of Distributed Solar Photovoltaics (PV) in India: A Review of Technical Aspects, Best Practices and the Way forward; Prayas (Energy Group): Pune, India, 2014. [Google Scholar]
- Long, C.; Ochoa, L.F. Voltage control of PV-rich LV networks: OLTC-fitted transformer and capacitor banks. IEEE Trans. Power Syst. 2015, PP, 1–10. [Google Scholar] [CrossRef]
- Aggarwal, M.; Gupta, S.K.; Madhusudan; Kasal, G. D-STATCOM Control in Low Voltage Distribution System with Distributed Generation. In Proceedings of the 2010 3rd International Conference on Emerging Trends in Engineering and Technology (ICETET), Goa, India, 19–21 November 2010.
- Efkarpidis, N.; Wijnhoven, T.; Gonzalez, C.; De Rybel, T.; Driesen, J. Coordinated Voltage Control Scheme for Flemish LV Distribution Grids Utilizing OLTC Transformers and D-STATCOM’s. In Proceedings of the 12th IET International Conference on Developments in Power System Protection (DPSP 2014), Copenhagen, Denmark, 31 March–3 April 2014.
- Alam, M.; Muttaqi, K.; Sutanto, D. Distributed Energy Storage for Mitigation of Voltage-Rise Impact Caused by Rooftop Solar PV. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012.
- Alam, M.; Muttaqi, K.M.; Sutanto, D. Mitigation of rooftop solar PV impacts and evening peak support by managing available capacity of distributed energy storage systems. IEEE Trans. Power Syst. 2013, 28, 3874–3884. [Google Scholar] [CrossRef]
- Safitri, N.; Shahnia, F.; Masoum, M. Coordination of Single-Phase Rooftop PVs to Regulate Voltage Profiles of Unbalanced Residential Feeders. In Proceedings of the 2014 Australasian Universities, Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014.
- Vovos, P.N.; Kiprakis, A.E.; Wallace, A.R.; Harrison, G.P. Centralized and distributed voltage control: Impact on distributed generation penetration. IEEE Trans. Power Syst. 2007, 22, 476–483. [Google Scholar] [CrossRef]
- Vandoorn, T.; De Kooning, J.; Meersman, B.; Vandevelde, L. Soft Curtailment for Voltage Limiting in Low-Voltage Networks through Reactive or Active Power Droops. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012.
- Mansoor, V.M.; Nguyen, P.H.; Kling, W. An Integrated Control for Overvoltage Mitigation in the Distribution Network. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Istanbul, Turkey, 12–15 October 2014.
- Reeves, D.; Nourbakhsh, G.; Mokhtari, G.; Ghosh, A. A Distributed Control Based Coordination Scheme of Household PV Systems for Overvoltage Prevention. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013.
- Lew, D.; Bird, L.; Milligan, M.; Speer, B.; Wang, X.; Carlini, E.M.; Estanqueiro, A.; Flynn, D.; Gomez-Lazaro, E.; Menemenlis, N.; et al. Wind and Solar Curtailment. In Proceedings of the International Workshop on Large-Scale Integration of Wind Power into Power Systems, Denver, CO, USA, March 2013.
- Castillo-Cagigal, M.; Gutierrez, A.; Monasterio-Huelin, F.; Caamano-Martin, E.; Masa, D.; Jimenez-Leube, J. A semi-distributed electric demand-side management system with PV generation for self-consumption enhancement. Energy Convers. Manag. 2011, 52, 2659–2666. [Google Scholar] [CrossRef]
- Perera, B.K.; Ciufo, P.; Perera, S. Power Sharing among Multiple Solar Photovoltaic (PV) Systems in a Radial Distribution Feeder. In Proceedings of the 2013 Australasian Universities, Power Engineering Conference (AUPEC), Hobart, Australia, 29 September–3 October 2013.
- Zhao, J.; Golbazi, A.; Wang, C.; Wang, Y.; Xu, L.; Lu, A.J. Optimal and Fair Real Power Capping Method for Voltage Regulation in Distribution Networks with High PV Penetration. In Proceedings of the 2015 IEEE PES General Meeting, Denver, CO, USA, 26–30 July 2015.
- Viyathukattuva Mohamed Ali, M.M.; Nguyen, P.H.; Kling, W.L.; Chrysochos, A.I.; Papadopoulos, T.A.; Papagianni, G.K. Fair Power Curtailment of Distributed Renewable Energy Sources to Mitigate Overvoltages in Low-Voltage Networks. In Proceedings of the IEEE Eidhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015.
- PowerFactory, D. User’s Manual Version 15; DIgSILENT GmbH: Gomaringen, Germany, 2013. [Google Scholar]
- Conti, S.; Greco, A.; Raiti, S. Voltage Sensitivity Analysis in MV Distribution Networks. In Proceedings of the 6th WSEAS/IASME International Conference on Electric Power Systems, High Voltages, Electric Machines, Tenerife, Spain, 16–18 December 2006.
- Brenna, M.; de Berardinis, E.; Carpini, L.D.; Foiadelli, F.; Paulon, P.; Petroni, P.; Sapienza, G.; Scrosati, G.; Zaninelli, D. Automatic distributed voltage control algorithm in smart grids applications. IEEE Trans. Smart Grid 2013, 4, 877–885. [Google Scholar] [CrossRef]
- Papathanassiou, S.; Hatziargyriou, N.; Strunz, K. A Benchmark Low Voltage Microgrid Network. In Proceedings of the CIGRE Symposium: Power Systems with Dispersed Generation, Athens, Greece, 13–16 April 2005.
- Sanner, M.F. Python: A programming language for software integration and development. J. Mol. Graph. Model. 1999, 17, 57–61. [Google Scholar] [PubMed]




| Type | Inverter ID | Rating-KVA |
|---|---|---|
| PV | PV-Res01 | 45 |
| PV | PV-Res02 | 33 |
| PV | PV-Res03 | 27 |
| PV | PV-Res04 | 41 |
| PV | PV-Res05 | 50 |
| KPI | Local | CC1 | CC2 |
|---|---|---|---|
| TEC-kWh | 610.15 | 752.42 | 712.88 |
| CUI1-kWh | 77.99 | 11.24 | 33.58 |
| CUI2-h | 1.49 | 1.27 | 0.001 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latif, A.; Gawlik, W.; Palensky, P. Quantification and Mitigation of Unfairness in Active Power Curtailment of Rooftop Photovoltaic Systems Using Sensitivity Based Coordinated Control. Energies 2016, 9, 436. https://doi.org/10.3390/en9060436
Latif A, Gawlik W, Palensky P. Quantification and Mitigation of Unfairness in Active Power Curtailment of Rooftop Photovoltaic Systems Using Sensitivity Based Coordinated Control. Energies. 2016; 9(6):436. https://doi.org/10.3390/en9060436
Chicago/Turabian StyleLatif, Aadil, Wolfgang Gawlik, and Peter Palensky. 2016. "Quantification and Mitigation of Unfairness in Active Power Curtailment of Rooftop Photovoltaic Systems Using Sensitivity Based Coordinated Control" Energies 9, no. 6: 436. https://doi.org/10.3390/en9060436
APA StyleLatif, A., Gawlik, W., & Palensky, P. (2016). Quantification and Mitigation of Unfairness in Active Power Curtailment of Rooftop Photovoltaic Systems Using Sensitivity Based Coordinated Control. Energies, 9(6), 436. https://doi.org/10.3390/en9060436







