Realistic Quantum Control of Energy Transfer in Photosynthetic Processes
Abstract
:1. Introduction
2. Model of the Physical System
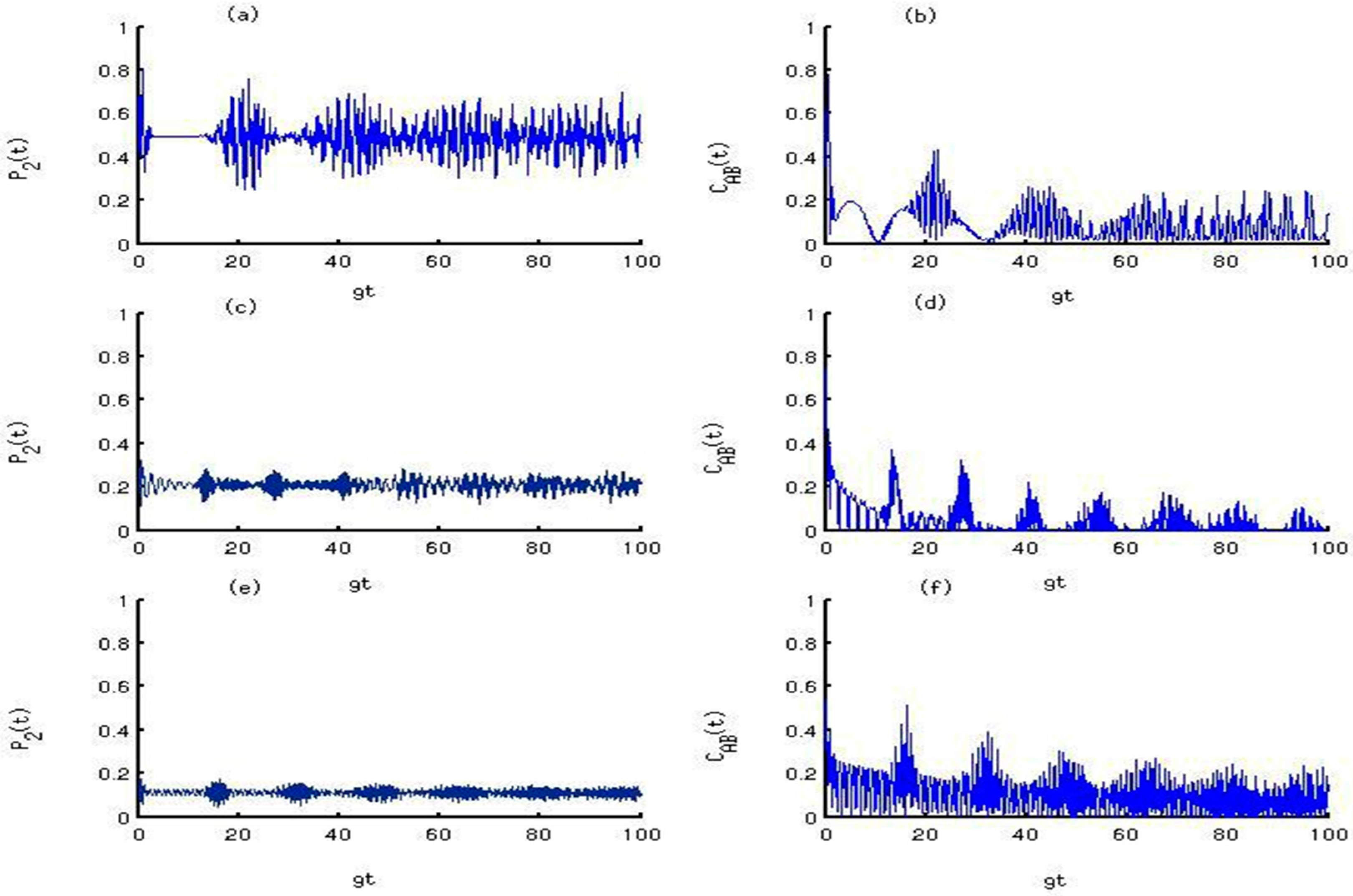
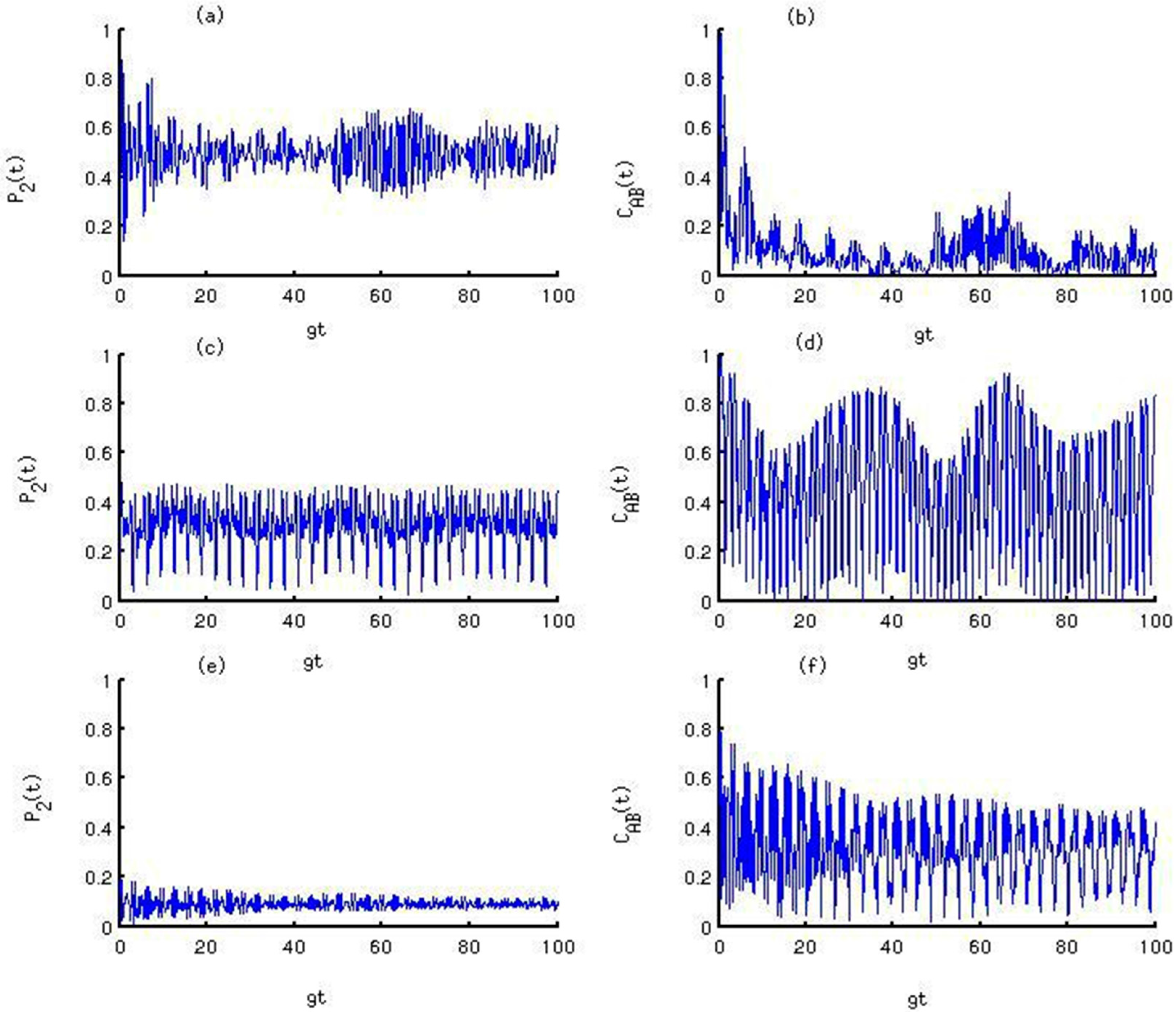
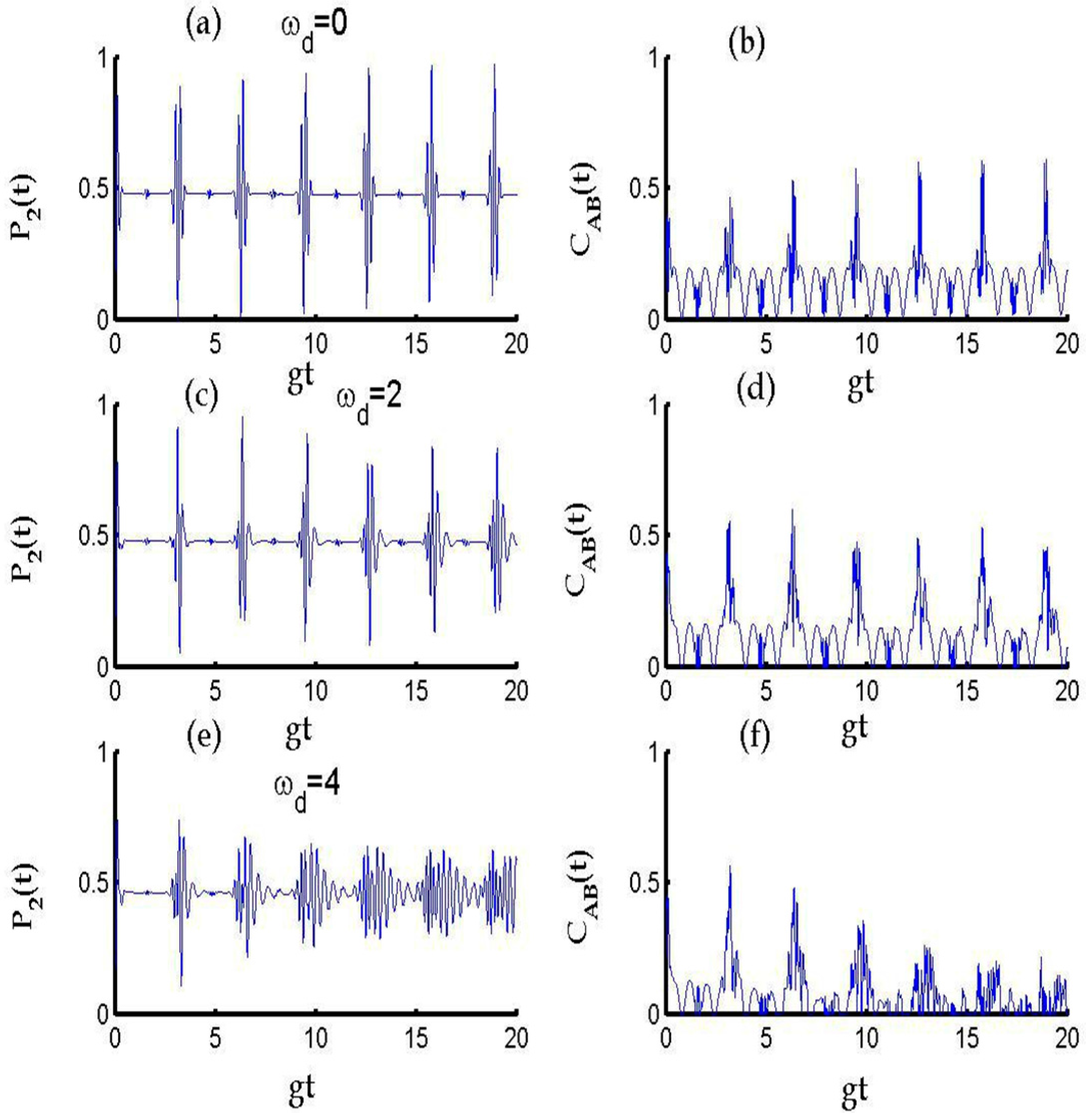
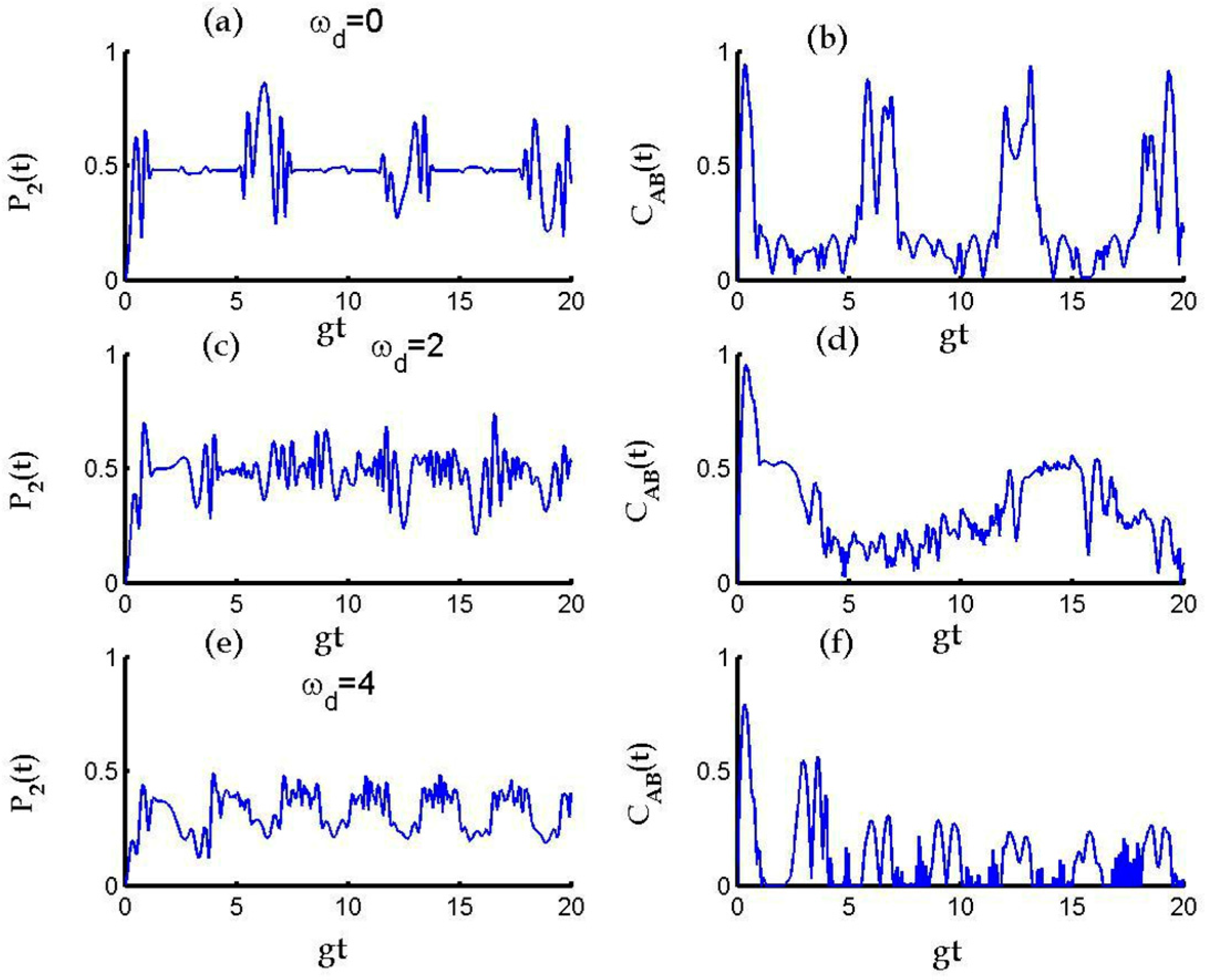
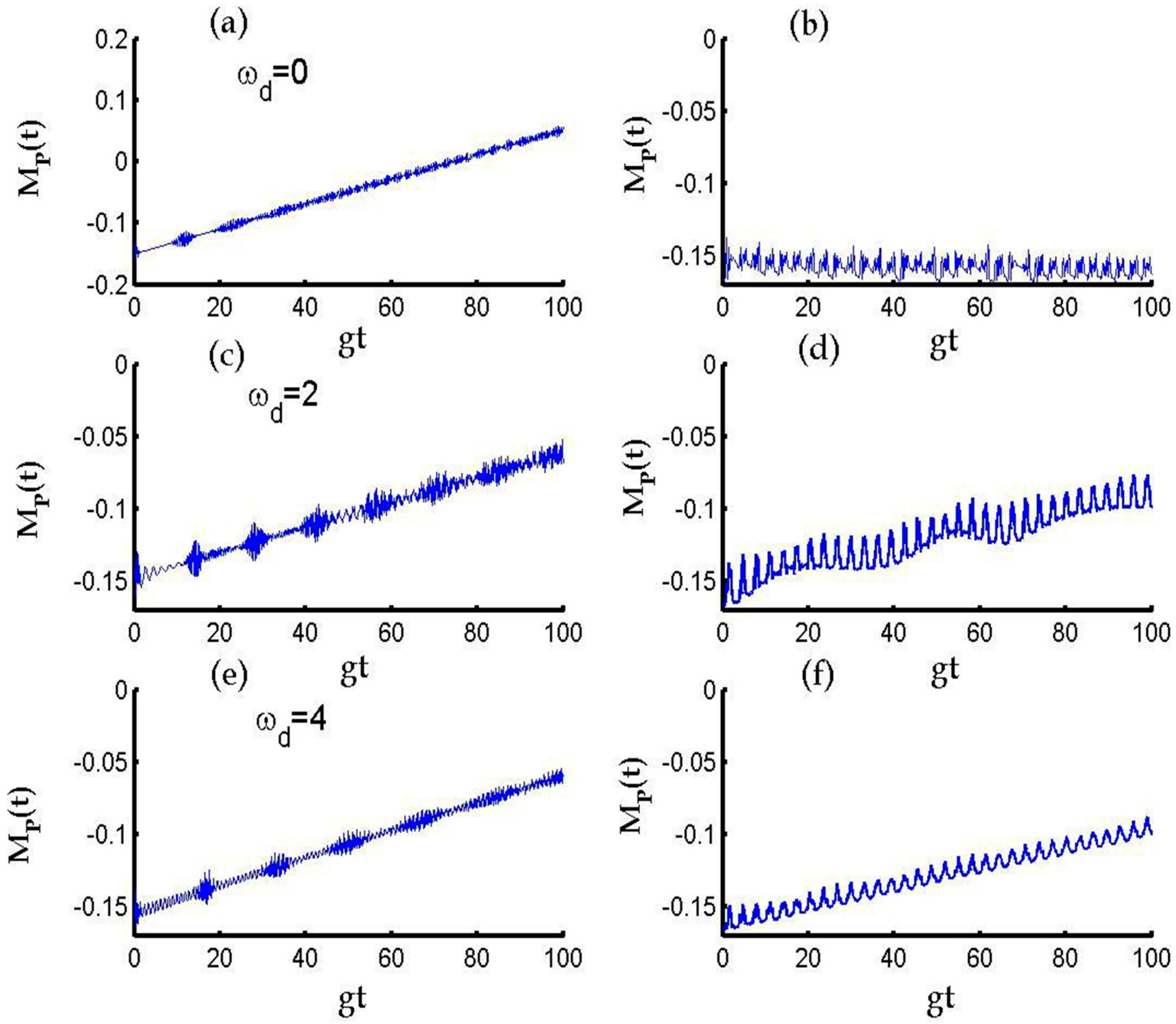
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Mancal, T.; Cheng, Y.-C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Cheng, Y.-C.; Fleming, G.R. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 2007, 316, 1462–1465. [Google Scholar] [CrossRef] [PubMed]
- Collini, E.; Wong, C.; Wilk, K.; Curmi, P.; Brumer, P.; Scholes, G. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Aspuru-Guzik, A. Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. 2009, 113, 9942–9947. [Google Scholar] [CrossRef] [PubMed]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.; Caram, J.; Harel, E.; Wen, J.; Blankenship, R.; Engel, G. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766–12770. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.-Q.; Huang, J.-F.; Kuang, L.-M.; Sun, C.P. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Richards, G.H.; Wilk, K.E.; Curmi, P.M.G.; Quiney, H.M.; Davis, J.A. Coherent vibronic coupling in light-harvesting complexes from photosynthetic marine algae. J. Phys. Chem. Lett. 2012, 3, 272–277. [Google Scholar] [CrossRef] [PubMed]
- Calhoun, T.; Ginsberg, N.; Schlau-Cohen, G.; Cheng, Y.-C.; Ballottari, M.; Bassi, R.; Fleming, G. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 2009, 113, 16291–16295. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Calhoun, T.; Schlau-Cohen, G.; Fleming, G. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Phys. Chem. Chem. Phys. 2010, 12, 7319–7335. [Google Scholar] [CrossRef] [PubMed]
- Scholak, T.; de Melo, F.; Wellens, T.; Mintert, F.; Buchleitner, A. Efficient and coherent excitation transfer across disordered molecular networks. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Olaya-Castro, A.; Lee, C.F.; Olsen, F.F.; Johnson, N.F. Efficiency of energy transfer in a light-harvesting system under quantum coherence. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Liang, X.T.; Zhang, W.M.; Zhuo, Y.Z. Decoherence dynamics of coherent electronic excited states in the photosynthetic purple bacterium Rhodobacter sphaeroides. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Plenio, M.; Huelga, S.F. Dephasing assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Quantum coherence in photosynthetic light harvesting. Annu. Rev. Condens. Matter Phys. 2012, 3, 333–361. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G. Quantum superpositions in photosynthetic light harvesting: Delocalization and entanglement. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Jang, S. Theory of multichromophoric coherent resonance energy transfer: A polaronic quantum master equation approach. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef] [PubMed]
- Caram, J.R.; Engel, G.S. Extracting dynamics of excitonic coherences in congested spectra of photosynthetic light harvesting antenna complexes. Faraday Discuss. 2011, 153, 93–104. [Google Scholar] [CrossRef] [PubMed]
- Sarovar, M.; Cheng, Y.-C.; Whaley, K. Environmental correlation effects on excitation energy transfer in photosynthetic light harvesting. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New. J. Phys. 2009, 11. [Google Scholar] [CrossRef]
- Olaya, A.C.; Scholes, G.D. Energy transfer from Förster–Dexter theory to quantum coherent light-harvesting. Int. Rev. Phys. Chem. 2011, 30, 49–77. [Google Scholar] [CrossRef]
- Harel, E.; Engel, G.S. Quantum coherence spectroscopy reveals complex dynamics in bacterial light-harvesting complex 2 (LH2). Proc. Natl. Acad. Sci. USA 2012, 109, 706–711. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47. [Google Scholar] [CrossRef]
- Shrdinger, E. Discussion of probability relations between separated systems. Proc. Camb. Philos. Soc. 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bell, J. On the Einstein podolsky rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Clauser, J.; Horne, M.; Shimony, A.; Holt, R. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Huver, S.D.; Wildfeuer, C.F.; Dowling, J.P. Entangled Fock states for robust quantum optical metrology, imaging, and sensing. Phys. Rev. A 2008, 78. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum. Inform. Comput. 2001, 1, 27–44. [Google Scholar]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Thermodynamics and the measure of entanglement. Phys. Rev. A 1997, 56. [Google Scholar] [CrossRef]
- Zyczkowski, K.; Horodecki, P.; Sanpera, A.; Lewenstein, M. Volume of the set of separable states. Phys. Rev. A 1998, 58. [Google Scholar] [CrossRef]
- Berrada, K. Classical and quantum correlations for two-mode coherent-state superposition. Opt. Commun. 2011, 285, 2227–2235. [Google Scholar] [CrossRef]
- Berrada, K.; Khalek, S.A.; Ooi, C.H.R. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80. [Google Scholar] [CrossRef]
- Groisman, B.; Popescu, S.; Winter, A. Quantum, classical, and total amount of correlations in a quantum state. Phys. Rev. A 2005, 72. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M.D. Quantum mutual information and the one-time pad. Phys. Rev. A 2006, 74. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2001, 88. [Google Scholar] [CrossRef] [PubMed]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A 2001, 34. [Google Scholar] [CrossRef]
- Bylicka, B.; Chruscinski, D. Non-Markovianity and reservoir memory of quantum channels: A quantum information theory perspective. Phys. Rev. A 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, R.; Saitoh, A. Single-experiment-detectable nonclassical correlation witness. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S. Entanglement of atom–field interaction for nonlinear optical fields. Physica E 2011, 44, 628–634. [Google Scholar] [CrossRef]
- Obada, A.S.F.; Abdel-Khalek, S.; Abo-Kahla, D.A.M. New features of entanglement and other applications of a two-qubit system. Opt. Commun. 2010, 283, 4662–4670. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Alkhateeb, S. Quantum correlations between each two-level system in a pair of atoms and general coherent fields. Results Phys. 2016, 6, 780–788. [Google Scholar] [CrossRef]
- Abdel-Khalek, S. Quantum entanglement and geometric phase of two moving two-level atoms. Open Syst. Inf. Dyn. 2015, 22. [Google Scholar] [CrossRef]
- Nielsen, M.A. Conditions for a class of entanglement transformations. Phys. Rev. Lett. 1999, 83. [Google Scholar] [CrossRef]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40. [Google Scholar] [CrossRef]
- Friedrich, B.; Herschbach, D. Alignment and trapping of molecules in intense laser fields. Phys. Rev. Lett. 1995, 74. [Google Scholar] [CrossRef] [PubMed]
- Eleuch, H.; Guerin, S.; Jauslin, H.R. Effects of an environment on a cavity-quantum-electrodynamics system controlled by bichromatic adiabatic passage. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Barzanjeh, S.; Eleuch, H. Quantum entanglement sudden death and sudden birth in semiconductor microcavities. Int. J. Theor. Phys. 2011, 50, 2939–2950. [Google Scholar] [CrossRef]
- Giacobino, E.; Karr, J.P.; Messin, G.; Eleuch, H.; Baas, A. Quantum optical effects in semiconductor microcavities. Comptes Rendus Phys. 2002, 3, 41–52. [Google Scholar] [CrossRef]
- Eleuch, H. Entanglement and autocorrelation function. Int. J. Mod. Phys. B 2010, 24, 5653–5662. [Google Scholar] [CrossRef]
- Eleuch, H.; Rostovtsev, Y.V.; Scully, M.O. New analytic solution of Schrödinger’s equation. Europhys. Lett. Assoc. (EPL) 2010, 89. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Shishtawy, R.M.; Haddon, R.; Al-Heniti, S.; Raffah, B.; Abdel-Khalek, S.; Berrada, K.; Al-Hadeethi, Y. Realistic Quantum Control of Energy Transfer in Photosynthetic Processes. Energies 2016, 9, 1063. https://doi.org/10.3390/en9121063
El-Shishtawy RM, Haddon R, Al-Heniti S, Raffah B, Abdel-Khalek S, Berrada K, Al-Hadeethi Y. Realistic Quantum Control of Energy Transfer in Photosynthetic Processes. Energies. 2016; 9(12):1063. https://doi.org/10.3390/en9121063
Chicago/Turabian StyleEl-Shishtawy, Reda M., Robert Haddon, Saleh Al-Heniti, Bahaaudin Raffah, Sayed Abdel-Khalek, Kamal Berrada, and Yas Al-Hadeethi. 2016. "Realistic Quantum Control of Energy Transfer in Photosynthetic Processes" Energies 9, no. 12: 1063. https://doi.org/10.3390/en9121063
APA StyleEl-Shishtawy, R. M., Haddon, R., Al-Heniti, S., Raffah, B., Abdel-Khalek, S., Berrada, K., & Al-Hadeethi, Y. (2016). Realistic Quantum Control of Energy Transfer in Photosynthetic Processes. Energies, 9(12), 1063. https://doi.org/10.3390/en9121063






