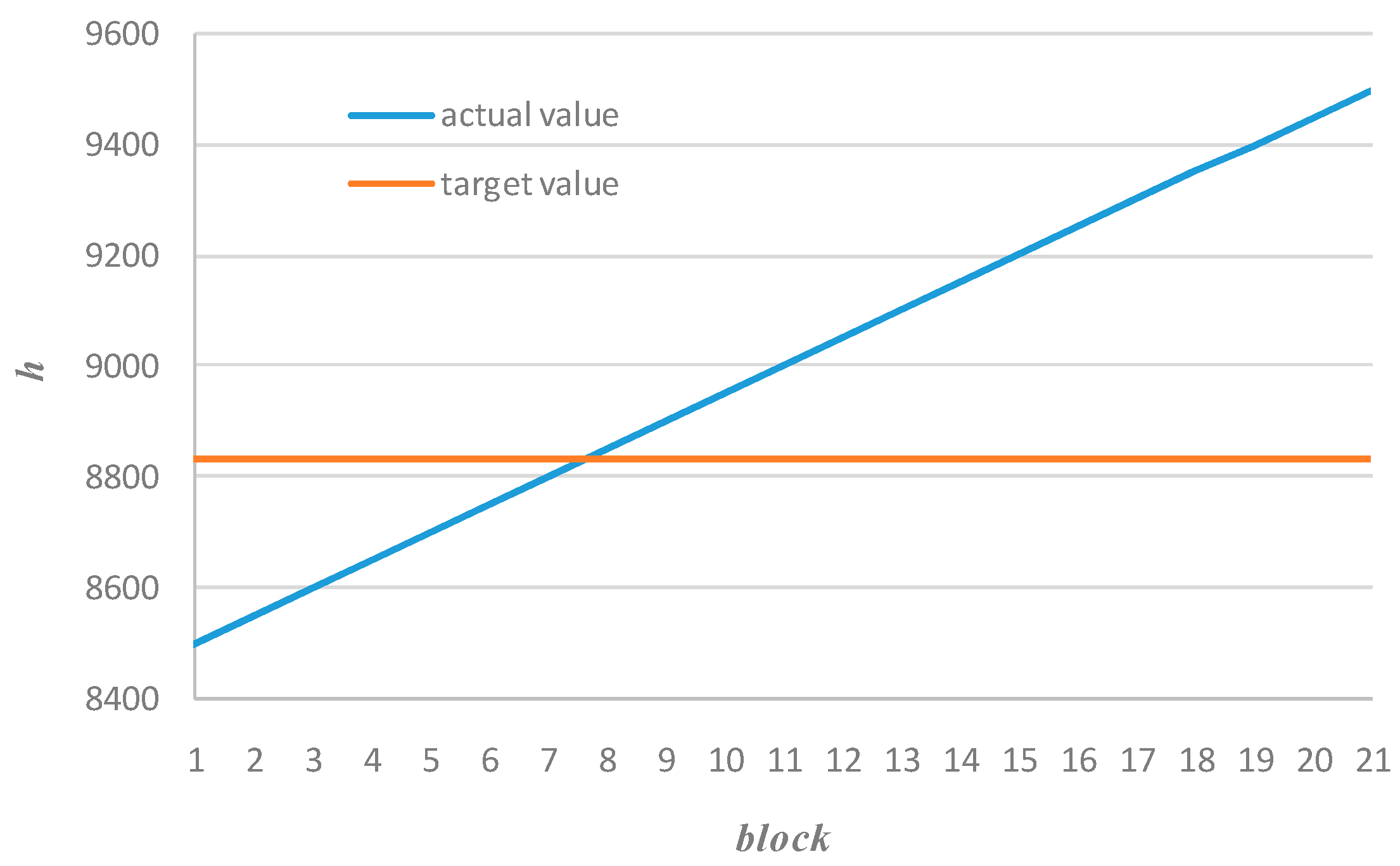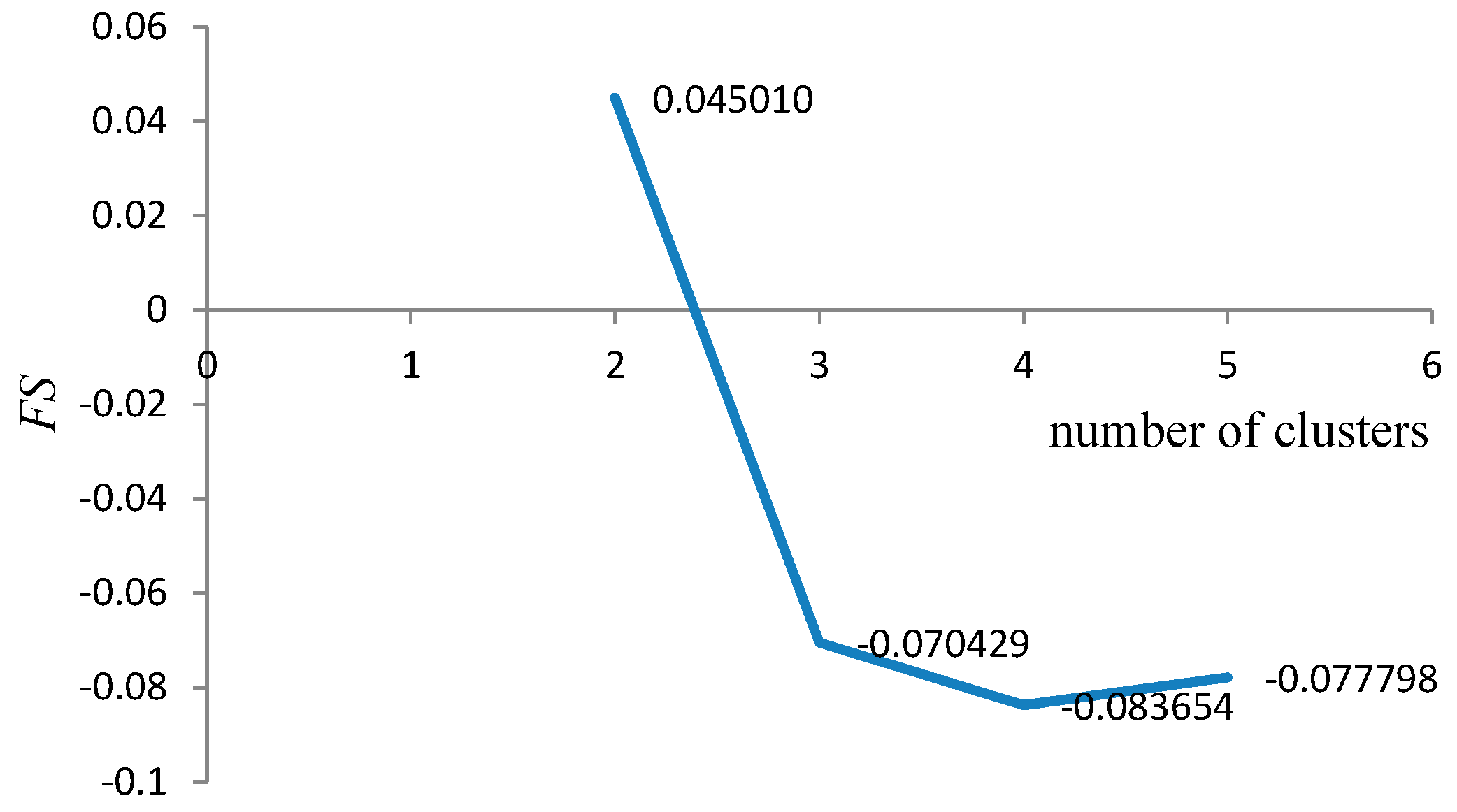2.1. The Concept of the Model
Creating the technological model of a coal deposit represents the approach that documents variability within a coal deposit with respect to the multi-attribute technological requirements of the coal customer, primarily related to the coal quality, ash and sulfur content; in our case these are coal thermal power plant requirements. Building the model can be treated as technological mapping. It is used to assist with new mine project development or major operating mine expansion prior to significant capital investment. The approach allows the location and quantification of zones of quality in 3D space, efficient mine production planning, economic analysis forecasting, reduction of project risks and even better environmental planning. Technological mapping is undertaken during the feasibility planning stages for a new mine project development or mine expansion as a support function for production planning. At this point geostatistical block model of deposit is developed and attributes are estimated and we use geostatistical information to build up our model. Since the technological model represents the basis for production planning it can be used for both short and long-term planning. In the presence of multiple customers the model must be modified. In such case the number of clusters is strictly equal to the number of customers and the fuzzy TOPSIS method measuring the relative closeness must be replaced by the fuzzy multi-attribute distance function measuring the distance between each block and the requirements of each customer. Clustering is now performed over the set of obtained distances. This algorithm does not allow criteria to be divided.
The traditional block model of coal deposit means the deposit is divided into an adequate number of blocks having the same size. Such a model is created using the data obtained from exploration drilling and application of geostatistical methods. Supposing what portion of the coal deposit is defined to be mineable in economical way (mineable reserves), i.e., the ultimate number of mineable blocks is defined.
Let be the set of mineable blocks in the coal deposit. Each block is characterized by a certain number of attributes, such as dimensions, location, density, tonnage, heating value, sulfur and ash content. Without loss of generality we suppose the density and tonnage are the same for every block. With respect to the thermal power plant’s requirements, heating value, sulfur and ash content are the main modeling attributes of. Such attributes are used to determine the possible technological value of every block in B.
One of methods of reducing the size of the production planning problem is to first combine all mineable blocks into block aggregates based on relative closeness of their attributes to the given technological requirements.
Definition 1. Let be a sequence of mineable blocks. A subsecuence of is a sequence with for all [
14].
Definition 2. A point c is called a cluster point or accumulation point of a sequence if for any and any there is an such that [
14].
Considering Definitions 1 and 2 we can create cluster composed of mineable blocks. We refer to this cluster composed of blocks as a technological mining cut. Obviously, the mineable reserves can be represented by the set composed of all technological mining cuts. Formally, the clustering structure of the coal deposit is represented as a set of the following subsets of such that: and for . Consequently, any mineable block in B belongs to exactly one and only one technological mining cut.
Definition 3. Let be a set of the triangular fuzzy numbers describing actual values of heating value, sulfur and ash content of the block respectively, where k is the total number of mineable blocks.
Definition 4. Let be a set of the triangular fuzzy numbers describing the target values of attributes required by the thermal power plant.
Definition 5. Let be a set of the triangular fuzzy numbers describing the relative closeness of every mineable block to the .
Considering Definitions 3–5 we can define technological mining cut (cluster) as a three attributes spatial object, composed of mineable blocks, with relative closeness belonging to one and only one predefined cluster interval. Therefore, the problem statement is to divide the area of the coal deposit into
N technological mining cuts. The procedure of the solving the problem is divided into two main phases:
calculation of the relative closeness of every mineable block to the target values based on the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) method,
clustering the obtained values based on the fuzzy C-mean clustering method.
2.2. The Relative Closeness
In order to define the relative closeness of block to the target values we apply the concept of multi-criteria decision making. To decrease the uncertainty of the input attributes we apply fuzzy set theory i.e., triangular fuzzy numbers [
15,
16]. Application of the fuzzy set theory has found wide use for solving problems in the mining industry [
17,
18,
19,
20,
21].
Let
X be a classical set of objects, called the universe, whose generic elements are denoted by
x. The membership in a crisp subset
X is often viewed as characteristic function
from
X to {0, 1} such that:
where {0, 1} is called a valuation set. If the valuation set is allowed to be real interval [0, 1],
A is called a fuzzy set and denoted by
and
is the degree of membership of
x in
.
A triangular fuzzy number is created according to probability-possibility transformation [
22,
23,
24]. In order to calculate the relative closeness,
, between the
i-th mineable block and requirements of the thermal power plant we apply the modified TOPSIS method. Modification refers primarily to the different sequence of steps and calculation of attribute weights than the ones used in the original method. The TOPSIS method is a technique for order preference by similarity to an ideal solution proposed by Hwang and Yoon (1981) [
25]. The basic concept of this method is that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution.
Application of fuzzy TOPSIS can be found in many scientific papers. Chen [
26] extended the use of TOPSIS to the fuzzy environment and gave numerical examples of system analysis engineer selection for a software company. Chu [
27] presented a fuzzy TOPSIS model under group decisions for solving the facility location selection problem. Yang and Hung [
28] proposed the use of TOPSIS and fuzzy TOPSIS methods for plant layout design problem.
The modified fuzzy TOPSIS method is based on the following steps:
Step 1: Normalization of the input data
The space of the input data is defined by the union of the mineable block attributes and target values. It can be represented by the following input data matrix:
where
k is the total number of the mineable blocks in the coal deposit and
m is the total number of the attributes. In our case the input data matrix is as follows:
Note, in the input data matrix, requirement of the thermal power plant is treated as a fictitious mineable block. Each element of the matrix
is transformed using the following equations:
Equation (4) refers to the block attributes while Equation (5) refers to the targets. The normalized input data matrix is as follows:
Step 2: Weights of the attributes and targets
In the original TOPSIS method the global weight of each criterion is calculated, while in our model we calculate the local weight of each attribute within the mineable block and technological requirement (targets) separately. The weight of a block attribute is calculated as follows:
The weight of target value is calculated as follows:
The weights of target attributes are assumed to have equal importance.
Step 3: Construct the decision matrix
The first phase in solving the problem of the coal deposit partitioning into finite number of technological mining cuts can be treated as an Alternatives, Criteria, Evaluations model. A finite set of alternatives is defined by the set , i.e., each mineable block represents one alternative. A finite set of criteria is defined by the set , where each element represents the distance function between the j-th block attribute and the j-th target value. A set of evaluations of alternatives with respect to given criteria is defined by the set , where each element represents the rating of the alternative with respect to defined criterion.
Heating value, sulfur and ash content are used as three main attributes in the calculation of distance functions, i.e., in the process of the block evaluation. Accordingly we have the set
F composed of three basic distance functions, i.e., the set of criteria is defined as
. Evaluation of each element of the set
is obtained as follows:
where term
refers to the weighted normalized target value of the
j-th attribute while
to the actual value of the mineable block.
The criterion based on the heating value (
f1) is divided into two criteria with respect to the sign of the distance function (
f1 > 0;
f1 < 0). Suppose there is a sequence of mineable blocks with ascending order of the heating value and required (target) value, see
Figure 1.
According to Equation (9) we obtain descending order of the distance function values, see
Figure 2. The sign of the distance function is defined by the following sign function of
f1:
By the sign of the heating value distance function we generally separate the mineable blocks into two subsets, where the first subset is composed of the mineable blocks having a heating value greater than the target (
), while the second are the blocks having a lower value (
). Accordingly, we obtain the two following criteria
and
. It is very important to emphasize that one and only one of these two criteria exists in the
i-th mineable block. It is defined as follows:
Note, [0, 1] indicates only the existence of the criterion in the
i-th mineable block not the evaluated values. Criterion
should be maximized while
is minimized. Accordingly, the set of criteria is transformed and is as follows;
. Evaluation of each element of the set
with respect to criteria based on the sulfur and ash content (
f3,
f4) is also evaluated by Equation (11). Both criteria should be maximized. Finally we obtain the following decision matrix:
Step 4: Define the ideal and the negative-ideal solutions
Let us suppose that
identifies the ideal solution and
the negative one. They are defined as follows:
where:
With benefit and cost attributes, we discriminate between criteria that the decision maker desires to maximize or minimize, respectively.
Step 5: Measure the distance between alternatives and ideal solutions
To calculate the
m-Euclidean distance from each alternative (mineable block) to
and
the following equations can be easily adopted:
Step 6: Measure of the relative closeness to the ideal solution
The elements of the set
are calculated by the following equation:
A very important concept related to the applications of triangular fuzzy numbers is the process of defuzzification. It converts a triangular fuzzy number into a crisp value The most commonly used defuzzification method is the centroid defuzzification method, which is also known as center of gravity [
29]. The defuzzification formula of triangular fuzzy numbers (
a,
b,
c) is:
and it will be used to express the fuzzy relative closeness as crisp value. Finally, we obtain the set of the relative closeness
that should be partitioned into adequate number of clusters.
Applying the same concept to the sulfur and ash content attribute we can obtain the following decision matrix:
2.3. Coal Deposit Partitioning Model
In order to divide a coal deposit into an adequate number of technological mining cuts we apply the fuzzy C-mean clustering algorithm [
30,
31,
32,
33] over the set
.
Algorithm aims to determine cluster centers
cn(
n = 1, 2, …,
N) and fuzzy partition matrix
U by minimizing the following function:
subject to:
The exponent
is used to adjust the weighting effect of membership values. A large
will increase the fuzziness of the function
J. The value of
is often set to 2. Applying partial derivative to the function
J with respect to variable
and
the following update equations are obtained:
Based on Equations (21)–(26) we describe the model to coal deposit partitioning into technological mining cuts as follows:
- Step 1:
select an integer number of technological mining cuts i.e., clusters (N) and threshold value ; let ω = 2;
- Step 2:
input a set of initial cluster centers , composed of the increasing order values randomly chosen from the interval ;
- Step 3:
compute all and then all uni according to Equation (26);
- Step 4:
update the set of initial cluster centers according to Equation (25);
- Step 5:
compute the value of the objective function J according to Equation (21) and compare J(t+1) with J(t), where t is the iteration number. If then stop otherwise return to Step 2.
Determination of the optimal number of technological mining cuts (
N) is based on the fuzzy validity criterion. The Fukuyama-Sugeno validity functional is used to define it [
34,
35,
36]:
Since we have two clustering approaches based on four and six criteria, respectively, it is necessary to compare them. There are numerous measures for comparing clustering results. In this paper the adjusted Rand index (
ARI) is used for comparison [
37,
38,
39,
40].
The range of ARI is , with only extreme values below zero. A value 0 indicates that there is no similarity, whereas a value of 1 indicates a similarity. If the value of ARI is high (ARI > 0.85) then mine production planners can select any one of the obtained models, otherwise it is necessary to select the optimal partitioning.
The selection is based on the entropy as a measure of quality of the obtained clusters [
41,
42]. This measure considers the overlaps between clusters
P and
E. The entropy of cluster
P and
E is
H(
P) and
H(
E). The optimal technological model of the coal deposit is selected according to:
. If there is no significant difference between
H(
P) and
H(
E), (<20%), then some additional way of selection have to be employed. For that purpose we can use Fukuyama-Sugeno validity functional (
FS). For compact and well separated clusters it is expected small value of
FS. Optimal technological model of coal deposit is selected according to:
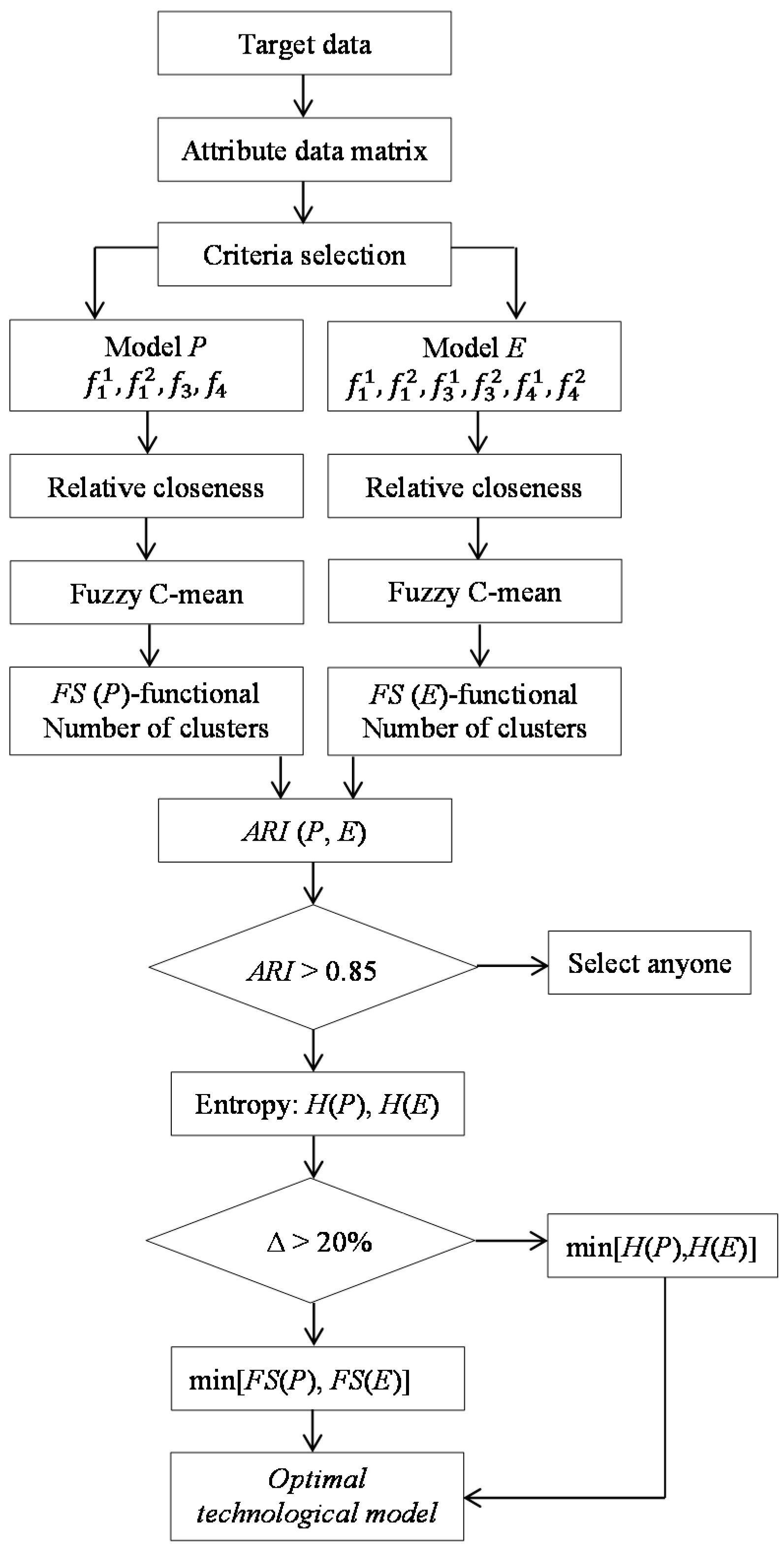
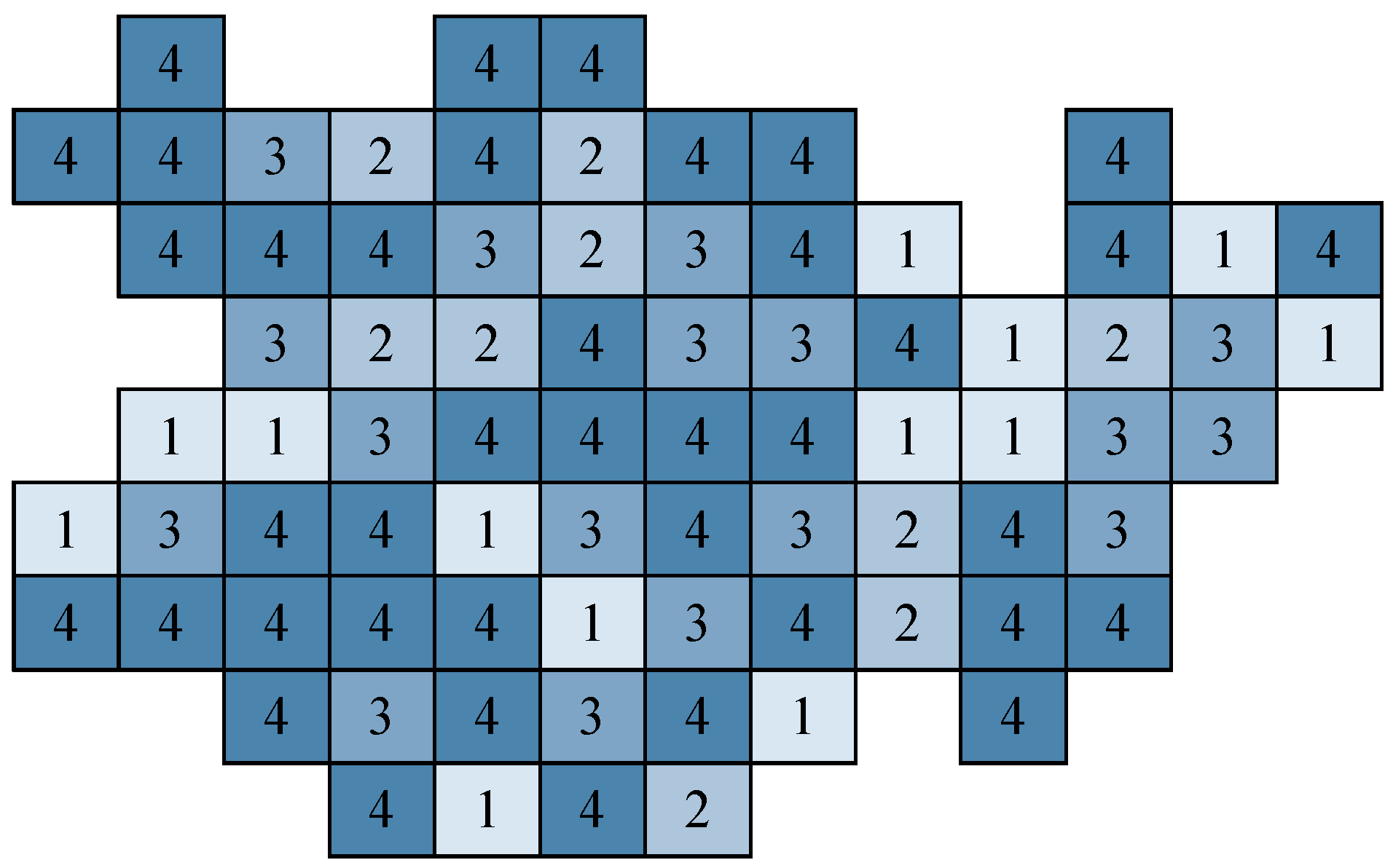
. A model of multi-attribute technological model of a coal deposit is represented in
Figure 3.