A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site
Abstract
:1. Introduction
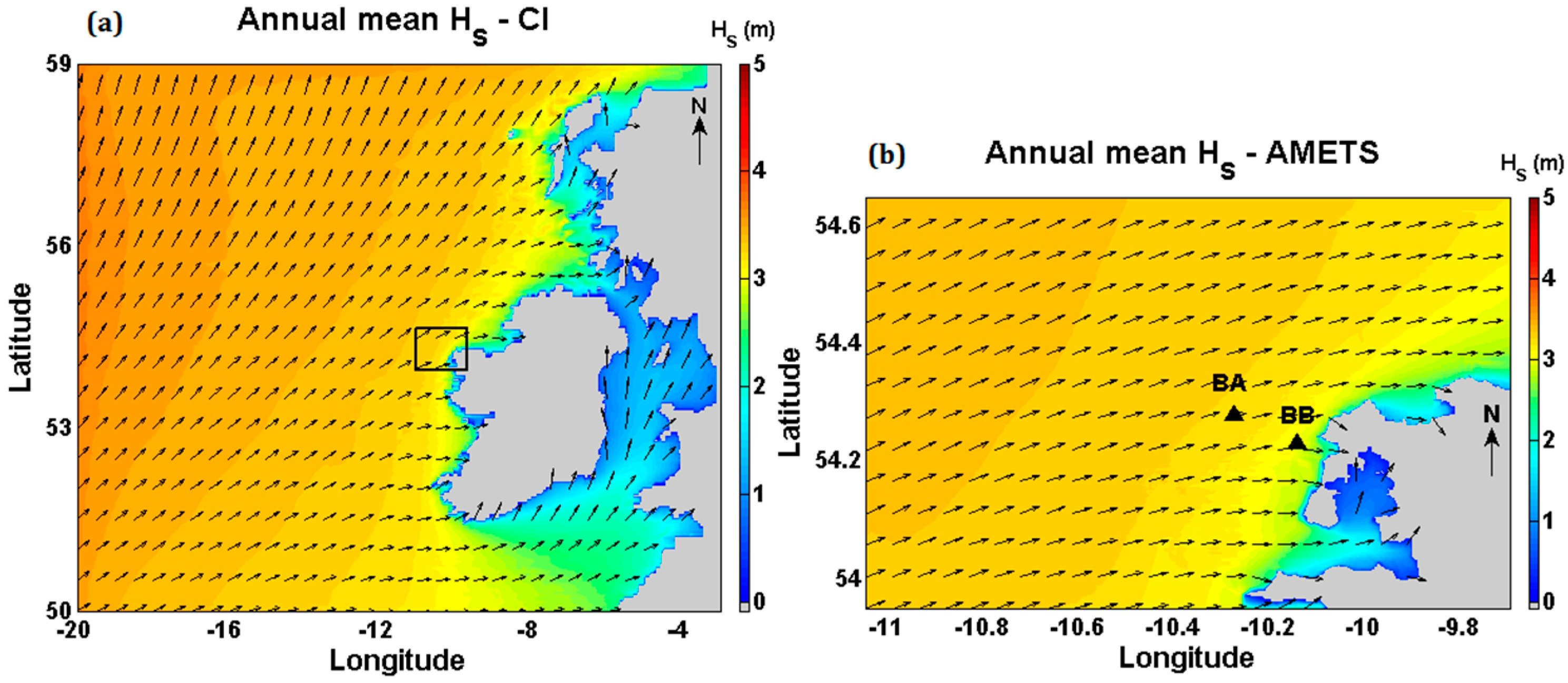
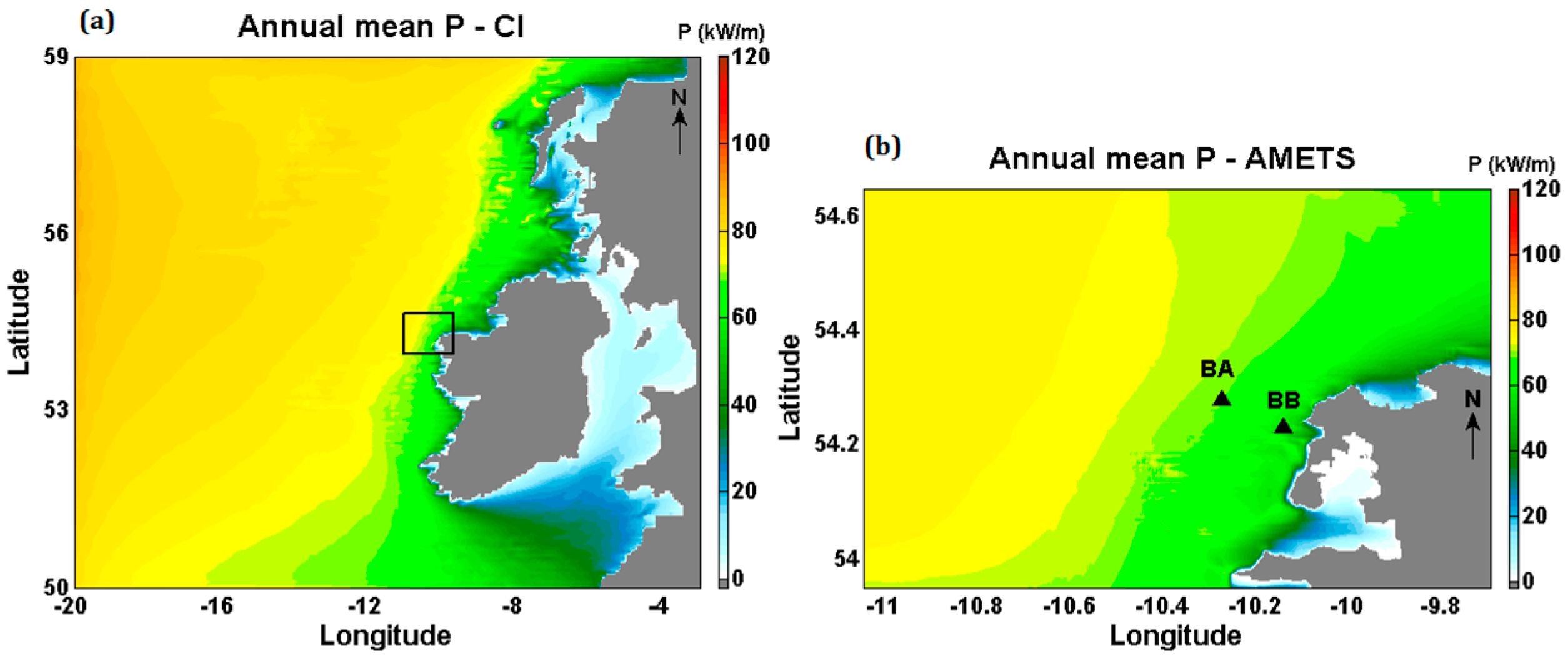
- Berth A (BA): approximately 16 km offshore, 100 m water depth, and covering 6.9 km2;
- Berth B (BB): approximately 6 km offshore, 50 m water depth, and covering 1.5 km2.
2. Material and Methods
2.1. Wave Model Description
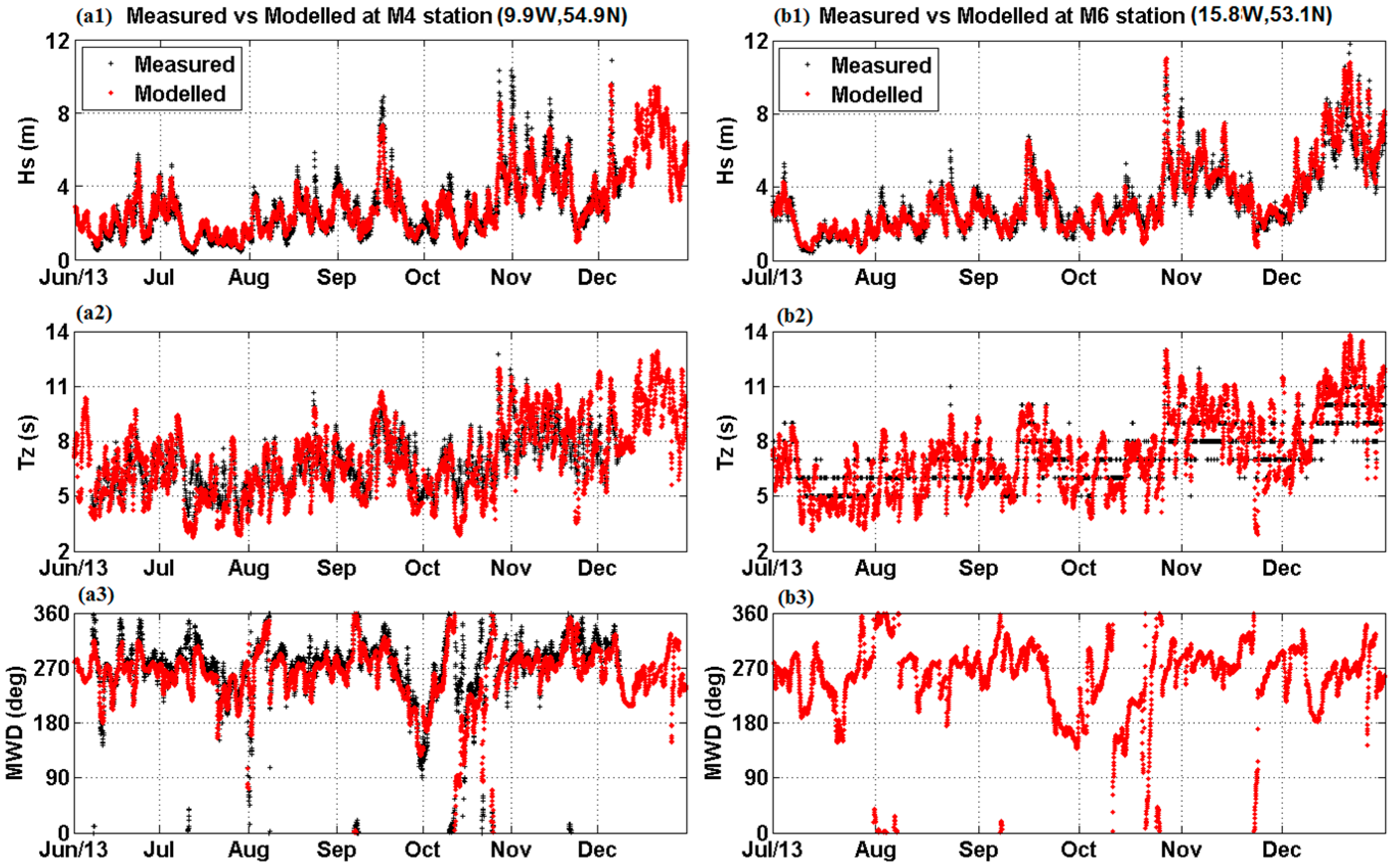
2.2. Coarse Ireland Model Development and Validation
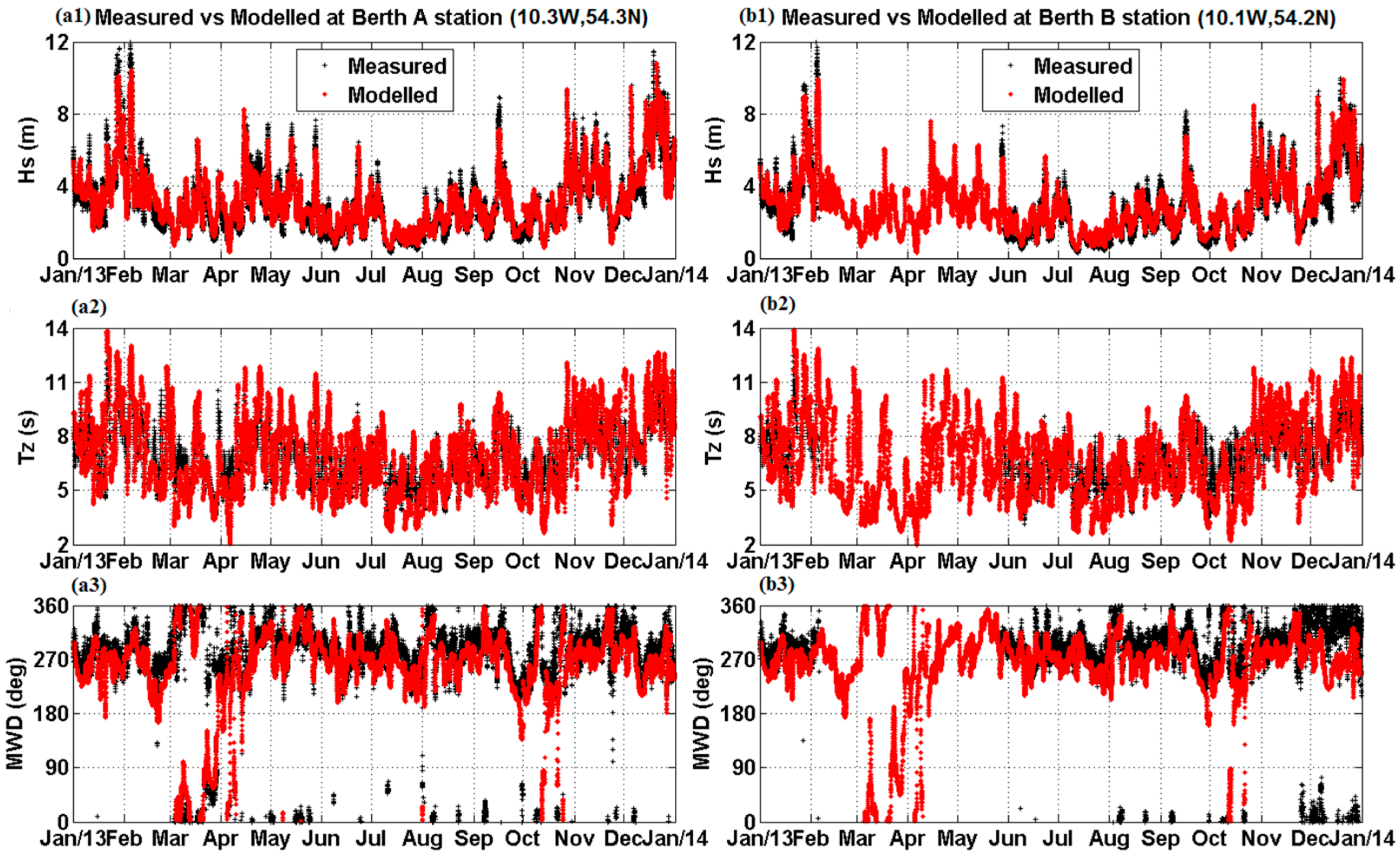
2.3. Atlantic Marine Energy Test Site Model Development and Validation
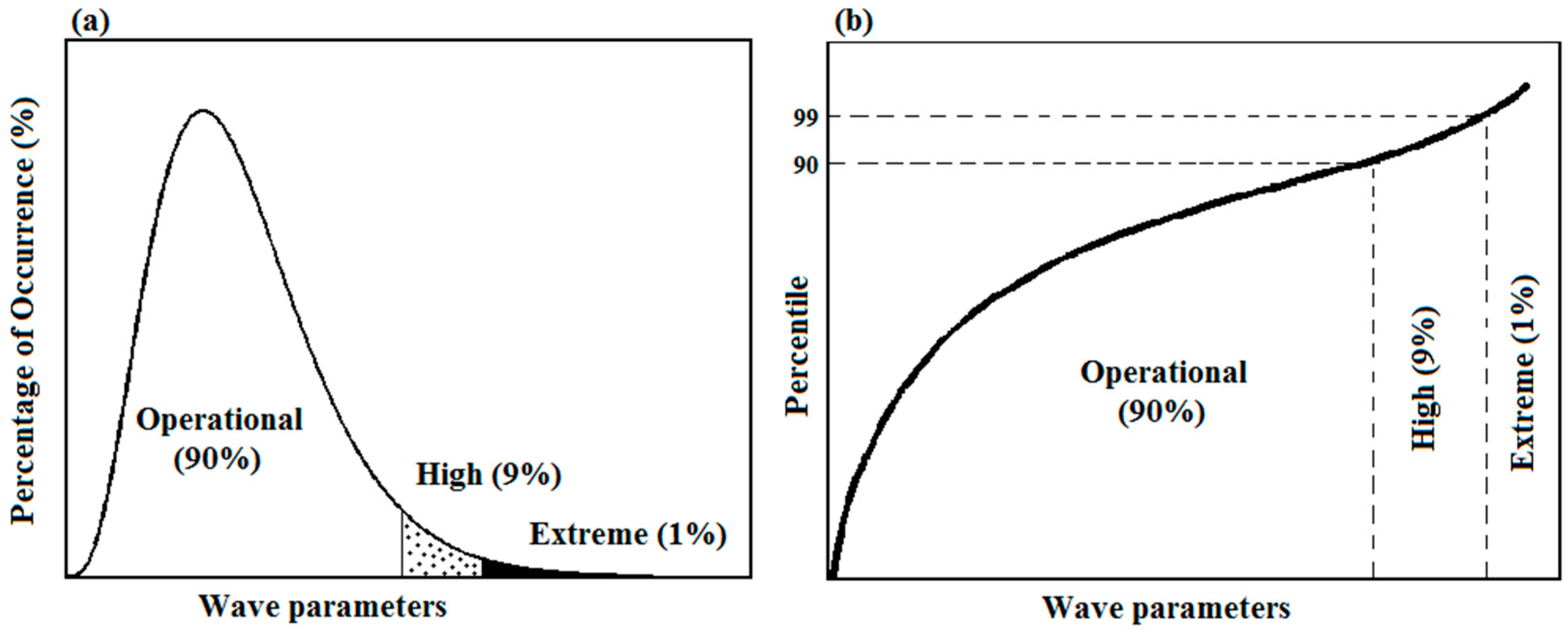
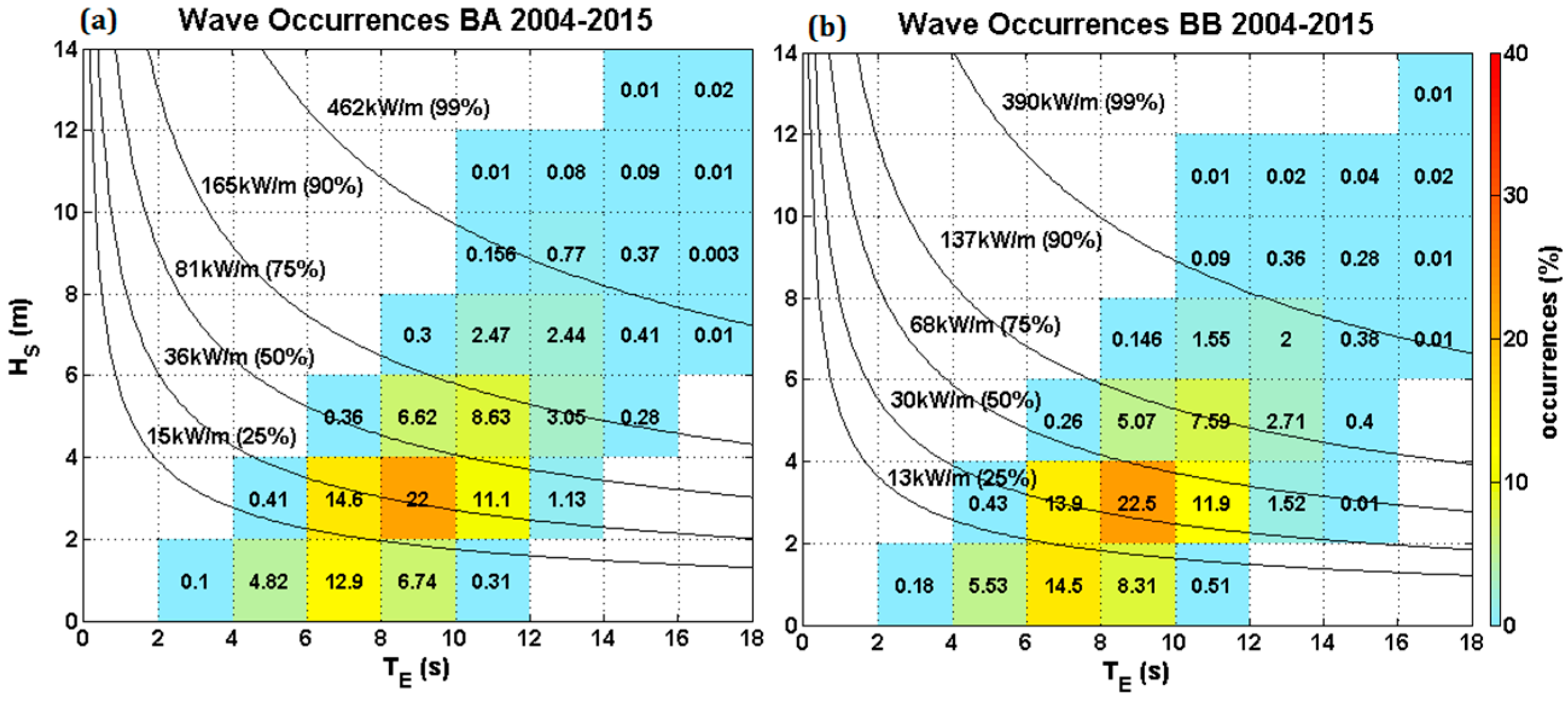
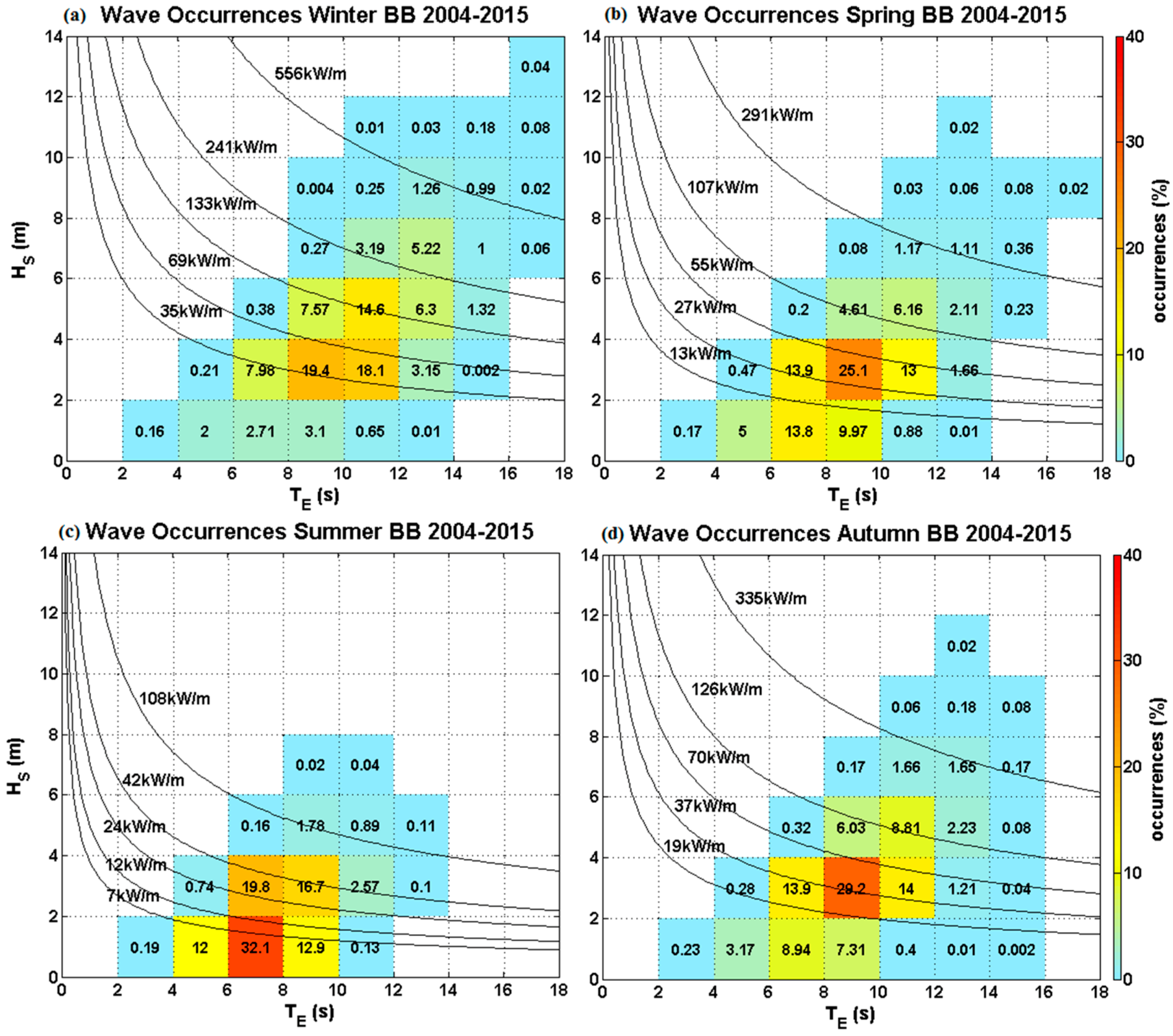
3. Resource Assessment Results
- (1)
- Assessment of mean conditions;
- (2)
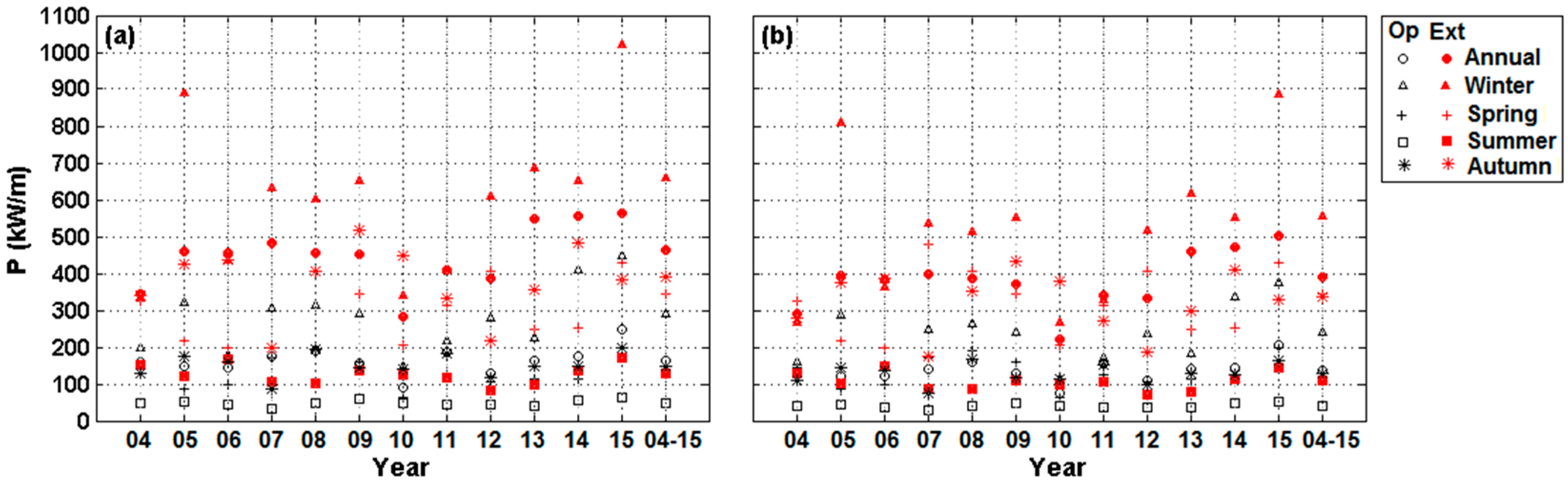
- Characterisation of operational, high and extreme conditions;
- (3)
- Joint occurrence analyses—with MWD in the cases of Hs and TE and between Hs and TE in the case of P.
- ▪
- Annual period: January to December of current year;
- ▪
- Winter period: December of previous year, January and February of current year;
- ▪
- Spring period: March, April and May of current year;
- ▪
- Summer period: June, July and August of current year;
- ▪
- Autumn period: September, October and November of current year.
- ▪
- Operational events: events falling between 0th and 90th percentiles;
- ▪
- High events: events falling between 90th and 99th percentiles;
- ▪
- Extreme events: events falling between 99th and 100th percentiles.
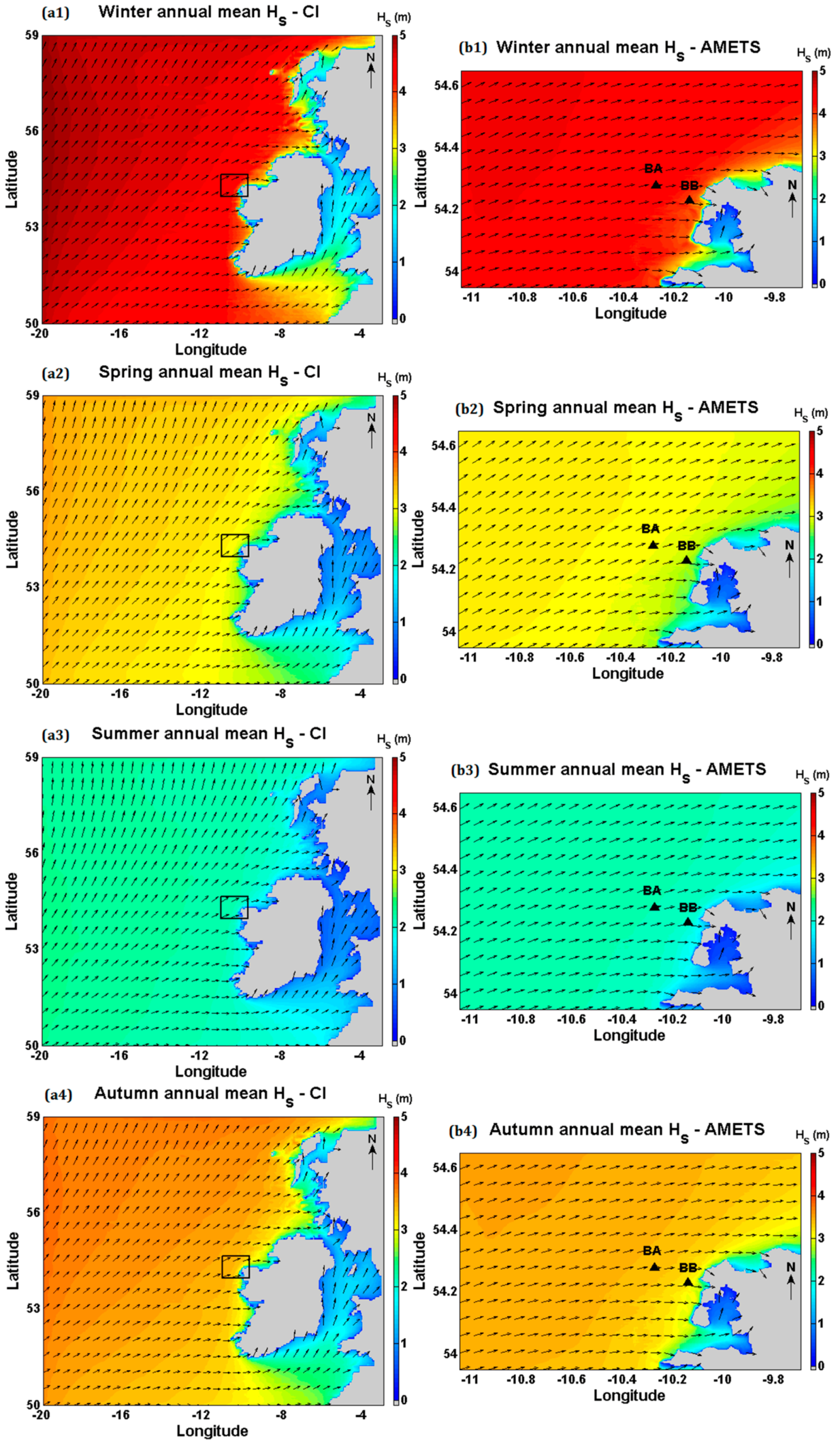
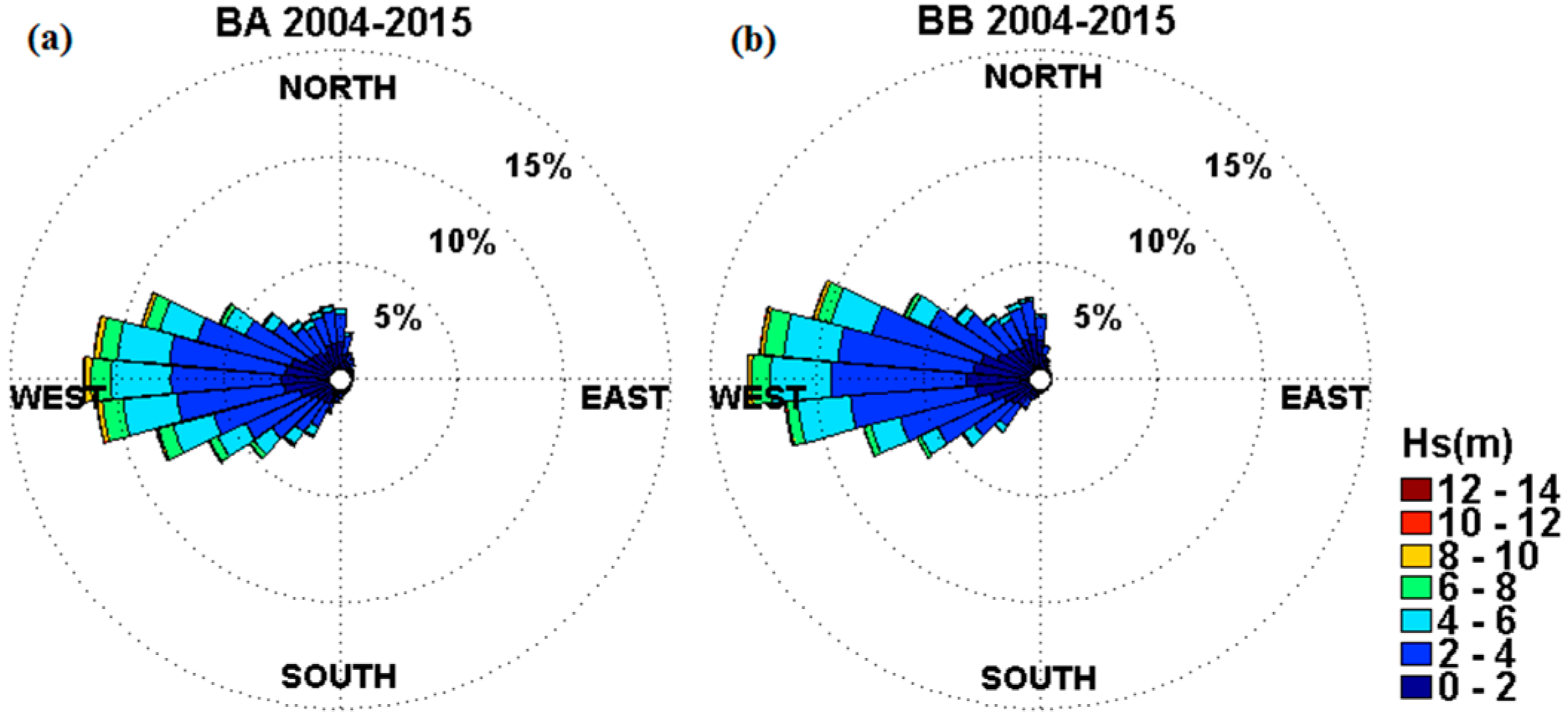
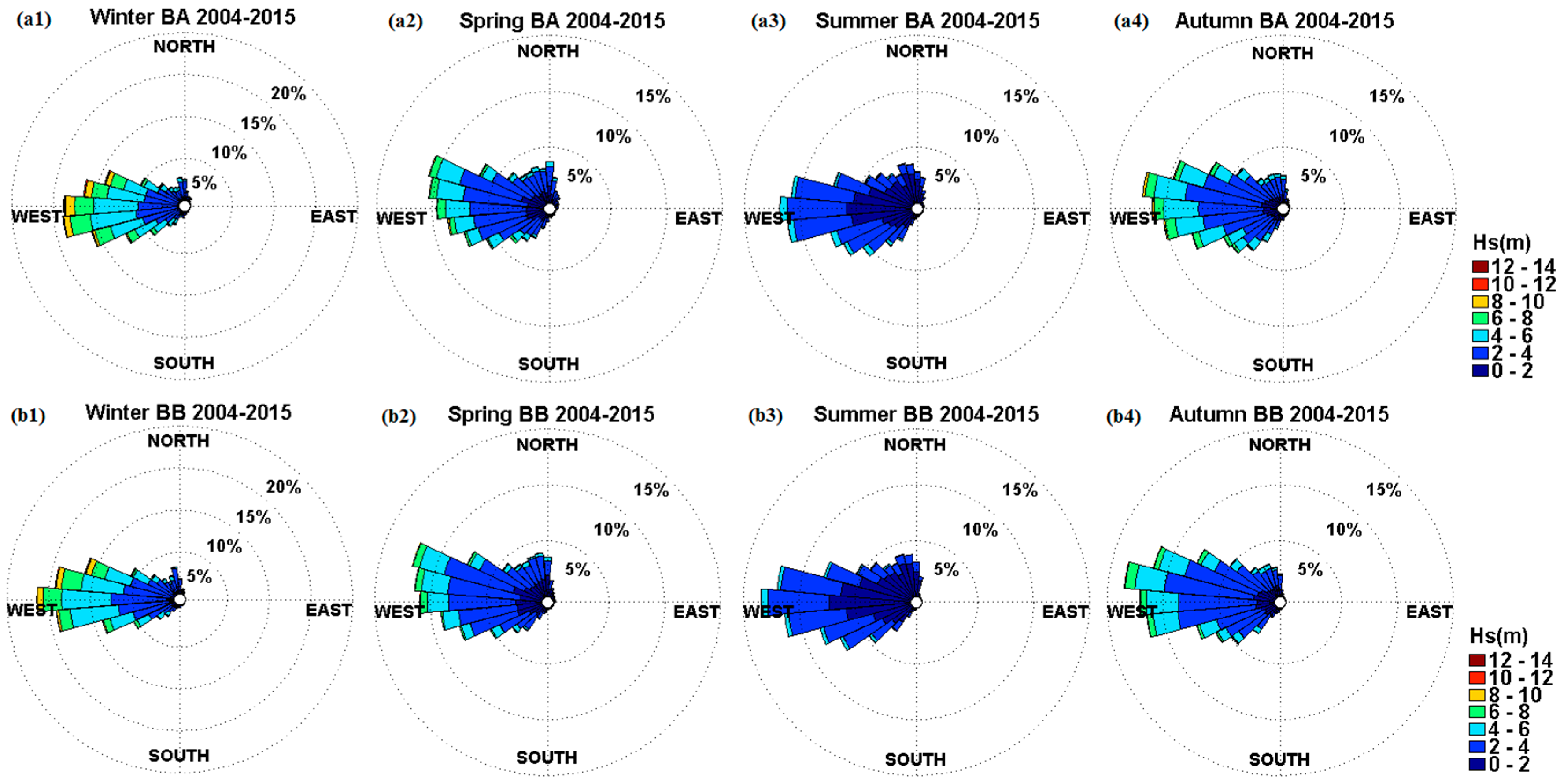
3.1. Significant Wave Height
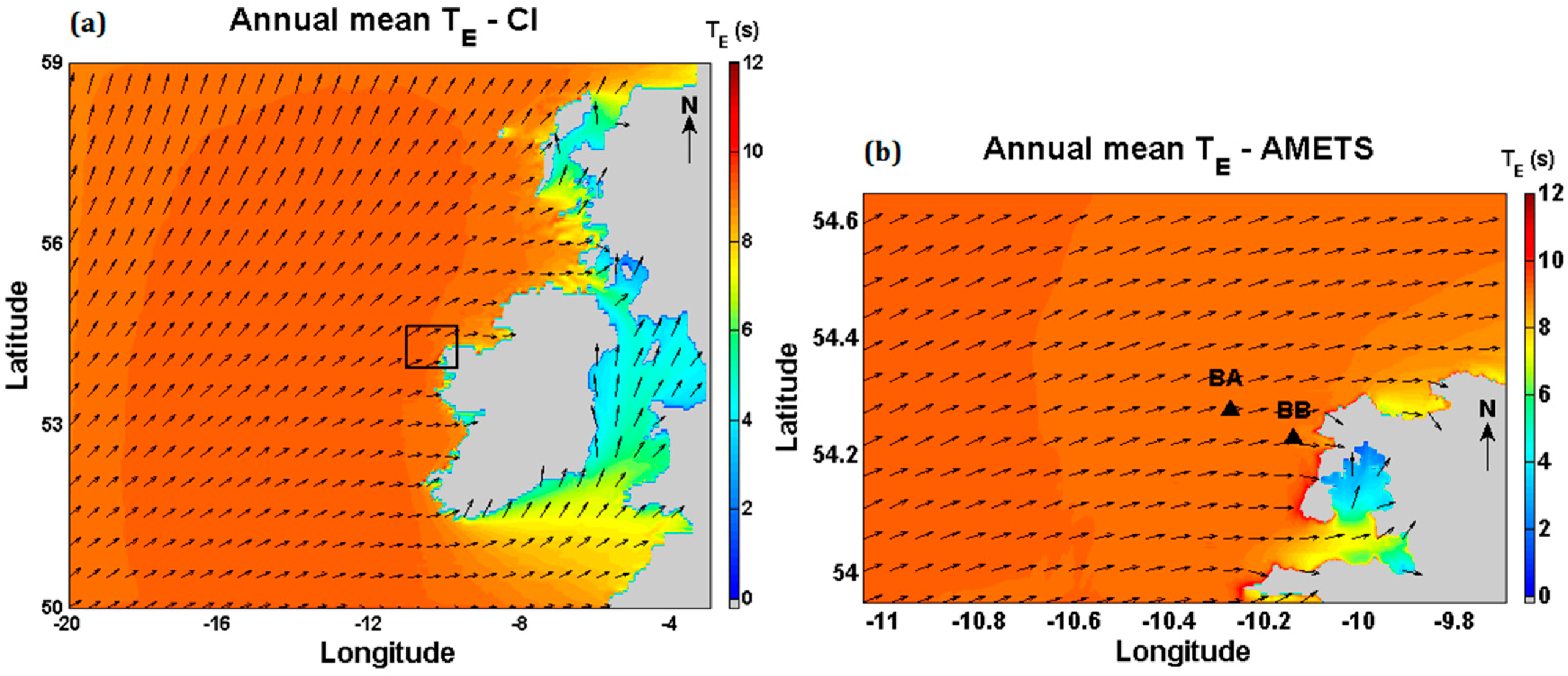
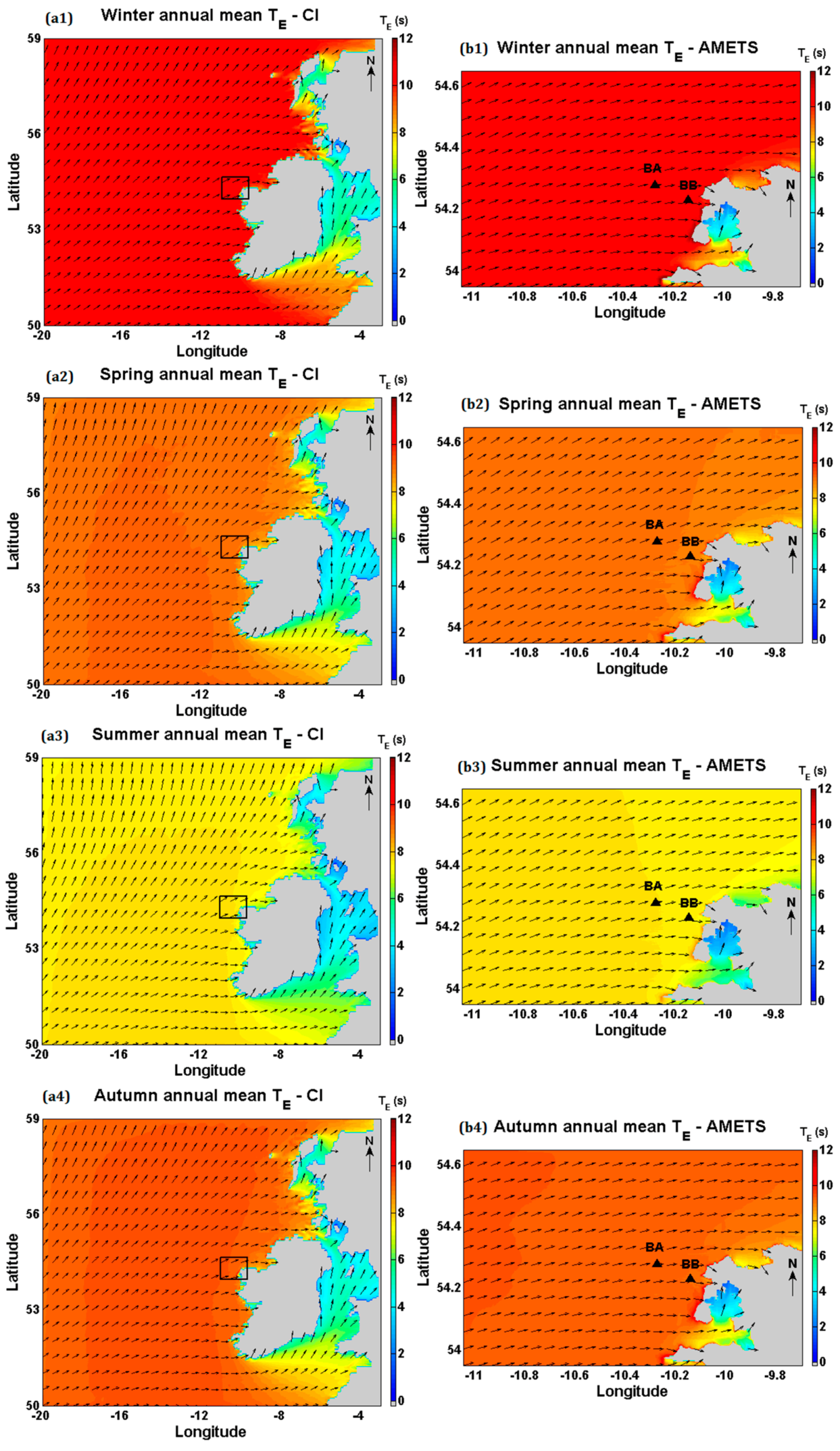
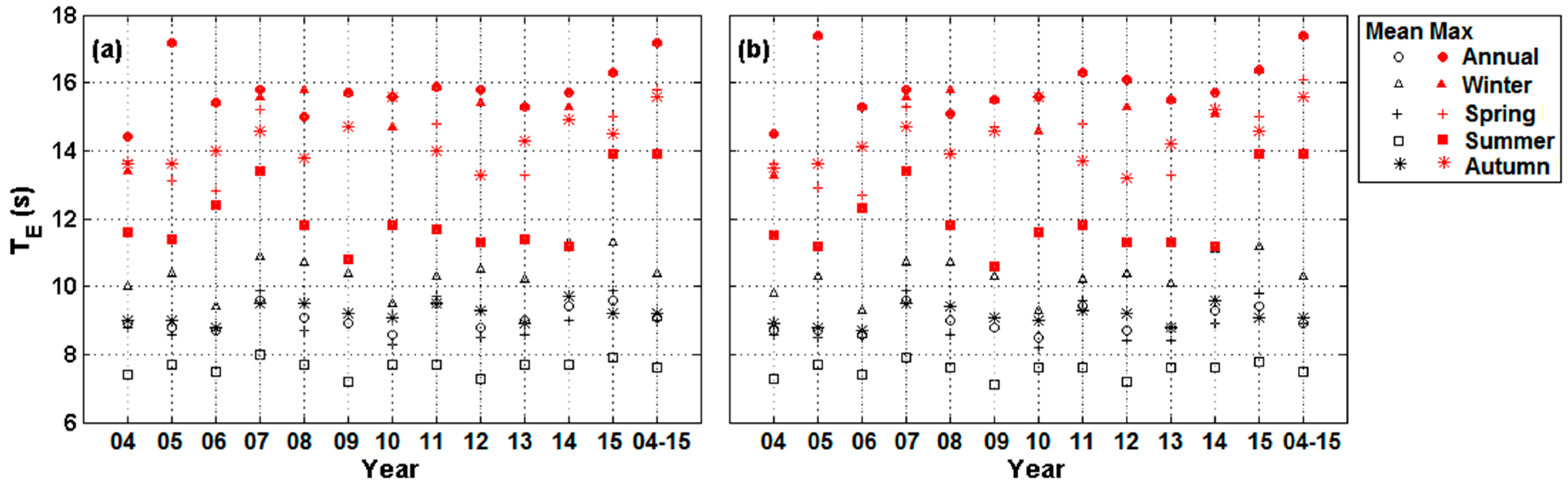
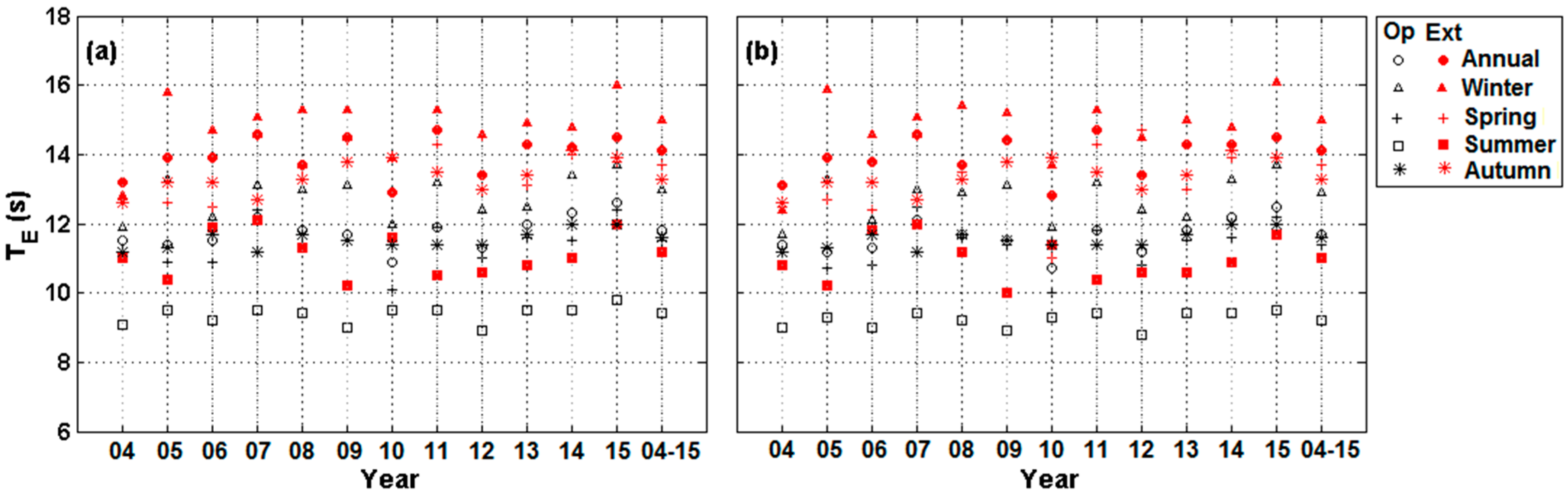
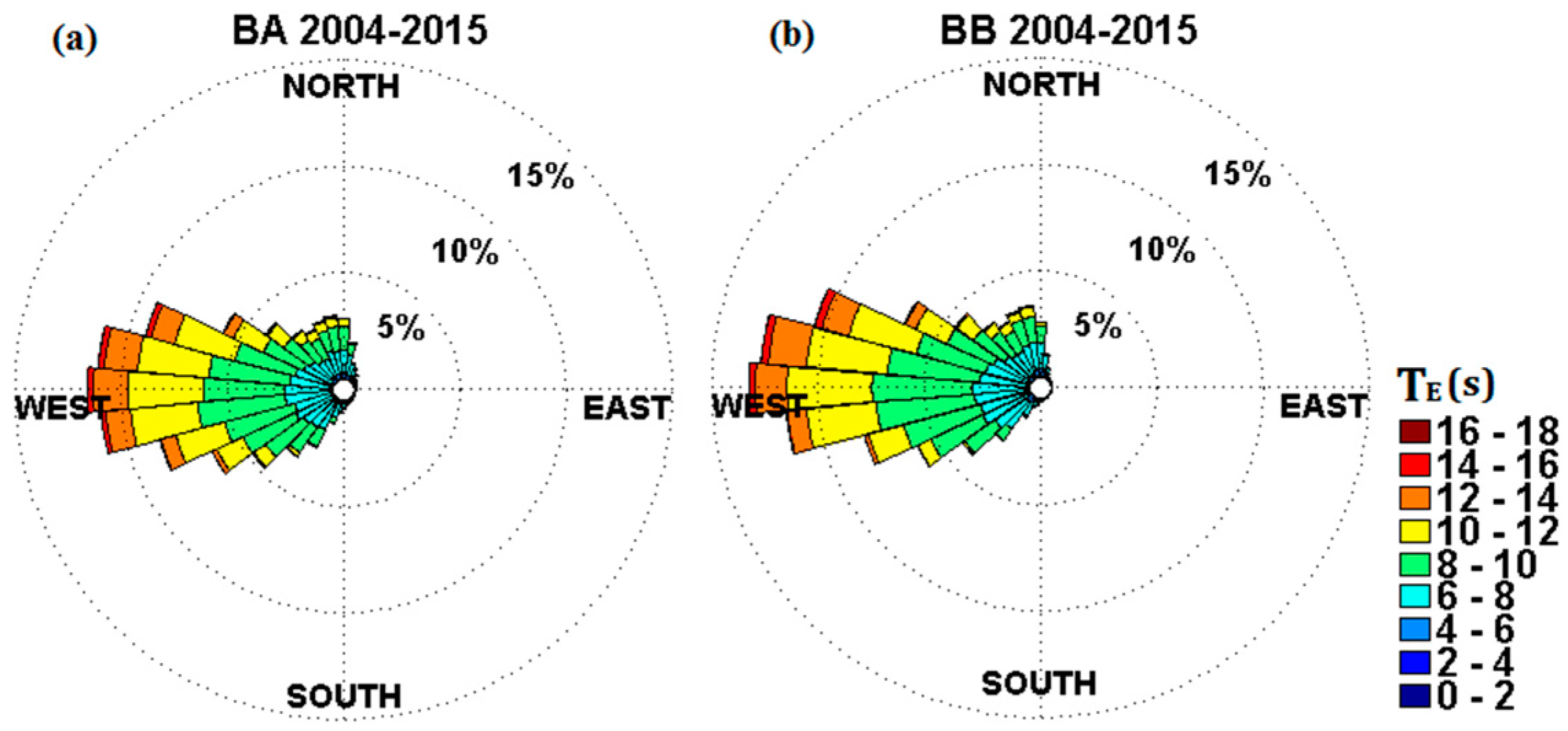
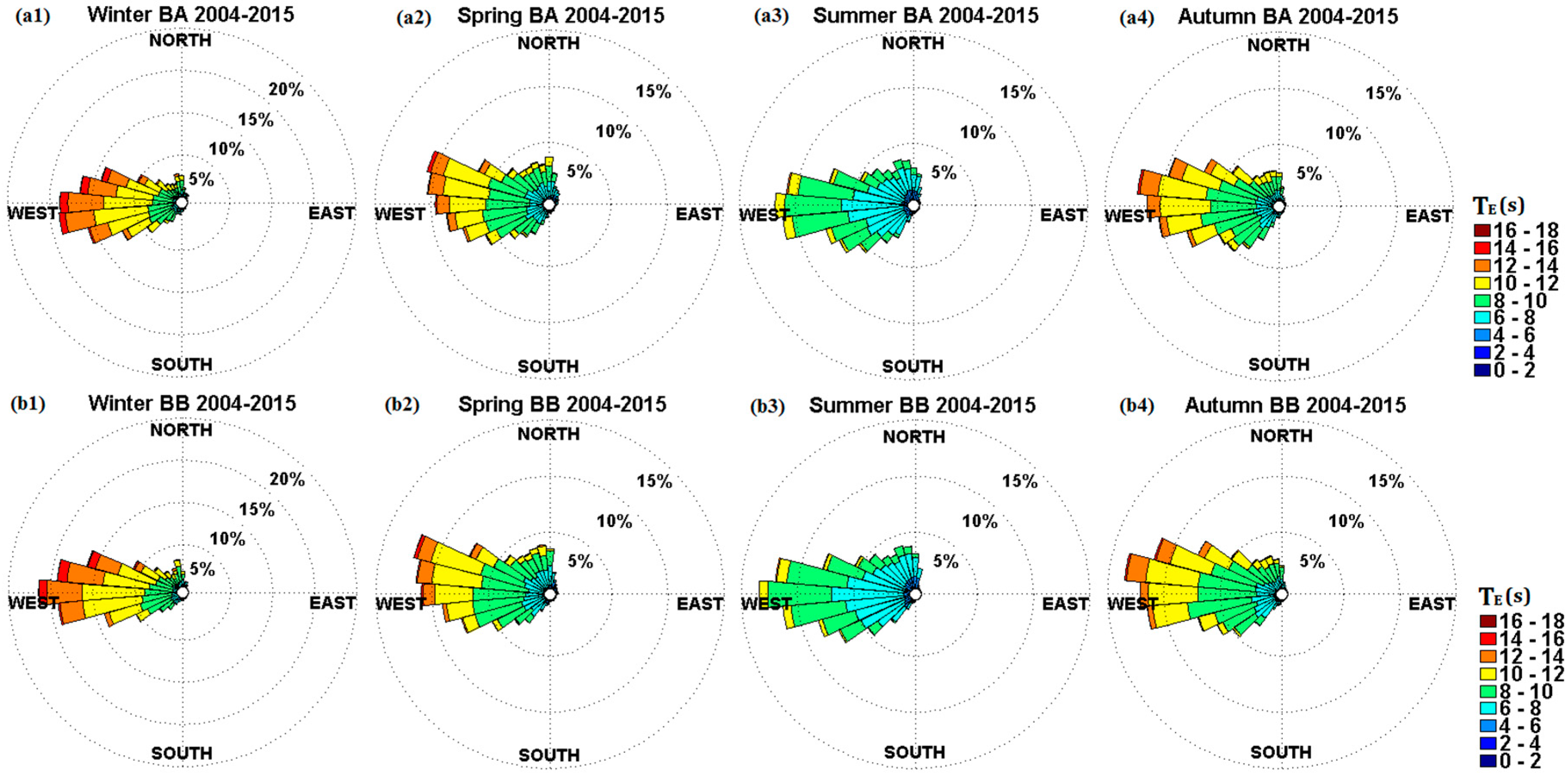
3.2. Energy Wave Period
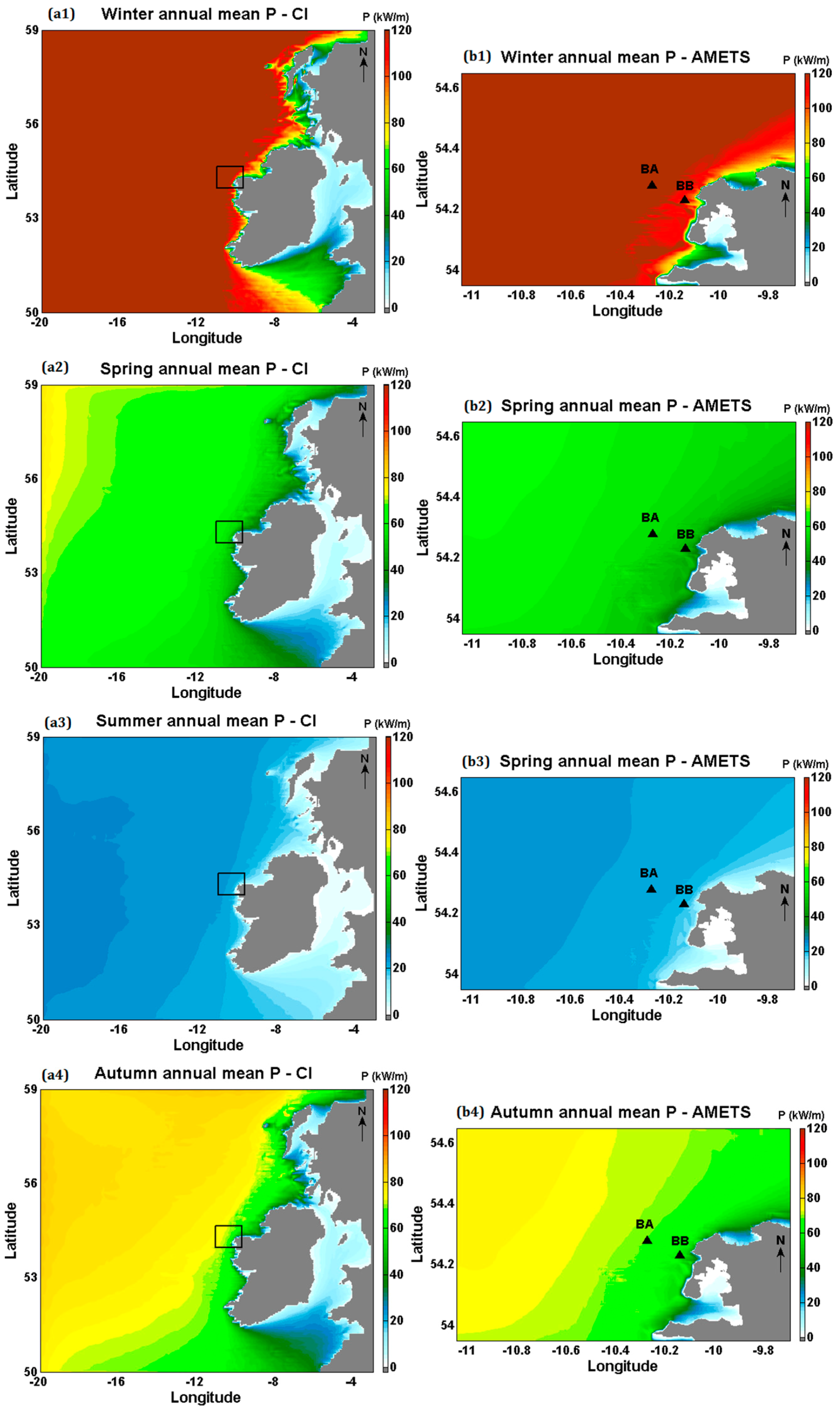
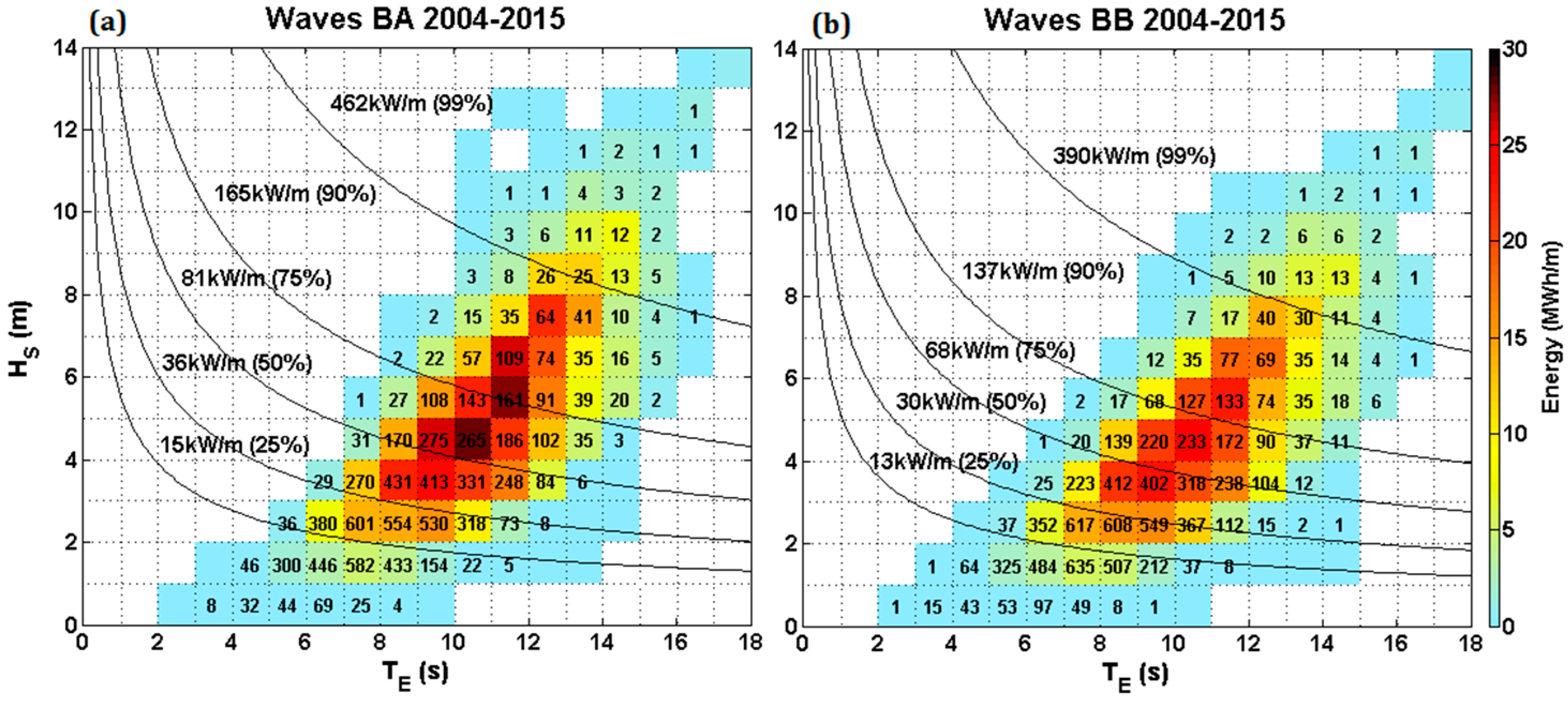
3.3. Wave Power
4. Discussion
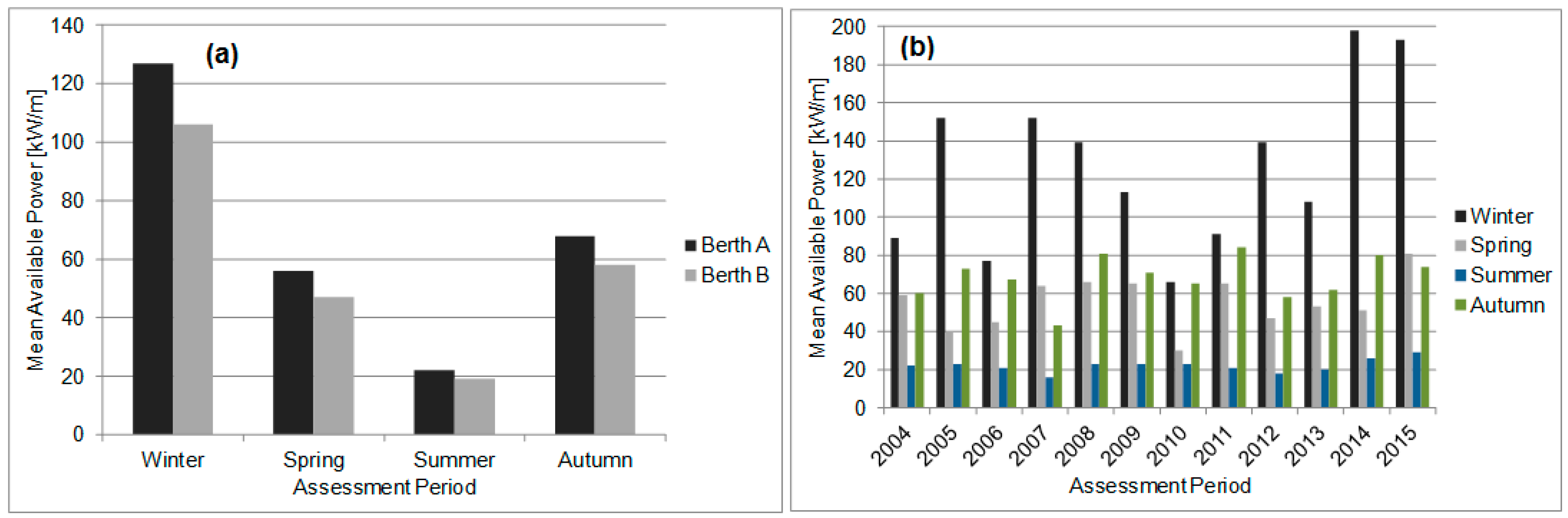
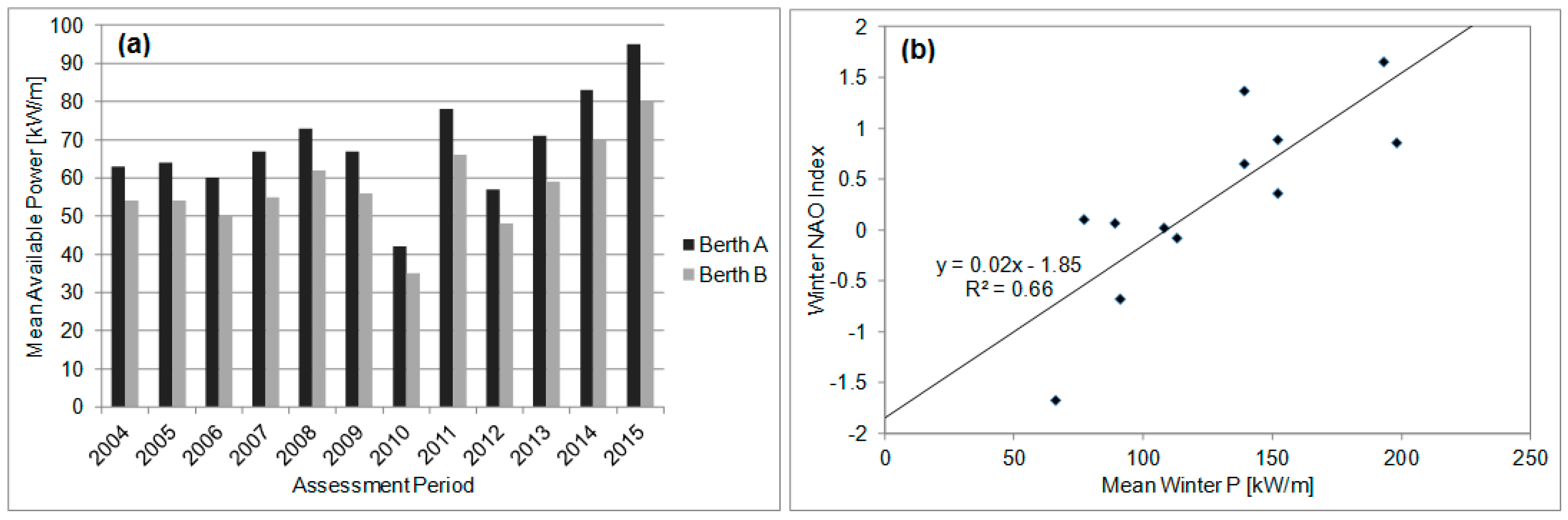
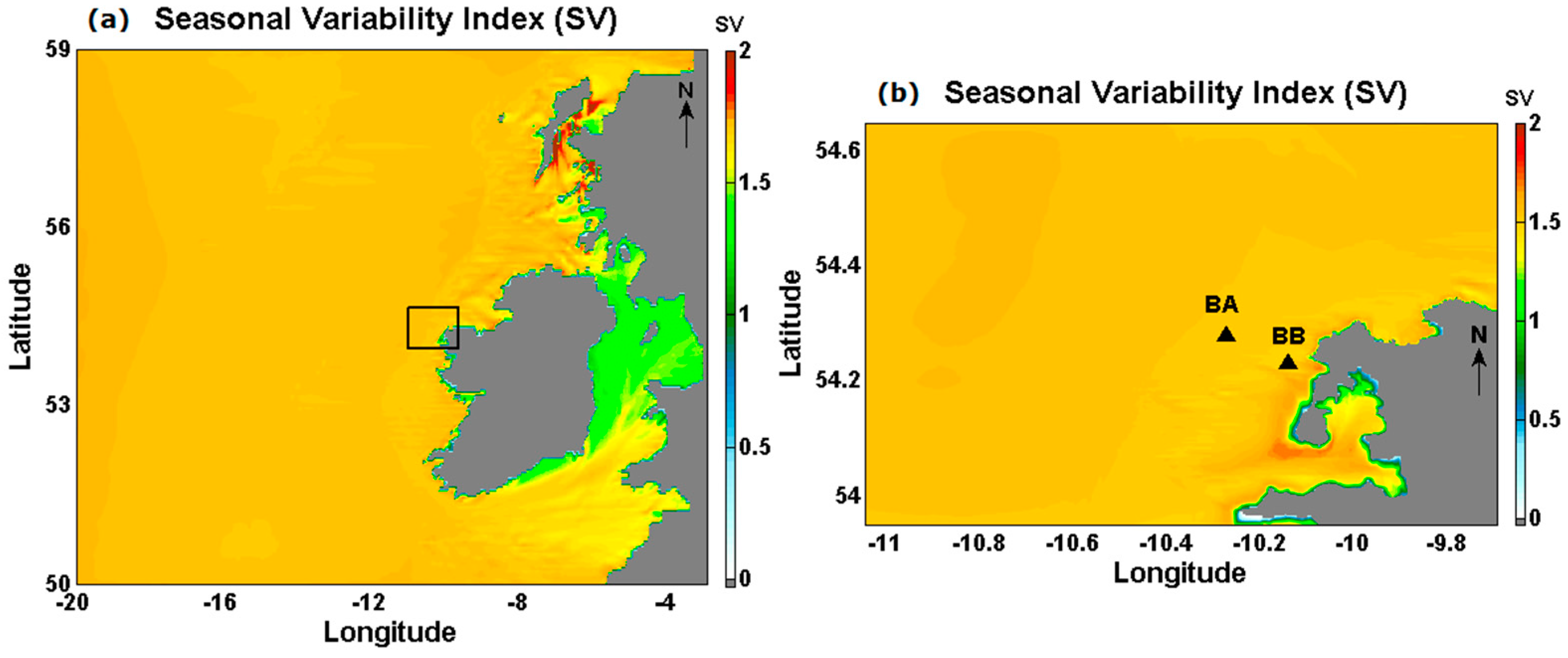
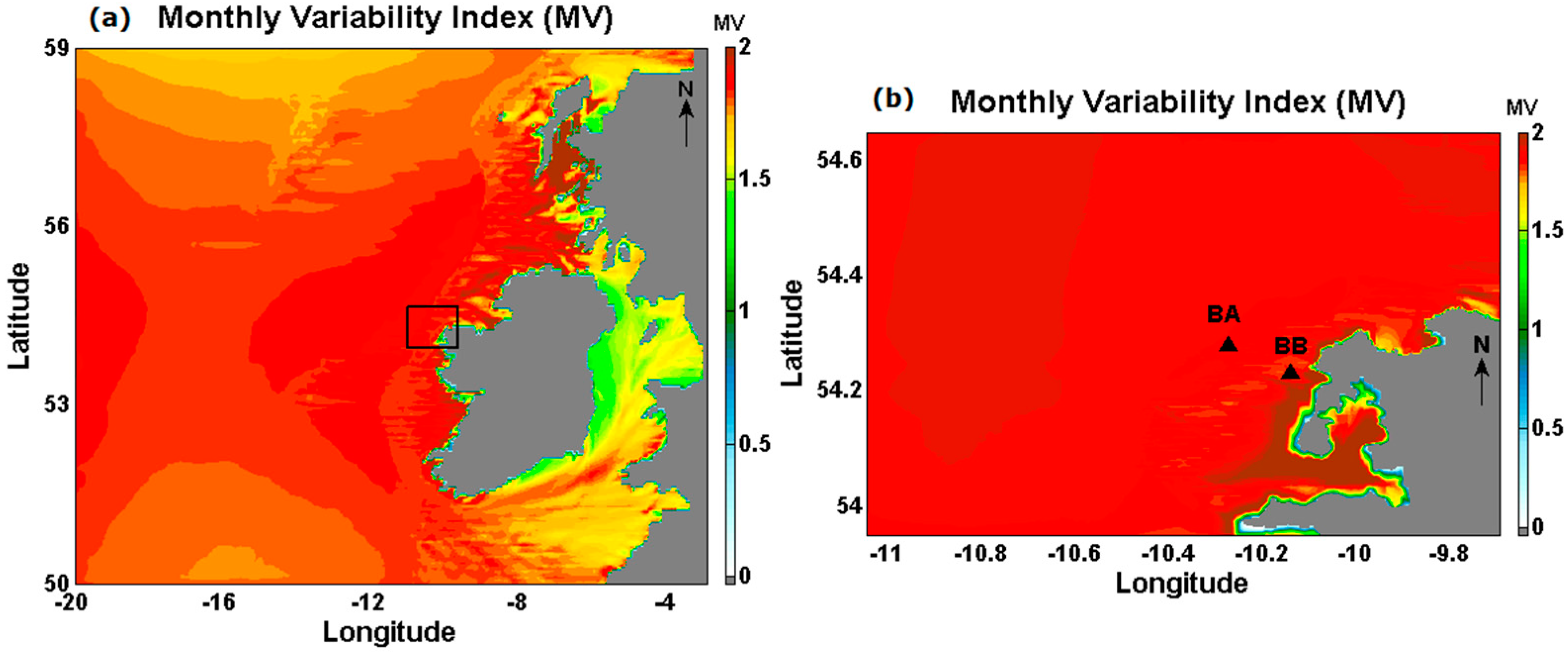
4.1. Resource Variability
4.2. Energy versus Power
5. Conclusions
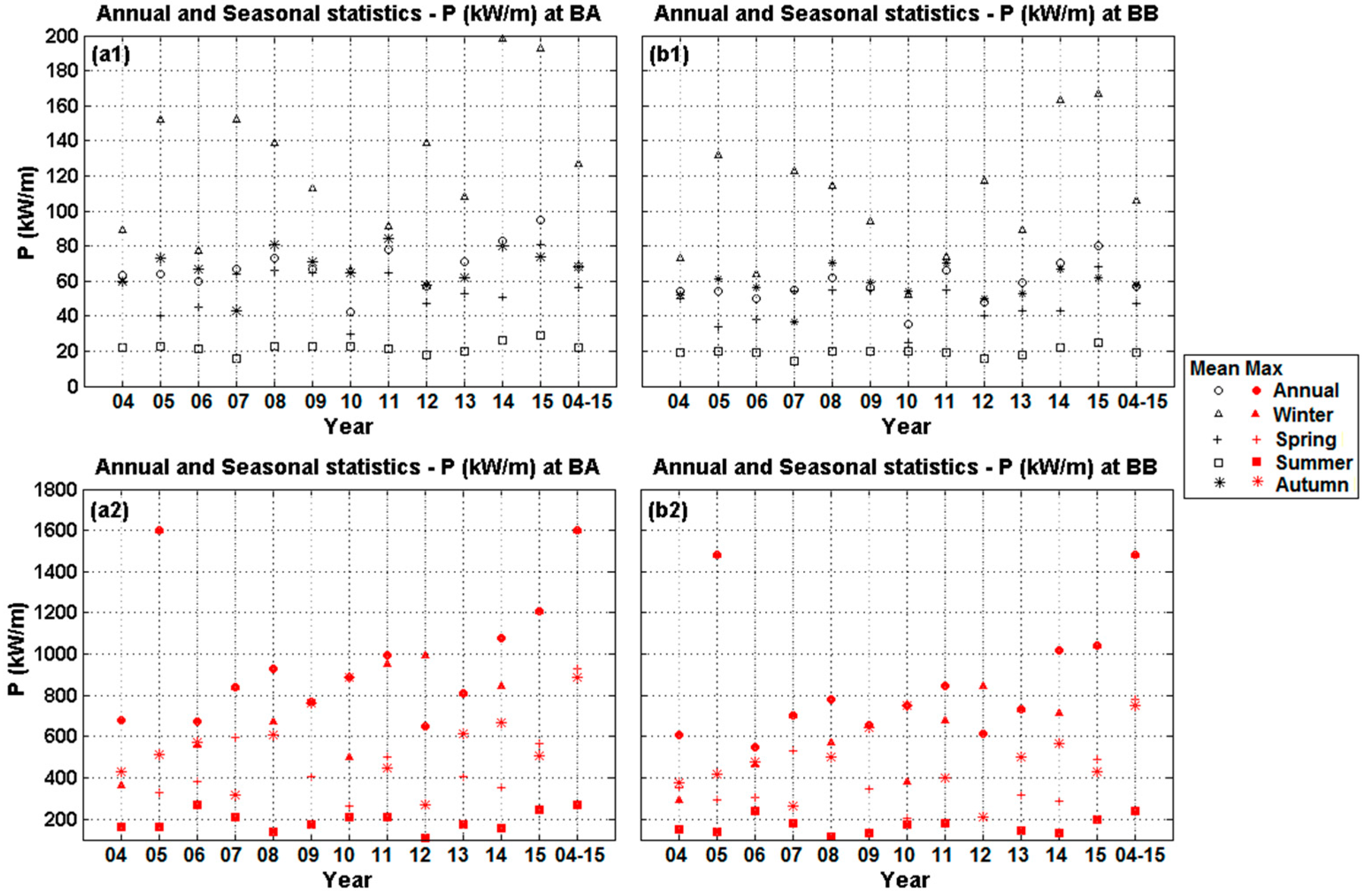
- The wave power resource at AMETS is substantial, with 12-year annual mean powers of 68 kW/m and 57 kW/m calculated at BA and BB, respectively; annual mean Hs were 3.2 m and 3.0 m, respectively, and annual mean TE were 9.1 s and 8.9 s, respectively.
- The determination of operational, high and extreme wave event thresholds as presented here is recommended for wave resource assessments as the thresholds can provide useful information for device developers for device survivability design and performance optimisation.
- There is significant seasonal variation in the wave resource at AMETS—the 12-year mean winter power at BA was 127 kW/m compared to 22 kW/m in summer while mean autumn and spring powers were approximately 60 kW/m. AMETS thus provides a wide range of conditions for testing devices from relatively benign summer sea states to the highly energetic winter sea states; this may provide a useful test strategy where devices are first deployed in summer, then spring/autumn and finally winter. It is also important for device developers to take account of this seasonal variability when designing wave devices for the highly energetic waters off the west coast of Ireland.
- There is significant annual variability in wave resource at AMETS. Given that conditions at AMETS would be reflective of conditions off the Irish west coast, it is recommended that any wave resource assessment of Irish Atlantic waters should be based on a minimum of 10 years data. The strong correlation was between mean winter wave powers and the winter NAO index means that where there is limited wave data at an Irish Atlantic site, the winter NAO index could be used to indicate whether the resource estimates are likely to be under- over-representative. Given the decadal variation in NAO it would also be interesting to conduct the AMETS resource assessment for a multi-decadal period.
- The sea states that contribute most energy at AMETS are not the same as those that occur most often; they are of slightly higher Hs and slightly longer TE. It is extremely important that this mismatch in conditions be considered by device developers when aiming to optimise device performance for particular sea states.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Year | Annual | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | |
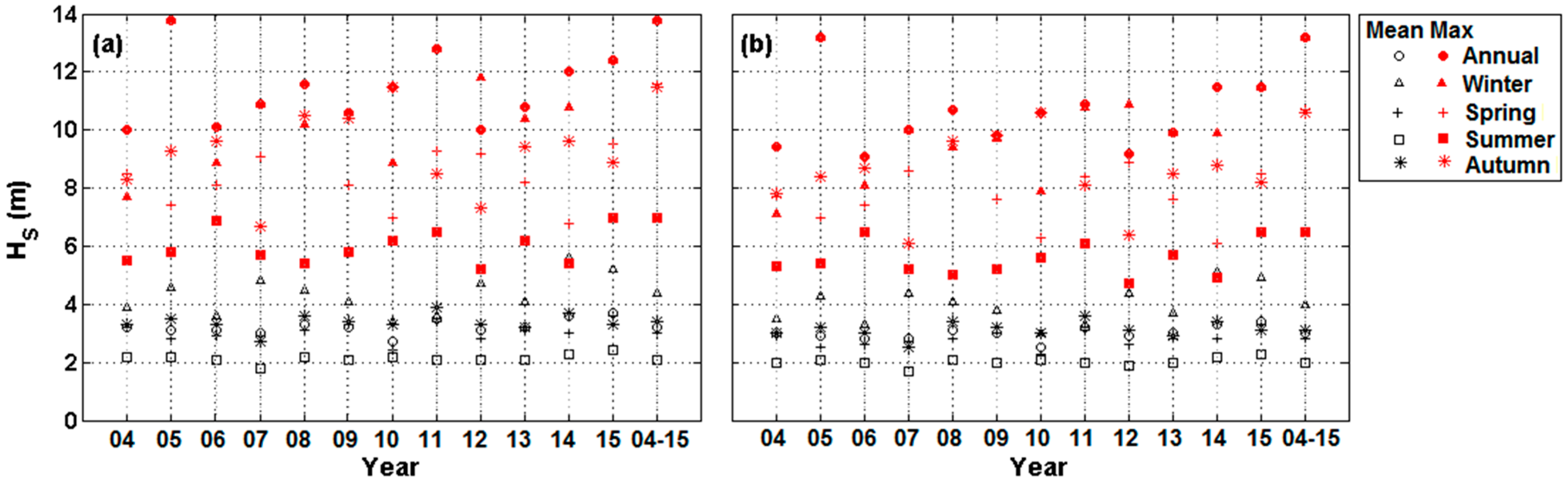
| 2004 | 3.2 | 1.6 | 10.0 | 3.9 | 1.5 | 7.7 | 3.2 | 1.5 | 8.5 | 2.2 | 0.9 | 5.5 | 3.3 | 1.3 | 8.3 |
| 2005 | 3.1 | 1.7 | 13.8 | 4.6 | 2.1 | 13.8 | 2.8 | 1.1 | 7.4 | 2.2 | 0.9 | 5.8 | 3.5 | 1.6 | 9.3 |
| 2006 | 3.1 | 1.6 | 10.1 | 3.6 | 1.4 | 8.9 | 2.9 | 1.2 | 8.1 | 2.1 | 1.0 | 6.9 | 3.3 | 1.6 | 9.6 |
| 2007 | 3.0 | 1.7 | 10.9 | 4.8 | 1.8 | 10.9 | 2.9 | 1.6 | 9.1 | 1.8 | 0.7 | 5.7 | 2.7 | 1.0 | 6.7 |
| 2008 | 3.3 | 1.7 | 11.6 | 4.5 | 1.9 | 10.2 | 3.1 | 1.8 | 11.6 | 2.2 | 0.8 | 5.4 | 3.6 | 1.6 | 10.5 |
| 2009 | 3.2 | 1.6 | 10.6 | 4.1 | 1.7 | 10.6 | 3.3 | 1.4 | 8.1 | 2.1 | 1.1 | 5.8 | 3.4 | 1.5 | 10.4 |
| 2010 | 2.7 | 1.3 | 11.5 | 3.4 | 1.4 | 8.9 | 2.4 | 1.0 | 7.0 | 2.2 | 0.9 | 6.2 | 3.3 | 1.5 | 11.5 |
| 2011 | 3.5 | 1.6 | 12.8 | 3.6 | 1.7 | 12.8 | 3.4 | 1.2 | 9.3 | 2.1 | 0.9 | 6.5 | 3.9 | 1.3 | 8.5 |
| 2012 | 3.1 | 1.5 | 10.0 | 4.7 | 1.6 | 11.8 | 2.8 | 1.4 | 9.2 | 2.1 | 0.8 | 5.2 | 3.3 | 1.1 | 7.3 |
| 2013 | 3.2 | 1.7 | 10.8 | 4.1 | 1.7 | 10.4 | 3.1 | 1.3 | 8.2 | 2.1 | 0.9 | 6.2 | 3.2 | 1.5 | 9.4 |
| 2014 | 3.6 | 1.7 | 12.0 | 5.6 | 1.7 | 10.8 | 3.0 | 1.2 | 6.8 | 2.3 | 0.9 | 5.4 | 3.7 | 1.3 | 9.6 |
| 2015 | 3.7 | 2.0 | 12.4 | 5.2 | 2.1 | 12.4 | 3.6 | 1.6 | 9.5 | 2.4 | 1.0 | 7.0 | 3.3 | 1.8 | 8.9 |
| 2004–2015 | 3.2 | 1.6 | 13.8 | 4.4 | 1.9 | 13.8 | 3.0 | 1.4 | 11.6 | 2.1 | 0.9 | 7.0 | 3.4 | 1.5 | 11.5 |
| Year | Annual | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | |
| 2004 | 3.0 | 1.4 | 9.4 | 3.5 | 1.3 | 7.1 | 2.9 | 1.4 | 7.7 | 2.0 | 0.9 | 5.3 | 3.0 | 1.2 | 7.8 |
| 2005 | 2.9 | 1.5 | 13.2 | 4.3 | 2.0 | 13.2 | 2.5 | 1.0 | 7.0 | 2.1 | 0.8 | 5.4 | 3.2 | 1.5 | 8.4 |
| 2006 | 2.8 | 1.5 | 9.1 | 3.3 | 1.3 | 8.1 | 2.6 | 1.1 | 7.4 | 2.0 | 0.9 | 6.5 | 3.0 | 1.5 | 8.7 |
| 2007 | 2.8 | 1.5 | 10.0 | 4.4 | 1.6 | 10.0 | 2.7 | 1.4 | 8.6 | 1.7 | 0.7 | 5.2 | 2.5 | 0.9 | 6.1 |
| 2008 | 3.1 | 1.6 | 10.7 | 4.1 | 1.8 | 9.4 | 2.8 | 1.7 | 10.7 | 2.1 | 0.8 | 5.0 | 3.4 | 1.5 | 9.6 |
| 2009 | 3.0 | 1.5 | 9.8 | 3.8 | 1.6 | 9.7 | 3.0 | 1.3 | 7.6 | 2.0 | 1.0 | 5.2 | 3.2 | 1.4 | 9.8 |
| 2010 | 2.5 | 1.1 | 10.6 | 3.0 | 1.2 | 7.9 | 2.3 | 0.9 | 6.3 | 2.1 | 0.8 | 5.6 | 3.0 | 1.4 | 10.6 |
| 2011 | 3.2 | 1.5 | 10.9 | 3.3 | 1.5 | 10.8 | 3.1 | 1.2 | 8.4 | 2.0 | 0.8 | 6.1 | 3.6 | 1.2 | 8.1 |
| 2012 | 2.9 | 1.3 | 9.2 | 4.4 | 1.5 | 10.9 | 2.6 | 1.3 | 8.9 | 1.9 | 0.7 | 4.7 | 3.1 | 1.0 | 6.4 |
| 2013 | 3.0 | 1.6 | 9.9 | 3.7 | 1.6 | 9.9 | 2.8 | 1.2 | 7.6 | 2.0 | 0.8 | 5.7 | 2.9 | 1.4 | 8.5 |
| 2014 | 3.3 | 1.6 | 11.5 | 5.1 | 1.6 | 9.9 | 2.8 | 1.1 | 6.1 | 2.2 | 0.8 | 4.9 | 3.4 | 1.2 | 8.8 |
| 2015 | 3.4 | 1.8 | 11.5 | 4.9 | 2.0 | 11.5 | 3.3 | 1.5 | 8.5 | 2.3 | 0.9 | 6.5 | 3.1 | 1.6 | 8.2 |
| 2004–2015 | 3.0 | 1.4 | 13.2 | 4.0 | 1.7 | 13.2 | 2.8 | 1.3 | 10.7 | 2.0 | 0.8 | 6.5 | 3.1 | 1.4 | 10.6 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
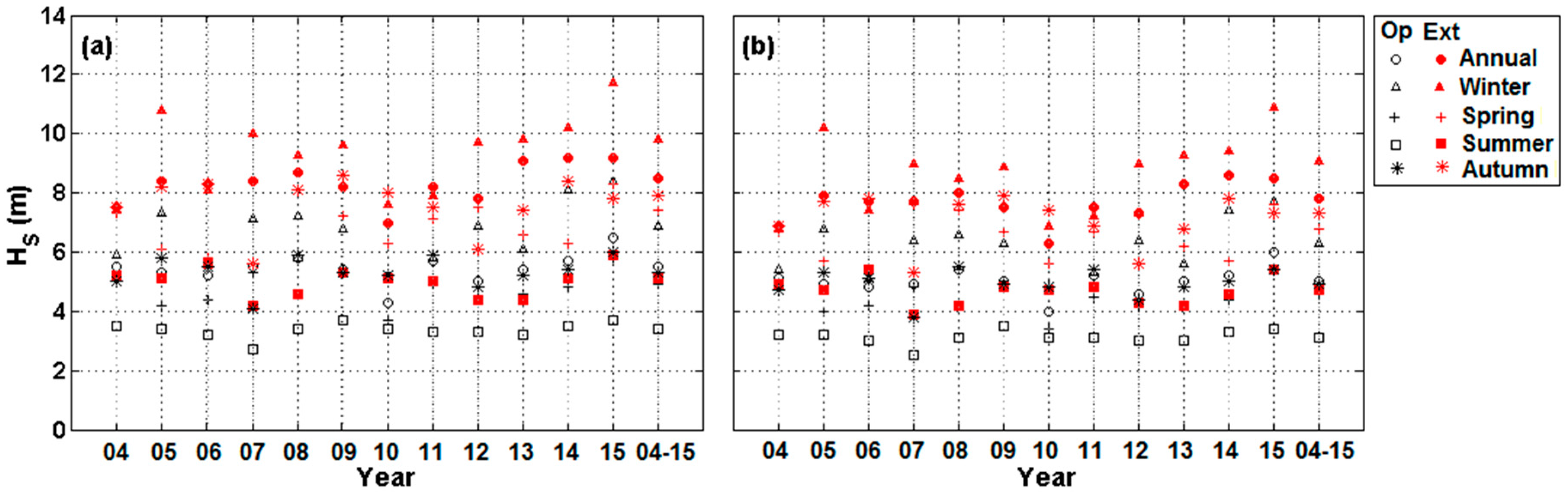
| 2004 | 5.5 | 7.5 | 5.9 | 7.4 | 5.2 | 7.3 | 3.5 | 5.2 | 5.0 | 7.5 |
| 2005 | 5.3 | 8.4 | 7.3 | 10.8 | 4.2 | 6.1 | 3.4 | 5.1 | 5.8 | 8.2 |
| 2006 | 5.2 | 8.3 | 5.6 | 8.1 | 4.4 | 5.8 | 3.2 | 5.6 | 5.5 | 8.3 |
| 2007 | 5.5 | 8.4 | 7.1 | 10.0 | 5.3 | 8.4 | 2.7 | 4.2 | 4.1 | 5.6 |
| 2008 | 5.8 | 8.7 | 7.2 | 9.3 | 5.7 | 8.1 | 3.4 | 4.6 | 5.9 | 8.1 |
| 2009 | 5.4 | 8.2 | 6.8 | 9.6 | 5.4 | 7.2 | 3.7 | 5.3 | 5.3 | 8.6 |
| 2010 | 4.3 | 7.0 | 5.2 | 7.6 | 3.7 | 6.3 | 3.4 | 5.1 | 5.2 | 8.0 |
| 2011 | 5.7 | 8.2 | 5.8 | 7.9 | 4.9 | 7.1 | 3.3 | 5.0 | 5.9 | 7.5 |
| 2012 | 5.0 | 7.8 | 6.9 | 9.7 | 4.5 | 7.5 | 3.3 | 4.4 | 4.8 | 6.1 |
| 2013 | 5.4 | 9.1 | 6.1 | 9.8 | 4.6 | 6.6 | 3.2 | 4.4 | 5.2 | 7.4 |
| 2014 | 5.7 | 9.2 | 8.1 | 10.2 | 4.8 | 6.3 | 3.5 | 5.1 | 5.4 | 8.4 |
| 2015 | 6.5 | 9.2 | 8.4 | 11.7 | 5.8 | 8.3 | 3.7 | 5.9 | 6.0 | 7.8 |
| 2004–2015 | 5.5 | 8.5 | 6.9 | 9.8 | 4.9 | 7.4 | 3.4 | 5.1 | 5.3 | 7.9 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
| 2004 | 5.1 | 6.9 | 5.4 | 6.8 | 4.9 | 6.7 | 3.2 | 4.9 | 4.7 | 6.9 |
| 2005 | 4.9 | 7.9 | 6.8 | 10.2 | 4.0 | 5.7 | 3.2 | 4.7 | 5.3 | 7.7 |
| 2006 | 4.8 | 7.7 | 5.1 | 7.4 | 4.2 | 5.4 | 3.0 | 5.4 | 5.1 | 7.8 |
| 2007 | 4.9 | 7.7 | 6.4 | 9.0 | 4.8 | 7.6 | 2.5 | 3.9 | 3.8 | 5.3 |
| 2008 | 5.4 | 8.0 | 6.6 | 8.5 | 5.4 | 7.4 | 3.1 | 4.2 | 5.5 | 7.6 |
| 2009 | 5.0 | 7.5 | 6.3 | 8.9 | 5.0 | 6.7 | 3.5 | 4.8 | 4.9 | 7.9 |
| 2010 | 4.0 | 6.3 | 4.7 | 6.9 | 3.4 | 5.6 | 3.1 | 4.7 | 4.8 | 7.4 |
| 2011 | 5.2 | 7.5 | 5.3 | 7.2 | 4.5 | 6.7 | 3.1 | 4.8 | 5.4 | 6.9 |
| 2012 | 4.6 | 7.3 | 6.4 | 9.0 | 4.2 | 7.2 | 3.0 | 4.3 | 4.4 | 5.6 |
| 2013 | 5.0 | 8.3 | 5.6 | 9.3 | 4.2 | 6.2 | 3.0 | 4.2 | 4.8 | 6.8 |
| 2014 | 5.2 | 8.6 | 7.4 | 9.4 | 4.4 | 5.7 | 3.3 | 4.6 | 5.0 | 7.8 |
| 2015 | 6.0 | 8.5 | 7.7 | 10.9 | 5.4 | 7.6 | 3.4 | 5.4 | 5.4 | 7.3 |
| 2004–2015 | 5.0 | 7.8 | 6.3 | 9.1 | 4.6 | 6.8 | 3.1 | 4.7 | 4.9 | 7.3 |
| Year | Yearly | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | |
| 2004 | 8.9 | 1.9 | 14.4 | 10.0 | 1.6 | 13.4 | 8.8 | 1.7 | 13.7 | 7.4 | 1.3 | 11.6 | 9.0 | 1.7 | 13.6 |
| 2005 | 8.8 | 1.9 | 17.2 | 10.4 | 2.4 | 17.2 | 8.6 | 1.6 | 13.1 | 7.7 | 1.3 | 11.4 | 9.0 | 1.7 | 13.6 |
| 2006 | 8.7 | 2.0 | 15.4 | 9.4 | 2.1 | 15.4 | 8.7 | 1.7 | 12.8 | 7.5 | 1.4 | 12.4 | 8.8 | 2.0 | 14.0 |
| 2007 | 9.6 | 2.0 | 15.8 | 10.9 | 1.8 | 15.6 | 9.9 | 1.8 | 15.2 | 8.0 | 1.3 | 13.4 | 9.5 | 1.4 | 14.6 |
| 2008 | 9.1 | 2.0 | 15.0 | 10.7 | 2.0 | 15.8 | 8.7 | 2.0 | 15.0 | 7.7 | 1.3 | 11.8 | 9.5 | 1.7 | 13.8 |
| 2009 | 8.9 | 2.1 | 15.7 | 10.4 | 2.1 | 15.7 | 9.2 | 1.9 | 14.7 | 7.2 | 1.4 | 10.8 | 9.2 | 1.7 | 14.7 |
| 2010 | 8.6 | 1.7 | 15.6 | 9.5 | 2.0 | 14.7 | 8.3 | 1.4 | 11.8 | 7.7 | 1.4 | 11.8 | 9.1 | 1.7 | 15.6 |
| 2011 | 9.5 | 2.0 | 15.9 | 10.3 | 2.2 | 15.9 | 9.7 | 1.7 | 14.8 | 7.7 | 1.3 | 11.7 | 9.5 | 1.6 | 14.0 |
| 2012 | 8.8 | 1.9 | 15.8 | 10.5 | 1.6 | 15.4 | 8.5 | 2.0 | 15.8 | 7.3 | 1.2 | 11.3 | 9.3 | 1.6 | 13.3 |
| 2013 | 9.0 | 2.2 | 15.3 | 10.2 | 1.8 | 15.3 | 8.6 | 2.1 | 13.3 | 7.7 | 1.4 | 11.4 | 8.9 | 2.0 | 14.3 |
| 2014 | 9.4 | 2.1 | 15.7 | 11.3 | 1.7 | 15.3 | 9.0 | 1.9 | 15.7 | 7.7 | 1.4 | 11.2 | 9.7 | 1.7 | 14.9 |
| 2015 | 9.6 | 2.2 | 16.3 | 11.3 | 1.9 | 16.3 | 9.9 | 1.8 | 15.0 | 7.9 | 1.4 | 13.9 | 9.2 | 2.1 | 14.5 |
| 2004–2015 | 9.1 | 1.9 | 17.2 | 10.4 | 2.0 | 17.2 | 9.0 | 1.9 | 15.8 | 7.6 | 1.4 | 13.9 | 9.2 | 1.8 | 15.6 |
| Year | Yearly | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | Mean | ±SD | Max | |
| 2004 | 8.7 | 1.9 | 14.5 | 9.8 | 1.5 | 13.3 | 8.6 | 1.7 | 13.6 | 7.3 | 1.3 | 11.5 | 8.9 | 1.7 | 13.5 |
| 2005 | 8.7 | 1.9 | 17.4 | 10.3 | 2.4 | 17.4 | 8.5 | 1.5 | 12.9 | 7.7 | 1.3 | 11.2 | 8.8 | 1.7 | 13.6 |
| 2006 | 8.6 | 2.0 | 15.3 | 9.3 | 2.1 | 15.3 | 8.5 | 1.7 | 12.7 | 7.4 | 1.4 | 12.3 | 8.7 | 2.0 | 14.1 |
| 2007 | 9.6 | 2.0 | 15.8 | 10.7 | 1.8 | 15.6 | 9.9 | 1.8 | 15.3 | 7.9 | 1.3 | 13.4 | 9.5 | 1.4 | 14.7 |
| 2008 | 9.0 | 2.0 | 15.1 | 10.7 | 2.0 | 15.8 | 8.6 | 2.0 | 15.1 | 7.6 | 1.3 | 11.8 | 9.4 | 1.7 | 13.9 |
| 2009 | 8.8 | 2.1 | 15.5 | 10.3 | 2.2 | 15.5 | 9.1 | 1.9 | 14.7 | 7.1 | 1.4 | 10.6 | 9.1 | 1.7 | 14.6 |
| 2010 | 8.5 | 1.7 | 15.6 | 9.3 | 2.0 | 14.6 | 8.2 | 1.4 | 11.5 | 7.6 | 1.3 | 11.6 | 9.0 | 1.7 | 15.6 |
| 2011 | 9.4 | 2.0 | 16.3 | 10.2 | 2.3 | 16.3 | 9.6 | 1.7 | 14.8 | 7.6 | 1.3 | 11.8 | 9.3 | 1.6 | 13.7 |
| 2012 | 8.7 | 1.9 | 16.1 | 10.4 | 1.6 | 15.3 | 8.4 | 2.0 | 16.1 | 7.2 | 1.2 | 11.3 | 9.2 | 1.6 | 13.2 |
| 2013 | 8.8 | 2.2 | 15.5 | 10.1 | 1.9 | 15.5 | 8.4 | 2.2 | 13.3 | 7.6 | 1.4 | 11.3 | 8.8 | 2.0 | 14.2 |
| 2014 | 9.3 | 2.1 | 15.7 | 11.1 | 1.8 | 15.1 | 8.9 | 1.9 | 15.7 | 7.6 | 1.4 | 11.2 | 9.6 | 1.8 | 15.2 |
| 2015 | 9.4 | 2.2 | 16.4 | 11.2 | 2.0 | 16.4 | 9.8 | 1.8 | 15.0 | 7.8 | 1.4 | 13.9 | 9.1 | 2.1 | 14.6 |
| 2004–2015 | 8.9 | 1.9 | 17.4 | 10.3 | 2.1 | 17.4 | 8.9 | 1.9 | 16.1 | 7.5 | 1.4 | 13.9 | 9.1 | 1.8 | 15.6 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
| 2004 | 11.5 | 13.2 | 11.9 | 12.8 | 11.0 | 12.7 | 9.1 | 11.0 | 11.2 | 12.6 |
| 2005 | 11.4 | 13.9 | 13.3 | 15.8 | 10.9 | 12.6 | 9.5 | 10.4 | 11.3 | 13.2 |
| 2006 | 11.5 | 13.9 | 12.2 | 14.7 | 10.9 | 12.5 | 9.2 | 11.9 | 11.7 | 13.2 |
| 2007 | 12.2 | 14.6 | 13.1 | 15.1 | 12.4 | 14.5 | 9.5 | 12.1 | 11.2 | 12.7 |
| 2008 | 11.8 | 13.7 | 13.0 | 15.3 | 11.7 | 13.6 | 9.4 | 11.3 | 11.7 | 13.3 |
| 2009 | 11.7 | 14.5 | 13.1 | 15.3 | 11.5 | 14.4 | 9.0 | 10.2 | 11.5 | 13.8 |
| 2010 | 10.9 | 12.9 | 12.0 | 13.9 | 10.1 | 11.4 | 9.5 | 11.6 | 11.4 | 13.9 |
| 2011 | 11.9 | 14.7 | 13.2 | 15.3 | 11.9 | 14.3 | 9.5 | 10.5 | 11.4 | 13.5 |
| 2012 | 11.3 | 13.4 | 12.4 | 14.6 | 11.0 | 14.5 | 8.9 | 10.6 | 11.4 | 13.0 |
| 2013 | 12.0 | 14.3 | 12.5 | 14.9 | 11.6 | 13.1 | 9.5 | 10.8 | 11.7 | 13.4 |
| 2014 | 12.3 | 14.2 | 13.4 | 14.8 | 11.5 | 14.0 | 9.5 | 11.0 | 12.0 | 14.1 |
| 2015 | 12.6 | 14.5 | 13.7 | 16.0 | 12.4 | 13.8 | 9.8 | 12.0 | 12.0 | 13.9 |
| 2004–2015 | 11.8 | 14.1 | 13.0 | 15.0 | 11.5 | 13.7 | 9.4 | 11.2 | 11.6 | 13.3 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
| 2004 | 11.4 | 13.1 | 11.7 | 12.4 | 10.8 | 12.5 | 9.0 | 10.8 | 11.2 | 12.6 |
| 2005 | 11.2 | 13.9 | 13.3 | 15.9 | 10.7 | 12.7 | 9.3 | 10.2 | 11.3 | 13.2 |
| 2006 | 11.3 | 13.8 | 12.1 | 14.6 | 10.8 | 12.4 | 9.0 | 11.8 | 11.7 | 13.2 |
| 2007 | 12.1 | 14.6 | 13.0 | 15.1 | 12.5 | 14.5 | 9.4 | 12.0 | 11.2 | 12.7 |
| 2008 | 11.7 | 13.7 | 12.9 | 15.4 | 11.6 | 13.5 | 9.2 | 11.2 | 11.7 | 13.3 |
| 2009 | 11.5 | 14.4 | 13.1 | 15.2 | 11.4 | 14.4 | 8.9 | 10.0 | 11.5 | 13.8 |
| 2010 | 10.7 | 12.8 | 11.9 | 13.7 | 10.0 | 11.0 | 9.3 | 11.4 | 11.4 | 13.9 |
| 2011 | 11.8 | 14.7 | 13.2 | 15.3 | 11.8 | 14.3 | 9.4 | 10.4 | 11.4 | 13.5 |
| 2012 | 11.2 | 13.4 | 12.4 | 14.5 | 10.8 | 14.7 | 8.8 | 10.6 | 11.4 | 13.0 |
| 2013 | 11.8 | 14.3 | 12.2 | 15.0 | 11.5 | 13.0 | 9.4 | 10.6 | 11.7 | 13.4 |
| 2014 | 12.2 | 14.3 | 13.3 | 14.8 | 11.6 | 13.9 | 9.4 | 10.9 | 12.0 | 14.1 |
| 2015 | 12.5 | 14.5 | 13.7 | 16.0 | 12.2 | 13.9 | 9.5 | 11.7 | 12.0 | 13.9 |
| 2004–2015 | 11.7 | 14.1 | 13.0 | 15.0 | 11.4 | 13.7 | 9.2 | 11.0 | 11.6 | 13.3 |
| Year | Annual | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | |
| 2004 | 63 | 75 | 679 | 89 | 76 | 363 | 59 | 68 | 429 | 22 | 25 | 164 | 60 | 61 | 427 |
| 2005 | 64 | 106 | 1599 | 152 | 177 | 1599 | 40 | 41 | 327 | 23 | 24 | 163 | 73 | 87 | 515 |
| 2006 | 60 | 82 | 673 | 77 | 83 | 563 | 45 | 45 | 381 | 21 | 29 | 267 | 67 | 83 | 570 |
| 2007 | 67 | 94 | 841 | 152 | 132 | 841 | 64 | 91 | 594 | 16 | 20 | 210 | 43 | 38 | 319 |
| 2008 | 73 | 96 | 927 | 139 | 130 | 674 | 66 | 100 | 927 | 23 | 21 | 136 | 81 | 86 | 607 |
| 2009 | 67 | 90 | 769 | 113 | 121 | 769 | 65 | 71 | 404 | 23 | 28 | 173 | 71 | 92 | 765 |
| 2010 | 42 | 57 | 888 | 66 | 65 | 500 | 30 | 34 | 264 | 23 | 25 | 212 | 65 | 90 | 888 |
| 2011 | 78 | 91 | 993 | 91 | 103 | 951 | 65 | 59 | 503 | 21 | 24 | 207 | 84 | 68 | 446 |
| 2012 | 57 | 72 | 651 | 139 | 125 | 993 | 47 | 73 | 651 | 18 | 17 | 110 | 58 | 45 | 272 |
| 2013 | 71 | 101 | 811 | 108 | 126 | 811 | 53 | 54 | 405 | 20 | 21 | 173 | 62 | 75 | 612 |
| 2014 | 83 | 105 | 1077 | 198 | 147 | 846 | 51 | 50 | 354 | 26 | 26 | 159 | 80 | 77 | 668 |
| 2015 | 95 | 127 | 1211 | 193 | 193 | 1211 | 81 | 89 | 564 | 29 | 32 | 244 | 74 | 88 | 505 |
| 2004–2015 | 68 | 94 | 1599 | 127 | 136 | 1599 | 56 | 69 | 927 | 22 | 25 | 267 | 68 | 77 | 888 |
| Year | Annual | Winter | Spring | Summer | Autumn | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | Mean | SD | Max | |
| 2004 | 54 | 63 | 606 | 73 | 61 | 293 | 50 | 56 | 354 | 19 | 22 | 148 | 52 | 52 | 376 |
| 2005 | 54 | 93 | 1480 | 132 | 158 | 1480 | 34 | 36 | 293 | 20 | 20 | 138 | 61 | 73 | 418 |
| 2006 | 50 | 69 | 548 | 64 | 68 | 465 | 38 | 38 | 305 | 19 | 25 | 241 | 56 | 70 | 478 |
| 2007 | 55 | 77 | 705 | 123 | 109 | 705 | 54 | 77 | 532 | 14 | 17 | 178 | 37 | 33 | 265 |
| 2008 | 62 | 81 | 780 | 114 | 109 | 572 | 55 | 84 | 780 | 20 | 17 | 112 | 70 | 73 | 501 |
| 2009 | 56 | 76 | 657 | 94 | 103 | 657 | 55 | 61 | 344 | 20 | 23 | 134 | 59 | 77 | 641 |
| 2010 | 35 | 47 | 753 | 52 | 51 | 385 | 25 | 27 | 204 | 20 | 21 | 174 | 54 | 75 | 753 |
| 2011 | 66 | 76 | 845 | 74 | 81 | 681 | 55 | 51 | 401 | 19 | 21 | 183 | 70 | 57 | 403 |
| 2012 | 48 | 61 | 617 | 117 | 105 | 845 | 40 | 66 | 617 | 16 | 14 | 87 | 50 | 38 | 211 |
| 2013 | 59 | 86 | 732 | 89 | 110 | 732 | 43 | 45 | 318 | 18 | 18 | 145 | 53 | 64 | 504 |
| 2014 | 70 | 90 | 1019 | 163 | 122 | 717 | 43 | 41 | 290 | 22 | 21 | 131 | 67 | 65 | 565 |
| 2015 | 80 | 108 | 1045 | 167 | 170 | 1045 | 68 | 74 | 490 | 25 | 26 | 196 | 62 | 74 | 429 |
| 2004–2015 | 57 | 80 | 1480 | 106 | 116 | 1480 | 47 | 58 | 780 | 19 | 21 | 241 | 58 | 65 | 753 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
| 2004 | 159 | 346 | 199 | 335 | 143 | 325 | 50 | 151 | 127 | 341 |
| 2005 | 147 | 458 | 320 | 890 | 88 | 217 | 51 | 121 | 174 | 424 |
| 2006 | 144 | 454 | 179 | 437 | 97 | 200 | 43 | 166 | 159 | 435 |
| 2007 | 175 | 484 | 306 | 632 | 171 | 480 | 32 | 106 | 87 | 200 |
| 2008 | 189 | 454 | 313 | 601 | 190 | 405 | 47 | 103 | 193 | 405 |
| 2009 | 157 | 453 | 291 | 652 | 160 | 345 | 59 | 137 | 143 | 516 |
| 2010 | 90 | 282 | 148 | 339 | 63 | 204 | 50 | 126 | 139 | 448 |
| 2011 | 187 | 408 | 217 | 408 | 124 | 312 | 45 | 117 | 181 | 332 |
| 2012 | 129 | 386 | 279 | 609 | 105 | 405 | 43 | 82 | 116 | 218 |
| 2013 | 165 | 547 | 224 | 688 | 114 | 250 | 42 | 97 | 149 | 355 |
| 2014 | 174 | 555 | 410 | 652 | 115 | 251 | 55 | 138 | 148 | 483 |
| 2015 | 250 | 565 | 448 | 1023 | 198 | 427 | 62 | 173 | 200 | 384 |
| 2004–2015 | 165 | 462 | 290 | 658 | 127 | 346 | 49 | 129 | 150 | 389 |
| Year | Annual | Winter | Spring | Summer | Autumn | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op | Ex | Op | Ex | Op | Ex | Op | Ex | Op | Ex | |
| 2004 | 134 | 289 | 158 | 269 | 143 | 325 | 40 | 127 | 110 | 277 |
| 2005 | 122 | 394 | 287 | 810 | 88 | 217 | 45 | 101 | 146 | 375 |
| 2006 | 121 | 383 | 148 | 365 | 97 | 200 | 38 | 149 | 136 | 385 |
| 2007 | 142 | 400 | 247 | 536 | 171 | 480 | 28 | 88 | 75 | 175 |
| 2008 | 159 | 386 | 263 | 513 | 190 | 405 | 41 | 86 | 167 | 351 |
| 2009 | 130 | 373 | 240 | 552 | 160 | 345 | 50 | 111 | 118 | 433 |
| 2010 | 74 | 222 | 112 | 266 | 63 | 204 | 42 | 100 | 114 | 378 |
| 2011 | 157 | 340 | 173 | 329 | 124 | 312 | 38 | 106 | 151 | 271 |
| 2012 | 109 | 331 | 236 | 517 | 105 | 405 | 35 | 72 | 97 | 188 |
| 2013 | 139 | 460 | 183 | 617 | 114 | 250 | 37 | 78 | 129 | 300 |
| 2014 | 145 | 471 | 337 | 551 | 115 | 251 | 47 | 112 | 124 | 411 |
| 2015 | 207 | 503 | 375 | 886 | 198 | 427 | 51 | 143 | 164 | 328 |
| 2004–2015 | 137 | 390 | 241 | 557 | 127 | 346 | 42 | 108 | 127 | 335 |
References
- Coe, R.G.; Neary, V.S. Review of Methods for Modeling Wave Energy Converter Survival. In Proceedings of the 2nd Marine Energy Technology Symposium (METS), Seattle, WA, USA, 15–18 April 2014.
- Folley, M.; Babarit, A.; Child, B.; Forehand, D.; Boyle, L.O.; Silverthorne, K.; Spinneken, J.; Stratigaki, V.; Troch, P. A Review of Numerical Modelling of Wave Energy Converter Arrays. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Rio de Janeiro, Brazil, 1–6 July 2012; pp. 535–545.
- Barstow, S.; Mørk, G.; Lønseth, L.; Mathisen, J.P. WorldWaves wave energy resource assessments from the deep ocean to the coast. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 149–159.
- National Oceanic and Atmospheric Administration (NOAA). National Weather Service: Environmental Modelling Center—NOAA WaveWatch III, NE Atlantic (Global). Available online: http://polar.ncep.noaa.gov/waves/viewer.shtml?-multi_1-NE_atlantic- (accessed on 23 April 2014).
- O’Brien, L.; Dudley, J.M.; Dias, F. Extreme wave events in Ireland: 14 680 BP-2012. Nat. Hazards Earth Syst. Sci. 2013, 13, 625–648. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; Martínez de Alegría, I.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Fugro. World Wide Wave Statistics (WWWS). Available online: http://www.oceanor.com/Services/WWWS (accessed on 21 April 2014).
- Met Éireann. Met Eireann Weather News: Another Record Wave Height Set Today South of Cork. Available online: http://www.met.ie/news/display.asp?ID=243 (accessed on 15 December 2014).
- WestWave. WestWave: Converting Ireland’s Wave Energy Potential. Available online: http://www.westwave.ie/location/ (accessed on 28 November 2013).
- Met Éireann. The Irish Meteorological Service Online: Display and Download Historical Data. Available online: http://www.met.ie/climate-request/ (accessed on 27 January 2015).
- Gulev, S.K.; Grigorieva, V. Variability of the winter wind waves and swell in the North Atlantic and North Pacific as revealed by the voluntary observing ship data. J. Clim. 2006, 19, 5667–5685. [Google Scholar] [CrossRef]
- Cahill, B. Characteristics of the Wave Energy Resource at the Atlantic Marine Energy Test Site. Ph.D. Thesis, University College Cork, Cork, Ireland, 2013. [Google Scholar]
- The Wamdi Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Tolman, H. Technical Note: User Manual and System Documentation of WAVEWATCH III; Version 4.18; U.S. Department of Commerce: College Park, MD, USA, 2014.
- DHI. Wave Modelling in Oceans and Coastal Areas. Available online: http://www.mikebydhi.com/products/mike-21/waves (accessed on 3 July 2014).
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Rusu, E. Strategies in using numerical waves model in ocean/coastal applications. J. Mar. Sci. Technol. 2011, 19, 58–75. [Google Scholar]
- TUDelft. Hydraulic Engineering: SWAN. Available online: http://www.swan.tudelft.nl/ (accessed on 2 February 2014).
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: New York, NY, USA, 2009; pp. 24–52. [Google Scholar]
- Zijlema, M. Computation of wind-wave spectra in coastal waters with SWAN on unstructured grids. Coast. Eng. 2010, 57, 267–277. [Google Scholar] [CrossRef]
- Wolf, J.; Hargreaves, J.C.; Flather, R.A. Application of the SWAN Shallow Water Wave Model to Some U.K Coastal Sites; Proudman Oceanographic Laboratory Report No. 57; Proudman Oceanographic Laboratory (POL): Prenton, UK, 2000. [Google Scholar]
- Gleizon, P.; Campuzano, F.J.; García, P.C.; Gomez, B.; Martinez, A. Wave energy mapping along the European Atlantic coast. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nante, France, 6–11 September 2015.
- Rusu, L.; Guedes Soares, C. Impact of assimilating altimeter data on wave predictions in the western Iberian coast. Ocean Model. 2015, 96, 126–135. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the Death Coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Marine Institute. Online Wave Forecasts. Available online: http://www.marine.ie/Home/site-area/data-services/marine-forecasts/wave-forecasts (accessed on 24 February 2015).
- Atan, R.; Goggins, J.; Nash, S. A preliminary assessment of the wave characteristics at the Atlantic Marine Energy Test Site (AMETS) using SWAN. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015.
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- U.S. Navy Fleet Numerical Meteorology and Oceanography Center (FNMOC)’s Wave Watch 3 (WW3). Available online: http://gcmd.nasa.gov/records/GCMD_FNMOC_WaveWatchIII.html (accessed on 2 October 2014).
- Amante, C.; Eakins, B. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. Available online: http://www.ngdc.noaa.gov/mgg/global/global.html (accessed on 8 May 2014).
- National Research Council Canada (NRC). Blue KenueTM: Software Tool for Hydraulic Modellers. Available online: http://www.nrc-cnrc.gc.ca/eng/solutions/advisory/blue_kenue_index.html (accessed on 4 February 2014).
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the existence of a fully developed wind-sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Yan, L. An Improved Wind Input Source Term for Third Generation Ocean Wave Modelling (Wetenschapplijke Rapport); WR-No 87-8; Koninklijk Nederlands Meteorologisch Inistituut: De Bilt, The Netherlands, 1987. [Google Scholar]
- Janssen, P.A.E.M. Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- TUDelft. SWAN Scientific and Technical Documentation—Cycle III Version 41.01A. Available online: http://swanmodel.sourceforge.net/online_doc/swantech/swantech.html (accessed on 25 January 2014).
- Hasselmann, K. On the spectral dissipation of ocean waves due to whitecapping. Bound.-Layer Meteorl. 1974, 6, 107–127. [Google Scholar]
- Atan, R.; Goggins, J.; Nash, S. Development of a Nested Local Scale Wave Model for a 1/4 Scale Wave Energy Test Site using SWAN. J. Oper. Oceanogr. 2016. submitted. [Google Scholar]
- Marine Institute. Wave Buoy Network Real Time Data 30 Minute. Available online: http://data.marine.ie/Dataset/Details/20969# (accessed on 20 January 2015).
- Kuik, A.J.; Van Vledder, G.P.; Holthuijsen, L.H. A method for the routine analysis of pitch-and-roll buoy wave data. J. Phys. Oceanogr. 1988, 18, 1020–1034. [Google Scholar] [CrossRef]
- Krogstad, H.E.; Trulsen, K. Interpretations and observations of ocean wave spectra. Ocean Dyn. 2010, 60, 973–991. [Google Scholar] [CrossRef]
- Gallagher, S.; Gleeson, E.; Tiron, R.; McGrath, R.; Dias, F. Wave climate projections for Ireland for the end of the 21st century including analysis of EC-Earth winds over the North Atlantic Ocean. Int. J. Climatol. 2016, 36, 4592–4609. [Google Scholar] [CrossRef]
- Guide to Wave Analysis and Forecasting, 2nd ed.; World Meteorological Organization (WMO): Geneva, Switzerland, 1998.
- Data and Products—Data Processing and Interpretation. Available online: http://www.infomar.ie/data/DataProcessing.php (accessed on 5 October 2014).
- Atan, R.; Goggins, J.; Nash, S. Development of a high resolution wave model at AMETS using SWAN. In Proceedings of the Civil Engineering Research in Ireland (CERI) Conference, Galway, Ireland, 29–30 August 2016.
- Bento, A.R.; Martinho, P.; Campos, R.; Guedes Soares, C. Modelling Wave Energy Resources in the Irish West Coast. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 945–953.
- Demirbilek, Z.; Vincent, C.L. Coastal Engineering Manual, Part II, Water Wave Mechanics, 2nd ed.; Engineer Manual 1110-2-1100; U.S. Army Corps of Engineers: Washington, DC, USA, Chapter 1.
- Cornett, A.M. A global wave energy resource assessment. In Proceedings of the Eighteen International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008; International Society of Offshore and Polar Engineers (ISOPE): Cupertino, CA, USA, 2008; pp. 1–9. [Google Scholar]
- Atan, R.; Goggins, J.; Harnett, M.; Agostinho, P.; Nash, S. Assessment of wave characteristics and resource variability at a 1/4-scale wave energy test site in Galway Bay using Waverider and high frequency radar (CODAR) data. Ocean Eng. 2016, 117, 272–291. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Ocean Energy Systems (OES). Offshore Installations Worldwide. Available online: http://www.ocean-energy-systems.org/ocean-energy-in-the-world/gis-map/ (accessed on 24 February 2015).
- Cahill, B.G.; Lewis, T. Wave energy resource characterisation of the Atlantic Marine Energy Test Site. Int. J. Mar. Energy 2013, 1, 3–15. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation: Regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Tsimplis, A.M.N.; Woolf, D.K.; Osborn, T.J.; Wakelin, S.; Wolf, J.; Flather, R.; Shaw, A.G.; Woodworth, P.; Challenor, P.; Blackman, D.; et al. Towards a vulnerability assessment of the UK and northern European coasts: The role of regional climate variab. Philos. Trans. Math. Phys. Eng. Sci. 2005, 363, 1329–1358. [Google Scholar] [CrossRef] [PubMed]
- Neill, S.P.; Lewis, M.J.; Hashemi, M.R.; Slater, E.; Lawrence, J.; Spall, S.A. Inter-annual and inter-seasonal variability of the Orkney wave power resource. Appl. Energy 2014, 132, 339–348. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration (NOAA). National Weather Service: North Atlantic Oscilation (NOA). Available online: http://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml (accessed on 12 June 2016).
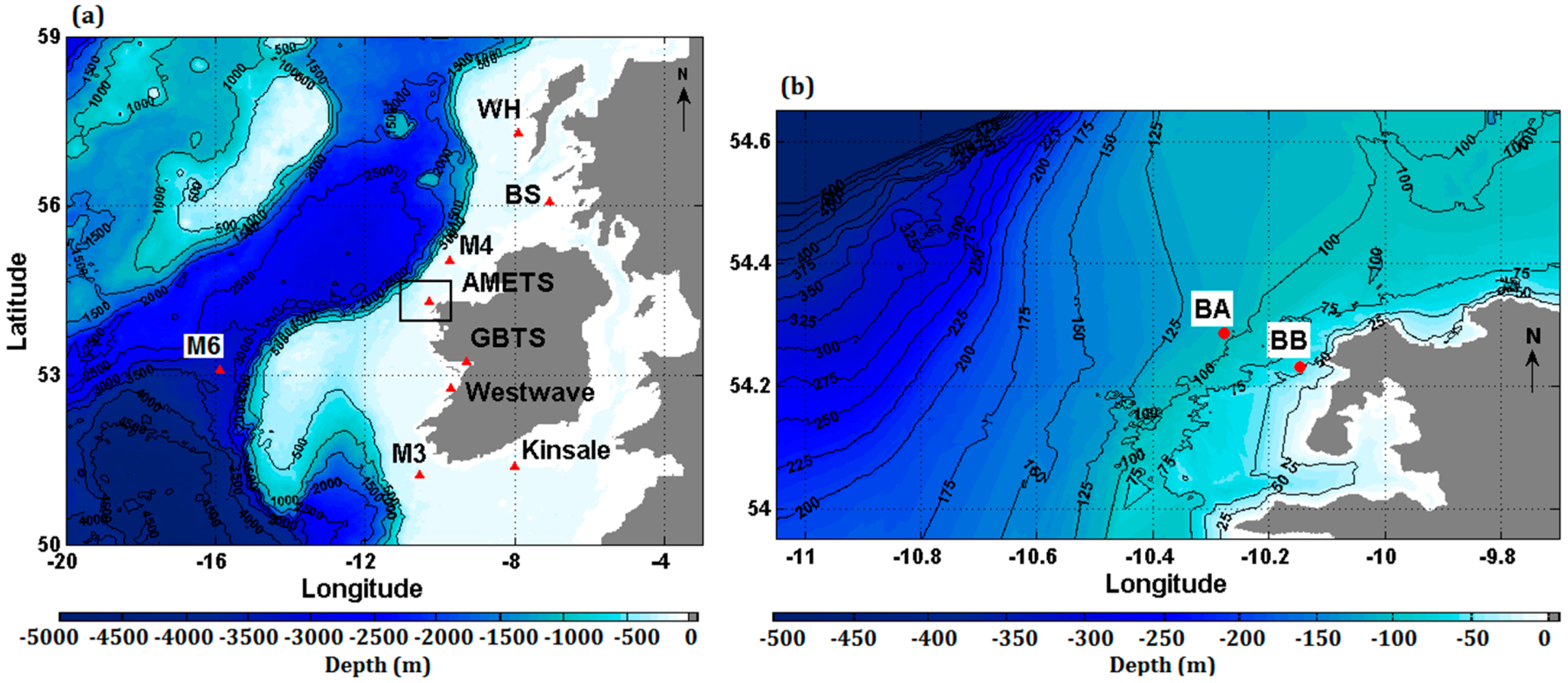

| Station | Locations | Depth (m) | Availability | Measured Data Resolution | Modelled Data Resolution |
|---|---|---|---|---|---|
| BA | 10.3 W, 54.28 N | 100 | January 2012 to date | 30 min | 30 min |
| BB | 10.15 W, 54.23 N | 50 | January 2010 to date | 30 min | 30 min |
| M3 | 10.55 W, 51.22 N | 155 | January 2007 to date | 1 h | 1 h |
| M4 | 9.99 W, 54.99 N | 80 | January 2008 to date | 1 h | 1 h |
| M6 | 15.88 W, 53.07 N | 3280 | January 2007 to date | 1 h | 1 h |
| WH | 7.91 W, 57.29 N | 83 | January 2009 to date | 1 h | 1 h |
| BS | 7.06 W, 56.06 N | 93 | January 2009 to date | 1 h | 1 h |
| Station | Waves | Mean | R2 | RMSE | Bias | SI |
|---|---|---|---|---|---|---|
| BA | Hs (m) | 3.01 m | 0.95 | 0.55 m | −0.02 m | 0.18 |
| Tz (s) | 6.82 s | 0.84 | 1.22 s | 0.23 s | 0.18 | |
| MWD (°) | 285° | 0.61 | 28° | −12° | 0.10 | |
| BB | Hs (m) | 2.80 m | 0.92 | 0.69 m | −0.40 m | 0.24 |
| Tz (s) | 6.98 s | 0.77 | 1.74 s | 0.23 s | 0.25 | |
| MWD (°) | 292° | 0.57 | 25° | −4° | 0.09 | |
| M3 | Hs (m) | 2.99 m | 0.95 | 0.51 m | 0.11 m | 0.17 |
| Tz (s) | 6.91 s | 0.85 | 1.16 s | 0.37 s | 0.17 | |
| MWD (°) | 266° | 0.79 | 27° | 6° | 0.10 | |
| M4 | Hs (m) | 3.09m | 0.92 | 0.65 m | 0.07 m | 0.21 |
| Tz (s) | 6.97s | 0.84 | 1.16 s | 0.27 s | 0.17 | |
| MWD (°) | 260° | 0.61 | 60° | 2° | 0.20 | |
| M6 | Hs (m) | 3.09 m | 0.92 | 0.67 m | 0.33 m | 0.22 |
| Tz (s) | 7.26 s | 0.84 | 1.06 s | 0.39 s | 0.15 | |
| MWD (°) | NA | NA | NA° | NA | NA | |
| WH | Hs (m) | 2.84 m | 0.90 | 0.85 m | 0.01 m | 0.30 |
| Tz (s) | 6.64 s | 0.80 | 1.47 s | 0.13 s | 0.22 | |
| MWD (°) | 265° | 0.40 | 82° | −15° | 0.30 | |
| BS | Hs (m) | 2.49 m | 0.93 | 0.60 m | 0.31 m | 0.24 |
| Tz (s) | 1.54 s | 0.86 | 1.42 s | 0.51 s | 0.23 | |
| MWD (°) | 268° | 0.62 | 54° | −4° | 0.20 |
| Station | Waves | Mean | R2 | RMSE | Bias | SI |
|---|---|---|---|---|---|---|
| BA | Hs (m) | 3.01 m | 0.95 | 0.58 m | 0.10 m | 0.19 |
| Tz (s) | 6.82 s | 0.87 | 1.21 s | 0.19 s | 0.18 | |
| MWD (°) | 285° | 0.66 | 27° | −8° | 0.09 | |
| BB | Hs (m) | 2.80 m | 0.95 | 0.52 m | 0.17 m | 0.22 |
| Tz (s) | 6.98 s | 0.80 | 1.40 s | 0.01 s | 0.20 | |
| MWD (°) | 292° | 0.64 | 26° | −9° | 0.09 | |
| [44] at BB | Hs (m) | 2.08 m | 0.89 | 0.48 m | 0.17 m | 0.23 |
| Tz (s) | 8.47 s | 0.77 | 1.42 s | 1.12 s | 0.17 | |
| MWD (°) | NA | NA | NA° | NA | NA | |
| [12] at BB | Hs (m) | NA | 0.84 | 0.73 m | −0.11 m | 0.31 |
| Tz (s) | NA | 0.52 | 1.82 s | −1.15 s | 0.21 | |
| MWD (°) | NA | NA | NA° | NA | NA | |
| [40] at BB | Hs (m) | 2.87 m | 0.95 | 0.41 m | 0.19 m | 0.14 |
| Tz (s) | 7.06 s | 0.89 | 0.86 s | 0.65 s | 0.12 | |
| MWD (°) | NA | NA | NA° | NA | NA |
| Period/Location | Depth, d (m) | Mean Wavelength, λ (m) | d/λ > 1/2 |
|---|---|---|---|
| 12-year BA | 100 | 89.0 | 1.1 |
| 12-year BB | 50 | 81.7 | 0.6 |
| 12-year Winter BB | 50 | 106.3 | 0.5 |
| 12-year Spring BB | 50 | 79.8 | 0.6 |
| 12-year Summer BB | 50 | 57.4 | 0.9 |
| 12-year Autumn BB | 50 | 83.7 | 0.6 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atan, R.; Goggins, J.; Nash, S. A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site. Energies 2016, 9, 967. https://doi.org/10.3390/en9110967
Atan R, Goggins J, Nash S. A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site. Energies. 2016; 9(11):967. https://doi.org/10.3390/en9110967
Chicago/Turabian StyleAtan, Reduan, Jamie Goggins, and Stephen Nash. 2016. "A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site" Energies 9, no. 11: 967. https://doi.org/10.3390/en9110967
APA StyleAtan, R., Goggins, J., & Nash, S. (2016). A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site. Energies, 9(11), 967. https://doi.org/10.3390/en9110967






