1. Introduction
As global warming has raised more critical concerns in recent years, refrigerants, such as R22, R410A and R134a with high global warming potential (GWP), are facing the challenge of being phased out. Hydrocarbons, such as R290 and R600a, have a zero ozone depletion potential (ODP) and an extremely low GWP, but they are not safe. The use of water (R718) as a type of natural refrigerant, which is environmentally-friendly, safe, and cheap, has attracted more and more attention recently [
1,
2]. Water vapor compression refrigeration and heat pump systems, which use water as the refrigerant, run at sub-atmospheric pressure. In the published literature, experimental data indicated that when the heat flux was constant, the boiling heat transfer coefficient gradually decreased with decreasing pressure [
3,
4,
5]. So it plays a significant role for the optimization of the whole system that the evaporator heat transfer enhancement in refrigeration and heat pump systems working at sub-atmospheric pressure. Even though the literature on evaporation of water is extensive, data on the characteristics of water evaporation under vacuum conditions are still scarce [
6,
7]; the heat flux is much higher than that of an evaporator. Moreover, the design of these evaporators still remains mainly empirical [
6]. So research on water boiling heat transfer at sub-atmospheric pressure has become an important issue.
In the past 80 years, nucleate boiling has been one of the most important researches in thermal science. In spite of collecting a lot of data and developing different theoretical models, it is not possible to predict nucleate boiling very accurately [
7]. Some of the experimental research on water boiling heat transfer at sub-atmospheric pressure have been summarized in
Table 1. It shows that there was correlation research, but the research that applies to work conditions of the evaporator in water vapor compression refrigeration or heat pump systems is still blank.
In the literature [
5,
6,
7], there have been several pressure points that could be applied to evaporators, but the heat transfer surfaces were all horizontal plates or finned surfaces. In water vapor compression refrigeration and heat pump systems, whether flooded evaporator or falling film evaporator, the heat transfer surfaces are all horizontal tubes. So the experiment conclusions did not completely apply to the research on the evaporator heat transfer.
Table 1.
Experimental researches on water nucleate boiling at sub-atmospheric pressure.
Table 1.
Experimental researches on water nucleate boiling at sub-atmospheric pressure.
| Author | Pressure (kPa) | Heating Surface | Specials |
|---|
| Raben et al. (1965) [8] | 4–100 | copper | |
| Mitrovic (1984) [9] | 3–101.3 | copper | flate plate with channels, tubes |
| McGillis et al. (1991) [10] | 4–9 | copper | |
| Hetsroni et al. (2004) [11] | 7–47 | copper | different tubes |
| Choon et al. (2006) [12] | 18 | copper-foam | |
| Lena Schnabel et al. (2008) [7] | 1 and 2 | copper | raw copper, sand blasted, finned surface |
| Mark Aaron Chan (2010) [5] | 2,4,9 | copper | Plain and finned surface |
| Florine Giraud et al. (2015) [6] | 0.85–100 | copper | plain surface |
Meanwhile, the experiments in
Table 1 constitute all the research on heat transfer mechanism and enhancement, and they rarely involved the calculation of the boiling heat transfer coefficient. In paper [
13], there were correlations, which were tested in [
7], but the heat transfer surface was still a horizontal plate. So the correlations of water boiling heat transfer coefficient on a horizontal copper tube surface at sub-atmospheric pressure are still unknown.
In order to research the evaporator heat transfer in water vapor compression refrigeration and heat pump systems, experiments are carried out. Regression equations of the boiling heat transfer coefficient are educed based on the experimental data, which are convenient for the practical application. To a certain extent, this experiment will guide the heat transfer enhancement of the evaporator working at sub-atmospheric pressure.
2. Experimental System
The experimental system is shown in
Figure 1. The major component in the system is a sealed chamber. The vacuum in the test section is realized by using a vacuum pump. The bottom and top parts of the test section are the evaporation boiling section and condensation section, respectively. In the evaporation boiling section, the surface of a horizontal copper rod, which has an external diameter of 20.8 mm, is used as the heating surface. It is heated by an electric heater, which is inside the rod and has a diameter of 11.8 mm and a length of 190 mm. They are in close contact with each other and heat-conducting medium is between them. The heating power is adjusted by a voltage regulator and measured by a power meter. The experimental medium is deionized water. In the condensation section, cooling water from a low-temperature thermostat bath is used to condense water vapor from the evaporation boiling section. The condensing surface is a horizontal copper plate between the evaporation boiling section and condensation section. The whole experimental system is covered by a 30 mm rubber insulation board to avoid heat loss. Heat loss is evaluated by calculation, and the maximum heat loss rate is 1.92% in this experiment.
Figure 1.
Experimental system 1. Test section; 2. Low-temperature thermostat bath; 3. Voltage regulator; 4. Flowmeter; 5. Valve for vacuum; 6. Vacuum pump; 7. Data acquisition instrument (Agilent 34970A); 8. Computer; a. Horizontal copper rod; b. Cooling water chamber; P. vacuum pressure transmitter; W. power meter.
Figure 1.
Experimental system 1. Test section; 2. Low-temperature thermostat bath; 3. Voltage regulator; 4. Flowmeter; 5. Valve for vacuum; 6. Vacuum pump; 7. Data acquisition instrument (Agilent 34970A); 8. Computer; a. Horizontal copper rod; b. Cooling water chamber; P. vacuum pressure transmitter; W. power meter.
In the test section, pressure is measured by a vacuum pressure transmitter, as shown in
Figure 1. The temperatures of water vapor and deionized water are measured by Pt 100. The temperatures of the heating surface are measured by sheathed thermocouples. To calculate the mean heat transfer coefficient, eight temperature test points are used on the heating surface in different directions (
Figure 2) to get the mean temperature of the surface. To minimize the effects of surrounding fluids on the measurement results, at the locations of measurement points in
Figure 2, small pits are dug, the probes of thermocouples are buried in them with solders while welded, the thermal performance of which is very good. The temperature standard deviation among the test points is 0.831 and the relative standard deviation is 2.96% (
q = 7162 W·m
−2,
p = 2.93 kPa). The inlet and outlet temperatures of cooling water are measured by thermocouples, and the flow rate is measured by a flow meter. The experimental data of all test points are collected by a data acquisition instrument (Agilent 34970A), and are given by a computer.
Figure 2.
Temperature test point distribution on the copper rod surface (e: equal).
Figure 2.
Temperature test point distribution on the copper rod surface (e: equal).
The boiling heat transfer coefficients of water on the heating surface can be calculated as follows:
In this experiment, run conditions of the evaporator in water vapor compression refrigeration and heat pump systems are simulated. A horizontal copper rod is used as the heating surface. The pressure in the test section can be controlled by heating capacity and cooling water flow rate. When heating capacity equals the heat removed by cooling water, the pressure is steady. When heating capacity is higher, the pressure will increase. When the pressure reaches a certain value, cooling water flow rate is adjusted to reach a new heat balance, and the pressure is steady again. The pressure range is 1.8–3.3 kPa. The heat flux range is 4000–10000 W·m−2, which is suitable for the evaporator.
3. Reliability Analysis
3.1. Error Analysis
The boiling heat transfer coefficients of water on the heating surface,
h, can be calculated by correlation (1). The relative error of
h is derived to be:
Heating power input on the surface,
Q, is measured by a power meter; the size of the heat transfer surface is measured by a micrometer. So the relative error of heat flux, δ
q/
q is:
In this experiment, the calibrated error of copper-constantan thermocouple is 0.2 °C. The precision of Pt100 is 0.198 °C. So the temperature difference absolute error is 0.4 °C. The smallest wall superheat is 2.088 °C. Therefore, the relative error of wall superheat, δΔ
t/Δ
t is:
Thus, the uncertainty of heat transfer coefficient is:
3.2. Experiment Repeated Test
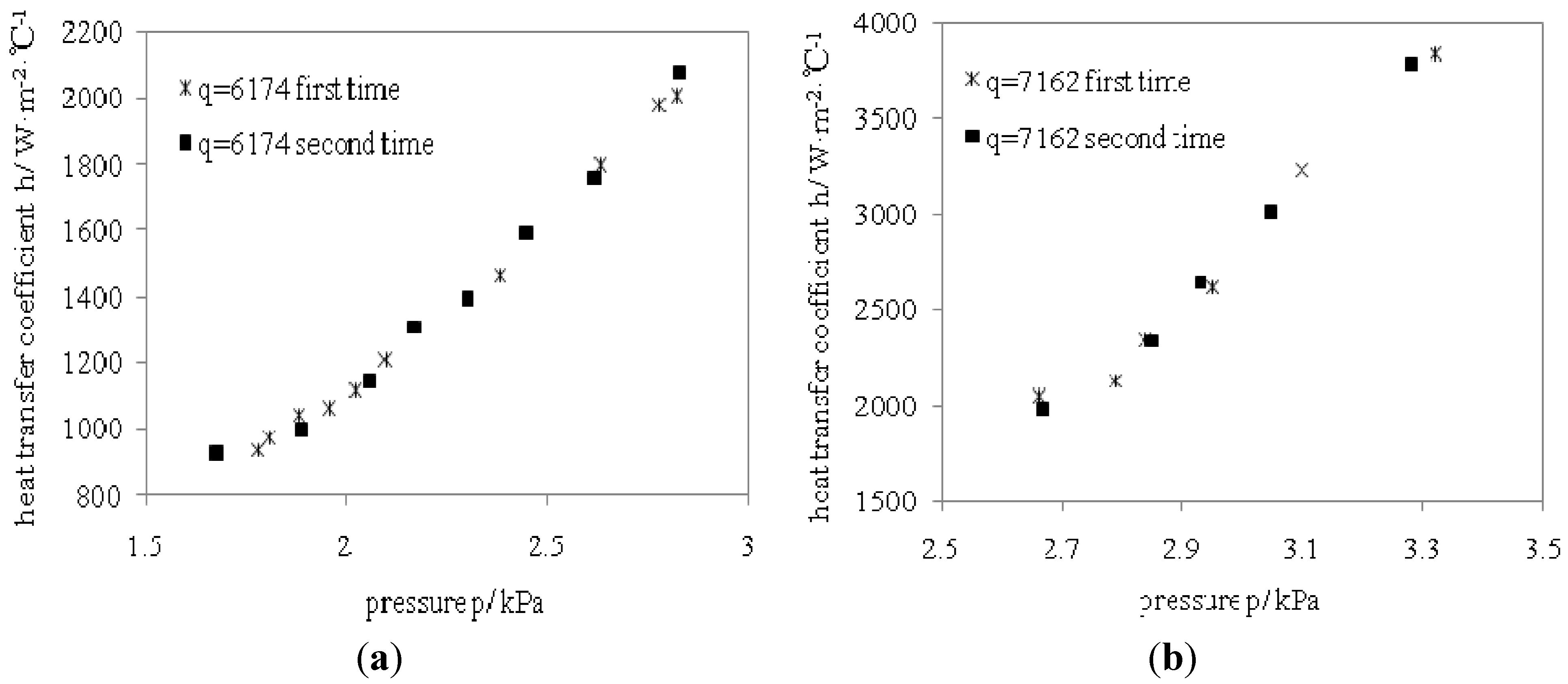
The experiment repeated test is an important measure for ensuring the experimental data are reliable and valid. As shown in
Figure 3, the resulting test data of the two experiments are so approximate. In the experiment process, the pressures on both experiments cannot be exactly the same since pressure is controlled by heating capacity and cooling capacity. The heat transfer coefficient errors under the same work conditions are showed in
Table 2. All errors are within ±5%, thus making the data in this experiment reliable and valid.
Figure 3.
Experimental data repeated test. (a) Comparison of experiment results when q = 6174 W·m−2; (b) Comparison of experiment results when q = 7162 W·m−2.
Figure 3.
Experimental data repeated test. (a) Comparison of experiment results when q = 6174 W·m−2; (b) Comparison of experiment results when q = 7162 W·m−2.
Table 2.
Experimental errors in the same work conditions.
Table 2.
Experimental errors in the same work conditions.
| q/W·m−2 | 6174 | 7162 |
|---|
| Number | 1 | 2 | 3 | 1 | 2 | 3 |
| p/kPa | 1.88 | 2.63 | 2.82 | 2.66 | 2.85 | 2.95 |
| h/ W·m−2 °C−1 | 1043.583 | 1795.243 | 2003.193 | 2048.055 | 2341.94 | 2615.652 |
| 994.978 | 1761.941 | 2080.836 | 1976.174 | 2345.008 | 2650.501 |
| Error/% | 4.66 | 1.86 | −3.88 | 3.51 | −0.13 | −1.33 |
4. Results and Discussion
In this experiment, the boiling heat transfer coefficients of water on a horizontal copper rod at sub-atmospheric pressure are calculated by Equation (1) according to the experimental data.
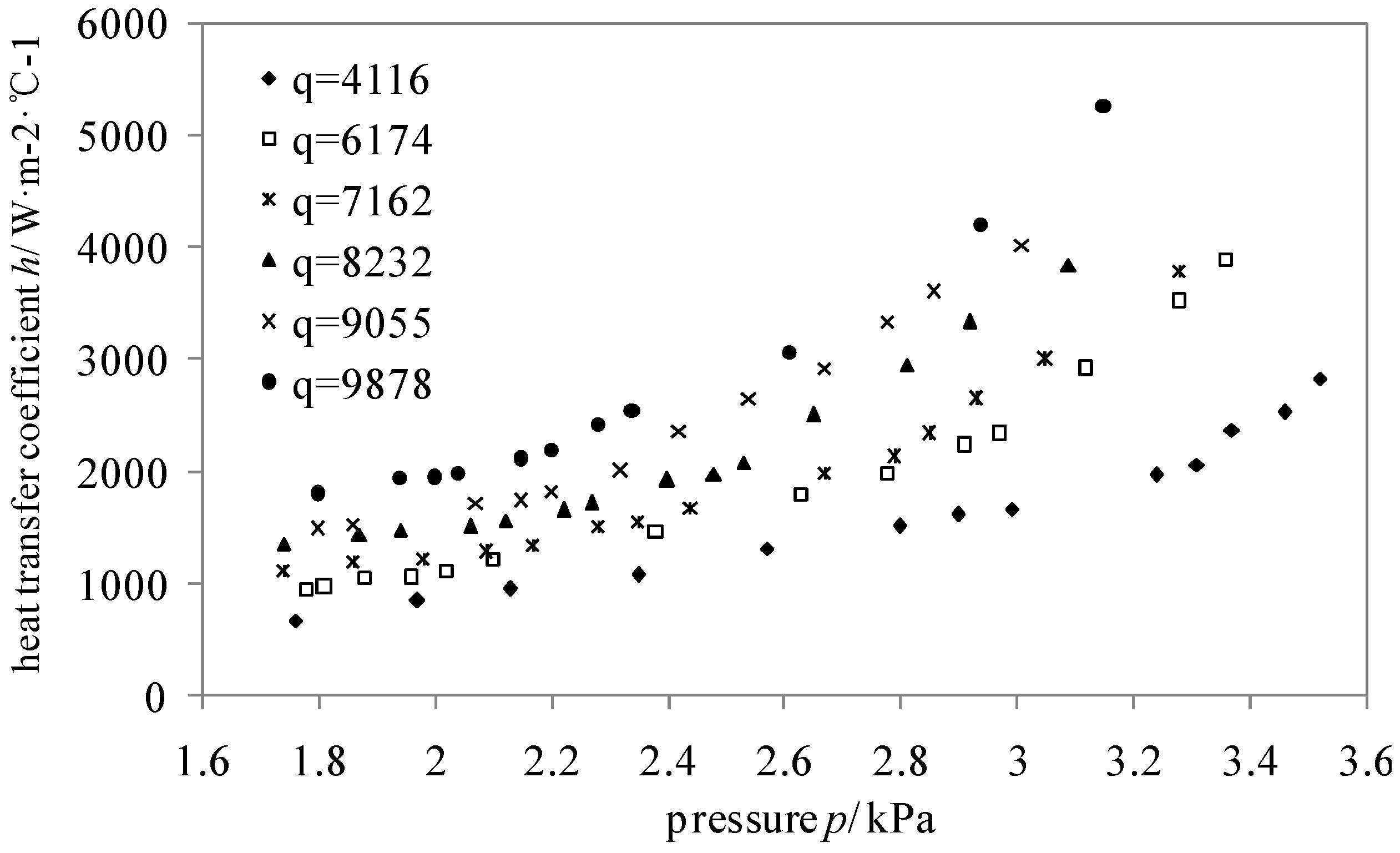
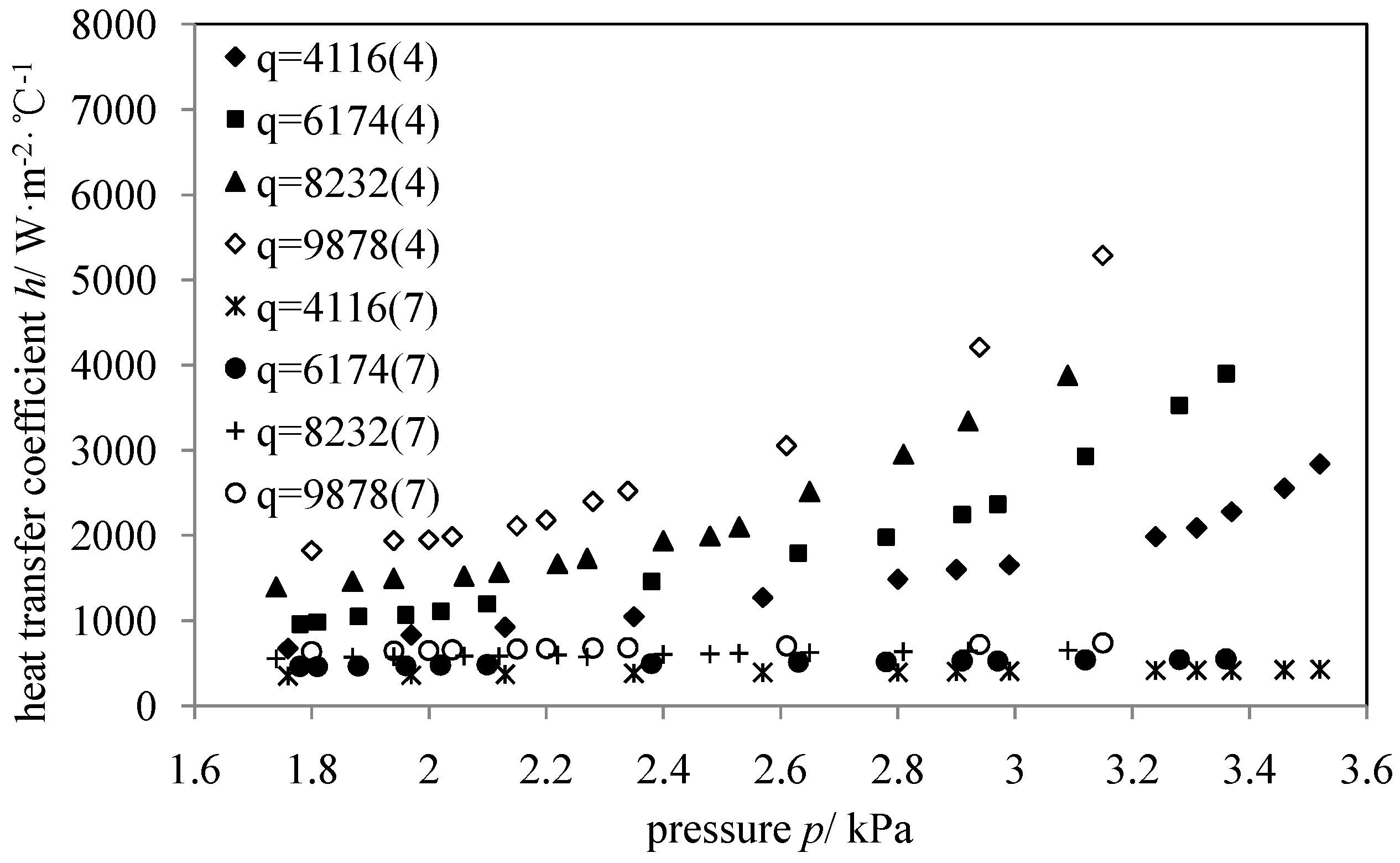
Figure 4 shows the variation of heat transfer coefficient with increasing pressure and heat flux. When the heat flux is constant, the heat transfer coefficient increases with increasing pressure, which is in accord with previous research results [
3,
4,
5]. Thus, when the heat flux is constant, water boiling heat transfer coefficient increases with increasing pressure at sub-atmospheric, atmospheric, and positive pressures. When the pressure is constant, the heat transfer coefficient increases with increasing heat flux.
Figure 4.
Variation of water boiling heat transfer coefficient with pressure and heat flux (q is in W·m−2).
Figure 4.
Variation of water boiling heat transfer coefficient with pressure and heat flux (q is in W·m−2).
Meanwhile, when the pressure is low, the increase of heat transfer coefficients with increasing pressure is slow. However, when the pressure reaches a certain value, the increase is enhanced,
i.e., there is an inflection point on the change curve. And with the heat flux increasing, the pressure value of the inflection point decreases gradually, which is showed as
Figure 4.
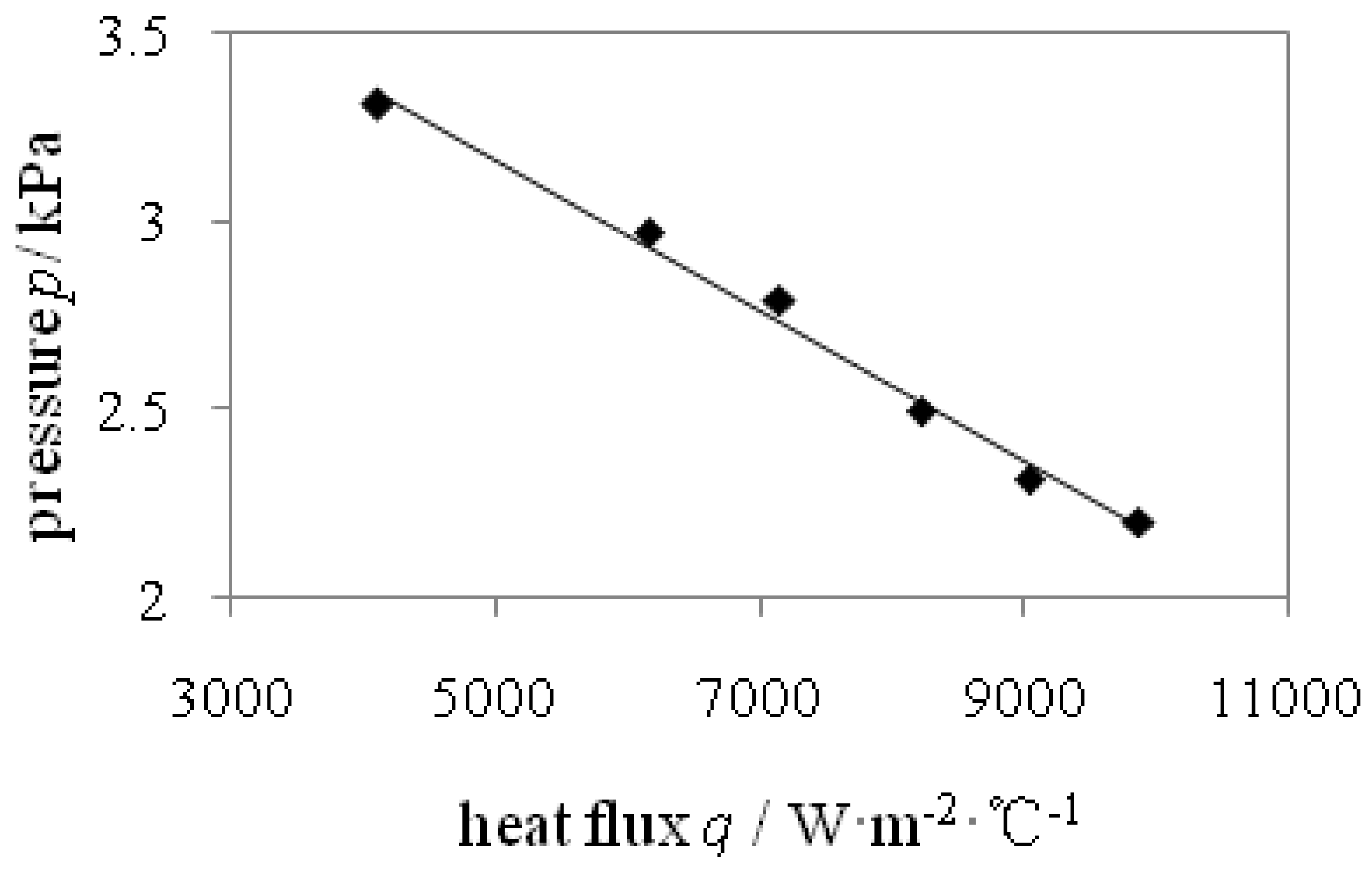
Figure 5 shows the relations between the pressure value and the heat flux. The pressure value approximately linearly decreases with increasing heat flux.
The change of increase trend of the boiling heat transfer coefficient with increasing pressure and heat flux may be due to the change of heat transfer mode. When the heat flux is small, and the pressure is lower, the heat transfer mode between water and the heating surface is natural convection. At this time, the heat transfer coefficient is smaller. With the pressure increasing, the local heat transfer mode perhaps changes to nucleate pool boiling gradually where the temperature difference between the surface and water is higher. As the pressure further increases, nucleate pool boiling is more intense [
3,
4,
5], which rapidly enhances the mean heat transfer coefficient between water and surface. Hence, there is an inflection point on the curve. With the heat flux increasing, the nucleate pool boiling is already obvious when the pressure is lower. So the pressure of the inflection point decreases with the heat flux increasing.
In the flooded evaporator of refrigeration and heat pump systems, the heat exchanges between refrigerant and cooled water through the tube wall. The refrigerant gradually changes from liquid state to gas state. Its temperature is the saturation temperature all the time under the conditions of taking no account of outlet superheat. However, the temperature of cooled water in evaporator is not constant, which decreases along the flow direction. The temperature difference between inlet and outlet is about 5–10 °C. So the heat transfer of refrigerant on tube wall is not homogeneous in the evaporator. It is the synthesis of natural convection and nucleate pool boiling.
Figure 5.
Relation between pressure value on the inflection point and heat flux.
Figure 5.
Relation between pressure value on the inflection point and heat flux.
5. Experimental Data Fitting
To calculate the boiling heat transfer coefficient of water on a horizontal copper rod at sub-atmospheric pressure conveniently, the experimental data are fitted to get the regression equations. Thus, the heat transfer coefficients can be calculated when just knowing the work conditions.
The important pool boiling regimes for water as refrigerant are the region of convective and nucleate boiling. In the region of convection, the Nusselt number can be calculated by the empirical correlation (3). The main parameters affecting nucleate pool boiling are the heat flux,
q, saturation pressure,
p, properties of working fluid and the characteristics of boiling surface and material,
etc. [
7,
14].
The experimental data are fitted using the least-squares method, and the regression equations are showed as correlation (4).
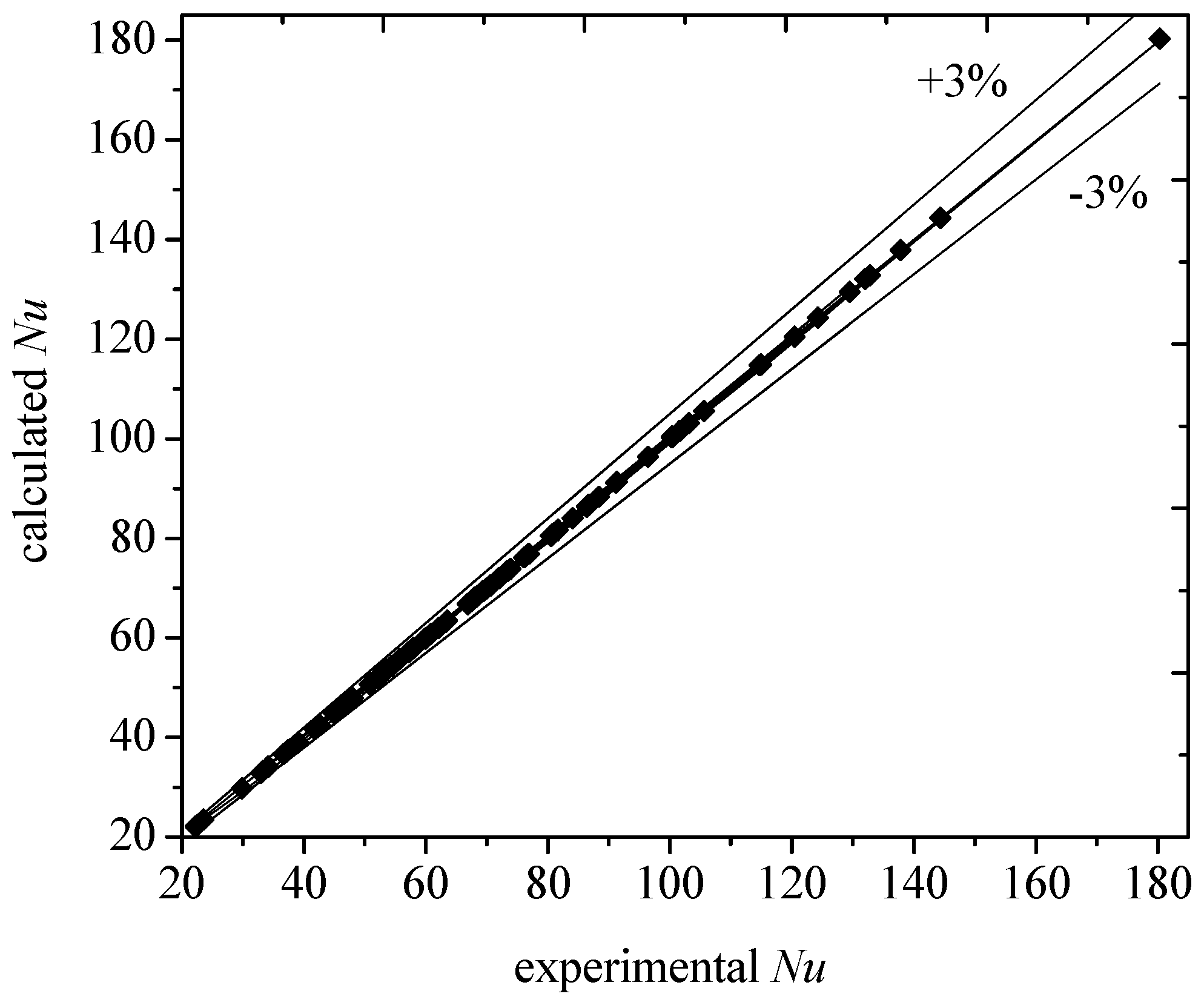
Figure 6 shows the comparisons of boiling heat transfer coefficient between experimental data and calculation results by correlation (4). All errors of the two are within ±3%, and the biggest error is −2.99%, which shows the calculation results are in good agreement with the experimental data. Thus, the regression equations are available
Here, pr is the ratio of pressure in kPa to 1kPa; qr is the ratio of heat flux in W·m−2 to 1 W·m−2.
Correlation (4) can be expressed by the correlation between the heat transfer coefficient and main influence parameters (liquid state), which is showed as correlation (5).
Figure 6.
Comparisons of experimental data and calculation results by regression equations.
Figure 6.
Comparisons of experimental data and calculation results by regression equations.
In correlation (5), the value of water properties is determined by the pressure. And the superheat of the heating surface is not a work condition but an experiment result, which cannot be determined without experimental data.
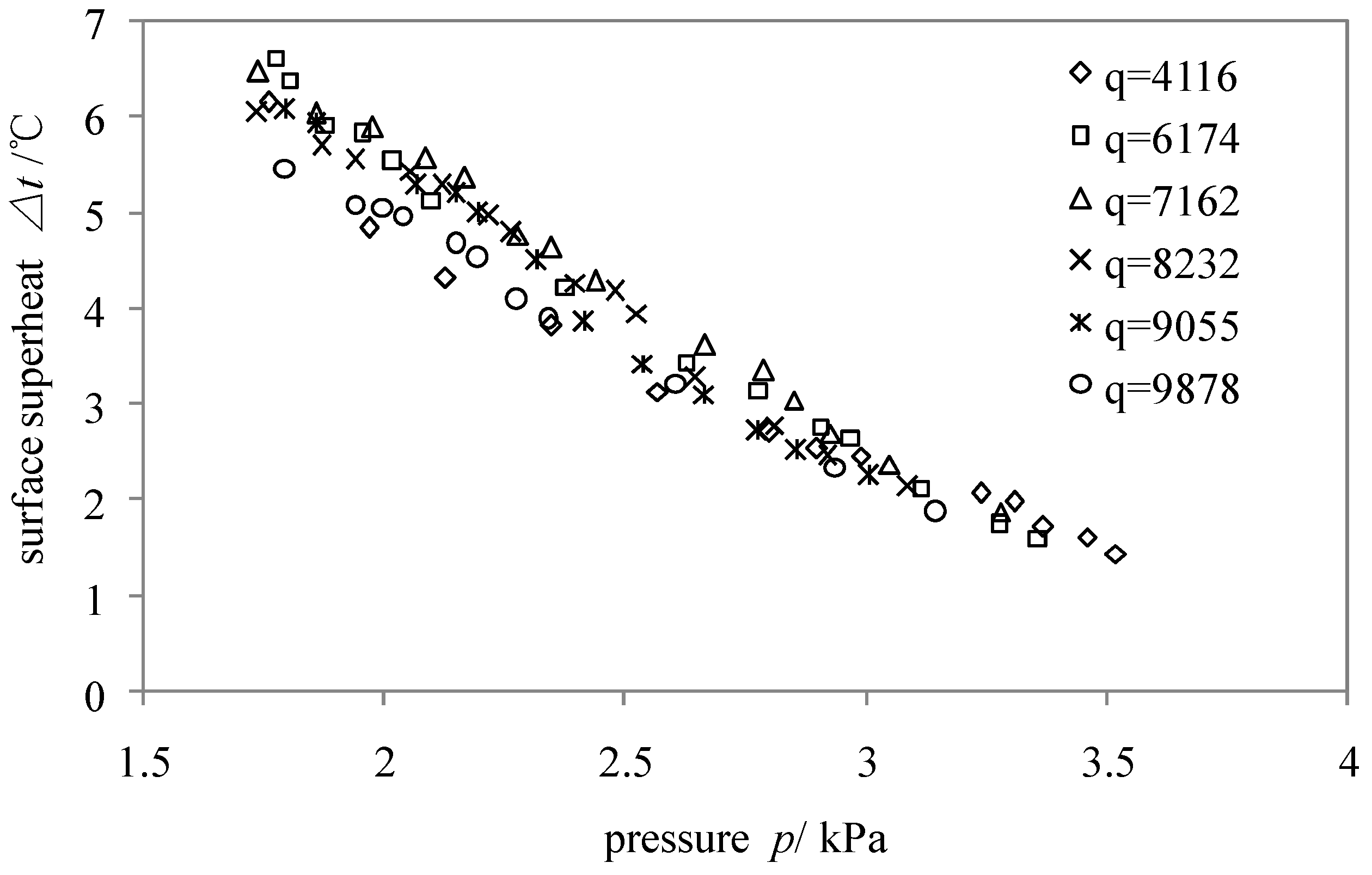
Figure 7 shows that there are similar correlations between pressures and superheats. Correlation (6) is educed using the least-squares method. At the work conditions of this experiment, the mean superheat of the heating surface can be calculated by correlation (6) according to the experimental pressure. It benefits the system reduction and vacuum guarantee due to cancel the heating surface temperature measurement, which is very practical.
Figure 7.
Superheat changes on the copper rod surface with pressure (q is in W·m−2).
Figure 7.
Superheat changes on the copper rod surface with pressure (q is in W·m−2).
Meanwhile, the correlation between boiling heat transfer coefficient,
h, and superheat of wall, in correlation (1) can be changed to the correlation between
h and pressure,
p, by correlation (6) for practical application.
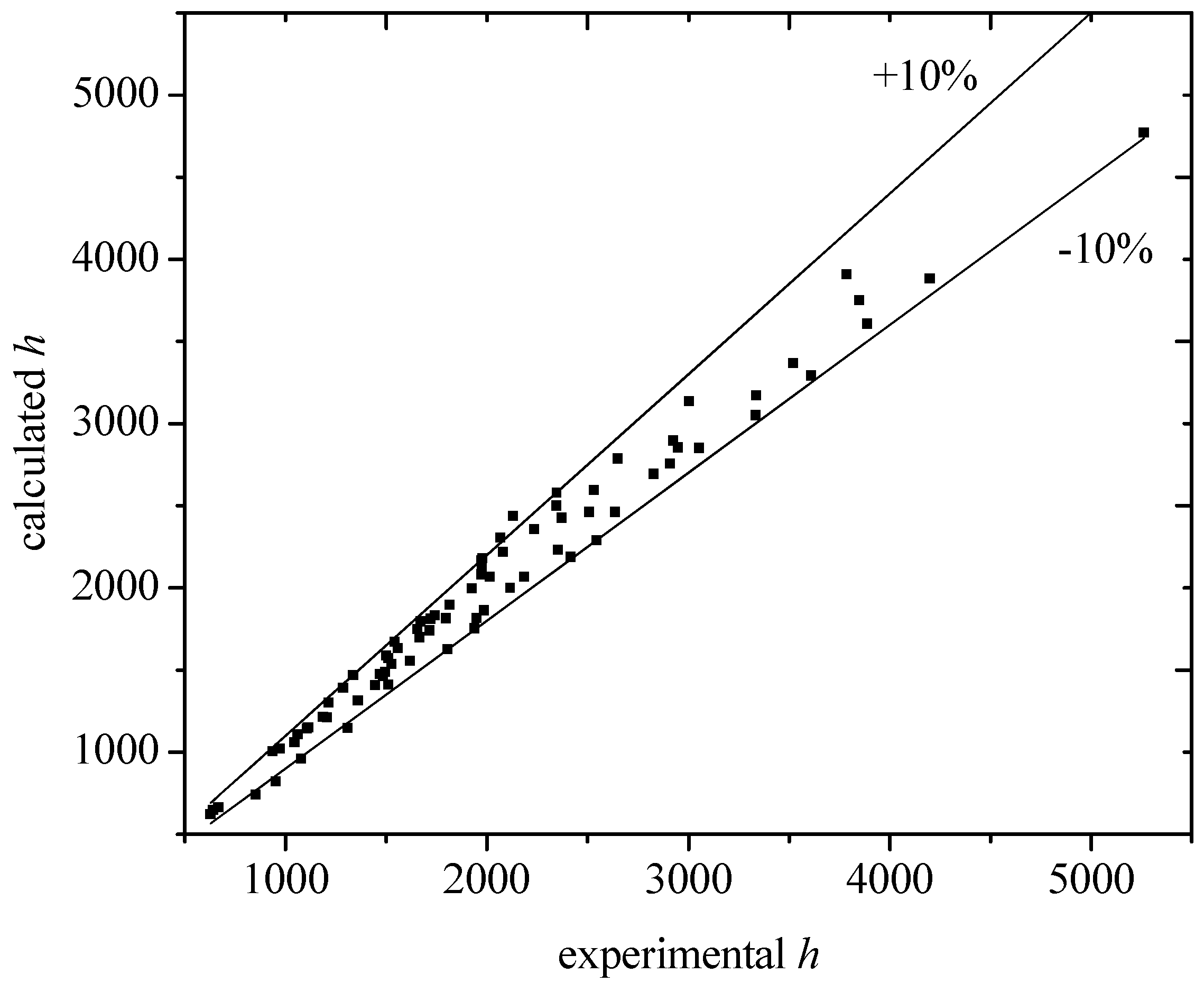
Figure 8 shows the comparisons between experimental data and calculation results by correlation (1) and (6). The errors are within ±10%. Thus, in the range of work conditions of this experiment, it is very practical that the boiling heat transfer coefficient of water is calculated by correlation (1) and (6).
Figure 8.
Comparisons of experimental data and calculation results.
Figure 8.
Comparisons of experimental data and calculation results.
6. Correlation between Experimental Data and Calculation Results by Cooper Correlation
In the existing literature, Cooper correlation is used by many scholars to calculate the pool boiling heat transfer coefficient of refrigerants such as R134a,
etc. [
15,
16,
17]. In the boiling heat transfer section of the textbook [
18], correlation (7) is also provided. However, there are work mediums and conditions apply to it. For water, there are different expressions according to the characteristics and materials of boiling surface [
19,
20]. In [
20], only a horizontal copper plate is used as the boiling surface under the conditions including the pressures of this experiment.
Figure 9 shows the comparisons of calculation results by correlation (4) and correlation (7) at the same work conditions.
The difference of calculation results by these two correlations is so obvious, and it will increase with increasing pressure. For example, when q = 8232 W·m−2, p = 1.87 kPa, h(4)/h(7) = 2.54. When p = 3.09 kPa, h(4)/h(7) = 5.91. Thus, the correlation (7) is not suitable for the refrigerant (R718) in water vapor compression refrigeration and heat pump systems.
Figure 9.
Comparisons of calculation results by correlation (4) and correlation (7) (q is in W·m−2, Rp = 0.4 μm).
Figure 9.
Comparisons of calculation results by correlation (4) and correlation (7) (q is in W·m−2, Rp = 0.4 μm).
7. Conclusions
To research the evaporator heat transfer and its enhancement in water vapor compression refrigeration and heat pump systems, in this experiment, water boiling heat transfer on a horizontal copper rod surface at corresponding work conditions (1.8–3.3 kPa, 4000–10,000 W·m
−2) is researched by experiments. The conclusions are drawn as follows:
- (1)
At sub-atmospheric pressure, when the heat flux is constant, the boiling heat transfer coefficient of water increases with increasing pressure. It agrees with that at atmospheric pressure and positive pressure.
- (2)
When the pressure is low, the increase of boiling heat transfer coefficient with increasing pressure is slow. When the pressure reaches a certain value, the increase is enhanced. Moreover, with the heat flux increasing, this pressure value approximately linearly decreases with increasing heat flux. The change of increase trend of boiling heat transfer coefficient may be due to the change of heat transfer mode.
- (3)
The experimental data are fitted using the least-squares method, and the regression equations are showed as follows:
- (4)
The Cooper correlation used for calculating the pool boiling heat transfer coefficient of refrigerants extensively is not suitable for this experiment, i.e., this correlation is not suitable for the calculation of evaporator heat transfer coefficients in water vapor compression refrigeration and heat pump systems.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos. 51376010).
Author Contributions
Li-Hua Yu made experiments and wrote the main part of the paper. Shu-Xue Xu and Guo-Yuan Ma revised the paper. Jun Wang gave great suggestions. All authors read and approve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | heating surface area (m2) |
| c | specific heat capacity (J·kg−1·K−1) |
| d | diameter of the copper rod (m) |
| g | acceleration of gravity (m·s−2) |
| h | heat transfer coefficient (W·m−2·°C−1) |
| p | pressure (kPa) |
| Q | heating power (W) |
| q | heat flux (W·m−2) |
| t | temperature (°C) |
| ∆t | temperature difference (°C) |
| ρ | density (kg·m−3) |
| λ | thermal conductivity (W·m−1·K−1) |
| ν | kinematic viscosity (m2·s−1) |
| αv | volume expansion coefficient (K−1) |
| Nu | Nusselt number |
| Gr | Grashof number |
| Pr | Prandtl number |
Subscripts
| wall | heat transfer surface |
| w | water |
References
- Kharazi, A.A.; Müller, N. Implementation of 3-Port Condensing Wave Rotors in R718 Cycles. J. Energy Resour. Technol. 2006, 128, 325–334. [Google Scholar] [CrossRef]
- Sarevski, M.N.; Sarevski, V.N. Preliminary study of a novel R718 refrigeration cycle with single stage centrifugal compressor and two-phase ejector. Int. J. Refrig. 2014, 40, 435–449. [Google Scholar] [CrossRef]
- Das, S.K.; Roetzel, W.A. Composite Heat Transfer Model for Pool Boiling on a Horizontal Tube at Moderate Pressure. Can. J. Chem. Eng. 2004, 82, 316–322. [Google Scholar] [CrossRef]
- Liu, Z.H.; Liao, L. Enhancement Boiling Heat Transfer Study of a Newly Compact In-line Bundle Evaporator under Reduced Pressure Conditions. Chem. Eng. Technol. 2006, 29, 408–413. [Google Scholar] [CrossRef]
- Chan, M.A.; Yap, C.R.; Ng, K.C. Pool Boiling Heat Transfer of Water on Finned Surfaces at Near Vacuum Pressures. J. Heat Transf. 2010, 132. [Google Scholar] [CrossRef]
- Giraud, F.; Rullière, R.; Toublanc, C.; Clausse, M.; Bonjour, J. Experimental evidence of a new regime for boiling of water at sub-atmospheric pressure. Exp. Therm. Fluid Sci. 2015, 60, 45–53. [Google Scholar] [CrossRef]
- Schnabel, L.; Scherr, C.; Weber, C. Water as Refrigerant-Experimental Evaluation of Boiling Characteristics at Low Temperatures and Pressures. In Proceeding of the VII Minsk International Seminar Heat Pumps, Refrigerators, Power Sources, Minsk, Belarus, 8–11 September 2008.
- Raben, I.A.; Beaubouef, R.T.; Commerford, G.E. A study of heat transfer in nucleate pool boiling of water at low pressure. Chem. Eng. Prog. Symp. Ser. 1965, 61, 249–257. [Google Scholar]
- Mitrovic, J. Intensivierung Des Wärmeübergangs Bei Verdampfung in Freier Strömung; VDI-Verlag: Düsseldorf, Germany, 1984. [Google Scholar]
- McGillis, W.R.; Carey, V.P.; Fitch, J.S.; McGillis, W.R. Pool boiling enhancement techniques for water at low pressure. In Proceeding of 7th IEEE Semiconductor Thermal Measurement and Management Symposium, Phoenix, AZ, USA, 12–14 February 1991; pp. 64–72.
- Hetsroni, G.; Gurevich, M.; Mosyak, A.; Rozenblit, R.; Segal, Z. Boiling enhancement with environmentally acceptable surfactant. Int. J. Heat Fluid Flow 2004, 25, 841–848. [Google Scholar] [CrossRef]
- Choon, N.K.; Chakraborty, A.; Aye, S.M.; Xiaolin, W. New pool boiling data for water with copper-foam metal at sub-atmospheric pressure: Experiment and correlation. Appl. Therm. Eng. 2006, 36, 1286–1290. [Google Scholar] [CrossRef]
- VDI Gesellschaft. VDI-Wärmeatlas; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Gorenflo, D. Wärmeübergangs Bei Blasensieden, Filmsieden und Einphasiger Freier Konvektion in Einemgroßen Druckbereich; Müller-Verlag: Karlsruhe, Germany, 1977. [Google Scholar]
- Zhang, D.C.; Wang, K.; He, Y.L.; He, Y.; Tao, W. Boiling heat transfer of R134a outside horizontal doubly-enhanced tubes. J. Chem. Ind. Eng. (China) 2007, 58, 2710–2714. [Google Scholar]
- Tian, H.; Liu, Z.Y.; Ma, Y.T. Experimental research on falling film evaporating characteristic outside the horizontal enhanced tube. J. Eng. Thermophys. 2012, 33, 1924–1928. [Google Scholar]
- Chen, T.L. Water-Heated Pool Boiling of Different Refrigerants on the Outside Surface of a Horizontal Smooth Tube. J. Heat Transf. 2012, 134. [Google Scholar] [CrossRef]
- Yang, S.M.; Tao, W.Q. Heat Transfer, 4th ed.; Higher Education Press: Beijing, China, 2006; p. 322. [Google Scholar]
- Cooper, M.G. Saturation Nucleate Pool Boiling—A Simple Correlation. Int. Chem. Eng. Symp. Ser. 1984, 86, 785–792. [Google Scholar]
- Cooper, M.G. Heat flow rates in saturated nucleate pool boiling—A wide ranging examination using reduced properties. Adv. Heat Transf. 1984, 16, 157–239. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).