Investigation of the Promotion of Wind Power Consumption Using the Thermal-Electric Decoupling Techniques
Abstract
:1. Introduction
2. Problem Statement (Concept of the Thermal-Electric Coupling of CHPs)
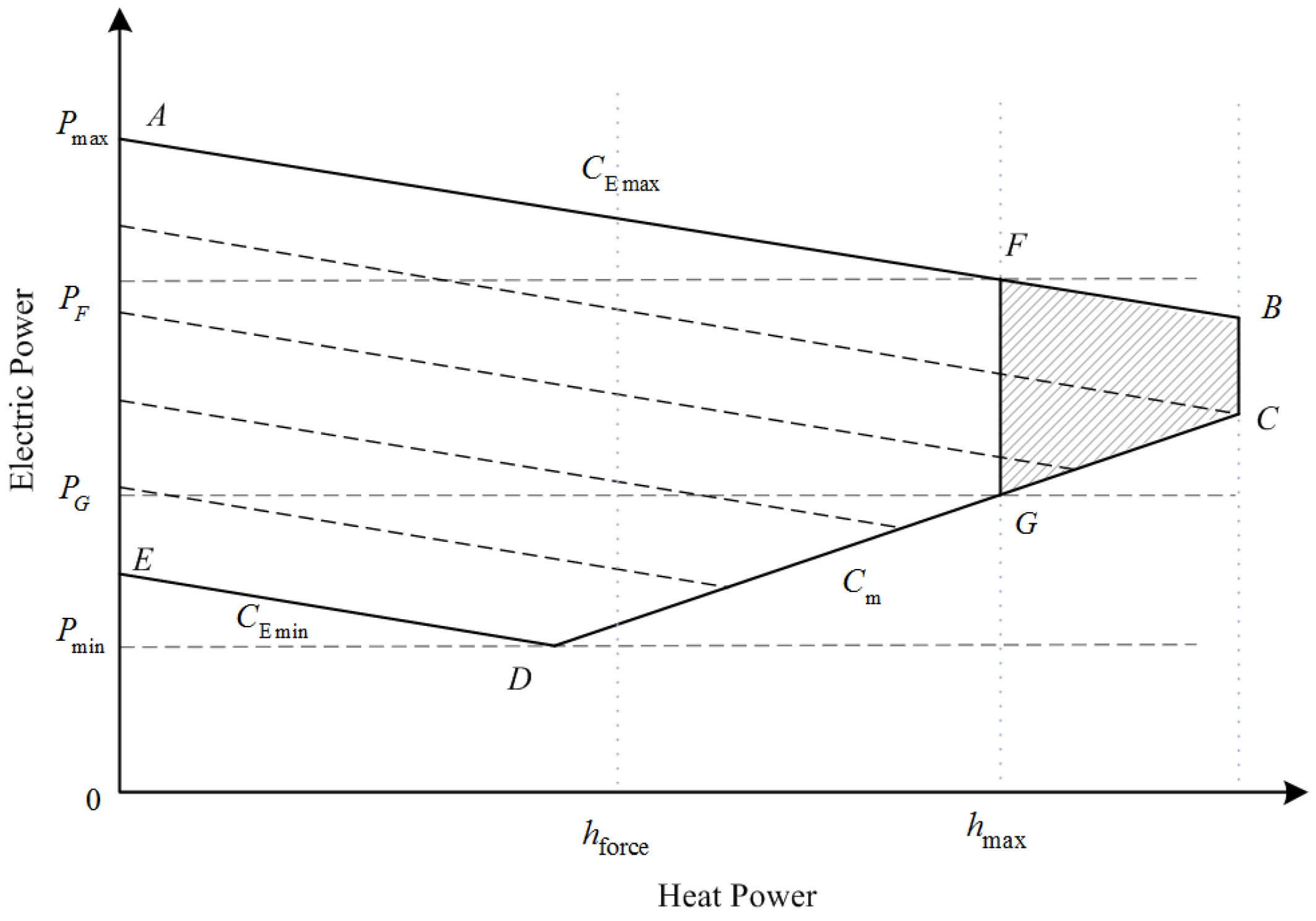
3. Proposed Schemes to Reduce the Thermal-Electric Coupling of CHPs
3.1. Principle of Thermal-Electric Decoupling
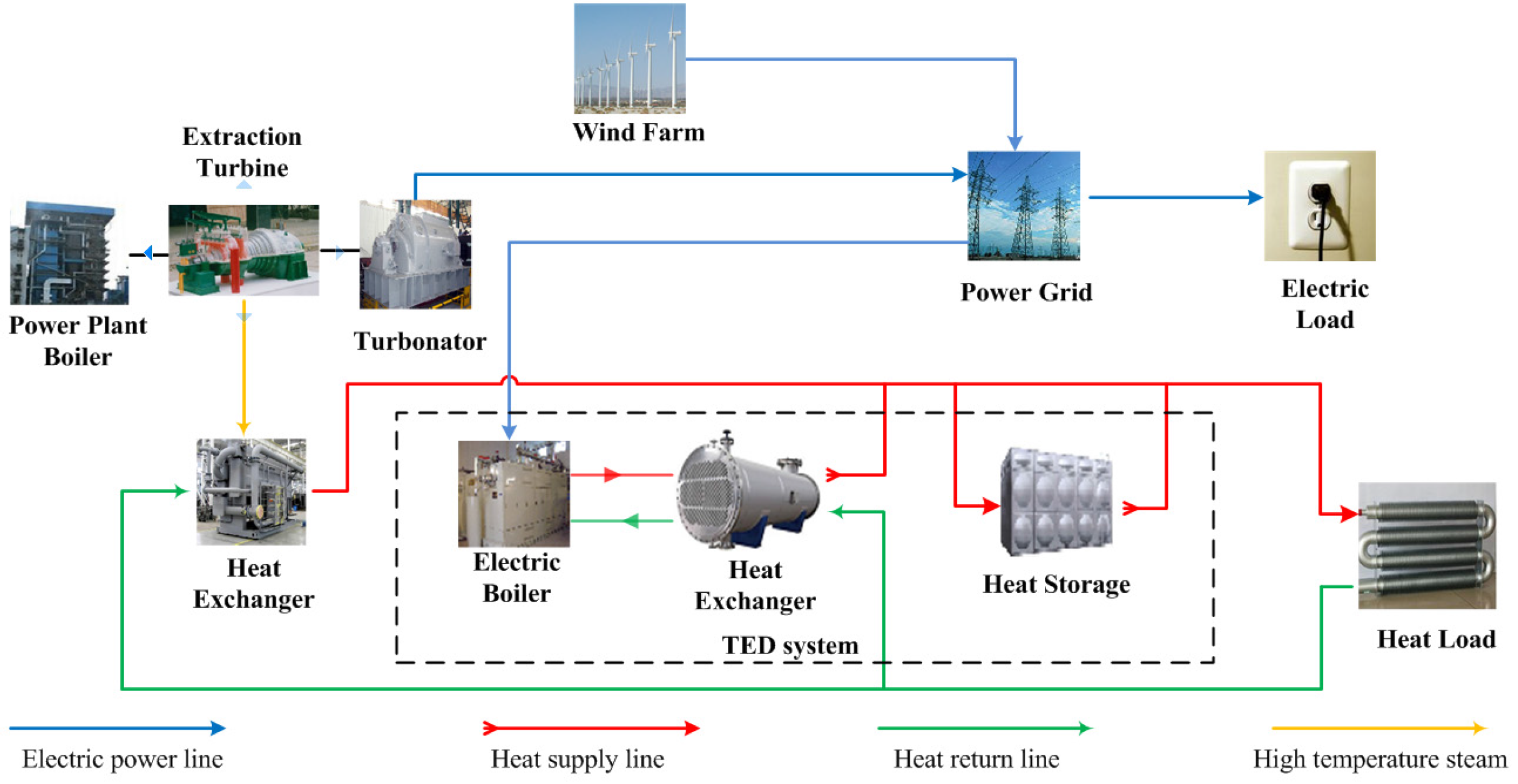
3.2. Effects of the Analysis of Auxiliary Thermal Sources on CHPs
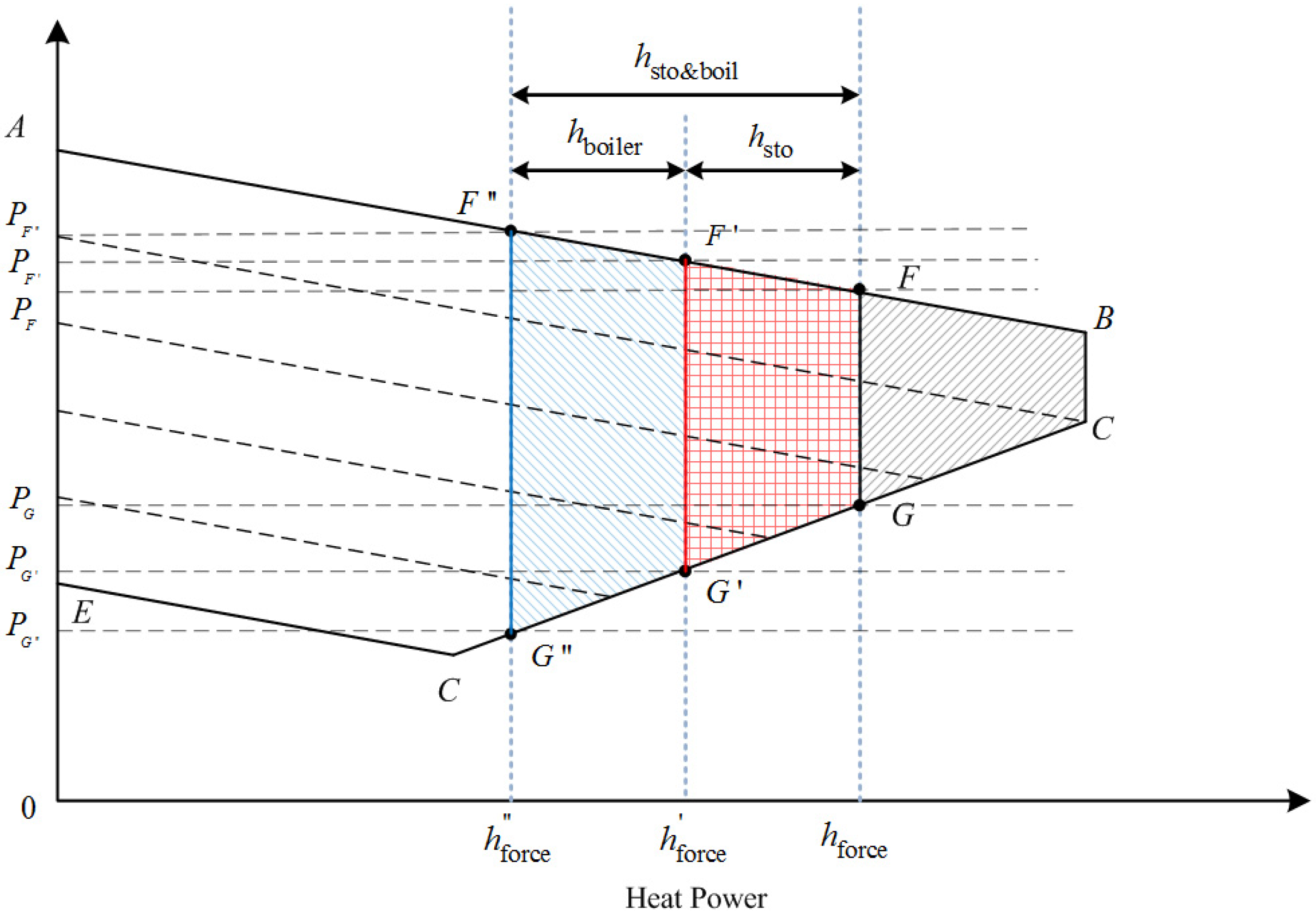
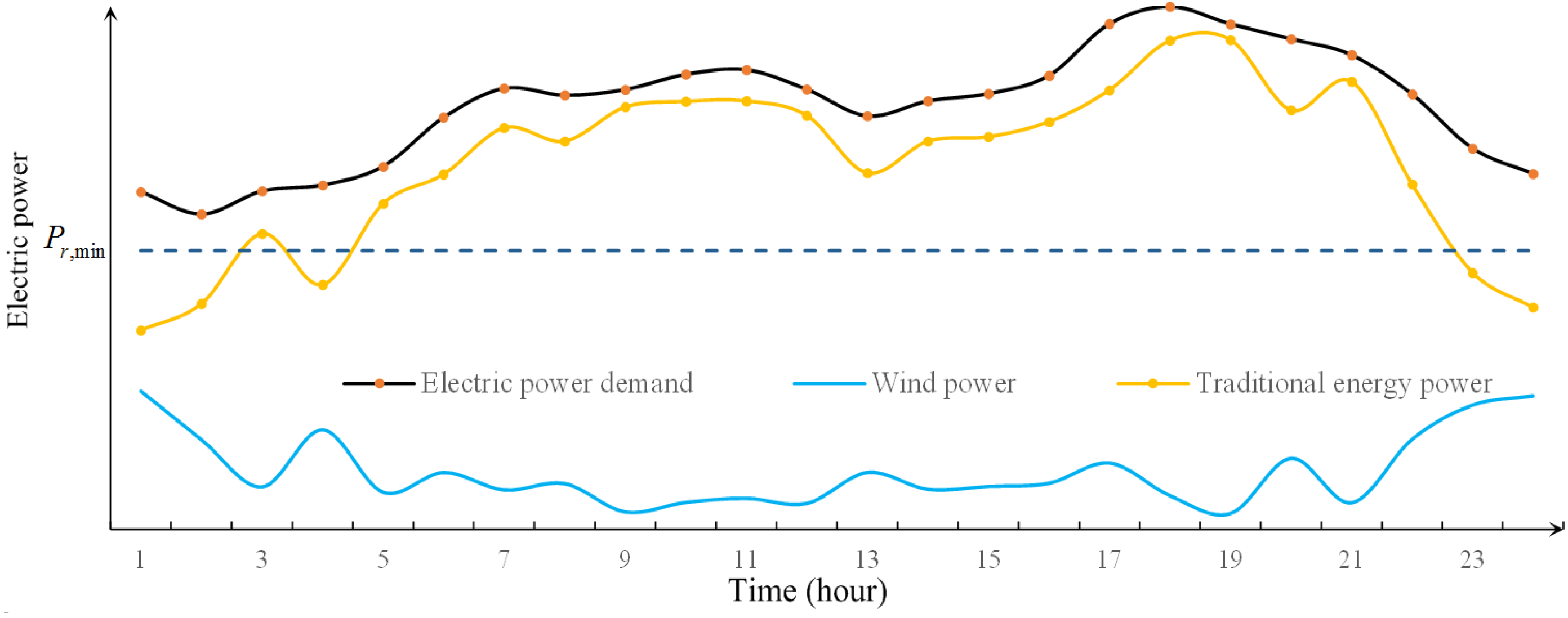
3.3. Technical Analysis of Auxiliary Thermal Sources on Wind Power Curtailment
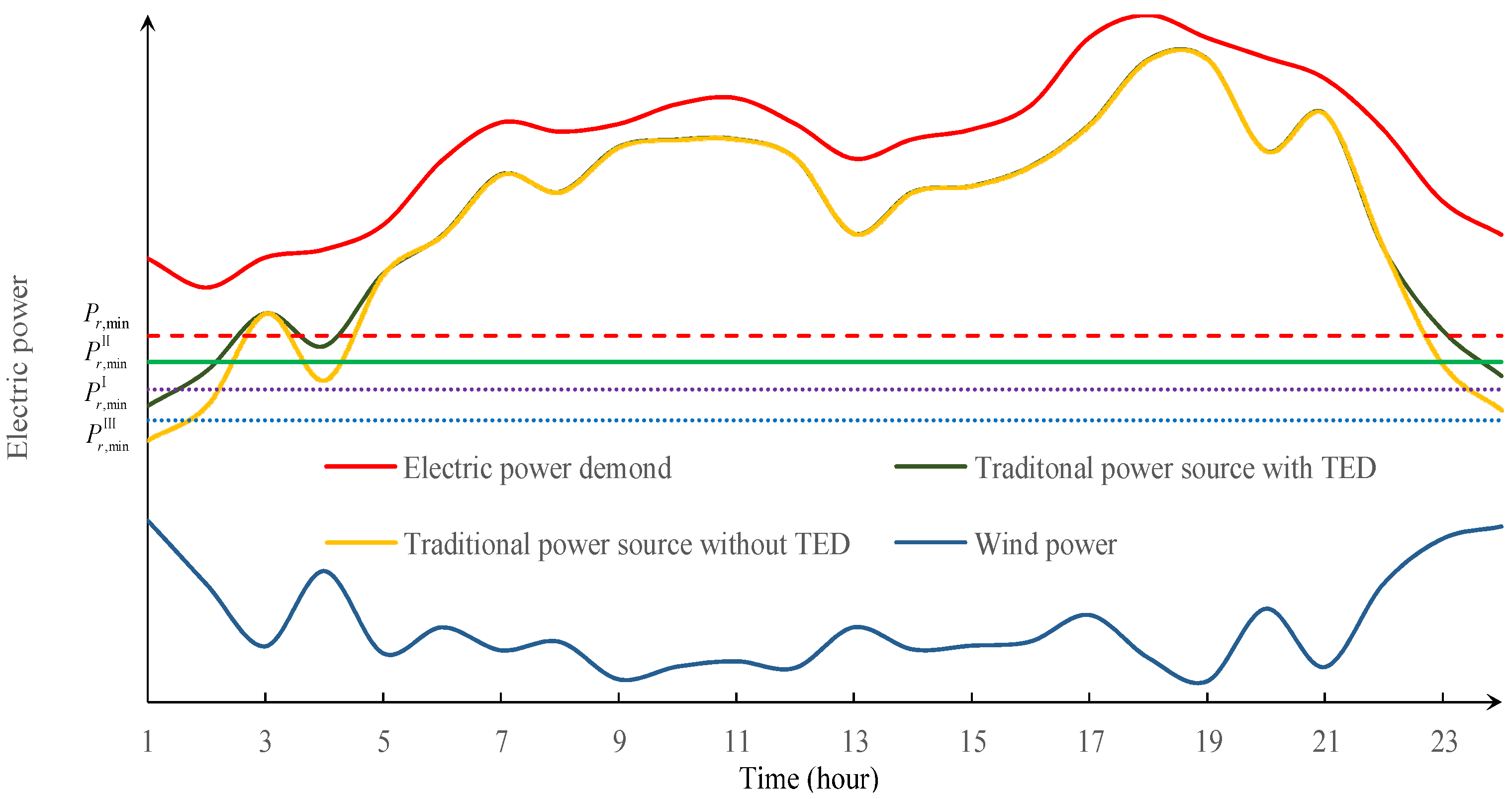
| Measure | Wind Power Curtailment |
|---|---|
| No measure | 1 a.m., 2 a.m., 4 a.m., 11 p.m., 12 p.m. |
| HS only | 1 a.m., 2 a.m., 12 p.m. |
| EB only (EB store the heat) | 1 a.m., 2 a.m., 4 a.m., 12 p.m. |
| EB only (EB release the heat) | 1 a.m., 2 a.m., 12 p.m. |
| HS & EB (EB store the heat) | 1 a.m., 12 p.m. |
| HS & EB (EB release the heat) | 1 a.m. |
4. Technical Evaluation of Thermal-Electric Decoupling
4.1. Assessment Indexes
| Scenario | Discrimination | Heat Storage Status | |||
|---|---|---|---|---|---|
| A | 0 | 0 | Out of work | ||
| B | 0 | 0 | Out of work | ||
| C | 0 | Out of work | |||
| D | 0 | 0 | Work | ||
| E | 0 | Work | |||
| F | 0 | Work | |||
| G | Work | ||||
| H | 0 | 0 | 0 | N/A |
4.2. Calculating Procedures

5. Modeling and Numerical Simulations
5.1. System Modeling
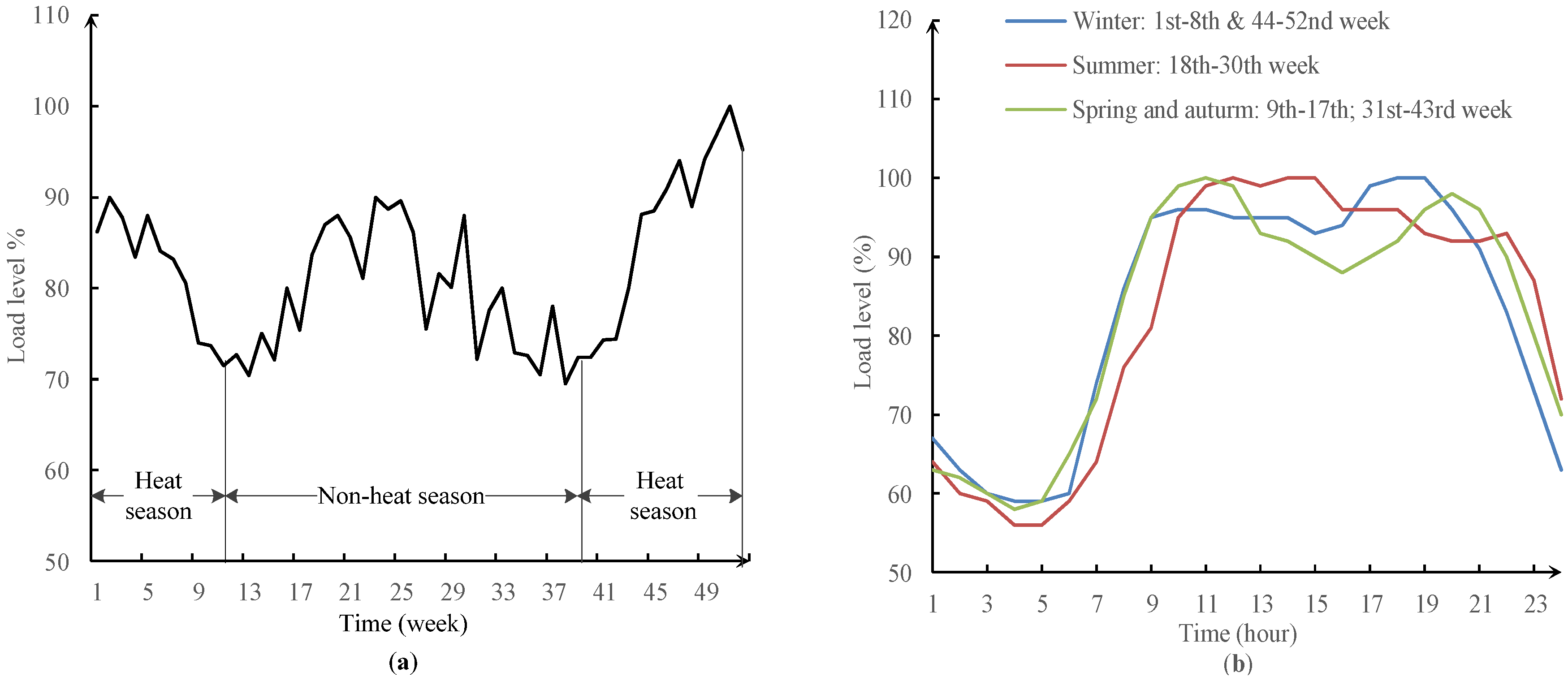
5.1.1. Electric Load Model
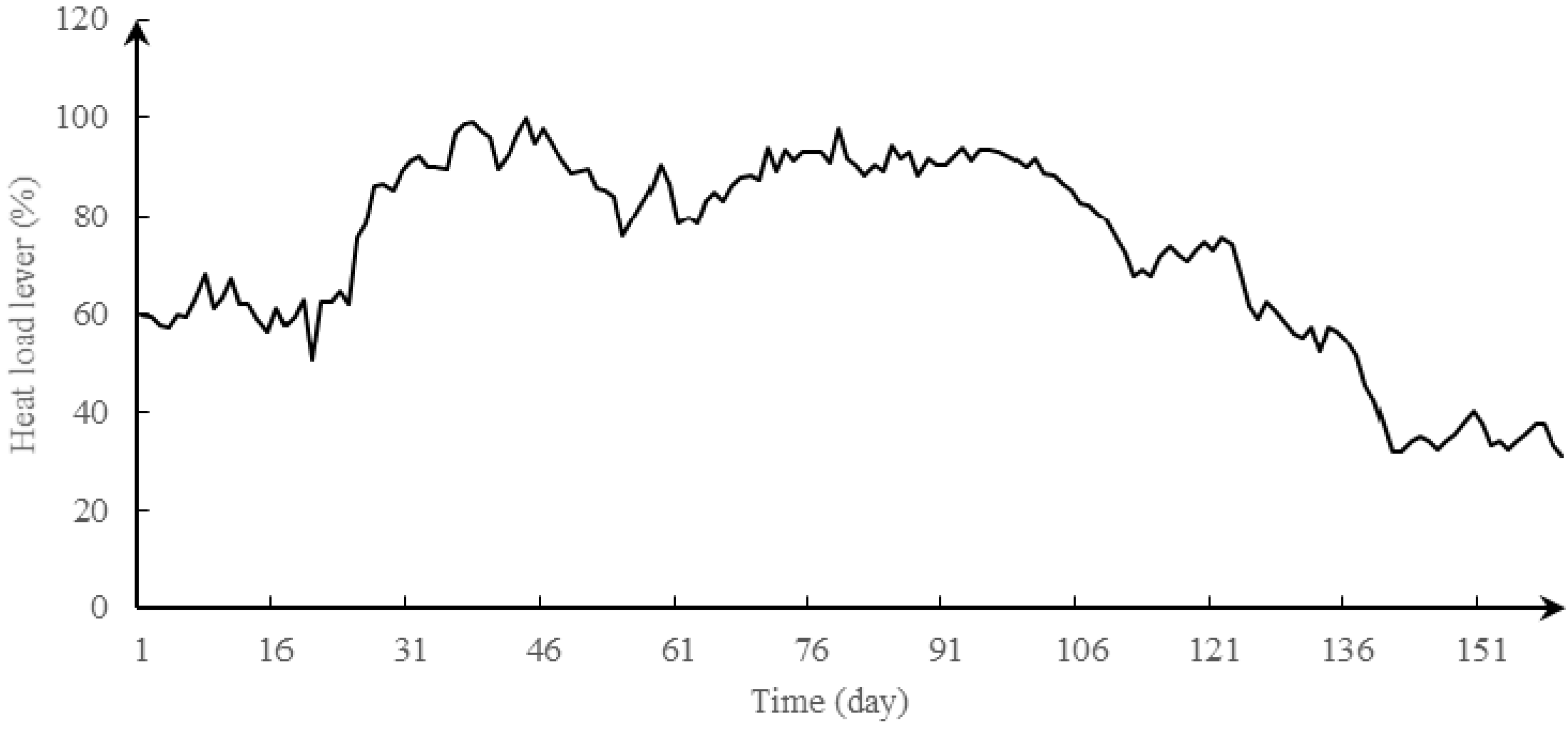
5.1.2. Heat Load Model
5.1.3. Wind Farms Model
5.2. General Situation of Simulation
| Area and Power Source Type | Installed Capacity | Electric Power Output Change Interval (MW, Non-Heat Season) | Electric Power Output Change Interval (MW, Heat Season) |
|---|---|---|---|
| Heat zone A (CHPs) | 300 MW × 2 | 300, 600 | 420, 492 |
| Heat zone B (CHPs) | 350 MW + 200 MW | 275, 550 | 385, 460 |
| Heat zone C (CHPs) | 200 MW × 2 | 200, 400 | 280, 340 |
| Pure condensing steam units | 200 MW × 3 + 500 MW × 1 | 440, 1100 | 440, 1100 |
| Wind farm | 1.5 MW × 400 | 0, 600 | 0, 600 |
| Total | 3250 MW | 1215, 3250 | 1525, 2992 |
| Capacity (MW) | Model | Electric Power Output Interval (MW, Rated) | Heat Power Output Interval (MW, Rated) | Electric Power Output Interval (MW, Heat Season) | Heat Power Output Interval (MW, Heat Season) |
|---|---|---|---|---|---|
| 200 | C240/N200-12.75/1.08/0.245 | 100, 200 | 0, 250 | 140, 170 | 0, 220 |
| 300 | C240/N300-16.7/535/538/0.4 | 300, 150 | 0, 400 | 210, 246 | 0, 280 |
| 350 | C330N350-17.75/540/540/0.981 | 175, 350 | 0, 450 | 245, 290 | 0, 400 |
5.3. Simulation Results
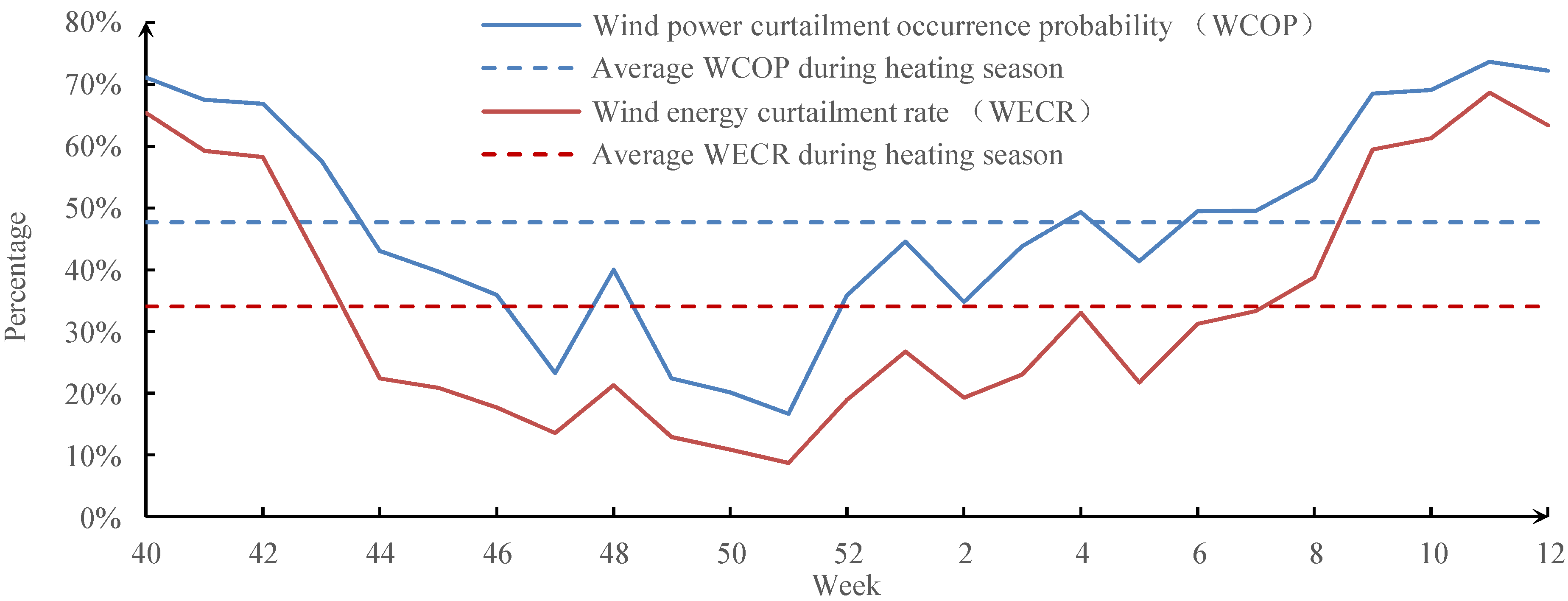
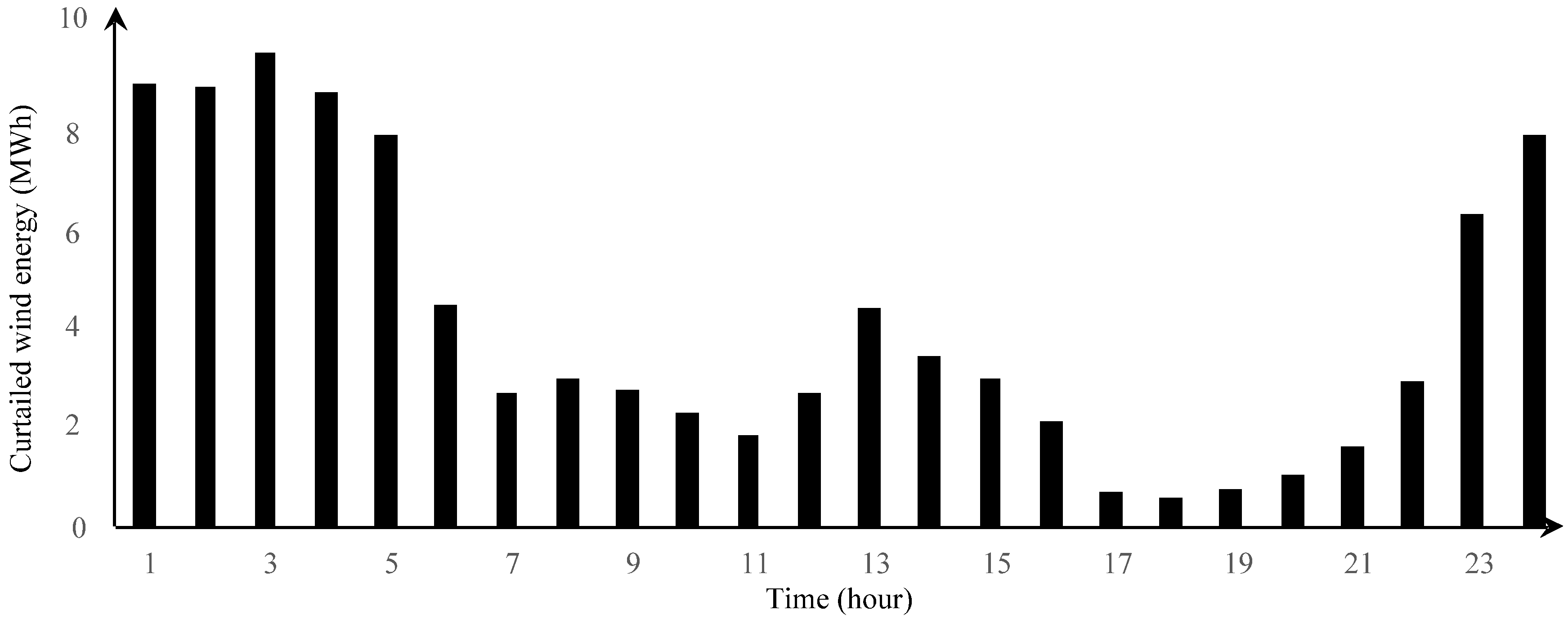
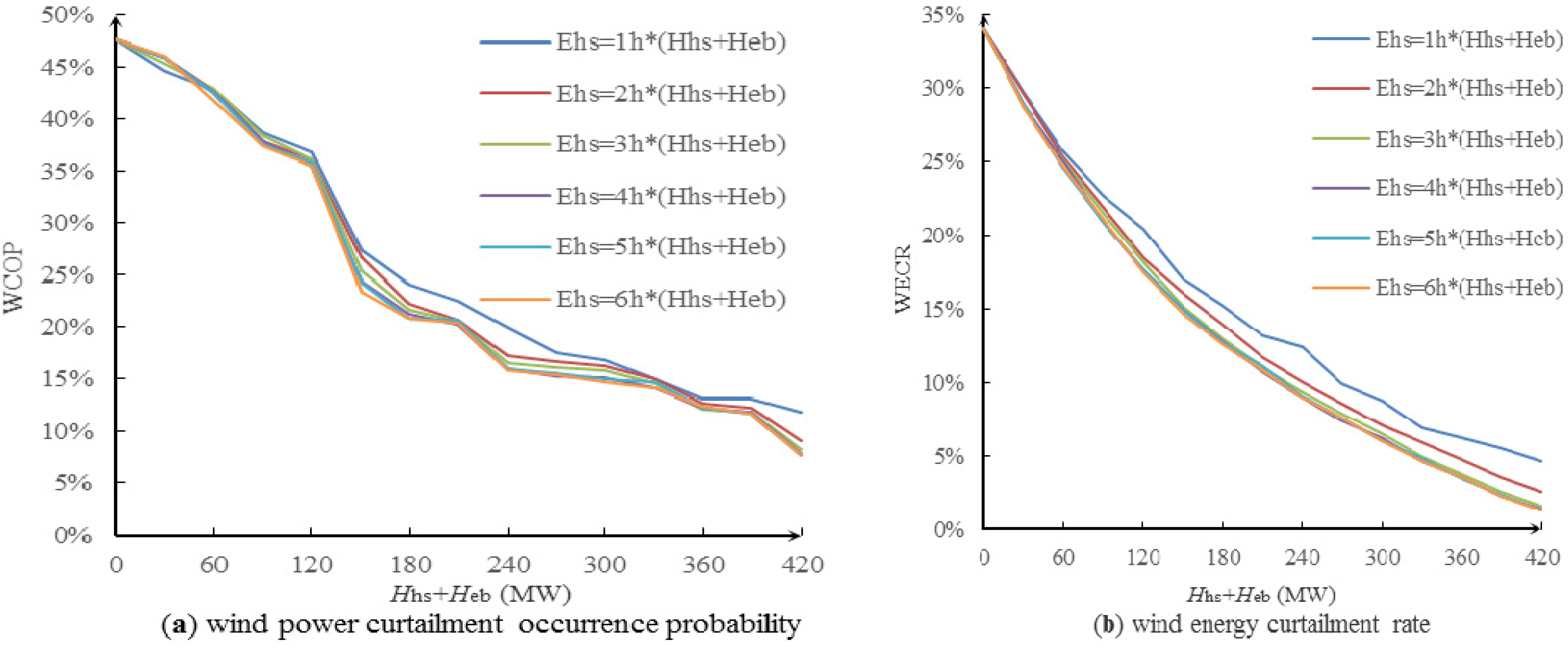
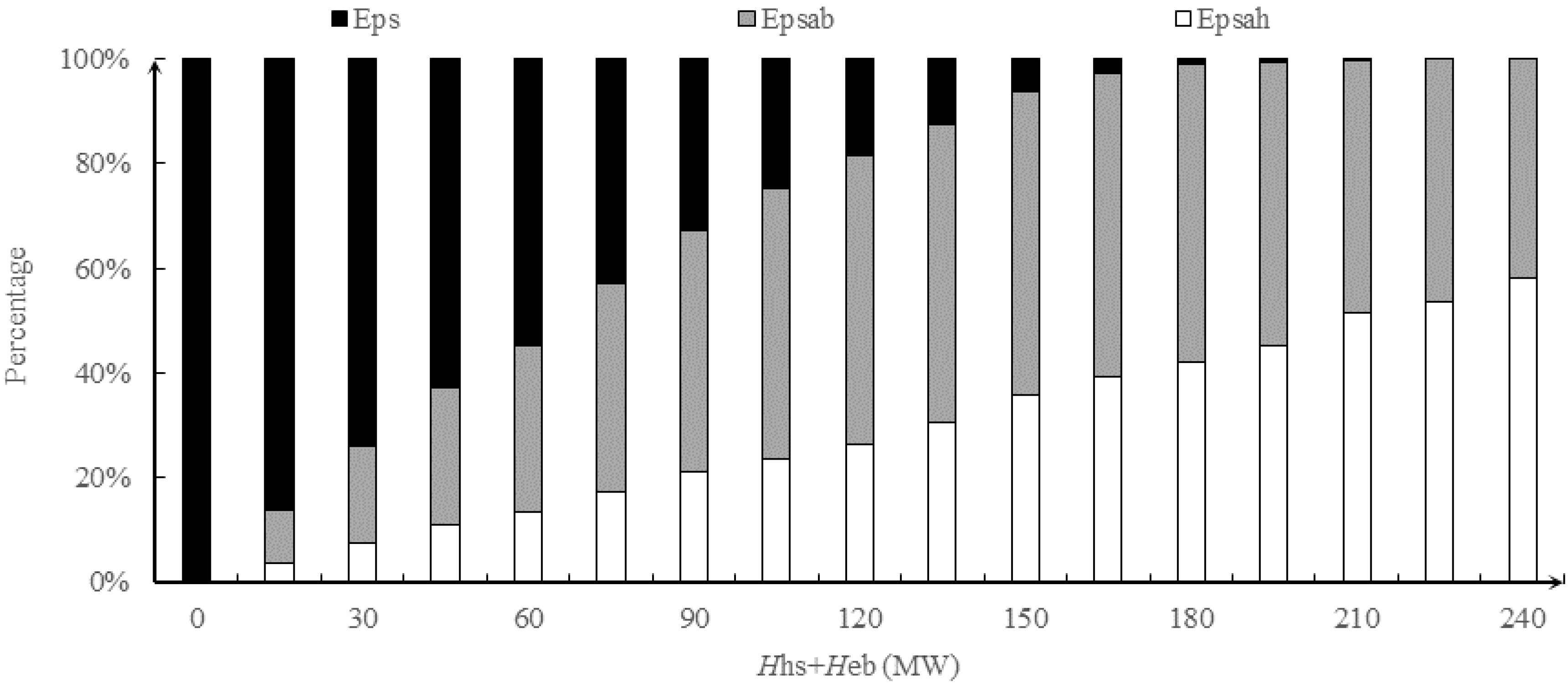
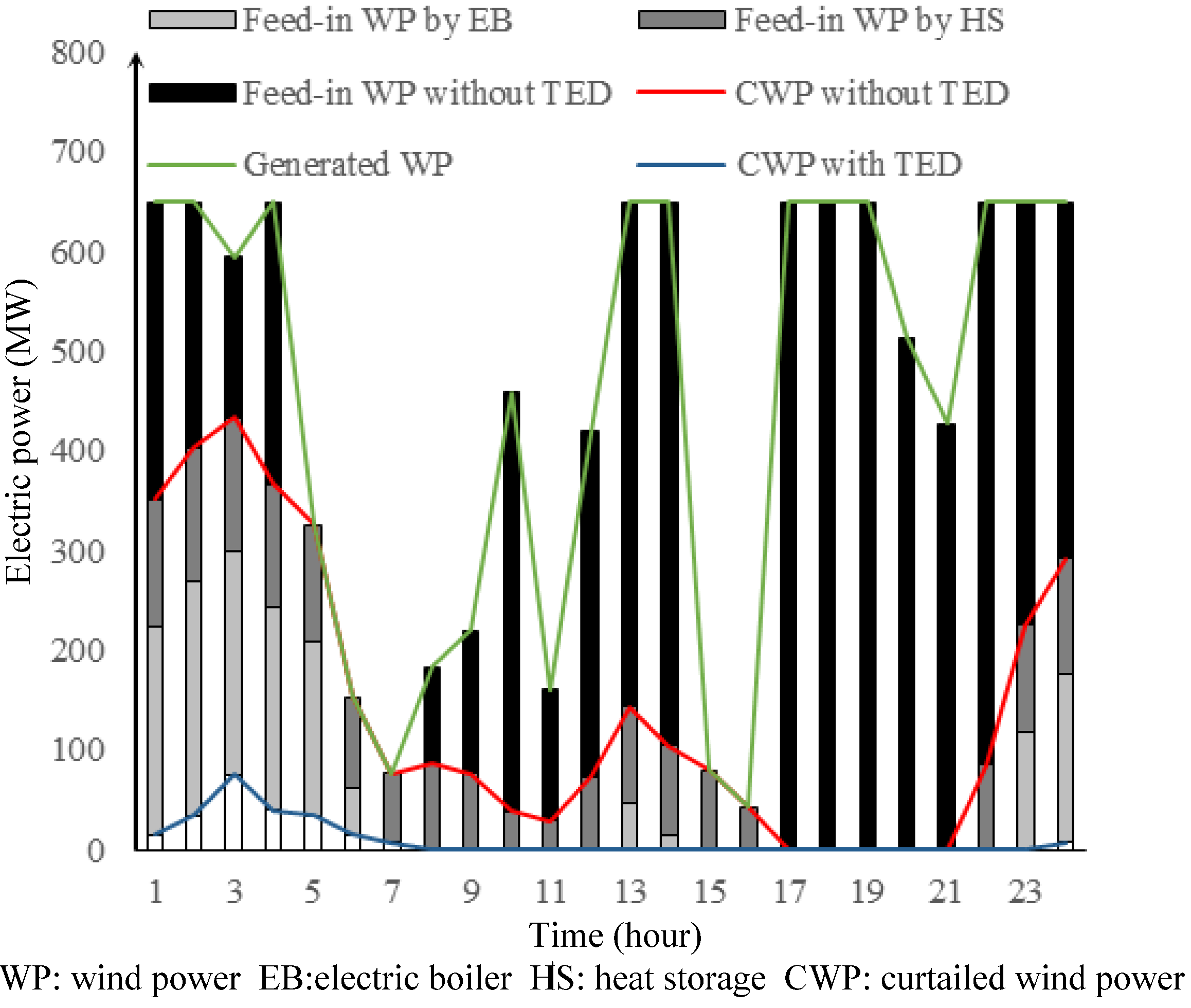
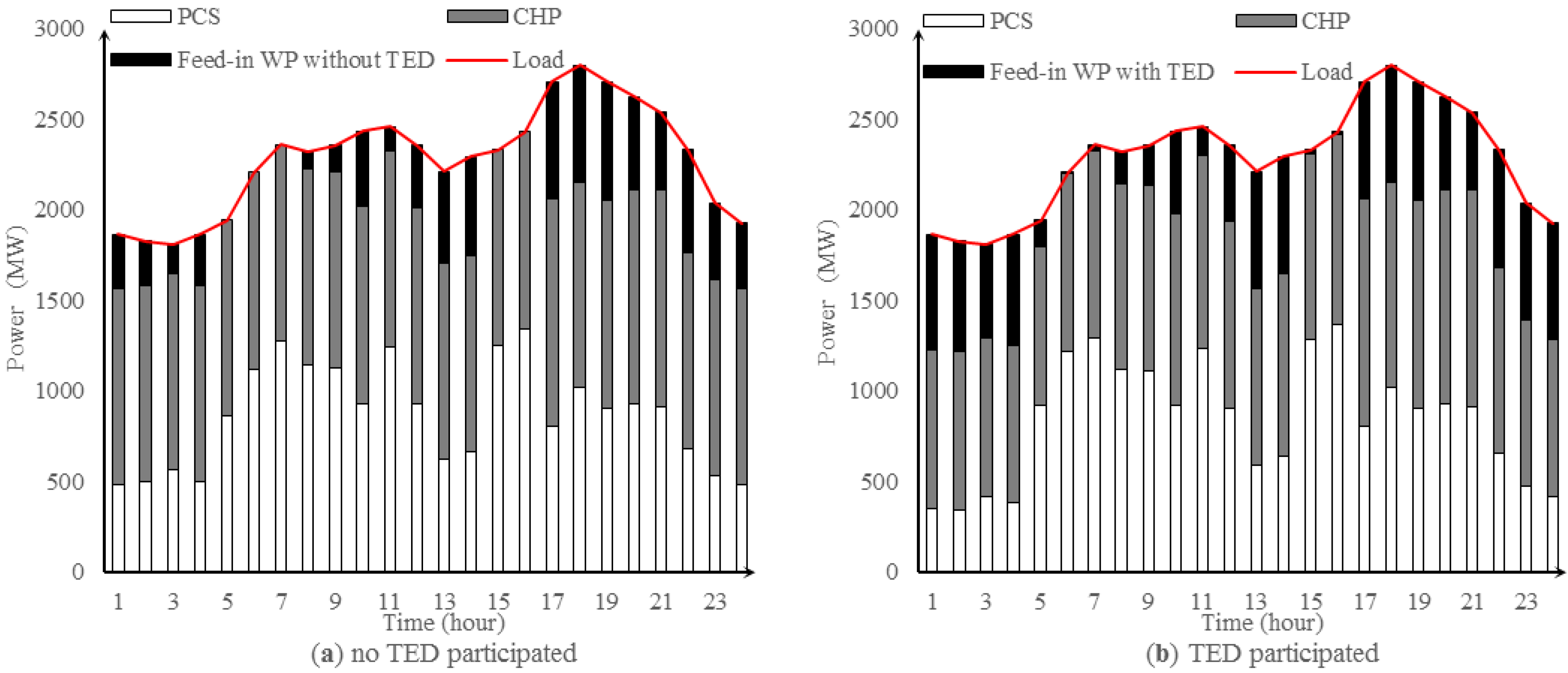
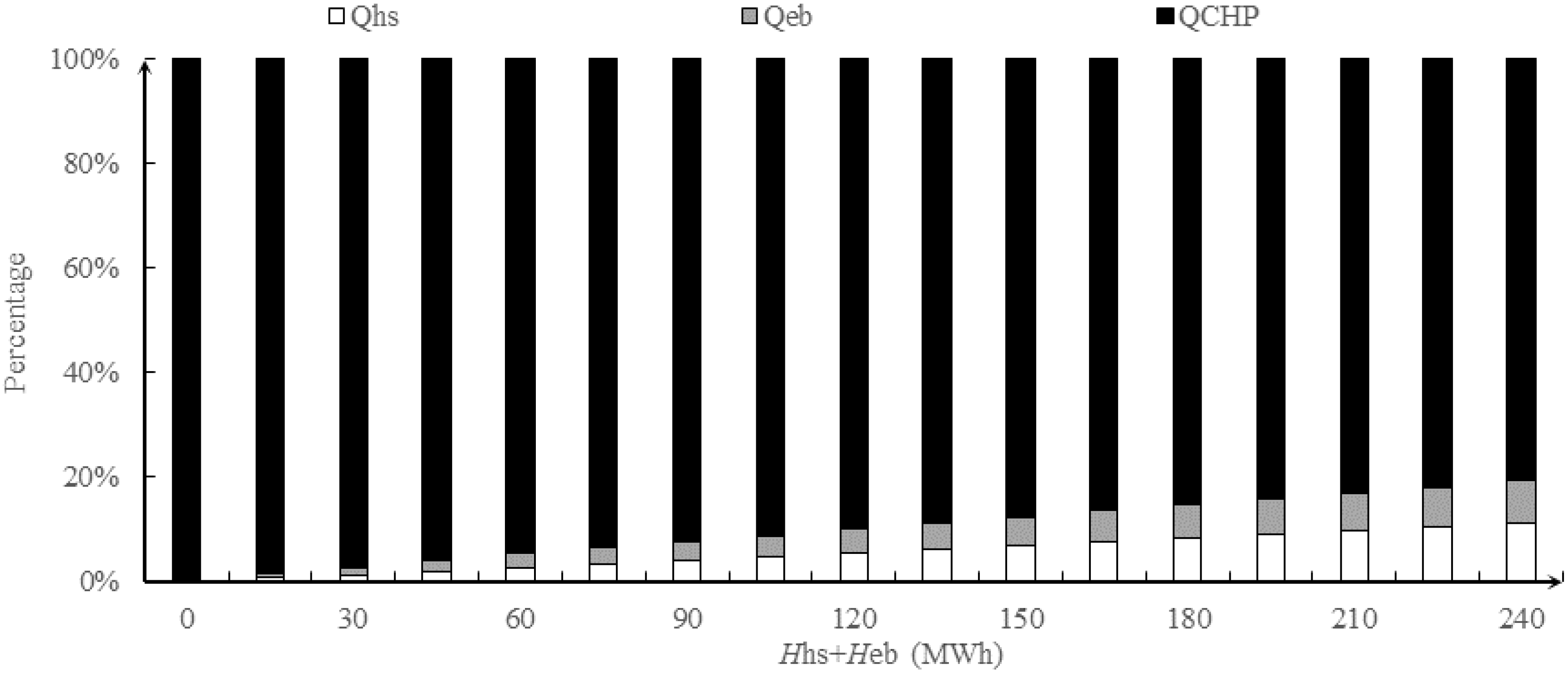
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ding, J.; Qiu, Y.F.; Sun, H.D.; Zhou, H.C.; Ma, S.Y.; Wang, Z.; Shen, H.; Li, B.; Song, Y.T. Consideration of wind generator tripping under Large-scale wind power integration. Proc. CSEE 2011, 19, 25–36. (In Chinese) [Google Scholar]
- Liu, X.D.; Fang, K.; Chen, H.Y.; She, C.Q. Research on rational wind power casting theory for large-scale wind power integration improvement. Power Syst. Prot. Control 2012, 6, 35–39. [Google Scholar]
- Li, J.F.; Cai, F.B.; Qiao, L.M.; Wang, J.X.; Gao, H.; Tang, W.Q.; Peng, P.; Geng, D.; Li, X.Q.; Li, Q.H. 2014 China Wind Power Review and outlook. Available online: http://www.doc88.com/p-9435193811067.html (accessed on 12 June 2015).
- Zhang, W.L.; Qiu, M.; Lai, X.K. Application of energy storage technologies in power grids. Power Syst. Technol. 2008, 7, 1–9. [Google Scholar]
- Teng, J.; Chen, C.; Martinez, I.C. Utilising energy storage systems to mitigate power system vulnerability. IET Génér. Transm. Distrib. 2013, 7, 790–798. [Google Scholar] [CrossRef]
- Francisco, D.; Andreas, S.; Oriol, G.; Roberto, V. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar]
- Khodayar, M.E.; Abreu, L.; Shahidehpour, M. Transmission-constrained intra hour coordination of wind and pumped-storage hydro units. IET Génér. Transm. Distrib. 2013, 7, 755–765. [Google Scholar] [CrossRef]
- Kushnir, R.; Dayan, A.; Ullmann, A. Temperature and pressure variations within compressed air energy storage caverns. Int. J. Heat Mass Transf. 2012, 55, 5616–5630. [Google Scholar] [CrossRef]
- Kassa, I.; Djamila, R.; Toufik, R.; Abdelmounaim, T. Wind energy conversion system associated to a flywheel energy storage system. Analog. Integr. Circuits Signal Proc. 2011, 69, 67–73. [Google Scholar]
- Nirmal-Kumar, C.; Niraj, G. Battery energy storage systems: Assessment for small-scale renewable energy integration. Energy Build. 2010, 42, 2124–2130. [Google Scholar]
- Hedegaard, K.; Mathiesen, B.; Lund, H.; Heiselberg, P. Wind power integration using individual heat pumps—Analysis of different heat storage options. Energy 2012, 47, 284–293. [Google Scholar] [CrossRef]
- Ruan, J.P.; Zhang, J.C.; Wang, J.H. Improvement of stability of wind farms connected to power grid using flywheel energy storage system. Electr. Power Sci. Eng. 2008, 3, 5–8. [Google Scholar]
- Gholami, A.; Ansari, J.; Jamei, M.; Kazemi, A. Environmental/economic dispatch incorporating renewable energy sources and plug-in vehicles. IET Génér. Transm. Distrib. 2014, 8, 2183–2198. [Google Scholar] [CrossRef]
- Li, Q.Y. Wind power consumption mode based on water source heat pump technology. Automat. Electr. Power Syst. 2012, 36, 25–27. [Google Scholar]
- Lund, H.; Munster, E. Modelling of energy systems with a high percentage of CHP and wind power. Renew. Energy 2003, 28, 2179–2193. [Google Scholar] [CrossRef]
- Meibom, P.; Kiviluoma, J.; Barth, R.; Brand, H.; Weber, C.; Larsen, H. Value of electric heat boilers and heat pumps for wind power integration. Wind Energy 2007, 10, 321–337. [Google Scholar] [CrossRef]
- Mathiesen, B.V.; Lund, H. Comparative analyses of seven technologies to facilitate the integration of fluctuating renewable energy sources. IET Renew. Power Génér. 2008, 3, 190–204. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Hasche, B.; Nabe, C. Potential of heat pumps for demand side management and wind power integration in the German electricity market. IEEE Trans. Sustain. Energy 2012, 3, 636–642. [Google Scholar] [CrossRef]
- Akmal, M.; Fox, B.; Morrow, J.D. Impact of heat pump load on distribution networks. IET Génér. Transm. Distrib. 2014, 8, 2065–2073. [Google Scholar] [CrossRef] [Green Version]
- Blark, M. Towards an intermittency-friendly energy system: Comparing electric boilers and heat pumps in distributed cogeneration. Appl. Energy 2012, 91, 354–365. [Google Scholar] [CrossRef]
- Kiviluoma, J.; Meibom, P. Influence of wind power, plug-in electric vehicles, and heat storages on power system investments. Energy 2010, 35, 1244–1255. [Google Scholar] [CrossRef]
- Østergaard, P.A. Wind power integration in Aalborg Municipality using compression heat pumps and geothermal absorption heat pumps. Energy 2013, 49, 502–508. [Google Scholar] [CrossRef]
- Jing, T.Y. The Research on Active Power Balance of Power System under Large-Scale Integration of Wind Power. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- Yang, T.H.; Zhou, J.H.; Cao, X.Y.; Cen, K.F. Application of heat-electricity ratio in energy-saving analysis of thermal power station. Power Syst. Eng. 2001, 6, 329–332. [Google Scholar]
- Cai, G.W.; Du, Y.; Li, C.S.; Gu, X.G.; Li, Y. Middle and long-term daily load curve forecasting based on support vector machine. Power Syst. Technol. 2006, 23, 56–60. [Google Scholar]
- Freris, L.; Infield, D. Renewable Energy in Power Systems, 1st ed.; John Wiley & Sons Ltd Publication: Chester, UK, 2008; pp. 27–33. [Google Scholar]
- Zhang, N.; Kang, C.Q.; Duan, C.G. Simulation methodology of multiple wind farms operation considering wind speed correlation. In Proceedings of the third IASTED Asian Conference on Power and Energy Systems, Beijing, China, 12–14 October 2009; pp. 35–42.
- Zhang, R.S.; Qi, G.G.; Li, C.B.; Li, L.; Bao, Y.P.; Zhu, Y.S. Forecasting of load model based on typical daily load profile and BP neural network. In Proceedings of the International Conference on System Engineering and Modeling, Kuala Lumpur, Malaysia, 7–8 April 2012; pp. 125–134.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, S.; Li, Z.; Li, W. Investigation of the Promotion of Wind Power Consumption Using the Thermal-Electric Decoupling Techniques. Energies 2015, 8, 8613-8629. https://doi.org/10.3390/en8088613
Rong S, Li Z, Li W. Investigation of the Promotion of Wind Power Consumption Using the Thermal-Electric Decoupling Techniques. Energies. 2015; 8(8):8613-8629. https://doi.org/10.3390/en8088613
Chicago/Turabian StyleRong, Shuang, Zhimin Li, and Weixing Li. 2015. "Investigation of the Promotion of Wind Power Consumption Using the Thermal-Electric Decoupling Techniques" Energies 8, no. 8: 8613-8629. https://doi.org/10.3390/en8088613





