A Real-Time Joint Estimator for Model Parameters and State of Charge of Lithium-Ion Batteries in Electric Vehicles
Abstract
:1. Introduction
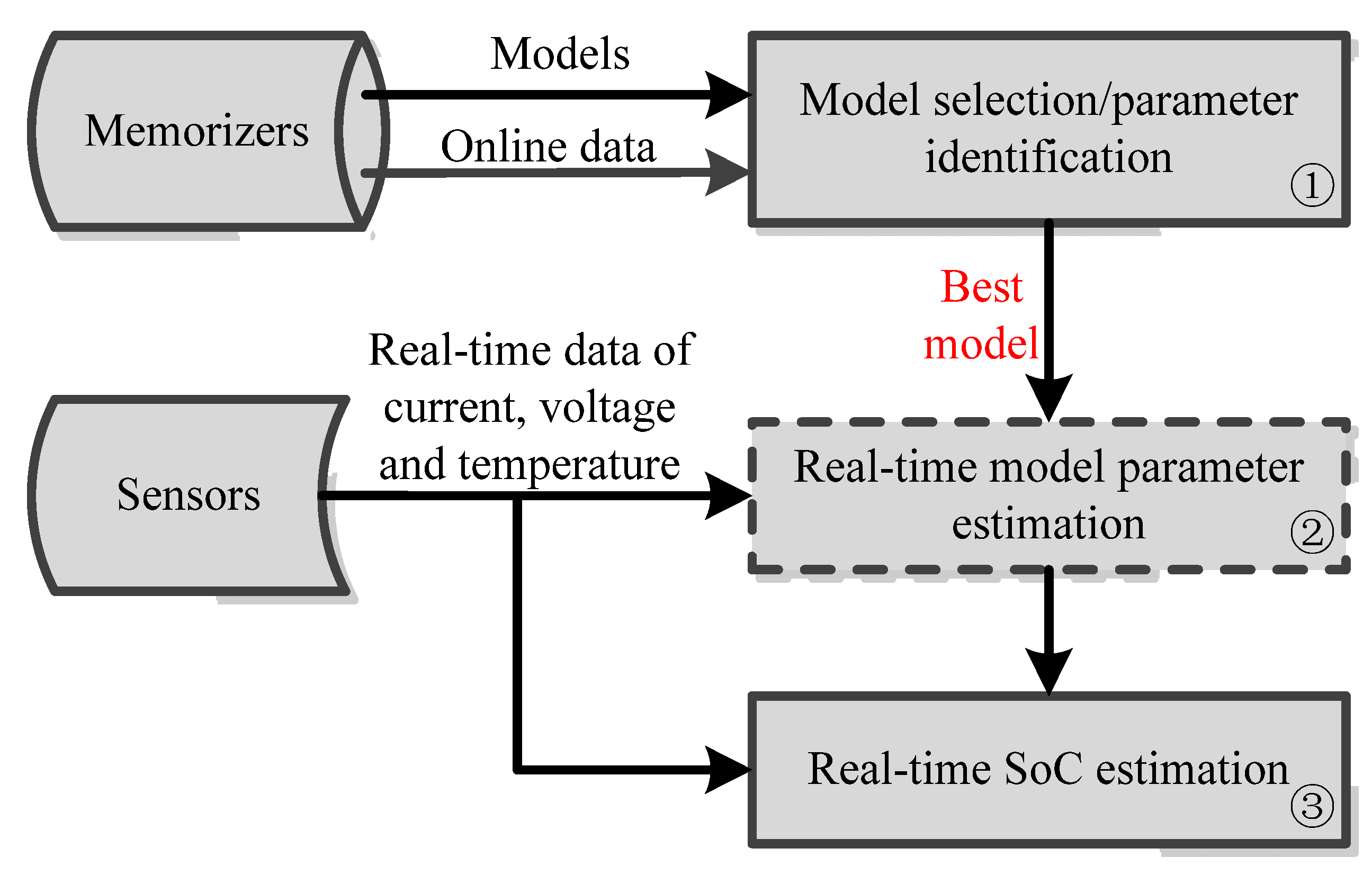
1.1. Contribution of the Paper
1.2. Organization of the Paper
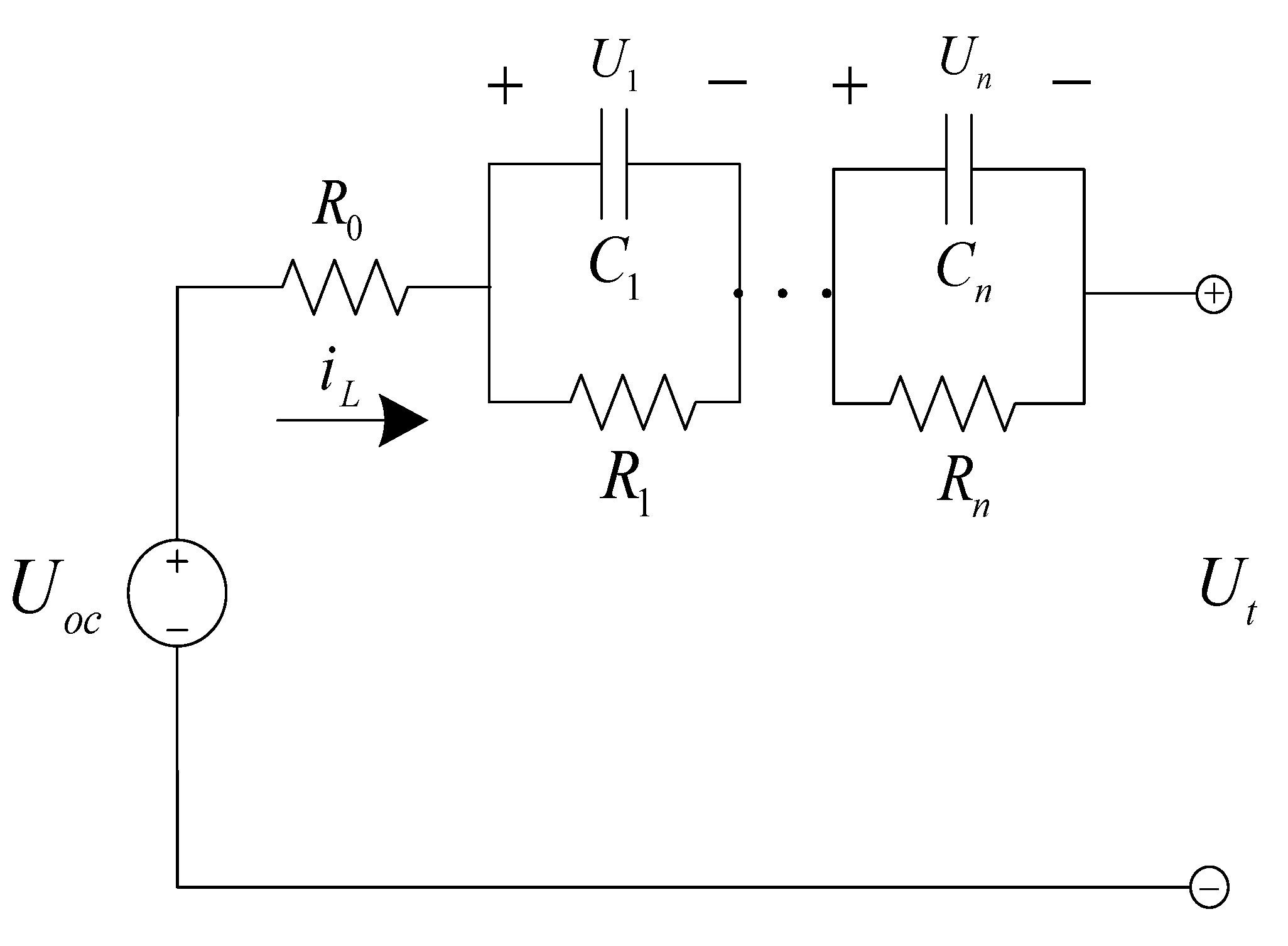
2. Battery Modeling and Real-Time Parameter Identification
3. Central Difference Kalman Filter (CDKF)-Based State of Charge (SoC) Estimator
3.1. State of Charge Definition
3.2. State-Space Modeling
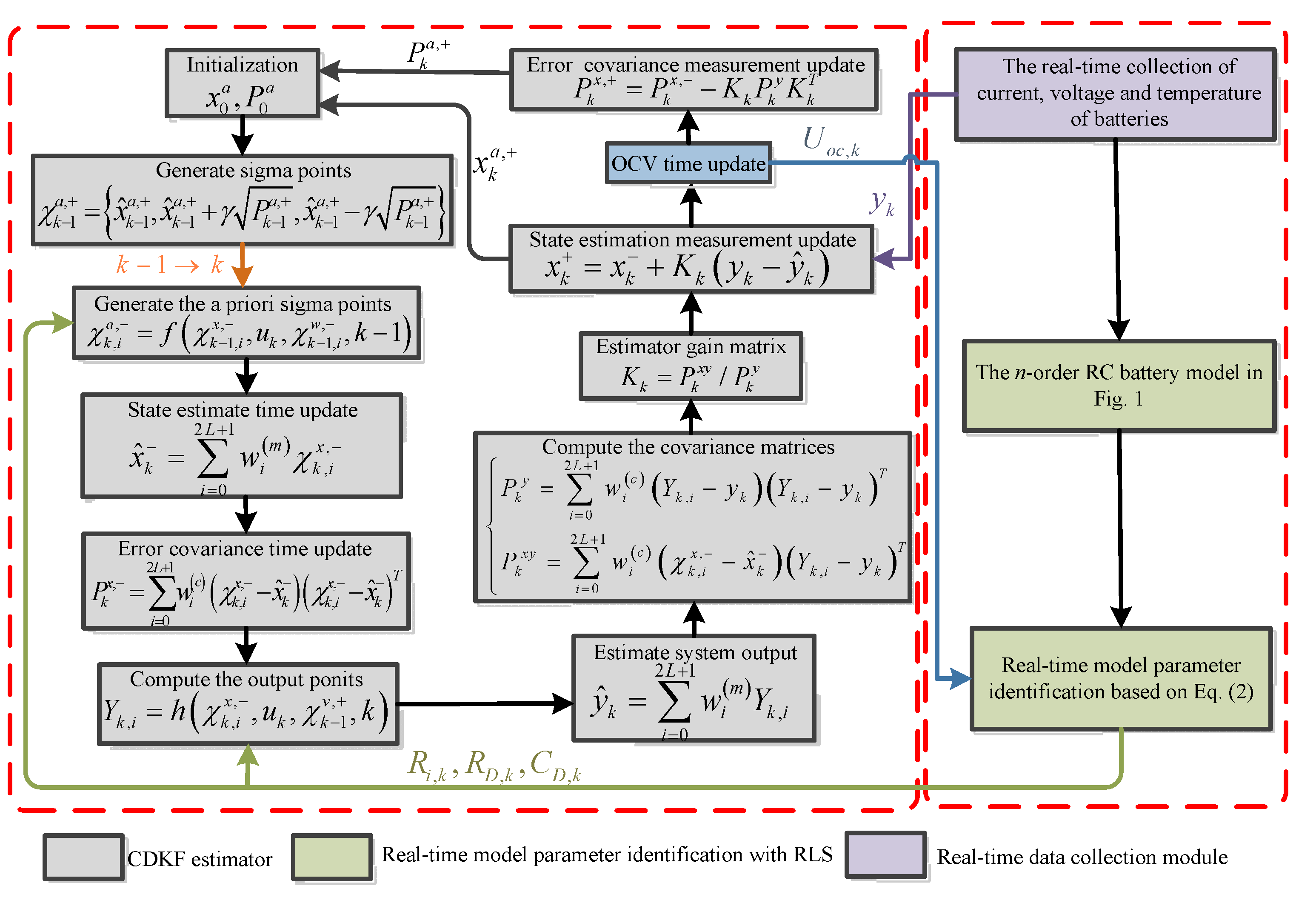
3.3. SoC Estimation Using the Central Difference Kalman Filter Algorithm
- Data measurement. The sensors collect the real-time data on current, voltage and temperature at each sampling time, and then the collected data are applied to identify the model parameters and estimate the SoC real-timely.
- Model parameter identification. The RLS method is used to realize real-time model parameter identification based on the collected data of current and voltage. Then the identified model parameters are transferred to the CDKF-based SoC estimator and the estimated OCV value is transferred back in turn. Herein, a stable and accurate RLS-based model parameter identification process can ensure, and at the same time is based on the good stability and high accuracy of the CDKF estimator.
- CDKF-based SoC estimator. The CDKF algorithm is used to estimate the SoC based on the identified model parameters. In this process, if model parameters are not identified correctly, the CDKF estimator will not work normally, thus leading to the wrong returned OCV value. However, the RLS and CDKF automatically correct the wrong estimates based on the big observer errors and gain matrices simultaneously, then both estimates of them will converge to the true values quickly, which realizes the close-loop SoC estimation process. Herein the proposed estimator in this paper is able to estimate the SoC accurately against different operating environment disturbances.
4. Data Set of Lithium-Ion Cell for Verification
4.1. Experiment Setup
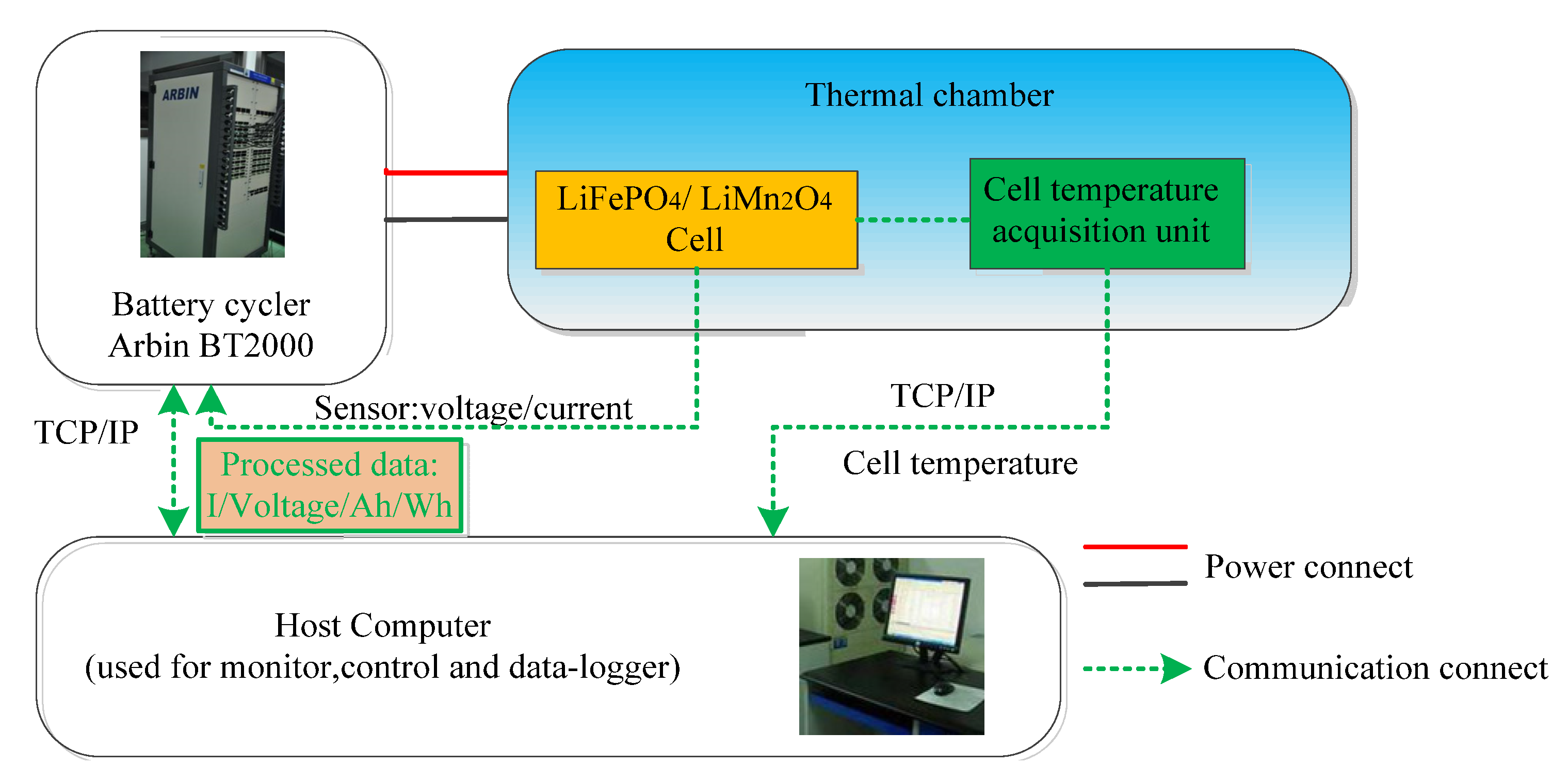
4.2. Battery Test
| Lithium-Ion Battery Cell | LiFePO4 | LiMn2O4 |
|---|---|---|
| Nominal capacity (Ah) | 2.3 | 35 |
| Maximum available capacity (Ah) | 2.2 | 31.81 |
| Nominal voltage (V) | 3.3 | 3.7 |
| Upper cut-off voltage (V) | 3.8 | 4.2 |
| Lower cut-off voltage (V) | 1.6 | 3.0 |
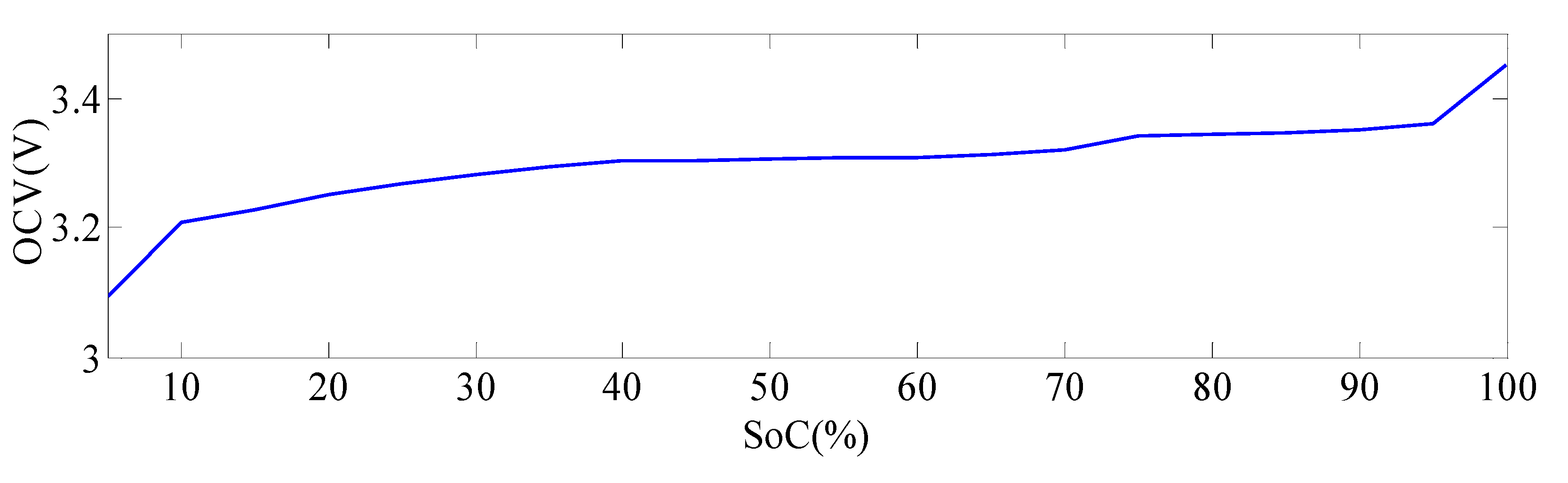
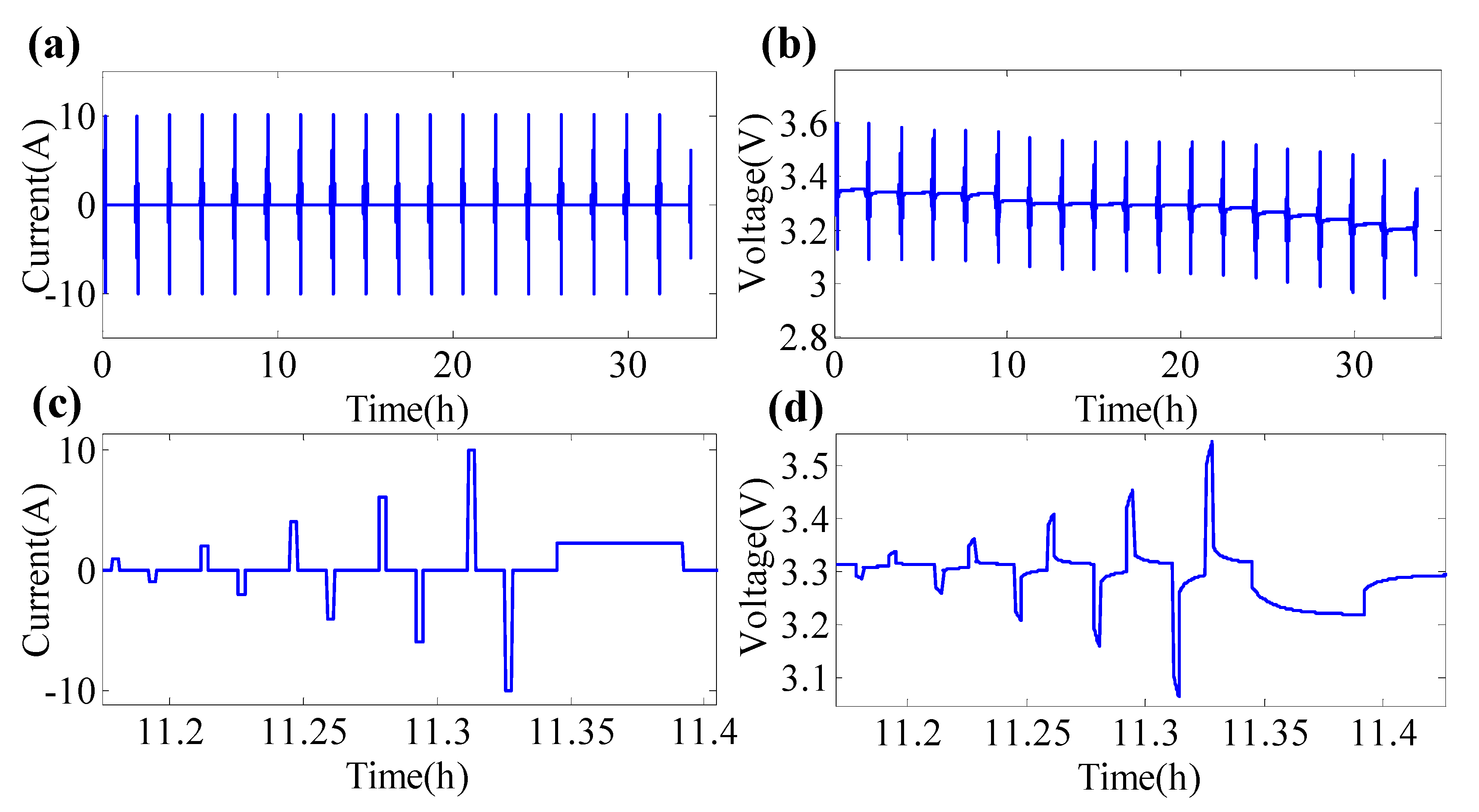
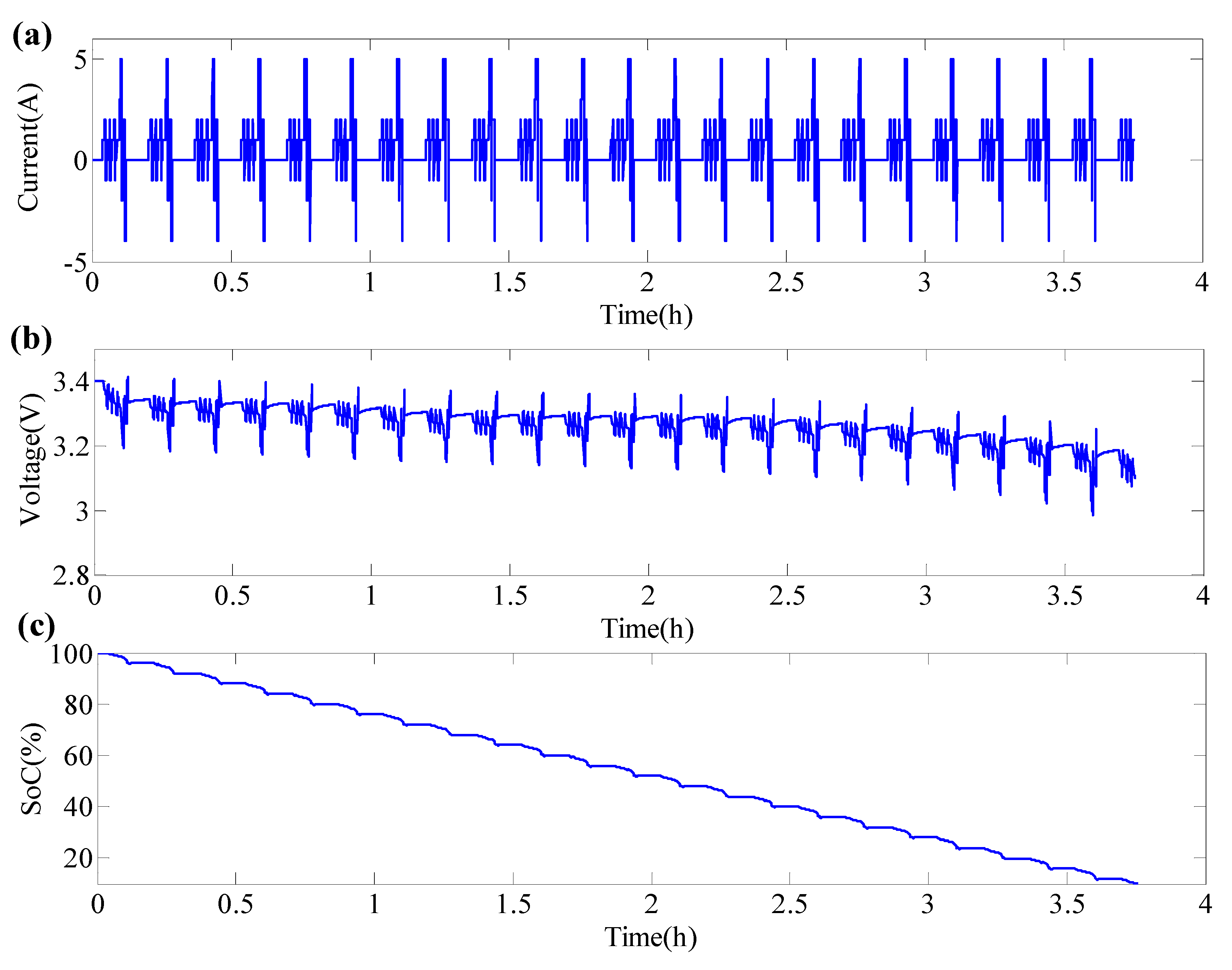
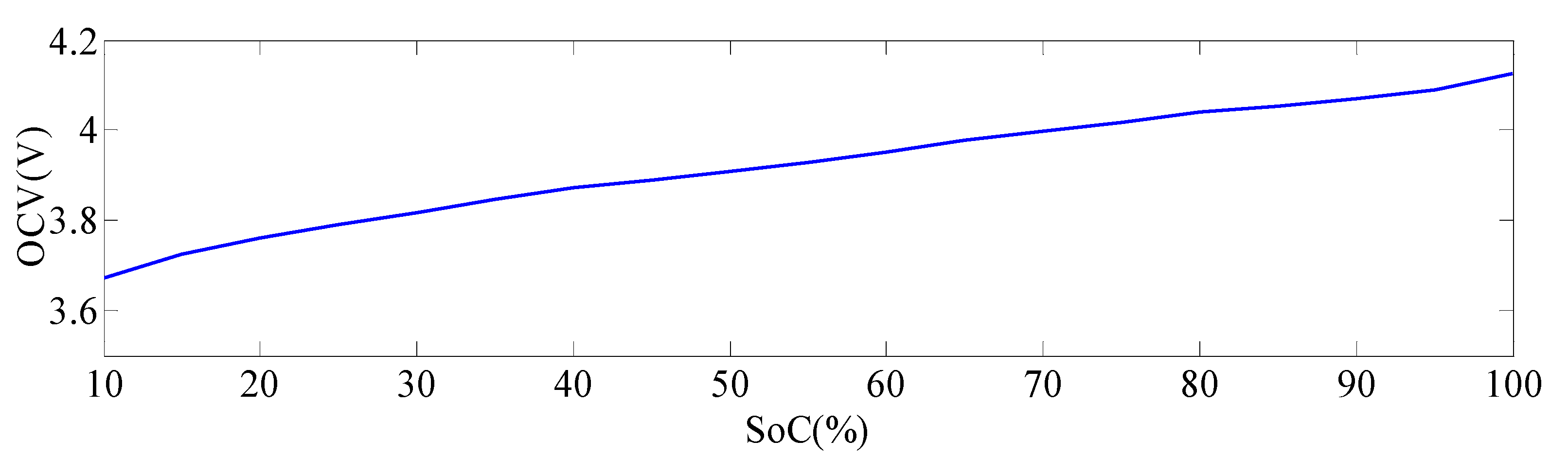
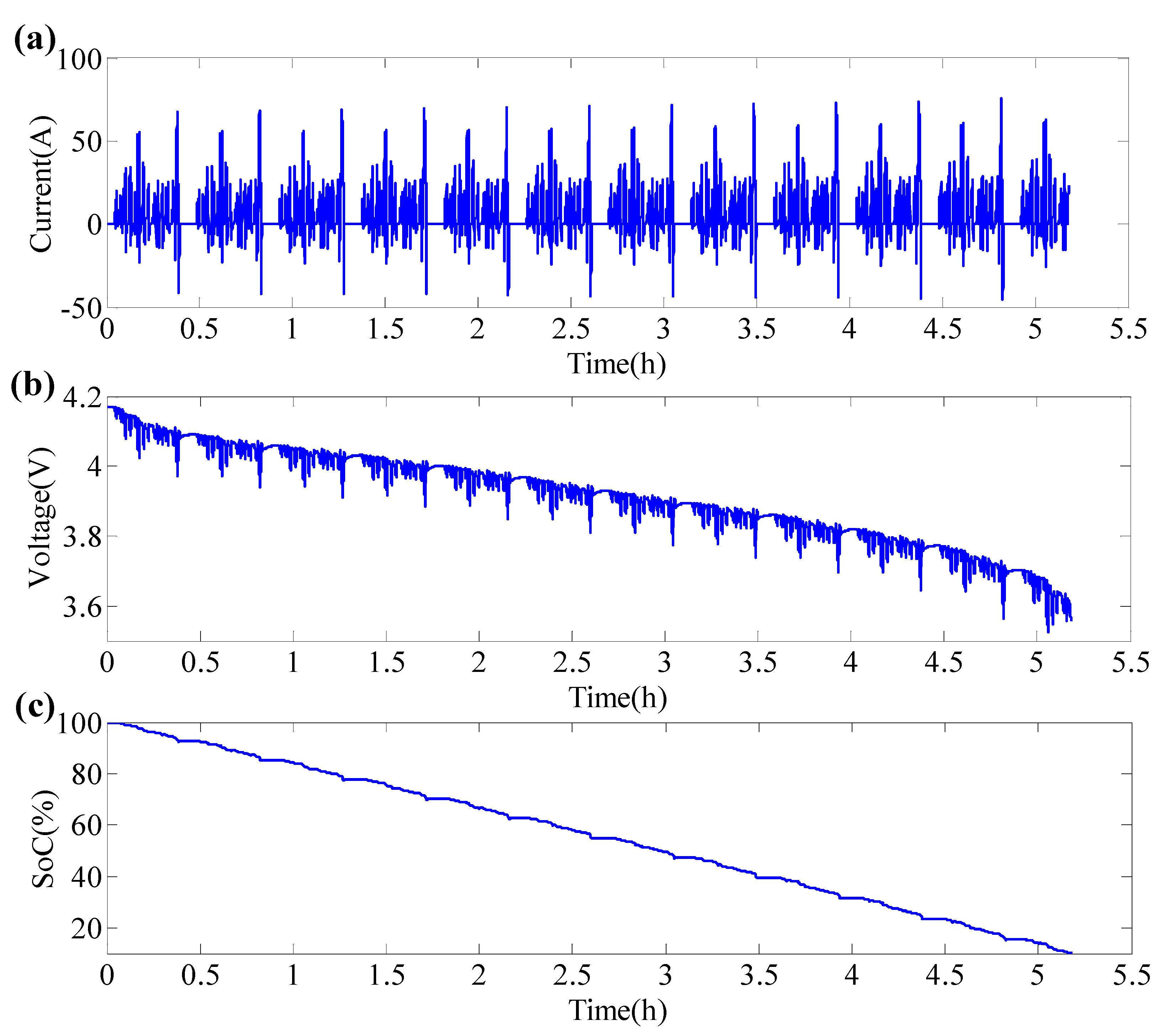
5. Verification and Discussion
5.1. Model Selection
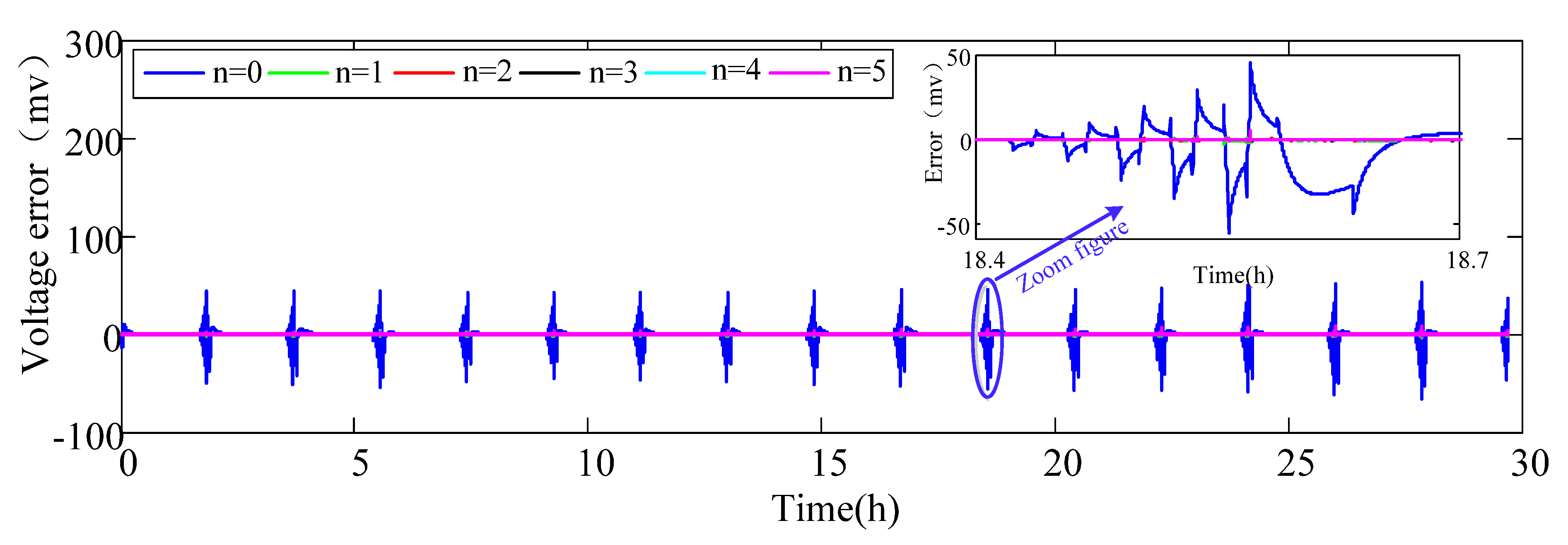
| n | Maximum (mV) | Mean (mV) | Standard Deviation (mV) | AIC | Duration (s) |
|---|---|---|---|---|---|
| 0 | 67.02 | −0.30 | 6.02 | 7.18 | 4.64 |
| 1 | 7.68 | 7.9 × 10−3 | 0.18 | −4.80 | 4.75 |
| 2 | 8.82 | 9.3× 10−3 | 0.15 | −3.67 | 4.93 |
| 3 | 8.81 | 7.2 × 10−3 | 0.14 | −1.93 | 5.28 |
| 4 | 8.77 | 5.7 × 10−3 | 0.13 | −0.04 | 5.54 |
| 5 | 8.74 | 4.4 × 10−3 | 0.13 | 1.88 | 5.90 |
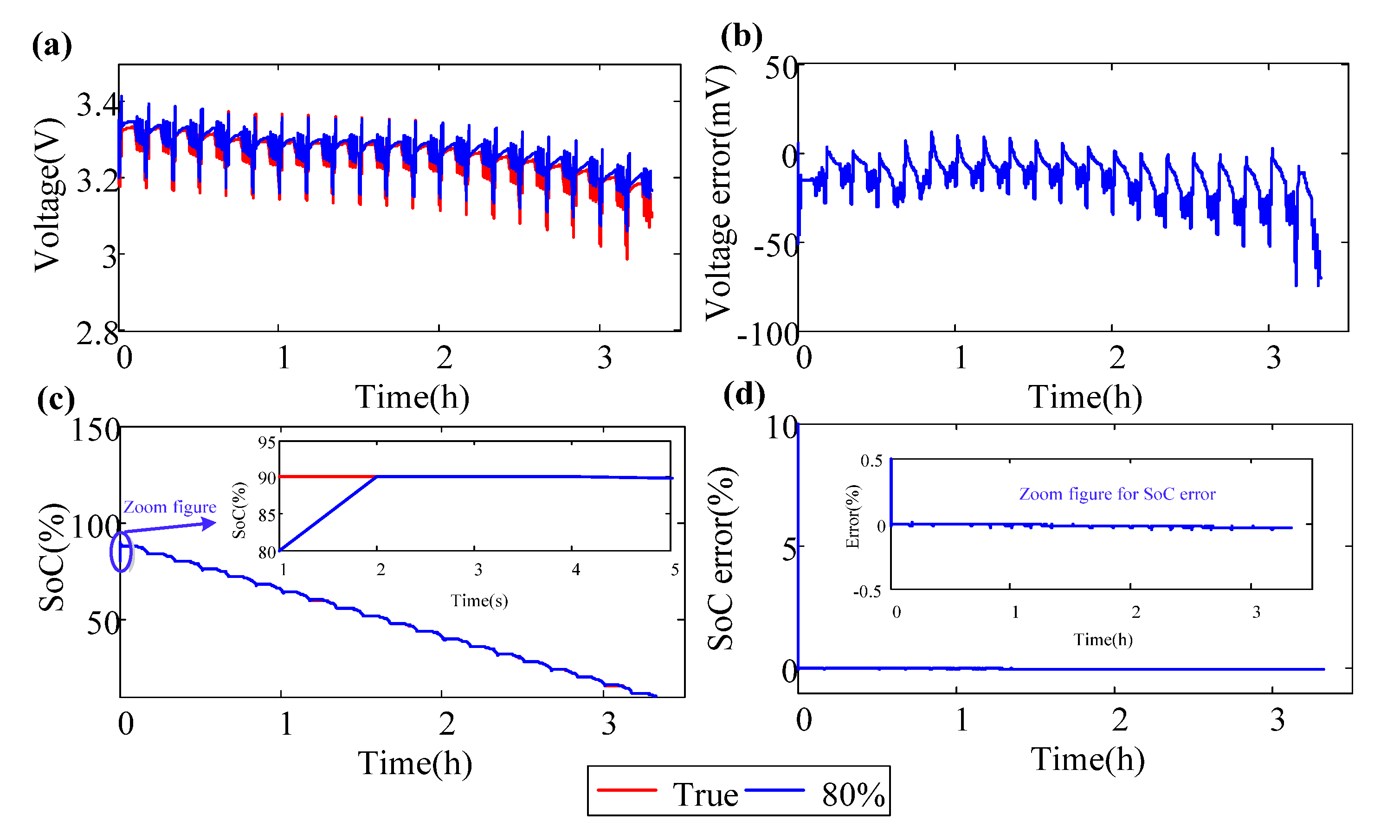
5.2. SoC Estimation
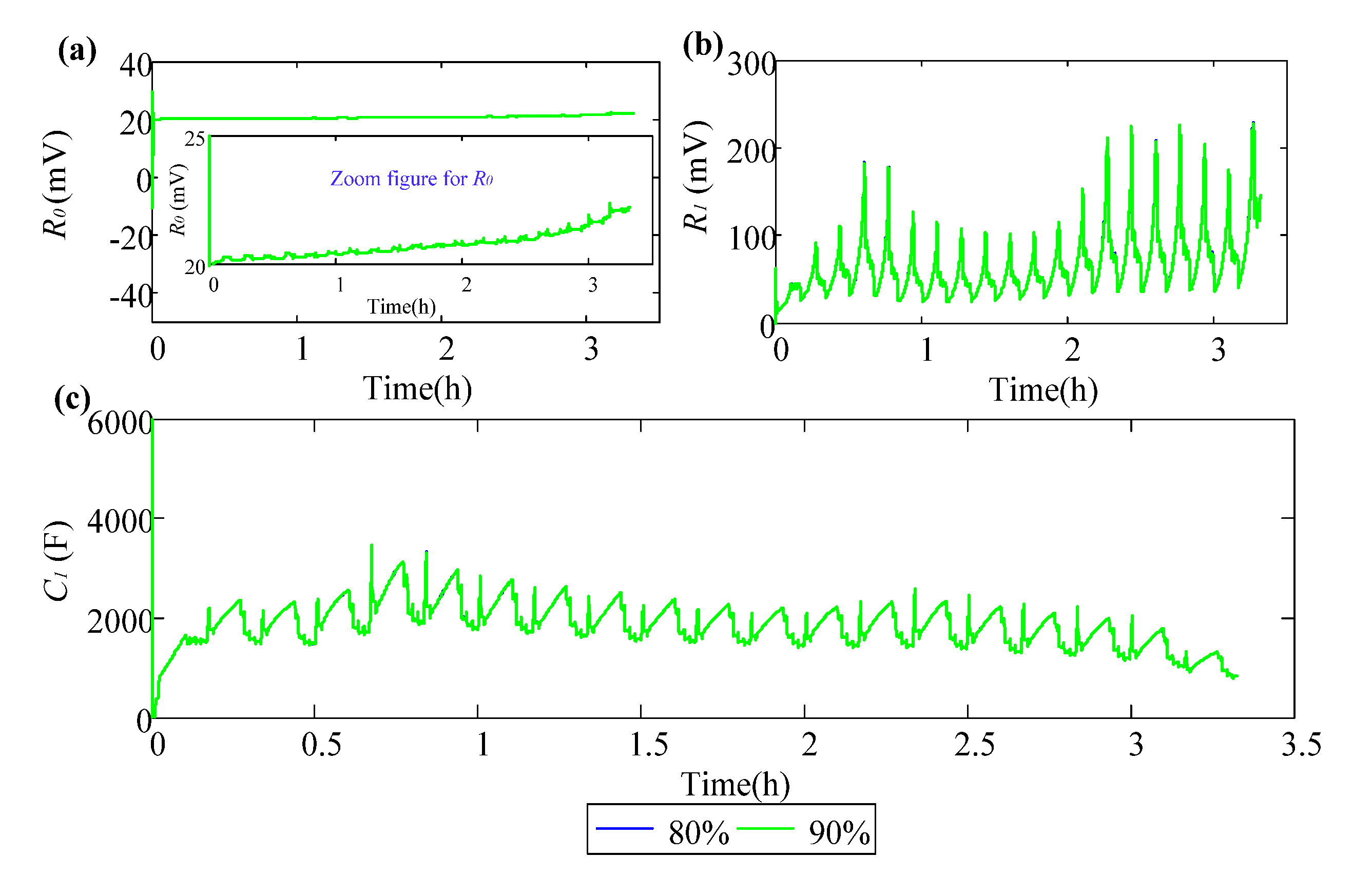

| Initial SoC (%) | Maximum (mV) | Mean (mV) | Standard Deviation (mV) |
|---|---|---|---|
| 90% | 4.71 | −8.42 × 10−2 | 3.56 × 10−2 |
| 80% | 4.72 | –8.43 × 10−2 | 3.56 × 10−2 |

| Index | Maximum | Mean | Standard Deviation | Duration (s) |
|---|---|---|---|---|
| SoC (%) | 0.04 | −0.01 | 0.01 | 48.585 |
| Voltage (mV) | 74.63 | −14.30 | 11.32 |
| Index | Maximum | Mean | Standard Deviation | Duration (s) |
|---|---|---|---|---|
| SoC (%) | 0.05 | −0.02 | 0.01 | 49.115 |
| Voltage (mV) | 74.67 | −14.31 | 11.32 |
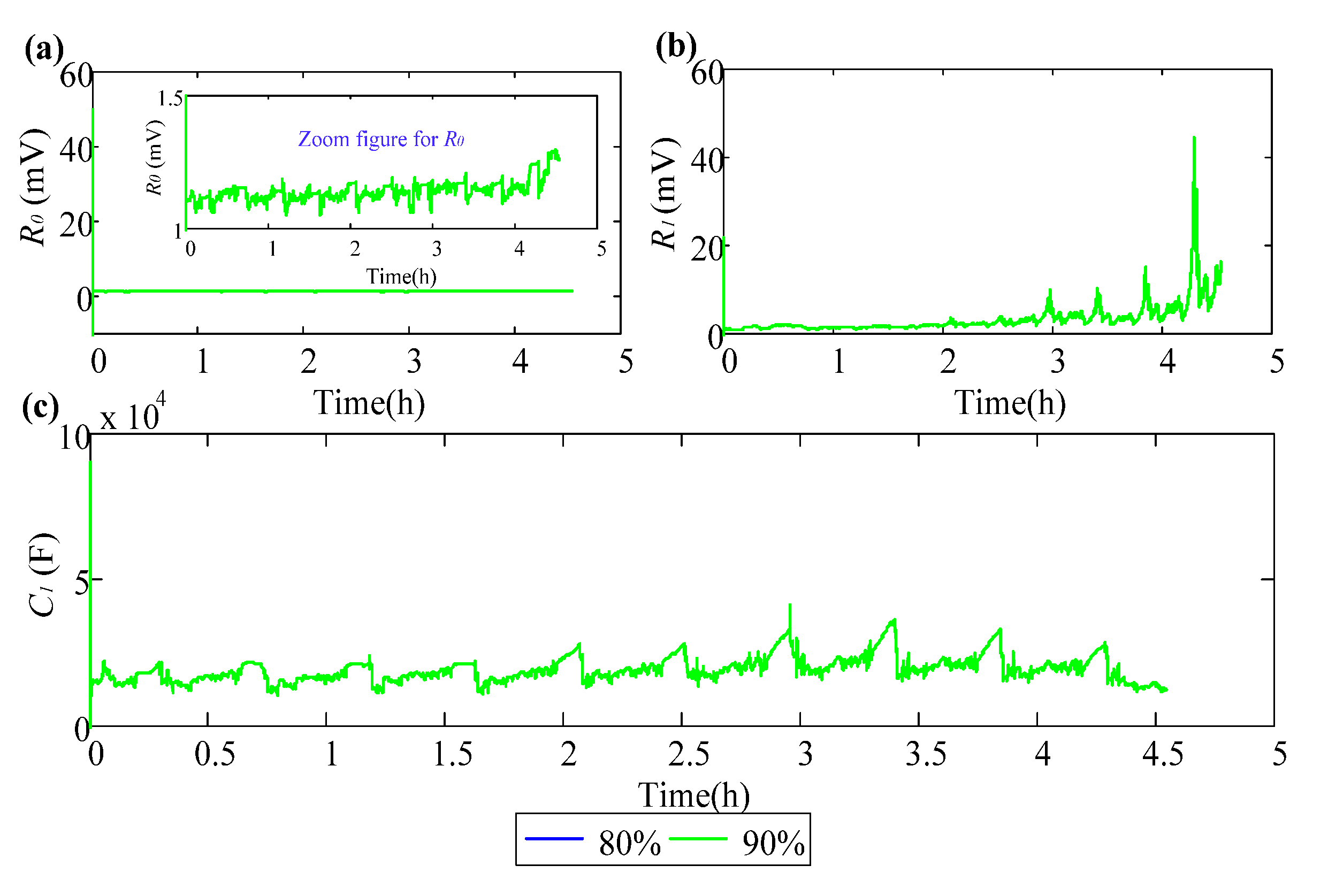
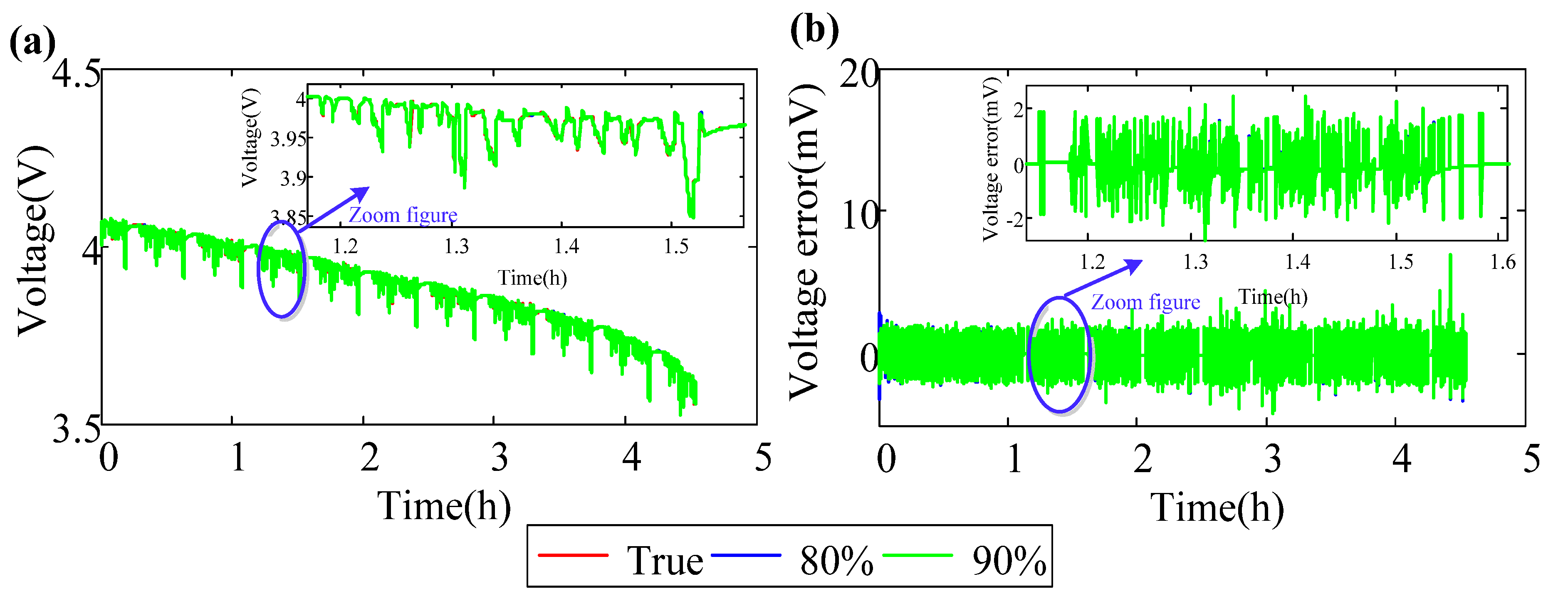
| Initial SoC (%) | Maximum (mV) | Mean (mV) | Standard (mV) |
|---|---|---|---|
| 90% | 6.95 | −8.16 × 10−2 | 0.74 |
| 80% | 6.85 | −8.58 × 10−2 | 0.74 |
| Initial SOC (%) | Voltage Prediction Error (mV) | SOC Estimation Error (%) | Duration (s) | ||||
|---|---|---|---|---|---|---|---|
| Maximum | Mean | Standard Deviation | Maximum | Mean | Standard Deviation | ||
| 80 | 73.98 | −4.83 | 9.29 | 0.77 | −0.28 | 0.23 | 63.017 |
| 90 | 72.93 | −4.89 | 9.36 | 0.65 | −0.40 | 0.21 | 62.900 |
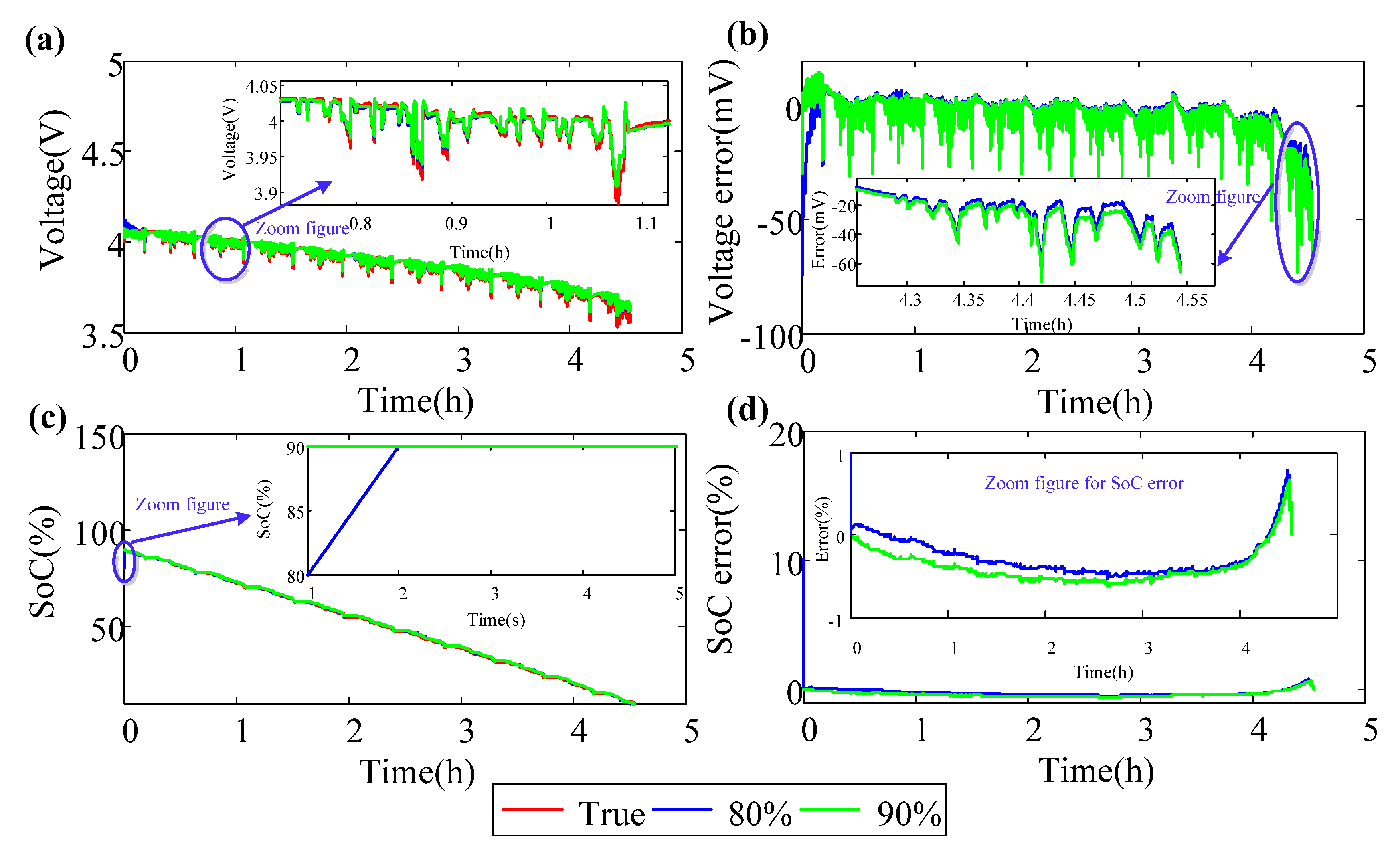
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| SoC | State of charge |
| AIC | Akaike information criterion |
| PNGV | Partnership for New Generation Of Vehicles |
| RC | Resistance-capacitance |
| OCV | Open circuit voltage |
| CDKF | Central difference Kalman filter |
| HPPC | Hybrid pulse power characteristic |
| DST | Dynamic Stress Test |
| BJDC | Beijing Driving cycles |
References
- Scrosati, B.; Garche, J. Lithium batteries: Status, prospects and future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
- Rydh, C.J.; Sandén, B.A. Energy analysis of batteries in photovoltaic systems. Part I: Performance and energy requirements. Energy Convers. Manag. 2005, 46, 1957–1979. [Google Scholar] [CrossRef]
- Shao, S.; Bi, J.; Yang, F.; Guan, W. On-line estimation of state-of-charge of Li-ion batteries in electric vehicle using the resampling particle filter. Transp. Res. D Transp. Environ. 2014, 32, 207–217. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Vasebi, A.; Partovibakhsh, M.; Bathaee, S.M.T. A novel combined battery model for state-of-charge estimation in lead-acid batteries based on extended Kalman filter for hybrid electric vehicle applications. J. Power Sources 2007, 174, 30–40. [Google Scholar] [CrossRef]
- ThermoAnalytics Inc. Battery Modeling for HEV Simulation by Thermo-Analytics Inc. Available online: http://www.thermoanalytics.com/support/publications/batterymodelsdoc.html (accessed on 7 August 2015).
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ionics 2004, 175, 835–839. [Google Scholar]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 186, 500–507. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B.J. A technique for dynamic battery model identification in automotive applications using linear parameter varying structures. Control Eng. Pract. 2009, 17, 1190–1201. [Google Scholar] [CrossRef]
- Moss, P.L.; Au, G.; Plichta, E.J.; Zheng, J.P. An electrical circuit for modeling the dynamic response of Li-ion polymer batteries. J. Electrochem. Soc. 2008, 155, A986–A994. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Hu, X.S.; Li, S.B.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- He, H.W.; Xiong, R.; Fan, J.X. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; Chow, M.-Y. Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar]
- Feng, F.; Lu, R.G.; Wei, G.; Zhu, C.B. Online estimation of model parameters and state of charge of LiFePO4 batteries using a novel open-circuit voltage at various ambient temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Pei, L.; Zhu, C.B. An integrated approach for real-time model-based state-of-charge estimation of lithium-ion batteries. J. Power Sources 2015, 283, 24–36. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhang, C.B.; Chen, Z.H. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter. J. Power Sources 2015, 279, 306–311. [Google Scholar] [CrossRef]
- Aung, H.; Low, K.S.; Goh, S.T. State-of-charge estimation of lithium-ion battery using square root spherical unscented Kalman filter (Sqrt-UKFST) in Nanosatellite. IEEE Trans. Power Electron. 2015, 30, 4774–4783. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384. [Google Scholar] [CrossRef]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison study on the battery SoC estimation with EKF and UKF algorithms. Energies 2013, 6, 5088–5100. [Google Scholar] [CrossRef]
- Li, J.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Seo, B.H.; Nguyen, T.H.; Lee, D.C.; Lee, K.B.; Kim, J.M. Condition monitoring of lithium polymer batteries based on a sigma-point Kalman filter. J. Power Electron 2012, 12, 778–786. [Google Scholar] [CrossRef]
- Rigatos, G.G. Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles. Robot. Auton. Syst. 2012, 60, 978–995. [Google Scholar] [CrossRef]
- Jaechan, L. CDKF approach for estimating a static parameter of carrier frequency offset based on nonlinear measurement equations in OFDM systems. Nonlinear Dyn. 2014, 78, 703–711. [Google Scholar]
- Xiong, R.; Sun, F.; Gong, X.; He, H. Adaptive state of charge estimator for lithium-ion cells series battery pack in electric vehicles. J. Power Sources 2013, 242, 699–713. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Bossche, P.V.D.; Hegazy, O.; Smekens, J.; Coosemans, T.; Mierlo, J.V. Rechargeable energy storage systems for plug-in hybrid electric vehicles—Assessment of electrical characteristics. Energies 2012, 5, 2952–2988. [Google Scholar] [CrossRef]
- Hendrik, K.; Robinson, K.; Philipp, S. A Simple Specification Procedure for the Transition Function in Persistent Nonlinear Time Series Models; Springer: Berlin, Germany, 2014. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Zhang, Y.; He, H. A Real-Time Joint Estimator for Model Parameters and State of Charge of Lithium-Ion Batteries in Electric Vehicles. Energies 2015, 8, 8594-8612. https://doi.org/10.3390/en8088594
Gao J, Zhang Y, He H. A Real-Time Joint Estimator for Model Parameters and State of Charge of Lithium-Ion Batteries in Electric Vehicles. Energies. 2015; 8(8):8594-8612. https://doi.org/10.3390/en8088594
Chicago/Turabian StyleGao, Jianping, Yongzhi Zhang, and Hongwen He. 2015. "A Real-Time Joint Estimator for Model Parameters and State of Charge of Lithium-Ion Batteries in Electric Vehicles" Energies 8, no. 8: 8594-8612. https://doi.org/10.3390/en8088594






