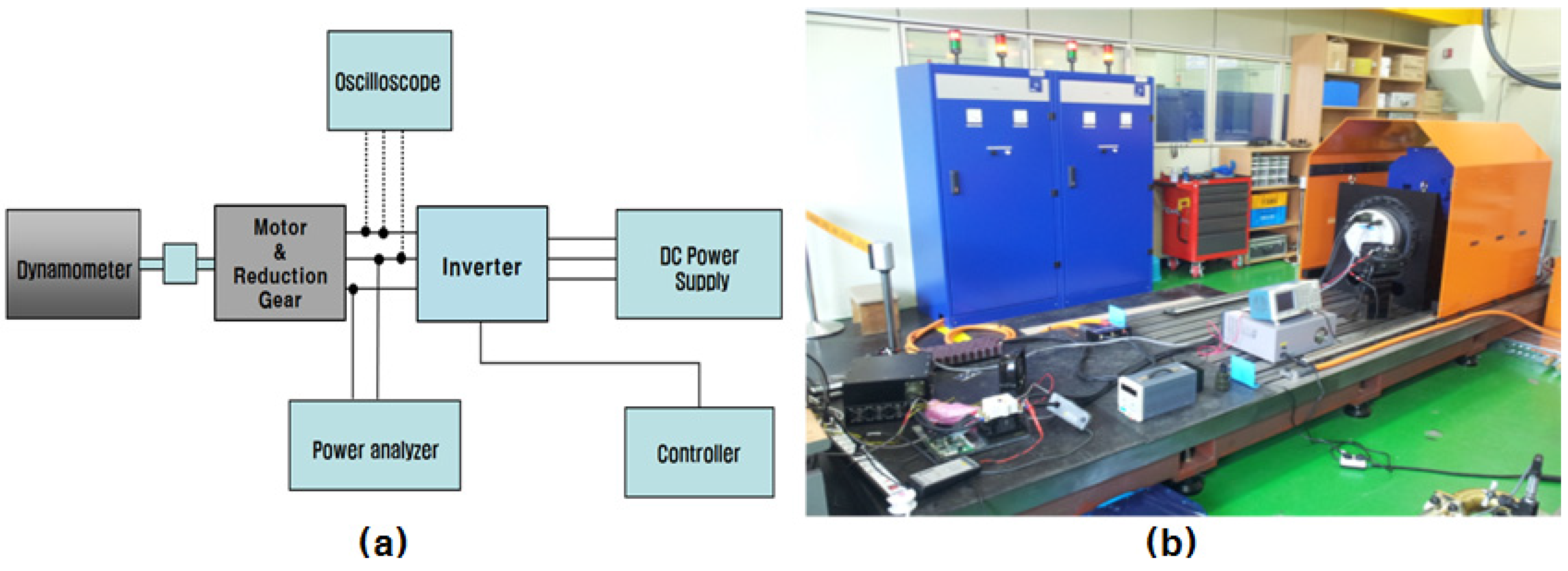
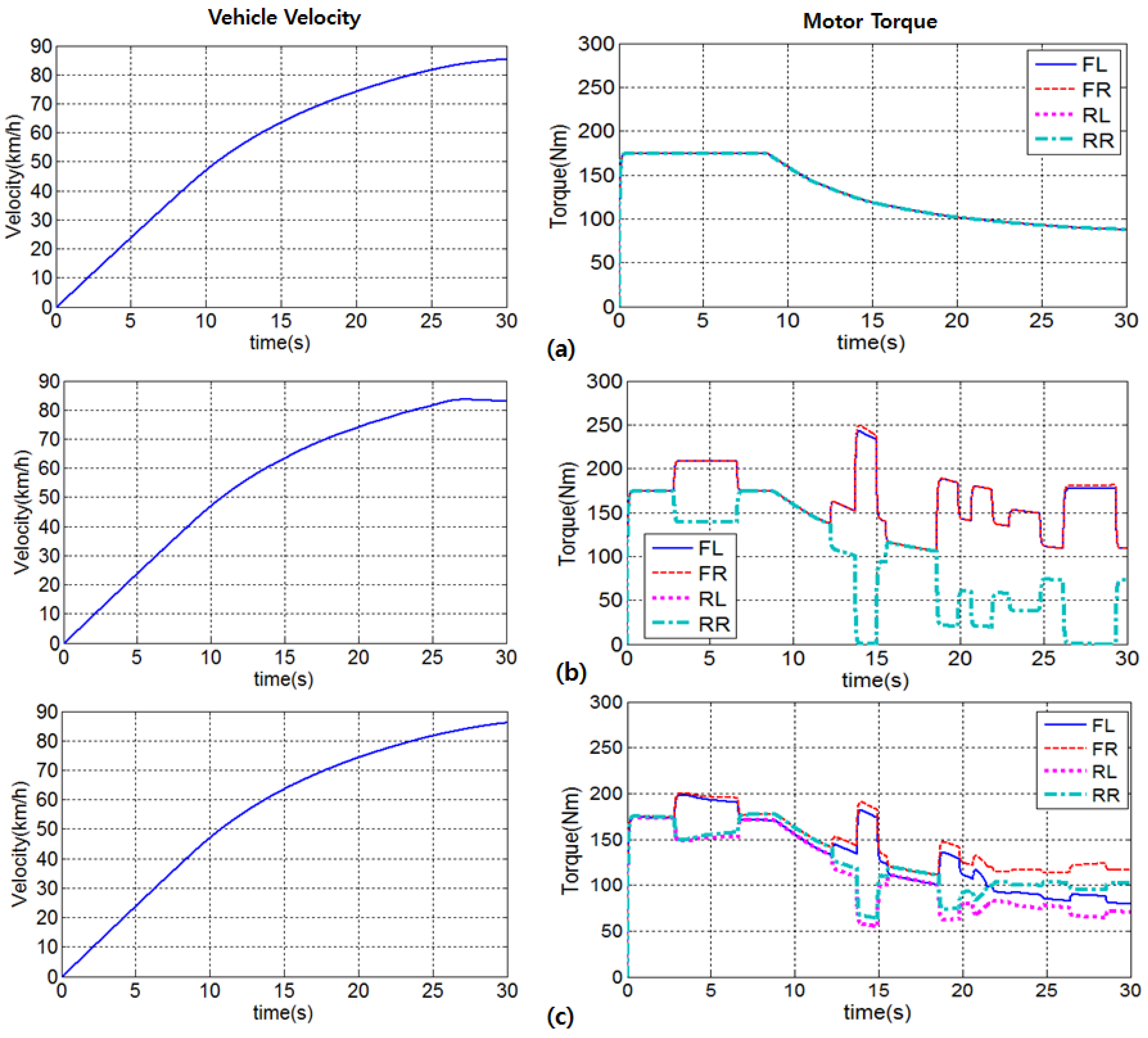
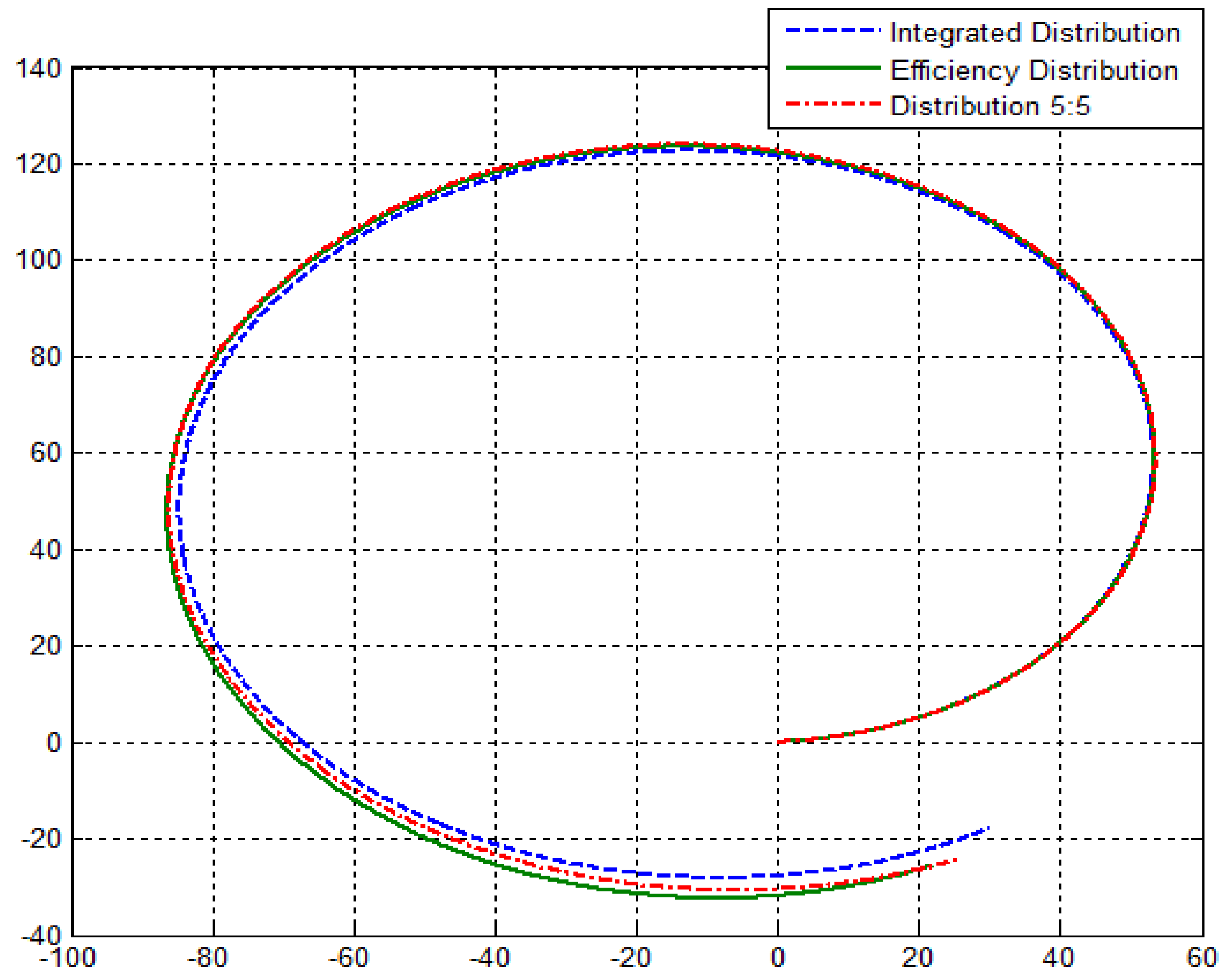
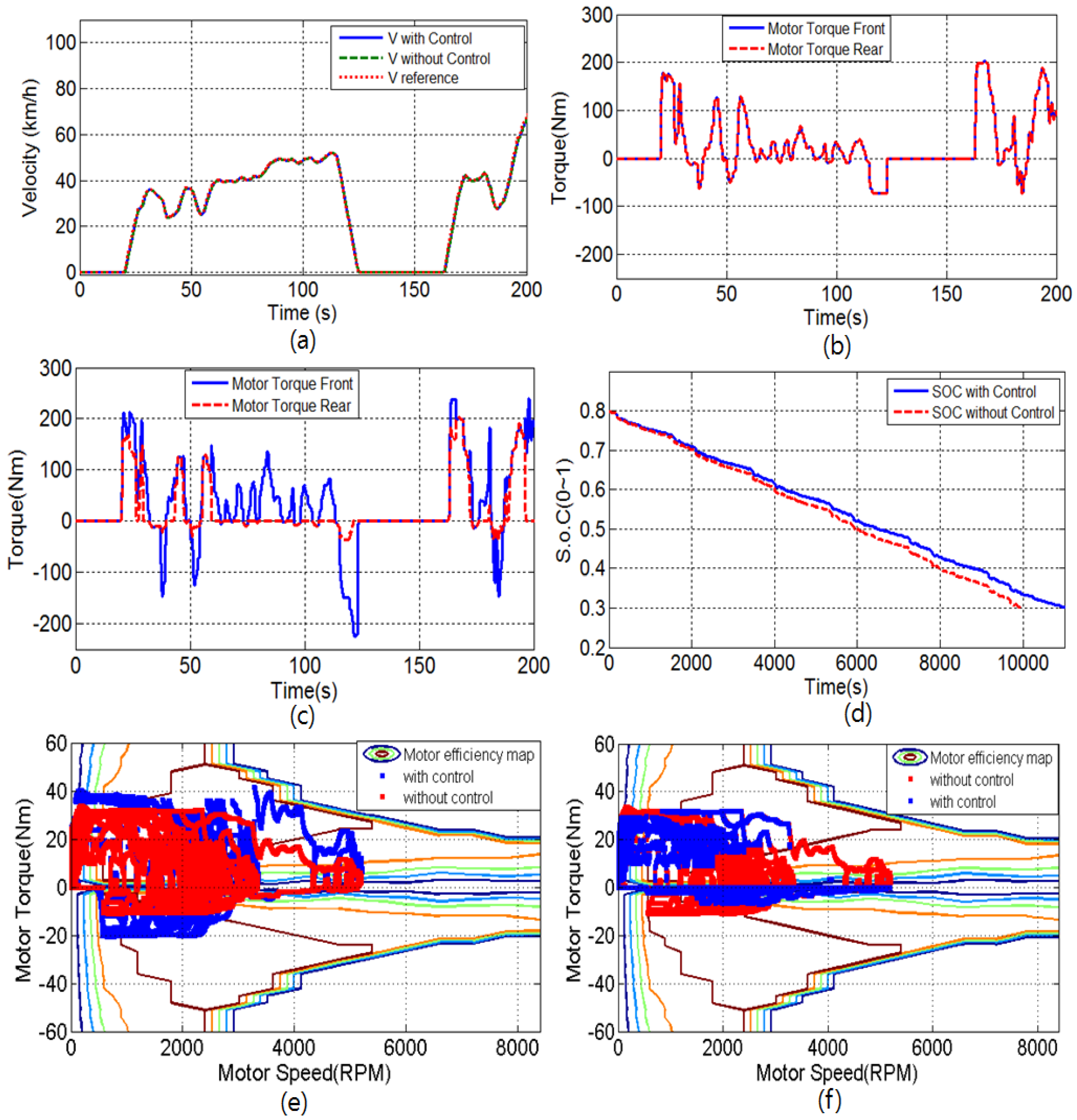
Since electric vehicles equipped with in-wheel motors allow for independent driving and braking of each wheel, the vehicle can be actively controlled through control of the driving/braking torque depending on the situation. Also, the efficiency of the vehicle can be increased by distributing the torque for each motor or selecting between two wheels and four wheels [
13,
14,
15,
16]. However, the stability of the vehicle can be greatly reduced by independent driving of the wheels if the driving/braking torque cannot be stably controlled during acceleration or braking. In order to resolve this problem, this study proposes a control strategy to judge different driving situations using Fuzzy logic and to differentiate the distribution of the torque.
3.1. Torque Distribution Strategy for Optimizing Driving Efficiency
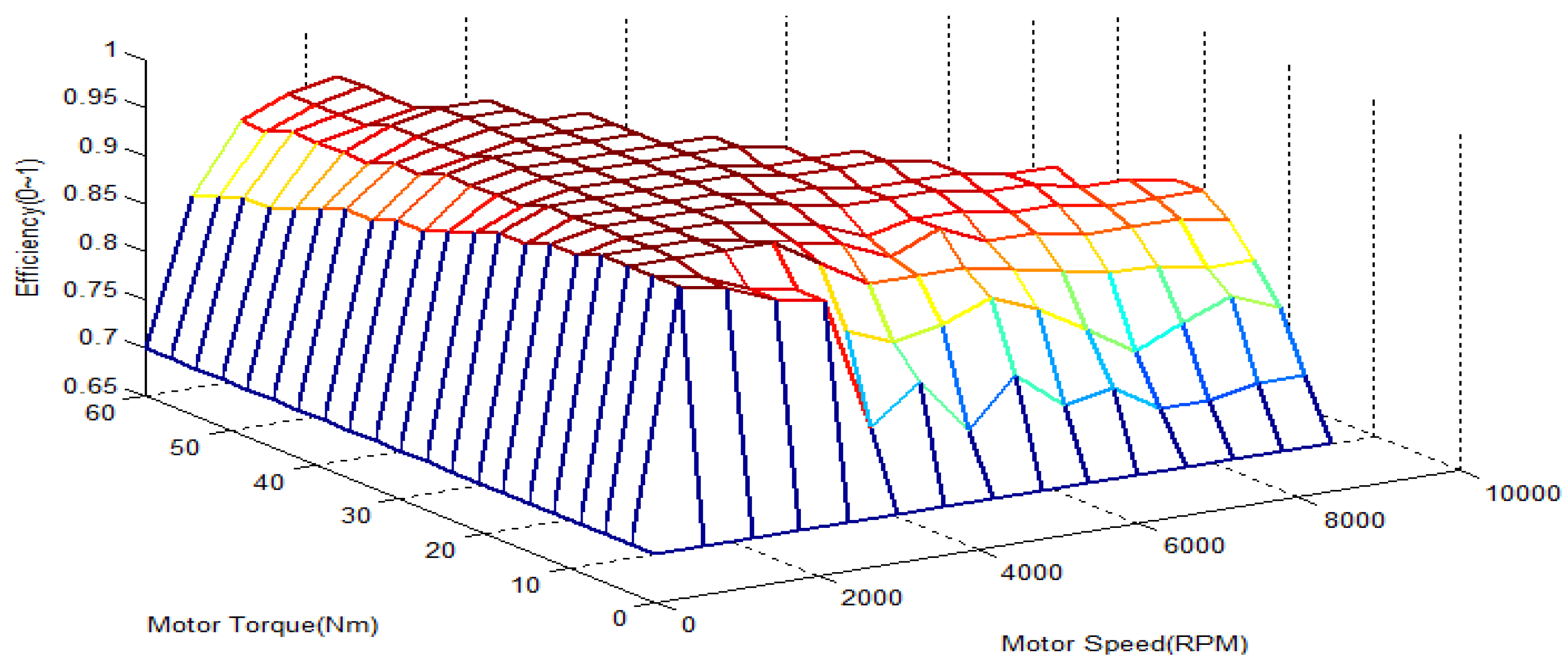
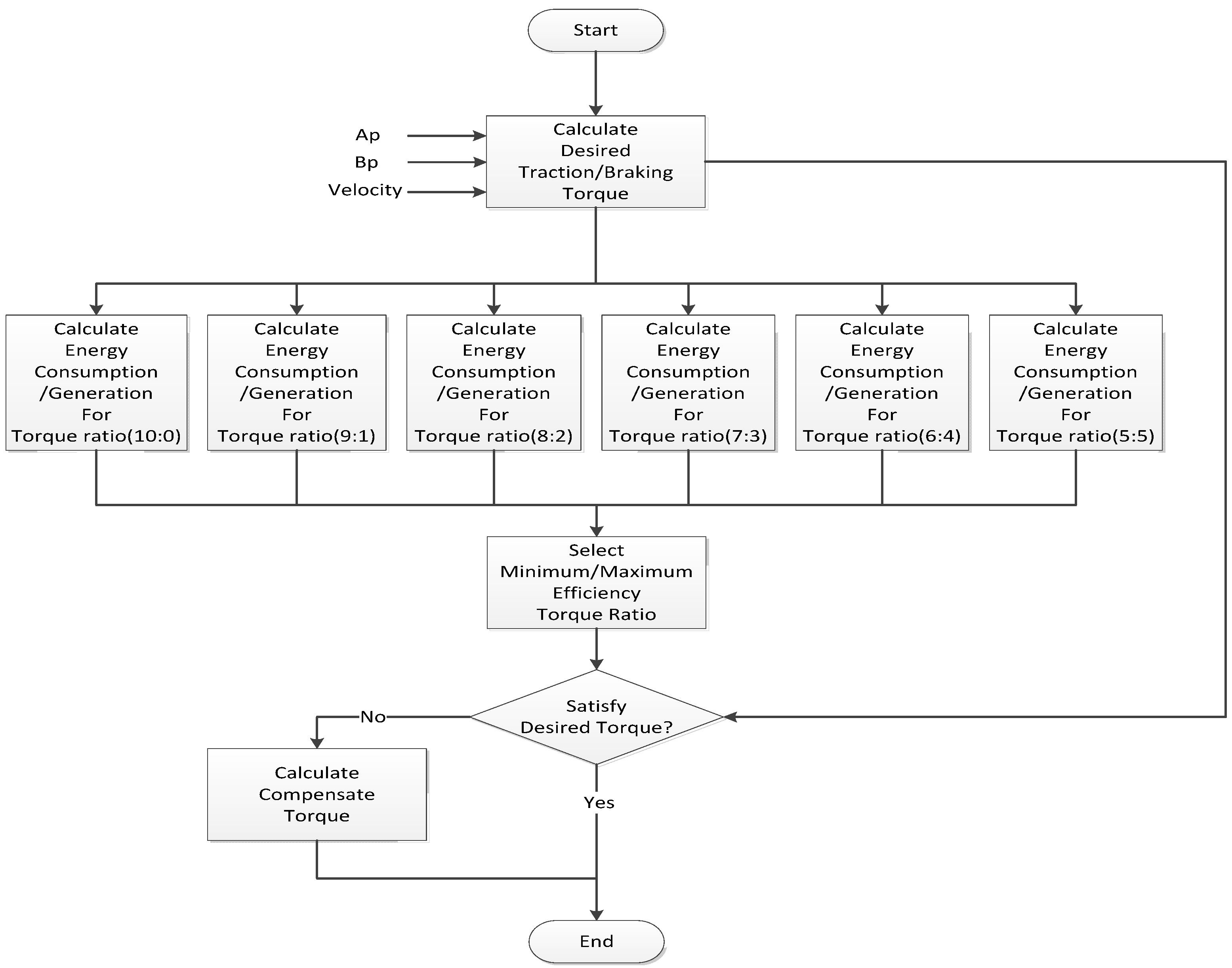
Vehicles attached with four in-wheel motors can drive each motor with independent torque, and the total torque wanted by the driver can be distributed at different ratios. This advantage can be used to increase the efficiency driving stability of the vehicle, as well as the efficiency. This study aims to present a control strategy that increases the efficiency by differentiating the ratio between the front and rear wheels and operating the driving torque output for efficient domain of the motor when the driver wants a certain driving torque. For instance, when a driver is expecting a total driving torque of 60 Nm, if the total driving efficiency of the motors are 85% when each motor has an output of 15 Nm and 90% when two motors have outputs of 20 Nm and the other two motors have outputs of 10 Nm, this method yields an efficient driving ratio. The efficiency characteristics of the overall system must first be understood in order to create such an algorithm. In this study, an algorithm was formed to control the torque distribution ratio in the efficiency domain of actual motors using the efficiency characteristics of the motor-inverter system found through the experiment described in
Section 2.2. The total driving/braking torque is calculated using the accelerator/brake pedal values of the driver and the velocity of the vehicle. The calculated total driving/braking torque and the efficiency curve of
Figure 2 are used to estimate the actual power consumption according to the driving ratio. The control algorithm was prepared to increase the driving efficiency of the vehicle by selecting the driving ratio that consumes and regenerates optimum energy.
Figure 7 shows the flow chart of the control algorithm.
Figure 7.
Flow chart of the strategy for optimizing driving efficiency.
Figure 7.
Flow chart of the strategy for optimizing driving efficiency.
3.2. Torque Distribution Strategy Considering Driver’s Acceleration Demand
If a driving torque distribution strategy is developed by considering a vehicle’s efficiency only, there may occur such a problem as failing to meet the driver demanded torque for acceleration or causing driving stability to be decreased due to driving torque concentrated on the front or rear wheel when accelerated. Therefore, it is vital to develop a control strategy ensuring that the driver demand for acceleration or cruise driving is determined by using the driver’s accelerator pedal signals, thereby producing driving torque appropriate to such driver demand.
Information able to be made available to determine driver demand for acceleration includes the vehicle’s current velocity and the driver’s accelerator pedal position value (Ap). However, the simple use of these data values gives rise to difficulty in accurately determining the driver’s acceleration demand. For instance, the magnitude of the driver’s demand for acceleration may be big at lower speeds although signals are input with low pedal values; likewise, the magnitude of the driver’s demand for acceleration may be small at higher speeds although signals are input with comparatively high pedal values. Quantitative reference values are necessary to distinguish between acceleration and cruise modes according to the accelerator pedal value. To compute quantitative values, an evaluation index of the acceleration demand, α, is defined as follows.
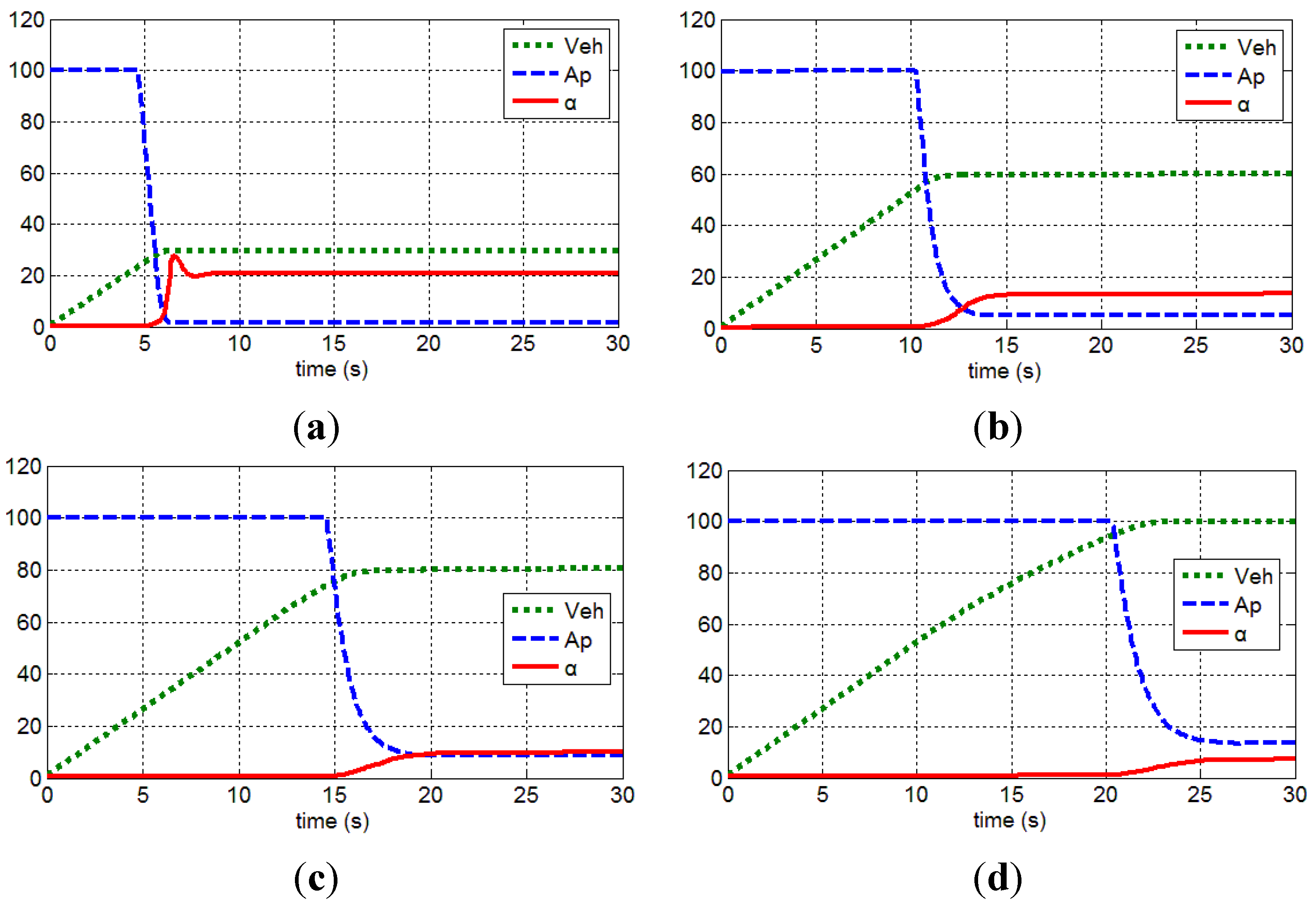
The term, α, in Equation (18) is defined as a value of the vehicle’s current velocity divided by the current Ap value, where the bigger the value α, the stronger the driver demand for cruising. At low vehicle speed, the input of even lower Ap value can be interpreted as having stronger demand for acceleration since the value α is relatively small, whereas at high speed of vehicle, the input of even higher AP value can be interpreted as having weaker demand for acceleration since the value α is relatively big. To investigate the range of the value α depending speeds in the cruise mode, a simple simulation was performed. The simulation pertains to assumptions of accelerating the vehicle from the stop position to 30 kph, 60 kph, 80 kph, and 100 kph for cruise drive.
Figure 8 shows respective simulation speeds, Ap’s and α values, while
Table 2 shows α values by simulation speed.
Resulting from the simulation, it can be known that values are overly small while accelerating, but α-values by speed remain constant when accelerated to specific speed and then cruised. Moreover, although the higher the cruising speed, the greater the AP values, it can be verified that the increased input value is small comparatively with the increased speed, resultantly causing the α-value to be lowered. Therefore, it is allowed to first set the reference α-values respectively matching the simulated speed levels, and then use them to judge as acceleration mode if the actual α-value is smaller than the reference value and as cruise mode if the actual α-value is equal to or bigger than the reference value. Nevertheless, as α-values during cruise mode vary with simulated speeds, reliance on α-values only makes it difficult to accurately determine whether the driver demand is for acceleration or for cruise driving. As a means to solve this problem, a fuzzy logic, as shown in
Table 3, is presented to make the driver demand for acceleration verifiable by using the vehicle’s speed and α-values [
19].
Figure 8.
Variations of index α under various vehicle speed and accelerator position conditions; (a) 0–30 kph acceleration and cruise drive; (b) 0–60 kph acceleration and cruise drive; (c) 0–80 kph acceleration and cruise drive; (d) 0–100 kph acceleration and cruise drive.
Figure 8.
Variations of index α under various vehicle speed and accelerator position conditions; (a) 0–30 kph acceleration and cruise drive; (b) 0–60 kph acceleration and cruise drive; (c) 0–80 kph acceleration and cruise drive; (d) 0–100 kph acceleration and cruise drive.
Table 2.
Index α at different vehicle speeds.
Table 2.
Index α at different vehicle speeds.
| Vehicle speed | α |
|---|
| 30 kph | 21 |
| 60 kph | 13 |
| 80 kph | 10 |
| 100 kph | 8 |
Table 3.
Torque distribution strategy that reflects driver’s acceleration demand.
A rule-based control is configured by using input membership functions, i.e., vehicle speed and α-values to determine driver demand for acceleration. The output membership function outputs torque ratio between 1 and 0, where values closer to 1 are judged closer to the cruise driving condition, thereby producing driving torque for which an efficiency-optimized torque distribution strategy is applied, while values closer to 0 are judged closer to the acceleration driving condition, thereby producing driving torque in which torque is distributed 5:5 to the front and rear wheels.
3.3. Torque Distribution Strategy Considering Tire Slip
When the vehicle is driving, slip occurs between the tires of the vehicle and the road surface. Here, the friction coefficient differs according to the amount of slip between the tires and the road surface. The torque delivered from the wheels is determined based on the friction coefficient. Therefore, when the torque that needs to be distributed into four wheels is excessively concentrated on the front or rear wheels, the slip ratio can increase rapidly. If the vehicle velocity is
V and the velocity of each wheel is
Vω, the slip ratio, λ, is defined as shown below.
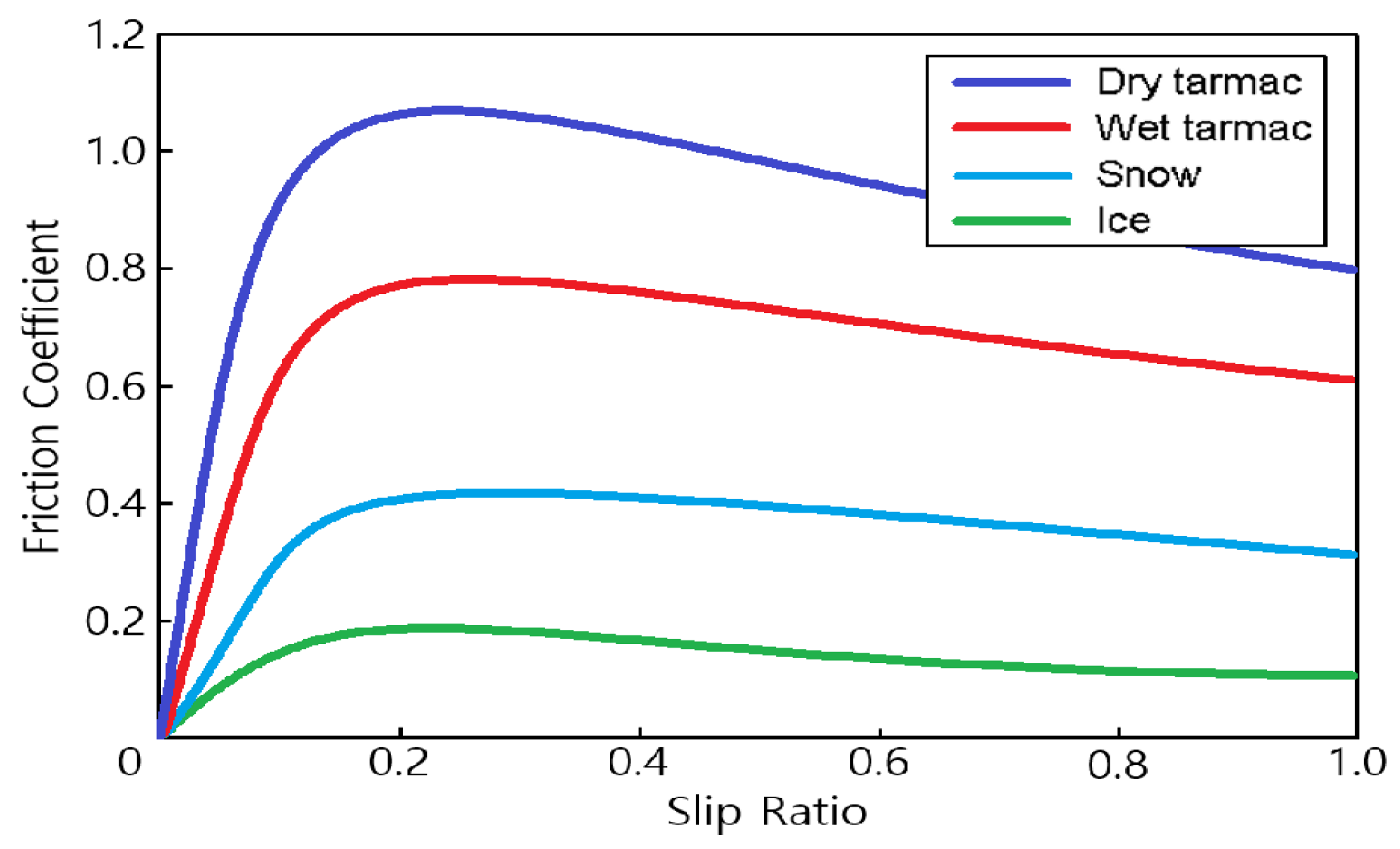
The friction coefficient between tires and the road surface has a general trend of increasing proportionally until a slip ratio of 0.2, reaching a maximum friction coefficient near 0.2, and rapidly decreasing after the maximum.
Figure 9 is a graph that shows the rough relationship between the slip ratio and the friction coefficient [
20]. Therefore, the slip controller generally controls the slip ratio so that it is maintained near 0.2. However, as mentioned earlier, this paper determines how to distribute the given total torque into each wheel prior to the intervention of the slip controller instead of maintaining the slip ratio through active control of the torque. Instability of the vehicle can be increased by controlling the slip ratio to 0.18–0.2, which is similar to an ordinary slip controller. For more active control intervention, a slip domain of about 0.08–0.12 was selected as the transient section, and a slip section of about 0.15 was selected as the unstable domain. The output membership function was configured to an output torque ratio between 1 and 0 as in the torque distribution strategy that reflects the will of the driver.
Table 4 shows the developed Fuzzy logic.
Figure 9.
Relationship between slip ratio and friction coefficient.
Figure 9.
Relationship between slip ratio and friction coefficient.
Table 4.
Torque distribution strategy considering tire slip.
3.4. Torque Distribution Strategy Considering Vehicle Cornering
When the vehicle turns, the rotational speed of each wheel is affected by the difference in the turning radius between the inner wheel and outer wheel. Thus, in the case of vehicles with a general driving mechanism that delivers torque to each wheel using a single driving source, it is essential to attach a differential gear to deliver torque while overcoming the difference in wheel speed between the inner and outer wheels of the vehicle when cornering. Differential gear is also used by the recent AWD (All-Wheel Drive) method. A difference in turning radius not only occurs between the inner and outer wheels, but also between the front and rear wheels. Even if there is a difference in rotational speed between the propeller shaft that drives the rear wheels and the propeller shaft that drives the front wheels upon cornering of the vehicle, the difference between the front and rear wheels can be compensated through application of the differential gear. This allows for soft cornering at high velocity. However for independently driven vehicles, the differential gear is removed and the turning performance can be reduced because the power source independently drives each wheel. This study proposes a control algorithm for a virtual electronic differential gear to resolve such a problem.
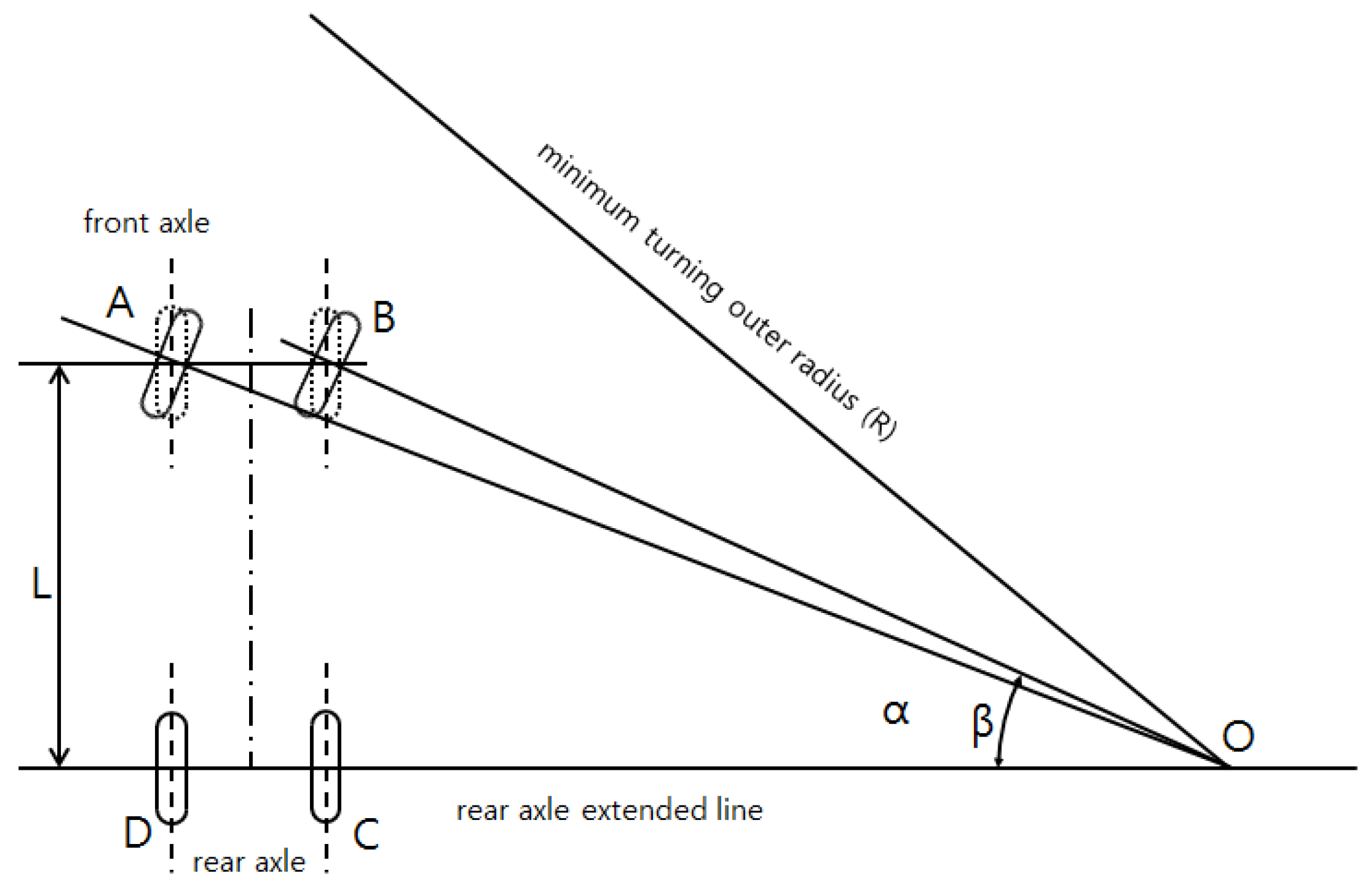
When the vehicle turns, a difference in turning radius is generated between the inner and outer wheels. A difference in turning radius between the front and rear wheels is generated as well. As shown in
Figure 10, the turning radius (
) of the outer front wheel(A) is largest, and is therefore defined as the representative turning radius(R) of the vehicle.
In
Figure 10, the turning radius of each wheel can be found by drawing a central extension line for each wheel from the central point O of the turning radius. The lines for the inner rear wheel(C) and outer rear wheel (D) can be assumed as
and
, respectively. For the front wheels, a triangle is formed with the central point O by drawing an extension line with a length that is identical to the wheel space(L) from each rear wheel. According to the Pythagorean Theorem, the turning radius
of the outer front wheel (A) and the turning radius
of the inner front wheel(B) are as follows.
Figure 10.
Turning radius of each wheel.
Figure 10.
Turning radius of each wheel.
The turning radius of the vehicle can be estimated as shown below using the steering angle(δ) and yaw rate (γ) [
21].
The estimated turning radius(R) uses the center of the rear wheel axle on the rear axle as the reference. When the wheel tread of the vehicle is defined as t, the turning radius of each wheel is as follows.
The angular velocity of the vehicle is calculated using the vehicle velocity and turning radius as shown below.
Ultimately, the wheel velocity of each wheel can be expressed as follows using the angular velocity of the vehicle.
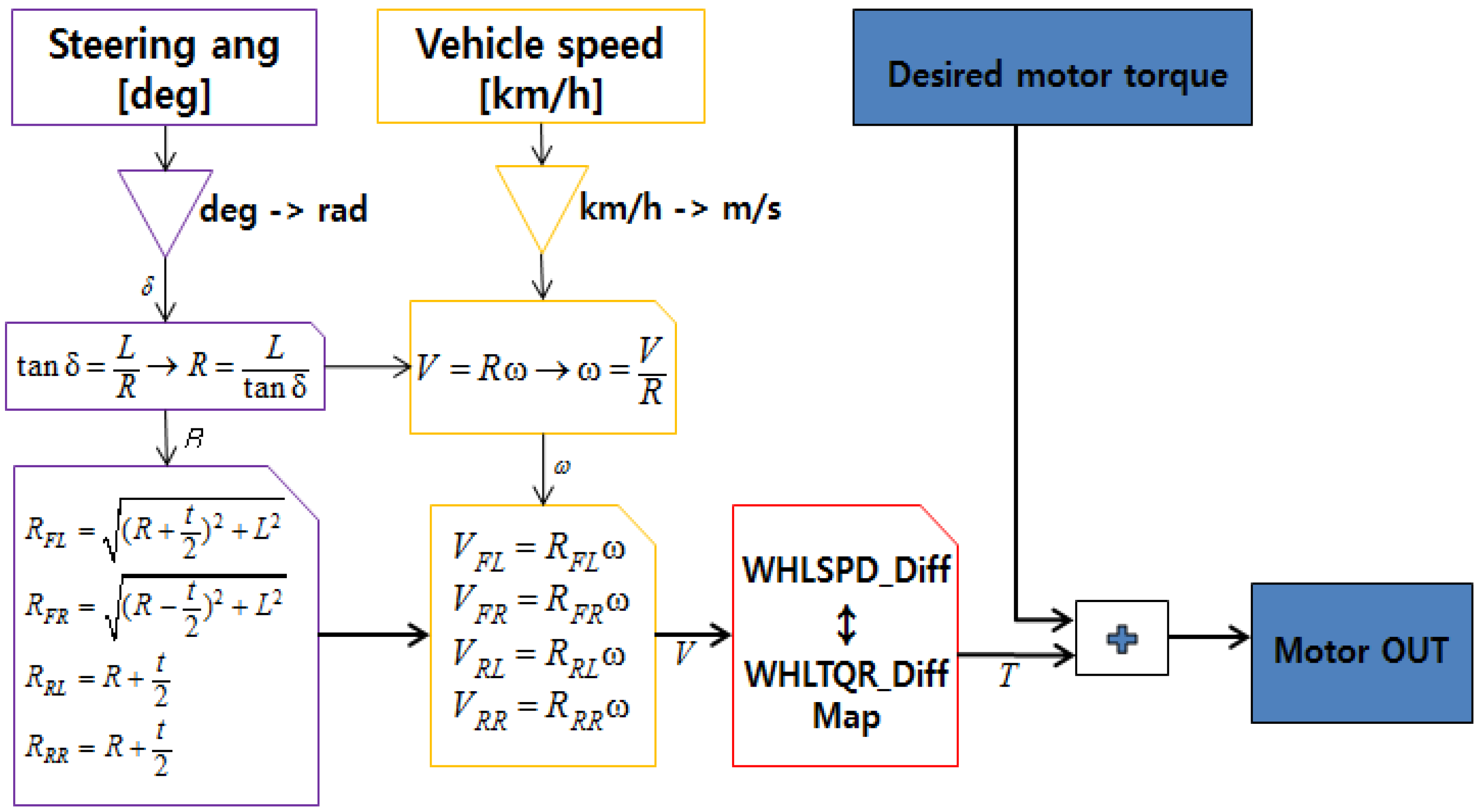
In order to track the velocity of each wheel calculated as shown above, the control logic shown in
Figure 11 was created to output a different driving torque for each wheel. The wheel velocity-torque relationship was converted into a map through experimentation to apply the control algorithm to a vehicle, and the reliability of the algorithm was increased by applying the map to the actual control algorithm.
Figure 11.
Control concept of electric differential gear.
Figure 11.
Control concept of electric differential gear.
The torque distribution strategy based on Fuzzy logic was formed using the steering value of the driver and the vehicle velocity to determine the application of driving torque found using the control logic to the vehicle.
Table 5 shows the torque distribution strategy considering a cornering situation. Like the two distribution strategies presented earlier, the driving torque delivered by an efficient distribution strategy is output as the output value is closer to 1, and a driving torque that reflects a cornering situation is output as the output value is closer to 0.
Table 5.
Torque distribution strategy considering vehicle cornering.
3.5. Integrated Algorithm for Torque Distribution
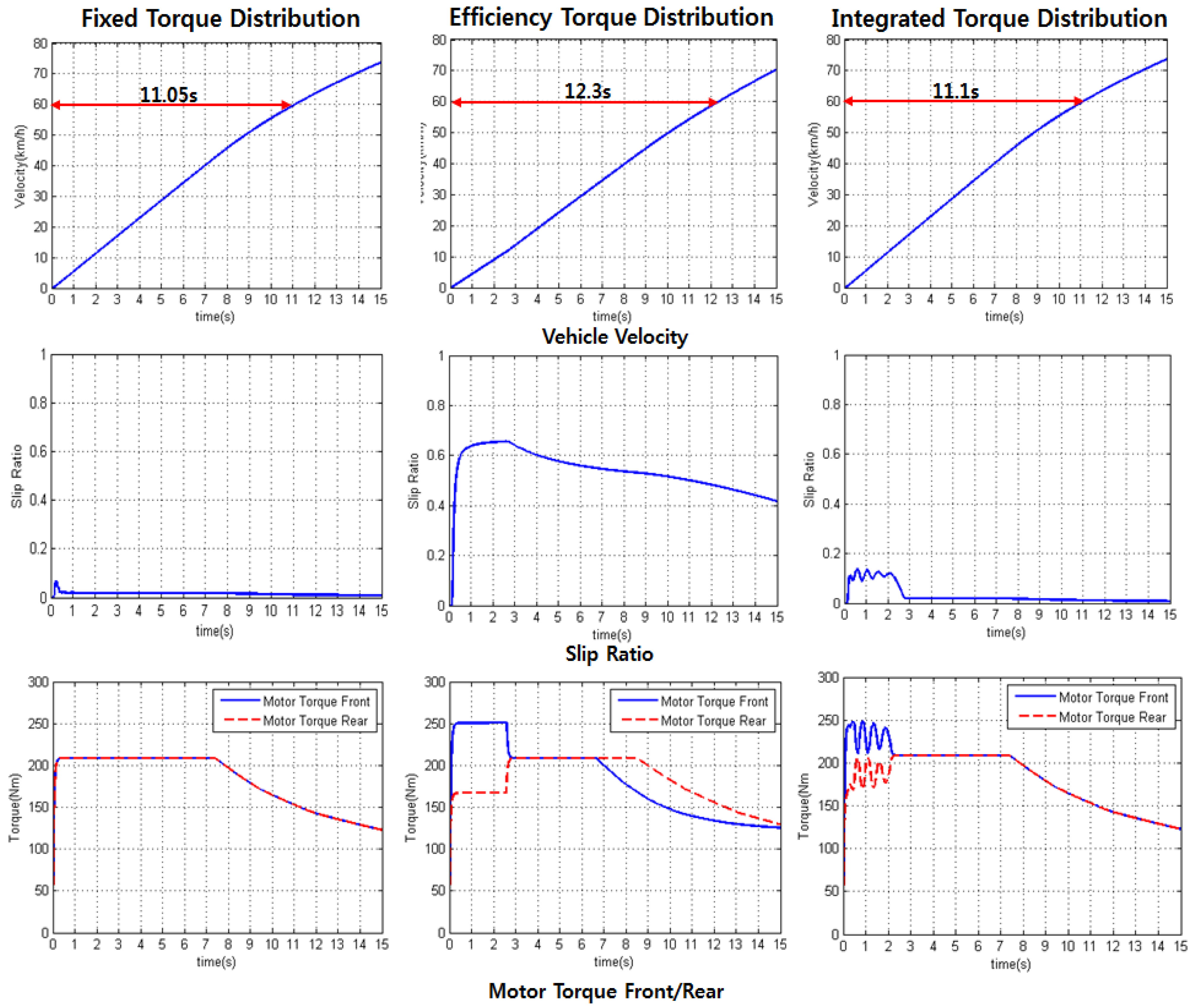
Torque distribution logic considering the efficiency of the driving system, torque distribution logic reflecting the acceleration will and braking will of the driver, and torque distribution logic considering the slip of the vehicle were developed. The effect of individual logic sets on the performance of the vehicle can differ according to how they are integrated. In this paper, each logic set was given a priority, and the distribution strategy with the highest priority was placed in the latter part so as to have greater impact on the final torque distribution. For example, since the energy efficiency algorithm determines the driving/braking torque without considering the stability of the vehicle, it was arranged to be the first algorithm to determine the torque, as it had the lowest importance in the final torque decision. Since slip of the vehicle is very likely to create unstable vehicle behavior, it was chosen to be the last algorithm such that it will have the greatest discretion.
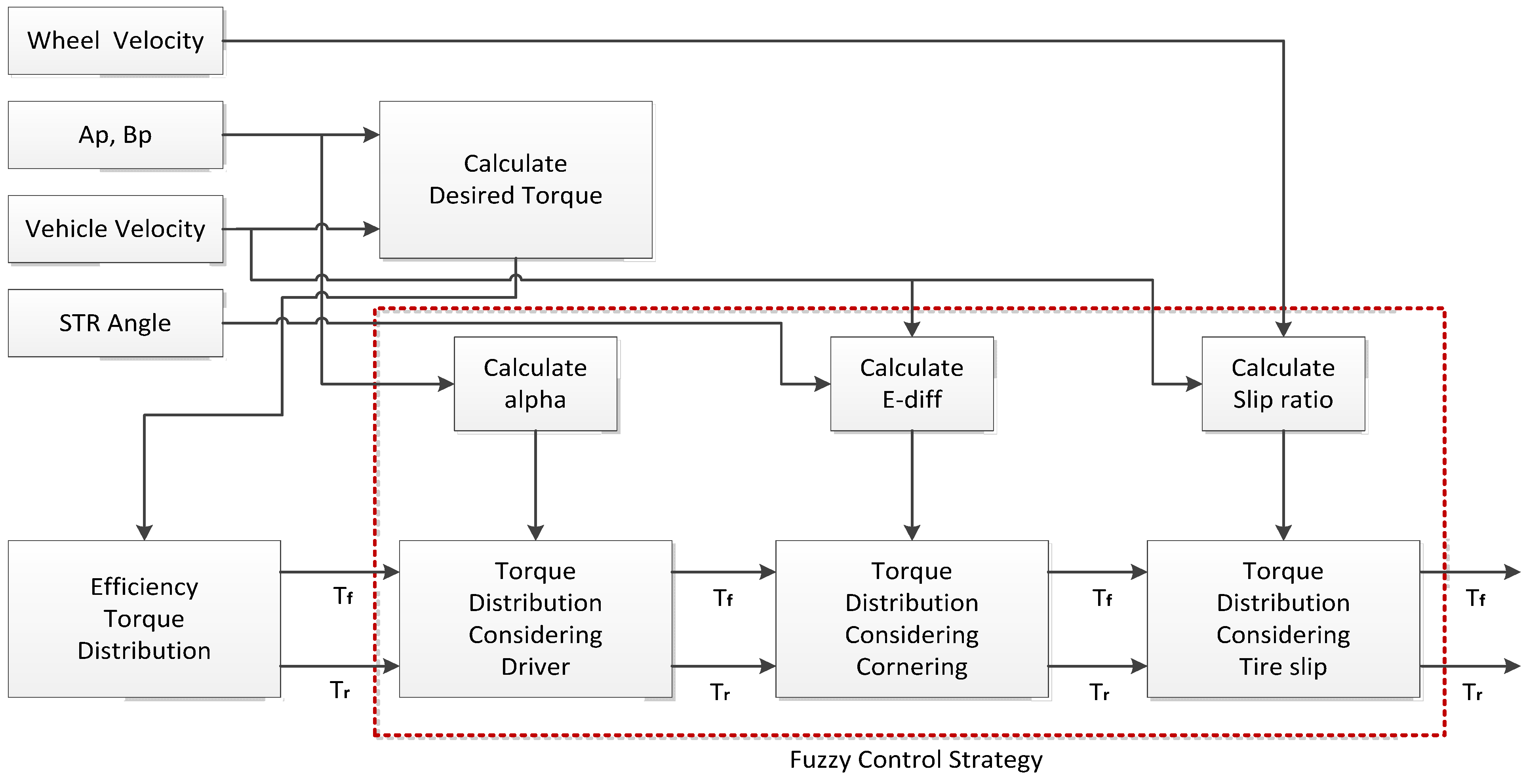
Figure 12 shows a block diagram of the integrated algorithm. The priorities of the algorithms were arranged in the following order: efficiency distribution strategy, distribution strategy considering the driving will of the driver, distribution strategy considering cornering of the vehicle, and distribution strategy considering slip. The part indicated by red dotted lines reflects the Fuzzy control strategy.
Figure 12.
Integrated torque distribution algorithm.
Figure 12.
Integrated torque distribution algorithm.