Next Article in Journal
State-of-Charge Estimation for Lithium-Ion Batteries Using a Kalman Filter Based on Local Linearization
Previous Article in Journal
The Future of Solar Power in the United Kingdom
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 8
Issue 8
10.3390/en8087833
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Comparison of Numerical Modelling Techniques for Tidal Stream Turbine Analysis

by
Ian Masters
,
Alison Williams
,
T. Nick Croft
,
Michael Togneri
,
Matt Edmunds
*,
Enayatollah Zangiabadi
,
Iain Fairley
and
Harshinie Karunarathna
Zienkiewicz Centre for Computational Engineering, Swansea University, Swansea SA2 8PP, UK
*
Author to whom correspondence should be addressed.
Energies 2015, 8(8), 7833-7853; https://doi.org/10.3390/en8087833
Submission received: 2 April 2015 / Revised: 24 July 2015 / Accepted: 24 July 2015 / Published: 30 July 2015
Browse Figures
Versions Notes

Abstract

:
To fully understand the performance of tidal stream turbines for the development of ocean renewable energy, a range of computational models is required. We review and compare results from several models of horizontal axis turbines at different spatial scales. Models under review include blade element momentum theory (BEMT), blade element actuator disk, Reynolds averaged Navier Stokes (RANS) CFD (BEM-CFD), blade-resolved moving reference frame and coastal models based on the shallow water equations. To evaluate the BEMT, a comparison is made to experiments with three different rotors. We demonstrate that, apart from the near-field wake, there are similarities in the results between the BEM-CFD approach and a coastal area model using a simplified turbine fence at a headland case.

1. Introduction

The attempt to fully understand the mechanics of extraction of energy from tidal currents is a challenging engineering problem. Conventional tidal stream energy devices take the form of an axial flow turbine using hydrofoils that generate lift and drag. Two aspects need to be considered: the effect of the flow on the turbine and the effect of the turbine on the flow field.
We may regard the torque that drives the rotation of the turbine as a function of the hydrodynamic forces that arise due to relative motion between the fluid and the rotating blades. Describing this relative motion, and thereby estimating the hydrodynamic forces, is therefore the primary requirement of a numerical scheme that models a tidal stream turbine (TST). One CFD approach is to utilise a moving reference frame containing the rotating turbine blades, which we describe in this paper. Difficulties in implementing this scheme may occur at the boundary of the moving part of the mesh, which manifests itself as a pressure discontinuity. More computationally-efficient schemes treat the rotor as an actuator disk, blade element disk or actuator line. These schemes are also discussed, with a focus on the blade element disk approach, which we refer to as BEM-CFD (blade element momentum-CFD). Finally, the least computationally-intensive numerical scheme is a blade element momentum theory (BEMT) approach, which is widely used for the analysis of propellers and other rotors. In this scheme, the flow field is assumed, and the computation reduces to a 1D treatment of the blade elements, comparing tabulated lift and drag coefficients with axial and rotational induction factors.
The BEMT scheme is computationally very fast, for instance running a tip speed ratio (TSR) sweep (roughly 400 individual simulations) in plug flow requires only around twenty minutes on a desktop computer, and can be used to study in detail time-varying effects, such as the effects of waves and rotor control strategies. By contrast, a TSR sweep in the BEM-CFD model takes around five days on a 32-core cluster. CPU times for coastal area models vary significantly based on the scale and resolution of the scenario being investigated.
The principal difficulty in validating these schemes is the lack of field data. Several sets of results are in the literature based on experiments with relatively small diameter rotors. Calculation of the Reynolds number based on the blade chord length shows that Reynolds numbers are significantly lower than those found in typical datasets for aerofoils in air [1]. Computationally-efficient schemes, such as the BEMT and BEM-CFD approaches, rely on pre-determined lift and drag data and, thus, can only capture the effects of changes in sectional properties (e.g., as a result of biofouling or pitting) if these data are altered. We present a sensitivity study of these effects and propose some solutions to improve such schemes.
CFD models can be used to investigate the second aspect in the near-field: wake characteristics, recovery and interaction can all be modelled. Larger scale changes can be determined using coastal area models that can predict changes over hundreds of kilometres with much lower spatial resolution.

2. BEMT

The basic theory of BEMT is widely described in the literature [2,3], so we do not go into detail here. Briefly, one may describe the principle of the approach as reconciling two different models of a horizontal-axis turbine: a blade element (BE) model that treats the turbine as a collection of foil sections generating lift and drag forces in response to the oncoming flow and a momentum theory (MT) model that treats the turbine as a series of annular elements that absorb linear momentum (representing the slowing-down of the current due to the turbine) and impart angular momentum (representing the swirl induced in the turbine wake).
Two parameters are defined that capture the salient details in both models, and we obtain our solution by determining the values of these parameters that bring the two models into closest agreement. Our BEMT code [4] incorporates several extensions to the classical theory, including tip/hub losses, high induction effects [5] and the ability to model an arbitrary inflow. Here, we present its ability to capture the sensitivity of turbine performance to small changes in the hydrodynamic properties of the blade profiles.
We begin by considering three rotors for which experimental results have already been published. These turbines will be referred to by the institute at which the experimental work has been carried out. Thus, we have the rotors designed by Cardiff University [6] and tested in the recirculating flume at Liverpool, which are reported in [7,8]; the IFREMER turbine, reported in [9]; and the Manchester turbine, reported in [10,11]. All rotors have a three-bladed configuration, and the blade geometries for each are shown in Figure 1.
Energies 08 07833 g001 1024
Figure 1. Blade geometries for the (top) Liverpool, (middle) IFREMER and (bottom) Manchester turbines. Chord length (distance from the section leading edge to the trailing edge) is shown with solid lines and the twist angle with dashed lines (90° meaning the section is parallel to the rotor plane).
Figure 1. Blade geometries for the (top) Liverpool, (middle) IFREMER and (bottom) Manchester turbines. Chord length (distance from the section leading edge to the trailing edge) is shown with solid lines and the twist angle with dashed lines (90° meaning the section is parallel to the rotor plane).
Energies 08 07833 g001
The Liverpool rotor uses a Wortmann FX63-137 section for the entire blade length; the IFREMER rotor uses a NACA 63418 section; and the Manchester rotor uses a Göttingen 804 foil. BEMT relies on a table of lift and drag coefficients to calculate the forces generated by the blade elements, and the data for each of these foils were taken from different sources. The coefficients for the Wortmann foil were taken from a flume study carried out at Swansea [12] at Re = 5 × 104; for the NACA 63418 section, data were taken from standard tables [1] for moderate angles of attack with Re = 9 × 106, with flat-plate theory used for extreme angles of attack; for the Göttingen foil, data were taken from a wind tunnel study [13] at Re = 3 × 104. Data for the Göttingen foil are much less complete than those for the other sections; additionally, the section stalls very abruptly and at an unusually low angle of 8°. To ensure a fast runtime, the data are not smoothed, and linear interpolation is used to estimate lift and drag between data points. As a result of the sparse data and the interpolation, the BEMT results contain many small discontinuities, since in many cases, a relatively small change in inflow angle results in a large jump in the lift and drag properties of the foil. This is also noticeable in the BEMT work carried out at Manchester, as can be seen in the studies that report their experimental results [10].
As we mention above, the purpose of the work presented here is to investigate the sensitivity of turbine performance to small changes in the lift and drag properties of the hydrofoils used in the rotor blades. For each rotor, we calculated four sets of performance data: One with the original geometry, one with decreased lift (i.e., CL decreased by 10% at all inflow angles), one with increased drag (i.e., CD increased by 50% at all inflow angles) and one with both lift and drag altered. These cases are intended as a simple representation of the degradation of section performance due to factors such as biofouling or surface pitting due to cavitation, and the magnitude of the changes are in line with those found in experimental investigations [14]. Note that an earlier numerical investigation by Batten et al. [15] treated drag in a similar fashion, but did not consider the effects of roughness on lift. 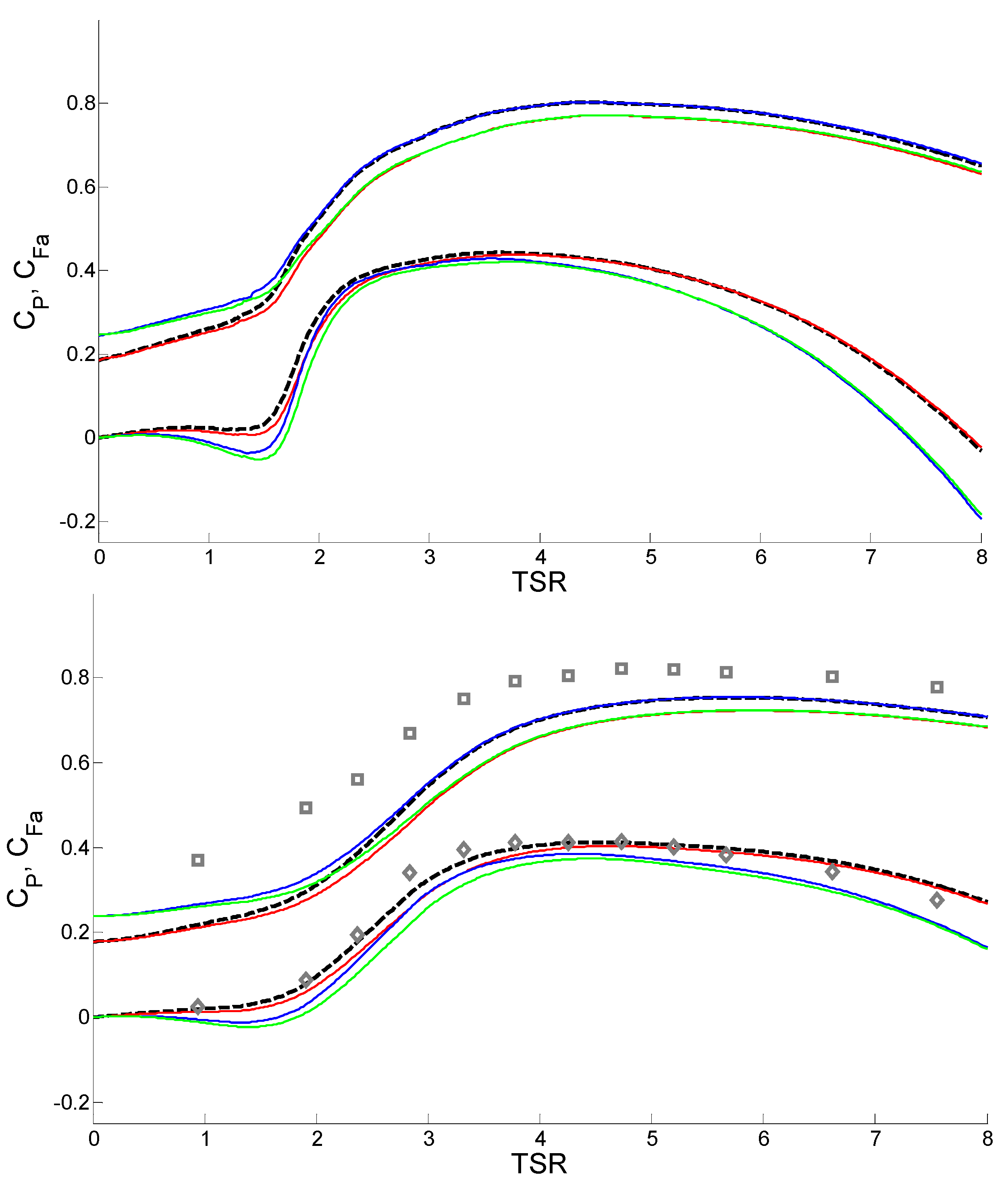These results are presented graphically in Figure 2, along with experimental data for the IFREMER and Manchester turbines.
Energies 08 07833 g002a 1024Energies 08 07833 g002b 1024
Figure 2. Power (CP) and axial force (CFa) coefficients for (top) Liverpool, (middle) IFREMER and (bottom) Manchester turbines. In all cases, the upper cluster of lines shows CFa, and the lower shows CP. Black dashed lines show original turbine performance; red lines show the 90% CL case; blue lines show the 150% CD case; green lines show the combined lift decrease and drag increase case. Experimental results are also shown for the IFREMER and Manchester turbines (in grey), with data taken from [9,11], respectively. Note that for the range of TSR values investigated, both the Liverpool and Manchester turbines go beyond the freewheeling state (i.e., CP = 0); in a real turbine, this operating condition cannot be reached.
Figure 2. Power (CP) and axial force (CFa) coefficients for (top) Liverpool, (middle) IFREMER and (bottom) Manchester turbines. In all cases, the upper cluster of lines shows CFa, and the lower shows CP. Black dashed lines show original turbine performance; red lines show the 90% CL case; blue lines show the 150% CD case; green lines show the combined lift decrease and drag increase case. Experimental results are also shown for the IFREMER and Manchester turbines (in grey), with data taken from [9,11], respectively. Note that for the range of TSR values investigated, both the Liverpool and Manchester turbines go beyond the freewheeling state (i.e., CP = 0); in a real turbine, this operating condition cannot be reached.
Energies 08 07833 g002aEnergies 08 07833 g002b
It is immediately apparent that there are few large changes in turbine performance as a result of lift/drag changes of this magnitude. This is reassuring from an operational point of view, as it implies that relatively small changes to the blade characteristics that may occur as a result of biofouling or blade erosion/pitting are unlikely to cause a large drop in performance.
The details of the performance changes vary between rotors: we tabulate the most important parameters in Table 1. In CP terms, the IFREMER rotor is more sensitive to lift/drag changes than the Liverpool rotor, although their CFa sensitivities are very similar. The Manchester rotor CP drops more significantly with degradation of section performance, particularly when drag is increased. It should be remembered that the Manchester rotor was designed in order to replicate full-scale thrust characteristics, rather than power characteristics, and so, changes in its CP curve are likely to be atypical. It is clear from this table, and from Figure 1, that across all rotor geometries, CP is more affected by an increase in sectional drag, whereas sectional lift has a greater influence on CFa.
It is not only the value of the optimum CP that is altered by these changes in blade profile properties, but also the TSR at which this optimum is attained. An increase in sectional drag coefficient always results in a downwards shift of the optimum TSR, while a decrease in lift has different effects: for the Manchester rotor, the optimum TSR shifts slightly downwards, but for the IFREMER and Liverpool rotors, the shift is upward. A sophisticated control scheme, then, may be able to use sensitivity analyses, such as those presented here, to partially compensate for blade degradation by altering the TSR at which the turbine is operated.
Table
Table 1. Changes to maximum power and thrust coefficients and optimum TSR for Liverpool, IFREMER and Manchester turbines in response to small changes in the lift and drag properties of blade sections.
Table 1. Changes to maximum power and thrust coefficients and optimum TSR for Liverpool, IFREMER and Manchester turbines in response to small changes in the lift and drag properties of blade sections.
LiverpoolIFREMERManchester
Max CPOriginal0.44310.41220.3350
CL − 10%0.4377 (−1.22%)0.4035 (−2.12%)0.3119 (−6.88%)
CD + 50%0.4287 (−3.26%)0.3848 (−6.66%)0.2157 (−35.62%)
Both0.4213 (−4.92%)0.3736 (−9.37%)0.1866 (−44.3%)
Max CFaOriginal0.80180.75310.9761
CL − 10%0.7707 (−3.88%)0.7224 (−4.07%)0.9175 (−6.00%)
CD + 50%0.8024 (+0.08%)0.7540 (+0.13%)0.9643 (−1.21%)
Both0.7714 (−3.79%)0.7234 (−3.95%)0.9185 (−5.90%)
Optimum TSROriginal3.644.524.64
CL − 10%3.84 (+5.50%)4.62 (+2.21%)4.54 (−2.15%)
CD + 50%3.52 (−3.30%)4.32 (−4.42%)4.10 (−11.64%)
Both3.70 (+1.65%)4.50 (−0.44%)4.40 (−5.17%)
We can also see that the agreement between the BEMT code’s predictions of the unmodified rotor performance and the experimental data for the IFREMER and Manchester turbines is good throughout the range of experimental TSR values. Taking the peak values as representative, for the Manchester results, power agrees to within 2.9% and thrust to within 3.0%; for the IFREMER turbine, power agrees to within 0.3%. The apparent exception is the axial force coefficient for the IFREMER turbine, but this discrepancy is attributable to the fact that the measured axial force included the force on the supporting structure and not simply the rotor disc itself. Despite this difference, it can nevertheless be seen that the trend of axial force’s dependence on TSR matches the experimental observations. Note that the IFREMER results have been corrected for blockage using the method of Glauert [2]. In order to apply this correction, the power and thrust coefficients must correspond to the same TSR values; the experimental values provided by Stallard et al [11] do not satisfy this condition, and thus, the correction cannot be carried out in this case. However, the blockage in this experiment was only 2.5% and, thus, would not greatly alter the results reported. In fact, we can specify upper bounds on its influence for this blockage ratio: no CFa value would change by more than 1.4%, and no CP value by more than 2.2%. Overall, the agreement between BEMT predictions and experimental results allows us to be confident in our numerical model.

3. CFD and BEM-CFD

The most complete computational model of a full-scale tidal turbine that can feasibly be run is a large eddy simulation (LES) [16], although unsteady RANS remains more common [17,18]. Such a model will necessarily rely on a moving mesh to account for blade rotation. The moving boundary in the mesh may present difficulties, manifesting as a pressure discontinuity and greater computational costs. An alternative method is the BEM-CFD model in which the flow properties are resolved by interaction of the BEM and CFD methods [19,20,21,22]. As BEM by itself does not provide any useful information about the effect of a turbine in the far-field, we use CFD to resolve the full domain [23]. In other words, the BEM method is used to model the turbine, and CFD is employed to model the flow properties elsewhere in the domain, thus giving us a time-averaged estimate of the turbine wake while significantly reducing the computational cost compared to a geometry-resolved CFD model. Here, we will present two sets of results from a BEM-CFD model validated against CFD and against experimental measurements.
We start by modelling a single tidal turbine configuration in both the BEM-CFD method and a blade-resolved geometry (BRG) CFD method. In the comparison between these two models, we are primarily interested in the velocity deficit in the turbine wake. An understanding of turbine wakes is vital if tidal turbines are to be deployed in arrays [24] (as turbine wakes will inevitably impinge on other turbines located downstream), and such arrays are the only way tidal turbines can be economically viable [25].
The CFD finite volume model is constructed and set up in ANSYS Fluent. This was provided by the Marine Energy Research Group of Cardiff University. The turbine used in this model is the based on the Liverpool rotor described in Section 2, but scaled up to a diameter of 10 m. The details of this blade, including the performances and mesh details, are provided in [6,17,18]. The computational domain has dimensions 506 m × 50 m × 50 m, in which the turbine is located 104 m from the inlet to allow the flow to settle before reaching the turbine. This domain is chosen based on the studies published previously, which have shown that with this distance from the side walls, there would be minimum effects from the boundary on the turbine [6]. The inlet boundary condition is set as a uniform flow of 3.086 m/s (equivalent to six knots, a typical flow speed of a potential TST deployment site), and a no-slip condition is imposed at the bed and blade surfaces. For all of the side walls and the top of the domain, symmetry boundary conditions have been enforced. At the outlet boundary, a zero diffusion flux condition for all flow variables is imposed. The rotational speed of the blade was set to 2.25 rad∙s−1 or TSR 3.64, the design optimum rotational speed for the rotor in normal operation. Note that this is identical to the optimum TSR found in BEMT simulations of the Liverpool rotor (see Table 1). The zone that represents the rotation of the rotor is set to have a 17 m diameter and a 6 m width. The properties of the mesh for this model are discussed in detail in [6].
An equivalent model has also been implemented using the BEM-CFD method. The domain geometry is the same and is meshed with 6.03 million tetrahedral elements. The mesh sizing for the both cases is different in the vicinity of the blades. Unstructured tetrahedral elements have been adopted in a way to be able to capture the geometry of the blade properly for the BRG-CFD model. The boundary conditions are the same as those used in the Fluent model. Rather than representing the geometry of the turbine directly as in the CFD model, we treat the rotor as a momentum source/sink in the domain based on the geometry and hydrodynamic properties of the blade. This BEM-CFD method has been validated in the previous research of the group, together with a mesh independence study [25].
Both the BRG-CFD and BEM-CFD models employ a standard finite volume approach with a k-ε turbulence model. Note also that in both cases, we are modelling only the rotor itself: no support structure (nacelle, tower, etc.) is included. The rotors rotate clockwise in both models viewed from upstream.
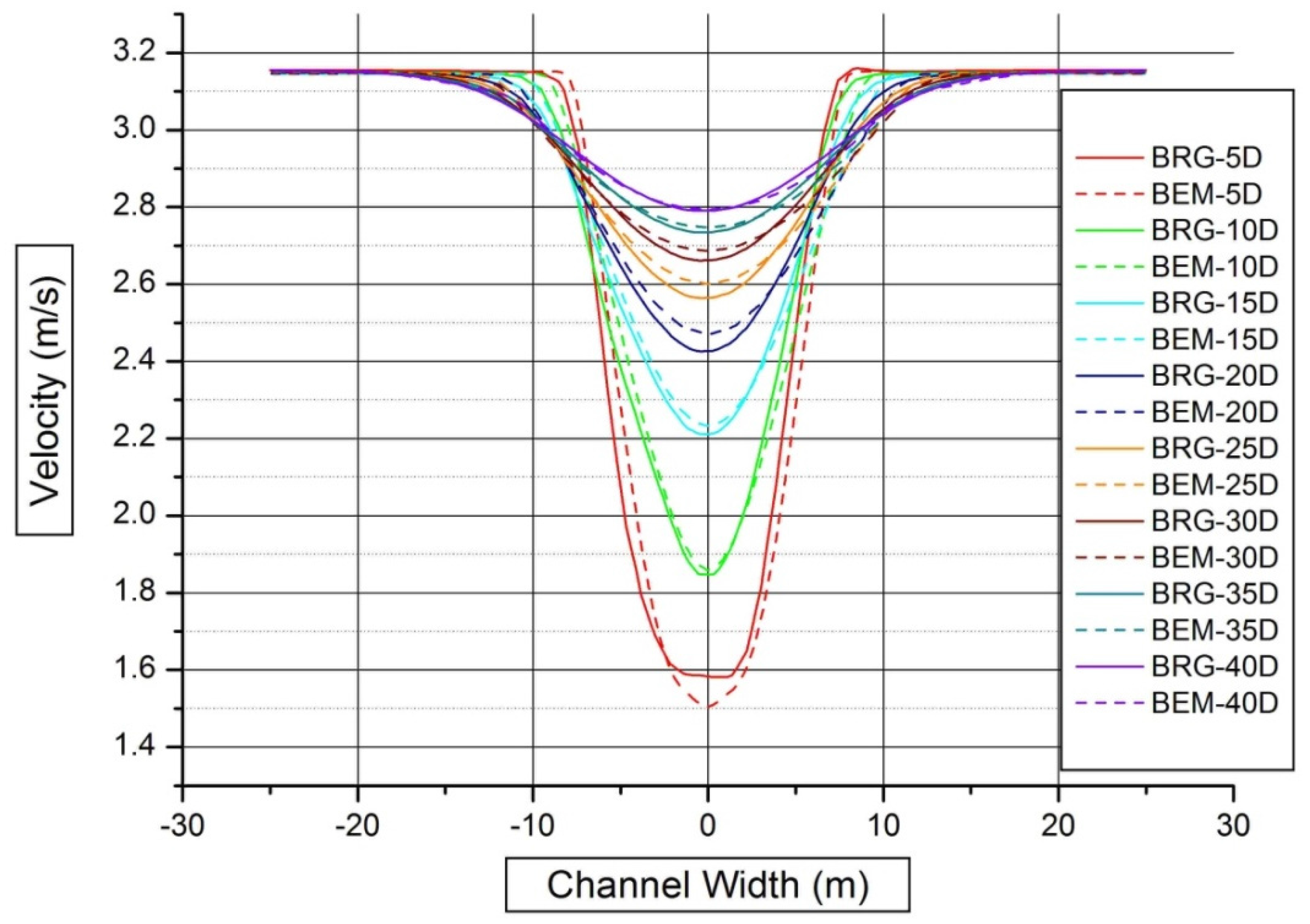
In Figure 3, we compare the two models’ predictions of velocity deficit at five diameter (5D) intervals between the distances of 5D and 40D behind the turbine. The values are extracted along the horizontal line passing behind the turbine at the hub level. We see that the models agree well throughout most of the wake. Five diameters downstream of the rotor, the velocity has dropped by more than 50% in comparison to the inlet velocity, although on the centreline, the BRG predicts a higher wake velocity than the BEM-CFD. Further downstream, the wake profiles are very similar across the span of the domain, both in terms of the magnitude of velocity deficit and wake spreading. The results also show that the wake shape for the BEM-CFD method is symmetric, while the BRG method’s wake is slightly asymmetric. The lower minimum velocity observed in the BEM-CFD method could be linked to relative over-prediction of turbine power in the BEM-CFD method compared to the BRG model. Comparison of CP and CFa for both models shows that the BEM-CFD method predicts a slightly higher CP value of 0.44 compared to 0.40 for the BRG-CFD, and the CFa for the BEM-CFD and BRG-CFD is 0.81 and 0.83, respectively. The BRG-CFD results are published in [18] and also have good agreement with the BEMT results shown in the top panel of Figure 2. It should be borne in mind that for simplicity, this comparison is done in a uniform flow above a flat bed; in the real environment, non-uniform flows and sloped surfaces will influence the results [9,26]. 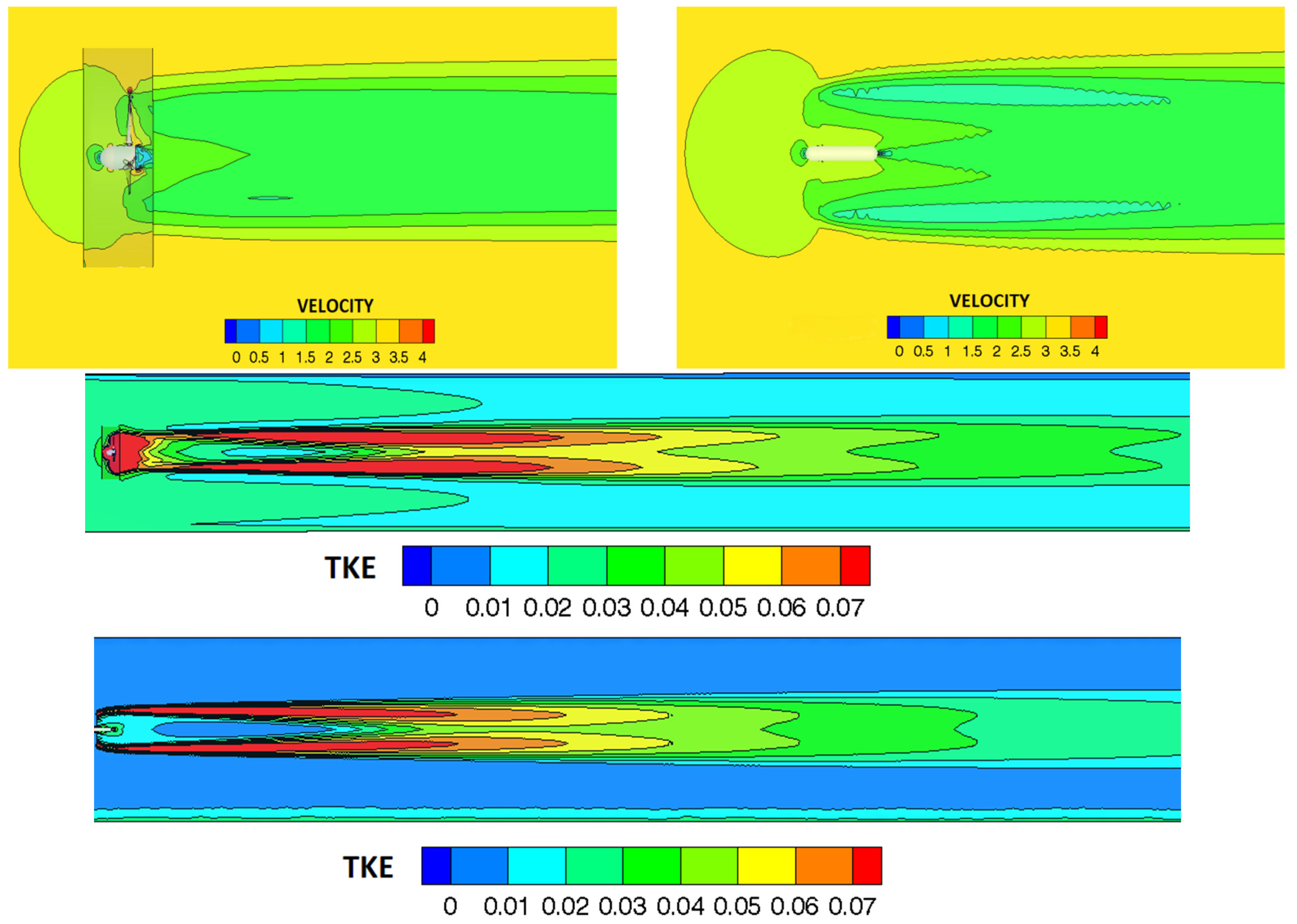Figure 4 shows the velocity deficit and the turbulent kinetic energy for each of the models.
Energies 08 07833 g003 1024
Figure 3. Comparison of the velocity deficit in the rotor wake from BEM-CFD and blade-resolved geometry (BRG) models at a range of downstream locations.
Figure 3. Comparison of the velocity deficit in the rotor wake from BEM-CFD and blade-resolved geometry (BRG) models at a range of downstream locations.
Energies 08 07833 g003
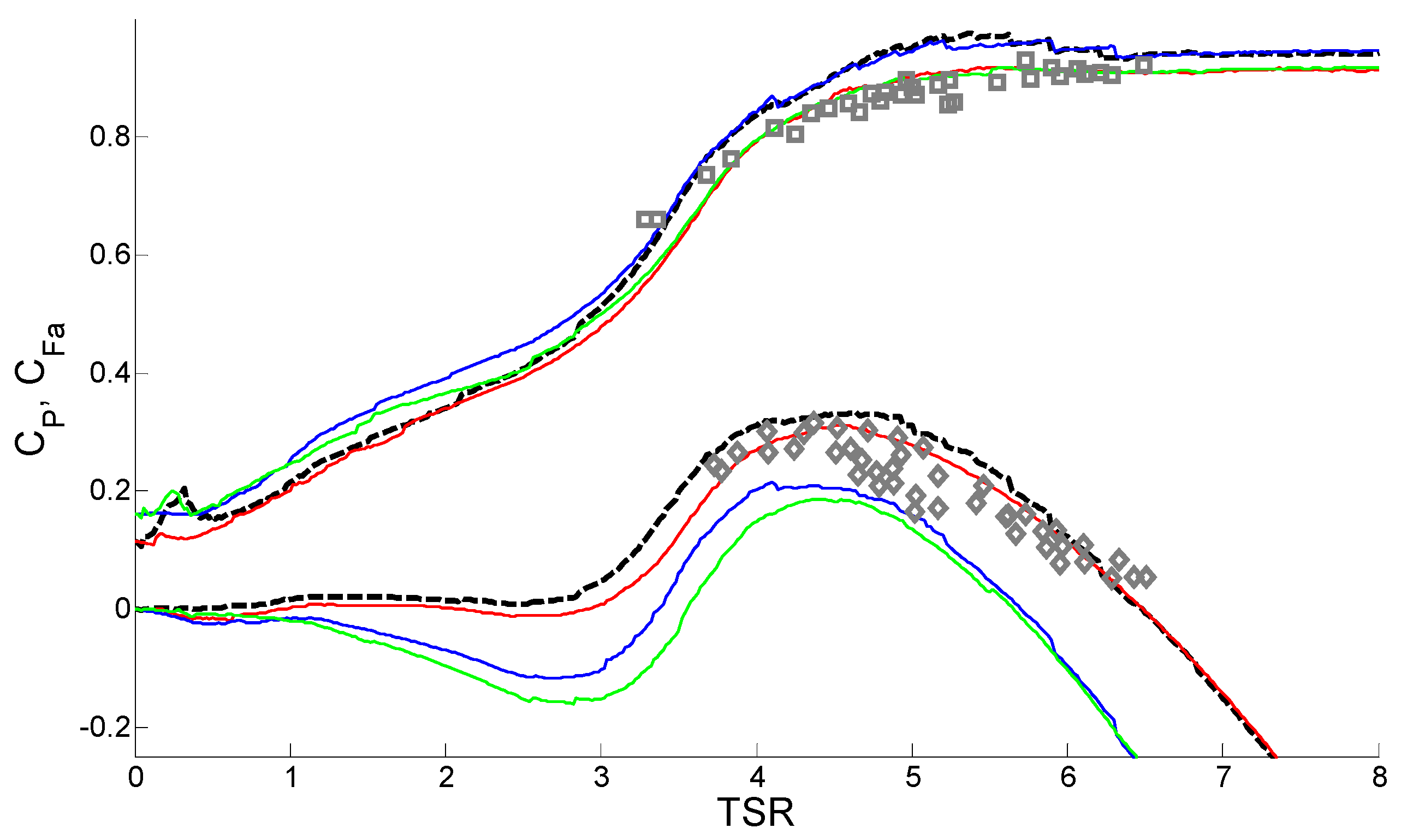
In addition to validating the BEM-CFD model against the BRG-CFD results, we have also carried out a comparison with experimental results carried out in the IFREMER flume, the same results used as one of the test cases for the BEMT simulations reported in Section 2. Figure 5 demonstrates that results from the BEM-CFD method match experimental measurements well, in comparison to Figure 9a of [9]. A comparison of BEM-CFD and BEMT methods is also conducted using the rotor geometry from the IFREMER experimental study. 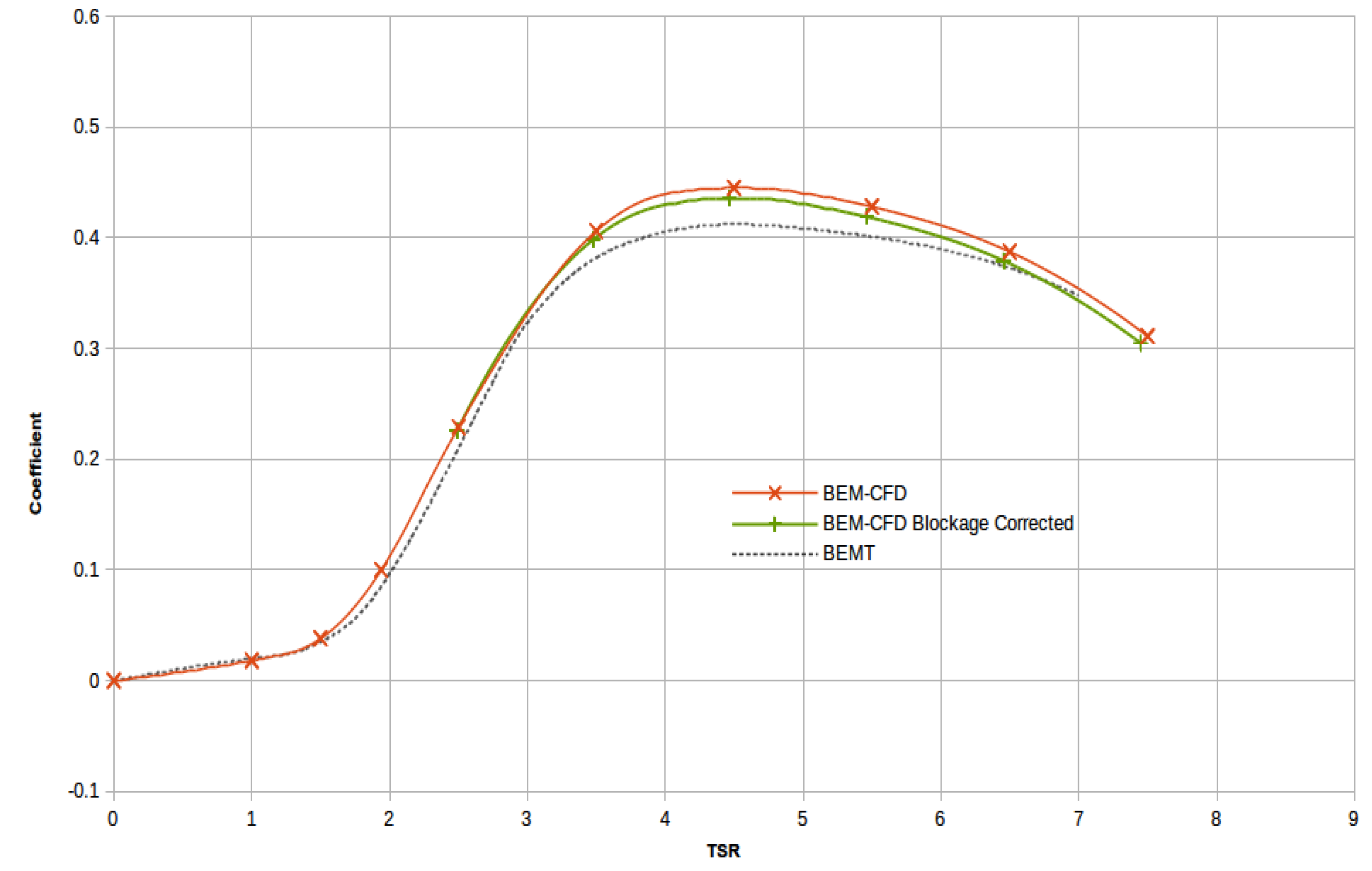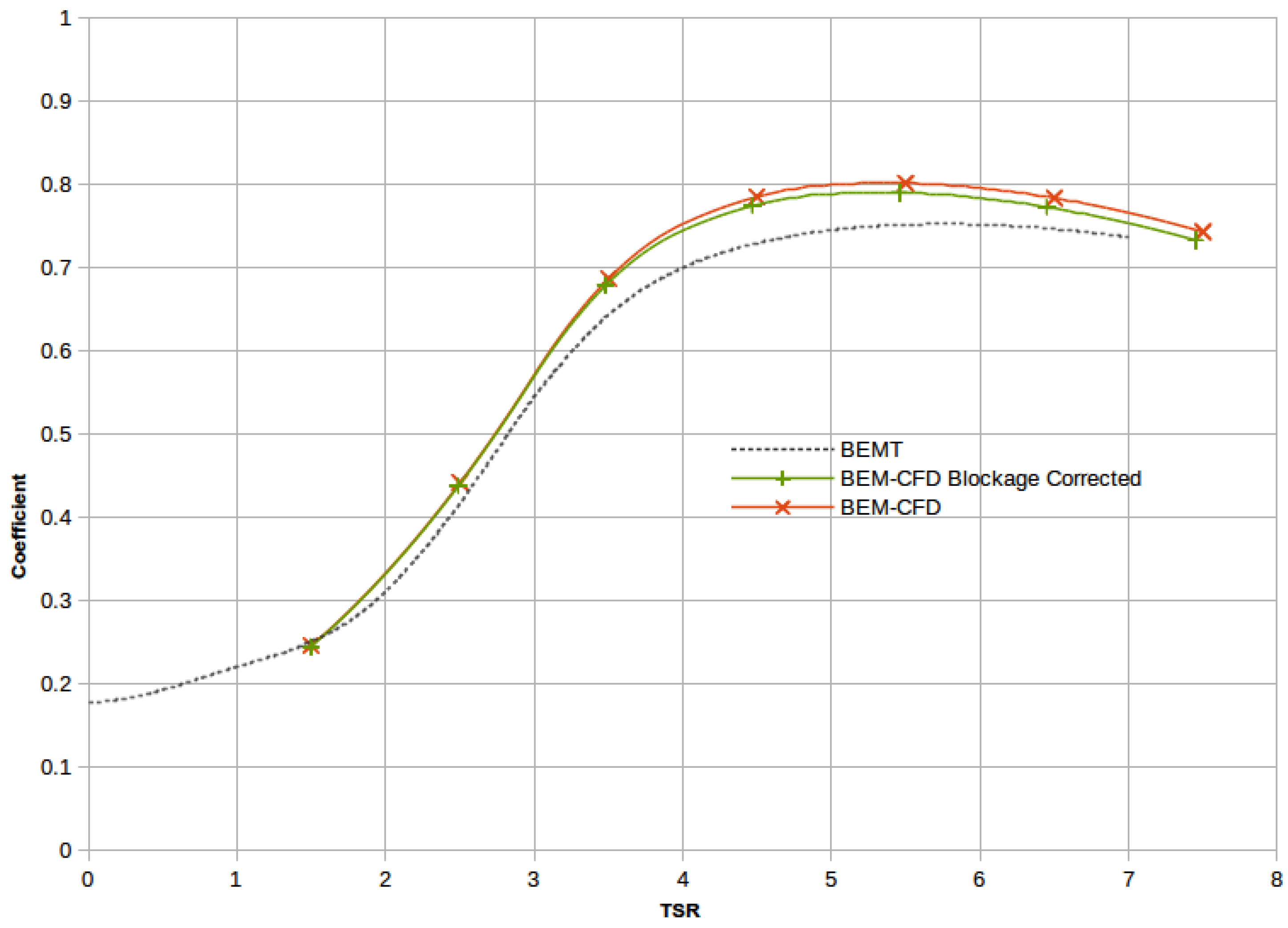Figure 6 and Figure 7 demonstrate the coefficient of power and coefficient of axial thrust plotted against TSR. The results show that BEMT under-predicts power in comparison to BEM-CFD. This under-prediction is largest near the optimum, with the model predictions varying by 5.4%.
Energies 08 07833 g004 1024
Figure 4. Comparisons of the velocity deficit between BRG (top right) and BEM-CFD (top left) and between turbulent kinetic energy (TKE) for BRG (middle) and BEM-CFD (bottom) in the Cardiff 10-m rotor wake.
Figure 4. Comparisons of the velocity deficit between BRG (top right) and BEM-CFD (top left) and between turbulent kinetic energy (TKE) for BRG (middle) and BEM-CFD (bottom) in the Cardiff 10-m rotor wake.
Energies 08 07833 g004
In comparing the BEMT, BEM-CFD and experimental results, it is important to bear in mind the effects of blockage and how this differs between the three cases. BEMT results always reflect a turbine operated in a theoretically perfect blockage-free state, whereas both experiments and CFD introduce a flow constriction (flume walls for experiment, domain boundaries for CFD) that forces more fluid through the turbine than in an equivalent unblocked condition. Thus, it is to be expected that we would find better agreement between BEMT and experiment when the blockage of the experiment is corrected, as is seen in the second panel of Figure 2, but better agreement between BEM-CFD and experiment if this correction is not applied, as is seen in Figure 7 and Figure 8. A slight complication arises in that, although the BEM-CFD simulations replicated almost all of the conditions of the experiments reported in [9], the mast on which the turbine was mounted was omitted for reasons of computational cost. The experimental measurements of thrust in fact included the drag on this mast, as well as the rotor thrust (as mentioned in Section 2), which explains the offset between numerical predictions of thrust and the corresponding measured values. Furthermore, the additional thrust on the mast means that blockage was more significant in the experiments than the BEM-CFD simulations. Thus, the changes in the experimental power and thrust curves due to the correction are larger. This is why we have better agreement between unblocked experiment and BEMT, and between blocked experiment and blocked BEM-CFD, than we see between unblocked BEM-CFD and BEMT.
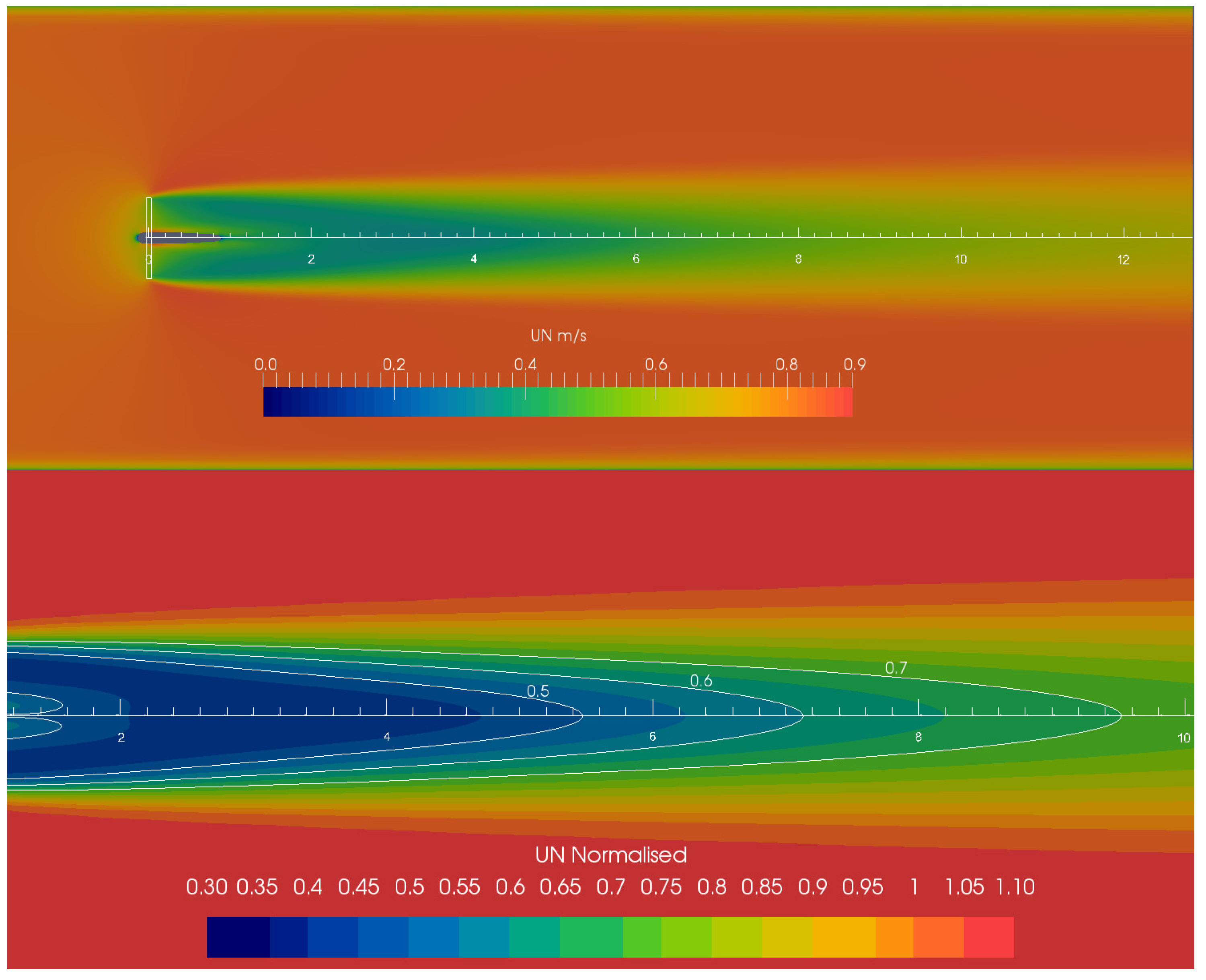
Energies 08 07833 g005 1024
Figure 5. BEM-CFD model of IFREMER wake characteristics: axial velocity slice taken at the hub centre. Free stream velocity is 0.8 m·s−1; TSR is 3.67; and background turbulence intensity is set at 3%. The top panel shows the full wake to the end of the domain, while the bottom panel is staged to compare with Figure 9a from [9] and includes isolines at 0.5, 0.6 and 0.7 normalised axial velocity.
Figure 5. BEM-CFD model of IFREMER wake characteristics: axial velocity slice taken at the hub centre. Free stream velocity is 0.8 m·s−1; TSR is 3.67; and background turbulence intensity is set at 3%. The top panel shows the full wake to the end of the domain, while the bottom panel is staged to compare with Figure 9a from [9] and includes isolines at 0.5, 0.6 and 0.7 normalised axial velocity.
Energies 08 07833 g005
Energies 08 07833 g006 1024
Figure 6. Comparison of IFREMER rotor results for CP (coefficient of power) between BEM-CFD and BEMT for a range of TSRs. Blockage corrected BEM-CFD results are included for reference.
Figure 6. Comparison of IFREMER rotor results for CP (coefficient of power) between BEM-CFD and BEMT for a range of TSRs. Blockage corrected BEM-CFD results are included for reference.
Energies 08 07833 g006
Energies 08 07833 g007 1024
Figure 7. Comparison of IFREMER rotor results for CFa (coefficient of axial thrust) between BEM-CFD and BEMT for a range of TSRs. Blockage-corrected BEM-CFD results are included for reference.
Figure 7. Comparison of IFREMER rotor results for CFa (coefficient of axial thrust) between BEM-CFD and BEMT for a range of TSRs. Blockage-corrected BEM-CFD results are included for reference.
Energies 08 07833 g007

4. Coastal Area Modelling

While CFD and BEMT approaches are focused very much on the turbine itself, whether in terms of structural loading, blade performance or detailed wake structures and intra-array interactions, computational limitations mean that different techniques are required for the modelling of larger-scale impacts or for long time period simulations. Coastal area models are therefore used, which typically solve the shallow water equations in two or three dimensions. Horizontal meshes are either rectangular or, increasingly, unstructured, and models are either 2D depth averaged or, in the 3D case, cater to vertical resolution with a series of layers. Model domain sizes for coastal area models range from the order of 10 km for site-specific modelling to the order to 1000 km for shelf-scale studies of multiple arrays or far-field impacts. Simulation durations typically range from a single tidal cycle to more than a year, with time steps of seconds to minutes and output periods of minutes to hours. Coastal scale modelling typically investigates available resource [27,28] or the impacts of energy extraction on the wider environment for array or inter-array scenarios. Resource modelling is conducted to provide greater spatiotemporal coverage than is achieved with field measurements [29].
Impacts on the hydrodynamic regime can be observed over a much larger area than covered by CFD. Hydrodynamic responses can be noticed on an ocean scale for tidal barrages and on a regional to shelf-sea scale for tidal stream turbines [30,31]. Changes to hydrodynamic regime can lead to second-order effects. Researchers have also investigated impacts on sediment transport and associated changes to morphology [32,33,34,35]. Wave-current interactions [36] can also be an important process, both in affecting the tidal resource and the changes to currents impacting the wave climate [37,38,39], the water quality [40] or aquatic organisms. More recently, optimal siting for power production over a large area has been considered [41].
A variety of methods have been used for the implementation of turbines in coastal array models: in two-dimensional models, the impact of turbines is often included as an additional component of bottom friction within the array footprint, either averaged over the whole array or as individual turbines [33,34,42]. The value used is often based on actuator disk theory with correction factors applied when array scale extraction is considered [43,44]. In three-dimensional models, such an approach would give unrealistic vertical velocity profiles, and thus, an additional sink term must be introduced to the model [35]. A review of the commonly-used methods is presented in [45]. Many coastal area models only consider the reduction in momentum; however, the rotor also generates additional turbulence, which some studies have also included to increase the realism of the impact of turbines on flow. Roc et al. [46] show that excluding turbulence reduces the accuracy in the simulation of wake recovery; thrust only leads to a faster recovery of the wake than shown in measurements, while inclusion of turbulence matches measurements well.
Currently, few turbines are installed in the real world, and no turbine arrays have been deployed. This means that few full-scale data exist on the impact of turbines on flow in the natural environment, and what data do exist re commercially sensitive. Therefore, it is not currently possible to conduct full-scale model-measurement comparisons relevant to coastal area models. This means that the two options to increase confidence in turbine formulations in coastal area models are comparison with scaled experiments, e.g., [47], or model-model comparison. In order to demonstrate the contrast between BEM-CFD and a coastal area model (Danish Hydraulic Institute’s MIKE3), the two techniques were used to model a simplified case of a fence of six turbines at an idealised headland. Such comparisons are useful to demonstrate the difference in outputs between the two techniques, to determine areas in which the coastal area model will give unrealistic results and to give credence to the simpler coastal area model approach given the lack of real full-scale turbine wake data available for model validation.
Both models use finite volume techniques to solve the incompressible Reynolds-averaged Navier–Stokes equations, but mesh resolution and turbine implementation is different. The other key differences are: the difference between time-stepping (coastal area model) and steady state (BEM-CFD) simulations; the free surface for the coastal area model; and that MIKE3 invokes the assumption of hydrostatic pressure, whereas the BEM-CFD considers dynamic pressure given the smaller mesh spacing. In the coastal area model, the Boussinesq assumption is invoked and turbulence catered to with eddy viscosity based on the Smagorinsky formulation. The BEM-CFD model used was that described in Section 3, and the coastal area model used was MIKE3 by the Danish Hydraulic Institute [48]. MIKE3 was chosen as the tested model, because it is a commercial piece of code regularly used in renewable energy applications.
The scenario tested in this paper was based on [49] and the BEM-CFD case more fully described in [25]. The domain was 770 m wide for both cases with the headland extending by 230 m. The offshore boundary was set to full slip condition in both cases. The bathymetry was set to be a constant 30 m, and the six turbines had a hub height of 15 m and a rotor diameter of 10 m. Turbine hub spacing was set at 20 m. The BEM-CFD case extended 450 m upstream and downstream of the headland centreline, whereas the coastal area model extended to 7000 m downstream. This difference is due to the lack of a similar boundary condition for the downstream boundary in the coastal area model compared to the BEM-CFD model. The BEM-CFD model implemented a zero pressure downstream boundary, whereas one could not specify this in the coastal area model, and hence, the extended domain with the same downstream boundary conditions as the upstream boundary. For both models, the upstream boundary was a plug flow with 3 m·s−1 velocity parallel to the shoreline and a still water level of zero (hence, a water depth of 30 m). The BEM-CFD model has a fixed lid at the zero water level, whereas the coastal area model has a free surface apart from the specified level at the boundary. In both models, bed resistance is set to zero.
In both the coastal area model and BEM-CFD simulations, only the rotor was considered with no support structures or nacelles included. MIKE3 has an inbuilt turbine tool based on actuator disk theory [38]. The drag force FD is calculated as:
F D = 1 2 ρ w α C D A e V 2
where ρw is the density of water, α is a correction factor that is equal to one in this study, CD is the drag co-efficient, Ae is the effective area of the turbine and V is the velocity. A constant drag co-efficient was specified as 0.9, which was equivalent to the thrust coefficient reported from the BEM-CFD simulation results. This co-efficient varied between devices in the BEM-CFD results, and thus, the average value across the fence was used in the coastal area model. The drag force, calculated by Equation (1), is then used to implement a sink in the momentum equations using an extra source term. No additional turbulence is generated by the energy extraction process in the coastal area model. Conversely, the BEM-CFD mesh has sufficiently fine resolution to capture the turbulence generation [26]. Full details of the representation of the turbines in the BEM-CFD model are described in Section 3.
The meshes used are shown in Figure 8 to demonstrate the difference in resolution. Since the BEM-CFD model is a fully-3D mesh, the figures show slices through the mesh at hub height, whereas the coastal area model uses a layered approach, and thus, the displayed mesh is the actual mesh. In the coastal area model, the turbines are implemented as sub-grid structures, and the triangular horizontal mesh in the fence region has an area of 68 m2, such that a 10-m diameter rotor fits within one triangle. By contrast, the BEM-CFD model has 50,000 elements representing each rotor.
Energies 08 07833 g008 1024
Figure 8. Meshes used in the headland case example: (a) the coastal area model; (b) the BEM-CFD model; and (c) a close up of the BEM-CFD mesh showing the gradation to finer regions around the turbines.
Figure 8. Meshes used in the headland case example: (a) the coastal area model; (b) the BEM-CFD model; and (c) a close up of the BEM-CFD mesh showing the gradation to finer regions around the turbines.
Energies 08 07833 g008
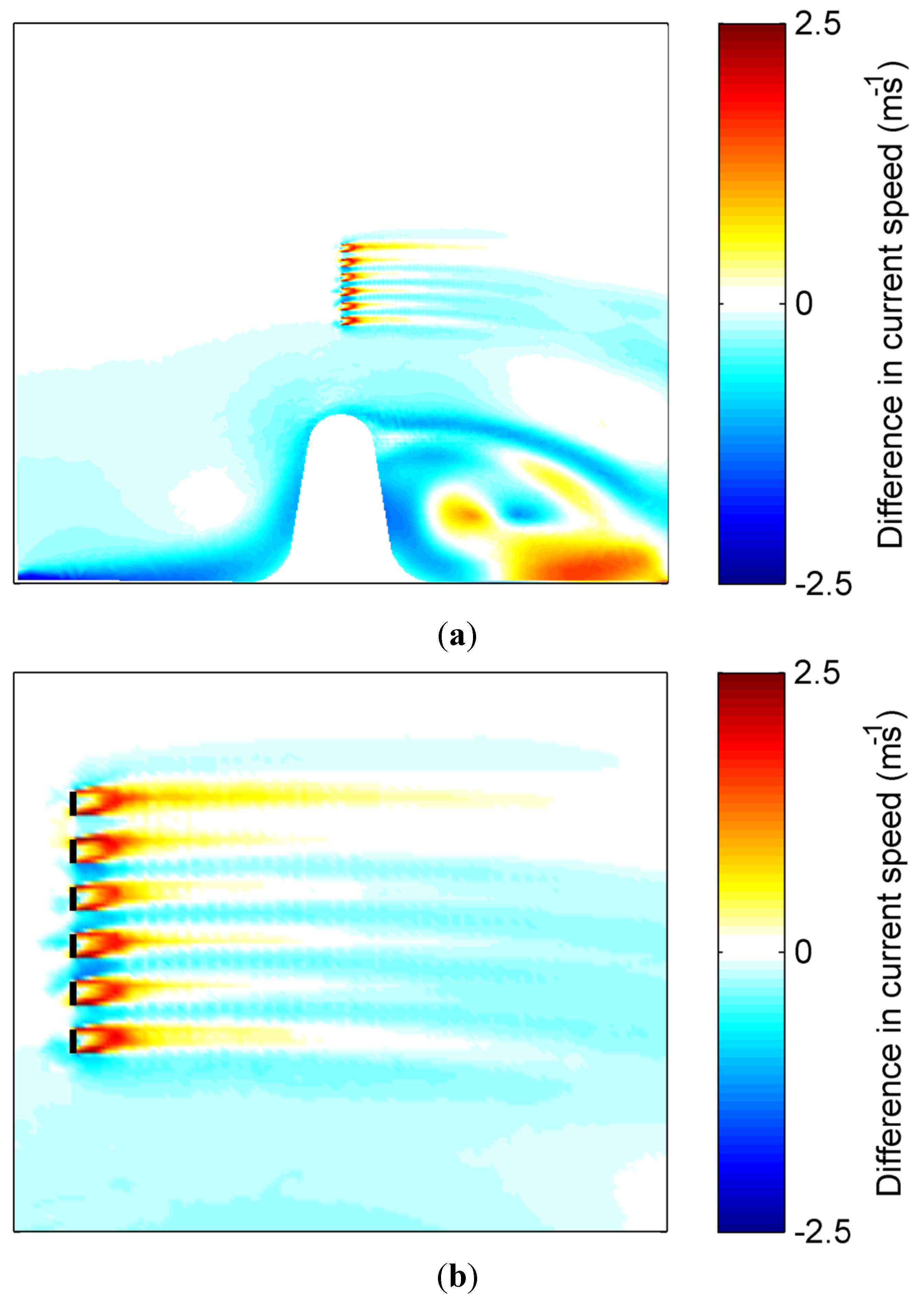
Figure 9 shows the velocity field at hub height for both simulations. Clearly, the BEM-CFD model resolves the turbine wakes in much greater detail; however, in the far-field, flows are similar. Figure 10 shows the difference in flow speeds between the two cases. Lower velocities are observable close to the land on the upstream side for the coastal area model. In both tests, the land boundary is specified as zero velocity; however, for the CFD case, the much finer mesh means that velocity can increase in greater proximity to the boundary. Within 1–2 cells away from the boundary, the coastal area model gives similar results. Flow velocities in the far-upstream and offshore of the turbine fence can be seen to be very similar. Flows between the headland and the turbine fence are slightly lower for the coastal area model than for the BEM-CFD. In this area, the difference in water level between the fixed lid of the BEM-CFD and the free surface of the coastal area model is greatest (Figure 11).
The shape and location of the vortex in the lee of the headland is visually similar for the selected time step, although Figure 10 shows that there are some large differences in magnitude. Comparison of a steady-state and time-varying model is somewhat arbitrary, since a method of selecting the appropriate time step to consider is not obvious. If the coastal area model is run for a long time period, a vortex develops and propagates downstream before a new vortex forms. Similar flow behaviour has been reported by [45]. Therefore, in this case, the time step where visually the vortices looked similar was chosen so that differences in vortex location did not affect the wake structures.
Energies 08 07833 g009 1024
Figure 9. Horizontal flow fields for the headland fence case: The images show velocity magnitude at hub height from: (a) the BEM-CFD model; and (b) the coastal area model. Flow is from left to right in the images.
Figure 9. Horizontal flow fields for the headland fence case: The images show velocity magnitude at hub height from: (a) the BEM-CFD model; and (b) the coastal area model. Flow is from left to right in the images.
Energies 08 07833 g009
Figure 10b shows a close up of the turbines. The coastal area model has very slightly lower velocities in front of the turbine for some areas. This may in part be due to the different treatment of pressure in the two models. Additionally, the triangular shape of the differences suggests that mesh resolution may be a contributing factor. Velocities are lower in the gaps between the turbines for the coastal area model. In the near wake, velocities are generally higher for the coastal area model, meaning that less energy is extracted from the flow in the coastal area model. The velocity minima behind the turbine is 76% of the upstream velocity for the coastal area model compared to 52% for the BEM-CFD. There are small areas of comparatively lower velocity directly behind the turbine locations; this is may be due to insufficient resolution in the MIKE mesh to capture the very near-field turbine effects, although differences in model formulation are also likely to affect the results. It is hypothesized that the difference in velocity deficit is partly due to the omission of the tangential component of drag. Swirl in the wake means that there are components of drag in both the axial and tangential directions. Wake rotation is not represented in the coastal area model, and hence, only drag in the axial direction was considered in defining the drag co-efficient used in the coastal area model.
Energies 08 07833 g010 1024
Figure 10. Differences in horizontal flow for the headland fence case: the images show the difference in velocity magnitude at hub height for: (a) the BEM-CFD model domain; and (b) a close up around the six turbines. Negative values indicate that velocity magnitude is lower in the coastal area model and positive values that velocity magnitude is higher in the coastal area model. Black lines indicate the turbine locations in (b).
Figure 10. Differences in horizontal flow for the headland fence case: the images show the difference in velocity magnitude at hub height for: (a) the BEM-CFD model domain; and (b) a close up around the six turbines. Negative values indicate that velocity magnitude is lower in the coastal area model and positive values that velocity magnitude is higher in the coastal area model. Black lines indicate the turbine locations in (b).
Energies 08 07833 g010
Other researchers [50] have recently shown that energy extraction in coastal area models is under-represented in coastal area models as mesh sizes are reduced. In Equation (1), actuator disk theory shows that the free stream velocity should be used; however, in the model formulation, the cell velocity is used instead. For situations where the cell size is very much greater than the turbine, this approximation is valid. As the cell size becomes comparable to the turbine, the cell velocity is no longer close to the free stream velocity due to the effect of the turbine. Hence, the force is underestimated, and so, the flow reduction is also under-represented.
The domain of the BEM-CFD model does not extend sufficiently far downstream to establish whether differences between coastal area model and BEM-CFD return to zero in the far-field. Differences in techniques mean that convergence in results may never occur. At the downstream extent of the BEM-CFD domain, the coastal area model results are at most 0.4 m·s−1 lower than the BEM-CFD results in the wake region. This is still a substantial difference given that the input boundary velocity is 3 m·s−1. It is uncertain how much of this difference is due to differences in the vortex affecting the wake structure: differences in wake velocities approach zero for the wakes of the two turbines located furthest from the headland at around 20 diameters downstream of the turbines. Given that the vortex is not identical in the two simulations, flows landward of the turbine array are dissimilar, which provides different lateral conditions and, hence, will affect wake recovery. Figure 11 shows that the difference at the downstream extent is unlikely to be due to the free surface given that the difference in water depth in this region of the domain is less than 2% of the total water depth.
Energies 08 07833 g011 1024
Figure 11. A plot showing the difference in water level between the coastal area model and the BEM-CFD model (fixed lid at a 30-m water depth).
Figure 11. A plot showing the difference in water level between the coastal area model and the BEM-CFD model (fixed lid at a 30-m water depth).
Energies 08 07833 g011
In terms of comparison between the two techniques, the primary complicating factors are the differences in spatial and temporal scales. The difference between steady-state and time-varying simulations makes comparison between results for scenarios with highly time-varying flow features difficult in terms of determining appropriate time steps of the unsteady model for comparison. The other shortfall of this comparison is that computational limitations on the size of the BEM-CFD domain means that the downstream section does not extend far enough to determine the point at which differences in flow velocities become negligible. The mesh size dependency on the applicability of the model formulation as raised by [50] is believed to be the key difference in the level of energy extraction.
Importantly, the complexity and detail available in coastal area modelling for near-field wake and wake interactions will always be lower than for CFD or similar techniques, meaning that the two methodologies are complementary given coastal area modelling’s greater ability to consider larger areas, complex bathymetries and long time period simulations. Coastal area models also routinely have the capability to include other phenomenon, such as wave action, sediment transport and morphological change.

5. Conclusions

Computer modelling has always been a compromise between three issues: the numerical description, computational resources and experimental validation. We have presented here several numerical schemes to describe the extraction of useful energy from a tidal turbine and the interaction that it has with the flow. The most appropriate choice of scheme depends on the physical scale where answers are required and the computational resources available.
It is clear that reasonable characterisation of lab-scale flows can be achieved with good instrumentation, and the experiments used for validation can be replicated with reasonable accuracy using the BEMT, BEM-CFD and BRG approaches. As noted in Section 2, there is good agreement between experiment and BEMT models of the Manchester and IFREMER rotors; as measured by optimum CP, the differences between the numerical model and empirical measurements are only 2.9% and 0.3%, respectively. This gives us confidence in our predictions regarding the effects of hydrofoil degradation on rotor performance, which we can briefly summarise by saying that rotor thrust is more sensitive to decreases in sectional lift and rotor power more sensitive to increases in sectional drag. The BEM-CFD has been shown to capture the wake dynamics well, both in comparison to experimental results (Figure 5, bottom panel) and to BRG-CFD (Figure 3 and Figure 4). In addition, the direct comparison of the BEMT and BEM-CFD models is reasonably satisfactory, with predictions of peak CP differing by only 5.4%.
However, attempts to model real flows have a very high uncertainty in the physical geometry of the problem and characterisation of the boundary conditions, and care should be taken when making comparisons to real turbines in real channels. For instance, although BEM-CFD and BRG-CFD show agreement in the distribution of turbulent kinetic energy (compare the last two panels of Figure 4), it is difficult for RANS-CFD to maintain a realistically high level of turbulence when compared to real flows [16].
Comparison between BEMT and the different CFD and experimental approaches is simpler than comparison between CFD and coastal area models due to the greater differences between CFD and coastal area modelling in terms of scale, mesh resolution and temporal discretisation. It is also important to understand the effects of flow blockage when selecting a tool for analysing performance characteristics. For instance, correcting the results of the IFREMER turbine for blockage in Section 2 meant that the BEMT and experimental results showed remarkably good agreement (to within 0.3%); however, as we discuss at the end of Section 3, the inclusion or omission of rotor support structures in the BEM-CFD model had a noticeable effect on the agreement between results of the experiment, BEMT and BEM-CFD, and it is incumbent on investigators to be careful in how they quantify blockage.
The coastal area model under-represented energy extraction compared to the BEM-CFD test (velocity minima of 76% and 52% of the upstream velocity, respectively). This is primarily caused by the use of cell velocity in the drag force calculation and the requirement for small cell sizes to resolve the wake. As has been reported by other researchers [50], small cell sizes mean that the cell velocity is reduced by the presence of the turbine, whereas theory requires the free-stream velocity to be used. Therefore, an incorrectly low velocity is used, reducing the implemented momentum sink term and, hence, the velocity deficit.
The choice of model will depend strongly on the availability of computational resources. The existence of efficient models is due to the limits on computational power available on a day to day basis to the turbine modelling community. While very large models are possible, they are not practical and may not add value when the uncertainties in boundary conditions are taken into account. The comparison presented here allows the reader to make more informed choices about the value of the modelling tools that are available to them.

Acknowledgments

Funding to support this research was provided by the Welsh Government and HEFCW through the Sêr Cymru National Research Network for Low Carbon, Energy and the Environment. Some activity has been conducted under the LCRI project, which is partly funded by the Welsh Government, the Higher Education Funding Council for Wales, the Welsh European Funding Office and the European Regional Development Fund (ERDF) Convergence Programmes. The work was also supported by the EPSRC Supergen-funded Terawatt project (EP/J010170/1) and the EPSRC Supergen-funded “The effects of realistic tidal flows on the performance and structural integrity of tidal stream turbines” project (EP/J010200/1). The authors would also like to acknowledge Allan Mason-Jones from Cardiff University for providing the BRG-CFD dataset.

Author Contributions

Ian Masters conceived of the paper and wrote the Introduction and Conclusions. Alison Williams and Nick Croft were both involved in model development. Michael Togneri conducted the BEMT work and wrote that section. Matt Edmunds conducted the BEM-CFD work and wrote that corresponding section. Enayatollah Zangaibadi also worked on the CFD model runs. Iain Fairley wrote the section on the coastal area modelling and conducted the coastal area comparison simulation. Harshinie Karunarathna reviewed the coastal area work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abbott, I.H.; von Doenhoff, A.E. Theory of Wing Sections, Including a Summary of Airfoil Data; Dover Publications Inc.: New York, NY, USA, 1959. [Google Scholar]
  2. Glauert, H. Airplane Propellers. In Aerodynamic Theory; Durand, W.F., Ed.; California Institute of Technology: Pasedena, LA, USA, 1934. [Google Scholar]
  3. Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: New York, NY, USA, 2001. [Google Scholar]
  4. Masters, I.; Chapman, J.C.; Orme, J.A.C.; Willis, M.R. A robust blade element momentum theory model for tidal stream turbines including tip and hub loss corrections. Proc. Inst. Mar. Eng. Sci. Tech. Part A 2011, 10, 25–35. [Google Scholar]
  5. Chapman, J.C.; Masters, I.; Togneri, M.; Orme, J.A.C. The Buhl correction factor applied to high induction conditions for tidal stream turbines. Renew. Energy 2013, 60, 472–480. [Google Scholar] [CrossRef]
  6. Mason-Jones, A. Performance assessment of a horizontal axis tidal turbine in a high velocity shear environment. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2010. [Google Scholar]
  7. Tedds, S.C.; Owen, I.; Poole, R.J. Near-wake characteristics of a model horizontal axis tidal stream turbine. Renew. Energy 2014, 63, 222–235. [Google Scholar] [CrossRef]
  8. Henriques, T.A.D.; Tedds, S.C.; Botsari, A.; Najafian, G.; Hedges, T.S.; Sutcliffe, C.J.; Owen, I.; Poole, R.J. The effects of wave-current interaction on the performance of a model horizontal axis tidal turbine. Int. J. Mar. Energy 2014, 8, 17–35. [Google Scholar] [CrossRef]
  9. Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
  10. Fernandez-Rodriguez, E.; Stallard, T.J.; Stansby, P.K. Experimental study of extreme thrust on a tidal stream rotor due to turbulent flow and with opposing waves. J. Fluid. Struct. 2014, 51, 354–361. [Google Scholar] [CrossRef]
  11. Stallard, T.; Feng, T.; Stansby, P.K. Experimental study of the mean wake of a tidal stream rotor in a shallow turbulent flow. J. Fluid. Struct. 2015, 54, 235–246. [Google Scholar] [CrossRef]
  12. Togneri, M.; Masters, I.; Malki, R.; Rio, A. Flume measurements of lift and drag for selected tidal turbine blade sections. Int. J. Mar. Energy 2015. submitted for publication. [Google Scholar]
  13. Hassan, U. A Wind Tunnel Investigation of the Wake Structure within Small Wind Turbine Farms; Technical Report ETSU WN 5113; Energy Technology Support Unit: London, UK, 1993. [Google Scholar]
  14. Walker, J.M.; Flack, K.A.; Lust, E.E.; Schultz, M.P.; Luznik, L. Experimental and numerical studies of blade roughness and fouling on marine current turbine performance. Renew. Energy 2014, 66, 257–267. [Google Scholar] [CrossRef]
  15. Batten, W.M.J.; Bahaj, A.S.; Molland, A.F.; Chaplin, J.R. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
  16. Afgan, I.; McNaughton, J.; Rolfo, S.; Apsley, D.D.; Stallard, T.; Stansby, P. Turbulent flow and loading on a tidal stream turbine by LES and RANS. Int. J. Heat Fluid Flow 2013, 43, 96–108. [Google Scholar] [CrossRef]
  17. O’Doherty, D.; Mason-Jones, A.; Morris, C.; O’Doherty, T.O.; Byrne, C.; Prickett, P.; Grosvenor, R. Interaction of marine turbines in close proximity. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011.
  18. Mason-Jones, A.; O’Doherty, D.; Morris, C.E.; O’Doherty, T.; Byrne, C.; Prickett, P.W.; Grosvenor, R.I.; Owen, I.; Tedds, S.; Poole, R.J. Non-dimensional scaling of tidal stream turbines. Energy 2012, 44, 820–829. [Google Scholar] [CrossRef]
  19. Willis, M.; Masters, I.; Thomas, S.; Glalie, R.; Loman, J.; Cook, A.; Ahmadian, R.; Falconer, R.; Lin, B.; Gao, G.; et al. Tidal turbine deployment in the Bristol Channel: A case study. Proc. ICE Energy 2010, 163, 93–105. [Google Scholar] [CrossRef]
  20. Harrison, M.E.; Batten, W.M.J.; Bahaj, A.S. A blade element actuator disc approach applied to tidal stream turbines. In Proceedings of the OCEANS 2010, Seattle, WA, USA, 20–23 September 2010.
  21. Malki, R.; Williams, A.J.; Croft, T.N.; Togneri, M.; Masters, I. A coupled blade element momentum-computational fluid dynamics model for evaluating tidal stream turbine performance. Appl. Math. Model. 2013, 37, 3006–3020. [Google Scholar] [CrossRef]
  22. Williams, A.J.; Croft, T.N.; Masters, I.; Bennet, C.R.; Patterson, S.G.; Willis, M.R. A combined BEM-CFD model for tidal stream turbine. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010.
  23. McCombes, T.R. An Unsteady Hydrodynamic Model for Tidal Current Turbines. Ph.D. Thesis, Univeristy of Strathclyde, Glasgow, UK, 2013. [Google Scholar]
  24. Malki, R.; Masters, I.; Williams, A.J.; Croft, T.N. Planning tidal stream turbine array layouts using a coupled blade element momentum—Computational fluid dynamics model. Renew. Energy 2014, 63, 46–54. [Google Scholar] [CrossRef]
  25. Edmunds, M.; Malki, R.; Williams, A.J.; Masters, I.; Croft, T.N. Aspects of tidal stream turbine modelling in the natural environment using a coupled BEM-CFD model. Int. J. Mar. Energy 2014, 7, 20–42. [Google Scholar] [CrossRef]
  26. Masters, I.; Malki, R.; Williams, A.J.; Croft, T.N. The influence of flow acceleration on tidal stream turbine wake dynamics: A numerical study using a coupled BEM-CFD model. Appl. Math. Model. 2013, 37, 7905–7918. [Google Scholar] [CrossRef]
  27. Neill, S.P.; Hashemi, M.R.; Lewis, M.J. The role of tidal asymmetry in characterizing the tidal energy resource of Orkney. Renew. Energy 2014, 68, 337–350. [Google Scholar] [CrossRef]
  28. Lewis, M.; Neill, S.P.; Robins, P.E.; Hashemi, M.R. Resource assessment for future generations of tidal-stream energy arrays. Energy 2015, 83, 403–415. [Google Scholar] [CrossRef]
  29. Fairley, I.; Evans, P.; Wooldridge, C.; Willis, M.; Masters, I. Evaluation of tidal stream resource in a potential array area via direct measurements. Renew. Energy 2013, 57, 70–78. [Google Scholar] [CrossRef]
  30. Ahmadian, R.; Falconer, R.; Bockelmann-Evans, B. Far-field modeling of the hydro-environmental impact of tidal stream turbines. Renew. Energy 2012, 28, 107–116. [Google Scholar] [CrossRef]
  31. Ahmadian, R.; Falconer, R.A. Assessment of array shape of tidal stream turbines on hydro-environmental impacts and power output. Renew. Energy 2012, 44, 318–327. [Google Scholar] [CrossRef]
  32. Chatzirodou, A.C.; Karunarathna, H. Impacts of tidal energy extraction on sea bed morphology. In Proceedings of the 34th International Conference on Coastal Engineering, Seoul, Korea, 15–20 June 2014.
  33. Neill, S.P.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand banks. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
  34. Robins, P.E.; Neill, S.P.; Lewis, M.J. Impact of tidal-stream arrays in relation to the natural variability of sedimentary processes. Renew. Energy 2014, 72, 311–321. [Google Scholar] [CrossRef]
  35. Fairley, I.; Masters, I.; Karunarathna, H. The cumulative impact of tidal stream turbine arrays on sediment transport in the Pentland Firth. Renew. Energy 2015, 80, 755–769. [Google Scholar] [CrossRef]
  36. Wolf, J.; Prandle, D. Some observations of wave-current interaction. Coast. Eng. 1999, 37, 471–485. [Google Scholar] [CrossRef]
  37. Hashemi, M.R.; Neill, S.P.; Robins, P.E.; Davies, A.G.; Lewis, M.J. Effect of waves on the tidal energy resource at a planned tidal stream array. Renew. Energy 2015, 75, 626–639. [Google Scholar] [CrossRef]
  38. Fairley, I.; Ahmadian, R.; Falconer, R.A.; Willis, M.R.; Masters, I. The effects of a Severn Barrage on wave conditions in the Bristol Channel. Renew. Energy 2014, 68, 428–442. [Google Scholar] [CrossRef]
  39. Lewis, M.J.; Neill, S.P.; Hashemi, M.R.; Reza, M. Realistic wave conditions and their influence on quantifying the tidal stream energy resource. Appl. Energy 2014, 136, 495–508. [Google Scholar] [CrossRef]
  40. Kadiri, M.; Hashemi, M.R.; Bockelmann-Evans, B.; Rauen, W.; Falconer, R. A review of the potential water quality impacts of tidal renewable energy systems. Renew. Sustain. Energy Rev. 2012, 16, 329–341. [Google Scholar] [CrossRef]
  41. Neill, S.P.; Hashemi, M.R.; Lewis, M.J. Optimal phasing of the European tidal stream resource using the greedy algorithm with penalty function. Energy 2014, 73, 997–1006. [Google Scholar] [CrossRef]
  42. Martin-Short, R.; Hill, J.; Kramer, S.C.; Avdis, A.; Allison, P.A.; Piggott, M.D. Tidal resource extraction in the Pentland Firth, UK: Potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew. Energy 2015, 76, 596–607. [Google Scholar] [CrossRef]
  43. Vogel, C.R.; Willden, R.H.J.; Houlsby, G.T. A correction for depth-averaged simulations of tidal turbine arrays. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC), Aalborg, Denmark, 2–5 September 2013.
  44. Takafumi, N.; Willden, R.H.J. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 2012, 708, 596–606. [Google Scholar]
  45. Baston, S.; Waldman, S.; Side, J. Modelling Energy Extraction in Tidal Flows. MASTS Position Paper. Available online: http://www.masts.ac.uk/media/126430/140828_position_paper_tidal_energy_extraction_rev2.1.pdf (accessed on 15 May 2015).
  46. Roc, T.; Conley, D.; Greaves, D. Methodology of tidal turbine representation in ocean circulation model. Renew. Energy 2013, 51, 448–464. [Google Scholar] [CrossRef]
  47. Draper, S.; Stallard, T.; Stansby, P.; Way, S.; Adcock, T. Laboratory scale experiments and preliminary modelling to investigate basin scale tidal stream energy extraction. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC), Aalborg, Denmark, 2–5 September 2013.
  48. MIKE 21 and MIKE 3 Flow Model FM—Hydrodynamic and Transport Module—Scientific Documentation; Danish Hydraulic Insitute: Hørsholm, Denmark, 2012.
  49. Draper, S.; Borthwick, A.; Houlsby, G. Energy potential of a tidal fence deployed near a coastal headland. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [PubMed]
  50. Kramer, S.; Piggott, M.D.; Hill, J.; Kregting, L.; Pritchard, D.; Elsaesser, B. The modelling of tidal turbine farms using multi-scale, unstructured mesh models. In Proceedings of the 2nd International Conference on Environmental Interactions of Marine Renewable Energy Technologies, Stornoway, UK, 28 April–2 May 2014.

Share and Cite

MDPI and ACS Style

Masters, I.; Williams, A.; Croft, T.N.; Togneri, M.; Edmunds, M.; Zangiabadi, E.; Fairley, I.; Karunarathna, H. A Comparison of Numerical Modelling Techniques for Tidal Stream Turbine Analysis. Energies 2015, 8, 7833-7853. https://doi.org/10.3390/en8087833

AMA Style

Masters I, Williams A, Croft TN, Togneri M, Edmunds M, Zangiabadi E, Fairley I, Karunarathna H. A Comparison of Numerical Modelling Techniques for Tidal Stream Turbine Analysis. Energies. 2015; 8(8):7833-7853. https://doi.org/10.3390/en8087833

Chicago/Turabian Style

Masters, Ian, Alison Williams, T. Nick Croft, Michael Togneri, Matt Edmunds, Enayatollah Zangiabadi, Iain Fairley, and Harshinie Karunarathna. 2015. "A Comparison of Numerical Modelling Techniques for Tidal Stream Turbine Analysis" Energies 8, no. 8: 7833-7853. https://doi.org/10.3390/en8087833

Article Metrics

Back to TopTop